Introduction

Shale is a type of unconventional petroleum reservoir mainly composed of powdery or flaky clay minerals, which is characterized by low porosity and permeability1,2. Shale gas mainly exists in shale rocks under adsorption and capillary pressure. The exploration of shale gas resources is different from that of conventional resources due to the special characteristics of shale gas formation and storage. Currently, the shale resource potential is mainly characterized by identifying geological sweet spots or engineering sweet spots3.

Conventional logging methods can qualitatively identify shale reservoirs. The typical shale gas logging response characteristics generally include high natural gamma values, high resistivity, high acoustic time-difference values, low neutron logging response values, low density, and low photoelectric effects4. Bao-Ying Zhang summarized the sensitivity of each geological parameter by identifying the relationship between the response characteristics of well logs and each shale reservoir parameter5. Hong-Quan Xia and other researchers calculated geological sweet spot parameters based on natural gamma ray logging (GR), density logging (DEN), and true formation resistivity (RT) values to establish a mathematical model for identifying shale gas sweet spots6. Huan-Ming Wen extracted fractal information from well logs such as acoustic time difference logging (AC), compensated neutron logging (CNL), DEN, and GR through box dimension, correlation dimension, R/S dimension, and power spectrum dimension, and described the reservoir heterogeneity using the extracted results7. The shale attribute parameters used in these evaluation methods are obtained through conventional logging interpretation template calculations8,9,10,11. Conventional logging is easily affected by complex shale reservoir pore structures in terms of their response to lithology and identification sensitivity, which leads to the problems of low prediction accuracy and regional limitations. Additionally, the numerous evaluation parameters and complex model calculations in multiple processing methods may lead to overlooking of important information in the raw data, resulting in low shale reservoir classification accuracy.

Compared with conventional oil and gas reservoirs, the identification and prediction of shale oil and gas resource-rich zones pose significant challenges12. Currently, most of them are identified qualitatively, and it is difficult to characterize them quantitatively13. Moreover, the linear relationship between conventional logging responses is affected by organic matter and pore fluid properties14. Although advanced nuclear magnetic resonance (NMR) logging technology can quantitatively reflect the microscopic pore structure and fracture development of shale reservoirs15, its high cost is a significant drawback. Reservoir quantitative evaluation studies based on conventional logging data can utilize various artificial intelligence methods, such as image multiresolution clustering analysis16,17 and neural network methods18,19,20, to address this challenge. However, the fitting accuracy of such data-driven logging reservoir evaluation methods is constrained by the size of the trained base datasets due to small differences in shale logging responses, variable logging curve quality, and limited shale core labels.

Fractal theory is a mathematical method with unique advantages in characterizing complex irregularities, which has shown that the microstructure of shale reservoirs satisfies fractal features 21,22. Chen et al. utilized multiple fractal parameters from the T2 spectrum obtained by NMR experiments to reflect the differences in the pore structure of rocks and to classify the pore structure types23. Wang et al. classified the pore structure of carbonate rocks based on the fractal dimension of logging curves, and selected the weighted box dimension of porosity curves and the weighted R/S dimension rendezvous plot of resistivity curves to determine the pore structure classification criteria24. Ding et al. established a test well interpretation model for multi-stage fractured horizontal wells in fractured shale gas reservoirs, and analyzed the influence of parameters such as fractal index and fractal dimension on pressure dynamics25. Yin et al. explored the fractal characteristics and thermal evolution laws of shale pores based on the FHH fractal model, and fractal theory has made significant progress in the quantitative characterization of physical properties in shale reservoirs26.

In view of the limitations of traditional logging evaluation methods in regional geological influence, prediction accuracy and computational parameter complexity, this paper proposes a method for evaluating shale gas sweet spots after performing a comprehensive analysis of multifractal spectra. This method employs a multifractal approach to fractalize well logs with many different attributes. Taking Well JY6-2 and Well JY10-4 in the Fuling shale gas reservoir as examples, multiple fractal theory is used to analyze well logs and establish comprehensive fractal evaluation indices for the fractal spectral width ∆α and fractal dimension D for each type of well log based on qualitative fractal characterization. Then, a comprehensive evaluation criterion is constructed for the production capacity of three types of natural gas reservoirs. This approach avoids the problems associated with the traditional logging evaluation method, which uses a large number of parameters for reservoir formation evaluation and has a complicated calculation method. The multiple fractals of well logs combine information on both geological and engineering sweet spots so that the capacity profile can better correspond to the actual sweet spot area and reflect both the high and low levels of actual capacity.

Methods

Conventional logging evaluation methods

The AC method provides formation porosity information based on the time difference of longitudinal wave arrivals; the more complex the acoustic time-difference curve, the more complex the pore structure of the reservoir27,28. Lower intensity of the DEN scattered γ-rays indicates greater chance for occurrence of Compton-Woo scattering, and therefore, the bulk density of the formation rock will be greater. Natural GR data are obtained by measuring the intensity of natural gamma rays absorbed by clay particles in the formation, which reflects the distribution of shale content in a reservoir. Moreover, the natural gamma value is positively correlated with the organic carbon content (TOC)29. As the GR and TOC values increase in shale reservoirs, a purer shale will have a greater brittle mineral content5. The thermal neutron distribution in CNL data is inversely proportional to the hydrogen content in the formation. That is, the higher the thermal neutron distribution density, the lower the hydrogen content in the formation; the lower the porosity of the formation, the lower the reservoir gas content in theory. However, the relationship between porosity and gas content is not absolute. Although lower porosity implies less natural gas content, this is not a universal law, and it is also related to the type, composition and pressure of the rock. In this paper, multiple attributes of multiple sets of conventional logging curves are used to calibrate their relationship. The four kinds of well logs above are analyzed in detail to comprehensively evaluate reservoir pore structure, rock density, fluid distribution, and gas content.

In the case of the Fuling shale reservoir30, the conventional well logs in the target section indicate that GR is consistently above 150 API, AC exceeds 220 µs/m, CNL varies from 10 to 22%, and DEN ranges from 2.50 to 2.70 g/cm3. The logging data, complemented by the natural gamma energy spectrum, are utilized to establish an interpretation model for identifying shale reservoirs. The model accuracy is then fine-tuned to derive shale reservoir parameter correlation equations with improved applicability.

$$\begin{array}{c}{\rm TOC}=-3.337{\rm DEN}+0.122{\rm U}-0.083{\rm CNL}+11.351, {\text{R}}^{2}=0.8\end{array}$$
(1)
$$\begin{array}{c}{\text{POR}} t=0.045{\text{AC}}+0.042{\text{CNL}}-3.953{\text{DEN}}+3.882, {\text{R}}^{2}=0.73 \end{array}$$
(2)
$$\begin{array}{c}{\text{PORe}}=-20.607{\text{DEN}}-0.194{\text{TOC}}+58.709, {\text{R}}^{2}=0.74\end{array}$$
(3)
$$\begin{array}{c}{\text{Sg}} =2.546{\text{PORe}}-28.18{\text{DEN}}-0.49{\text{CNL}}+135.925, {\text{R}}^{2}=0.69\end{array}$$
(4)

In the above formulas, TOC represents the organic carbon content, expressed in %; PORt denotes the total porosity, also in %; PORe stands for the effective porosity, in %; Sg indicates the gas saturation, in %; DEN represents the density logging intensity in g/cm3; U denotes the radioactive uranium elemental content in ppm; CNL refers to the compensated neutron logging value, expressed in %; and AC represents the acoustic time difference logging data, in µs/m.

Equations (1)–(4) are derived from conventional well logs to establish an interpretation framework for evaluating shale reservoir parameters. However, this method may not be optimal for assessing shale reservoirs because of the low correlation of the interpretation model. In the Fuling shale gas reservoir, geological and engineering research has been integrated for its efficient three-dimensional development31. However, due to the poor correlation between engineering and geological sweet spots and actual gas production, one-third of the well sections have not produced gas and one-third of the well sections have produced gas from the fractured horizontal gas wells in the work zone. Therefore, Ting-Xue Jiang, Si-Ping Chen, Gui-Hua Chen and others have proposed a variety of comprehensive sweet spot evaluation methods8,9,10,11. Nevertheless, since the geological and engineering parameters involved are all derived from the parameters calculated by conventional logging interpretation templates, the evaluation parameters are numerous and the data calculations are complicated. Furthermore, due to the many processing methods, it is possible that important information hidden in the original data gets ignored. To address the above problems, a comprehensive evaluation method is proposed herein based on multifractal spectra to gather and collect multi-attribute information from conventional well logs in shale gas reservoirs; this approach simplifies the calculation steps of combining formation lithology selection and ranking and calculating a large number of formation parameters. At the same time, this method correlates geological sweet spots with engineering sweet spots and forms three types of capacity evaluation criteria for shale gas formations based on actual gas production, thus addressing the problems mentioned above and achieving the goal of quantitatively identifying high-quality shale gas reservoirs.

Integrated shale gas sweet spot logging evaluation

Production profile capacity contribution grading

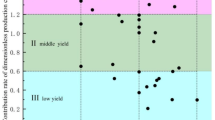
The raw datasets for this study are obtained from the Fuling shale work area database, which consists of test data related to the gas production profiles from 294 fractured sections of 20 fractured horizontal wells. However, the production profile capacity contribution must first be calculated to reflect the production profiles of different well sections. In this study, SPE155485 is used to define low-, medium-, and high-production sections in each well based on the average gas contribution rate of a single section; a gas contribution rate of more than 1.2 is classified as a high-production section, a gas contribution rate of less than 0.6 is classified as a low-production section, and a gas contribution rate of between 0.6 and 1.2 is classified as a medium-production section. The data processing information for Well JY10-4, Well JY6-2, and Well JY8-2, as examples, is shown in Table 1.

Table 1 Evaluation of the capacity contribution of some production profiles.
Full size table

Establishment of the comprehensive fractal evaluation index

Standardization of logging data

When performing data analysis, data with different characteristics often have different magnitudes. To eliminate the influence of singular sample data, it is necessary to standardize the logging data and limit the logging data to the range of [0,1]. The specific formula for this calculation is as follows32:

$$\begin{array}{c}{X}_{i}=\frac{{x}_{i}-{x}_{\min}}{{x}_{\max}-{x}_{\min}}\end{array}$$
(5)

In the above equation, \({X}_{i}\) is the data value after normalization, xi is the original logging data value, and xmax and xmin are the maximum and minimum values in the original logging data, respectively.

Acquisition of the multifractal spectrum

Multiple fractal analyses can be performed on logging data after standardization, according to the analysis method described by Chang-Chun Zou33 and Yong Chen34. However, during actual oil extraction, the reservoir’s pore structure and fluid distribution are not uniform, and only an approximate self-similarity exists in a statistical sense. Therefore, it is necessary to use the multiple fractal method to establish the fractal dimensions of a number of different fractal subsets to identify and characterize various non-uniform pore structures and fluid distributions at different scales.

However, the influence of noise and other factors in the actual logging process causes overlapping of well logs and noise spectra; therefore, wavelet denoising is required first. For wavelet denoising, db3 is chosen as the compactly supported orthogonal wavelet basis, and then the signal is reconstructed using the low-frequency coefficients obtained after wavelet decomposition and the high-frequency coefficients obtained after threshold quantification35. The wavelet modulus maximum transform is used to obtain the multifractal spectrum \(f(\alpha )\). First, the waveform data are polarized to obtain the corresponding maximum point, and all singularity indices are measured using db3 as an orthogonal wavelet basis. Then, the partition function \(Z(q,a)\) at each scale \({\alpha }\) is calculated and linearly regressed.

$$\begin{array}{c}{\text{log}}_{2}Z\left(q,a\right)\approx \tau \left(q\right){\text{log}}_{2}a+C\left(q\right) \end{array}$$
(6)

The exponential function \(\tau (q)\) can be calculated as follows.

$$\begin{array}{c}\tau \left(q\right)=min\left(q\left(\alpha +\frac{1}{2}-f\left(\alpha \right)\right)\right) \end{array}$$
(7)

The multifractal spectrum \(f(\alpha )\) is obtained from Eq. (8):

$$\begin{array}{c}f\left(\alpha \right)=min\left(q\left(\alpha +\frac{1}{2}-\tau \left(q\right)\right)\right)\end{array}$$
(8)
$$\begin{array}{c}\Delta \alpha ={{\alpha }}_{\text{max}}-{{\alpha }}_{\text{min}} \end{array}$$
(9)
$$\begin{array}{c}\Delta f\left(\alpha \right)=f\left({\alpha }_{\max}\right)-f\left({\alpha }_{\min}\right) \end{array}$$
(10)

In the above equation, \(a\) represents the scale parameter, \(a\in R\), and \(a \ne 0\); \(\alpha\) denotes the singular index and \(q\) represents the fractal scaling.

The four main extracted attributes that characterize the multifractal parameters are the spectral width ∆α, the multifractal spectrum f(α)max, the maximum and minimum probability subset fractal dimension difference ∆f(α), and the symmetry parameter |B|. When the multifractal spectrum is skewed to the right, it indicates a higher fractal dimension index, a refined structure, and a stronger ability to characterize reservoir heterogeneity. Moreover, a left-skewed spectrum has a lower fractal dimension index and a weaker fractal intensity36.

R/S analysis

R/S analysis37, or variable scale analysis, is suitable for analyzing data with continuous volatility. In the field of logging, the time scale is transformed into a scale of change in the well logs; in effect, logged values at different depths are used as variables in a sequence that varies with log depth. The non-homogeneity of logging data can be evaluated using the R/S fractal dimension; the larger the fractal dimension, the greater the non-homogeneity38.

To perform R/S analysis, it is first necessary to average the logging data and then calculate the accumulated deviation of the sampling points in each stratum section.

$$\begin{array}{c}Z\left(u,N\right)=\sum_{n=1}^{u}\left\{x\left(n\right)-\stackrel{-}{x\left(n\right)}\right\} \left(1\le u\le N, n=1, 2\dots , N\right) \end{array}$$
(11)

The extreme difference is then derived from the accumulated deviation, reflecting the well logs’ degree of variation.

$$\begin{array}{c}R\left(N\right)=\underset{0<u<N}{\max}Z\left(u,N\right)-\underset{0<u<N}{\min}Z\left(u,N\right) \end{array}$$
(12)

Finally, the standard deviation is calculated, which reflects the degree of deviation of each sampling point from the mean and characterizes the volatility of the overall well logs.

$$\begin{array}{c}S\left(N\right)=\sqrt{\frac{1}{N}\sum_{u=1}^{N}\left[x\left(u\right)-\right.\stackrel{-}{x\left(n\right)}{]}^{2}} \end{array}$$
(13)

In the above equation, \(u\) denotes the number of sample points increasing sequentially between \([1,N]\) from the endpoint.

Then, \(R(N)\) is divided by \(S(N)\) to obtain the dimensionless ratio R/S, and log(N) ~ log(R/S) is linearly regressed in the double logarithmic coordinate system. When R/S is approximately linear with N, it indicates a fractal feature in the well logs, and there exists a relationship \(D=2-H\); then, the fractal dimension D can be obtained.

Comprehensive fractal evaluation method establishment

The multifractal spectrum characterizes the pore structure, rock density, fluid distribution, and gas content of a reservoir, and must be evaluated together with the R/S fractal dimension due to the complexity of the actual reservoir structure. Taking Well JY6-2 as an example, fractal correlation information of AC, CNL, DEN and GR well logs are collected and calculated for each well section separately, revealing the relationships between the well logs and fractal-related parameters, as shown in Fig. 1. The comparison reveals that as the reservoir inhomogeneity increases, ∆α also increases, while the fractal dimension D remains relatively stable. Additionally, the fractal properties of the four well logs are also calculated for comparison with their yield contributions. The statistical results are shown in Table 2.

Fig. 1
figure 1

Graph of the relationship between well log and fractal-related parameters.

Full size image
Table 2 Fractal-related parameters and productivity contribution statistics for the fractured sections of Well JY6-2.
Full size table

Since numerous fractal parameters are obtained for each of the four conventional well logs reflecting reservoir properties, it is necessary to establish a comprehensive fractal characterization considering the weighting levels. According to the different production capacity of each well section, the production capacity contribution is taken as the parent sequence xi0(i = 1,2,3…n), and the fractal spectral width ∆α and fractal dimension D of each well log are taken as the sub-sequence xij(i = 1,2,3…n; j = 1,2,3…m) to determine the grey relational degree and then normalized to obtain the weight coefficients related to ∆α and D. Then, the parameters of the comprehensive fractal evaluation index are derived. The statistical results are shown in Tables 3 and 4.

Table 3 ∆α grey relational degree for well JY6-2.
Full size table
Table 4 D grey relational degree for well JY6-2.
Full size table
$$\begin{array}{c}\Delta X=\left|{x}_{ij}-{x}_{i0}\right| \end{array}$$
(14)
$$\begin{array}{c}\Delta {X}_{\max}={\max}\left|{x}_{ij}-{x}_{i0}\right| \end{array}$$
(15)
$$\begin{array}{c}\Delta {X}_{\min}= {\min}\left|{x}_{ij}-{x}_{i0}\right| \end{array}$$
(16)
$$\begin{array}{c}{R}_{co}=\frac{\Delta {X}_{\min}+\delta \Delta {X}_{\max}}{\Delta X+\delta \Delta {X}_{\max}} \end{array}$$
(17)

In the given equation, \(\Delta \text{X}\) represents the absolute difference between the factors of the sub-sequence and the parent sequence, \(\Delta {\text{X}}_{\text{max}}\) and \(\Delta {\text{X}}_{\text{min}}\) represent the maximum and minimum values of the absolute difference, respectively;\({\text{R}}_{\text{co}}\) denotes the gray correlation coefficient, and \(\updelta\) is the discriminant scale used to mitigate the impact of excessively large absolute differences. The value of \(\updelta\) falls within the range of [0.1, 1]. For this evaluation, the value 0.5 is chosen to enhance the significance of assessing the gray correlation coefficient.

The specific methodology is as follows:

(1) First, the grey relational degree is calculated.

$$\begin{array}{c}{R}_{j,0}=\frac{1}{n}\sum_{i=1}^{n}{R}_{co} \end{array}$$
(18)

The closer the grey relational degree is to 1, the more closely the subsequence is linked to the parent sequence. The degree of influence of different subsequences on the parent sequence can be determined based on the order of the grey relational degree.

(2) The weight coefficients are then calculated by normalizing the grey relational degree.

$$\begin{array}{c}{\omega }_{j}=\frac{{R}_{j,0}}{\sum_{j=1}^{m}{R}_{j,0}} \end{array}$$
(19)

(3) The ∆α' and D’ values are fitted according to the weighting coefficients to finally obtain the parameters of the comprehensive fractal evaluation index.

Results

The multifractal spectrum productivity grading statistics for Well JY6-2, as an example, are shown in Table 2. The multifractal spectra of four attribute well logs corresponding to the 15# well section of high-production, the 10# well section of low-production, and the 12# and 14# well sections of medium-production are calculated. Then, their characteristics are compared, as shown in Fig. 2.

Fig. 2
figure 2

Multifractal spectra of the four attribute well logs from well sections with different capacities in the JY6-2 fractured horizontal well.

Full size image

Combining the results of multiple fractals from the logging series attributes in some well sections (Fig. 2), and the fractal dimension D calculated by the R/S method (Table 2), the following fractal features are observed:

  1. 1.

    The multifractal spectral width ∆α of attributes AC and CNL is larger than that of attributes DEN and GR, which shows that the extracted attribute signals are more sensitive to the degree of irregularity of the fractal structure; the multifractal spectrum f(α)max of the four attribute signals varies little, which shows that the difference in the size and peak changes of the four attribute signals is not significant. The fractal dimension difference ∆f(α) < 0 of attribute AC indicates that its maximum peak signal frequency is greater than the minimum peak signal frequency; the fractal dimension difference ∆f(α) > 0 of attribute DEN indicates that its maximum peak signal frequency is less than the minimum peak signal frequency. The symmetry parameter B > 0 for the multifractal spectrum of attribute AC indicates that the fractal dimension index of the left-skewed spectrum is lower and the fractal strength is weaker than that of the normal spectrum; the symmetry parameter B < 0 for the multifractal spectrum of attribute DEN indicates that the fractal dimension index of the right-skewed spectrum is larger and the fractal strength is stronger than that of the normal spectrum.

  2. 2.

    The fractal dimension D value extracted by the R/S technique reflects the same pattern in each high, medium, and low productivity horizontal well section. The fractal dimension D corresponding to attribute AC is 1.399 in the high-production section and 1.441 in the low-production section; the fractal dimension D corresponding to attribute CNL is 1.595 in the high-production section and 1.648 in the low-production section; the fractal dimension D corresponding to attribute DEN is 1.445 in the high-production section and 1.547 in the low-production section; and the fractal dimension D corresponding to attribute GR is 1.498 in the high-production section and 1.587 in the low-production section. By comparing the above values of the fractal dimension D, it can be concluded that the pore structure of the reservoir in the high-production section is more uniform than that in the low-production section, and the reservoir has better homogeneity, higher permeability, and better fluidity.

In summary, the width of the multifractal spectrum ∆α and the fractal dimension D, which are more sensitive fractal parameters reflecting the production capacity level, can be selected to qualitatively evaluate the sweet spots of shale gas reservoirs with high production areas. To comprehensively consider the weight of each logging attribute signal, it is necessary to fit the ∆α’ and D’ values according to the weight coefficients. The evaluation indexes are calculated using Well JY6-2 and Well JY10-4 as examples to further delineate the production capacity into different sweet spots. The statistical results are shown in Table 5.

Table 5 Comprehensive fractal evaluation index parameters.
Full size table

According to the calculation results, Fig. 3 is divided into three types of gas reservoirs. The ∆α’ comprehensive fractal evaluation index of the class I gas reservoirs is 0.7 \(<\uplambda <\) 1, and the D’ comprehensive fractal evaluation index is 0 \(<\upgamma <\) 0.5; the ∆α’ comprehensive fractal evaluation index of the class II gas layer is 0.3 \(<\uplambda <\) 0.7, and the D’ comprehensive fractal evaluation index is 0.5 \(<\upgamma <\) 0.8; the ∆α’ comprehensive fractal evaluation index of the class III gas reservoirs is 0 \(<\uplambda <\) 0.3, and the D’ comprehensive fractal evaluation index is 0.8 \(<\upgamma <\) 1. Overall, the comprehensive fractal evaluation index of ∆α’ of the high-production wells is close to 1, and it shows a decreasing trend from high production to low production. The comprehensive fractal evaluation index of the R/S fractal dimension D’ of the low-production wells is close to 1, and it shows a decreasing trend from low to high production. The above comprehensive fractal evaluation method for identifying high-quality shale gas reservoir areas shows that the actual production capacity can be quantitatively reflected by combining actual production profiles, simplifying the calculation of stratigraphic evaluation parameters, and avoiding the problem of poor correlation between the predicted sweet spot areas and actual gas production. Therefore, this method has wide applicability.

Fig. 3
figure 3

Graph of integrated fractal evaluation index of the weighted fractal parameters.

Full size image

Discussion

According to the established comprehensive fractal evaluation method and classification standard, the production capacity of Well JY8-2 is zoned and evaluated. The fractal dimension calculation and evaluation results using conventional well logs are shown in Table 6. The fractal dimension D values of well logs AC and GR in the high-productivity section of Well JY8-2 are on the low side, while those of well logs CNL and DEN are on the high side. The multifractal spectral widths ∆α of well logs AC in the high-productivity section are on the high side, while those of well logs CNL, DEN, and GR are on the low side. The multifractal characteristics are basically consistent with the multifractal law of high-yield sweet spots summarized above.

Table 6 Contrasting multifractal dimensions and productivity contributions in Well JY8-2.
Full size table

The fractal parameters of the four well logs corresponding to the fractured well section are utilized in the grey correlation-modified comprehensive fractal expression, resulting in ∆α’ of 0.4389 and D’ of 0.7252 for the 3205.5–3283.375 m test well section (Table 7). With the ∆α’ comprehensive fractal evaluation index falling between 0.25 and 0.6 and the D’ comprehensive fractal evaluation index between 0.5 and 0.8, this section is classified as a Class II gas layer, whereas the intervals 3176.6438–3205.5 m and 3283.375–3338.125 m exhibit characteristics of Class III gas layers.

Table 7 Comprehensive fractal evaluation index parameters.
Full size table

From the comprehensive well logs in Fig. 4, the comprehensive fractal evaluation index of ∆α' shows a decreasing trend from medium to low production, while the comprehensive fractal evaluation index of R/S fractional dimension D’ of low production wells is close to 1, and shows a decreasing trend from low to high production. The validation results are consistent with the production capacity zoning law, proving the effectiveness of the comprehensive fractal evaluation method.

Fig. 4
figure 4

Relationships between well logs and comprehensive fractal evaluation index.

Full size image

Conclusion

  1. 1.

    Multiple fractals and R/S analysis methods were used to generate the multifractal spectra and fractal dimensions of various well logs; these can be used to qualitatively characterize high-quality reservoir areas in shale gas reservoirs by making use of geological characteristics reflected by various well logs and the production capacity contribution of the production section. The results show that the fractal dimension D values of the AC, CNL, and GR well logs in the high-production section are low, and the fractal dimension D value of the DEN well logs is high. Moreover, the multifractal spectral width ∆α of the AC well logs in the high-production section is large, and the multifractal spectral widths ∆α of the CNL, DEN, and GR well logs are low.

  2. 2.

    The grey relational degree between various types of well logs with respect to the two parameters ∆α and D were calculated separately based on the qualitative characterization of high-quality reservoir areas in shale gas reservoirs, and then a comprehensive fractal evaluation index was established based on the weighting coefficient fitting. The index directly corresponds to the contribution of the production profile capacity to the fractal dimension of the well logs, forming three production capacity evaluation criteria for the shale gas reservoirs. Overall, the comprehensive fractal evaluation index of the high-production wells ∆α’ is close to 1 and shows a decreasing trend from high to low production, while the comprehensive fractal evaluation index of the low-production wells with the R/S fractal dimension D’ is close to 1 and shows a decreasing trend from low-yielding to high-yielding.

  3. 3.

    The verification of the production capacity zoning and the logging data of Well JY8-2 demonstrate the validity of the integrated fractal evaluation method. The above research results can be helpful for improving gas production and for identifying high-quality reservoir areas in shale gas reservoirs.