Chaotic vibration control of an axially moving string of multidimensional nonlinear dynamic system with an improved FSMC

Abstract

A new control approach based on fuzzy sliding mode control (FSMC) is proposed to regulate the chaotic vibration of an axial string. Hamilton’s principle is used to formulate the nonlinear equation of motion of the axial translation string, and the von Kármán equations are used to analyse the geometric nonlinearity. The governing equations are nondimensionalized as partial differential equations and transformed into a nonlinear 3-dimensional system via the third-order Galerkin approach. An active control technique based on the FSMC approach is suggested for the derived dynamic system. By using a recurrent neural network model, we can accurately predict and effectively apply a control strategy to suppress chaotic movements. The necessity of the suggested active control method in the regulation of the nonlinear axial translation string system is proven using different chaotic vibrations. The results show that the study of the chaotic vibrations of axially translating strings requires nonlinear multidimensional dynamic systems of axially moving strings; the validity of the proposed control strategy in controlling the chaotic vibration of axially moving strings in a multidimensional form is demonstrated.

Introduction

Axially translating strings are extensively applied in various engineering fields. These structures are commonly found in strings¹, cables^2,3,4, and belts^5,6,7. In engineering practice, external disturbances and other variables can cause transverse responses of axially moving strings. These vibrations may harm the structure and degrade its operational precision.

The nonlinear dynamic behaviours of axially moving strings have been investigated by many researchers in past decades. Yang and Fang⁸ investigated nonlinear vibrations of an axially moving viscoelastic string under the control of a fractional differentiation law. The structure’s first second-order vibration modes are investigated, and the simulation results show that with increasing fractional order, the amplitude decreases and the frequency increases. Yang⁹ analysed axially moving strings using multiple-scale analysis and gyroscopic mode decoupling. A comparative study illustrates the need for a high-dimensional nonlinear system of axially moving strings. Ma¹⁰ introduced a novel numerical approach for handling issues related to coupled string vibrations using, the wavelet-Galerkin method followed by spectral delayed correction. The validity of this approach was proven using both numerical simulation and experiments based on the first-order Galerkin method. Chen¹¹ suggested an improved finite difference approach for simulating the transverse vibration of axially moving strings. The effect of transportation velocity on free nonlinear vibrations was quantitatively analysed using different truncated terms. Wang¹² studied the transverse vibration of moving strings using Hamiltonian dynamics and symplectic eigenvalue analysis. Both linear and nonlinear vibration responses may be obtained using symplectic modal functions. At critical speeds, the first three vibration modes were investigated. Koivurova¹³ investigated the nonlinear dynamic behaviour of axial motion bands by examining the relationships among the natural frequency, axial speed, and vibration amplitude and described the main difference between an axially moving string and a beam in the region of supercritical transport velocity. Yang¹⁴ investigated the nonlinear parametric resonance of viscoelastic strings moving axially in a two-dimensional dynamic system. The numerical findings show that the fractional order influences the steady-state response. Xia¹⁵ conducted experimental research on the nonlinear characteristics of axially travelling strings. The findings of the experiments reveal that transverse responses are affected by both the velocity profile and initial tension, and that all transverse motion behaviours depend on motion parameters. Kesimli¹⁶ examined the nonlinear response of spring-supported axially translating strings. It was found that, increasing the spring rigidity, axial speed, and number of midpoint supports results in substantial nonlinear effects. Yurddaş¹ examined the nonlinear responses of axially translating multi-supported strings. Different from the other studies, nonideal supports were investigated, which permits a negligible deviation from the supports at each end of the investigated string.

From the above, it can be concluded that axial vibration has a significant effect on strings, so that controlling axial vibration is particularly important. An effective control method should suppress string vibration¹⁷.

There have been many control methods proposed to suppress nonlinear vibrations of engineering structures subject to parametric uncertainties and external uncertainties^{18,19,20,21,22,23,24,25,26,27,28,29}. Nozaki¹⁸ implemented two control methods namely OLFC and SDRE to control the chaotic vibration of an atomic force microscope, and the influence of parametric errors was evaluated. Peruzzi¹⁹ proved that OLFC will effectively suppress the nonlinear vibration of an electronic circuit of a resonant MEMS mass subject to parametric errors. Zhao²⁰ investigated the vibration boundary control problem of a linear dynamic system of an axial string system related to outside disturbances and input constraints. The Lyapunov stability was applied to analyse and prove the stability of the controlled system without any reduction. Nguyen and Hong²¹ investigated the asymptotic stabilization of an axially translating string. Their method uses adaptive boundary control techniques to handle the complexities caused by nonlinear dynamics, variable tension, friction, and external disturbances. Li²² investigated the suppression of nonlinear responses of axially moving strings with upstream or downstream boundary suppression. It was demonstrated that boundary control, whether applied upstream or downstream, can result in exponential stabilization of the nonlinear vibration. Kelleche and Tatar²³ focused on the stabilization problem of nonlinear axially moving viscoelastic strings. They used the Leibniz rule to consider the net flux passing through boundaries. Shaalan²⁴ applied fuzzy sliding mode control (FSMC) in the polymer extrusion process. It was shown that this cutting-edge control method effectively addresses the complicated control demands and dynamics of the polymer extrusion system. Sun²⁵ investigated the synchronization of multi-induction motors with FSMC. This work highlighted how the performance of multiple motors may be enhanced and coordinated in industrial applications through the use of FSMC. Nguyen²⁶ introduced a novel control method that blends sliding control and adaptive fuzzy logic. The method ensures reliable and effective control in complicated and unpredictable contexts by efficiently addressing unknown system features. He and Meng²⁷ discussed the use of an adaptive strategy in a string system to handle input delay. This study highlighted the importance of resolving delay nonlinearities without creating a delay inverse, managing system parameter uncertainties, and reducing flexible string vibrations. Korayem²⁸ investigated the role that FSMC played in resolving issues with microcantilevers’ dynamic reactions in liquid environments, which enhanced performance and control in an atomic force microscope. Nguyen²⁹ emphasized the integration of FSMC to handle nonlinear factors and uncertain disturbances in a control system, proving its potential to increase performance and stability.

In addition to being suitable for tasks such as speech recognition, language modelling and text generation^30,31,32, recurrent neural networks (RNNs) can model and predict the behaviour of nonlinear dynamic systems^33,34,35, which is crucial for understanding and controlling axially moving string systems.

In the present study, a modified FSMC is proposed to suppress the nonlinear vibration of a multidimensional nonlinear dynamic system of strings^36,37. The string’s nonlinear dynamic system is derived using the Galerkin method. The influence of higher vibration modes on the nonlinear dynamic behaviour of the string is then investigated via numerical simulations based on the generated multidimensional nonlinear dynamic system. To reduce vibration in engineering practice^16,38,39, a modified control strategy is finally developed in response to a multidimensional nonlinear dynamic system and then used to manage the chaotic vibration of the dynamic system.

Equation of Motion

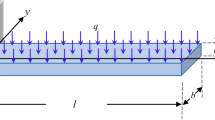
The axially moving string examined in this study is depicted in Fig. 1. The equations of motion for the string are derived using von Karman-type equations and the Hamiltonian principle. Figure 1 shows that the length of the translating string is l, and the string moves axially at a constant rate $v_{0}$; u and w are the displacement of a point on the string along x and z axes, respectively.

Fig. 1

Model of the axially translating string.

Prior to deformation, the position vector of a point on the translating string, denoted by ${\mathbf{r}}$, is presented as,

$${\mathbf{r}} = x(t){\text{i}} + 0{\text{k}}$$

(1)

where ${\text{i}}$ and ${\text{k}}$ are the unit vectors along x and z axes, respectively.

As a result, the displacement field for the string that is translating axially can be expressed as,

$${\mathbf{R}} = \left( {x\left( t \right) + u_{0} \left( {x\left( t \right),t} \right)} \right){\text{i}} + w_{0} \left( {x\left( t \right),t} \right){\text{k}}$$

(2)

where $u_{0} \left( {x\left( t \right),t} \right)$ and $w_{0} \left( {x\left( t \right),t} \right)$ are, for a point on the string.

Then, the following can be obtained:

$$\frac{{d{\mathbf{R}}}}{dt} = \left( {\frac{dx\left( t \right)}{{dt}} + \frac{{du_{0} \left( {x\left( t \right),t} \right)}}{dt}} \right){\text{i}} + \frac{{dw_{0} \left( {x\left( t \right),t} \right)}}{dt}{\text{k}}$$

(3)

where the rate of translation of the string is equal to the total derivative of $w_{0}$ with respect to time as shown below:

$$\frac{{dw_{0} \left( {x\left( t \right),t} \right)}}{dt} = \frac{{\partial w_{0} \left( {x\left( t \right),t} \right)}}{\partial t} + v_{0} \frac{{\partial w_{0} \left( {x\left( t \right),t} \right)}}{\partial x\left( t \right)}$$

(4)

As a result, the translating string’s kinetic energy over volume V of the string can be expressed as,

$$T = \int_{{0}}^{{l}} {\frac{1}{2}\left( {\rho \frac{{d{\mathbf{R}}}}{dt}\frac{{d{\mathbf{R}}}}{dt}} \right)dx}$$

(5)

where $\rho$ is the mass per length.

The strain associated with Eq. (2) is obtained below by considering the von Karman equations,

$$\varepsilon_{11} = \frac{{\partial u_{0} \left( {x\left( t \right),t} \right)}}{\partial x\left( t \right)} + \frac{1}{2}\left( {\frac{{\partial w_{0} \left( {x\left( t \right),t} \right)}}{\partial x\left( t \right)}} \right)^{2}$$

(6)

Thus, the string’s overall strain energy can be calculated using the following formula:

$$U = Q_{11} \int_{{0}}^{{l}} {\frac{1}{2}\left( {\varepsilon_{11} \varepsilon_{11} } \right)dx}$$

(7)

where the elastic coefficient $Q_{11}$ is in the same direction as $\varepsilon_{11}$.

The force has produced zero virtual work,

$$W = 0$$

(8)

Using Eqs. (5), (7), and (8), Hamilton’s principle can be expressed as,

$$\int_{{\;t_{1} }}^{{\;t_{2} }} {\;\;\left( {\delta L + \delta W} \right)\,} dt = 0$$

(9)

from which the entire Lagrangian function L is obtained as

$$L = T - E$$

(10)

Hereafter, $x\left( t \right)$, $w_{0} \left( {x\left( t \right),t} \right)$, and $u_{0} \left( {x\left( t \right),t} \right)$ will be replaced with x, $w_{0}$, and $u_{0}$, respectively, for clarity. Substitution of Eqs. (5), (7), and (8) into Eq. (9) yields,

$$\begin{aligned} \int_{{t{}_{1}}}^{{t_{2} }} {\delta Ldt} & = \int_{{t{}_{1}}}^{{t_{2} }} {\delta \left( {T - U} \right)dt} \\ & = \int_{{t{}_{1}}}^{{t_{2} }} {\delta \left\{ {\int_{0}^{l} {\left[ {\rho \left( {\frac{{d{\mathbf{R}}}}{dt}\frac{{d{\mathbf{R}}}}{dt}} \right) - Q_{11} \left( {\varepsilon_{11} \varepsilon_{11} } \right)} \right]} } \right\}dt} \\ & = \int_{{t{}_{1}}}^{{t_{2} }} {\int_{0}^{l} {\left[ {\rho \left( {\frac{{d{\mathbf{R}}}}{dt}\frac{{d\delta {\mathbf{R}}}}{dt}} \right)} \right]} dt} - \int_{{t{}_{1}}}^{{t_{2} }} {\int_{0}^{l} {\left[ {Q_{11} \left( {\varepsilon_{11} \delta \varepsilon_{11} } \right)} \right]} dt} \\ & = 0 - \int_{{V}} {\int_{{t_{1} }}^{{t_{2} }} {\rho \left( {\frac{{d^{2} {\mathbf{R}}}}{{dt^{2} }}} \right)\delta {\mathbf{R}}dt} dV} - \int_{{t{}_{1}}}^{{t_{2} }} {\int_{{V}} {Q_{11} } \varepsilon_{11} \delta \varepsilon_{11} dVdt} \\ & = - \int_{{t_{1} }}^{{t_{2} }} {\int_{{0}}^{{l}} {\rho \delta \left( {x + u_{0} } \right)\left( {\frac{{d^{2} x}}{{dt^{2} }} + \frac{{d^{2} u_{0} }}{{dt^{2} }}} \right)} dxdt} \\ & \quad - \int_{{t_{1} }}^{{t_{2} }} {\int_{{0}}^{{l}} {\rho \delta w_{0} \frac{{d^{2} w_{0} }}{{dt^{2} }}} dxdt} \\ & \quad - \int_{{t{}_{1}}}^{{t_{2} }} {\int_{{0}}^{{l}} {Q_{11} \delta \left( {\frac{{\partial u_{0} }}{\partial x} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} } \right)\varepsilon_{11} dxdt} } \\ & = L_{1} + L_{2} + L_{3} \\ \end{aligned}$$

where

$$L_{1} = - \int_{{t_{1} }}^{{t_{2} }} {\int_{{0}}^{{l}} {\rho \delta \left( {x + u_{0} } \right)\left( {\frac{{d^{2} x}}{{dt^{2} }} + \frac{{d^{2} u_{0} }}{{dt^{2} }}} \right)} dxdt}$$

(11a)

$$L_{2} = - \int_{{t_{1} }}^{{t_{2} }} {\int_{{0}}^{{l}} {\rho \delta w_{0} \frac{{d^{2} w_{0} }}{{dt^{2} }}} dxdt}$$

(11b)

$$L_{3} = - \int_{{t{}_{1}}}^{{t_{2} }} {\int_{{0}}^{{l}} {Q_{11} \delta \left( {\frac{{\partial u_{0} }}{\partial x} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} } \right)\varepsilon_{11} dxdt} }$$

(11c)

Because the string travels axially at a constant velocity ($\frac{{d^{2} v_{0} }}{{dt^{2} }} = 0$), it can be obtained from Eq. (11a) that:

$$\begin{aligned} L_{1} & = - \int_{{t_{1} }}^{{t_{2} }} {\int_{{0}}^{{l}} {\rho \delta \left( {x + u_{0} } \right)\left( {\frac{{d^{2} x}}{{dt^{2} }} + \frac{{d^{2} u_{0} }}{{dt^{2} }}} \right)} dxdt} \\ & = - \int_{{t_{1} }}^{{t_{2} }} {\int_{{0}}^{{l}} {\rho \left( {0 + \delta u_{0} } \right)\left( {0 + \frac{{d^{2} u_{0} }}{{dt^{2} }}} \right)} dxdt} \\ & = - \int_{{t_{1} }}^{{t_{2} }} {\int_{{0}}^{{l}} {\rho \frac{{d^{2} u_{0} }}{{dt^{2} }}\delta u_{0} } dxdt} \\ \end{aligned}$$

(12a)

Equation (11c) leads to the following,

$$\begin{aligned} L_{3} & = - \int_{{t{}_{1}}}^{{t_{2} }} {\int_{0}^{l} {Q_{11} \delta \left( {\frac{{\partial u_{0} }}{\partial x} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} } \right)\varepsilon_{11} dxdt} } \\ & = - \int_{{t{}_{1}}}^{{t_{2} }} {\int_{{0}}^{{l}} {Q_{11} \left( {\frac{{\partial \delta u_{0} }}{\partial x} + \frac{1}{2}\delta \left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} } \right)\varepsilon_{11} dxdt} } \\ & = - \int_{{t{}_{1}}}^{{t_{2} }} {\int_{0}^{l} {Q_{11} \varepsilon_{11} \frac{{\partial \delta u_{0} }}{\partial x}dxdt} } - \int_{{t{}_{1}}}^{{t_{2} }} {\int_{0}^{l} {Q_{11} \varepsilon_{11} \frac{{\partial w_{0} }}{\partial x}\frac{{\partial \delta w_{0} }}{\partial x}dxdt} } \\ & = - \int_{{t{}_{1}}}^{{t_{2} }} {\left[ {\left. {\left( {Q_{11} \varepsilon_{11} \delta u_{0} } \right)} \right|_{0}^{l} - \int_{{0}}^{{l}} {Q_{11} \delta u_{0} d\varepsilon_{11} } } \right]} dt \\ & \quad - \int_{{t{}_{1}}}^{{t_{2} }} {\left[ {\left. {\left( {Q_{11} \varepsilon_{11} \frac{{\partial w_{0} }}{\partial x}\delta w_{0} } \right)} \right|_{0}^{l} - \int_{0}^{l} {Q_{11} \varepsilon_{11} \delta w_{0} d\frac{{\partial w_{0} }}{\partial x}} } \right]} dt \\ & = - \int_{{t{}_{1}}}^{{t_{2} }} {\left( {0 - \int_{0}^{l} {Q_{11} \delta u_{0} d\varepsilon_{11} } } \right)} dt \\ & \quad - \int_{{t{}_{1}}}^{{t_{2} }} {\left( {0 - \int_{0}^{l} {Q_{11} \delta w_{0} d\left( {\varepsilon_{11} \frac{{\partial w_{0} }}{\partial x}} \right)} } \right)} dt \\ & = - \int_{{t{}_{1}}}^{{t_{2} }} {\left( { - \int_{0}^{l} {Q_{11} \frac{{\partial \varepsilon_{11} }}{\partial x}\delta u_{0} d} x} \right)} dt \\ & \quad - \int_{{t{}_{1}}}^{{t_{2} }} {\left( { - \int_{0}^{l} {Q_{11} \frac{{\partial \varepsilon_{11} }}{\partial x}\frac{{\partial w_{0} }}{\partial x}\delta w_{0} dx} } \right)} dt \\ & = - \int_{{t{}_{1}}}^{{t_{2} }} {\left( { - \int_{0}^{l} {Q_{11} \frac{\partial }{\partial x}\left( {\frac{{\partial u_{0} }}{\partial x} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} } \right)\delta u_{0} d} x} \right)} dt \\ & \quad - \int_{{t{}_{1}}}^{{t_{2} }} {\left( { - \int_{0}^{l} {Q_{11} \left( {\frac{{\partial u_{0} }}{\partial x} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} } \right)\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\delta w_{0} dx} } \right)} dt \\ & \quad - \int_{{t{}_{1}}}^{{t_{2} }} {\left( { - \int_{0}^{l} {Q_{11} \frac{\partial }{\partial x}\left( {\frac{{\partial u_{0} }}{\partial x} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} } \right)\frac{{\partial w_{0} }}{\partial x}\delta w_{0} dx} } \right)} dt \\ & = \int_{{t{}_{1}}}^{{t_{2} }} {\left( {\int_{0}^{l} {Q_{11} \left( {\frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + \frac{{\partial w_{0} }}{\partial x}\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right)\delta u_{0} d} x} \right)} dt \\ & \quad + \int_{{t{}_{1}}}^{{t_{2} }} {\left( {\int_{0}^{l} {Q_{11} \left( {\frac{{\partial u_{0} }}{\partial x}\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right)\delta w_{0} dx} } \right)} dt \\ & \quad + \int_{{t{}_{1}}}^{{t_{2} }} {\left( {\int_{0}^{l} {Q_{11} \left( {\frac{{\partial^{2} u_{0} }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial x} + \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} } \right)\delta w_{0} dx} } \right)} dt \\ \end{aligned}$$

(12b)

Then, the governing equation for an axially translating string can be derived from Eqs. (12a), (12b), and (11b) as follows

$$- \rho \frac{{d^{2} u_{0} }}{{dt^{2} }} + Q_{11} \left( {\frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + \frac{{\partial w_{0} }}{\partial x}\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right) = 0$$

(13a)

$$- \rho \frac{{d^{2} w_{0} }}{{dt^{2} }}+ Q_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }}\frac{{\partial w_{0} }}{\partial x} + Q_{11} \frac{{\partial u_{0} }}{\partial x}\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{3}{2}Q_{11} \left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} = 0$$

(13b)

The strain can be calculated using the boundary conditions and nonlinear dynamic equations, as follows:

$$\frac{{\partial u_{0} }}{\partial x} = - \frac{1}{2}\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} + \frac{1}{2l}\int_{{0}}^{{l}} {\left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} dx}$$

(14)

After substituting Eq. (14) into Eq. (13b), the string’s nonlinear governing equation is derived as:

$$- \rho \frac{{d^{2} w_{0} }}{{dt^{2} }} + \int_{0}^{l} {\frac{1}{2l}Q_{11} \left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} dx} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} = 0$$

(15)

Nondimensionalization

The nondimensional variables used to validate Eq. (15) are listed below:

$$\overline{t} = \sqrt {\frac{{Q_{11} }}{\rho }} t = \tau t,\quad \overline{x} = \frac{x}{l}\overline{w}_{0} = \frac{{w_{0} }}{l},\quad \frac{{d\overline{w}_{0} }}{{d\overline{t}}} = \frac{1}{\tau l}\frac{{dw_{0} }}{dt},\quad \frac{{d^{2} \overline{w}_{0} }}{{d\overline{t}^{2} }} = \frac{1}{{\tau^{2} l}}\frac{{d^{2} w_{0} }}{{dt^{2} }}$$

(16)

After substituting Eqs. (16) and (15), the axially translating string’s non-dimensional governing equation can be rewritten as follows:

$$- \frac{{d^{2} \overline{w}_{0} }}{{d\overline{t}^{2} }} + \eta \int_{0}^{1} {\left( {\frac{{\partial \overline{w}_{0} }}{{\partial \overline{x}}}} \right)^{2} d\overline{x}} \frac{{\partial^{2} \overline{w}_{0} }}{{\partial \overline{x}^{2} }} = 0$$

(17)

where, $\eta$ is given by:

$$\eta = \frac{1}{2}\frac{1}{l}Q_{11} \frac{1}{{\rho l\tau^{2} }}$$

Series of Solutions

Based on the Galerkin method, $\overline{w}_{0}$ is expanded in terms of comparison functions as follows:

$$\overline{w}_{0} = \sum\limits_{n = 1}^{\infty } {\varphi_{n} \left( {\overline{x}} \right)\overline{w}_{n} \left( {\overline{t}} \right)}$$

(18)

The following expression for $\varphi_{n} \left( {\overline{x}} \right)$ corresponds to the axially translating string’s pinned–pinned boundary:

$$\varphi_{n} \left( {\overline{x}} \right) = \sin \left( {n\pi \overline{x}} \right)$$

(19)

Introduce Eq. (18) into Eq. (17); for convenience, substitute $\phi_{n}$, $w_{n}$, $\dot{w}_{n}$, $\ddot{w}_{n}$, v, and t with $\varphi_{n} (\overline{x})$, $\overline{w}_{n} \left( {\overline{t}} \right)$, $\frac{{dw_{n} }}{dt}$, $\frac{{d^{2} w_{n} }}{{dt^{2} }}$, $\overline{v}_{0}$ and $\overline{t}$; using the third-order Galerkin method, the following transformation is obtained,

$$\begin{aligned} w_{1} & = w_{1,1} ,\quad w_{2} = w_{2,1} ,\quad w_{3} = w_{3,1} \\ \dot{w}_{1,1} & = w_{1,2} \quad \dot{w}_{2,1} = w_{2,2} ,\quad \dot{w}_{3,1} = w_{3,2} \\ \end{aligned}$$

The three-dimensional nonlinear dynamic system of an axially moving string with simply-supported boundaries is described by:

$$\left\{ {\begin{array}{l} {\dot{w}_{1,1} = w_{1,2} } \\ {\dot{w}_{1,2} = 2\left( {\chi_{1} + \eta \zeta_{1} } \right)} \\ {\dot{w}_{2,1} = w_{2,2} } \\ {\dot{w}_{2,2} = 2\left( {\chi_{2} + \eta \zeta_{2} } \right)} \\ {\dot{w}_{3,1} = w_{3,2} } \\ {\dot{w}_{3,2} = 2\left( {\chi_{3} + \eta \zeta_{3} } \right)} \\ \end{array} } \right.$$

(20)

where,

$$\begin{aligned} \chi_{1} &= \frac{8}{3}vw_{2,1} + \frac{1}{2}v^{2} \pi^{2} w_{1,1} \hfill \\ \chi_{2} &= \frac{24}{5}vw_{3,1} - \frac{8}{3}vw_{1,1} + 2v^{2} \pi^{2} w_{2,1} \hfill \\ \chi_{3} &= - \frac{24}{5}vw_{3,1} + \frac{9}{2}v^{2} \pi^{2} w_{3,1} \hfill \\ \zeta_{1} &= \left( { - \frac{1}{4}\eta \pi^{4} w_{1,1}^{3} - \frac{9}{4}\eta \pi^{4} w_{1,1} w_{3,1}^{2} - \eta \pi^{4} w_{1,1} w_{2,1}^{2} } \right) \hfill \\ \zeta_{2} &= \left( { - \eta \pi^{4} w_{2,1} w_{1,1}^{2} - 9\eta \pi^{4} w_{2,1} w_{3,1}^{2} - 4\eta \pi^{4} w_{2,1}^{3} } \right) \hfill \\ \zeta_{3} &= \left( { - \frac{9}{4}\eta \pi^{4} w_{3,1} w_{1,1}^{2} - \frac{81}{4}\eta \pi^{4} w_{3,1}^{3} - 9\eta \pi^{4} w_{3,1} w_{2,1}^{2} } \right) \hfill \\ \end{aligned}$$

Control design

If a nonlinear governing equation takes the following form,

$$\ddot{w} = \Phi \left( {w,\dot{w},t} \right)$$

(21)

The corresponding equation with control can be presented as

$$\ddot{w} = \Phi \left( {w,\dot{w},t} \right) + U + \Delta P\left( {w,\dot{w}} \right)$$

(22)

where U is the control input, and where $\Delta P\left( {w,\dot{w}} \right)$ is the unknown external disturbance acting on the string.

Using the n^th-order Galerkin technique, a set of second-order ordinary differential equations that account for Eq. (22) will be produced as follows:

$$\left\{ {\begin{array}{*{20}c} {\dot{w}_{1,1} = w_{1,2} } \\ {\dot{w}_{1,2} = \varphi_{1} \left( {{\mathbf{W}},t} \right) + u_{1} + \Delta f_{1} \left( {{\mathbf{W}},t} \right)} \\ {\dot{w}_{2,1} = w_{2,2} } \\ {\dot{w}_{2,2} = \varphi_{2} \left( {{\mathbf{W}},t} \right) + u_{2} + \Delta f_{2} \left( {{\mathbf{W}},t} \right)} \\ \vdots \\ {\dot{w}_{i,1} = w_{i,2} } \\ {\dot{w}_{i,2} = \varphi_{i} \left( {{\mathbf{W}},t} \right) + u_{i} + \Delta f_{i} \left( {{\mathbf{W}},t} \right)} \\ \vdots \\ {\dot{w}_{n,1} = w_{n,2} } \\ {\dot{w}_{n,2} = \varphi_{n} \left( {{\mathbf{W}},t} \right) + u_{n} + \Delta f_{i} \left( {{\mathbf{W}},t} \right)} \\ \end{array} } \right.$$

(23)

where $\varphi_{i} \left( {{\mathbf{W}},t} \right)$, $u_{i}$, and $\Delta f_{i} \left( {{\mathbf{W}},t} \right)$ are the results of $\Phi \left( {w,\dot{w},t} \right)$, U, and $\Delta P\left( {w,\dot{w}} \right)$ after the Galerkin method is used, and the column vector ${\mathbf{W}}$ in Eq. (23) is given below:

$${\mathbf{W}} = \left[ {w_{1,1} w_{1,2} w_{2,1} w_{2,2} \; \cdots \;w_{i,1} w_{i,2} \; \cdots \;w_{n,1} w_{n,2} } \right]^{T}$$

The nondimensional vibration of a specified point $w_{p}$ may be obtained based on Eqs. (18) and (23),

$$w_{p} = \sum\limits_{n = 1}^{\infty } {\varphi_{n} \left( {x_{p} } \right)w_{n} \left( t \right)}$$

(24)

where $x_{p}$ indicates the location of the chosen point.

A reference vibration is given as,

$$w_{r} = A_{r} \sin \left( {\omega_{r} t} \right)$$

(25)

where $A_{r}$ and $\omega_{r}$ are the frequency and amplitude of the reference signal, respectively.

U can be specified below:

$$U = U_{eq} - U_{r}$$

(26)

where $U_{eq}$ and $U_{r}$ are given by,

$$U_{eq} = - \left( {\left( {\dot{w}_{p} - \dot{\Psi }} \right) + \kappa \left( {w_{p} - \Psi } \right)} \right),\quad U_{r} = k_{fs} U_{fs}$$

(27)

In Eq. (27), $\kappa$ contains the control coefficients that regulate the sliding surface, $k_{fs}$ is given as $\left| {\Delta F\left( {w,\dot{w}} \right)} \right| < k_{fs} \in R^{ + }$, and $U_{fs}$ follows the fuzzy rule table in Table 1¹⁷.

Table 1 Fuzzy rule table.

Following Table 1, the specific membership functions of the fuzzy variables, $U_{eq}$, $\frac{{dU_{eq} }}{dt}$ , and $U_{fs}$ are further illustrated in Fig. 2, based on the previous studies^17,40,41.

Fig. 2

Membership functions of the input–output variables: (a) the membership functions of $U_{eq}$ and $\frac{{dU_{eq} }}{dt}$; (b) the membership function of $U_{fs}$.

Following the control developed in Eqs. (22–27), the vibration control of a translating string is conducted via Eq. (17) as shown below,

$$\ddot{w}_{0} = \eta \int_{0}^{1} {\left( {\frac{{\partial \overline{w}_{0} }}{{\partial \overline{x}}}} \right)^{2} d\overline{x}} \frac{{\partial^{2} \overline{w}_{0} }}{{\partial \overline{x}^{2} }} + U + \Delta F\left( {w,\dot{w}} \right)$$

(28)

The third-order Galerkin discretization yields the following expressions:

$$\left\{ {\begin{array}{*{20}c} {\dot{w}_{1,1} = w_{1,2} } \\ {\dot{w}_{1,2} = 2\left( {\chi_{1} + \eta \zeta_{1} } \right) + u_{1} + \Delta f_{1} \left( {{\mathbf{W}},t} \right)} \\ {\dot{w}_{2,1} = w_{2,2} } \\ {\dot{w}_{2,2} = 2\left( {\chi_{2} + \eta \zeta_{2} } \right) + u_{2} + \Delta f_{2} \left( {{\mathbf{W}},t} \right)} \\ {\dot{w}_{3,1} = w_{3,2} } \\ {\dot{w}_{3,2} = 2\left( {\chi_{3} + \eta \zeta_{3} } \right) + u_{3} + \Delta f_{3} \left( {{\mathbf{W}},t} \right)} \\ \end{array} } \right.$$

(29)

and $u_{1}$, $u_{2}$, and $u_{3}$ are obtained as follows:

$$u_{1} = \frac{2}{\pi }U,\quad u_{2} = 0 \cdot U,\quad u_{3} = \frac{2}{3\pi }U$$

As will be demonstrated in the next section, when a mathematical model is used, the chaotic vibration of the axially moving string at a specified position may be synchronized with the desired signal.

Vibration Control

To demonstrate the suitability and efficacy of the developed approach described in the last section, numerical studies are performed. In this study, the string’s nonlinear response is first highlighted, and a chaotic vibration is discovered. Then, the developed control method is applied to synchronize the chaotic vibration of the translating string.

The following parameters are used to study the response of the axially translating string:

$$Q_{11} = 2.9 \times 10^{4}\,\hbox{N},\quad l = 0.5\,\hbox{m},\quad \rho = 1.00\,\hbox{kg}/\hbox{m}$$

and the axially moving velocity is given by:

$$v_{0} = 2.02\,\hbox{m}/\hbox{s}$$

The initial conditions are given below:

$$\begin{aligned} w_{1,1} \left( 0 \right) & = 0.001,\quad w_{1,2} \left( 0 \right) = 0.005 \\ w_{2,1} \left( 0 \right) & = 0.0001,\quad w_{2,2} \left( 0 \right) = 0.0025 \\ w_{3,1} \left( 0 \right) & = 0.00005,\quad w_{3,2} \left( 0 \right) = 0.00125 \\ \end{aligned}$$

Based on Eqs. (18) and (29), the vibration of the specified point is 0.3125 m along x, and the corresponding response $w_{p}$ is given by:

$$\begin{aligned} w_{p} & = \sum_{n = 1}^{3} \varphi_{n} w_{n,1} = 0.92388w_{1,1} - 0.70711w_{2,1} + 0.38268w_{3,1} \\ & = 0.92388w_{1} - 0.70711w_{2} + 0.38268w_{3} \\ \end{aligned}$$

(30)

where, $w_{1,1}$, $w_{2,1}$, and $w_{3,1}$ are replaced with $w_{1}$, $w_{2}$, and $w_{3}$ for convenience.

Vibration prediction

RNNs have been a popular topic in neural network research in recent years and are composed of an input layer, a hidden layer and an output layer. The input of the hidden layer includes the output of the hidden layer at the previous moment so that the output of the hidden layer can reflect historical information to a certain extent, and this information flows through the next neuron together with new information to affect the final output.

The feature $\delta$ and the hidden state $H_{t}$ at time step t are sent into the fully connected layer to calculate the output variable $O_{t}$ of the current time step t, and $H_{t}$ will participate in the calculation of the hidden state $H_{t + 1}$ at the next time step $t + 1$ for iterative calculation. A diagram of a one-unit RNN is shown in Fig. 3. From bottom to top: input state, hidden state, and output state. $\alpha$, $\beta$, and $\gamma$ are the weights of the input layer, the hidden layer, and the output layer, respectively.

Fig. 3

Basic recurrent neural network.

Compute the hidden state $H_{t}$ at any time at time step t on the basis of the current input $\delta_{t}$ and the previous hidden state $H_{t - 1}$, where $b_{h}$ is the bias parameter of the hidden layer:

$$H_{t} = \phi \left( {\delta_{t} \beta_{1} + H_{t - 1} \beta_{2} + b_{h} } \right)$$

(31)

$b_{q}$ is the bias parameter of the output layer, and the output of the output layer $O_{t}$ is given by:

$$O_{t} = H_{t} \gamma + b_{q}$$

(32)

Chaotic motion

The responses of the selected point on the axially-translating string are investigated in this section, and a dynamic behaviour diagnostic method named the periodicity ratio (PR) method^{42,43,44,45,46,47} is employed for nonlinear dynamic behaviour characterization⁴⁸: when the PR value of a specific dynamic behaviour is 0, the corresponding behaviour is then characterized as chaotic.

At $v_{0} = {2}{\text{.02}}{m \mathord{\left/ {\vphantom {m s}} \right. \kern-0pt} s}$ from $t = 0$ to $t = 1{100}$, Fig. 4 shows the string’s response, for which the PR value is 0. The greatest amplitude of the string’s vibration can surpass 0.045. In Figs. 5 and 6, the 2D phase diagram, 3D phase diagram, and Poincaré map are presented. With the determined PR value, the wave diagram, the 2D phase diagram, the 3D phase diagram and the Poincaré map, the response of the selected point on the axially moving string is characterized as a chaotic vibration in an unstable state of the corresponding nonlinear dynamic system of the axially moving string.

Fig. 4

$w_{p}$ without control.

Fig. 5

Phase diagram: (a) 2D phase diagram; (b) 3D phase diagram.

Fig. 6

Poincaré map.

As shown in Fig. 4, the amplitude is very high when the displacement depicted in the figure is considered as non-dimensional. The string’s performance may therefore be enhanced by reducing and stabilizing the chaotic motion.

Furthermore, although $w_{1}$ in Fig. 7a has a greater impact compared to $w_{2}$ and $w_{3}$, as shown in Fig. 7b and c, the effects of $w_{2}$ and $w_{3}$ are still significant. In fact, $w_{2}$ and $w_{3}$ have a substantial effect on the actual vibration of the chosen spot. As a result, a nonlinear dynamic system in multiple dimensions is required for effective prediction of the dynamics of the nonlinear elastic string.

Fig. 7

First three mode vibrations without control: (a) $w_{1}$; (b) $w_{2}$; (c) $w_{3}$.

Chaotic time series prediction

After data processing, the data are divided into two parts: 70% of the data are included in the training set, for which the loss is shown by the blue line in Fig. 8, and 30% of the data are included in the test set, for which the loss is shown by the orange line in Fig. 8. All of the samples were trained 1300 times, and the number of samples in each sample batch was 256. The training is characterized by the string’s axial velocity and axial motion displacement.

Fig. 8

Prediction of $w_{p}$ without control.

Figure 8 shows that as the number of iterations increases, the loss value decreases, and the final loss function value is less than 2.5%, which provides a solid basis for a more accurate prediction and the effective application of the control to the chaotic vibration of the axially moving string.

Figure 9a shows the predicted displacement time series curves from 100 to 150 s and its subregions. Figure 9b shows the predicted velocity time series curves from 100 to 150 s and its subregions. The velocity and displacement of chaotic motion predicted using the RNN model are shown in Fig. 9. The blue curve, which shows the anticipated outcomes, can be compared with the red curve, which represents the actual dataset. Given the good agreement between the two curves, chaotic motion times can be effectively predicted using the developed method.

Fig. 9

Prediction results for the corresponding features. (a) Testing results for the displacement. (b) Testing results for the velocity.

Amplitude synchronization

The control is applied to demonstrate its effectiveness for amplitude synchronization. The desired amplitude of the reference signal is given three different values.

$$A_{r} = 0.0{2}0$$

When the control approach is used, the reference amplitude is set as

$$w_{r} = 0.0{20}\sin \left( {0.0369t} \right)$$

The remaining control coefficients, as well as the external disturbance, have the following values:

$$\kappa = {2}{\text{.90,}}\quad k_{fs} = {1}.0{0},\quad \Delta F\left( {w,\dot{w}} \right) = 0.001\sin (w_{p} )$$

The control is applied at $t = {140}$, as depicted in Fig. 10. The vibrations of the string at $v_{0} = {2}{\text{.02}}{m \mathord{\left/ {\vphantom {m s}} \right. \kern-0pt} s}$ are displayed in Figs. 10 and 11.

Fig. 10

$w_{p}$ with control.

Fig. 11

First three mode vibrations with control: (a) $w_{1}$; (b) $w_{2}$; (c) $w_{3}$.

Figure 10 shows that the string requires a certain time period for stabilization following the use of the control approach. The vibrations of the chosen point, $w_{p}$, are shown from $t = {0}$ to $t = 4000$. The chaotic vibration is stabilized into a periodic motion with an amplitude of 0.020 after the time period.

In Fig. 11a–c, the vibrations are presented for $w_{1}$, $w_{2}$, and $w_{3}$. These figures show that the control approach eventually stabilizes each displacement of the axially translating string, converting it from a chaotic motion into a periodic motion.

The comparison between $w_{r}$ and $w_{p}$ is depicted in Fig. 12. It is observed that the maximum amplitude of the string’s response changes after the string is stabilized by the use of the control approach. As observed from the figure, the maximum amplitude of $w_{p}$ is close to that of $w_{r}$.

Fig. 12

$w_{p}$ (blue continuous line) and the reference signal $w_{r}$ (red dashed line).

Figure 13 displays the input for control, U. Immediately after the control was applied, U first increased. As the system stabilizes, the maximum value of U, which is represented by a periodic wave diagram in the figure, decreased significantly to a relatively small number. The maximum value of U is 0.1.

$$A_{r} = 0.0{15}$$

Fig. 13

Control input U.

When the control approach is used, the reference intended amplitude is set as

$$w_{r} = 0.0{15}\sin \left( {0.0369t} \right)$$

With other control factors, as well as the unidentified outside disturbance, the following values are used:

$$\kappa = 3.4{0},\quad k_{fs} = {1}.0{0},\quad \Delta F\left( {w,\dot{w}} \right) = 0.001\sin (w_{p} )$$

The control is applied at $t = 140$, as depicted in Fig. 14. The vibrations of the string at $v_{0} = 2.02{m \mathord{\left/ {\vphantom {m s}} \right. \kern-0pt} s}$ are displayed in Figs. 14 and 15.

Fig. 14

$w_{p}$ with control.

Fig. 15

First three mode vibrations with control: (a) $w_{1}$; (b) $w_{2}$; (c) $w_{3}$.

Figure 14 shows that the string requires only a short time period for stabilization following the use of the control approach. The vibrations of the chosen point, $w_{p}$, are shown from $t = {0}$ to $t = 4000$. The chaotic vibration is stabilized into a periodic motion with a maximum amplitude of approximately 0.015.

Figure 15a–c present the vibrations for $w_{1}$, $w_{2}$, and $w_{3}$. These figures show that the control approach eventually stabilizes each displacement of the axially translating string, converting it from a chaotic motion into a periodic motion.

The applied $w_{r}$ and $w_{p}$ are compared in Fig. 16. It is observed that the maximum amplitude of the string’s response changes somewhat after the string is stabilized by the use of the control approach. As the shown in the figure, the maximum amplitude of $w_{p}$ is close to that of $w_{r}$.

Fig. 16

$w_{p}$ (blue continuous line) and the reference signal $w_{r}$ (red dashed line).

Figure 17 displays the input for control, U. Immediately after the control is applied, U first increases. As the system stabilized, the maximum value of U, which is represented by a periodic wave diagram in the figure, decreased to a relatively small value. The maximum value of U is 0.12, which is larger than the previous value.

$$A_{r} = 0.010$$

Fig. 17

Control input U.

The desired reference amplitude is set during the application of the control strategy as follows:

$$w_{r} = 0.0{10}\sin \left( {0.0369t} \right)$$

The other control variables, as well as the unidentified external disturbance, take the following values:

$$\kappa = 4.{00},\quad k_{fs} = {1}.0{0},\quad \Delta F\left( {w,\dot{w}} \right) = 0.001\sin (w_{p} )$$

The control is applied at $t = {140}$, as depicted in Fig. 18. The vibrations of the string at $v_{0} = {2}{\text{.02}}{m \mathord{\left/ {\vphantom {m s}} \right. \kern-0pt} s}$ are displayed in Figs. 18 and 19.

Fig. 18

$w_{p}$ with control.

Fig. 19

First three mode vibrations with control: (a) $w_{1}$; (b) $w_{2}$; (c) $w_{3}$.

Figure 18 shows that the string requires a relatively long period of time for stabilization following the use of the control approach. The vibrations of the chosen point, $w_{p}$, are shown from $t = {0}$ to $t = 4000$. The chaotic vibration is stabilized into a periodic motion with an amplitude of approximately 0.010 after the brief period.

Figure 19a–c present the vibrations for $w_{1}$, $w_{2}$, and $w_{3}$. It is observed that the control approach eventually stabilizes each displacement of the axially translating string, converting it from a chaotic motion into a periodic motion.

The applied $w_{r}$ and $w_{p}$ are compared in Fig. 20. It is observed that the maximum amplitude of the string’s response changes somewhat after the string is stabilized by the use of the control approach. The maximum amplitude of $w_{p}$ is close to that of $w_{r}$.

Fig. 20

$w_{p}$ (blue continuous line) and the reference signal $w_{r}$ (red dashed line).

Figure 21 displays the input for control, U. Immediately after the control was applied, U first increased. As the system stabilized, the maximum value of U, which is represented by a periodic wave diagram in the figure, decreased significantly to a small value. The maximum value of U is 0.50, which is four times larger than the previous value.

Fig. 21

Control input U.

Frequency synchronization

The control is applied to demonstrate its efficacy for frequency synchronization. The desired frequency of the reference signal is given one of three different values.

$$\omega_{r} = 0.0277$$

The preferred reference frequency is chosen when the control strategy is applied according to:

$$w_{r} = 0.01{2}\sin \left( {0.0277t} \right)$$

Considering other control factors, as well as unidentified outside disturbances, the following values are used:

$$\kappa = {2}{\text{.00}},\quad k_{fs} = {1}.0{0},\quad \Delta F\left( {w,\dot{w}} \right) = 0.001\sin (w_{p} )$$

The control is applied at $t = {140}$, as depicted in Fig. 22. The vibrations of the string at $v_{0} = {2}{\text{.02}}{m \mathord{\left/ {\vphantom {m s}} \right. \kern-0pt} s}$ are displayed in Figs. 22 and 23.

Fig. 22

$w_{p}$ with control.

Fig. 23

First three mode vibrations with control: (a) $w_{1}$; (b) $w_{2}$; (c) $w_{3}$.

Figure 22 shows that the string requires only a short period of time for stabilization following the use of the control approach. The vibrations of the chosen point, $w_{p}$, are shown from $t = {0}$ to $t = 4000$. The chaotic vibration is stabilized into a periodic motion with an angular velocity close to 0.0277.

Figure 23a–c present the vibrations for $w_{1}$, $w_{2}$, and $w_{3}$. These figures show that the control approach eventually stabilizes each displacement of the axially translating string, converting it from a chaotic motion into a periodic motion.

Figure 24 compares the applied $w_{r}$ and $w_{p}$. It is observed that the maximum amplitude of the string’s response changes somewhat after the string is stabilized by the use of the control approach. The angular velocity of $w_{p}$ is close to that of $w_{r}$.

Fig. 24

$w_{p}$ (blue continuous line) and the reference signal $w_{r}$ (red dashed line).

Figure 25 displays the input for control, U. Immediately after the control is applied, U first increases. As the system stabilized, the maximum value of U, which is represented by a periodic wave diagram in the figure, decreased significantly to a small value. The maximum value of U is 0.034.

$$\omega_{r} = 0.0184$$

Fig. 25

Control input U.

The desired frequency of the reference is set by the control strategy according to:

$$w_{r} = 0.01{2}\sin \left( {0.0184t} \right)$$

and other control parameters, as well as the unidentified outside disturbance, have the following values:

$$\kappa = {2}{\text{.50}},\quad k_{fs} = {1}{\text{.00}},\quad \Delta F\left( {w,\dot{w}} \right) = 0.001\sin (w_{p} )$$

The control is applied at $t = {140}$, as depicted in Fig. 26. The vibrations of the string at $v_{0} = {2}{\text{.02}}{m \mathord{\left/ {\vphantom {m s}} \right. \kern-0pt} s}$ are displayed in Figs. 26 and 27.

Fig. 26

$w_{p}$ with the control.

Fig. 27

First three mode vibrations with control: (a) $w_{1}$; (b) $w_{2}$; (c) $w_{3}$.

Figure 26 shows that the string needs only a relatively short period of time for stabilization following the use of the control approach. The vibrations of the chosen point, $w_{p}$, are shown from $t = {0}$ to $t = 4000$. The chaotic vibration is stabilized into a periodic motion with an angular velocity close to 0.0184.

Figure 27a–c present the vibrations for $w_{1}$, $w_{2}$, and $w_{3}$. These figures show that the control approach eventually stabilizes each displacement of the axially translating string, converting it from a chaotic motion into a periodic motion.

Figure 28 compares the applied $w_{r}$ and $w_{p}$. It is observed that the maximum amplitude of the string’s response changes somewhat after the string is stabilized by the use of the control approach. The maximum amplitude of $w_{p}$ is close to that of $w_{r}$.

Fig. 28

$w_{p}$ (blue continuous line) and the reference signal $w_{r}$ (red dashed line).

Figure 29 displays the input for control, U. Immediately after the control is applied, U first increases. As the system stabilized, the maximum value of U, which is represented by a periodic wave diagram in the figure, decreased significantly to a small value. The maximum value of U is 0.060, which is almost two times larger than the previous value.

$$\omega_{r} = 0.0092$$

Fig. 29

Control input U.

As the control strategy is implemented, the desired frequency of the reference is set according to:

$$w_{r} = 0.01{2}\sin \left( {0.0092t} \right).$$

For other control factors, as well as the unidentified outside disturbance, the following values are used:

$$\kappa = {2}{\text{.50}},\quad k_{fs} = {1}{\text{.00}},\quad \Delta F\left( {w,\dot{w}} \right) = 0.001\sin (w_{p} ).$$

The control is applied at $t = {140}$, as depicted in Fig. 30. The vibrations of the string at $v_{0} = {2}{\text{.02}}{m \mathord{\left/ {\vphantom {m s}} \right. \kern-0pt} s}$ are displayed in Figs. 30 and 31.

Fig. 30

$w_{p}$ with control.

Fig. 31

First three mode vibrations with control: (a) $w_{1}$; (b) $w_{2}$; (c) $w_{3}$.

Figure 30 shows that the string requires a short period of time for stabilization following the use of the control approach. The vibrations of the chosen point, $w_{p}$, are shown from $t = {0}$ to $t = 4000$. The chaotic vibration is stabilized into a periodic motion with an angular velocity close to 0.0092 after a brief period.

Figure 31a–c present the vibrations for $w_{1}$, $w_{2}$, and $w_{3}$. It is observed that the control approach eventually stabilizes each displacement of the axially translating string, converting it from a chaotic motion into a periodic motion.

Figure 32 compares the applied $w_{r}$ and $w_{p}$. It is observed that the maximum amplitude of the string’s response changes somewhat after the string is stabilized by the use of the control approach. The maximum amplitude of $w_{p}$ is close to that of $w_{r}$.

Fig. 32

$w_{p}$ (blue continuous line) and the reference signal $w_{r}$ (red dashed line).

Figure 33 displays the input for control, U. Immediately after the control is applied, U first increases. As the system stabilized, the maximum value of U, which is represented by a periodic wave diagram in the figure, decreased significantly to a small value. The maximum value of U is 0.068, which is slightly larger than the previous value.

Fig. 33

Control input U.

Influence of parametric errors

Following the previous research on the influence of parametric errors^18,19, chaotic vibration control is applied in the case of random parametric errors to further examine the validity of the control approach. With the same control configuration given in the first case of Amplitude Synchronization, the parameter in Eq. (17) now includes an error of ± 20% as follows:

$$\eta^{*} = \left( {1 + 0.20r\left( t \right)} \right)\eta$$

(33)

where, $r\left( t \right)$ is a normally distributed random function based on the previous research¹⁹.

With the coefficient in Eq. (33) substituted into Eq. (17), vibration control is applied, and the actual response at the selected point is shown in Fig. 34. Although the amplitude of the suppressed response at the selected point is slightly larger than that of the first case of Amplitude Synchronization, clearly $w_{p}$ can still be suppressed in the case of random parametric errors.

Fig. 34

$w_{p}$ with control.

The first three mode vibrations are shown in Fig. 35a–c, which also demonstrate the influence of the control on the response of the studied structure.

Fig. 35

First three mode vibrations with control: (a) $w_{1}$; (b) $w_{2}$; (c) $w_{3}$.

The comparison between $w_{r}$ and $w_{p}$ is depicted in Fig. 36. Although at the beginning of the control the maximum amplitude of the string’s response is more than 0.06, which is larger than that of the first case of Amplitude Synchronization, the difference between the suppressed $w_{p}$ and $w_{r}$ is still small.

Fig. 36

$w_{p}$ (blue continuous line) and the reference signal $w_{r}$ (red dashed line).

Figure 37 displays the input for control, U. Immediately after the control was applied, U first increased to a maximum value around 0.16, which is almost 50% higher than the observed value 0.11 in the first case of Amplitude Synchronization. However, once $w_{p}$ is stabilized, the demanded control value to maintain the control is still close to that in the first case of Amplitude Synchronization.

Fig. 37

Control input U.

Conclusions

Using a novel control strategy developed based on the FSMC, the present work provides an active control strategy for the chaotic motion control of an axially moving string. Using the third-order Galerkin approach, a multidimensional nonlinear system of an axially moving string is derived. A control strategy is subsequently established to synchronize the obtained multidimensional dynamic system. The numerical study demonstrated the efficacy of the control strategy in the case of both external disturbance and random parametric errors. The results obtained in this study will be beneficial for multidimensional nonlinear dynamic system vibration control of axially moving strings in engineering. Drawing on the results of this study, some additional conclusions can be made:

• (1) Higher-order vibrations must be introduced at this phase to analyse the vibration of an axially moving string under sinusoidal stimulation more thoroughly and precisely, particularly when chaotic vibrations must be considered. Consequently, while controlling the vibration of a nonlinear string system, the influence of higher-order vibrations must be considered.

• (2) The effectiveness of this control method is demonstrated by the ability of the established active control strategy to effectively synchronize the response of the axial moving strings in the multidimensional dynamic system with the desired reference signal, which is significantly controlled under both the frequency and amplitude parameters.

• (3) This multidimensional nonlinear dynamic system based on the FSMC control approach plays an important role in the research of chaotic vibrations of axially moving strings, significantly enhancing both the efficiency and reliability of control.

• (4) The modified control strategy is further validated in the case of both external disturbance and parametric errors. Though larger response amplitude is observed and higher control input is demanded at the beginning of the control, generally the response of the axially moving string subjected to parametric error can still remain suppressed with the control strategy.

• (5) By using the RNN model, we can accurately predict and effectively apply the control strategy to suppress chaotic movements; therefore, the amplitude of the string is continuously reduced, and the period of the string can also be increased.