The seepage model for CO₂ in Shale considering dynamic slippage, effective stress and gas adsorption

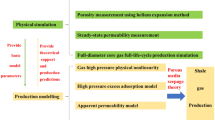
Abstract

This paper first conducted a shale injection CO₂ seepage experiment based on an improved single-vessel pressure pulse attenuation method. The experimental results reveal that the evolution pattern of shale permeability with respect to pore pressure can be divided into before and after phase change. The overall trend is that it first decreases and then increases, which is not a simple exponential form. The exponential fit of the permeability before and after the phase change alone is one-sided. A CO₂ adsorption deformation test was subsequently conducted on shale under the same temperature and gas pressure conditions. The results revealed that with increasing CO₂ pressure, the expansion and deformation of shale first increased but then decreased. The entire deformation process involves three deformation stages: a short compression stage, a slow expansion stage, and a stable deformation stage. The slip effect was corrected by combining adsorption expansion, effective stress, the real gas effect and the dynamic slip factor. The modified permeability model is more consistent with the relationship between permeability and pore pressure.

Introduction

Increasing the proportion of unconventional natural gas represented by shale gas in primary energy consumption is crucial to achieving the dual-carbon goal^1,2,3. China’s shale gas reserves below 3500 m account for more than 65% of total resources, and its recoverable volume ranks first in the world^4,5,6,7. Owing to the low porosity and low permeability of reservoirs, shale gas production is very difficult^8,9,10. The most common shale gas mining process is hydraulic fracturing. Allan Katende et al. studied the fracture proppant of hydraulic fracturing and explored the influence of fracture proppant on shale seepage characteristics considering multiple influencing parameters^11,12,13. However, owing to the large regional environmental differences in the distribution of shale gas, not all shale gas reservoirs, such as some shale gas reservoirs in water-deficient areas, are suitable for hydraulic fracturing technology. Hydraulic fracturing has problems such as high water consumption and reservoir damage^14,15. To solve the problems that occur when hydraulic fracturing is used to mine shale gas, efficient mining with supercritical CO₂, which uses supercritical CO₂to increase the permeability of shale reservoirs for shale gas production^16,17, has been proposed. At present, CO₂₋enhanced shale gas extraction, the law of CO₂ seepage and the evolution of shale permeability are not fully understood. For example, in the process of mining, the effective stress and slippage effect have competitive effects on the seepage of carbon dioxide in shale. Therefore, revealing the evolution of the permeability of shale considering the coupling of effective stress, the slippage effect and adsorption expansion is a key problem in engineering.

At present, the influence of effective stress on reservoir rock permeability has been widely verified¹⁸. Experimental results show that pore sensitivity is very important for the development of oil and gas resources and that microfractures in reservoirs are more sensitive to stress¹⁹. Zhou et al. reported that the effective stress is affected by the gas adsorption effect and subsequently affects the permeability of shale²⁰. The natural microfracture permeability of shale reservoirs is more obviously affected by the effective stress, which can reach 80%²¹. Experiments have shown that the effective stress affects the permeability of shale by affecting its porosity²². When most researchers conduct effective stress analysis, they believe that under the same external stress conditions, the change in permeability with gas pressure is monotonic. However, owing to the special characteristics of CO₂ in the pressure range with phase change, the change in permeability is not monotonic. It is necessary to further explore CO₂ seepage in shale and the change in shale permeability during the phase change process.

Through microscopic experiments, Zhang et al. and others reported that adsorption expansion causes changes in the pores of coal samples and reduces permeability²³. Many researchers have studied adsorption deformation in different gases, such as CO₂, CH₄, and N₂. The results show that the adsorption expansion of shale has obvious anisotropy, which is closely related to the bedding of shale^{24,25,26,27,28}. On the basis of adsorption experiments and adsorption deformation tests, scholars have introduced the adsorption effect into the permeability model to modify its effect on permeability^{29,30,31,32,33}. Although many previous studies have been conducted on the influence of the adsorption effect on permeability, the combination of adsorption expansion and slippage effects needs to be further explored.

For CO₂ storage projects, as the CO₂ storage time increases, CO₂ diffuses to the surroundings, the CO₂pressure continues to decrease, the gas slippage effect cannot be ignored, and the permeability of low-permeability reservoir rocks rebounds³⁴, which is related to the phase transition. The slip effect is a key factor in permeability changes. It is necessary to explore the slip effect under the influence of pore pressure coupled with a phase change pressure range to determine the CO₂seepage law in shale. For the slip effect, the Klinkenberg equation is widely used in research. However, some experimental permeability results deviate from the results of the Klinkenberg linear Eqs^35,36,37. For CO₂ seepage in shale, it is necessary to further verify whether this equation is also applicable to the phase change process. The change in permeability during the phase change process needs further study.

Since the permeability of shale reservoirs is extremely low, for indoor permeability measurement experiments, the most commonly used steady-state method takes a long time, has low accuracy, and has stringent requirements for the measurement of the gas outlet, so the transient method is usually used to measure the permeability of extremely dense rock. Compared with the steady-state method, the transient method takes less time and has higher accuracy. Among the transient methods, the pulse attenuation method is the most commonly used^38,39,40,41. The traditional pressure pulse attenuation method involves passing through two chambers upstream and downstream, and the pressure difference between the upstream and downstream chambers causes the upstream gas to automatically flow through the shale to the downstream chamber. This work uses an improved single-vessel pressure pulse attenuation method to conduct permeability measurement experiments. By reducing the number of chambers, the experimental error and experimental time are reduced^40,41.

In summary, scholars have conducted many experimental studies on shale gas seepage under different working conditions, and further research is needed on the seepage characteristics of CO₂ in shale. Most studies on CO₂ percolation do not consider phase changes; most of them are separate studies before and after phase change, which limits the study of the pattern of change in permeability, and this cannot represent the entire process from low pressure to high pressure. This work uses an improved single-vessel pressure pulse attenuation method to measure the shale injection CO₂ permeability experimentally and conduct CO₂ deformation tests on shale adsorption under the same temperature and gas pressure conditions. By introducing adsorption expansion, effective stress, the real gas effect and the dynamic slip factor, the impact of multiple factors on the evolution of the permeability of CO₂ injected into shale was explored.

Materials and experimental methods

Materials

The shale samples used in the experiments in this study were taken from an outcrop of tight shale in the Longmaxi Formation, Yanzi Village, Changning County, Yibin, Sichuan Province, China. The specific shale samples and sampling locations are shown in Fig. 1. Particle samples were cut from the same whole shale sample and crushed to less than 200 mesh (< 75 μm), and the crushed samples were thoroughly mixed to reduce inhomogeneity. The specific detailed parameters of the shale samples are shown in Tables 1, 2 and 3.

Fig. 1

Shale pickup locations and samples.

Table 1 Mineral compositions and TOC of the selected gas shale samples.

Table 2 Shale sample pore size distributions.

Table 3 Basic parameters and porosities of the shale samples.

Fig. 2

Pore structure of the shale samples.

Equipment, plan and steps for the seepage experiment

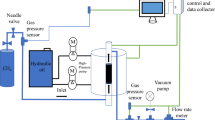
A diagram showing the device used in the seepage experiment is shown in Fig. 3. The purity of the gas used in the experiment is 99.99%. The maximum temperature that the water bath device can reach is 100 °C, and the accuracy is ± 0.01 °C. The upper limit of the pressure sensor is 100 MPa, the accuracy is ± 0.01 MPa, and the upper limit of the pressure that the core gripper can withstand is 60 MPa.

Fig. 3

Seepage experimental system.

CO₂ permeation experiment

CO₂ permeation experiments in shale were carried out at a constant temperature (35 °C, 40 °C) and a gas pressure of 2.5 ~ 16 MPa. The specific scheme is shown in Table 4.

Table 4 Seepage experiment settings, with a pulse pressure of 0.5 MPa.

Figure 5(b) shows the specific experimental process. The pressure difference (DP) between Pci and Psi should be less than 10% of Psi⁴². After the initial point pressure is balanced, the pressure can be directly increased to the next test point. The subsequent pressure balance time can be shortened appropriately to reduce the experimental time and save experimental gas.

Equipment, plan and steps for the adsorption swelling experiment

A diagram of the device used in the adsorption swelling experiment is shown in Fig. 4. The upper limit of the pressure that the adsorption chamber and the reference chamber can withstand is 60 MPa. The data collection system includes a data collector and a static strain gauge (the accuracy of the strain measurement at 0 ~ 50 °C is 0.5% of the indicated value). The other devices are consistent with the seepage experimental device.

Fig. 4

System used for the adsorption swelling experiment.

Adsorption swelling experiment

CO₂ adsorption deformation experiments were carried out on shale at a constant temperature (35 °C, 40 °C) and a gas pressure of 2.5 ~ 16 MPa. The specific scheme is shown in Table 5.

Table 5 Adsorption swelling experiment settings.

Fig. 5

Experimental flow chart: (a) upstream chamber volume correction; (b) seepage experiment; and (c) adsorption deformation experiment.

Figure 5(c) shows the specific experimental process.

Permeability theory

Basic assumptions for the permeability calculations

To facilitate the calculation, the following appropriate assumption is made:

• 1) After applying the pulse pressure, the physical properties of the gas before and after equilibrium remain unchanged.

• 2) The porosity of the shale sample before and after equilibrium remains unchanged.

• 3) Before and after equilibrium, the adsorption caused by the pressure difference is ignored.

• 4) The laboratory temperature error was ignored, and the experimental temperature was held constant.

The phase diagram of CO₂ is shown in Fig. 6(a). Owing to the particularity of CO₂, the physical properties of CO₂ differ under the experimental conditions of this study. Figure 6(b) shows the change curve of CO₂density with gas pressure under constant temperature conditions. For Hypothesis 1, when the added pressure is less than 10% of the original pressure^43,44, the physical properties of CO₂ change little. In the real gas correction section of this article, the effects of temperature and pressure on the CO₂ density, compressibility, compression factor, and dynamic viscosity are introduced. The results show that under the experimental conditions in this work, the change in CO₂physical properties before and after equilibrium is less than 1%, so this assumption is acceptable. For Hypothesis 2, since the pressure difference before and after equilibrium is less than 0.5 MPa, the change in porosity caused is less than 1%⁴⁵, so this part of the change can be ignored. Regarding Hypothesis 3, in the subsequent adsorption experiments, according to Fig. 21, the difference in adsorption capacity caused by the pressure difference before and after equilibrium is less than 0.85% on average; therefore, this part of the adsorption effect can be ignored. For Hypothesis 4, owing to the long experiment duration and the influence of the laboratory environment, the temperature difference in laboratory equipment caused by the temperature difference between the morning and evening is less than 1 °C and can be ignored.

Fig. 6

(a) Phase diagram of CO₂; (b) CO₂ density−pressure relationship.

Using the above assumption to make appropriate simplifications, the axial density distribution governing equation is^38,44

$$\frac{{\partial \rho (x,t)}}{{\partial t}}=K\frac{{{\partial ^2}\rho (x,t)}}{{{\partial ^2}x}}$$

(1)

The equilibrium equation for the gas amount is as follows:

$$\frac{{d{n_c}}}{{dt}}={\left. {K\phi A\frac{{\partial c}}{{\partial x}}} \right|_{x=0}}$$

(2)

The molar mass of the upstream chamber is n_c = ρ_cV_c/M where ρ_c is the chamber gas density (kg/m³) and V_c is the upstream chamber volume (volume correction is required, m³). M is the molecular weight of the gas (kg/mol). The CO₂ concentration in the sample is c=ρ/M, and Eq. (2) can be rewritten as

$$\lambda L\frac{{d{\rho _c}}}{{dt}}={\left. {K\frac{{\partial \rho }}{{\partial x}}} \right|_{x=0}}$$

(3)

where λ is the ratio of the volume of the upstream chamber to the pore volume of the shale and L is the length of the shale (m).

The boundary conditions are as follows:

$$\rho \left( {0,t} \right)={\rho _c}\left( t \right)$$

(4)

$$\lambda L\frac{{d{\rho _c}}}{{dt}}={\left. {K\frac{{\partial \rho }}{{\partial x}}} \right|_{x=0}}$$

(5)

$${\left. {\frac{{\partial \rho }}{{\partial x}}} \right|_{x=L}}=0$$

(6)

The initial conditions are $\rho_{c}\mid_{t=0}=\rho_{ci}$ and$\rho\mid_{t=0}=\rho_{si}$ .

The internal gas density model of a shale core sample is obtained via the Laplace transform of the above equation⁴⁵:

$$\frac{{\rho - {\rho _{{\text{si}}}}}}{{{\rho _\infty } - {\rho _{{\text{si}}}}}}=\left( {1+\sum\limits_{{n=1}}^{\infty } {\frac{{2(1+\lambda ){e^{\frac{{ - Ka_{n}^{2}t}}{{{L^2}}}}}\cos \left( {{a_n}\left( {1 - \frac{x}{L}} \right)} \right)}}{{\left( {1+\lambda +{\lambda ^2}a_{n}^{2}} \right)\cos \left( {{a_n}} \right)}}} } \right)$$

(7)

where ρ_∞ is the CO₂ density after the pressure is balanced. λ satisfies the equation $\tan(a_n)=-\lambda a_n$ .

$${\rho _\infty }=\frac{{{\rho _{{\text{ci}}}}{V_c}+{\rho _{si}}{V_\phi }}}{{{V_\phi }+{V_c}}}=\frac{{{\rho _{{\text{ci}}}}\lambda +{\rho _{si}}}}{{1+\lambda }}$$

(8)

Substituting Eq. (8) into Eq. (7) yields

$$\rho ={\rho _{si}}+\frac{{\lambda \left( {{\rho _{ci}} - {\rho _{si}}} \right)}}{{1+\lambda }}\left( {1+\sum\limits_{{n=1}}^{\infty } {\frac{{2(1+\lambda ){e^{\frac{{ - Ka_{n}^{2}t}}{{{L^2}}}}}\cos \left( {{a_n}\left( {1 - \frac{x}{L}} \right)} \right)}}{{\left( {1+\lambda +{\lambda ^2}a_{n}^{2}} \right)\cos \left( {{a_n}} \right)}}} } \right)$$

(9)

Substituting the above equation into$\lambda L\frac{{d{\rho _c}}}{{dt}}= K \frac{\partial\rho}{\partial x}\mid_{x=0}$ yields:

$$\lambda L\frac{{d{\rho _c}}}{{dt}}= - K\sum\limits_{{n=1}}^{\infty } {\frac{{2\left( {{\rho _{ci}} - {\rho _{si}}} \right)a_{n}^{2}{\lambda ^2}{e^{\frac{{ - Ka_{n}^{2}t}}{{{L^2}}}}}}}{{\left( {1+\lambda +{\lambda ^2}a_{n}^{2}} \right)L}}}$$

(10)

In Eq. (10), when t = 0, the gas density in the upstream chamber can be expressed as

$${\rho _c}={\rho _\infty }+\sum\limits_{{n=1}}^{\infty } {\frac{{2\lambda \left( {{\rho _{ci}} - {\rho _{si}}} \right)}}{{1+\lambda +{\lambda ^2}a_{n}^{2}}}} {e^{ - \frac{{Ka_{n}^{2}t}}{{{L^2}}}}}$$

(11)

Substituting the equality relation $\rho_\infty=\frac{\rho_{ci}V_c+\rho_{si}V_\phi}{V_{\phi}+V_c}=\frac{\rho_{ci} \lambda+\rho_{si}}{1+\lambda}$ into Equation (11) yields

$$\frac{\rho_c-\rho_\infty}{\rho_{ci}-\rho_\infty}=\sum\limits_{{n=1}}^{\infty } {\frac{{2\lambda \left( {{1+\lambda}} \right)}}{{1+\lambda +{\lambda ^2}a_{n}^{2}}}} {e^{ - \frac{{Ka_{n}^{2}t}}{{{L^2}}}}}$$

(12)

The mass fraction can be calculated via the following equation:

$${F_U}=\frac{{{M_t}}}{{{M_\infty }}}=\frac{{{\rho _{ci}} - {\rho _c}}}{{{\rho _{ci}} - {\rho _\infty }}}$$

(13)

The ratio of the remaining gas to the sample entering the shale core can be expressed as

$${F_R}=1 - {F_U}=\frac{{{\rho _c} - {\rho _\infty }}}{{{\rho _{ci}} - {\rho _\infty }}}$$

(14)

FR can be expressed as

$${F_R}=\sum\limits_{{n=1}}^{\infty } {\frac{{2\lambda (1+\lambda )}}{{1+\lambda +{\lambda ^2}a_{n}^{2}}}} {e^{\frac{{ - Ka_{n}^{2}t}}{{{L^2}}}}}$$

(15)

Then,

$$\begin{gathered} {F_R}=1 - \frac{{\left( {{\rho _{ci}} - {\rho _c}} \right)(1+\lambda )}}{{{\rho _{ci}} - {\rho _{si}}}}=1 - \frac{{(\lambda +1)\frac{M}{{{z_{av}}RT}}\left( {{P_{ci}} - {P_c}} \right)}}{{\frac{M}{{{z_{av}}RT}}\left( {{P_{ci}} - {P_{si}}} \right)}} \hfill \\ =1 - \frac{{(\lambda +1)\left( {{P_{ci}} - {P_c}} \right)}}{{\left( {{P_{ci}} - {P_{si}}} \right)}}=\sum\limits_{{n=1}}^{\infty } {\frac{{2\lambda (1+\lambda )}}{{1+\lambda +{\lambda ^2}a_{n}^{2}}}} {e^{\frac{{ - Ka_{n}^{2}t}}{{{L^2}}}}} \hfill \\ \end{gathered}$$

(16)

The density is expressed as pressure for convenience. On the basis of the first assumption, when a real gas is considered, it can still be replaced, which is more conducive to subsequent calculations.

To facilitate the calculation and processing of the experimental data, the expressions for the early solution and the later solution are given.

Early solution:

$${F_R}=1 - (1+\lambda )\left( {1 - {e^{\frac{\tau }{{{\lambda ^2}}}}}\operatorname{erfc} \left( {\sqrt {\frac{\tau }{{{\lambda ^2}}}} } \right)} \right)$$

(17)

where$\tau=\frac{Kt}{L^{2}}$ is dimensionless. Figure 7(a) shows the early solution and general solution at different volume ratios λ. When τ ≤ 0.15 , the previous solution is approximated to the general solution. With increasing λ, when τ ≥ 0.15, the early solution is the same as the general solution, which is most obvious at λ = 100.

Later solution:

When τ ≥ 0.15, Equation (16) converges rapidly; then, when n > 1, the value after the second term can be ignored, and the solution is approximately

$$F_R=\frac{2\lambda (1+\lambda )}{1+\lambda +{\lambda ^2}a_{1}^{2}}e^{-\tau{a_{1}^{2}}}$$

(18)

where a₁ is the first nonzero and nonextreme positive solution to $\tan(a_n)=-\lambda a_n$. Figure 7(b) compares the later solution and the general solution at different volume ratios (λ); when λ tends to infinity, Eq. (18) can be approximated as, where, , and⁴²$ln(F_R)=f+mt$, where $f=ln\left(\frac{2 \lambda(1+\lambda)}{1+\lambda+\lambda^{2}a^{2}_{1}} \right)$,$m=\frac{a^{2}_{1}K}{L^{2}}$, and$K=\frac{k}{\phi \mu c_g}$ .

The final permeability equation is as follows:

$$k= - \frac{{{L^2}\phi \mu {c_g}m}}{{a_{1}^{2}}}$$

(19)

where k is the permeability, (m²); c_g is the compression coefficient of CO₂, 1/Pa; µ is the dynamic viscosity of CO₂; and Φ is the porosity of the shale sample.

Fig. 7

(a) Early solution and general solution; (b) later solution and general solution.

Owing to the compressibility of the pores, the initial porosity is not accurate, so the porosity needs to be corrected before the carbon dioxide seepage experiment. Through He seepage experiments in shale, according to the initial and final equilibrium pressures of the experimental system, the porosity can be calculated via Boyle’s law, and because the amount of helium adsorbed is very small, it can be ignored; thus, the porosity can be calculated via the following formula:

$$\frac{{{V_u}\left( {{p_0}+\Delta p} \right)}}{{{Z_{{p_0}+\Delta p}}}}+\frac{{\phi ^{\prime}AL{p_0}}}{{{Z_{{p_0}}}}}=\frac{{\left( {{V_u}+\phi ^{\prime}AL} \right){p_f}}}{{{Z_{{p_f}}}}}$$

(20)

The compression factor of helium comes from NIST. Owing to the strong adsorption of CO₂, the porosity change caused by adsorption cannot be ignored. For carbon dioxide, the improved SRD model is more suitable; with the SRD adsorption model, the porosity caused by adsorption can be expressed as follows:

$${\phi _{ad}}=\frac{{{\rho _S}\left( {1 - \phi ^{\prime}} \right)}}{{{c_g}{\rho _a}}}\frac{{2D{n_{\hbox{max} }}}}{p}\frac{{d{\rho _a}}}{{dp}}\left\{ {{n_{max}}{e^{ - D{{\left[ {\ln \left( {{{{\rho _a}} \mathord{\left/ {\vphantom {{{\rho _a}} {{\rho _g}}}} \right. \kern-0pt} {{\rho _g}}}} \right)} \right]}^2}}} - {K_1}{\rho _g}} \right\}$$

(21)

where D, nmax, and $\frac{d\rho_a}{dp}$ can be obtained via adsorption experiments and real gas effects, as explained in the following chapters.

The apparent porosity of shale can be expressed as

$${\phi _a}=\phi ^{\prime}+{\phi _{ad}}$$

(22)

Adsorption calculation

The initial and final pressure values of each equilibrium point reference chamber and adsorption chamber were recorded under isothermal conditions. The schematic diagram is shown in Fig. 8, and the cumulative adsorption amount can be obtained via Eq. (23).

Fig. 8

Diagram of the adsorption experiment.

The adsorption capacity can be expressed as

$$\Delta {N_{{{\exp }^i}}}=\frac{1}{{R \cdot T}}\left( {\frac{{P_{r}^{i} \cdot {V_r}}}{{Z_{r}^{i}}}+\frac{{P_{e}^{j} \cdot {V_v}}}{{Z_{e}^{j}}} - \frac{{P_{e}^{i} \cdot \left( {{V_r}+{V_v}} \right)}}{{Z_{e}^{i}}}} \right)$$

(23)

The cumulative adsorption amount$N_{exp}^{i}=\sum_{i=1}^{n} \Delta N_{exp}^{i}$ . The total adsorption capacity is converted into the adsorption capacity of shale samples per unit mass, the gas volume under standard conditions (STP) is taken as the unit, and the adsorption capacity is$n_{exp}=\frac{22400N_{exp}}{m}$ .

Because the volume of the adsorption chamber and the reference room is much larger than the volume of the pipeline and the valve, this part of the volume can be ignored.

Results and discussion

Permeability results

Volume correction

The relationship between α and λ is shown in Fig. 9. Since the volume of the upstream chamber is very small, the volume of the pipeline and valve connected to it cannot be ignored, and the actual volume needs to be corrected, as shown in Fig. 10. The correction equation is as follows:

$$\frac{{{P_1}\left( {{V_1}+{V_2}} \right)}}{{{z_1}}}=\frac{{{P_2}\left( {{V_1}+{V_2}+{V_0}} \right)}}{{{z_2}}}$$

(24)

$$\frac{{{P_3}\left( {{V_1}+{V_2}} \right)}}{{{z_3}}}=\frac{{{P_2}\left( {{V_1}+{V_2}+{V_0}+{V_a}} \right)}}{{{z_4}}}$$

(25)

The correction process is shown in Fig. 5 (a).

Fig. 9

Relationship between λ and a₁.

Fig. 10

Schematic of the volume correction.

Real gas effects

Owing to the special nature of CO₂, the physical properties of supercritical CO₂ are very different from those of gaseous CO₂. Therefore, the difference in the physical properties of CO₂ at each measuring point (interval of 1.5 MPa) during the experiment in this paper cannot be ignored. Figure 11 (a) shows the compression factor of CO₂. Under the experimental temperature conditions in this work, the compression factor first decreases but then increases with increasing pressure. Figure 11 (b) shows the dynamic viscosity of CO₂. Unlike the compression factor, the dynamic viscosity gradually increases with increasing pressure. Figure 11 (c) is the compression coefficient of CO₂, which decreases first and then increases with increasing pressure. Figure 11 (d) shows the density of CO₂, and its change trend is consistent with that of the dynamic viscosity of CO₂. The physical properties of CO₂ change abruptly when it approaches the critical condition. To facilitate the calculation, the compression factor, compression coefficient and dynamic viscosity need to be determined. The equation for the compression factor Z is shown in Table 6.

Fig. 11

Physical properties of CO₂: (a) density; (b) dynamic viscosity; (c) coefficient of compressibility; (d) compressibility factor (a), (b) and (d) data from NIST.

Table 6 Methods used to calculate the compressibility factor Z in the literature.

Figure 12 (a) compares the compression factor Z fitting results and the Z (NIST) results of the three models. A comparison of the results of the three fitting equations reveals that the H−S−M method has the best fitting effect. Figure 12 (b) compares the H−S−M fitting results and the Z (NIST) data. The fitting error is shown in Fig. 14 (a). The overall error of the H−S−M method is less than 10%.

Fig. 12

(a) L101 fitting results of the three equations compared with the Z data. (b) Comparison of the H−S−M method fitting results and the Z data for L101 and L102.

The dynamic viscosity of gas can be expressed as⁴⁹

$$\mu =\eta \exp \left( {\alpha {\rho ^\beta }} \right)$$

(26)

where ρ = MP/ZRT , ρ is the gas density considering the real gas effect, kg/m³; M is the molar mass of the gas, kg/mol; and R is the general gas constant J/(mol·K).

The compression coefficient of gas can be expressed by Eq. (27)⁴⁰. The specific results are shown in Fig. 10 (c).

$${c_g}=\frac{1}{p}\left( {1 - \frac{{d\ln \left( z \right)}}{{d\ln \left( p \right)}}} \right)$$

(27)

Figure 13 (a) shows the L101 and L102 fitting results compared with µ (NIST). Figure 13 (b) shows that the relationship between the fitting results of L101 and L102 and the µ (NIST) data can be fit with the standard linear function under the experimental conditions. Figure 14 (b) shows that the overall average error is less than 15%, which is acceptable.

Fig. 13

(a) µ fitting results; (b) comparison between the fitting results and the µ data.

Fig. 14

(a) Error of the three models in fitting the compression factor and (b) error in fitting the µ value.

Data processing

Since the pressure‒time curves of the upstream chamber under different pressures are similar, we discuss the results for sample L101 at a pressure of 2.5 MPa. Figure 15 shows the pressure decay curve with time and the FR−time curve under L101 2.5 MPa. Figure 15(b) shows that after the early decline, the later solution for the later time corresponds well with the experimental value. Through the slope of the later solution, the permeability of the core can be calculated. Figure 16 shows the curve of the m values of the two shale cores as a function of pressure. The figure shows that the change in slope can be divided into two stages: the gas phase before the phase change and the supercritical phase after the phase change. The absolute value of the slope in the supercritical phase increases with increasing pressure and tends to be linear. This situation may be due to the special physical properties of CO₂, as shown in Fig. 11. When the pressure is close to the critical pressure, the physical properties change suddenly.

Figure 17 shows the permeability curves of two shale core samples with increasing CO₂ pressure. The permeability clearly has an extreme value when the CO₂pressure is close to the critical pressure, and the curves of the shale permeability and pore pressure are approximately ‘v’ shaped. The overall permeability change can be divided into two stages. 1: In the gas phase, when the pore pressure is low, the permeability decreases gradually. Ranathunga et al. suggested that the decrease in permeability was the result of matrix expansion. In the present work, we infer that the reduction is the common result of the Klinkenberg effect, expansion and effective stress⁵⁰. As the pore pressure continues to increase, the permeability decreases. 2: In the supercritical state, the permeability of shale corresponds to the physical properties of CO₂ (Fig. 11). There is a minimum inflection point near the critical pressure, and the permeability increases with increasing pressure. If the real properties of gas are ignored, the results will be greatly affected.

Fig. 15

L101 at 2.5 MPa: (a) pressure vs. time curve and (b) FR vs. time curve.

Fig. 16

Slope of each pressure point under experimental conditions: (a) m of L101 and (b) m of L102.

Fig. 17

Curves of the shale permeability with pressure (a) L101 and (b) L102.

Mechanism of stress and adsorption strain in shale

Adsorption capacity and adsorption strain

Figure 18 shows the absolute adsorption capacity of CO₂ in shale and the gas pressure curve. The diagram reveals that the amount of CO₂ adsorbed in shale first increases and then decreases with increasing CO₂ pressure, and the maximum value occurs near the critical pressure. A comparison of the adsorption capacity of the two shales revealed that under the same gas pressure conditions, the adsorption capacity in the early stage at 35 °C was greater than that at 40 °C. After exceeding the critical pressure, the adsorption amounts at the two temperatures tend to be equal.

Fig. 18

Isotherms of excess CO₂ adsorption in shale.

At present, the adsorption models of coal and shale are mostly assumed to satisfy the Langmuir model. However, owing to the particularity of CO₂, the Langmuir model cannot describe the adsorption of CO₂ above 6 MPa. This is because the Langmuir model cannot describe the phase transition of CO₂, whereas the supercritical DR model (SDR)^[[51,52]] can describe the supercritical adsorption of CO₂ by introducing density. The supercritical DR model is established with the conventional DR model. The conventional DR model is shown in Eq. (28).

$$n={n_{max}}{e^{ - D{{\left[ {\ln \left( {{{{p_0}} \mathord{\left/ {\vphantom {{{p_0}} p}} \right. \kern-0pt} p}} \right)} \right]}^2}}}$$

(28)

where n is the excess adsorption capacity of the sample; nmax is the maximum adsorption capacity; p₀ is the saturated vapour pressure of CO₂; p is the adsorption pressure; and D is the characteristic coefficient of CO₂ adsorption on the sample. Since the adsorption temperature exceeds the critical temperature of CO₂, CO₂ does not liquefy, and there is no saturated vapour pressure p₀; thus, the conventional DR model cannot describe the adsorption conditions in the supercritical state. Replacing the pressure with density and introducing the density of the adsorbed phase yields Eq. 29.

$$n={n_{max}}{e^{ - D{{\left[ {\ln \left( {{{{\rho _a}} \mathord{\left/ {\vphantom {{{\rho _a}} {{\rho _g}}}} \right. \kern-0pt} {{\rho _g}}}} \right)} \right]}^2}}} - {K_1}{\rho _g}$$

(29)

where ρ_a is the density of CO₂ and ρ_g is the density of the adsorbed phase.

The results of Reference⁵² show that the adsorption amount is linearly related to the deformation amount, and the correlation factor Q is introduced. Therefore, the model of adsorption deformation is as follows.

$$\varepsilon =Q\left( {{n_{max}}{e^{ - D{{\left[ {\ln \left( {{{{\rho _a}} \mathord{\left/ {\vphantom {{{\rho _a}} {{\rho _g}}}} \right. \kern-0pt} {{\rho _g}}}} \right)} \right]}^2}}} - {K_1}{\rho _g}} \right)$$

(30)

Let, $\epsilon_{max}=n_{max}Q$ and K=K₁Q ; then, it can be rewritten in the form of the SDR model.

$$\epsilon=\epsilon_{max}e^{-D[ln \frac{\rho_a}{\rho_g}]^{2}}-K \rho_g$$

(31)

Fig. 19

Linear strains of (a) L101 and (b) L102.

As shown in Fig. 19, the axial (vertical bedding direction) strain and radial (parallel bedding direction) strain of the shale samples are consistent in terms of the overall change trend but exhibit significant directionality in deformation. The strain of vertical bedding is greater than that of parallel bedding, which shows that the adsorption deformation of shale is anisotropic. The pores and fractures in shale mainly develop along the bedding, and the adsorption expansion of shale mainly involves changes in the width of fractures and pores; thus, expansion deformation occurs mainly in the vertical direction of pores and fractures. The adsorption strain of shale can be calculated from the axial strain and radial strain.$\epsilon=\epsilon_1=2\epsilon_2$ , where ε is the adsorption strain, ε₁ is the axial strain, and ε₂ is the radial strain.

Fig. 20

(a) Adsorption strain with pressure; (b) adsorption strain with density.

As shown in Fig. 20, (a) shows a curve of the change in the adsorption strain with pressure, and (b) can be obtained by substituting the experimental data into Eq. (28). (b) shows that the SDR model can describe the expansion deformation of shale that adsorbs CO₂.

The variation in the adsorption strain is $\Delta\epsilon=\epsilon-\epsilon_0$ :

$$\Delta \varepsilon ={\varepsilon _{max}}\left\{ {{e^{ - D{{\left[ {\ln \left( {{{{\rho _a}} \mathord{\left/ {\vphantom {{{\rho _a}} {{\rho _g}}}} \right. \kern-0pt} {{\rho _g}}}} \right)} \right]}^2}}} - {e^{ - D{{\left[ {\ln \left( {{{{\rho _0}} \mathord{\left/ {\vphantom {{{\rho _0}} {{\rho _g}}}} \right. \kern-0pt} {{\rho _g}}}} \right)} \right]}^2}}}} \right\}=d\varepsilon$$

(32)

The volumetric strain and fracture strain caused by adsorption deformation can be expressed as.

Volumetric strain:

$$d\varepsilon _{b}^{{ad}}= - \left( {1 - f} \right)\left( {1 - \phi } \right)d\varepsilon$$

(33)

Fracture strain:

$$d\varepsilon _{f}^{{ad}}=\frac{{f\left( {1 - \phi } \right)}}{\phi }d\varepsilon$$

(34)

where f is the internal expansion coefficient, which is used to measure the influence of shale adsorption deformation on the change in pore and fracture width, and its fluctuation range is usually 0−1. A schematic diagram of shale adsorption deformation is shown in Fig. 21. V_m is the matrix volume, V_f is the pore fracture volume, and the shale volume is V_b.

Fig. 21

Adsorption deformation of the shale matrix^3,53.

Stress sensitivity

With the continuous change in pore pressure, stress directly affects the closure and opening of pores and fractures in shale reservoirs, which is very important for the permeability evolution of reservoirs. The volumetric strain and fracture strain caused by effective stress can be expressed as^54,55

$$d\varepsilon _{b}^{s}=\frac{1}{{{K_b}}}\left( {d\overline {\sigma } - \alpha dp} \right)$$

(35)

$$d\varepsilon _{f}^{s}=\frac{1}{{{K_f}}}\left( {d\overline {\sigma } - \beta dp} \right)$$

(36)

where K_b is the bulk modulus of shale, MPa; $K_b=\frac{E}{[3(1-2\nu)]}$ ; E is the elastic modulus, MPa; v is Poisson’s ratio, dimensionless, $\alpha=\frac{1-K_b}{K_m}$ ; and $\beta=\frac{1-K_f}{K_m}$ . The total volumetric strain and rupture strain are as follows:

$$d{\varepsilon _b}=d\varepsilon _{{_{b}}}^{{ad}}+d\varepsilon _{{_{b}}}^{s}$$

(37)

$$d{\varepsilon _f}=d\varepsilon _{f}^{{ad}}+d\varepsilon _{{_{f}}}^{s}$$

(38)

Some scholars believe that the relationships among the porosity, volumetric strain and fracture strain can be expressed via Eq. (39)^3,43.

$$\frac{{d\phi }}{\phi }=d{\varepsilon _b} - d{\varepsilon _f}$$

(39)

Generally, the bulk modulus of shale itself is much greater than that of shale pores. The bulk modulus of fractures is much lower than that of the shale matrix: K_b > > K_f, and K_b < < K_m. When the rock porosity is far less than 1 and φ < < 1, the above equation can be integrated into

$$\int {\frac{{d\phi }}{\phi }} =\int_{{{\varepsilon _{b0}}}}^{{{\varepsilon _b}}} {d{\varepsilon _b}} - \int_{{{\varepsilon _{f0}}}}^{{{\varepsilon _f}}} {d{\varepsilon _f}}$$

(40)

where$C_f=\frac{1}{K_f}$.

$$\frac{\phi}{\phi_0}=exp\left[-C_f\left(\int_{\overline\sigma 0}^{\overline\sigma}d\overline\sigma-\int_{p0}^{p}dp\right)-\frac{(f+1)K_b}{K_f}\int^{\epsilon_{m}^{ad}}_{\epsilon_{m}^{ad}0}d\epsilon_{m}^{ad}\right]$$

(41)

Since K_b < < K_m, α is almost equal to 1. According to the Betty‒Maxwell reciprocity law, $K_f=\frac{\phi K_b}{\alpha}$ , and $K_f {\approx \phi K_b}$ .

Combined with the above equations, we can obtain

$$\frac{\phi }{{{\phi _0}}}=\exp \left\{ { - {C_f}\left[ {\left( {\overline {\sigma } - \overline {{{\sigma _0}}} } \right) - \left( {P - {P_0}} \right)+\left( {f+1} \right){K_b}{\varepsilon _{\hbox{max} }}\left\{ {{e^{ - D{{\left[ {\ln \left( {{{{\rho _a}} \mathord{\left/ {\vphantom {{{\rho _a}} {{\rho _g}}}} \right. \kern-0pt} {{\rho _g}}}} \right)} \right]}^2}}} - {e^{ - D{{\left[ {\ln \left( {{{{\rho _0}} \mathord{\left/ {\vphantom {{{\rho _0}} {{\rho _g}}}} \right. \kern-0pt} {{\rho _g}}}} \right)} \right]}^2}}}} \right\}} \right]} \right\}=\exp \kappa$$

(42)

The following relation is stipulated:

$$\exp \kappa = - {C_f}\left[ {\left( {\overline {\sigma } - \overline {{{\sigma _0}}} } \right) - \left( {P - {P_0}} \right)+\left( {f+1} \right){K_b}{\varepsilon _{\hbox{max} }}\left\{ {{e^{ - D{{\left[ {\ln \left( {{{{\rho _a}} \mathord{\left/ {\vphantom {{{\rho _a}} {{\rho _g}}}} \right. \kern-0pt} {{\rho _g}}}} \right)} \right]}^2}}} - {e^{ - D{{\left[ {\ln \left( {{{{\rho _0}} \mathord{\left/ {\vphantom {{{\rho _0}} {{\rho _g}}}} \right. \kern-0pt} {{\rho _g}}}} \right)} \right]}^2}}}} \right\}} \right]$$

(43)

Slippage effects

Compared with conventional reservoirs, shale reservoirs have smaller pores and microcracks. Under low pore pressure, the gas flow rate at the edge of the wall is not 0, which makes the gas improve the flow capacity during the seepage process, thereby increasing the permeability. The yellow part in Fig. 22 is the ideal flow state, and the flow velocity in the pore is evenly distributed at a distance from the wall surface. Obviously, this flow velocity distribution is not correct, and the green part is a linear distribution. Owing to the intermolecular force, the probability of the molecules colliding and the friction between the fluid and the wall surface, the flow velocity is not linear in the distribution of the distance from the wall surface, which needs further discussion. Therefore, the permeability of this part needs to be corrected.

Fig. 22

Diagram of the slippage effect.

In an experiment, Klinkenberg reported an obvious inverse linear relationship between the permeability and pore pressure and presented an empirical first-order permeability correction equation such as Eq. (44). However, with increasing Knudsen number (Kn > 0.001), the gas flow in shale does not fully follow the Klinkenberg correction equation. On the basis of the Klinkenberg correction equation, Moghadam and Chalaturnyk proposed a higher-order equation to describe the slip effect⁵⁶. The second-order permeability correction equation after correction is shown in Eq. (45).

$${k_{ap}}={k_\infty }\left( {1+\frac{b}{p}} \right)$$

(44)

$${k_{ap}}={k_\infty }\left( {1+\frac{b}{{{P_m}}} - \frac{a}{{P_{m}^{2}}}} \right)$$

(45)

where$b=\frac{4m}{r_{pore}}$ ,$a=\frac{4m^{2}}{r^{2}_{pore}}$,$m=c\mu_g \sqrt{\frac{\pi RTZ}{2M}}$⁵⁷, and c is a dimensionless parameter.

Then, a and b can be expressed as

$$\left\{ {\begin{array}{*{20}{c}} {a=\frac{{2{c^2}\mu _{g}^{2}\pi ZRT}}{{{r^2}M}}} \\ {b=\frac{{4c{\mu _g}}}{r}\sqrt {\frac{{\pi ZRT}}{{2 M}}} } \end{array}} \right.$$

(46)

According to Reference⁵⁸, we can obtain $\phi=\frac{6r}{d}$ and, $k=\frac{8r^{6}}{12d}$ .

Then, $r=3\left(\frac{k}{\phi}\right)^{0.5}$ can be obtained according to the following relationship: $\frac{k}{k_0}=\left(\frac{\phi}{\phi_0}\right)^{3}$ . Combined with Eq. (42), the following equation can be obtained:

$$r=3{e^\kappa }{\left( {\frac{{{k_0}}}{{{\phi _0}}}} \right)^{0.5}}$$

(47)

Substituting Eq. (47) into Eq. (46) yields

$$\left\{ {\begin{array}{*{20}{l}} {a=\frac{{2{\phi _0}{c^2}\mu _{{\text{g}}}^{2}\pi RTZ}}{{9{k_0}M\exp (2\kappa )}}} \\ {b=\frac{{2\sqrt 2 c{\mu _{\text{g}}}}}{{3\exp \kappa }}\sqrt {\frac{{{\phi _0}\pi RTZ}}{{{k_0}M}}} } \end{array}} \right.$$

(48)

The apparent permeability of shale modified by dynamic second-order slip can be obtained by substituting Eq. (48) into Eq. (45):

$${k_{{\text{ap}}}}={k_0}\exp (3\kappa )\left( {1+\frac{{2\sqrt 2 c{\mu _{\text{g}}}}}{{3{P_{\text{m}}}\exp \kappa }}\sqrt {\frac{{{\phi _0}\pi RTZ}}{{{k_0}M}}} } \right.\left. { - \frac{{2{\phi _0}{c^2}\mu _{{\text{g}}}^{2}\pi RTZ}}{{9P_{{\text{m}}}^{2}{k_0}M\exp (2\kappa )}}} \right)$$

(49)

Liu et al³⁶. and Heller et al⁵⁹. reported that the change in effective stress has a greater effect on permeability than slippage has on permeability. Therefore, we believe that the effective stress plays a dominant role in the evolution of permeability in environments with increasing pore pressure. The traditional exponential form is not suitable for global fitting. We use the following equation to construct the permeability fitting function^36,60,61.

$${k_{ap}}={k_{ap}}\left( {{P_c},{P_p}} \right)={a_1}+{a_2}{P_c}+{a_3}{P_P}+{a_4}P_{c}^{2}+{a_5}{P_c}{P_P}+{a_6}P_{p}^{2}+ \cdots +{a_{n+i}}P_{p}^{n}$$

(50)

Figure 23 compares the experimental data and the results of the three different fitting equations. Because the traditional exponential form cannot fit a nonmonotonic dataset with extreme values, the data before and after the extreme values are fitted piecewise. The construction function fits the global data well, and the fitting effect is good, which reflects the inflection point of the experiment well. However, for these two fitting methods, although the exponential form can reflect the monotonicity and trend of the data well, it cannot be defined globally when the pressures cross (covering low pressure, high pressure and the phase transition). Although the constructor can fit the global data well, its highest phase cannot be determined. Moreover, it cannot explain the problem, and the upper and lower limits of the order of magnitude of the fitting parameter are high. Figures 24 and 25 show the errors of the three fitting models. The numerical values indicate that the fitting degree of the three fitting models exceeds 95%, and the relationship between the fitting value and the experimental value is close to a linear function.

Fig. 23

Experimental data and fitting values.

Fig. 24

L101 error analysis: (a) Δ/k and (b) relationship between the results of the three fitting equations and the experimental values.

Fig. 25

L102 error analysis: (a) Δ/k and (b) relationship between the results of the three fitting equations and the experimental values.

Conclusion

In this study, we explored the seepage law of CO₂ in shale via an improved single-container pulse permeability measurement method and carried out shale adsorption CO₂ expansion tests under the same temperature and gas pressure conditions. Combined with the real gas effect, adsorption strain and the slippage effect, the permeability was corrected, and the results of three fitting equations were compared. The specific conclusions are as follows.

• 1. The evolution of permeability with respect to pore pressure after CO₂ injection into shale can be divided into two stages: before and after phase change. In the gaseous CO₂ stage, when the pore pressure is low, the permeability decreases gradually under the combined action of the slippage effect, adsorption expansion and effective stress. With the gradual increase in pore pressure, CO₂ nears the phase transition, the slippage effect is weakened, the effective stress effect gradually increases, the permeability change gradually decreases, and the minimum value is reached. During the supercritical CO₂ stage, the physical properties of CO₂ change abruptly, and the trend of the change in permeability with increasing pore pressure changes from a decrease in the gas phase to an increase. In the early stage of the supercritical state, the increasing trend is small. With increasing pore pressure, the permeability clearly tends to increase, and the overall trend tends to decrease first and then increase.

• 2. The expansion deformation of shale under CO₂ pressure can be described in the form of a supercritical DR (SDR) model with CO₂ density. The adsorption deformation of shale shows significant directionality. The strain of vertical bedding is greater than that of parallel bedding; that is, the adsorption deformation of shale is anisotropic. The trend of expansion deformation is similar to that of the adsorption capacity. Under the action of CO₂ pressure, the deformation of shale undergoes three deformation stages: the transient compression stage, the slow expansion stage, and the stable deformation stage.

• 3. In this work, the permeability model is corrected by considering the combined effects of adsorption expansion, effective stress and the slippage effect. Comparing two common fitting methods with the model in this paper shows that the model in this paper can not only better explain the evolution law of permeability after injection of CO₂ in shale but also correspond to the physical changes in CO₂, which can better explain the trend of the change in permeability.