Introduction

Medical imaging, particularly Magnetic Resonance Imaging (MRI), has emerged as a cornerstone in modern healthcare, enabling clinicians to visualize and analyze internal structures with unprecedented detail1,2. As the demand for precise diagnostics and personalized treatment plans continues to grow, the development of advanced image processing techniques becomes crucial. In this context, the focus of this research is on the intricate realm of MRI segmentation, specifically addressing the challenges inherent in multi-class segmentation.

Segmentation, the process of partitioning an image into meaningful and distinct regions, plays a pivotal role in medical image analysis. It provides a foundation for accurate organ delineation and pathology identification, laying the groundwork for subsequent diagnostic and treatment decisions. However, the complexity of the human anatomy, coupled with the subtle variations in tissue characteristics, presents a formidable task for segmentation algorithms.

This research endeavors to bridge the gap by proposing a novel multi-class MRI segmentation algorithm. A key innovation lies in the integration of diffusion models, harnessing the power of diffusion-based information to enhance segmentation accuracy. Diffusion models have proven effective in capturing microstructural details, making them invaluable in discerning subtle boundaries between different tissues3.

In the subsequent sections, we delve into the theoretical underpinnings of diffusion models and their application in the context of MRI segmentation. We explore the intricacies of multi-class segmentation challenges and elucidate how the proposed algorithm addresses these issues. Furthermore, a comprehensive evaluation is conducted, comparing the performance of the proposed algorithm against existing state-of-the-art methods.

As we navigate through the intricacies of this research, the ultimate goal is to contribute to the refinement of medical image segmentation techniques, fostering advancements that empower clinicians with more accurate and reliable tools for diagnosis and treatment planning.

Related work

The segmentation of image samples into distinct regions of interest is a crucial step in medical image analysis applications. Manual segmentation remains a clinical standard; however, it is essential to note that annotations made by multiple experts may exhibit significant variations due to differences in experience, domain knowledge, and subjective judgment. Deep learning methods have achieved state-of-the-art performance in medical image segmentation tasks. Among the most widely adopted approaches are those that employ U-Net4 or incorporate transformer models5 to generate segmentation masks for input images. nnU-Nets6 represent the latest advancements in the field of medical image segmentation, demonstrating the ability to autonomously analyze each specific dataset and select optimal architectures and hyperparameters to achieve superior performance on a given task.

The Noise Diffusion Probability Model, referred to as the Diffusion Model, belongs to a category of likelihood-based generative models7,8,9. Dhariwal et al., demonstrated their superiority in terms of sample quality and diversity across multiple datasets compared to state-of-the-art generative adversarial networks10. Due to this success, they have garnered significant interest in the research community and have been explored in various applications such as super-resolution11, restoration12, semantic segmentation13,14,15, anomaly detection16,17,18, and text-to-image generation19. There is a growing interest in utilizing the Diffusion Model for medical image analysis as well.

The diffusion model and GANs have previously been explored for medical image segmentation. Cirillo et al20, employed GANs for 3D brain tumor segmentation, using them to generate segmentation maps while penalizing the model for producing unrealistic segmentations. Wolleb et al21, introduced DDPM for brain MR image segmentation, providing a solution for DPM-based image segmentation by synthesizing labeled data and eliminating the need for per-pixel annotations. Despite being groundbreaking, this approach is time-consuming. Guo et al22, proposed PD-DDPM, accelerating the segmentation process by using pre-segmentation results and noise prediction based on forward diffusion rules. When combined with Attention Unet, this method outperformed previous DDPM even with fewer downsampling steps. MedSegDiff23 improved DPM for medical image segmentation by introducing a dynamic conditional encoding strategy that mitigates the negative impact of high-frequency noise components through an FF resolver. Subsequently, to achieve better convergence between noise and semantic features, they proposed MedSegDiff-V224, where a transformer-based architecture is combined with Gaussian spatial attention blocks for noise estimation. Diff-UNet25 introduced a universal end-to-end 3D medical image segmentation method, leveraging the advantages of the diffusion model to enhance segmentation robustness.

The diverse and meaningful nature of these research efforts in utilizing the diffusion model for medical image segmentation, especially for complex and blurry brain tumor images, is evident. But most studies have focused on straightforward segmentation tasks for the entire tumor or tackled the three-dimensional segmentation of tumors using high-end computational resources. In contrast, our work is dedicated to the efficient and high-precision realization of multi-class segmentation for brain tumors. Specifically, our research delves into a diffusion model-based technique for multi-class segmentation of brain tumors, aiming to address the challenge posed by the blurred boundaries of tumor sub-regions leading to decreased segmentation accuracy. To tackle this challenge, we leverage the stochastic nature of the diffusion model. By introducing elements of randomness, our model becomes more flexible, resulting in a substantial improvement in multi-class segmentation accuracy for tumors.

The unique properties of the diffusion model enable it to better capture subtle features and edge information in images, leading to enhanced performance when dealing with the boundary-blurred sub-regions of tumors. By introducing the randomness of the diffusion model during the training process, we have effectively increased the adaptability of the model to complex tumor structures and morphological variations, thereby improving the accuracy of multi-class segmentation.

This approach not only aids in a more detailed revelation of the structure and features of different sub-regions of brain tumors but also exhibits strong robustness in dealing with various uncertainties and noise in the images. Overall, by thoroughly exploiting the stochastic nature of the diffusion model, we have successfully optimized the multi-class segmentation task for brain tumors, providing robust support for further research and development in the field of medical image analysis.

Methods

Diffusion model for multi-class segmentation

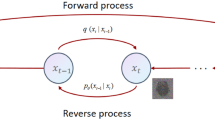
The segmentation denoising diffusion model employs two Markov chains: a forward chain that perturbs the true segmentation into noise and a backward chain that transforms noise into a predicted segmentation map. The former is typically manually designed with the aim of transforming any data distribution into a simple prior distribution (e.g., a standard Gaussian distribution), while the latter Markov chain reverses the former by learning a transition kernel parameterized by deep neural network parameters. Subsequently, this process involves sampling a random vector from the prior distribution and generating new data through ancestral sampling using the reverse Markov chain.

Mathematically formalizing this process, given the true segmentation data distribution \({\text{x}}_{0} \sim q({\text{x}}_{0} )\), the forward process generates a random sequence \({\text{x}}_{1} ,{\text{x}}_{2} ...{\text{x}}_{T}\) based on the transition kernel \(q({\text{x}}_{t} \left| {{\text{x}}_{t - 1} } \right.)\). Utilizing the probability chain rule and the Markov property, \({\text{x}}_{1} ,{\text{x}}_{2} ...{\text{x}}_{T}\) can be conditionally factorized given \({\text{x}}_{0}\) as:

$$q({\text{x}}_{1} ,...,{\text{x}}_{T} \left| {{\text{x}}_{0} } \right.) = \prod\limits_{t = 1}^{T} {q({\text{x}}_{t} \left| {{\text{x}}_{t - 1} } \right.)}$$
(1)

DDPM assumes that the transition kernel \(q({\text{x}}_{t} \left| {{\text{x}}_{t - 1} } \right.)\) progressively transforms the data distribution \(q({\text{x}}_{0} )\) into a tractable prior distribution. A typical transition kernel is the Gaussian perturbation \(q({\text{x}}_{t} \left| {{\text{x}}_{t - 1} } \right.) = N({\text{x}}_{t} ;\sqrt {1 - \beta_{t} } {\text{x}}_{t - 1} ,\beta_{t} {\text{I}})\), where \(\beta_{t} \in (0,1)\) is a hyperparameter pre-set before model training. Additionally, there are other types of transition kernels that can be applied within the same framework. However, research has shown that the Gaussian distribution can marginalize the joint distribution in \(q({\text{x}}_{1} ,...,{\text{x}}_{T} \left| {{\text{x}}_{0} } \right.) = \prod\limits_{t = 1}^{T} {q({\text{x}}_{t} \left| {{\text{x}}_{t - 1} } \right.)}\) to obtain an analytical form for \(q({\text{x}}_{t} \left| {{\text{x}}_{0} } \right.)\) with respect to \(t \in (0,1,...,T)\). Assuming \(\alpha_{t} : = 1 - \beta_{t}\),\(\overline{\alpha }_{t} : = \prod\nolimits_{s = 0}^{t} {\alpha_{s} }\) we have:

$$q({\text{x}}_{t} \left| {{\text{x}}_{0} } \right.) = N({\text{x}}_{t} ;\sqrt {\overline{\alpha }_{t} } {\text{x}}_{0} ,(\sqrt {1 - \overline{\alpha }_{t} } ){\text{I}})$$
(2)

Given \({\text{x}}_{0}\), it is easy to obtain \({\text{x}}_{t}\) by sampling a Gaussian vector \(\varepsilon \sim N(0,{\text{I}})\), which is calculated by Eq. (3).

$${\text{x}}_{t} = \sqrt {\overline{\alpha }_{t} } {\text{x}}_{0} + \sqrt {1 - \overline{\alpha }_{t} } \varepsilon$$
(3)

When \(\overline{\alpha }_{T} \approx 0\), \({\text{x}}_{T}\) is almost identical to a Gaussian distribution. Therefore, it can be calculated by Eq. (4).

$$q({\text{x}}_{T} ): = \int {q({\text{x}}_{T} \left| {{\text{x}}_{0} } \right.)} q({\text{x}}_{0} ){\text{dx}}_{0} \approx N({\text{x}}_{T} ;0,{\text{I}})$$
(4)

In essence, the forward process slowly injects noise into the data until the original data structure disappears, and no new data samples are generated. Specifically, the reverse Markov chain is parameterized by the prior distribution \(p({\text{x}}_{T} ) = N({\text{x}}_{T} ;0,{\text{I}})\) and the learnable transition kernel \(p({\text{x}}_{t - 1} \left| {{\text{x}}_{t} } \right.)\). The reverse transition kernel is represented as:

$$p({\text{x}}_{t - 1} \left| {{\text{x}}_{t} } \right.) = N({\text{x}}_{t - 1} ;\mu_{\theta } ({\text{x}}_{t} ,t),\Sigma_{\theta } ({\text{x}}_{t} ,t))$$
(5)

where \(\theta\) represents the model parameters, and the mean and variance are parameterized by the neural network model. We employ an architecture similar to U-Net, where at each step from \(t = T\) to \(t = 0\), we predict \({\text{x}}_{t - 1}\) until the denoising process concludes, generating the predicted segmentation mask. As shown in Fig. 1a, the training phase corresponds to the forward process, where the real segmentation mask \({\text{x}}_{0}\) is perturbed to obtain \({\text{x}}_{t}\). The original brain tumor image is used as a conditional image, combined with the perturbed segmentation mask at multiple scales. A denoising model (Denoising UNet) is employed to predict the segmentation mask. Specifically, the perturbed real segmentation mask \({\text{x}}_{t}\) serves as the input to the denoising network model. Simultaneously, the original brain tumor image with four modalities is encoded by the feature encoder to obtain multi-scale features. These features are combined with the encoded \({\text{x}}_{t}\) at the corresponding scale of the denoising network and used to predict the segmentation mask directly through the decoder. This process continues until the network can accurately predict the real segmentation distribution for each noise mask applied at every step \(t\).

Fig. 1
figure 1

Training and inference stages of the proposed brain tumor multi class segmentation algorithm based on diffusion model. (a) Training stage for generating predictive segmentation masks by denoising input masks, (b) The inference stage of gradually denoising from random noise to generate the final segmentation mask.

Full size image

The inference phase corresponds to the reverse process, as shown in Fig. 1b, starting from sampling random Gaussian noise and gradually denoising using the trained model until a clean predicted segmentation mask is generated.

Enhancing tumor blurred boundary recognition

In the course of our research, we observed the diverse morphological features of gliomas in the brain, alongside inherent issues of image blurring and low resolution in MRI imaging26,27,28. Among these challenges, the characteristics of the ET subregion are particularly pronounced and severe. Consequently, in the multi-class segmentation task of glioma subregions, the overall performance is compromised due to the ambiguous and challenging nature of the ET boundary, as evidenced in various research endeavors5,6,25,29.

To address this issue, we propose a unilateral net focused on ET boundary recognition, with the specific architecture illustrated in Fig. 2. Leveraging the stochastic properties of a diffusion model, this network generates a corrective mask through multiple samplings to enhance the precision of recognizing boundaries within the ET region. Through this innovative approach, we can significantly improve the multi-class segmentation accuracy of all subregions of gliomas in the brain.

Fig. 2
figure 2

Using ET boundary recognition to correct multi class segmentation results.

Full size image

In the diverse imaging modes of brain MRI, the t1 and t1ce modes have garnered significant attention due to their outstanding performance in ET visualization and the associated degree of correlation. These modes demonstrate remarkable advantages in capturing the correlation between ET features and the surrounding structures. Recognizing this, we judiciously opted to employ brain MRI images in t1 and t1ce modes as the conditioning images for training the diffusion segmentation model. This decision was rooted in our awareness of the exceptional performance of these imaging modes in ET visualization.

We employed real ET segmentation masks as the training targets for the diffusion model, allowing the model to specialize in the segmentation task specifically tailored for ET. Through multiple samplings of the diffusion model, we generated masks for ET boundary recognition. These masks were skillfully applied to refine and elevate the results of multi-class segmentation of brain tumors. This innovative approach resulted in a dual effect in the final outcomes, significantly enhancing both the overall segmentation accuracy and the precision of individual segmentations. This research methodology presents an effective strategy for improving the accuracy of glioma segmentation in the brain, with promising potential for clinical applications.

Design of combined loss function

During the training process of the diffusion segmentation model, we instruct the model to directly generate predictive segmentation masks instead of noise. We design a combined loss function to measure the closeness between the predicted results and the ground truth masks. Specifically, we integrate Weighted Cross-Entropy Loss (WCE) with Weighted Dice (WD) Loss. The design of WCE is intended to address the issue of class imbalance between segmentation targets and the background, adjusting for imbalances both among segmentation targets and between segmentation targets and the background, it can be expressed as Eq. (6).

$$L_{WCE} ({\text{X}},{\text{P}};\theta_{S} ) = - \sum\limits_{c = 1}^{C} {\sum\limits_{h = 1}^{H} {\sum\limits_{w = 1}^{W} {{\text{w}}_{c} {\text{P}}_{h,w,c} \log \hat{P}_{h,w,c} } } } \,$$
(6)

where \({\text{X,P}}\) denote the input data and the corresponding ground truth, respectively, \({\text{w}}_{c}\) denote the weight of class \(C\), \(\hat{P} = N\left( {{\text{X}},\theta_{S} } \right)\) denotes predicted segmentation probability mask, \(\theta_{S}\) denotes network parameters.

Similarly, WD is adjusted based on the proportion of the corresponding class, aiding the model during training to detect small lesions and reduce false negatives, it can be expressed as Eq. (7).

$$L_{WD} {\text{(X,P;}}\theta_{s} ) = 1 - 2\frac{{\sum\limits_{c = 1}^{C} {\pi_{c} } \sum\limits_{h = 1}^{H} {} \sum\limits_{w = 1}^{W} {P_{h,w,c} \hat{P}_{h,w,c} } }}{{\sum\limits_{c = 1}^{C} {\pi_{c} } \sum\limits_{h = 1}^{H} {} \sum\limits_{w = 1}^{W} {P_{h,w,c} + \hat{P}_{h,w,c} } }} \,$$
(7)

where \(\pi_{c}\) denotes the balance weight of class \(C\), set as \(\pi_{c} = 1/\left( {\sum\limits_{h = 1}^{H} {\sum\limits_{w = 1}^{W} {P_{h,w,c} } } } \right)^{2}\).

Finally, add the weighted cross-entropy loss and the weighted Dice loss to get a combined loss to train our model, which is calculated by Eq. (8).

$$L_{c} = L_{WCE} + L_{WD} \,$$
(8)

Experiments

Data and evaluation metrics

The Brain Tumor Segmentation Challenge BraTS2020 dataset26,27,28 is a benchmark dataset widely utilized in the field of medical image analysis, specifically for brain tumor segmentation tasks. The dataset encompasses multi-modal MRI scans acquired from various medical centers. These modalities include T1-weighted, T1-weighted with contrast enhancement, T2-weighted, and fluid-attenuated inversion recovery (FLAIR) images, and the volume size of each modality is 240⨯240⨯155 and co-aligned to the same space, interpolated to the same resolution (1 mm3 isotropic) and skull stripped. These imaging modalities collectively provide a comprehensive view of the anatomical and pathological characteristics of brain tumors.

BraTS2020 contains 369 brain glioma subjects of varying degrees of disease with highly heterogeneous sub-regions30. Each subject is associated with expert-annotated ground truth segmentation labels. These labels delineate distinct subregions of the tumors, including background as label 0, necrotic and non-enhancing tumor (NCR/NET) as label 1, peritumoral edema (ED) as label 2, and ET as label 4. The segmentation annotations serve as a reference standard for evaluating the performance of segmentation algorithms.

For clinical diagnostic purposes, performance metrics were established based on the segmentation results of the model for the following tumor sub-regions: (1) ET, (2) Tumor Core (TC) comprising NCR/NET and ET, and (3) the entire tumor (WT, which encompasses TC and ED). This research employs the Dice similarity coefficient (DICE) and the 95th percentile of the Hausdorff Distance (HD95) as evaluation metrics to assess the model’s performance. The Dice score was calculated in 3D, as it more accurately reflects the segmentation performance across the entire glioma volume, providing a better evaluation of the model’s ability to handle volumetric data.

Implementation details

The dataset was then split into a training set with 332 subjects and a testing set with 37 subjects, maintaining a ratio of 9:1. The four modalities were used as the four channels for training the multi-class segmentation diffusion model, and the images from the t1 and t1ce modes were employed as the channels for training the ET boundary recognition model.

We employed PyTorch for training our network on an RTX3090 with 24 GB of memory, utilizing the Adam optimizer with an initial learning rate of 1e-4 to optimize the network. The architecture comprises an encoder with four layers featuring 32, 64, 128, and 256 channels, respectively, along with a corresponding decoder structure. For the diffusion-based model, masks of noise corruption and images were concatenated along the feature channels, and sine positional embeddings were used to encode time. Our model contains approximately 52.6 million trainable parameters. In the DDPM, T (the number of iterations) was set to 1000, and a linear β schedule ranging from 0.0001 to 0.02 was applied. During both training and inference, default settings were used, employing 5 steps for variance resampling. The model was trained over approximately 3 days, and inference for the entire test set took around 16 h. The hyperparameters for our model are as follows: a batch size of 12, a weight decay of 1e-5, and an image size of 224 × 224. Notably, no data augmentation was applied during training.

Results and discussion

During the testing phase, we initially utilized the multi-class segmentation network to generate preliminary predictive segmentation masks for the four subregions, as shown in Fig. 3. In Fig. 3, dark brown, red, and blue represent the necrotic part of glioma NCR/NET, ET, and ED, respectively. A visual comparison in the last two columns of the Fig. 3 reveals that while the WT and TC segmentation achieved precise results, directly performing multi-class segmentation for the complexly distributed ET region, especially at the adjacent boundary of NCR/NET, fails to accurately locate and classify boundary pixels, resulting in a decreased accuracy of multi-class segmentation for glioma subregions.

Fig. 3
figure 3

Example of multi class segmentation results for brain glial tumor sub regions.

Full size image

To validate the feasibility and effectiveness of our proposed approach using ET boundary recognition for multi-class glioma segmentation, we conducted comparative experiments on the predicted number of ET boundary recognition. The numerical results are presented in Table 1. We calculated multi-class segmentation results for 1, 3, and 5 predictions, demonstrating a substantial improvement in the segmentation effectiveness for ET as the number of predictions increases. Since TC is composed of both ET and NCR, the segmentation accuracy of TC is also enhanced simultaneously. Considering the efficiency issues during inference with diffusion-based segmentation models, we ultimately adopted a strategy with 5 predictions as the final segmentation result. The DICE for subregions are as follows: WT-92.4%, TC-90.7%, ET-88.1%, and the mean-90.4%. The corresponding HD95 values are: WT-3.65, TC-4.64, ET-3.09, and the mean-3.79. It is noteworthy that, with an increase in the number of predictions, segmentation performance further improves.

Table 1 Ablation research on number of ET boundary recognition predictions.
Full size table

The results of ET boundary recognition are depicted in Fig. 4, showcasing two selected predictions from the recognition results. After conducting 5 predictions for ET subregions in the test set, the boundary distribution variance maps and the final mean segmentation results are presented in the last two columns of Fig. 4. Our method effectively improves the segmentation accuracy for the challenging-to-identify ET boundaries, providing a valuable reference for clinicians and experts who utilize segmented images. This is crucial as it highlights the complex and difficult-to-distinguish distribution of ET boundary masks.

Fig. 4
figure 4

Subregions of brain gliomas-ET boundary recognition results.

Full size image

Finally, we compared our method with advanced U-Net-based and diffusion model-based algorithms, including numerical results presented in Table 2. Our method achieved optimal DICE for each subregion, particularly improving the segmentation effectiveness for ET by 9.2% compared to the second-best result. While our HD95 metric for ET reached the optimum, the average HD95 is slightly lower than the second-best algorithm at 3.97. The potential reason for this could be attributed to the fact that the second-best algorithm, Diff-UNet, directly employs a 3D model and data for multi-class segmentation. It can extract continuous 3D features during feature recognition, providing better resolution of detailed features compared to 2D methods. However, it comes with the drawbacks of a large model size, low processing efficiency, and high equipment requirements, making it less suitable for clinical implementation. In contrast, our method achieves precise multi-class segmentation effects while maintaining a simple and efficient model design.

Table 2 Quantitative comparison on BraTS2020 dataset.
Full size table

Conclusion

In this research, we introduce an approach to enhance the accuracy of multi-class segmentation for brain tumors using ET boundary recognition. By training a multi-class segmentation model alongside a dedicated unilateral network for ET boundary recognition, we aim to improve the segmentation accuracy of complex and challenging ET regions. This method is specifically designed to achieve efficient and accurate segmentation results in the multi-class segmentation task for glioma subregions. Notably, our approach does not require high-end equipment, making it a practical support for clinical diagnosis and treatment. Our methodology involves the integration of a multi-class segmentation model and a specialized network for ET boundary recognition. Through this synergy, we enhance the precision of segmenting complex and challenging ET regions within glioma subregions. The seamless integration of these components enables the achievement of both efficiency and accuracy in the segmentation task. Moreover, our method provides valuable insights into the localization of ET boundaries with fuzzy edges. This information serves as a crucial reference point for clinicians, enhancing the interpretability and reliability of segmentation results in a clinical context. The ability to offer interpretable and reliable segmentation results is essential for medical professionals in making informed decisions about patient care.