Clearance distribution and contact characteristics of misaligned gear couplings considering hob feed path

Abstract

Gear couplings are usually machined using hob and slotting cutter in a predetermined circular path. The tool feed path determines tooth profile. This article designs a new feed path. A new mathematical model of tooth surface is constructed based on path and tooth profile parameters. Calculation method for minimum normal design clearance is proposed, and furthermore, theoretical model for the clearance under misalignment conditions is developed. The calculation of the tooth surface coordinates and minimum clearance in the circumferential direction, the distribution of the minimum clearance in the circumferential is studied under the new path. The clearance of the tooth surface and circumferential direction are obtained, and the contact characteristics of teeth in the circumferential direction are analyzed. The results show that the new path can reduce the dependence of misalignment angle on clearance and tooth width compared to conventional path. A high load-carrying contact with full involute is more easily achieved on the tooth surface, and the load-carrying performance are more evenly distributed across the teeth.

Introduction

Due to their high power density and misalignment compensation capabilities, gear couplings are widely applied in the transmission systems of key modern equipment, such as rolling mills and subway systems¹. However, because of the uneven clearance distribution on the tooth surfaces of crowned teeth, meshing under misalignment conditions results in only partial contact, causing a sharp decline in contact performance as the misalignment angle increases^2,3. This reduction in load-carrying capacity particularly constrains the application range of crowned gear couplings.

In order to improve the performance of gear couplings, after more than a hundred years of development, scientists have made many contributions in the areas of lubrication and wear^4,5, vibration⁶ and optimization of geometrical parameters^7,8. The wear performance directly determines the usability of the product⁹, and multi-objective optimization design can obtain the best geometric parameters under mechanical properties^10,11. These methods are widely used to improve the usability of the product. However, existing research has yet to effectively address the rapid decline in load-carrying capacity of crowned gears under misalignment conditions. In recent years, research into the tooth profile morphology of gear couplings has been gradually developed. Fumihiro¹² studied tooth profile shapes and concluded that good tooth contact could be obtained when the tooth shape was between involute and trapezoidal. Guan¹³ carried out a series of studies on the forming methods for crowned teeth, proposing three different spreading principles and investigating the geometry and contact characteristics, giving three methods of evaluating tooth surfaces. Iñurritegui¹⁴ studied highly convex tooth surfaces with high misalignment angles of the Spherical gear couplings. Guan¹⁵ studied three-arc gear couplings and analyzed the effect of the three arc segments on the geometric parameters and mechanical properties. The feed path of the hob directly determines the drumming distribution of the crowned tooth, which in turn affects its geometrical characteristics and mechanical properties. However, there is a lack of research on path and geometric characteristics of crowned tooth surface in the past. To improve the meshing performance of crowned gears under misalignment conditions, this study optimizes the Hobbing method¹⁶ by analyzing key factors affecting tooth surface geometry¹⁷, including cutter profile and feed path. A novel elliptical-arc feed path is proposed to reconstruct the tooth surface profile. Additionally, a method for calculating the tooth surface clearance and analyzing contact characteristics is presented, with a focus on how path parameters influence surface contact performance.

The geometric design of the gear couplings under the elliptical-arc feed path is mainly focused on the clearance and tooth width. The clearance is one of the most important design parameters, too large clearance will affect the operational stability and destroy the joint bearing mechanism of the circumferential tooth pairs, too small clearance cannot meet the compensation of the rated misalignment angle, and may even produce extrusion plastic damage. Conventional design methods such as the gear handbook¹⁶ construct a relationship between clearance as a function of inclination angle based on geometric parameters such as displacement circle radius and malalignment angle, and calculate the permissible clearance at the maximum offset angle. In the 1960s, Renzo⁷ developed a calculation model of clearance for the geometrical characteristics of equiaxial misalignment of gear couplings. Also, the offset motion of the tooth meshing is studied and the distribution of the clearance is investigated^18,19. However, the geometrical calculation method does not accurately represent the surface under the combined effect of involute and feed path, especially in the case of new feed path that are not circular arcs, which can easily lead to greater design errors. By establishing the coordinate system and transformation matrix of the tooth surface, the position of the contact point for the minimum clearance is determined, and the coordinate transformation is used to calculate the clearance, which can significantly improve the calculation accuracy^20,21. Alfares²² and Wei²³ obtained a model for the calculation of distance between two nodes by establishing a global coordinate system for teeth and determining the coordinates of nodes on outer tooth and inner tooth profile of sleeve with respect to the global frame. Kelemen²⁴ used the profile shift method and the two-parameter envelope method to construct a mathematical model of the crowned tooth and demonstrated that the modelling accuracy of both models was generally consistent. However, the above mathematical models are generated based on circular path, and when the feed path are changed, the conventional modelling method cannot be used for the new feed path of crowned tooth.

Gear contact analysis often uses finite element methods and semi-analytical methods^25,26, but it is difficult to accurately obtain the contact characteristics of crowned tooth due to the complex contact surfaces. At present, the theoretical calculation method is usually based on the Hertz theory, without considering the inclination angle between the shafts, and the end line of the crowned tooth in the pitch circle tangent is equivalent to circular arc, and along the direction of the tooth height is equivalent to the cylindrical and planar contact, to carry out the calculation of the contact stress¹⁶. Kelemen²⁷ used the tool surface curvature characteristics and motion parameters to determine the curvature characteristics of the enveloped tooth surface to obtain the exact position and curvature of the contact point and calculated the tooth contact stresses using Hertz theory. The above research has improved the calculation accuracy of tooth contact, but due to the complexity of the crowned tooth surface, the tooth surface stiffness is a time-varying parameter. At present, it is difficult to accurately provide the time-varying characteristics of tooth contact load and area during tooth meshing. This paper establishes the relationship between tooth clearance and contact to accurately reflect the meshing characteristics of crowned teeth.

Therefore, this paper studies the influence of feed path on the geometric parameters such as clearance, tooth width and contact characteristics of gear couplings, and provides guidance for the development of high-performance gear couplings. The research objectives of this paper are:

• (1) Propose a new tool feed path, construct a mathematical model of the crowned tooth and calculate the minimum normal design clearance under the new feed path.

• (2) Propose high-precision calculation method for clearance, establish the mapping relationship between tooth surface clearance and contact, analysis the contact performance under new feed path.

• (3) Develop mathematical model of the tooth pair clearance of gear couplings at any position in the circumferential direction. Analyze the remaining clearance and contact characteristics of each tooth.

Analytical formulae

The analytical formulas described include a mathematical model of crowned tooth surface in the new feed path and the calculation of tooth face clearance and clearance in the circumferential direction. And, by constructing the coordinates of tooth surface under new feed path and proposing a high-precision calculation method for the clearance based on the coordinate transformation of angular misalignment.

New feed path

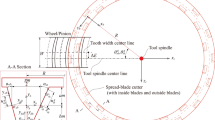
In this paper, a new hob feed path is proposed. Figure 1a shows schematic diagram of Hobbing machining, where Path A is a conventional feed path with the tool moving along a circular arc of radius R. Path B is the new feed path, where the tool moves along an elliptical curve consisting of the path parameters a and b. Figure 1b shows crowned tooth surface made by sweeping an involute along path B.

Fig. 1

Diagram of the formation of crowned tooth: (a) Hob feed path. (b) Forming mechanism.

As shown in Fig. 1, define the coordinates of the point M with respect to the O_hub coordinate system as (x, y, z). The tool moves along path B to z = 0 where y reaches its maximum value.

$$y_{\max } = r_{0} + r_{1}$$

(1)

where r₀ is the radius of pitch cylinder for the hob. r₁ is the radius of pitch circle for the workpiece.

The distance MO_hob between the point M and the origin of the feed path is:

$$\left\{ \begin{gathered} MO_{hobA} = R\quad \left( {\text{Path A}} \right) \hfill \\ MO_{hobB} = R_{B} = \sqrt {\frac{{a_{{}}^{2} b_{{}}^{2} }}{{\left( {a\cos \beta } \right)^{2} + \left( {b\sin \beta } \right)^{2} }}} \quad \left( {\text{Path B}} \right) \hfill \\ \end{gathered} \right.$$

(2)

where R is the radius of path A. β is the angle between the MO_hob and y_hob-axis.

Mathematical model of crowned tooth surface

As shown in Fig. 2, define the equation of the involute tooth profile at z₁ = 0²²:

$$\left\{ \begin{gathered} x_{1} = r_{y1} \sin \theta_{1} \hfill \\ y_{1} = r_{y1} \cos \theta_{1} \hfill \\ z_{1} = 0 \hfill \\ \end{gathered} \right.$$

(3)

Fig. 2

The coordinate system of crowned tooth: (a) The profile with z₁ = 0. (b) The profile with x₁ = 0.

As shown in Fig. 2a, Calculate the angle θ₁ between point A to O_hub and the y₁ axis:

$$\theta_{1} = \frac{s}{{2r_{1} }} + inv\alpha - inv\alpha_{y1}$$

(4)

where s is the tooth thickness along the pitch circle. α is the standard pressure angle. α_y1 is the pressure angle at radius r_y1.

Calculate tooth thickness along the pitch circle and pressure angle α_y1 at any position on the tooth profile:

$$\left\{ \begin{gathered} s = s_{0} - 2\left[ {\left( {R_{B} - r_{0} } \right) - \sqrt {\left( {R_{B}^{{}} - r_{0} } \right)^{2} - z_{1}^{2} } } \right]\tan \alpha \hfill \\ \alpha_{y1} = a\cos \frac{{r_{b1} }}{{r_{y1} }} \hfill \\ \end{gathered} \right.$$

(5)

where r_b1 denotes the radius of base circle. s₀ is the tooth thickness of the dividing circle.

Any point A (x_A, y_A, z_A) on the involute tooth profile at z₁ = 0 rotates along an elliptical path with semi-long axis a and semi-short axis b. The ellipse at any point has independent long and short semi-axes and is solved for by the following equation based on the fundamental properties of the ellipse:

$$\left\{ \begin{gathered} 1 = \frac{{z_{1}^{2} }}{{R_{11}^{2} }} + \frac{{y_{1}^{2} }}{{R_{21}^{2} }} \hfill \\ R_{11}^{{}} = a - t \hfill \\ R_{21} = b - t \hfill \\ \end{gathered} \right.$$

(6)

where R₁₁, R₂₁ are the distances from the intersection of ellipse at any point with the y_hob and z_hob axes to O_hob. t is an auxiliary calculation parameter that varies with tooth profile coordinates and path parameters.

Suppose that any point A₁(x_A1, y_A1, z_A1) is rotated along path B around the x₁ axis by an angle β to point A₂, with the x-axis coordinates unchanged. Calculate the distance between point A₁ and A₂ to the O_hob:

$$\left\{ \begin{gathered} R_{BA1} = \sqrt {\frac{{R_{11}^{2} R_{21}^{2} }}{{\left( {R_{11} \cos \nu } \right)^{2} + \left( {R_{21} \sin \nu } \right)^{2} }}} \hfill \\ R_{BA2} = \sqrt {\frac{{R_{11}^{2} R_{21}^{2} }}{{\left( {R_{11} \cos (\nu + \beta )} \right)^{2} + \left( {R_{21} \sin (\nu + \beta )} \right)^{2} }}} \hfill \\ \end{gathered} \right.$$

(7)

where ν is the angle between the A₁O_hob and the z_A-axis.

Obtain the coordinates of point A₂:

$$\left\{ \begin{gathered} x_{A2} = x_{A1} \hfill \\ y_{A2} = y_{A1} \frac{{R_{BA2} }}{{R_{BA1} }}\cos \beta + z_{A1} \frac{{R_{BA2} }}{{R_{BA1} }}\sin \beta \hfill \\ z_{A2} = - x_{A1} \frac{{R_{BA2} }}{{R_{BA1} }}\sin \beta + z_{A1} \frac{{R_{BA2} }}{{R_{BA1} }}\cos \beta \hfill \\ \end{gathered} \right.$$

(8)

The involute profile model is obtained by the above equation. According to the method of forming the crowned tooth, the profile model is rotated along the feed path to obtain the crowned tooth. Determine the mathematical model for crowned tooth surface relative to the tool feed path origin O_hob as:

$$\left[ \begin{gathered} x_{1h} \hfill \\ y_{1h} \hfill \\ z_{1h} \hfill \\ \end{gathered} \right] = M\left( \beta \right)\left[ \begin{gathered} x_{1} \\ y_{1} + (b - 0.5mz) \\ z_{1} \\ \end{gathered} \right]$$

(9)

where (x_h, y_h, z_h) are the coordinates of a point on a tooth surface in the new feed path. b is the tooth width. m is the module. z is the number of teeth.

$$M\left( \beta \right) = \left( {\begin{array}{*{20}c} 1 & {\quad 0} & {\quad 0} \\ 0 & {\quad Q\cos \left( \beta \right)} & {\quad Q\sin \left( \beta \right)} \\ 0 & {\quad - Q\sin \left( \beta \right)} & {\quad Q\cos \left( \beta \right)} \\ \end{array} } \right)$$

(10)

is the rotational matrix for a position angle β.

where Q is used to simplify the operation, Q = R_BA2/R_BA1.

The above analysis yields a mathematical model of crowned tooth surface with respect to the hub center coordinate system:

$$\left[ \begin{gathered} x_{h} \hfill \\ y_{h} \hfill \\ z_{h} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} x_{1h} \\ y_{1h} \\ z_{1h} \\ \end{gathered} \right] - \left[ \begin{gathered} 0 \\ b - 0.5mz \\ 0 \\ \end{gathered} \right]$$

(11)

Minimum normal clearance

The clearance directly affects the tooth meshing, especially for crowned tooth which affects meshing and misalignment angle^28,29. It has been shown that most of the research in the literature is focused on the minimum design clearance under the circular path. The gear design manual gives the calculation of the minimum normal clearance J_nmin¹⁶.

$$J_{n\min } = 2R\phi_{t} \left( {\frac{{\tan^{2} \eta }}{\cos \alpha } + \sqrt {\cos^{2} \alpha - \tan^{2} \eta } - \cos \alpha } \right)$$

(12)

where R is the displacement circle radius. ϕ_t is the curvature coefficient, the gear design manual provides reference values. η is the misalignment angle.

However, the method provided in the gear design handbook is only used to calculate gear couplings with conventional path and does not provide a reasonable clearance for the new feed path. In order to calculate the clearance under the new feed path, spatial coordinates and transformation matrices are used to analyse the change in tooth surface coordinates and the position of the contact point based on the characteristics of the involute tooth profile. Assume that the hub coordinate system is (x_h, y_h, z_h), the global coordinate system is (X_h, Y_h, Z_h). The transformation relationship between the hub coordinate system and the global coordinate system was described by:

$$\left[ \begin{gathered} X_{h} \hfill \\ Y_{h} \hfill \\ Z_{h} \hfill \\ \end{gathered} \right] = R\left( \eta \right)\left[ \begin{gathered} x_{h} \hfill \\ y_{h} \hfill \\ z_{h} \hfill \\ \end{gathered} \right]$$

(13)

R(η) is a rotation matrix with misalignment angle η:

$$R\left( \eta \right) = \left( {\begin{array}{*{20}c} {\cos \left( \eta \right)} & {\quad 0} & {\quad \sin \left( \eta \right)} \\ 0 & {\quad 1} & {\quad 0} \\ { - \sin \left( \eta \right)} & {\quad 0} & {\quad \cos \left( \eta \right)} \\ \end{array} } \right)$$

(14)

The contact range on the y₁-axis is determined by the radii of the crest of the inner and outer teeth:

$$\left\{ \begin{gathered} Y_{h} \le rd_{a1} = \frac{{mz + 2h_{a1} }}{2} \hfill \\ Y_{h} \ge r_{f1} = \frac{{mz - 2h_{f1} }}{2} \hfill \\ \end{gathered} \right.$$

(15)

where h_a1 is the addendum. h_f1 is the dedendum.

As shown in Fig. 3, three sections are selected in the direction of tooth width, with section A-A at the centre, A-C at the edge and A-B in the middle of A-A and A-C. The normal clearance on the tooth profile at A-A is equal, with the maximum circumferential clearance at crest and decreasing circumferential clearance along the tooth profile to the root. Due to the drumming, the clearance at the A-B gradually decreases from the crest to the tooth root. The maximum circumferential clearance occurs at the crest in section A-C, and the normal and circumferential clearance at the crest is much greater than at the tooth root. According to the clearance distribution along the tooth profile on the different sections, the tooth profile of the section A-A is in full contact due to the equal normal clearance, and the tooth profile of section A-B and section A-C is not completely contacted. Section A-C shows the contact of maximum misalignment angle, with the tooth profile contact position concentrated near the crest of inner tooth. From the above analysis it is easy to see that first contact point in misalignment conditions is at the crest of inner tooth.

Fig. 3

Clearance distribution on the tooth profile.

Since the first contact with the crest of inner tooth, the tooth surface coordinates under misalignment conditions are calculated according to Eq. (14), the coordinates with vertical coordinate r_f1 are obtained, the maximum coordinate X_e of each node on the x-axis is analyzed and the circumferential clearance at the crest of inner tooth is calculated as follows:

$$e_{cr} = 2\left( {X_{e} - x_{h1} } \right)$$

(16)

where x_h1 is the maximum coordinate of the involute on the x₁-axis.

As shown in Fig. 4, A-A is an involute standard tooth profile with a minimum pressure angle at the root and a maximum pressure angle at the crest. Point B is the contact point of the tooth profile on the indexing circle, where the pressure angle is the standard pressure angle. The pressure angle at any position on the tooth profile is not the same. Assuming that point N is any point on the involute tooth profile, calculate the pressure angle at point N as:

$$\alpha_{N} = \arccos \frac{{x_{N} }}{{\sqrt {x_{N}^{2} + y_{N}^{2} } }} - \arcsin \frac{{r_{2} }}{{\sqrt {x_{N}^{2} + y_{N}^{2} } }}$$

(17)

where x_N and y_N are the coordinates of the point N on the tooth surface on the x₁-axis. r₂ is the radius of the base circle.

Fig. 4

Pressure angle on involute tooth profile.

Calculate the pressure angle at the crest of inner tooth:

$$\alpha_{h1} = \arccos \frac{{x_{h1} }}{{\sqrt {x_{h1}^{2} + r_{f1}^{2} } }} - \arcsin \frac{{r_{2} }}{{\sqrt {x_{h1}^{2} + r_{f1}^{2} } }}$$

(18)

As the normal clearance on involute tooth profile is the same, calculate minimum normal clearance:

$$e = e_{cr} \cos \alpha_{h1}$$

(19)

It is worth noting that the denser the nodes on the tooth surface, the more accurate the calculation of the minimum design clearance.

Contact width

The contact point of the gear couplings moves from the center of the tooth to both ends with the misalignment angle. The design of the tooth width requires consideration of the contact width, the contact width being the key to determining the size of the tooth width. The tooth width design methods commonly are mainly based on empirical formulas provided by gear handbook¹⁶.

$$b = \left( {0.1 {-} 0.2} \right)mz$$

(20)

However, this design method does not provide greater accuracy, in particular, lacks scientific guidance for the design of gear couplings in the new feed path. The contact point under new feed path is calculated by constructing geometry and rotation matrix under misalignment.

$$b = 2z_{h}$$

(21)

In recent years, a number of new numerical methods have been applied to the calculation of complex contacts, including the finite element method³⁰ and the boundary element method³¹, which have greatly improved the accuracy of the calculation of crowned tooth. Among them, the finite element method is widely used in the design calculation of gear couplings, especially the geometric design parameters of tooth are checked with very high accuracy. Guan^32,33 all used the FEM to carry out numerical simulation analysis of the gear couplings to verify the accuracy of the theoretical calculation results and carry out optimized design. Therefore, the new crowned tooth will be analyzed using the FEM in subsequent studies and validated against the model presented in this paper.

Clearance distribution of tooth surface

The clearance is not the same at any position on the tooth surface. As shown in Fig. 5a, n_i and n_k nodes are set in the tooth height direction and tooth width direction respectively. The larger the value of n_i and n_k, the higher the density of nodes and the higher the accuracy of the mathematical model.

Fig. 5

Division of nodes of crowned tooth: (a) Tooth surface nodes. (b) Tooth contact.

As shown in Fig. 5b, the crowned tooth and inner tooth are the first to make point contact. As the load increases, the tooth surface undergoes elastic or elastic–plastic deformation and the clearance in the area adjacent to the contact point gradually decreases to 0 mm, and then contact. Therefore, the clearance distribution of the tooth surface provides a visual representation of the load-carrying performance. The tooth surface shape varies with the hob feed path, so the contact characteristics under the new feed path are analyzed by clearance distribution and comparing it with the conventional path.

Based on Eq. (11), the tooth surface coordinates of the crowned tooth are obtained when the misalignment angle is 0°:

$$x_{ik} = \left( {\begin{array}{*{20}c} {x_{11} } & \ldots & {x_{1k} } \\ \vdots & \ddots & \vdots \\ {x_{i1} } & \cdots & {x_{ik} } \\ \end{array} } \right),\;\;y_{ik} = \left( {\begin{array}{*{20}c} {y_{11} } & \ldots & {y_{1k} } \\ \vdots & \ddots & \vdots \\ {y_{i1} } & \cdots & {y_{ik} } \\ \end{array} } \right),\;\;z_{ik} = \left( {\begin{array}{*{20}c} {z_{11} } & \ldots & {z_{1k} } \\ \vdots & \ddots & \vdots \\ {z_{i1} } & \cdots & {z_{ik} } \\ \end{array} } \right)$$

(22)

To simulate the actual misalignment conditions, the crowned tooth is rotated along the y_hob-axis at an angle of η, with the y-axis coordinates remaining constant before and after the rotation. Based on Eq. (13), the tooth surface coordinates after rotation are obtained as follows:

$$X_{ik} = \left( {\begin{array}{*{20}c} {X_{11} } & \ldots & {X_{1k} } \\ \vdots & \ddots & \vdots \\ {X_{i1} } & \cdots & {X_{ik} } \\ \end{array} } \right),\;\;Y_{ik} = y_{ik} ,\;\;Z_{ik} = \left( {\begin{array}{*{20}c} {Z_{11} } & \ldots & {Z_{1k} } \\ \vdots & \ddots & \vdots \\ {Z_{i1} } & \cdots & {Z_{ik} } \\ \end{array} } \right)$$

(23)

Calculate the circumferential clearance e_ci at point i on tooth profile L₀ at z_ik = 0 based on the minimum normal design clearance e:

$$e_{ci} = \frac{e}{{\cos a_{i} }}$$

(24)

where α_i is the pressure angle at the ith point on the tooth profile L₀.

The x-coordinate of any point on the inner tooth profile in tooth width direction remains unchanged. Based on the circumferential clearance e_ci and x-coordinate of each point on the tooth profile L₀, the coordinates of the nodes on the inner tooth profile are calculated as follows:

$$x_{nik} = \left( {\begin{array}{*{20}c} {x_{11} + e_{c1} } & \ldots & {x_{11} + e_{c1} } \\ \vdots & \ddots & \vdots \\ {x_{i1} + e_{ci} } & \cdots & {x_{i1} + e_{ci} } \\ \end{array} } \right),y_{nik} = \left( {\begin{array}{*{20}c} {y_{{1\frac{k}{2}}} } & \ldots & {y_{{1\frac{k}{2}}} } \\ \vdots & \ddots & \vdots \\ {y_{{i\frac{k}{2}}} } & \cdots & {y_{{i\frac{k}{2}}} } \\ \end{array} } \right),z_{nik} = z_{ik}$$

(25)

Assume that the coordinate of a node of crowned tooth surface after rotation is (X_ab, Y_ab, Z_ab), and calculate the node coordinate (x_nab, y_nab, z_nab) of the inner tooth profile when y_nab is equal to Y_ab. Calculate the circumferential clearance of this node:

$$e_{cab} = x_{nab} - X_{ab}$$

(26)

The calculation to obtain the circumferential clearance at any point on the tooth surface is as follows:

$$e_{cik} = x_{nik} - X_{ik}$$

(27)

Clearance of circumferential teeth

Tooth surface coordinates (x_ik, y_ik, z_ik) and (x_nik, y_nik, z_nik) of crowned tooth C₁ and inter tooth T₁ with an misalignment angle of 0° obtained according to “Clearance distribution of tooth surface”. The coordinates of tooth pairs in the circumferential direction of the gear couplings can be obtained from the coordinate of teeth C₁ and T₁ centered at the O_hub and rotated at an angle ζ along the z_hob-axis.

$$\left\{ \begin{gathered} x_{tik} = x_{ik} \cos \zeta - y_{ik} \sin \zeta \hfill \\ y_{tik} = x_{ik} \sin \zeta + y_{ik} \cos \zeta \hfill \\ z_{tik} = z_{ik} \hfill \\ \end{gathered} \right.$$

(28)

$$\left\{ \begin{gathered} x_{tnik} = x_{nik} \cos \zeta - y_{nik} \sin \zeta \hfill \\ y_{tnik} = x_{nik} \sin \zeta + y_{nik} \cos \zeta \hfill \\ z_{tnik} = z_{nik} \hfill \\ \end{gathered} \right.$$

(29)

In this study the sleeve is set fixed and the hub rotates. Therefore, based on Eq. (13) the coordinates of the tooth surface in the circumferential direction after the rotation angle η along the y_hob-axis are calculated as:

$$\left[ \begin{gathered} X_{tik} \hfill \\ Y_{tik} \hfill \\ Z_{tik} \hfill \\ \end{gathered} \right] = R\left( \eta \right)\left[ \begin{gathered} x_{tik} \hfill \\ y_{tik} \hfill \\ z_{tik} \hfill \\ \end{gathered} \right],\;\;\left[ \begin{gathered} X_{tnik} \hfill \\ Y_{tnik} \hfill \\ Z_{tnik} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} x_{tnik} \hfill \\ y_{tnik} \hfill \\ z_{tnik} \hfill \\ \end{gathered} \right]$$

(30)

The minimum normal design clearance e is obtained through the tooth pair on the y_hob-axis. From Fig. 5, it can be seen that the clearance under actual misaligned contact is the circumferential clearance, therefore, the tooth pairs in the circumferential direction should be calculated parallel to the x_hob-axis. According to the analysis in “Minimum normal clearance”, the contact point is located at the crest of inner tooth, and contact between the crowned tooth and the inner tooth only occurs at the tooth surface on the load side at any angle in the circumferential direction. Assume that the coordinate of the crest of inter tooth at any angle in the circumferential direction are C (X_c, Y_c, Z_cnik), to obtain the coordinate of the point on the crowned tooth surface at y_cik = Y_c as (x_cik, y_c, z_cik). Calculate the clearance at any angle in the circumferential direction e_c:

$$e_{c} = \min \left( {x_{cik} - X_{c} } \right)$$

(31)

Validation model

The study in this paper is based on gear couplings with a module of 5 mm, a tooth number of 52 and a pressure angle of 20°. The key parameters a and b of new feed path are introduced for the study. The study was carried out on the basis of a reference conventional gear couplings, which was chosen as a basic comparison case for the scope of this research. The range of values selected together with the reference value were determined in regards to the following considerations and are shown in Table 1:

Table 1 Parameter table for gear couplings.

• Tooth Number, z. Module, m. Reference value: z = 52, m = 5 mm.

• Pressure angle, α. Reference value: 20°, most used in gear couplings for heavy-duty applications³⁴.

Range: 20–37.5°. The range of pressure angles is taken from the standard ISO 4156³⁴.

• Misalignment angle, η. Reference value: 1.5°, a higher misalignment angle will enable a bigger clearance.

The common misalignment angle standard for heavy machinery such as rolling mills is 0–1.5°³⁴.

• Path parameters, a and b. Reference value: 0.9mz.

The path parameters a and b were proposed in this study and are not currently available for reference. Based on the conventional path parameter R setting.

Range: 0.4–1.5 mz. There is no relevant reference, and the design range is given by initial values.

The geometry of the crowned tooth is generated from the mathematical model described in “Analytical formulae” and the accuracy of the mathematical model is verified by means of a finite element model and a gear design manual. Here, geometries were generated with the corresponding parameters:

• Constant parameters: m = 5 mm, z = 52, α = 20°, η = 1.5°, b = 240 mm. Variable parameters: a.

Based on the above parameters the mathematical model of the crowned tooth is constructed, and based on the calculation method in “Contact width”, minimum tooth width with misalignment angle of 1.5° is obtained. The accuracy of the minimum tooth width determines the design accuracy of clearance. The minimum tooth width under the new feed path is shown in Fig. 6, where 240–240 are the conventional path. It is not difficult to find that the use of empirical Eq. (20) cannot meet the new feed path under the design of the gear couplings, the accuracy of the calculation with the path parameters decreases or increases less and less. When the path parameter a is taken as 100 mm, the result of the empirical formula is much larger than the finite element result, and the minimum value of the empirical formula exceeds the finite element by 68.0%, the error between the algorithm proposed in this study and the finite element is 3.5%. When the parameter a is 160 and 200 mm, the results of finite element and this study are between empirical formulas.

Fig. 6

Contact width.

As the path parameter a takes value greater than 240 mm, the result of the empirical formula is gradually smaller than that of the finite element result. When the path parameter a is taken as 280, 320, 380 mm, the result of the empirical formula is much smaller than the finite element result, and the maximum value of the empirical formula is 29.2%, 46.0%, 57.2% lower than that of the finite element method. Therefore, as the path parameters a and b become larger or smaller, the empirical formulae are no longer able to carry out the design at all.

The finite element model is able to visualize the contact of crowned tooth and the accuracy of contact point improves with mesh density. The calculation method of the contact width proposed in this study has a small error with the results of the finite element method, which verifies that the theoretical model of the contact point of new feed path proposed is highly accurate and can provide support for the study of geometric parameters and contact characteristics under the new feed path.

Influence of path parameters on the minimum design clearance

The minimum design clearance referred to in the design of gear couplings refers to the normal clearance at the standard pressure angle, which determines the number of contact teeth and load-carrying capacity. Based on the clearance calculation method proposed in this study, the effect of different misalignment angles, modulus and pressure angles on the clearance is investigated for the new path parameters.

Here, geometries were generated with the corresponding parameters:

• Constant parameters: m = 5, z = 52, α = 20°, η = 1.5°, R = 240 mm. Variable parameters: a, b.

The path parameters directly change the geometrical characteristics of the crowned tooth surface and therefore directly influence the minimum design clearance. As shown in Fig. 7, the contour lines show the distribution of clearances where the a = b. The red points are the clearances under the conventional path. The dashed line represents the range covered by the maximum and minimum design clearance. Other contour lines represent the minimum design clearance under each path. The conventional path is too small or too large, which will reduce the load-carrying capacity of gear couplings. And, the conventional path parameter is closely related to the clearance, and the clearance increases with the increase of conventional path parameter. Excessive clearance will affect the operation stability of gear couplings.

Fig. 7

Law of path parameters and minimum normal clearance.

Analyzing the contours of Fig. 7, the minimum design clearance increases with increasing path parameter a and decreases with increasing path parameter b. The top left corner shows the minimum clearance design area and the bottom right corner shows the maximum clearance design area. Analysis of the contour distribution and the clearance of the conventional path shows that for the same clearance, the conventional path correspond to only one set of design parameter, while the new feed path have an unlimited number of semi-major and semi-minor axis. For example, when the conventional path parameter is 240 mm, the minimum design clearance is 1.56336 mm, and the value of the contour line marked 240–240 in the diagram is 1.56336 mm, on which the corresponding horizontal and vertical coordinates can be selected according to the needs of loaded etc. At 240 mm for parameter a, the clearance becomes smaller and smaller with increasing b. In theory, when b is taken to infinity, the clearance is infinitely close to 0 mm.

The histogram in Fig. 8a visualizes the variation of the clearance from the conventional path for path parameter a at misalignment angle of 1.5°. When a is taken to be smaller than conventional path parameter, the clearance is gradually reduced, and when a is taken to be 100 mm, the clearance is reduced by 85.36% compared to the conventional path. The clearance gradually increases when a is greater than conventional path parameter, and when a is taken to be 380 mm, the clearance increases by 114.64% compared to the conventional path. The histogram in Fig. 8b also shows the change in clearance for path parameter b compared to conventional path. The clearance decreases as the path parameter b increases, with 109.96% increase in clearance compared to the conventional path for path parameter b of 100 mm. With path parameter b of 380 mm, the clearance is reduced by 32.94% compared to the conventional path. The path parameters a and b are taken in equal proportions above and below 240 mm and the increase in clearance is higher than the decrease. For example, for values of b ranging from 240 to 280 mm and 200 mm, the clearance increases and decreases by 17.04% and 11.43% respectively, with the increase being 1.49 times greater than the decrease. At the same time, a and b do not affect clearance to the same extent, with a and b taking values from 240 to 100 mm and 380 mm reducing the clearance by 85.36% and 32.94%. Under the same conditions, the reduction in clearance under the action of a is 2.59 times greater than that of b. Of course, reducing a or increasing b will reduce minimum design clearance. Therefore, the new feed path is capable of achieving the small clearance required for large misalignment angle.

Fig. 8

Influence of path parameters on the minimum design clearance: (a) Path parameter a. (b) Path parameter b.

Circumferential clearance distribution of tooth surface

The clearance at any position on the tooth surface is not the same under misalignment conditions. Thus, point contact occurs first at locations with small clearance. As the tooth surface undergoes elastic or elastic–plastic deformation under load, it continues to expand into surface contact. Therefore, by analyzing the clearance distribution of the tooth surface, the contact characteristics of teeth can be obtained.

According to the above research ideas, the contact characteristics are studied through the clearance distribution of tooth surface, and the mechanical properties under the new feed path are evaluated.

The distribution of circumferential clearance is shown in Fig. 9, with the horizontal coordinate being the half-width of the crowned tooth and the vertical coordinate being the area from the crest of the inner tooth to crowned tooth. The circumferential clearance on the tooth surface increases gradually in the direction of the tooth height of the crowned tooth. The clearance increases gradually in the direction of tooth width from the midpoint to the ends. The maximum circumferential clearance is located at crest on the end and the minimum circumferential clearance is located at the center of crowned tooth near the tooth root. The contact area range is covered by the circumferential clearance contour in Fig. 9.

Fig. 9

Clearance distribution of tooth surface.

When z is not equal to 0, the vertical tooth profiles along the tooth height direction are not involute, the yellow line in the Fig. 9 are the involutes on the crowned tooth surface, the red line are the involutes on the inner tooth surface. It is easy to see that the angle of the involutes between the crowned and inner teeth on the surface exists, and the angle increases gradually from the middle of the tooth width to both ends from 0°. When the angle is 0°, the involutes of the inner tooth and crowned tooth are in full contact and the gear couplings has the strongest load-carrying capacity. However, when the clamping angle is greater than 0°, the contact between the inner and crowned teeth does not achieve involute contact and the load-carrying capacity is significantly reduced. And the larger the angle, the worse the contact and the weaker the load-carrying capacity, which is one of the important reasons for limiting the misalignment compensation capacity of gear couplings.

As shown in Fig. 10a, the theoretical calculation results of the tooth surface clearance and finite element contact results under the misalignment angle of 0°, 0.5°, 1.0° and 1.5°. According to theoretical calculations, contact first occurs at the position with the smallest clearance, and as the tooth surface undergoes elastic deformation, the contact area expands along the contour distribution, the theoretical calculation is consistent with the distribution of contact area of finite element, which proves the feasibility of analyzing contact characteristics through clearance.

Fig. 10

Analysis of contact characteristics of tooth surface: (a) Finite element simulation. (b) Misalignment meshing test.

As shown in Fig. 10b, the test of the crowned gear under misalignment conditions was conducted. The crowned gear was tested with m = 5, z = 30, a = 20°, η = 1.5°, and the test torque was 100N·m at a speed of 200r/min. The contact surface morphology of the crowned teeth obtained after the test is basically consistent with the theoretical calculation results, further proving that the contact area of the crowned teeth is transferred to the tooth root under misaligned working conditions.

Influence of path parameters on tooth clearance

The distribution of circumferential clearance at different paths for a misalignment angle of 1.5° is shown in Fig. 11. The path parameter b remains unchanged and the path parameter a is changed to 100 mm, 240 mm and 380 mm, where a takes 240 mm as the conventional path parameter. The red five stars are the location of the first contact point and the contact width increases with increasing path parameter a. When the path parameter a is less than 240 mm, the clearance and contact width of the new feed path is smaller than that of the conventional path, while the contour of the circumferential clearance is smaller and closer to the involute contact, resulting in a larger contact surface and better load-carrying capacity under the same load. With path parameter a greater than 240 mm, crowned tooth of the new feed path has greater clearance and contact width than the conventional path, with increasing demands on tooth width at equal inclination.

Fig. 11

Influence of path parameter a on tooth clearance.

The black line connecting the first contact point is the contact guide line after deformation of the tooth surface under load, the clearance magnitudes on the curves are 0.1 mm, 0.59 mm and 1.49 mm respectively. This means that full tooth height contact becomes increasingly difficult to achieve as a. When parameter a increases to a certain threshold, the deformation required to achieve full tooth high contact can even exceed the yield limit of the material, resulting in plastic deformation followed by crushing. Full tooth high contact is the ideal form of contact to maximize the mechanical properties. Reducing a makes it easier to achieve full tooth height contact and can increase the load-carrying capacity at misalignment conditions.

In the meshing process of crowned gears, the contact initially begins as point contact, which progressively evolves into elastic deformation under the applied load, eventually leading to surface contact. As shown in Fig. 12, this study investigates the distribution of the contact region and the contact area of crowned gears under different path parameters and equal deformation conditions. Figure 12a illustrates that when the path parameter a is set to 240 mm and 380 mm, and the tooth surface deformation reaches 150 μm, the contact is confined to the root area, forming a narrow strip-shaped contact with a small contact area. However, when the path parameter a is 100 mm, full tooth height contact is achieved at a deformation of 100 μm, resulting in a substantial increase in the contact area. Thus, as the path parameter a decrease, the crowned gear is more likely to achieve full tooth height contact, exhibiting superior contact performance. Further analysis of the contact area (see Fig. 12b) reveals that when the path parameter a decrease from 240 to 100 mm, the contact area under equal deformation increases by a maximum of 162.0%. Conversely, when the path parameter a increases from 240 to 380 mm, the reduction in contact area becomes more pronounced with increasing deformation, and at a deformation of 150 μm, the contact area decreases by as much as 30.1%. These findings suggest that reducing the path parameter a significantly increases the contact area, thereby improving the meshing performance of crowned gears.

Fig. 12

Gear meshing contact characteristics with different path parameters: (a) Contact region. (b) Contact area.

Clearance distribution of circumferential teeth

Here, geometries were generated with the corresponding parameters:

• Constant parameters: m = 5 mm, z = 50, α = 20°, η = 1.5°, b = 240 mm. Variable parameters: a.

When the misalignment angle is 0°, the clearance of the circumferential tooth is the same and thus each tooth has the same contact characteristics. However, the minimum clearance of circumferential tooth changes in the misalignment conditions. For example, crowned tooth in the pure flip area (0°/180°) are the first to make contact, while in the pure roll area (90°/270°) last contact or even no contact.

Figure 13a shows the distribution of the remaining clearance and tooth surface load at different angles in the circumferential direction under misalignment conditions, with the load in the horizontal coordinate and the clearance in the vertical coordinate. It is easy to see that the circumferential clearance distribution resembles the shape of a water drop and is consistent from 0–90°, 90–180°, 180–270° and 270–360°, with the clearance increasing with increasing path parameters at any angle in the circumferential direction. The rate of change of the circumferential clearance from 0° to 90° first increases and then decreases, while the contact of the gear couplings is characterized by an elastic deformation after the first contact at 0°, the deformation makes up for the minimum clearance of the adjacent tooth and thus causes contact, the number of contact teeth is thus iterated until the transmitted torque is satisfied. Therefore, the smaller the rate of change in clearance, the smaller the clearance required for adjacent tooth to make contact and the more likely the tooth will make contact.

Fig. 13

Clearance distribution of circumferential tooth pairs: (a) Distribution of clearance and load. (b) The law of clearance.

Figure 13b shows the clearance distribution of the tooth pairs under paths from 0 to 180°. κ and χ are the angles of the tangents to the horizontal axis of the clearance distribution curves in the 0° and 90°. The larger the κ and χ, the greater the rate of change of the clearance with angle, where κ₁ > κ₂ > κ₃ > κ₄, χ₁ < χ₂ < χ₃ < χ₄. Therefore, the clearance change rate in the 0° region gradually increases with the decrease of the path parameter a, and the adjacent tooth pairs are more difficult to contact under the action of torque. The clearance change rate in the 90° region gradually decreases with the decrease of the path parameter a, and the adjacent tooth pairs are more likely to contact, which is easy to realize the full tooth pairs meshing under misalignment conditions. According to the above analysis, when the path parameter a decrease to a certain threshold, κ may continue to increase to 90°, and χ approaches or is equal to 0°. At this time, the clearance between 0° and 90° is exactly the same, and the clearance is 0 mm.

Conclusions

In this paper, to improve the performance of gear couplings, a new hob feed path is proposed, and the mathematical model of tooth surface and the calculation method of geometric parameters such as minimum normal design clearance are constructed. Compared with the conventional path, the following conclusions can be obtained:

• (1) A calculation method suitable for elliptical-arc feed path is proposed and its high precision is verified. However, although the elliptical-arc feed path can flexibly design gear couplings with different properties, the machining accuracy of gear hobbing machine must be considered in actual production.

• (2) The clearance under the new path decreases as the path parameter a decrease and increases as the path parameter b decreases. The path parameter a has a higher influence on the clearance than b. The minimum design clearance is usually reduced by decreasing a. b has more influence on the load-carrying performance of tooth surface.

• (3) Initial contact is a point contact due to the drumming. The tooth surface is deformed under load, resulting in a surface contact. The contact width decreases with the decrease of parameter a, making it easier to achieve full tooth height contact under misalignment conditions. With the decrease of a, the change rate of clearance in the pure flip area gradually increases, and the change rate of clearance in the pure roll area gradually decreases. Because clearance decreases with the decrease of a, the number of contact teeth is more and more, and it is easier to achieve full tooth contact.