Optimization of working parameters of high-pressure roller mill based on entropy weight method and response surface method

Abstract

In order to improve the crushing efficiency of high-pressure roller mill and reduce energy consumption, the optimal parameter combination of high-pressure roller mill is sought, GM160-140 high-pressure roller mill is taken as the research object, and the discrete element simulation calculation model of high-pressure roller mill is established to simulate the crushing process. Taking the roll surface pressure, productivity, and the proportion of discharge particle diameter as the performance evaluation indexes, the simulation data are used to analyze the influence of each working condition parameter of the high-pressure roller mill on its performance law. Through the entropy weighting method to determine the weights of high-pressure roller mill productivity, roll surface pressure, the proportion of discharge particle diameter, and through the extreme difference analysis to get the optimal parameter combination. Minitab software is used to carry out the response surface method (RSM) experimental design, the optimal parameter combinations are derived from the optimization using the response surface apparatus, the optimal parameter combinations derived from the two optimization methods are compared and analyzed, and ultimately it is concluded that the optimization of the response surface is the global optimal, and the optimal parameter combinations are as follows: the roller speed is 2.50 rad/s, the roller gap is 28.87 mm, and the feed size is 31.97 mm, Under the above optimal parameters, the roll surface pressure is 150450.00 N, the productivity is 1268.00t/h, the percentage of the material less than 6 mm is 58.14%, so as to achieve the purpose of optimizing the parameters of the high-pressure roller mill, It is of significance to save resources and respond to the national green development and intelligent development.

Introduction

With the rapid economic growth, the demand for mineral resources in China is increasing¹, and the crushing and processing of ore has been paid more and more attention by scholars at home and abroad. High-pressure roller mill is an indispensable and important equipment in mining production, with low energy consumption per unit of crushing, strong processing capacity, equipment operating efficiency and so on². It is widely used in ferrous metals, non-ferrous metals and inorganic non-metallic mines and other industry sectors³, plays a very important role in industrial production. In 2020, China will “double carbon” goal into the overall layout of ecological civilization construction to promote the new development concept of green low-carbon⁴, high-pressure roller mill in mining equipment as a representative of high efficiency and energy saving, to carry out the performance evaluation and analysis of high-pressure roller mill performance analysis of basic research and optimization of operating conditions parameters, in order to improve the efficiency of the equipment, reduce energy consumption, respond to the national intelligent development, green development is of great significance.

Mathematical methods are an important way to study high-pressure roller mills. In theoretical modeling of high-pressure roller mills, Torres et al.⁵ proposed a series of relevant mathematical models to predict the performance of the high-pressure roller mill in terms of production, power consumption and discharge size based on the properties of the ore itself, the structural parameters of the high-pressure roller mill and the working condition parameters. Daniel et al.⁶ analyzed the roller pressure principle of high-pressure roller mill and established productivity model, power consumption model and particle size distribution model on this basis. Thivierge et al.^7,8 established a high-pressure roller mill performance test dataset through a large number of experiments and developed a high-pressure roller mill modeling framework, which includes a working gap model, a mass flow model, a power consumption model, and a product particle size distribution model. Kumar et al.⁹ used EDEM software to establish a crushing model of high-pressure roller mill and studied the crushing process of mineral particles during rolling, as well as the effect of structural parameters and working condition parameters on the production capacity and energy consumption. Barrios et al.¹⁰ coupled the discrete unit method with a multibody dynamics approach to investigate the effects of roll shape, hydraulic spring system activation parameters and material loading response on productivity, working clearance and roll pressure distribution. Zhang et al.¹¹ combined the discrete unit method and particle crushing model to simulate the kinetic properties of particles in a high-pressure roller mill and carried out a study on this basis, verifying that increasing the roll speed can enhance the output and increase the energy consumption, but it has almost no effect on the working gap, the product size, and the energy of particles fracture. Xu et al.¹² used a fractal theory approach to establish and validate a mathematical model of the particle size distribution of the discharge from a high-pressure roller mill, and further investigated the effect of high-pressure lift mill operating factors on the fractal dimension of the only parameter in the mathematical model. Bilgili et al.¹³ investigated multi-particle contact comminution using a mathematical model that resulted in a comminution process matrix. In terms of optimization methods, RSM was first proposed by Box and Wilson¹⁴ in 1951, and has now been widely used as an optimization method in chemistry, industry, medical and other industries. F. Khanramaki et al.¹⁵ used the response surface method to optimize the process parameters for the extraction of thorium from feed solution using cyanex272, and obtained the optimal parameter values. Pouyan Zoghiet al.¹⁶ employed the response surface method to optimize the variables influencing process efficiency during the study of soil cleaning methods for petroleum hydrocarbons in contaminated soil around oil storage tanks. Wang et al.¹⁷ established an air pollution emission level evaluation model based on entropy weight method, and evaluated the air pollution emission level of Wuhan City in central China. Gao et al.¹⁸ established an infectious disease risk analysis and assessment method based on information entropy theory. However, these optimization methods are rarely applied to ore crushing. In summary, scholars at home and abroad have studied the theoretical modeling and performance prediction modeling of high-pressure roller mill, and have studied the crushing process using discrete elements, but relatively few studies have been conducted on the performance evaluation and parameter optimization of high-pressure roller mill.

In this paper, based on the simulation of orthogonal test data, the entropy weight method is used to construct a comprehensive evaluation system for the performance of high-pressure roller mill, and the optimal parameter combinations obtained are compared and analyzed with the optimal parameter combinations obtained based on the response surface method to obtain the optimal parameter combinations of the global optimal parameter combinations, so as to achieve the purpose of optimizing the parameters of the high-pressure roller mill and realize the goals of improving efficiency and reducing energy consumption, and provide a reference for the research of optimizing parameters of the high-pressure roller mill and the application of the project. Provide reference for the research and engineering application of high-pressure roller mill parameter optimization.

High pressure roller mill working principle and performance evaluation parameters

Working principle

Fig. 1

Schematic diagram of high-pressure roller mill structure.

The main structure of the high-pressure roller mill is shown in Fig. 1, which mainly includes the frame, hydraulic system, guide trough, pressure roller and other devices. The two pressure rollers of the high-pressure roller mill are called fixed roller and dynamic roller. The fixed roller is fixed on a fixed shaft and rotates on the fixed shaft by means of a drive unit, and the movable roller is fixed on a floating shaft and is driven to rotate by another drive unit, which will move in the horizontal direction under the pressure generated by the hydraulic unit. The working gap between the movable and fixed rollers is called the roller gap. During the working process of the high-pressure roller mill, the material enters into the guide chute, fed by the top of the pressure roller, and discharged from the bottom of the pressure roller after crushed by the roller pressure.

Fig. 2

Working principle diagram of high-pressure roller mill.

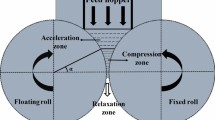
The principle of material crushing is shown in Fig. 2. The material pulverization interval is divided into three region^19,20, which are the acceleration region (the region corresponding to the rounding angle α), the compression region (the region corresponding to the rounding angle β) and the release region (the region corresponding to the rounding angle γ). In the material particles roll pressure process, the material first in the acceleration region above the contact with the two rollers, due to the existence of friction between the two, the material is therefore accelerated with the rollers for the accelerated movement, when the movement to the compression region, the speed of the material and roller surface speed is basically the same (assuming that there is no sliding between the material and the rollers), at this time the material began to be crushed by the two rollers squeezed and crushed, and always arrived at the smallest gap rollers, as the rollers gap increases. With the increase of roller gap, the compressed crushed material will rebound in the release region, and released to the end of the release region to the loose state or discharged in the form of material cake.

Main evaluation parameters

The main performance parameters of the high-pressure Roller Mill are production rate, power consumption and percentage of discharge size, which can be predicted based on material characteristics, structural dimensions and operating parameters.

• (1) Productivity.

The mathematical model of productivity of high-pressure roller mill is modeled based on parameters such as roll gap, roll speed, roll diameter, roll width, roll speed and cake density of high-pressure roller mill. Figure 3 is a schematic diagram of material extrusion and crushing, according to the law of conservation of mass, the material in the extrusion region, the quality does not change, and assuming that there is no relative sliding between the roller surface and the material, then the productivity Q of the high-pressure roller mill can be expressed as:

$$Q\left( \beta \right)=3600x\left( \beta \right)\rho \left( \beta \right)LV\cos \beta$$

(1)

Where, $\:Q\left(\beta\:\right)$ is the productivity of the high-pressure roller mill at any center angle $\:\beta\:$,t/h;$\:\rho\:\left(\beta\:\right)$ is the bulk density of the material at the horizontal cross section corresponding to any angle of the center of the circle $\:\beta\:$,t/m³;$\:x\left(\beta\:\right)$ is the roller gap at the horizontal cross-section corresponding to an arbitrary center angle $\:\beta\:$,m; $\:L$ is the roll width, m;$\:V$ is the linear speed of the pressure roller, m/s.

Fig. 3

Schematic diagram of material crushing.

In the calculation, the production capacity of the high-pressure roller mill is generally pointed out at the location of the material outlet, i.e., when $\:\beta\:$=0, the productivity of the high-pressure roller mill Q($\:\beta\:$=0) is²¹:

$$Q=3600\rho \left( \beta \right){x_0}LV$$

(2)

Where, $\:{x}_{0}$ is the outlet gap($\:\beta\:$=0),m.

• (2) Power consumption.

Power consumption refers to the difference between the input power and output power of the equipment, under the same productivity, the lower the power consumption, the better. The power consumption of high-pressure roller mill is related to the pressure roller force.

Fig. 4

Schematic diagram of the force on the pressure roller of the high-pressure roller mill.

Figure 4 shows a schematic diagram of the force on the pressure rollers of a high-pressure roller mill, The shaded area is the influence area of the working pressure, in the region of the pressure roller on the material squeezing pressure $\:F$ can be obtained through the working pressure of the pressure roller. Due to the working characteristics of the high-pressure roller mill, the material is squeezed by the pressure roller only in the compression area, so the corresponding force area is the upper part of the pressure roller, and thus the squeezing pressure $\:f$ of the pressure roller is:

$$f = 1000{\rm{}}F\frac{D}{2}L$$

(3)

Where,$\:f$ is the pressure of the pressure roller on the material, kN;$\:F$ is the working pressure of the pressure roller, MPa;$\:D$ is the roll diameter, m.

According to the results of the force analysis in Fig. 4, the torque $\:T$ caused by the squeezing force $\:f$ in the vertical direction is:

$$T=F\sin \left( \beta \right)\frac{D}{2}$$

(4)

Where,$\:T$ is the torque, kN; $\:\beta\:$ is half the angle at which laminar pulverization occurs.

Since a high-pressure roller mill has two counter-rotating pressure rollers, the total power of the high-pressure roller mill is twice the tangential force multiplied by the linear speed of the rollers. Therefore, the total power $\:P$ can be expressed as:

$$P=2\sin \left( \beta \right)U$$

(5)

The energy consumption is the ratio of the total power $\:P$ to the handling capacity $\:Q$, i.e.:

$$W=\frac{P}{Q}$$

(6)

Where, $\:W$ is the theoretical unit energy consumption, kW·h/t;$\:Q$ is productivity, t/h.

• (3) Proportion of discharge particle diameter.

Proportion of discharge particle diameter as a percentage is an important parameter used to measure the crushing effect of the mill equipment on the material. In the process of laminated crushing, part of the material is crushed into particles of different sizes in the area of the current crushing layer, and the other part of the material that is not crushed enters into the next crushing layer or other crushing layers behind it for crushing. Within each fragmentation layer within the compression zone is represented by two mechanisms, selection and breaks²². In any one of the crushing event, part of the material involved in the crushing process, this part of the material will be crushed into different particle size particles, the other part of the material is not involved in the crushing into the next crushing event, these processes are represented by the selection function and the crushing function, the specific process is shown in Fig. 5. Where the discharge from one crushing event is the feed for the next crushing event.

Fig. 5

Laminated Crushing Model.

In the laminated crushing model, the feed size distribution of each crushing layer is represented by $\:{f}_{i}(i=1-N)$, the incoming material of each layer is the outgoing material of the previous layer, i.e. $\:{f}_{i}={p}_{i-1}(i=2-N)$ .

The crushing and selection mechanisms in the laminated crushing process are represented by the crushing function $\:{S}_{i}(i=1-N)$ and the selection function $\:{B}_{i}(i=1-N)$. $\:{S}_{i}$ is the proportion of particles involved in crushing in each particle size in the crushed layer $\:i$. $\:{B}_{i}$ is the proportion of particles of each size in crushing layer $\:i$ after completion of crushing. Therefore, each crushing event can be described by Eq. (7), i.e.:

$${p_i}={f_{i+1}}=\left[ {{B_i}{S_i}+\left( {I - {S_i}} \right)} \right]{f_i}$$

(7)

In the study of the laminar crushing process of materials, a normalized standard deviation $\:{\sigma\:}_{s}$ of the particle size distribution is assumed in order to eliminate the influence of the specific values of the material size distribution on the two functions²³. The normalized standard deviation always takes values within the interval $0\sim 1$, and its expression is as follows:

$${\sigma _s}=\frac{\sigma }{x}$$

(8)

$\:\sigma\:$ in Eq. (8) is the standard deviation of the particle size distribution, $\:\stackrel{-}{x}$ is the mean value of the particle size, and $\:\sigma\:$ and $\:\stackrel{-}{x}$ are defined as:

$$\left\{ \begin{gathered} \sigma =\sqrt {\frac{1}{{N - 1}}\sum\nolimits_{{i=1}}^{n} {{f_i}{{\left( {{x_i} - \overline {x} } \right)}^2}} } \hfill \\ \overline {x} =\frac{1}{N}\sum\nolimits_{{i=1}}^{n} {{f_i}{x_i}} \hfill \\ N=\sum\nolimits_{{i=1}}^{n} {{f_i}} \hfill \\ \end{gathered} \right.$$

(9)

The values of the elements in the above two function matrices vary with different positions within the compression zone of the high-pressure roller mill. The value of the selection function and the compression ratio are related to the particle size distribution of the material to be crushed. The value of the selection function varies with the particle size distribution, independent of the particle size within a given size distribution, and related to the normalized standard deviation of the particle size distribution.

The crushing behavior of particles is described by the crushing function, which is a cumulative value. For a given initial incoming particle size distribution, it is assumed that the crushing behavior depends only on the compression ratio $\:{\epsilon\:}_{s}$. According to Evertsson’s results²⁴, the mathematical models of the selection function and the crushing function are shown in Eq. (10):

$$\left\{ \begin{gathered} S\left( {{\varepsilon _s},{\sigma _s}} \right)={a_1}\varepsilon _{s}^{2}\sigma _{s}^{2}+{a_2}\varepsilon _{s}^{2}{\sigma _s}+{a_3}\sigma _{s}^{2}+{a_4}{\varepsilon _s}\sigma _{s}^{2}+{a_9} \hfill \\ B\left( {{\varepsilon _s},{\sigma _s}} \right)=\left( {1 - \left( {{\alpha _3}+{\alpha _4}{\varepsilon _s}} \right)} \right)x_{s}^{{{\alpha _1}+{\alpha _2}{\varepsilon _s}}}+\left( {{\alpha _3}+{\alpha _4}{\varepsilon _s}} \right){x_s} \hfill \\ \end{gathered} \right.$$

(10)

Where, $\:{x}_{s}$ is the dimensionless value of the particle with size x relative to the initial size $\:{x}_{0}$, denoted as:

$${x_s}=\frac{{{{\log }_2}\left( {{x \mathord{\left/ {\vphantom {x {{x_{\hbox{min} }}}}} \right. \kern-0pt} {{x_{\hbox{min} }}}}} \right)}}{{{{\log }_2}\left( {{{{x_0}} \mathord{\left/ {\vphantom {{{x_0}} {{x_{\hbox{min} }}}}} \right. \kern-0pt} {{x_{\hbox{min} }}}}} \right)}}$$

(11)

Where, $\:{x}_{0}$ is the initial particle size for the compression test; $\:{x}_{min}$ is the minimum reference particle size (usually $\:{x}_{min}$=0.008 mm). Therefore, given a set of incoming particle size distributions, the particle size distribution of the discharged material from a high-pressure roller mill can be predicted by using Eq. ($7\sim 11$).

Main working parameters of high- pressure roller mill

From the analysis of subsection 2.2, it can be obtained that the performance of the high-pressure roller mill is affected by process parameters and working condition parameters. The process parameters of high-pressure roller mill mainly refers to the ratio of the diameter and width of the pressure roller, that is, the diameter and width ratio. In different diameter and width ratio of the material in the roll gap residence time and force situation is not the same, and thus the crushing effect also has an impact, usually, the larger the diameter and width ratio, the better the crushing effect, but the output will be reduced, but also will bring more energy consumption, and vice versa.

The main working condition parameters of high-pressure roller mill include roller speed, roller gap, feed particle diameter, pressure roller force, etc. The roller speed is related to the output, power consumption and smoothness of operation. Roller speed and production, power consumption and smoothness of operation, the lower the roller speed, the more stable and reliable operation of the equipment; the higher the roller speed, the greater the productivity, but too high a roller speed will also make the pressure roller and the material between the relative sliding increase, bad bite, so that the pressure roller surface wear increased, and even have a negative impact on the yield. The smaller the difference between the roll gap and the feed size of the high-pressure roller mill, the finer the size of the discharged product, and the larger the difference, the larger the size of the discharged product. The size of the roll gap is not adjustable in the working process, the roll gap when the high-pressure roller mill works stably depends on the dynamic balance between the force of the hydraulic system and the reaction force of the extruded material layer on the pressure roller. The larger the pressure roller force of the high-pressure roller mill, the better the crushing effect, the finer the discharged particle size of the middle material and the edge material, the more centralized particle size distribution of the middle material and the more uniform particle size distribution of the edge material, but the larger the pressure roller force, the greater the wear and tear of the roll surface.

Therefore, reasonable process parameters and working condition parameters can make the equipment reach the best state in terms of performance, cost and efficiency.

High pressure roller mill simulation modeling

High pressure Roller Mill Simulation Model

In this paper, the discrete element software EDEM is used to establish the simulation crushing model of high-pressure roller mill. At present, there are two kinds of models used to simulate the crushing of material particles in EDEM software, which are Bonding key model and Tavares energy crushing model. In the Bonding model, small particles are connected into large particles by bonding bonds, and the breaking of bonds reflects the crushing of particles. It can show the shape of the crushed material and more accurately react to the crushing of the material particles, but it can not count the particle size of the crushed particles and the amount of calculation is large. Tavares model is an empirical crushing model, when the impact energy is greater than the crushing energy, the material is crushed. It can be used in the post-processing panel to directly obtain the particle size distribution, crushing rate and other data, more intuitive display of the crushing effect and fast simulation speed.

High-pressure roller mill in the simulation of crushing, the number of particles is huge, and the need to analyze the crushed discharge size distribution and other data, Tavares model can be convenient for the discharge particle size statistics, and can also meet other simulation needs. Tavares model principle is shown in Fig. 6:

Fig. 6

Schematic diagram of Tavares model fragmentation.

In the Tavares model, each particle has a specific crushing energy that is distributed according to its size, mean and standard deviation. This energy varies according to the distribution described by the following Eqs^25,26:

$$P\left( E \right)=\frac{1}{2}\left[ {1 - erf\left( {\frac{{\ln {e^ * } - \ln {E_{50}}}}{{\sqrt {2\sigma _{E}^{2}} }}} \right)} \right]$$

(12)

$${E^*}=\frac{{{E_{\hbox{max} }}E}}{{{E_{\hbox{max} }}}}$$

(13)

Where, $\:E$ is the crushing energy distribution, J/kg;$\:{E}_{max}$ is the upper limit of the energy distribution, J/kg;$\:{E}_{50}$ is the median value of the energy distribution, J/kg;$\:{\sigma\:}_{E}$ is the standard deviation.

The median value of crushing energy is given by the following equation:

$$E=\frac{{{E_\infty }}}{{1+{{{k_p}} \mathord{\left/ {\vphantom {{{k_p}} {{k_s}}}} \right. \kern-0pt} {{k_s}}}}}\left[ {1+{{\left( {\frac{{{d_o}}}{{{d_p}}}} \right)}^\varphi }} \right]$$

(14)

Where, E_∞ is the ultimate crushing energy, J/kg;$\:\phi\:$ is a parameter adjusted from experimental data; $\:{k}_{p}$ and $\:{k}_{s}$ are the particle steeliness and geometry stiffness, respectively, GPa;$\:{d}_{p}$ is the size of the particle, mm;$\:{d}_{o}$ is the size of the particles in the ore characterization, ,mm. It should be noted that the elasticity of the geometry must be close to the true value of the physical test, and if the particles are compressed, the geometry should be compressed accordingly to maintain the ratio between the two.

When a particle is crushed without fragmentation, it will be damaged, after which the particle will develop a new fragmentation ${E'_f}$, the new fragmentation energy will be lower than its original fragmentation energy $\:{E}_{f}$, and this new fragmentation energy will be an intrinsic property of the particle until the next damage event occurs, given by the following equation:

$$E_{f}^{\prime }={E_f}\left( {1 - D} \right)$$

(15)

$$D={\left[ {\frac{{2r}}{{2r - 5D+5}} \cdot \frac{{e{E_K}}}{{{E_f}}}} \right]^{\frac{{2r}}{5}}}$$

(16)

Where, $\:{E}_{f}$ is the crushing energy of the particles, J;$\:{eE}_{k}$ is the effective impact energy, J;$\:D$ is the damage value; $\:{\rm\:Y}$ is the damage accumulation factor, which characterizes the ability of the material to withstand damage before fracture; finally, $\:e$ is the proportion of energy involved in the collision, which is assigned to the particle according to its stiffness.

$$e=\frac{1}{{1+{{{k_p}} \mathord{\left/ {\vphantom {{{k_p}} {{k_s}}}} \right. \kern-0pt} {{k_s}}}}}$$

(17)

Where, $\:{k}_{p}$ is the particle stiffness,$\:{k}_{s}$ is the surface stiffness of the geometry. When two particles of the same substance collide, $\:e$ = 0.5 in Eq. (17) because the energies between them are equal.

The Tavares crushing model is mainly based on the parameter $\:{t}_{10}$, which represents the proportion of fragments in the product that are smaller than 1/10 of the parent particle size, and is described by Eq:

$${t_{10}}=A\left[ {1 - \exp \left( { - b\frac{{e{E_k}}}{{{E_f}}}} \right)} \right]$$

(18)

Where $\:A$ and $\:b$ are parameters adjusted to the experimental data, and the larger the value of $\:{t}_{10}$, the finer the newly produced particles.

In the simulation process Tavares model crushing parameters are crucial, this paper uses iron ore for simulation, according to the research results of Tavares team, refer to the model crushing parameters calibrated by RODRIGUEZ et al.²⁷ to the crushing parameters of iron ore, as shown in Table 1:

Table 1 Crushing parameters of Tavares model.

Simulation parameters of high pressure roller mill

This paper is based on the modeling of GM160-140 high-pressure roller mill. In order to better simulate the material crushing process, the motion parameters and structural parameters of the high-pressure roller mill are simplified, and the parts that have no effect on the simulation process and have little effect are simplified or removed, and only the main part of the high-pressure roller mill is modeled, and its main structural parameters and simulation parameters are shown in Table 2²⁷:

Table 2 Structural parameters and simulation parameters of high-pressure roller mill.

Establishment of simulation crushing model of high-pressure roller mill

(1) Model establishment.

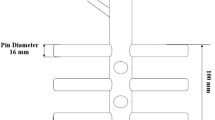
The model of the high-pressure roller mill was simplified, and the geometry was created by using the three-dimensional modeling software Solidworks. The guide groove, press roll and aggregate groove of the high-pressure roller mill were shown in Fig. 7, and the stud on the surface of the press roller was shown in Fig. 8:

Fig. 7

Solid model of high-pressure roller mill. (a) guide groove (b) press roll (c) aggregate groove.

Fig. 8

Stud on the surface of the pressure roller.

(2) Contact parameter setting.

The physical properties are defined as particles interacting with particles and particles interacting with geometry, and the direction of gravitational acceleration is -9.81 m/s² along the Y-axis. Define the properties of particles and geometry. The material of the particles is iron ore, whose property is Poisson’s ratio of 0.27, shear modulus of 2.46e + 7 Pa, density of 4400 kg/m³; The material of the geometry is 45 steel, Poisson ratio is 0.3, elastic modulus is 1e + 10 Pa, density is 7850 kg/m³; Define the contact coefficient between particles: recovery coefficient 0.2, static friction coefficient 0.55, rolling friction coefficient 0.51; contact coefficient between particles and geometry: recovery coefficient 0.15, static friction coefficient 0.49, rolling friction coefficient 0.47, as shown in Fig. 9:

Fig. 9

Particle properties and contact parameter Settings.

(3) Simulation parameter setting.

Use the Particle Factory tool to define the particle generation factory and the particle generation mode, and define the size and position of the particle factory to coincide with the material guide trough, as shown in Fig. 10:

Fig. 10

Particle factory Settings.

Import the created pressure model into EDEM software, EDEM Simulator supports dynamic time step and parallel calculation, set the particle simulation time step to 3.99e-05s, and the total simulation time is 3s, as shown in Fig. 11:

Fig. 11

Simulation Step Size Settings.

The final model is shown in Fig. 12:

Fig. 12

Simulation modeling diagram of high-pressure roller mill.

Simulation experiment design and data analysis

In the actual engineering cases, the value of the working condition parameters of the high-pressure roller mill are within a certain range, for example, the roller speed needs to be selected within the range of the equipment, low roll speed leads to lower productivity, the roller speed is too high will lead to the instability of the equipment, etc., in the practical application of the project and the efficiency of the simulation of a number of considerations, the simulation of the final selection of the roller speed, the roller gap and the feeding size of a total of three major working condition parameters as a variables²⁸. Orthogonal test is a mathematical statistics approach, which is primarily utilized to examine multiple factors. By means of rational arrangement of test times and conditions, the key factors influencing the test results and the optimal process parameters can be identified at a lower cost. A 3-factor, 3-level test was designed, and L₉(3⁴) orthogonal table was chosen to analyze the simulation results (roll surface pressure, productivity, and proportion of discharge particle diameter) of the high-pressure roller mill in a total of 9 tests. The specific parameter ranges of the three factors can be calculated by empirical formulas²⁹. The working condition parameter setting levels are shown in Table 3. Because the simulation can not calculate the power consumption of the high-pressure roller mill, so the roll surface pressure is used to replace the evaluation index of power consumption, in terms of the proportion of discharge particle diameter, the proportion of the discharge particle diameter less than or equal to 6 mm is selected, and the simulation results are shown in Table 4; Fig. 13:

Table 3 Experimental Scheme Orthogonal table L9 (3⁴).

Table 4 Results of the orthogonal scheme.

Fig. 13

Simulation result graph. (a) Roll surface pressure (b) Productivity (c) Particle diameter proportion.

The simulation data of each parameter of the high-pressure roller mill in Table 4 is analyzed in terms of range R, and the results are shown in Tables 5, 6 and 7. It can be obtained that the degree of influence of the three working conditions parameters on the roll surface pressure in the following order: roller speed > roller gap > feed particle diameter; the degree of influence on the productivity in the following order: feed particle diameter > roller gap > roller speed; the degree of influence on the proportion of discharge particle diameter in the following order: feed particle diameter > roller gap > roller speed.

Table 5 Results of roll surface pressure range analysis.

Table 6 Productivity range analysis table.

Table 7 Discharge particle size ratio range analysis table.

Parameter optimization method and result analysis

Parameter optimization method based on entropy weighting method with comprehensive weighting and result analysis

When measuring the performance of high-pressure roller mill, it is necessary to comprehensively consider a number of factors, such as productivity, power consumption, particle diameter distribution of the discharge material, roll surface pressure, etc., however, we are unable to determine the relative importance of the impact of each factor on the performance. Therefore, when dealing with the problem of multi-indicator empowerment, entropy weighting can be used for the measurement of a number of indicators, which can avoid the influence of the subjective factors, eliminate the results of the bias of the human subjective assignment of the results and improve the objectivity and accuracy of the evaluation results.

There are several steps to go through when applying the entropy weight method for decision making:

(1)According to the high-pressure roller mill performance evaluation index, the original data matrix X is constructed, as shown in Eq. (19):

$$X={\left( {{X_{ij}}} \right)_{mn}}=\left( {\begin{array}{*{20}{c}} {{x_{11}}}& \ldots &{{x_{1n}}} \\ \vdots & \ddots & \vdots \\ {{x_{m1}}}& \cdots &{{x_{mn}}} \end{array}} \right)$$

(19)

Where, $\:{X}_{ij}$ is the result of the comparative judgment of the scale of importance of the $\:i$th and $\:j$th indicators,$\:i$= 1,2…,$\:m$, $\:j$= 1,2,…,$\:n$,both $\:{X}_{ij}$>0;$\:m$ is the number of samples and $\:n$ is the number of indicators, in this paper $\:n$=3. (2)Standardize the original data set to eliminate the differences in the scale of the indicators, according to the meaning of the indicators, the indicators can be divided into upward indicators (the larger the value the better) and downward indicators (the smaller the value the better), in this paper, the roll surface pressure is a downward indicator, the productivity and the proportion of discharge particle diameter is a upward indicator, respectively, through the following methods for standardization:

For upward indicators:

$$x_{{ij}}^{\prime }=\frac{{{X_{1j}} - \hbox{min} \left( {{X_{1j}} \cdot \cdot \cdot {X_{mj}}} \right)}}{{\hbox{max} \left( {{X_{1j}} \cdot \cdot \cdot {X_{mj}}} \right) - \hbox{min} \left( {{X_{1j}} \cdot \cdot \cdot {X_{mj}}} \right)}}$$

(20)

For downward indicators::

$$x_{{ij}}^{\prime }=\frac{{\hbox{max} \left( {{X_{1j}} \cdot \cdot \cdot {X_{mj}}} \right) - {X_{1j}}}}{{\hbox{max} \left( {{X_{1j}} \cdot \cdot \cdot {X_{mj}}} \right) - \hbox{min} \left( {{X_{1j}} \cdot \cdot \cdot {X_{mj}}} \right)}}$$

(21)

Where, $\:{X}_{ij}$ is the element in row $\:i$ and column $\:j$ of the evaluation matrix;$\:min\left({X}_{1j},\dots\:{X}_{mj}\right)$is the minimum value in the matrix;$\:max\left({X}_{1j},\dots\:{X}_{mj}\right)$ is the maximum value in the matrix.

After processing, a new data matrix is obtained:

$${X^1}={\left( {\begin{array}{*{20}{c}} {x_{{_{{11}}}}^{1}}& \ldots &{x_{{_{{1n}}}}^{1}} \\ \vdots & \ddots & \vdots \\ {x_{{_{{m1}}}}^{1}}& \cdots &{x_{{_{{mn}}}}^{1}} \end{array}} \right)_{mn}}$$

(22)

(3)Find the ratio of each indicator under each program.

Calculate the weight of the $\:i$th sample under the $\:j$th indicator and consider it as the probability used in the information entropy calculation.

$${P_{ij}}=\frac{{x_{{ij}}^{1}}}{{\sum\nolimits_{{i=1}}^{m} {x_{{ij}}^{1}} }}\left( {i,j=1,2, \cdot \cdot \cdot ,m,n} \right)$$

(23)

(4)Calculating entropy.

Calculate the value of $\:k$, the entropy of the $\:j$th indicator:

$$k=\frac{1}{{\ln \left( m \right)}}$$

(24)

$${e_j}= - k\sum\nolimits_{{i=1}}^{m} {{P_{ij}}\ln \left( {{P_{ij}}} \right)}$$

(25)

Where, $\:k$>0; $\:{e}_{j}$>0. If $\:{P}_{ij}$=0, define $\:{e}_{j}$=0 and $\:m$ is the number of influences considered.

(5)Determination of the weights of the indicators.

The weight $\:{W}_{j}$ of the $\:j$th indicator is:

$${W_j}=\frac{{1 - {e_j}}}{{m - \sum\nolimits_{{j=1}}^{m} {{e_j}} }}\left( {j=1,2, \cdot \cdot \cdot ,n} \right)$$

(26)

(6)Calculating the composite score.

The weights of the integrated equipment performance, the orthogonal test results are comprehensively scored, and the integrated scoring value $\:{W}_{j}$ of the $\:i$th evaluation object is:

$${S_i}=\sum\nolimits_{{j=1}}^{n} {{W_j}} {P_{ij}}$$

(27)

The larger the value of the composite score value function $\:{S}_{i}$, the better the performance of the device.

The weight vector $\:{W}_{j}$ = (0.24 0.51 0.25) of the performance of the high-pressure roller mill is obtained by entropy weight method, from which it is known that the weights of the roll surface pressure, productivity, and the proportion of discharge particle diameter in the comprehensive evaluation system are 0.24, 0.51 and 0.25.

Based on Eqs. (20) and (21), the data of the three indicators for the performance evaluation of the high-pressure roller mill were standardized and combined with the weights, and then substituted into Eq. (27), thereby obtaining the comprehensive scores of these nine groups of simulation results, as shown in Table 8:

Table 8 Comprehensive score results.

Table 9 Horizontal response of working condition parameters after comprehensive evaluation.

Combined with the comprehensive weighted level response of the working condition parameters, compare and analyze the size of the extreme difference, and get the degree of influence of the working condition parameters on the comprehensive performance of the high-pressure roller mill in the following order: feed particle size > roll gap > roll speed. The optimal parameter combination is: roller speed 1.25 rad/s, roller gap 27 mm, feed particle diameter 35 mm. With the weighted composite score (comprehensive evaluation) of this single indicator to measure the advantages and disadvantages of the operating parameters, the operating parameters of the comprehensive evaluation of the average value of the maximum level in which the parameters in the level of the response to the maximum impact, when the level of the high-pressure roller mill operating parameters for the optimal level.

Response surface-based parameter optimization method and result analysis

Response surface method optimization is to use reasonable experimental design methods and get certain data through experiments, and use multiple quadratic regression equations to fit the functional relationship between the factors and the response values, and seek the optimal solution through the analysis of the regression equations. In the optimization process, Minitab software is used to design the experiment. The simulation test design is as follows: each processing parameter is selected as the highest level and the lowest level, the roller speed interval [1.25 rad/s, 2.5 rad/s], the roller gap interval [22 mm, 32 mm], and the feed particle diameter interval [25 mm, 35 mm], a total of 15 groups are designed, and the number of centers is 3, and the simulation test design of the Response Surface Method is shown in Table 10: The simulation results are shown in Table 11; Fig. 14:

Table 10 Response surface simulation test design.

Table 11 Simulation results of response surfaces.

Fig. 14

Simulation result graph. (a) Roll surface pressure (b) Productivity (c) Particle diameter proportion.

The three-dimensional response surface diagram can visualize the influence of multiple factors, and can also find out the optimal range more intuitively. Figures 15, 16 and 17 show the solution surface diagrams of the three evaluation indexes, and the highest point of the surface is the optimal solution.

Roller speed, roller gap and feed particle diameter on roll surface pressure, productivity, and proportion of discharge particle diameter are shown in Figs. 15, 16 and 17:

Fig. 15

Surface diagram of the effect of roller speed, roller gap, and feed particle diameter on roll surface pressure.

Fig. 16

Surface diagram of the effect of roller speed, roller gap, and feed particle diameter on productivity.

Fig. 17

Surface diagram of the effect of roller speed, roller gap, and feed particle diameter on proportion of discharge particle diameter.

R-sq (R2) is the percentage of variation in the response explained by the model, and R2 is used to determine the goodness of fit of the model to the data, and the higher the value of R2 the better the model fits the data. The 15 sets of data obtained from the simulation were analyzed by ANOVA and model optimization, and the fit of the regression equations for the three performance evaluation indexes of the high-pressure roller mill were 96.36% for the roller surface pressure, 96.57% for the productivity, and 99.71% for the proportion of discharge particle diameter, which were all excellent fits. The performance evaluation indexes of the high-pressure roller mill are predicted by Minitab response optimizer, in which the roller surface pressure is expected to be small, the productivity and the percentage of discharge size are expected to be large.

Fig. 18

Schematic diagram of response optimization.

Figure 18 is the response optimizer prediction diagram, through Fig. 18 can be seen, the three evaluation indicators of the high-pressure roller mill to achieve the optimal parameters of the optimization, the use of the response optimizer optimization of the final parameter combinations for the roller speed of 2.5 rad/s, the roller gap 28.8687 mm, the feed particle diameter of 31.9697 mm, the predicted value of the roll surface pressure of 155,909 N, the productivity of 1354 t/h, the proportion of discharge particle diameter for 55.42%, the complex consensual is 0.66, indicating that the optimization prediction results are better.

Optimization results analysis and validation

The optimal combinations obtained from the two optimization methods are simulated and verified and the results are shown in Table 12:

Table 12 Simulation verification results.

Comparing the simulation data after the optimization of response surface method with the prediction data after the optimization of the previous paper, the errors between the predicted values and the simulation values can be obtained, which are 3.6% of the roll surface pressure, 6.8% of the productivity, and 4.7% of the proportion of discharge particle diameter, which proves the accuracy of the optimization model of the response surface method.

Table 12 in the response surface optimization combination of simulation results and orthogonal test optimization results for comparison, it can be concluded that the integrated weighted optimization of the roll surface pressure, productivity and the proportion of discharge particle diameter are not as good as the response surface optimization. The main reason for this result is that only the weights are considered, the interaction between the factors is not considered, and the entropy weighting method can only be optimized on the existing data, which leads to bias in the interpretation and prediction of the experimental results. In contrast, the response surface is first optimized by designing reasonable experiments and then fitting the equations based on the experimental data, the fitted equations are continuous and the interaction between factors is considered, so that the global optimization can be achieved.

Conclusion

(1)Based on the discrete element method to establish the particle crushing simulation model of the mine high-pressure roller mill, get the simulation data of the particle crushing process of the high-pressure roller mill, and analyze the range R of the simulation data of the high-pressure roller mill at each level, and get the influence degree of the working condition parameters on the pressure of the roll surface in the following order: roller speed > roller gap > feed particle diameter; the influence degree of the working condition parameters on the proportion of the discharged particle diameter in the following order: feed particle diameter > roller gap > roller speed > roller gap. The influence of working condition parameters on productivity is as follows: feed particle size > roller gap > roller speed.

(2) Using entropy weighting method to determine the comprehensive evaluation system of each high-pressure roller mill evaluation indicators of the weight of the roll surface pressure of 0.24, the productivity of 0.51, the proportion of discharge particle diameter of 0.25, combined with the level of response of the working condition parameters, the degree of influence of the working condition parameters on the comprehensive performance of the high-pressure roller mill in the following order: feed particle diameter > roller gap > roller speed. The optimal level of working condition parameters obtained by comprehensive evaluation is: roller speed 1.25 rad/s, roller gap 27 mm, feed particle diameter 35 mm, and the optimal level of working condition parameters obtained by response surface optimization design is: roller speed 2.5 rad/s, roller gap 28.8687 mm, feed particle diameter 31.9697 mm.

(3) This paper analyzes the differences between two optimization methods and compares their optimization results. Ultimately, we aim to determine the optimal parameter combinations through response surface methodology to achieve a global optimum. By focusing on multi-objective optimization, we strive to enhance efficiency while reducing energy consumption. The findings provide valuable insights for parameter optimization research and engineering applications in high-pressure roller mills.