Introduction

Characteristic x-ray emission, as a consequential result of decay of inner-shell vacancy produced in ion-atom interactions, has been extensively investigated over the past few decades for the viewpoint of fundamental research and some practical applications1,2,3,4,5,6,7,8. Especially for protons, the K, L and some M-shell x-ray production cross sections have been extensively measured in numerous studies9,10,11,12,13,14,15, because, as the simplest ion, it can be regarded as a perturbation caused by a point charge during collision, and this can significantly simplify the complexity of theoretical simulations. The related experiments are required to test and verify the theoretical models, and provide a usable basis for the study of heavy ion- atom collisions. Furthermore, such data are important for the analytical techniques based on Particle Induced X-ray Emission (PIXE)16. H+ ions are generally produced through the ionization of hydrogen, and proton beams can easily be mixed with hydrogen molecular ions (H2+), which may affect the quantitative analysis of PIXE. Accurate data on the x-ray production cross section by H2+ ions is essential to enrich the PIXE databases and improve the accuracy of analysis. However, the experimental data on this subject are relatively scarce, necessitating further research.

The theoretical x-ray production cross section can be derived from the inner-shell ionization cross section, which can be caused by direct Coulomb ionization, electron capture, or quasi-molecular promotion. The specific mechanism depends on the collision parameters of the collisional system. In asymmetric systems of Z1 < < Z2, direct ionization is predominant, and this can be described by Binary Encounter Approximation (BEA)17, Plane Wave Born approximation (PWBA)18, and the corrected PWBA model that accounts for energy loss, Coulomb repulsion, perturbed stationary states and relativistic effects (ECPSSR), along with the refined ECPSSR considering the united and separated atom approximation (ECUSAR) theories19,20,21. In addition, multiple ionization can be induced by the impact of charged ions, and the atomic parameters, such as fluorescence yield and Coster-Kronig yield, may be changed because of the absence of outer-shell electrons, and this affects the theoretical estimations22,23,24. There are various available databases of atomic parameters for selection in cross section calculations25,26,27,28,29,30. The discrepancies arising from these parameter selections can lead to significant deviations, and this should be considered carefully.

This work intends to contribute with new experimental data for Te L-subshell x-ray emission induced by H2+ ions in the 150–300 keV range with a step of 50 keV. The multiple ionization induced by lower energy light ions is demonstrated by the experimental energy shift and relative intensity ratio change of L-subshell x rays. The new measurement of the x-ray production cross sections is presented and compared with various theoretical simulations along with theoretical and semi-empirical atomic parameters. The corrections of the united atomic approximation and multi-ionization atomic parameters on the simulations are studied. Additionally, due to the low dissociation energy of the molecular H2+, which is only 2.7 eV, the projectile H2+ ions are expected to be dissociated at a certain depth after passing by the surface of the target31,32,33. So, in the present work, the H2+ ion is considered as two H+ ions during the collisional ionization process with target atoms, and each of them has half the energy of the incoming molecular beam.

Experiment setup

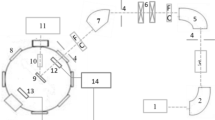
The present work was performed at the 320 kV high voltage experimental platform at the Institute of Modern Physics, Chinese Academy of Science (IMP, CAS) in Lanzhou, China34. Detailed methods and techniques have been introduced in previous work. H2+ ions are generated by ionizing hydrogen gas with 14.5 GHz microwaves in an Electron Cyclotron Resonance (ECR) ion source, and extracted by a primary voltage of 15 kV and selected by a 90° analyzing magnet. After acceleration, deflection, focusing, and beam limiting, the ion beam is introduced into the ultrahigh vacuum target chamber and vertically incident on the target surface, with a beam spot diameter of approximately 5 mm. The count of incident ions is determined indirectly by combining a penetrating Faraday cup and a conventional one. The x rays are collected by a Silicon Drift Detector (SDD), which is placed at a 45° angle with respect to the target normal, and has a solid angle of about 0.0066 rad and energy resolution of about 136 eV.

Results and discussion

Te L-shell x-ray spectra induced by H2 + ions.

Figure 1 shows the typical x-ray spectra induced by H2+ ions at various incident energies, which are actually produced by dissociated protons with half of the incident energies. As a comparison, the spectrum excited by 300 keV protons is also given. The spectra are well fitted by a nonlinear curve Gaussian fitting program with the help of origin software. One can find that the structures of the spectra are almost the same and similar to that of proton. They are identified as the L-subshell x rays of Te. It mainly contains six distinct lines and can be marked as Lι, Lα1,2, Lβ1,3,4, Lβ2,15, Lγ1, Lγ2,3,4,4ʹ x ray, which are the results of radiation transitions od M1–M3, M5, 4-L3, M4-L3/M3, 2-L1, N5, 4-L3, Lγ1, N4-L2, N3, 2-L1/ O3, 2-L1, respectively35,36.

Fig. 1
figure 1

Typical L-subshell x-ray spectra of Tellurium induced by H2+, compared with the result of proton.

Full size image

As evident from Fig. 1, despite the similarity in the overall spectral line structure, there are notable differences in their shapes and positions. Specifically, the central position of the spectral lines shifts towards higher energies compared to that of the protons. The relative intensity of Lβ x ray compared to Lα gradually is enhanced as the incident energy decreases. It is proposed that this variation can be attributed to the multiple ionization of outer-shell electrons.

Multiple ionization of Te atom produced by H2 + ions

Multiple ionization refers to the simultaneous ejection of another inner-shell or one or more outer-shell electrons accompanied by the ionization of a single inner-shell electron in the same atom, which can be induced in ion- atom collision37,38. The multiple vacancies in the outer-shells act as spectators and may not be fully filled prior to the decay of the inner-shell vacancy. Consequently, the screening of nuclear charge is reduced, leading to an increase in the binding energy of the remaining orbital electrons. As a result, the x-ray energies from the multiple ionized atoms are considerably enlarged compared to that of single ionized atom.

Table 1 presents the measured L-subshell x-ray energies of Te excited by H2+ ions at various incident energies, which are actually produced by dissociated protons with half of the incident energies, as well as those of 300 keV H+ and the data from singly ionized atoms36,39. There is no discernible regular variation in the experimental values as the projectile energy increases, and they are basically a constant within the limits of error, but are greater than the atomic data and proton data, which can also be used as single ionization data. Previous works have confirmed that the multiple ionization on the outer-shells, such as M-, N- and O-shells, can also be induced by the bombardment of lower energy light ions, such as H+ and He2+ ions, in the energy range of 75–250 keV/u, and the degree of this multiple ionization decreases with the increase of incident energy40,41. It is proposed that the same trend is expected for H2+ ions. Therefore, the observed blue shift mainly results from the outer-shell multiple ionization.

Table 1 Te L x-ray energies induced by H2+ ions (That is actually induced by the dissociated protons, and the actual proton energies are also given below that of H2+ ions.) and 300 keV H+, as well as the atomic data36,39.
Full size table

In addition to energy shift, the enhancement in relative intensity ratio of subshell x rays is another important consequence of multiple ionization, because the non-radiation process is inhibited due to the absence of outer shell electrons. Figures 2, 3, 4 present the relative intensity ratios of Lβ, Lι to Lα x rays as a function of the energy of dissociated protons. The experimental values are greater than those of theory of single ionization and the proton results39. This can be understood in terms of multiple ionization.

Fig. 2
figure 2

Relative intensity ratio of Te Lβ1, 3, 4 to Lα1, 2 x ray.

Full size image
Fig. 3
figure 3

Relative intensity ratio of Te Lβ2, 15 to Lα1, 2 x ray.

Full size image
Fig. 4
figure 4

Relative intensity ratio of Lι to Lα1, 2 x ray.

Full size image

Lβ1,3,4 x ray can be treated as two group lines from the decay of L1 and L2 vacancy, Lβ1 resulting from the radiation transition of M4-L2 and Lβ3,4 from that of M3, 2-L1. Lβ1 and Lα1,2 are mainly the radiation from the decay of L2 and L3 vacancy filled by the same 3d electrons, and the radiative yield of ωLβ1 and ωLα1, 2 is 0.020 and 0.036 for Te, respectively42. Correspondingly, The Auger yield a2 and a3 is 0.771 and 0.926. They are not much different in the same order of magnitude. In the case of multiple ionization on outer-shells, a2 and a3 will decrease by the same amplitude, and this will cause the same proportion increase of ωLβ1 and ωLα1, 2. This effect will not cause significant changes in the experimental relative intensity ratio of Lβ1,3,4 to Lα1,2. However, apart from x-ray emission and Auger transitions, the decay of L2 holes has one more non-radiative transition process than that of L3, namely the CK transition of L2-L3X. Due to the absence of outer-shell electrons caused by multiple ionizations, the CK transition here is weakened, which lead to an increase in the fluorescence yield ωLβ1, and experimentally, the emission of Lβ1 x ray is enhanced. Furthermore, for the decay of L1 hole corresponding to Lβ3, 4  x ray, the radiation transition probability is enlarged due to the suppression of multi-ionization non-radiation transition. This results in an enhanced emission of Lβ3, 4 x ray. As a result, the relative intensity ratios of Lβ1,3,4 and Lα1,2 x ray are enlarged, as presented in Fig. 3, and such enlargement is diminished with increasing energy of the dissociated protons, as aforementioned, the degree of multiple ionization decreases with the increase of incident energy of light ions in lower energy range.

Lβ2, 15 and Lα1, 2  x rays are the radiative transitions that occur when the same lower energy level L3 vacancies are filled by the N4, 5 and M4, 5 electrons, respectively. When the outer-shells such as M and N are in a state of multiple vacancies, the Auger yield a3 will weaken, leading to an enhancement of the fluorescence yield ω3. The Auger yield a3 of Te is one order of magnitude larger than ω342. When a3 decreases, ω3 will increase significantly, resulting in a remarkable enhancement of the corresponding x-ray emission. The single ionization fluorescence yield ωLα1, 2 is 6 times greater than that of ωLβ2, 15, and the change in ωLβ2, 15 is more sensitive to the effect of multiple ionization. So, the increase in ωLβ2, 15 caused by multiple ionizations is greater than that of ωLα1, 2, and this lead to a greater enhancement for Lβ2, 15 x-ray emissions than that of Lα1, 2. As a result, the observed relative intensity ratios of Lβ2, 15 to Lα1, 2 x ray are higher than the atomic data and proton result, as shown in Fig. 3.

Similar as above, Lι and Lα1, 2 x rays originate from the transitions of different M-subshell electrons to the L3 vacancy, respectively. The increase in fluorescence yield for these two x rays is mainly affected by the change in the Auger yield a3. The fluorescence yield ωLι is significantly smaller than ωLα1,2, accounting for merely 4% of the later42. Under the multiple ionization, ωLι exhibits a greater amplification compared to ωLα1,2. Therefore, the experimental emission increase in Lι x ray is greater than that of Lα1, 2. As shown in Fig. 4, the relative intensity of Lι to Lα1, 2  x ray is enlarged, and deceases as a function of the energy of dissociated protons due to the decreasing extent of multiple ionization. In a word, the observed enhancement of the relative intensity ratios of the L-subshell x rays provides further evidence for the multiple ionization of Te induced by lower energy H2+ ions.

Te L-subshell x-ray production cross section excited by H2 + ions

As mentioned in the introduction, the projectile H2+ ions have already been dissociated before exciting the ionization of the target atoms31,32,33. So, the H2+ ions are treated as H+ ions in the following calculations, for instance, the simulation of stopping power and ionization cross section. Additionally, the energy of this H+ ion is half of that of the incident H2+ ions.

In the present experiment, the projected ranges of dissociated protons in Te are much less than the target thickness. The target is regarded as a thick target. The x-ray production cross section at the incident energy E, defined as σx(E), can be extracted from the x-ray yield using the thick-target formula as following43:

$$\sigma_{{{\text{LX}}}} {(}E{)} = \frac{{1}}{n}\frac{dY}{{dE}}\frac{dE}{{dR}} + \frac{\mu }{n}\frac{\cos \theta }{{\cos \phi }}Y{(}E{)}$$
(1)
$$Y = \frac{{N_{X} }}{{N_{p} \eta {(}\Omega {/4}\pi {)}}}$$
(2)

where, n represents the atom density of target. Y is defined as the x-ray yield per incident ion, however, in reality, it is the yield per H+ ion because the incoming molecular H2+ ions are dissociated into protons. dY/dE is the derivative of Y(E) with respect to the energy of H+ ions which originates from the dissociation of molecular H2+ ions and has half the energy of H2+ ions, and it is extracted from the derivative of the calculated lnY versus lnE curve, i.e. dY/dE = Y[d(lnY)/d(lnE)]/E. The derivative d(lnY)/d(lnE) is obtained by fitting the polynomials to lnY = A(lnE-B)C, A, B and C are fitting parameters34. dE/dR is the stopping power of H+ ions with half the energy of the incident H2+ ions and is calculated using the software of SRIM44. μ is the self-absorption coefficient of characteristic x ray45. θ is the angle between the ion incident direction and target normal. φ is the SDD detection angle from the target normal. Nx is x-ray counts detected by SDD. Np is the number of H+ ions involved in the collision, which is twice the number of incident H2+ ions, because at the impact with sample a H2+ ion is immediately dissociated into two protons. Ω and η are the solid angle and efficiency of SDD, respectively. The SDD intrinsic efficiency, which combines the effects of transmission through the Be window and interaction in the silicon detector, is determined and provided by the manufacturer of Amptek Company46. The experimental uncertainty mainly comes from x-ray counts (< 5%), projectile ion statistic (< 3%), detection efficiency (≈10%), solid angel measurement (≈2%), stopping power estimation (≈10%), and derivative calculation of the experimental yield curve (< 2%). The maximum uncertainty in the yield is approximately 12%, while that in the cross-section is about 16%.

The experimental L-subshell and total x-ray production cross sections in Te excited by H2+ ions, which is actually produced by the dissociated protons, are listed in Table 2, and also shown in Fig. 5 as a function of the energy of dissociated protons. The values of the observed six distinguished L-subshell x rays are obtained directly from the x-ray counts with the help of Eqs. (1) and (2). The results of Lβ and Lγ are calculated by summing the data of Lβ1,3,4 and Lβ2,15, and that of Lγ1 and Lγ2,3,44ʹ, respectively. The LTotal is the summation of all the result of individual L-subshell x ray. All of those increase rapidly with increasing energy of the dissociated protons. It is at the magnitude of about 10–4–10–2 barn for Lι and Lγ x ray, and 10–3–10–1 barn for Lα, Lβ and LTotal. In addition, compared with the previous work39, as shown in Fig. 5, one can find that the present measured cross sections are almost equal for those of protons with half of the original energy of incoming H2+ ions within the uncertainty intervals.

Table 2 Experimental Te L-subshell and total L-shell x-ray production cross section induced by H2+ ions, which is actually excited by the dissociated protons with half energy of H2+ ions.
Full size table
Fig. 5
figure 5

Experimental Te L-subshell and total x-ray production cross section as a function of the actual energy of the dissociated protons, and compared with theoretical simulations.

Full size image

The theoretical x-ray production cross section, σLx (x = ι, α, β, γ), can be converted from the Li-subshell ionization cross section σLi (i = 1, 2, 3) by the following expressions47:

$$\sigma_{L\iota } = [\sigma_{L1} \left( {f_{13} + f_{12} f_{23} } \right) + \sigma_{L2} f_{23} + \sigma_{L3} ]\omega_{3} F_{3\iota }$$
(3)
$$\sigma_{L\alpha } \, = \,[\sigma_{L1} (f_{13} \, + \,f_{12} f_{23} )\, + \,\sigma_{L2} f_{23} \, + \,\sigma_{L3} ]\omega_{3} F_{3\alpha }$$
(4)
$$\sigma_{L\beta } \, = \,\sigma_{L1} \omega_{1} F_{1\beta } + (f_{12} \sigma_{L1} + \sigma_{L2} )\omega_{2} F_{2\beta } + [\sigma_{L1} (f_{13} \, + \,f_{12} f_{23} )\, + \,\sigma_{L2} f_{23} \, + \,\sigma_{L3} ]\omega_{3} F_{3\beta }$$
(5)
$$\sigma_{Lg} = \sigma_{L1} \omega_{1} F_{1\gamma } + (f_{12} \sigma_{L1} + \sigma_{L2} ) \, \omega_{2} F_{2\gamma }$$
(6)
$$\sigma_{LTot} \, = \,[\omega_{1} + \omega_{2} f_{12} \, + \,\omega_{3} (f_{13} \, + \,f_{12} f_{23} \, + \,f^{\prime}_{13} )]\sigma_{L1} + (\omega_{2} + f_{23} \omega_{3} )\sigma_{L2} + \omega_{3} \sigma_{L3}$$
(7)

Where, σLi is the theoretical ionization cross section induced by the H+ ions with half the energy of the incident H2+ ions after considering the dissociation of the molecule H2+, and that of PWAB, ECPSSR and ECUSAR are obtained using the ISICS program48. fij is the Coster-Kronig yield, ωi is the i-subshell fluorescence yield. FiX is the fraction of the radiative width of the subshell Li contained in the Xth spectral line. In the present calculations, the single-ionized data of ω0i and f0ij are taken from semi-empirical data collected by Krause25, and the theoretical calculation based on the relativistic Dirac-Hartree-Slater model collected by Campbell28,29, which can also be referenced from the calculations of Chen et al. and Puri et al.26,27. Meanwhile, the data of FiX comes from the tables of Scofield49,50.

As introduced above, multiple ionization in the target atom can substantially change the atomic parameters, such as increasing the fluorescence yield and decreasing CK transition rates, along with change of Auger yield, which in turn enhances the efficient x-ray production cross section. In the present calculations, the atomic parameters ωi and fij are modified for multiple ionization according to the model proposed by Lapicki et al.23, and these are listed in the Tables 3 and 4. In the present experimental energy range, the fluorescence yield ωi is larger than ω0i and decreases with the increase of proton energy, while fij is getting larger and larger, and continuously approaching the atomic data.

Table 3 Corrected atomic parameters by the multiple ionization for the semi-empirical data (Krause’s data).
Full size table
Table 4 Corrected atomic parameters by the multiple ionization for the theoretical data of relativistic Dirac-Hartree-Slater (DHS data).
Full size table

Figure 5 graphically illustrates the theoretical estimations of BEA, PWBA, ECPSSR and ECUSAR using the single ionization atomic parameters of theoretical DHS database, as well as the predictions of ECPSSR-MI and ECUSAR-MI that employ the corrected atomic parameters derive from multiple ionization. It is obvious that the PWBA simulation is higher than the experimental result. The discrepancy between the PWBA theory and the experiment is diminished as the dissociated proton energy increases, but it remains consistently larger than the experiment in the present energy range. For instance, it is still larger than the experiment by about one order of magnitude at the energy of 150 keV. The BEA estimation is equivalent to the experimental data in magnitude, but deviates significantly from the experiment in the tendency as a function of the energy of dissociated protons. It is relatively close to the experiment at 150 keV, but greater than the experiment when the proton energy is less than 150 keV, and then it is lower than the experiment with the increase of the energy of dissociated protons. The ECPSSR model displays superior agreement with experiment compared to BEA and PWBA, albeit with a slight underestimation relative to the experimental outcomes. Both the modification of united atom approximation and the correction of multiple ionization on atomic parameters lead to an enhancement in ECPSSR calculations. Overall, the ECUSAR-MI provides the best prediction to the experimental results.

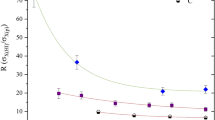
To facilitate a clearer comparison of the effects of multi-ionized atomic parameter correction and united atom approximation modification on the theoretical calculations, the ratios of experimental data to ECPSSR values employing distinct corrections is given in Fig. 6 as a function of the energy of dissociated protons. It is evident that the ratio of Exp/ECUSAR-MI is closest to 1, and this is smaller than that of Exp/ECPSSR-MI which is smaller than that of Exp/ECPSSR, and this is larger than that of Exp/ECUSAR. The separation between Exp/ECPSSR and Exp/ECUSAR is greater than that between Exp/ECPSSR and Exp/ECPSSR-MI. These intervals all decrease with increasing energy. The results indicate that the both corrections result in an increase in theory simulations. The modification of UA is stronger than the correction of MI. All corrections are more effective at lower energy and weaken as the dissociated protons energy increases. The ECUSAR-MI model combined both corrections of UA and MI is in the best agreement with the experiment.

Fig. 6
figure 6

The ratios of experimental x-ray production cross section to the estimation of ECPSSR and ECUSAR using Campbell’s atomic parameters and those with multiple ionization atomic parameters.

Full size image

To further evaluate the discrepancy in theoretical simulation arising from the use of various atomic parameters, the detailed comparisons between the experiment and the theoretical calculations using the different atomic parameters of Krause and DHS database, as well as the corrections of multiple ionization are shown in Fig. 7. The ratio derived from Krause’s data is larger than that obtained using the DHS data. With the same atomic parameters, the ratio involving UA modification is smaller. The ratio of Exp/ECUSAR-MI is the smallest. The interval between Exp/ECPSSR-MI using different atomic parameter is smaller than that caused by the UA modification. Similarly, the spacing between Exp/ECUSAR using different databases is also smaller than that modified by UA. The deviations among various ratios decrease with energy due to the weakening of the corrections. The change produced by parameter selection is less than that of UA modification. Although selecting different databases of atomic parameters can lead to variations in the estimation of x-ray production cross section, it does not affect the choice of a suitable theory for the simulation of ionization in ion-atom collisions.

Fig. 7
figure 7

The measured x-ray production cross section compared with theoretical calculations of ECPSSR-MI and ECUSAR-MI using Krause’s and DHS atomic parameters.

Full size image

Conclusion

The study has delved into the L-shell x-ray emission of Te excited by He2+ ions in the lower energy range of 150–300 keV. The energy shifts and the relative intensity ratios of the subshell x rays are investigated. The new experimental data of x-ray production cross section are acquired and compared with various theoretical calculations with different corrections. It is found that the Te atoms are multiply ionized by the impact of the dissociated protons, resulting in a blue shift of the energy and an enhancement of the relative intensity ratio of the L-subshell x-ray. The extent of this multiple ionization is decreased with increasing incident energy. The measured cross sections are approximately those of protons with half of the original energy of H2+ ions. The ECUSAR-MI using the DHS data is in a best agreement with the experiment. The L-shell ionization of Te can be simulated using the ECPSSR model with the modification of united atom approximation. In the prediction of x-ray production cross section, it is needed to incorporate the correction of multiple ionization atomic parameters, and the influence of selecting different databases should be considered carefully.