Rainfall data modeling using improved adaptive type-II progressively censored Weibull-exponential samples

Abstract

To get enough data from experiments that last for a long time, a recently unique improved adaptive Type-II progressive censoring technique has been suggested. This study, taking this scheme into consideration, concentrates on some conventional and Bayesian estimation tasks for parameter and reliability indicators, where the underlying distribution is the Weibull-exponential. From a traditional point of view, the likelihood methodology is explored for gaining point and approximate confidence interval estimates. Apart from the standard method, the Bayesian methodology is investigated to obtain the Bayesian point and credible intervals by taking advantage of the Markov chain Monte Carlo technique and the squared error loss function. To differentiate between the traditional and Bayesian estimates, a simulation analysis proceeds under various conditions. In order to put the suggested strategies into application, a pair of rainfall data sets are evaluated and numerous precision criteria are employed to pick the best progressive censoring plan.

Introduction

In recent times, dozens of lifetime distributions, featuring various forms for the probability density function (PDF) and hazard rate function (HRF), have been offered to boost modelling capability for actual life data sets. Among the ways to achieve this is to add additional parameters to already existing distributions or to combine them. A novel three-parameter Weibull-exponential (WEx) lifetime model was released by Oguntunde et al.¹, leveraging the exponential (Ex) distribution as a basis for the model in the Weibull-G family of distributions.

The WEx distribution

Suppose Y is a lifetime of a product that follows the $\hbox {WEx}(\varvec{\psi })$, where $\varvec{\psi }=(\rho ,\xi ,\mu )^\top$, where $\rho$ and $\mu$ are scale parameters and $\xi$ is shape parameter. Let $\varpi (y;\mu )=e^{\mu y}-1$, then its PDF and cumulative distribution function (CDF), can be defined as

$$\begin{aligned} g(y;\varvec{\psi })=\rho \xi \mu [\varpi (y;\mu )]^{\xi -1} e^{\mu y-\rho [\varpi (y;\mu )]^{\xi }},\ y>0,\ \rho ,\xi ,\mu >0 \end{aligned}$$

(1)

and

$$\begin{aligned} G(y;\varvec{\psi })=1-e^{-\rho [\varpi (y;\mu )]^{\xi }}, \end{aligned}$$

(2)

respectively. The reliability function (RF), and HRF (at a specific time $t>0$) of the WEx distribution are, respectively, given by

$$\begin{aligned} R(t;\varvec{\psi })=e^{-\rho [\varpi (t;\mu )]^{\xi }}\ t>0,\ \rho ,\xi ,\mu >0 \end{aligned}$$

(3)

and

$$\begin{aligned} h(t;\varvec{\psi })=\rho \xi \mu e^{\mu t} [\varpi (t;\mu )]^{\xi -1}. \end{aligned}$$

(4)

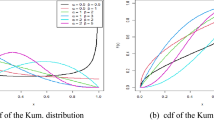
By setting $\rho =1$, the WEx model returns to the Gompertz distribution with shape parameter $\theta >0$. Additionally, by putting $\rho =1$, the WEx model reduces to the modified Kies exponential distribution by Al-Babtain et al.². Taking several options of $\rho$ and $\xi$ when $\mu =1$, several shapes of the density and hazard rate functions of the WEx distribution are depicted in Fig. 1. Figure 1a indicates that the WEx density (1) has a unimodal, bimodal or decreasing shape. Figure 1b shows that the HRF in (4) has a increasing or bathtub shape. Consequently, the WEx model became one of the most useful and applicable distributions for purposes of dependability and data analysis; for instance, based on progressive, hybrid, and adaptive progressive censored samples, Rastogi³, Abushal⁴, EL-Sagheer et al.⁵, respectively, studied some estimation issues of the WEx distribution.

Fig. 1

Shapes of the WEx distribution at $\mu =1$ (a) PDF and (b) HRF.

Reliability estimation and censoring strategy

Since reliability evaluation can yield a quantitative assessment of a product’s durability, it is crucial to life-testing studies. To ensure that the product satisfies stated reliability criteria and to forecast potential shortcomings, this estimation can be very helpful. For a long-lasting reliable product, the investigator can use a portion of data to assess the product’s reliability without wasting time waiting until all of the sample data fails. The literature offers numerous strategies for stopping the experiment before the entire sample fails in order to save both cash and time, see Maswadah⁶. We call these processes “censorship procedures”. One of the most commonly employed ways for getting data is the Progressive Type-II censoring (TII-PC) scheme. This plan enables the removal of some still-living units at certain prearranged points throughout the trial. For more detail, see Balakrishnan and Cramer⁷. A different kind of multi-stage censoring was suggested by Ng et al.⁸ and is referred to as adaptive progressive Type-II censoring (ATII-PC). This strategy resolves the problem of getting a few observed failures in progressive Type-I hybrid censorship plan proposed by Kundu and Joarder⁹. According to Ng et al.⁸, the ATII-PC plan performs well in statistical induction when test length is not a significant factor. However, when the test units are incredibly reliable, the testing period will be excessively lengthy, and the APT-IIC will not have worked in guaranteeing an appropriate total test duration. According to Ng et al.⁸, the APT-IIC performs well in statistical inference when test length is not a significant factor. However, if the test units are incredibly reliable, the testing period will be excessively lengthy, and the APT-IIC will not have succeeded in guaranteeing an appropriate total test duration. Yan et al.¹⁰ developed a fresh censoring technique termed an improved adaptive progressive Type-II censoring (ITII-APC) mechanism in order to address this problem.

A detailed explanation of the ITII-APC sample is provided as follows: Assume that two boundaries, $T_{1}<T_{2}$, a progressive censoring plan (PCP) ${{\textbf {S}}}=\left( S_{1},\dots ,S_{m}\right)$, and the number of observed failures $m<n$ are prefixed before starting the test which contains n independent and identical units at time zero. When the first failure occurred with time $Y_{1:m:n}$, a random selection of the remaining items $S_{1}$ is eliminated from the test. Once more, after the second failure occurred with time $Y_{2:m:n}$, $S_{2}$ items are randomly dropped from the test, and so forth. The ITII-APC plan gives us one of the three possible outcomes: Case-1: if $Y_{m:m:n}<T_{1}$, the experiment stops at $Y_{m:m:n}$ and all the remaining items are removed at the $m^{th}$ failure, i.e. $S_{m}=n-m-\sum _{i=1}^{m-1}S_{i}$. It is clear that this case presents the TII-PC sample. Case-2: if $T_{1}<Y_{m:m:n}<T_{2}$, the test stops at $Y_{m:m:n}$ and all items that did not fail are removed at the $m^{th}$ failure, i.e. $S_{m}=n-J_{1}-\sum _{i=1}^{J_{1}}S_{i}$. Here $J_{1}$ refers to the number of failures before the first boundary $T_{1}$. It is important to mention here that no items are removed from the test after observing $Y_{J_{1}:m:n}$, which means that the PCP is adapted to be ${{\textbf {S}}}=\left( S_{1},\dots ,S_{J_{1}},0,\dots ,0,S_{m}\right)$. This case describes the APT-IIC sample. Case 3: if$T_{1}<T_{2}<Y_{m:m:n}$, the test stops at the boundary $T_{2}$ and all remaining items at this threshold are removed, i.e. $S^{\star }=n-J_{2}-\sum _{i=1}^{J_{1}}S_{i}$, where $J_{2}$ denotes the number of observed failures acquired before $T_{2}$. The adaption of the PCP is applied here also as Case-2, once the experiment reaches $T_{1}$. This means the PCP becomes ${{\textbf {S}}}=\left( S_{1},\dots ,S_{J_{1}},0,\dots ,0,S^{\star }\right)$.

Reviewing the literature related to the ATII-PC and ITII-APC schemes reveals that numerous studies took into account the estimations of some lifetime models in the presence of ATII-PC data. Conversely, not much work has been done on the ITII-APC plan. Sobhi and Soliman¹¹ Nassar and Abo-Kasem¹², Chen and Gui¹³, Panahi and Moradi¹⁴, Kohansal and Shoaee¹⁵, Du and Gui¹⁶, and Alotaibi et al.¹⁷ are some studies that are relevant to the ATII-PC scheme. On the other hand, Nassar and Elshahhat¹⁸, Elshahhat and Nassar¹⁹, Elbatal et al.²⁰, Alam and Nassar²¹, Dutta and Kayal²², Asadi et al.²³, Alotaibi et al.²⁴, Alqasem et al.²⁵ and Elbatal et al.²⁶. considered some estimation issues using the ITII-APC samples. Now, suppose that ${{{\underline{\varvec{y}}}}}=(y_{1}<\dots<y_{J_{1}}<T_{1}<\dots<y_{J_{2}}<T_{2}$) refers to the observed ITII-APC data with PCP ${{\textbf {S}}}$. Then, the likelihood function (LF) of the unknown parameters $\varvec{\psi }$ can be formulated as

$$\begin{aligned} L(\varvec{\psi }|{{{\underline{\varvec{y}}}}})= C\prod _{i=1}^{D_2} g(y_{i})\prod _{i=1}^{D_1} \left[ 1-G(y_{i})\right] ^{S_i} \left[ 1-G(T^*)\right] ^{S^*}, \end{aligned}$$

(5)

where $y_{i}=y_{i:m:n}$ for simplicity and C is a constant. The possible choices of $T^*$, $D_{1}$, $D_{2}$ and $S^*$ for Cases 1, 2 and 3 are presented in Table 1.

Table 1 Possible values of $T^*$, $D_{1}$, $D_{2}$ and $S^*$.

Four key points highlight the significance of this study. First, the ITII-APC scheme demonstrates effectiveness in statistical inference when the tested units show high reliability. In these instances, the testing period often becomes excessively long, and traditional censoring methods like TII-PC and ATII-PC schemes may not adequately ensure a sufficient total test duration. The analysis of real data sets collected using the ITII-APC scheme allows us to obtain a comprehensive understanding of the variable of interest without requiring all tested units to fail. Second, the importance of the WEx distribution in fitting real-life data. Unlike the gamma distribution and its generalizations as well as the modifications of the Weibull distribution, the WEx distribution is particularly easy to use with censored data due to its simple forms of PDF and CDF. Third, to the best of our knowledge, this is the first study to examine the reliability estimations of the WEx distribution using the ITII-APC data, which may be of interest to many readers. Fourth, this study generalizes several existing studies, including the work of Rastogi³ and EL-Sagheer et al.⁵, which can be viewed as special cases of the current research. The main contributions of this study are summarized below:

• 1. Estimating the parameter vector $\varvec{\psi }$ and the reliability metrics using the maximum likelihood (ML) estimation method. Additionally, the approximate confidence intervals (ACIs) of various quantities are developed.

• 2. Employing the Markov chain Monte Carlo (MCMC) approach to obtain Bayes estimates using the squared error loss function. Additionally, we calculate the Bayes highest posterior density (HPD) credible intervals for the various parameters.

• 3. Comparing the classical and Bayes estimates through a simulation study based on various precision standards.

• 4. To provide evidence of the value of the suggested methodologies, two applications using real-life data are investigated.

• 5. Considering four optimality standards to investigate the problem of selecting the optimal PCP for the WEx model in the presence of ITII-APC data.

The remaining sections of this study are organized in the following manner: The ML estimations (MLEs) and ACIs for various parameters and the reliability measures are covered in Section “Likelihood approach”. The Bayesian estimations with the squared error loss function and the MCMC algorithm are dealt with in Section “Bayesian approach”. The simulation results based on various experimental scenarios are shown in Section “Monte Carlo evaluations”. The results of the analysis of two real-world data sets are presented in Section “Rainfall data analysis”. In Section “Optimal progressive censoring”, we look into the problem of selecting the optimal PCP based on four optimality criteria with applications. Some conclusions are displayed in Section “Concluding remarks”.

Likelihood approach

For statistical models, one of the most frequently employed methods for estimating parameters is the ML estimation approach. Based on an ITII-APC sample ${{{\underline{\varvec{y}}}}}$ along with PCP ${{\textbf {S}}}=\left( S_{1},\dots ,S_{J_{1}},0,\dots ,0,S^{*}\right)$, this section is considered the ML estimation of the WEx parameters including RF and HRF. This sections considers both point and interval estimations of the mentioned parameters.

Point estimation

Acquiring the observed ITII-APC sample ${{{\underline{\varvec{y}}}}}$, the LF can be written from the PDF given by (1), the CDF in (2) and the joint LF provided by (5) as given below, without the constant term,

$$\begin{aligned} L(\varvec{\psi }|{{{\underline{\varvec{y}}}}})= (\rho \xi \mu )^{D_{2}}\exp \left[ \mu \sum _{i=1}^{D_{2}}y_{i}+(\xi -1)\sum _{i=1}^{D_{2}}\log [\varpi (y_{i};\mu )]-\rho Q({{{\underline{\varvec{y}}}}};\mu ,\xi ) \right] , \end{aligned}$$

(6)

where $Q({{{\underline{\varvec{y}}}}};\mu ,\xi )=\sum _{i=1}^{D_{2}}[\varpi (y_{i};\mu )]^{\xi }+\sum _{i=1}^{D_{1}}S_{i}[\varpi (y_{i};\mu )]^{\xi }+S^{*}[\varpi (T^{*};\mu )]^{\xi }$. The log-LF of (6) can be expresses as follows

$$\begin{aligned} l(\varvec{\psi }|{{{\underline{\varvec{y}}}}})= D_{2}\log (\rho \xi \mu )+\mu \sum _{i=1}^{D_{2}}y_{i}+(\xi -1)\sum _{i=1}^{D_{2}}\log [\varpi (y_{i};\mu )]-\rho Q({{{\underline{\varvec{y}}}}};\mu ,\xi ). \end{aligned}$$

(7)

From (7), the normal equations of $\rho , \xi$ and $\mu$ are

$$\begin{aligned} & \frac{\partial l(\varvec{\psi }|{{{\underline{\varvec{y}}}}})}{\partial \rho }= \frac{D_{2}}{\rho }-Q({{{\underline{\varvec{y}}}}};\mu ,\xi )=0, \end{aligned}$$

(8)

$$\begin{aligned} & \frac{\partial l(\varvec{\psi }|{{{\underline{\varvec{y}}}}})}{\partial \xi }=\frac{D_{2}}{\xi }+\sum _{i=1}^{D_{2}}\log [\varpi (y_{i};\mu )]-\rho Q_{1}({{{\underline{\varvec{y}}}}};\mu ,\xi )=0 \end{aligned}$$

(9)

and

$$\begin{aligned} \frac{\partial l(\varvec{\psi }|{{{\underline{\varvec{y}}}}})}{\partial \mu }=\frac{D_{2}}{\mu }+(\xi -1)\sum _{i=1}^{D_{2}}\varpi ^{*}(y_{i};\mu )+\sum _{i=1}^{D_{2}}y_{i}-\rho Q_{2}({{{\underline{\varvec{y}}}}};\mu ,\xi )=0, \end{aligned}$$

(10)

where $\varpi ^{*}(y_{i};\mu )=y_{i}/(1-e^{-\mu y_{i}})$, $Q_{1}({{{\underline{\varvec{y}}}}};\mu ,\xi )$ and $Q_{2}({{{\underline{\varvec{y}}}}};\mu ,\xi )$ are defined as follow

$$\begin{aligned} Q_{1}({{{\underline{\varvec{y}}}}};\mu ,\xi )=\sum _{i=1}^{D_{2}}\varpi _{1}(y_{i};\mu )+\sum _{i=1}^{D_{1}}S_{i}\varpi _{1}(y_{i};\mu )+\varpi _{1}(T^{*};\mu ) \end{aligned}$$

and

$$\begin{aligned} Q_{2}({{{\underline{\varvec{y}}}}};\mu ,\xi )=\sum _{i=1}^{D_{2}}\varpi _{2}(y_{i};\mu )+\sum _{i=1}^{D_{1}}S_{i}\varpi _{2}(y_{i};\mu )+\varpi _{2}(T^{*};\mu ), \end{aligned}$$

with $\varpi _{1}(y_{i};\mu )=[\varpi (y_{i};\mu )]^{\xi }\log [\varpi (y_{i};\mu )]$ and $\varpi _{2}(y_{i};\mu )=\xi y_{i}e^{\mu y_{i}}[\varpi (y_{i};\mu )]^{\xi -1}$. From equation (8), the MLE of the parameter $\rho$ can be determined as a function of the parameters $\xi$ and $\mu$ as

$$\begin{aligned} \hat{\rho }(\xi ,\mu )=\frac{D_{2}}{Q({{{\underline{\varvec{y}}}}};\mu ,\xi )}. \end{aligned}$$

(11)

Substitute (11) in (9) and (10), the MLEs of $\xi$ and $\mu$ can be obtained by solving the following nonlinear system of equations

$$\begin{aligned} \frac{1}{\xi }+\frac{1}{D_{2}}\sum _{i=1}^{D_{2}}\log [\varpi (y_{i};\mu )]-\frac{Q_{1}({{{\underline{\varvec{y}}}}};\mu ,\xi )}{Q({{{\underline{\varvec{y}}}}};\mu ,\xi )}=0 \end{aligned}$$

(12)

and

$$\begin{aligned} \frac{1}{\mu }+\frac{\xi -1}{D_{2}}\sum _{i=1}^{D_{2}}\varpi ^{*}(y_{i};\mu )+\frac{1}{D_{2}}\sum _{i=1}^{D_{2}}y_{i}- \frac{Q_{2}({{{\underline{\varvec{y}}}}};\mu ,\xi )}{Q({{{\underline{\varvec{y}}}}};\mu ,\xi )}=0, \end{aligned}$$

(13)

Upon getting the MLEs $\hat{\xi }$ and $\hat{\mu }$ by solving (12) and (13) numerically, the MLE of $\rho$, denoted by $\hat{\rho }$, can be acquired directly from (11). The MLEs of the RF in (3) and HRF in (4) can be obtained also using the invariance property of the MLEs as given below

$$\begin{aligned} {\hat{R}}(t)=e^{-\hat{\rho }[\varpi (t;\hat{\mu })]^{\hat{\xi }}} \end{aligned}$$

and

$$\begin{aligned} {\hat{h}}(t)=\hat{\rho }\hat{\xi }\hat{\mu } e^{\hat{\mu } t} [\varpi (t;\hat{\mu })]^{\hat{\xi }-1}. \end{aligned}$$

Interval estimation of $\rho , \xi$ and $\mu$

The ACIs of the unknown parameters are constructed using the asymptotic normality of the MLEs. Given the log-LF in (7), we have the following second derivatives

$$\begin{aligned} & \frac{\partial ^{2} l(\varvec{\psi }|{{{\underline{\varvec{y}}}}})}{\partial \rho ^{2}}= -\frac{D_{2}}{\rho ^{2}},\,\,\, \frac{\partial ^{2} l(\varvec{\psi }|{{{\underline{\varvec{y}}}}})}{\partial \rho \partial \xi }= -Q_{1}({{{\underline{\varvec{y}}}}};\mu ,\xi ),\,\,\,\frac{\partial ^{2} l(\varvec{\psi }|{{{\underline{\varvec{y}}}}})}{\partial \rho \partial \mu }= -Q_{2}({{{\underline{\varvec{y}}}}};\mu ,\xi ),\\ & \frac{\partial ^{2} l(\varvec{\psi }|{{{\underline{\varvec{y}}}}})}{\partial \xi ^{2}}=-\frac{D_{2}}{\xi ^{2}}-\rho Q_{11}({{{\underline{\varvec{y}}}}};\mu ,\xi ),\,\,\, \frac{\partial ^{2} l(\varvec{\psi }|{{{\underline{\varvec{y}}}}})}{\partial \xi \partial \mu }= \sum _{i=1}^{D_{2}}\varpi ^{*}(y_{i};\mu )-\rho Q_{12}({{{\underline{\varvec{y}}}}};\mu ,\xi ), \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^{2} l(\varvec{\psi }|{{{\underline{\varvec{y}}}}})}{\partial \mu ^{2}}=-\frac{D_{2}}{\mu ^{2}}+(\xi -1)\sum _{i=1}^{D_{2}}\varpi ^{**}(y_{i};\mu )-\rho Q_{22}({{{\underline{\varvec{y}}}}};\mu ,\xi ), \end{aligned}$$

where $\varpi ^{**}(y_{i};\mu )=e^{-\mu y_{i}}[\varpi ^{*}(y_{i};\mu )]^{2}$ and

$$\begin{aligned} & Q_{11}({{{\underline{\varvec{y}}}}};\mu ,\xi )=\sum _{i=1}^{D_{2}}\varpi _{11}(y_{i};\mu )+\sum _{i=1}^{D_{1}}S_{i}\varpi _{11}(y_{i};\mu )+\varpi _{11}(T^{*};\mu ),\\ & Q_{22}({{{\underline{\varvec{y}}}}};\mu ,\xi )=\sum _{i=1}^{D_{2}}\varpi _{22}(y_{i};\mu )+\sum _{i=1}^{D_{1}}S_{i}\varpi _{2}(y_{i};\mu )+\varpi _{22}(T^{*};\mu ),\\ & Q_{12}({{{\underline{\varvec{y}}}}};\mu ,\xi )=\sum _{i=1}^{D_{2}}\varpi _{12}(y_{i};\mu )+\sum _{i=1}^{D_{1}}S_{i}\varpi _{12}(y_{i};\mu )+\varpi _{12}(T^{*};\mu ), \end{aligned}$$

with $\varpi _{11}(y_{i};\mu )=[\varpi (y_{i};\mu )]^{\xi }\log ^{2}[\varpi (y_{i};\mu )]$, $\varpi _{22}(y_{i};\mu )=y_{i}\varpi _{2}(y_{i};\mu )+\xi (\xi -1)y_{i}^{2}e^{2\mu y_{i}}[\varpi (y_{i};\mu )]^{\xi -2}$ and $\varpi _{12}(y_{i};\mu )=y_{i}e^{\mu y_{i}}[\varpi (y_{i};\mu )]^{\xi -1}\{1+\xi \log [\varpi (y_{i};\mu )]\}$.

As is well known, the inverse Fisher information matrix provides the asymptotic variance-covariance matrix for the MLEs. The Fisher information matrix is difficult to define exactly in our case due to the complex forms of the second derivatives, thus we utilize the approximation asymptotic variance-covariance matrix, which is shown below

$$\begin{aligned} {\varvec{I}}^{-1}(\hat{\varvec{\psi }})=\left[ \begin{array}{ccc} -\frac{\partial ^{2}l(\varvec{\psi }) }{\partial \rho ^{2}} & -\frac{\partial ^{2}l(\varvec{\psi }) }{\partial \rho \partial \xi } & -\frac{\partial ^{2}l(\varvec{\psi }) }{\partial \rho \partial \mu } \\ & -\frac{\partial ^{2}l(\varvec{\psi }) }{\partial \xi ^{2}} & -\frac{\partial ^{2}l(\varvec{\psi }) }{\partial \xi \partial \mu } \\ & & -\frac{\partial ^{2}l(\varvec{\psi }) }{\partial \mu ^{2}} \end{array} \right] _{\varvec{\psi }=\hat{\varvec{\psi }}}^{-1}, \end{aligned}$$

where $\hat{\varvec{\psi }}=(\hat{\rho },\hat{\xi },\hat{\mu })^\top$. The asymptotic normality of the MLEs stated that $(\hat{\rho },\hat{\xi },\hat{\mu })\sim N\left[ (\rho ,\xi ,\mu ),{\varvec{I}}^{-1}(\hat{\varvec{\psi }})\right]$. Then, the $100(1-\tau )\%$ ACIs of $\rho ,\xi$ and $\mu$ can be constructed as

$$\begin{aligned} \left( \hat{\rho }\pm z_{\tau /2}\sqrt{{\hat{V}}_{1}}\right) , \,\,\,\,\left( \hat{\xi }\pm z_{\tau /2}\sqrt{{\hat{V}}_{2}}\right) \,\,\,\,\text {and}\,\,\, \left( \hat{\mu }\pm z_{\tau /2}\sqrt{{\hat{V}}_{3}}\right) , \end{aligned}$$

where ${\hat{V}}_{j}, j=1,2,3$ are the main diagonal elements of ${\varvec{I}}^{-1}(\hat{\varvec{\psi }})$ and $z_{\tau /2}$ is determined from the standard normal distribution.

Interval estimation of R(t) and h(t)

The delta method, see Greene²⁷, is considered to get the approximate estimates of the variances for the MLEs of RF and HRF. Let $\Delta _{1}$ and $\Delta _{2}$ two vectors consist of the first partial derivatives of R(t) and h(t) with respect to $\rho , \xi$ and $\mu$, where

$$\begin{aligned} \Delta _{1}=\left[ \frac{\partial R(t)}{\partial \rho }\,\,\frac{\partial R(t)}{\partial \xi }\,\,\frac{\partial R(t)}{\partial \mu } \right] _{\varvec{\psi }=\hat{\varvec{\psi }}}\,\,\text {and}\,\, \Delta _{2}=\left[ \frac{\partial h(t)}{\partial \rho }\,\,\frac{\partial h(t)}{\partial \xi }\,\,\frac{\partial h(t)}{\partial \mu }\right] _{\varvec{\psi }=\hat{\varvec{\psi }}}, \end{aligned}$$

where

$$\begin{aligned} & \frac{\partial R(t)}{\partial \rho }=-[\varpi (t;\mu )]^{\xi }e^{-\rho [\varpi (t;\mu )]^{\xi }},\, \frac{\partial R(t)}{\partial \xi }=-\rho \log [\varpi (t;\mu )] [\varpi (t;\mu )]^{\xi }e^{-\rho [\varpi (t;\mu )]^{\xi }}\\ & \frac{\partial R(t)}{\partial \mu }=-\xi \rho t e^{\mu t}[\varpi (t;\mu )]^{\xi -1}e^{-\rho [\varpi (t;\mu )]^{\xi }},\, \frac{\partial h(t)}{\partial \rho }=\xi \mu e^{\mu t} [\varpi (t;\mu )]^{\xi -1}\\ & \frac{\partial h(t)}{\partial \xi }=\frac{\rho \mu \varpi _{12}(t;\mu )}{t},\, \frac{\partial h(t)}{\partial \mu }=\xi \rho e^{\mu t} [\varpi (t;\mu )]^{\xi -2}\left[ e^{\mu t}-\mu t(1-\xi e^{\mu t})-1\right] . \end{aligned}$$

Then, the approximate estimates of the variances of the MLEs of RF and HRF, can be computed, respectively, as

$$\begin{aligned} {\hat{V}}_{4}=\left[ \Delta _{1} {\varvec{I}}^{-1}(\hat{\varvec{\psi }})\acute{\Delta }_{1}\right] \,\,\text {and}\,\, {\hat{V}}_{5}=\left[ \Delta _{2} {\varvec{I}}^{-1}(\hat{\varvec{\psi }})\acute{\Delta }_{2}\right] . \end{aligned}$$

Consequently, the $100(1-\tau )\%$ ACIs correspond to the RF and HRF are

$$\begin{aligned} \left( {\hat{R}}(t)\pm z_{\tau /2}\sqrt{{\hat{V}}_{4}}\right) , \,\,\,\text {and}\,\,\, \left( {\hat{h}}(t)\pm z_{\tau /2}\sqrt{{\hat{V}}_{5}}\right) . \end{aligned}$$

Since the proposed MLEs (or their ACIs) cannot be obtained in explicit expressions, we apply some numerical procedures to evaluate them, such as the Newton-Raphson (N-R) iterative method. In brief, we now list some of the advantages and disadvantages of the N-R method, such as

• (a) Advantages:

  • One of the quickest approaches that gets to the source immediately.

  • Converges quadratically on the root.

  • The number of significant digits roughly doubles with each step as we move closer to the root.

  • The ability to acquire exact results for a root that was previously obtained from another.

  • Simple to convert to other dimensions.

• (b) Disadvantages:

  • It requires identifying the derivative.

  • Inadequate features of global convergence.

  • Depending on an initial guess value.

Bayesian approach

In addition to providing a different kind of analysis, the Bayesian approach incorporates prior information on the parameters employing informative priori densities. Non-informative priori are taken into consideration when this knowledge is unclear. The posterior marginal distributions are used in the Bayesian methodology to acquire information about the model parameters. Finding Bayes estimations, including point and HPD credible interval estimates, for the unknown parameters, RF and HRF are the focus of this part of the paper.

Prior and posterior distributions

Since the prior distribution represents the information that already exists about the unknown parameter, it is essential to Bayesian estimation. By checking the likelihood function in (6), one can easily see that the parameter $\rho$ has a conjugate gamma prior distribution. On the other hand, no related conjugate priors are available for the unknown parameters $\xi$ and $\mu$. In our case, we consider using the gamma prior distribution for these parameters because it adjusts their support while staying simple. In our case, we choose to use the gamma prior distribution for these parameters because it effectively adjusts their support while maintaining simplicity. The gamma prior is flexible and can accommodate a variety of prior knowledge. It provides closed-form expressions for both the mean and variance, which facilitates the easy determination of hyper-parameter values in simulations or during empirical data analysis. The closed form of the variance also allows for an examination of how the degree of variation in the prior distribution impacts estimation performance. Additionally, using the gamma prior distribution does not significantly impact posterior evaluation or computation, particularly when employing the MCMC method. As a result, the three unknown parameters in our study, $\rho , \xi$, and $\mu$, are assumed to be independent random variables that each follows gamma distribution with known and non-negative hyper-parameters. Let $\rho \sim Gamma(a_{1},b_{1})$, $\xi \sim Gamma(a_{2},b_{2})$ and $\mu \sim Gamma(a_{3},b_{3})$. Then, the joint prior distribution can be expressed as

$$\begin{aligned} p(\varvec{\psi })\propto \rho ^{a_{1}-1}\xi ^{a_{2}-1}\mu ^{a_{3}-1}e^{-(b_{1}\rho +b_{2}\xi +b_{3}\mu )}, \rho , \xi , \mu >0, \end{aligned}$$

(14)

$a_{j}, b_{j}>0, j=1,2,3$. The non-informative case can be applied by equating $a_{j}$ and $b_{j}, j=1,2,3$ to zero. Adding the observed data acquiring by the LF provided by (6) to the available prior knowledge given by the joint prior distribution in (14), one can derive the joint posterior distribution of the unknown parameters as

$$\begin{aligned} H(\varvec{\psi }|{{{\underline{\varvec{y}}}}})= & \frac{1}{A} \rho ^{D_{2}+a_{1}-1}\xi ^{D_{2}+a_{2}-1}\mu ^{D_{2}+a_{3}-1}e^{ -(b_{1}\rho +b_{2}\xi +b_{3}\mu )} \nonumber \\ & \times \exp \left\{ \mu \sum _{i=1}^{D_{2}}y_{i}+(\xi -1)\sum _{i=1}^{D_{2}}\log [\varpi (y_{i};\mu )]-\rho Q({{{\underline{\varvec{y}}}}};\mu ,\xi ) \right\} , \end{aligned}$$

where $A=\int _{0}^{\infty }\int _{0}^{\infty }\int _{0}^{\infty }p(\varvec{\psi })L(\varvec{\psi }|{{{\underline{\varvec{y}}}}})d\rho d\xi d\mu$. Utilizing the squared error loss function, the Bayes estimator of the parametric function $\omega (\varvec{\psi })$ can be defined as the posterior mean obtained as

$$\begin{aligned} \tilde{\omega }(\varvec{\psi })=\frac{\int _{0}^{\infty }\int _{0}^{\infty }\int _{0}^{\infty }\omega (\varvec{\psi })p(\varvec{\psi })L(\varvec{\psi }|{{{\underline{\varvec{y}}}}})d\rho d\xi d\mu }{\int _{0}^{\infty }\int _{0}^{\infty }\int _{0}^{\infty }p(\varvec{\psi })L(\varvec{\psi }|{{{\underline{\varvec{y}}}}})d\rho d\xi d\mu }. \end{aligned}$$

(15)

The squared error loss function is the most commonly used loss function in the literature. Its simplicity makes it particularly suitable for situations where overestimation and underestimation are treated equally. Additionally, it is easy to employ other loss functions, such as LINEX and general entropy, among others. The ratio of integrals in (15) causes the impossibility of getting the Bayes estimator of $\omega$ in a closed form. In order to get around this problem, we propose implementing the MCMC technique to obtain both the necessary Bayes estimates and the HPD credible intervals. This subject is covered in the next part.

MCMC and Bayes estimates

In Bayesian inference,the MCMC techniques are highly effective Monte Carlo methods. It can be used to sample from posterior distributions and calculating posterior values of interest. To make use of the law of large numbers, the MCMC uses repeating random sampling, just as other Monte Carlo approaches. Using this method, the joint posterior distribution must be partitioned into full conditional distributions for each model parameter. A sample has to be obtained from each of these conditional distributions in order to acquire the required estimates. For the unknown parameters $\rho , \xi$, and $\mu$, the full conditional distributions are given, respectively, by

$$\begin{aligned} & H_{1}(\rho |\varvec{\psi }_{-\rho },{{{\underline{\varvec{y}}}}})\propto \rho ^{D_{2}+a_{1}-1}e^{-\rho [Q({{{\underline{\varvec{y}}}}};\mu ,\xi )+b_{1}]}, \end{aligned}$$

(16)

$$\begin{aligned} & H_{2}(\xi |\varvec{\psi }_{-\xi },{{{\underline{\varvec{y}}}}})\propto \xi ^{D_{2}+a_{2}-1}\exp \left[ \xi \sum _{i=1}^{D_{2}}\log [\varpi (y_{i};\mu )]-\rho Q({{{\underline{\varvec{y}}}}};\mu ,\xi ) -b_{2}\xi \right] \end{aligned}$$

(17)

and

$$\begin{aligned} H_{3}(\mu |\varvec{\psi }_{-\mu },{{{\underline{\varvec{y}}}}})\propto \mu ^{D_{2}+a_{3}-1}\exp \left[ \mu \sum _{i=1}^{D_{2}}y_{i}+(\xi -1)\sum _{i=1}^{D_{2}}\log [\varpi (y_{i};\mu )]-\rho Q({{{\underline{\varvec{y}}}}};\mu ,\xi ) -b_{3}\mu \right] . \end{aligned}$$

(18)

One can easily observe that the full conditional distribution of $\rho$ is gamma distribution, with shape parameter $\delta _{1}=(D_{2}+a_{1})$ and scale parameter $\delta _{1}=[Q({{{\underline{\varvec{y}}}}};\mu ,\xi )+b_{1}]$. As a result, obtaining samples from (16) with any gamma-generating algorithm is simple. On the other hand, the distributions in (17) and (18) cannot be reduced to any well-known distribution. In this situation, the Metropolis-Hastings (M-H) algorithm is suitable to get the required samples from $H_{2}(\xi |\varvec{\psi }_{-\xi },{{{\underline{\varvec{y}}}}})$ and $H_{3}(\mu |\varvec{\psi }_{-\xi },{{{\underline{\varvec{y}}}}})$. We can obtain the required samples in accordance with the next steps by using the M-H algorithm with the Gibbs sampling scheme

• Step 1. Set the initial values as $(\rho ^{(0)},\xi ^{(0)},\mu ^{(0)})=(\hat{\rho },\hat{\xi },\hat{\mu })$.

• Step 2. Put $l=1$.

• Step 3. Generate $\rho ^{(l)}$ from $Gamma(\delta _{1},\delta _{2})$.

• Step 4. Simulate $\xi ^{(l)}$ using $H_{2}(\xi |\varvec{\psi }_{-\xi },{{{\underline{\varvec{y}}}}})$ via the M-H algorithm with normal proposal distribution $N\left( \hat{\xi },{\hat{V}}_{2}\right)$.

• Step 5. Generate $\mu ^{(l)}$ from $H_{3}(\mu |\varvec{\psi }_{-\mu },{{{\underline{\varvec{y}}}}})$ using the M-H algorithm with $N\left( \hat{\mu },{\hat{V}}_{3}\right)$.

• Step 6. Employ $\rho ^{(l)},\xi ^{(l)},\mu ^{(l)}$ to calculate $R^{(l)}$ and $h^{(l)}$.

• Step 7. Replace l by $l+1$.

• Step 8. Implement the steps 3 to 7, M replications acquire

  $$\begin{aligned} \left( \rho ^{(l)},\xi ^{(l)},\mu ^{(l)},R^{(l)},h^{(l)}\right) , l=1,\dots ,M. \end{aligned}$$

For any parameter $\rho ,\xi ,\mu ,R(t)$ and h(t), say $\omega$, the Bayes estimate based on the squared error loss function after a suitable burn-in period B can be expressed as given below

$$\begin{aligned} \tilde{\omega }=\frac{1}{M-B}\sum _{l=B+1}^{M}\omega ^{(l)}. \end{aligned}$$

The HPD credible interval approach provides threshold values from the posterior distribution that indicate an interval containing a specified probability centered around the distribution. This method assumes that all values within the interval are more likely to represent the parameter than any values outside of it. The HPD credible interval is described as the shortest interval that contains a determined percentage of the posterior probability, usually describing the highest-density region. Suppose that $H^{*}(\omega |{{{\underline{\varvec{y}}}}})$ denotes the posterior distribution of the unknown parameter $\omega$. Then, the $100(1-\tau )\%$ HPD credible interval $(L^{*},U^{*})$ for $\omega$ can be obtained by solving the following two equations simultaneously

$$\begin{aligned} \int _{L^{*}}^{U^{*}}H^{*}(\omega |{{{\underline{\varvec{y}}}}})d\omega =1-\tau \end{aligned}$$

and

$$\begin{aligned} H^{*}(L^{*}|{{{\underline{\varvec{y}}}}})=H^{*}(U^{*}|{{{\underline{\varvec{y}}}}}). \end{aligned}$$

As it is seen, we cannot obtain the marginal distribution for any of the unknown parameters, which prevents us from theoretically deriving the required HPD credible intervals. Instead, we can adopt the approach proposed by Chen and Shao²⁸ to utilize the generated MCMC samples to obtain these intervals numerically. In order to compute the HPD credible interval, sort $\omega ^{(l)}$ to be $\omega _{(l)}, l=B+1,\dots ,M$. Then, the HPD credible interval of $\omega$ is

$$\begin{aligned} \left\{ {\omega _{\left( {l^* } \right) },\omega _{\left( {l^* + \left( {1 - \tau } \right) (M-B) } \right) } }\right\} , \end{aligned}$$

where

$$\begin{aligned} \omega _{(l^* + [(1-\tau )(M-B)] )} - \omega _{(l^*)} = \mathop {\min }\limits _{1 \leqslant l \leqslant \tau (M-B)} \left\{ {\omega _{( {l + [(1-\tau )(M-B)]} )} - \omega _{(l)} }\right\} , \end{aligned}$$

at which $[\kappa ]$ is determined to be the largest integer that is either less than or equal to $\kappa$.

Monte Carlo evaluations

This section provides various simulations to test the accuracy of the estimates of $\rho$, $\xi$, $\mu$, R(t) , and h(t) proposed in the previous sections.

Simulation designs

Drawing 1,000 samples from $\hbox {WEx}(0.8,0.5,0.2)$, all estimators of the WEx parameters or reliability features are assessed based on different choices of n, m, ${{\textbf {S}}}$, and $T_{i},\ i=1,2$. At time $t=0.1$, the real value of (R(t), h(t) ) is taken as (0.89252,0.57423). Without loss of generality, we take the actual values of $\rho$, $\xi$, and $\mu$ as starting points in the all simulation experiments.

Besides $(T_{1},T_{2})=(2,4)$ and (4,6), we consider several values of n, m, and ${{\textbf {S}}}$ such as $n(=40,80)$, m is taken as a failure percent, i.e., $\frac{m}{n}=50\%$ and 75%, and three different censoring schemes ${{\textbf {S}}}$ namely:

$$\begin{aligned} \begin{array}{l} \hbox {Scheme-1}: \left( n-m,0^{m-1}\right) ,\\ \hbox {Scheme-2}: \left( 0^{\frac{m}{2}-1},n-m,0^{\frac{m}{2}}\right) ,\\ \hbox {Scheme-3}: \left( 0^{m-1},n-m\right) , \end{array} \end{aligned}$$

where the proposed schemes 1, 2, and 3 represent the left, middle, and right censoring, respectively, and $0^{m}$ means no removals in m stages.

To draw an ITII-APC sample from the WEx distribution, do the following steps:

• Step 1. Set the actual values of $\hbox {WEx}(\varvec{\psi }).$

• Step 2: Simulate a TII-PC sample as (a)-(d):

  • a. Generate $\alpha$ independent observations as ${{\alpha }_{1}},{{\alpha }_{2}},\dots ,{{\alpha }_{m}}$ from uniform distribution.

  • b. Set ${{\gamma }_{i}}=\alpha _{i}^{{{\left( i+\sum \nolimits _{r=m-i+1}^{m}{{{S}_{r}}} \right) }^{-1}}},\ i=1,2,\dots ,m$.

  • c. Set ${{u}_{i}}=1-{{\gamma }_{m}}{{\gamma }_{m-1}}\cdots {{\gamma }_{m-i+1}}$ for $i=1,2,\dots ,m$.

  • d. Set ${{Y}_{i}}=\mu ^{-1}\log \left( 1+(-\rho ^{-1}\log (1-{u}_{i}))^{\xi ^{-1}}\right) ,\ i=1,2,\dots ,m$, is the TII-PC sample from $\text {WEx}(\varvec{\psi })$.

• Step 3. Discard the staying sample $Y_{i},\ i={{J}_{1}}+2,\dots ,m,$ when ${{J}_{1}}$ is recorded at ${{T}_{1}}$.

• Step 4. Obtain the first $m-{{J}_{1}}-1$ order statistics (say ${{Y}_{{{J}_{1}}+2}},\dots ,{{Y}_{m}}$) from a truncated distribution ${\left[ R\left( {{y}_{{{J}_{1}}+1}} \right) \right] }^{-1}{g\left( y\right) }$ with sample size $n-{{J}_{1}}-1-\sum \nolimits _{i=1}^{{{J}_{1}}}{{{S}_{i}}}$.

• Step 5. Stop the ITII-APC life-test at:

  • a. ${{Y}_{m}}$ when ${{Y}_{m}}<{{T}_{1}}<{{T}_{2}}$; that is Case-1.

  • b. ${{Y}_{m}}$ when ${{T}_{1}}<{{Y}_{m}}<{{T}_{2}}$; that is Case-2.

  • c. ${{T}_{2}}$  when ${{T}_{1}}<{{T}_{2}}<{{Y}_{m}}$; that is Case-3.

  In R software version 4.2.2, to evaluate the theoretical inferences developed by maximum likelihood and Bayesian approaches, including point and interval estimations of the unknown parameters $\rho , \xi$, and $\mu$, as well as of the unknown reliability indices R(t) and h(t) (for $t>0$), we recommend two statistical packages, namely:

  • (a) The ‘$\textsf {maxLik}$’ package (by Henningsen and Toomet²⁹) that employs the Newton-Raphson method via ‘$\textsf {maxNR()}$’ function in maximizations;

  • (b) The ‘$\textsf {coda}$’ package (by Plummer et al.³⁰) that employs the ‘$run\_metropolis\_MCMC()$’ function in the Markovian process.

  Now, we use the M-H algorithm to run a process called MCMC sampler up to 12,000 times and ignore the first 2,000 results. Once the 10,000 MCMC iterations of each WEx parameter are gathered, the Bayes and 95% HPD interval estimates of WEx parameters are obtained. To highlight the performance of the Bayes hyper-parameters, besides the non-informative priors (say, P0), two separate informative sets of $(a_{i},b_{i})$ are used, namely:

  • P0: $a_{i}=b_{i}=0$ for $i=1,2,3$;

  • P1: $(a_{1},a_{2},a_{3})=(4,2.5,1)$ and $b_{i}=5$ for $i=1,2,3$;

  • P2: $(a_{1},a_{2},a_{3})=(8,5,2)$ and $b_{i}=10$ for $i=1,2,3$.

  Following the idea presented by Kundu³¹, the given hyper-parameter values of $a_{i},b_{i},\ i=1,2,3,$ of the unknown WEx parameters are chosen in such a way that the prior mean matches the expected value of the given actual parameter values. It is better to note here that if one takes P0 into account, the joint posterior density will then be in proportion to the likelihood function (6), i.e., $H(\varvec{\psi }|{{{\underline{\varvec{y}}}}})\propto (\rho \xi \mu )^{-1} L(\varvec{\psi }|{{{\underline{\varvec{y}}}}})$. Generally, if the proper prior information is available, it is better to use the informative prior(s) than the non-informative prior(s).

In Bayes’ MCMC calculations, the convergence assessment involves making sure that the sequence of numbers is the main focus in order to get a typical sample from the target distribution. For this aim, different convergence tools are used: (i) Auto-correlation function (ACF), (ii) Trace, and (iii) Brooks-Gelman-Rubin (BGR) diagnostic; see Fig. 2. These diagrams are displayed from mbox WEx(0.8, 0.5, 0.2), n[FP%]=80[50%], Scheme-1, P1, and $(T_{1},T_{2})=(2,4)$. Moreover, using the acceptance rate of the MH sampler based on two different samples when $m = 20$, P1, and Scheme-1 (as an example) generated at $(T_{1},T_{2})=(2,4)$ and (4,6), we found that the acceptance rates are 99.25% and 99.13%, respectively. It is evident that both MCMC samples provide an acceptable approximation for the posterior density; thus, the inferential results are effective.

Fig. 2

Three convergence plots of WEx model in Monte Carlo simulation (a) ACF, (b) Trace, and (c) BGR.

Figure 2a illustrates that the simulated chains are thoroughly combined and the outcomes are coherent; Fig. 2b shows that the chains for all WEx parameters are mixed together properly; Fig. 2c shows that there is no big difference between the variance–within each chain and the variance–between the chains. It also shows that using a bigger initial sample can help get rid of the effects of starting points. Subsequently, the results of $\rho$, $\xi$, $\mu$, R(t) , or h(t) that were given are reliable and good enough.

Now, the average estimates (Av.Es) of $\rho$ (as an example) are given by

$$\begin{aligned} Av.E{(\rho )}=\frac{1}{1000}\sum \limits _{q=1}^{1000}{\breve{\rho }^{(i)}}, \end{aligned}$$

where $\breve{\rho }^{(i)}$ is the estimate of $\rho$ at ith sample.

Comparison between point estimates of $\rho$ is done based on their (i) root mean squared-errors (RMSEs) and (ii) mean absolute biases (MABs) as

$$\begin{aligned} \text {RMSE}(\breve{\rho } )=\sqrt{\frac{1}{1000}\sum \nolimits _{q=1}^{1000}{{{\left( \breve{\rho }^{(i)}-{{\rho }}\right) }^{2}}}}, \end{aligned}$$

and

$$\begin{aligned} \text {MAB}(\breve{\rho } )=\frac{1}{1000}\sum \nolimits _{q=1}^{1000}{\left| \breve{\rho }^{(i)}-{{\rho }} \right| }, \end{aligned}$$

respectively.

Further, the comparison between interval estimates of $\rho$ is done based on their (i) average confidence lengths (AILs) and (ii) coverage percentages (CPs) as

$$\begin{aligned} \text {AIL}_{(1-\tau )\%}(\rho )=\frac{1}{1000}\sum \nolimits _{q=1}^{1000}{\left( {{\mathcal {U}}_{\breve{\rho }^{(i)}}}-{{\mathcal {L}}_{\breve{\rho }^{(i)}}}\right) }, \end{aligned}$$

and

$$\begin{aligned} \text {CP}_{(1-\tau )\%}{(\rho )}=\frac{1}{1000}\sum \nolimits _{q=1}^{1000}{{\varvec{I}}_{\left( {{\mathcal {L}}_{\breve{\rho }^{(i)}}};{{\mathcal {U}}_{\check{\rho }^{(i)}}}\right) }^{\diamond }\left( {\rho }\right) }, \end{aligned}$$

respectively, where ${\varvec{I}}^{\diamond }(\cdot )$ denotes the indicator operator, $({\mathcal {L}}(\cdot ),{\mathcal {U}}(\cdot ))$ denote the (lower,upper) limits of $(1-\tau )\%$ an interval estimate of ${\rho }$. For any helpful information regarding the R coding process implemented in the current work, we recommend following the workshop presented by Elshahhat³².

Simulation results and discussions

From Tables 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11, in terms of the lowest level of RMSEs, MABs, and AILs, as well as the highest level of CPs, several comments are listed as:

• All the estimates made using likelihood or Bayesian methods have shown good behavior. This is a common occurrence.

• As m(or n) increases, all estimates get better. The same result is recorded when $\sum _{i=1}^{m}S_{i}$ is reduced.

• As T increased, it is noted that

  • All simulated values of RMSEs and MABs for all estimates of all WEx parameters decreased.

  • All simulated values of AILs for all estimates of all WEx parameters decreased, while the simulated values of CPs increased.

• The most simulated results of CPs are near the specified nominal level.

• Comparing the different methods of estimating WEx parameters, we found that using the Bayes method with gamma information gave better results than using the likelihood estimates, just like we expected.

• Bayesian inferences derived from P2 are more effective than those from P1, and both outperform those developed from P0. This significant fact is due to P2 having a variance smaller than the others.

• The Bayes results (including MCMC and HPD interval estimates) with non-informative priors (P0) behave like the frequentist estimates, whereas those with informative priors (P$i,\ i=1,2$) behave satisfactorily better than others.

• Due to the prior assumption of WEx parameters, it is clear that the HPD interval estimates of all unknown quantities performed satisfactorily compared to others.

• Comparing the proposed schemes 1, 2, and 3, it is noted that:

  • All estimates of $\rho$, R(t) , or h(t) behaved better using Scheme-3 (i.e., right-removal) than others.

  • All estimates of $\xi$ and $\mu$ behaved better using Scheme-1 (i.e., left-removal) and Scheme-2 (i.e., middle-removal), respectively, than others.

• Ultimately, we recommend implementing the Bayes’ method with informative priors to evaluate the unknown parameters, reliability, and failure rate functions of the WEx model in the presence of data collected via the proposed strategy.

Table 2 The Av.Es ($1^{st}$ column), RMSEs ($2^{nd}$ column), and MABs ($3^{rd}$ column) of $\rho$.

Table 3 The Av.Es ($1^{st}$ column), RMSEs ($2^{nd}$ column), and MABs ($3^{rd}$ column) of $\xi$.

Table 4 The Av.Es ($1^{st}$ column), RMSEs ($2^{nd}$ column), and MABs ($3^{rd}$ column) of $\mu$.

Table 5 The Av.Es ($1^{st}$ column), RMSEs ($2^{nd}$ column), and MABs ($3^{rd}$ column) of R(t) .

Table 6 The Av.Es ($1^{st}$ column), RMSEs ($2^{nd}$ column), and MABs ($3^{rd}$ column) of h(t) .

Table 7 The ACLs ($1^{st}$ column) and CPs ($2^{nd}$ column) of 95% interval estimates of $\rho$.

Table 8 The ACLs ($1^{st}$ column) and CPs ($2^{nd}$ column) of 95% interval estimates of $\xi$.

Table 9 The ACLs ($1^{st}$ column) and CPs ($2^{nd}$ column) of 95% interval estimates of $\mu$.

Table 10 The ACLs ($1^{st}$ column) and CPs ($2^{nd}$ column) of 95% interval estimates of R(t) .

Table 11 The ACLs ($1^{st}$ column) and CPs ($2^{nd}$ column) of 95% interval estimates of h(t) .

Rainfall data analysis

Rainfall reliability analysis is crucial for water resource management, flood risk assessment, infrastructure planning, and disaster preparedness. It improves decision-making, promotes sustainability, and reduces climate variability impacts, ensuring resources are available during dry spells. For this purpose, this part investigates the significance and application of the suggested inferential approaches in actual practical settings using two separate rainfall data sets.

Rainfall in Minneapolis/St.

This application examines actual data regarding thirty successive values of the March rainfall (in inches) in Minneapolis/St. Paul; see Hinkley³³. We shall refer to the given rainfall in Minneapolis/St. by ’RMS’ for simplicity. Recently, the RMS data set has also been discussed by Elshahhat et al.³⁴ and Nassar et al.³⁵. To see the validity of the WEx model for the RMS data reported in Table 12, the Kolmogorov–Smirnov (K–S) statistic (along its P-value) is calculated. Before proceeding, we calculate the MLEs (along with their standard–errors (Std.Errs)) of $\rho$, $\xi$, and $\mu$. Then we get $\hat{\rho }=22.957(40.041)$, $\hat{\xi }=1.6722(0.2357)$, and $\hat{\mu }=0.0744(0.0643)$. Consequently, the K–S(P-value) result is 0.0783(0.9928). This fact shows that the WEx model matches the RMS very well.

Table 12 March rainfall in Minneapolis/St. Paul.

Following goodness data visualizations, Fig. 3 displays the estimated/empirical reliability lines, March rainfall data histograms with fitted density lines, and estimated/empirical scaled–TTT lines. Figure 3a,b indicates that the WEx model is appropriate to analyze the RMS data. Figure 3c exhibits that the entire March rainfall provides a growing failure rate. Additionally, to show the existence and uniqueness features of the acquired MLEs $\hat{\rho }$, $\hat{\xi }$, and $\hat{\mu }$, the profile log-likelihood plots are depicted in Fig. 4. It shows that the estimates of $\rho$, $\xi$, and $\mu$ used in the K–S test exist and are unique. We also suggest considering (22.957,1.6722,0.0744) of ($\rho ,\xi ,\mu$) as a suitable starting point.

Fig. 3

Goodness plots from RMS data (a) RF, (b) PDF, and (c) TTT.

Fig. 4

Profile log-likelihood plots from RMS data.

To examine the proposed theoretical results of the WEx parameters, we are creating different ITII-APC samples (with $m=10$) by choosing specific values of ${{\textbf {S}}}$ and $T_{i},\ i=1,2$; see Table 13. We use the M-H algorithm to make 40,000 MCMC samples and throw away the first 1,000 samples. For each artificial sample, the maximum likelihood and Bayes’ estimates, in addition to their Std.Errs are obtained; see Table 14. Further, the bounds of 95% ACI/HPD estimates of the same unknown parameters are also obtained and provided in Table 14. Since we do not have any priori information about the $\hbox {WEx}(\varvec{\psi })$ population from the given RMS data set, all Bayes computations are created using non-informative assumptions. In this part, the initial values of the parameters $\rho$, $\xi$, and $\mu$ are chosen as their maximum likelihood values obtained from the complete sampling. The findings reported in Table 14 showed that the offered point/interval estimates of $\rho$, $\xi$, $\mu$, R(t) , or h(t) are very similar to each other, just as we expected.

Table 13 Three ITII-APC samples from RMS data.

Table 14 Estimates of $\rho$, $\xi$, $\mu$, R(t) , and h(t) from RMS data.

To show that the suggested estimates of $\rho$, $\xi$, and $\mu$ (given in Table 14) exist and are unique, Fig. 5 displays the profile log-likelihood for each unknown quantity for every created sample. It is shown that, for all RMS samples, the given estimates $\rho$ , $\xi$ and $\mu$ exist and are unique.

Fig. 5

Profile log-likelihoods of $\rho$, $\xi$, and $\mu$ from RMS data (a) S1, (b) S2, and (c) S3.

To check if the M-H algorithm is working well, using the staying 30,000 iterations from S1 (as an example), we made two graphs called trace and conditional-density plots for all unknown parameters; see Fig. 6. In every graph, the average of the sample as well as 95% HPD limits are shown by solid and dashed lines, respectively. All trace graphs showed that all MCMC iterations were mixed effectively, and the range of 95% HPD bounds covered the calculated Bayes estimate. Furthermore, Fig. 6 shows that the iterations of $\rho$, $\xi$, and $\mu$ are fairly symmetrical, while those of R(t) and h(t) are negatively and positively skewed, respectively. Also, in Table 15, several statistics of the WEx parameters (including mean, mode, 1st quartile, 2nd quartile, 3rd quartile, standard deviation (SD), and skewness (Skew.)) are reported. It confirms the same findings provided in Table 14.

Fig. 6

MCMC plots using S1 from RMS data (a) $\rho$, (b) $\xi$, (c) $\mu$, (d) R(t) , and (e) h(t) .

Table 15 Statistics of $\rho$, $\xi$, $\mu$, R(t) , and h(t) from RMS data.

Rainfall in New South Wales

This application looks at a data set that shows how much rain fell each month from January 2000 to February 2007 at Carrol, a rain gauge station in New South Wales, Australia; see Table 16. We shall refer to the given rainfall in New South Wales by ’RNSW’ for simplicity. This data was provided by Jodra et al.³⁶ and earlier reanalyzed by Elshahhat et al.³⁷. Firstly, we need to see if the RNSW data matches the WEx lifetime model or not. However, we found that the MLEs(Std.Errs) of $\rho$, $\xi$, and $\mu$ are 0.7658(0.5856), 0.9765(0.1883), and 0.0210(0.0109), respectively, while the K–S(P-value) is 0.0498(0.9861). It implies that the WEx distribution fits the entire RNSW reasonably well.

Table 16 Monthly rainfall in New South Wales, Australia.

Using the complete RNSW data set, the reliability and density lines depicted in Fig. 7 support the same fitting results. The scaled–TTT plot in Fig. 7 indicates that the RNSW data set provides an increasing failure rate. The log-likelihood plots of $\rho$, $\xi$, and $\mu$ depicted in Fig. 8 indicate that the MLEs ${\hat{\rho }}$, ${\hat{\xi }}$, and ${\hat{\mu }}$ developed from the RNSW data exist and are unique, as well as that their values may be taken as suitable starting values.

Fig. 7

Goodness plots from RNSW data (a) RF, (b) PDF, and (c) TTT.

Fig. 8

Profile log-likelihood plots from RNSW data.

From Table 16, based on various options of $T_{i},\ i=1,2,$ and ${{\textbf {S}}}$, three ITII-APC samples (with $m=33$) from the full RNSW data are generated; see Table 17. The maximum likelihood, Bayes, and associated 95% ACI/HPD estimates of $\rho$, $\xi$, $\mu$, R(t) , and h(t) (at $t=0.3$) are computed; see Table 18. All Bayes’ calculations developed based on the RNSW data are performed based on the same scenarios reported in Subsection “Rainfall in Minneapolis/St.”. Table 18 indicates that the results obtained from the likelihood approach are very close to those obtained from the competitive Bayes’ approach. Figure 9 shows the log-likelihoods of $\rho$, $\xi$, and $\mu$ and confirms that all estimates of ${\hat{\rho }}$, ${\hat{\xi }}$, and ${\hat{\mu }}$, developed based on Si for $i=1,2,3,$ from RNSW data, existed and are unique.

Table 17 Three ITII-APC samples from RNSW data.

Table 18 Estimates of $\rho$, $\xi$, $\mu$, R(t) , and h(t) from RNSW data.

Fig. 9

Profile log-likelihoods of $\rho$, $\xi$, $\mu$ from RNSW data (a) S1, (b) S2, and (c) S3.

Figure 10 displays the density (with MCMC histogram) and trace plots for the remaining 30,000 MCMC variates of $\rho$, $\xi$, $\mu$, R(t) , and h(t) . As a consequence, the MCMC algorithm converges successfully, and the resulting histograms of each unknown parameter are pretty symmetrical. All findings listed in Table 19 support all facts shown in Fig. 10.

Fig. 10

MCMC plots using S1 from RNSW data (a) $\rho$, (b) $\xi$, (c) $\mu$, (d) R(t) , and (e) h(t) .

Table 19 Statistics of $\rho$, $\xi$, $\mu$, R(t) , and h(t) from RNSW data.

Optimal progressive censoring

Selecting the “optimal” PCP among a set of potential schemes is crucial in reality. At this point “potential schemes” refer to the various $(S_{1},\dots ,S_{m})$ selections for specified n, m, and the two thresholds. To be clear, if PCP S1 offers more details about the unknown parameters than PCP S2, then S1 is considered superior to S2. In this part, we present four precision criteria $({\mathcal {C}})$ to compare four censoring methods and identify the best one for use with the real data sets examined in the previous section. For more information about the optimal PCP, see for more detail Pradhan and Kundu³⁸, Ashour et al.³⁹, Alotaibi et al.⁴⁰. The following are four optimality standards used in this study:

• 1. ${\mathcal {C}}_{1}$: Maximizes the trace of the observed Fisher information matrix as:

  $$\begin{aligned} {\mathcal {C}}_{1}=Max\left( -\frac{\partial ^{2} l(\varvec{\psi }|{{{\underline{\varvec{y}}}}})}{\partial \rho ^{2}}-\frac{\partial ^{2} l(\varvec{\psi }|{{{\underline{\varvec{y}}}}})}{\partial \xi ^{2}}-\frac{\partial ^{2} l(\varvec{\psi }|{{{\underline{\varvec{y}}}}})}{\partial \mu ^{2}}\right) . \end{aligned}$$

• 2. ${\mathcal {C}}_{2}$: Minimizes the trace of ${\varvec{I}}^{-1}(\hat{\varvec{\psi }})$ as

  $$\begin{aligned} {\mathcal {C}}_{2}=Min\left( {\hat{V}}_{1}+{\hat{V}}_{2}+{\hat{V}}_{3}\right) . \end{aligned}$$

• 3. ${\mathcal {C}}_{3}$: Minimizes the determinant of ${\varvec{I}}^{-1}(\hat{\varvec{\psi }})$ as

  $$\begin{aligned} {\mathcal {C}}_{3}=Min\left| {\varvec{I}}^{-1}(\hat{\varvec{\psi }})\right| . \end{aligned}$$

• 4. ${\mathcal {C}}_{4}$: Minimizes the approximate estimated variance of the MLE of $\log (\hat{\phi }_{p})$, where $\hat{\phi }_{p}$ is the quantile function of the WEx distribution with $0<p<1$, and

  $$\begin{aligned} \log (\hat{\phi }_{p})=-\log (\hat{\mu })+\log \left\{ \log \left[ 1+\left( -\frac{\log (1-p)}{\hat{\rho }}\right) ^{1/\hat{\xi }} \right] \right\} . \end{aligned}$$

  The approximate estimated variance of $\hat{\phi }_{p}$ is obtained using the delta method as ${\hat{V}}_{6}=[\Delta _{3}{\varvec{I}}^{-1}(\hat{\varvec{\psi }})\acute{\Delta }_{3}$], where

  $$\begin{aligned} \Delta _{3}=\left[ \frac{\partial \log (\phi _{p})}{\partial \rho }\,\,\frac{\partial \log (\phi _{p})}{\partial \xi }\,\,\frac{\partial \log (\phi _{p})}{\partial \mu } \right] _{\varvec{\psi }=\hat{\varvec{\psi }}}. \end{aligned}$$

On the basis of the proposed censored samples created from the RMS and RNSW data sets, Tables 20 and 21 provide the issue of selecting the optimal PCP. As a result, from Tables 20 and 21, we can decide that:

• (i) From RMS data:

  • Via criteria ${\mathcal {C}}_2$ and ${\mathcal {C}}_4$; the left censoring (used in S1) is the optimum plan than others.

  • Via criteria ${\mathcal {C}}_1$ and ${\mathcal {C}}_3$; the right censoring (used in S3) is the optimum plan than others.

• (ii) From RNSW data:

  • Via criterion ${\mathcal {C}}_1$; the left censoring (used in S1) is the optimum plan than others.

  • Via criteria ${\mathcal {C}}_i$ for $i=2,3,4$; the right censoring (used in S3) is the optimum plan than others.

Moreover, the ideal PCP proposed based on the given RMS (or RNSW) data confirm the same findings developed from the proposed Monte Carlo comparisons.

Table 20 Optimum censoring plans from RMS data.

Table 21 Optimum censoring plans from RNSW data.

The analysis of two real rainfall data sets demonstrated that the WEx distribution effectively models this type of data, as evidenced by the high P-values obtained from the Kolmogorov-Smirnov test. This modeling suitability can be utilized to estimate the reliability of rainfall data, especially when the HRF has an increasing shape, at any given point, which is critical for water resource management. Understanding rainfall patterns facilitates the effective management of water supply, storage, and distribution, ensuring that resources are available during dry periods. Moreover, accurately estimating rainfall reliability is essential for flood risk assessment, as it improves predictions of flood events and supports better infrastructure planning and disaster preparedness. Additionally, the analysis revealed that the Bayesian estimation method with the gamma prior yielded more accurate reliability estimates compared to traditional approaches. As a result, we recommend using this approach when estimating the reliability of rainfall data. Finally, when collecting rainfall data with the ITII-APC scheme, it is recommended to use the right-removal pattern. Analysis indicated that estimating reliability measures with this pattern provided better results compared to the left-removal and middle-removal patterns.

Concluding remarks

In the context of improved adaptive progressively Type-II censored data, the current research supplied a variety of statistical inference methodologies for estimating the parameters and some reliability benchmarks, namely the hazard and reliability functions, of the Weibull-exponential distribution. To get the point and interval estimates of the unknown parameters, both conventional and Bayesian deductive procedures are considered. Using the observed Fisher information matrix the approximate confidence intervals are created. Such intervals are obtained for the reliability metrics by approximating the variances related to the estimators using the delta method. The Markov Chain Monte Carlo sampling procedure is carried out to collect data from the full conditional distributions for Bayesian estimation. The collected samples are subsequently utilized to obtain the highest posterior density intervals. All of the techniques are reviewed through detailed simulations and two real-world example situations. Based on the criteria of root mean square error, interval length, and coverage probability, the analysis yielded the following numerical findings:

• As the number of observed failures increases, both classical and Bayesian estimates improve.

• As the threshold times increase, all the estimates show improved performance.

• Bayesian inferences derived from prior 2 are more effective than those from prior 1, which is significant given that prior 2 shows less variability than prior 1.

• Taking into account the prior information about the Weibull-exponential distribution parameters, it is evident that the highest posterior density credible interval estimates for all unknown quantities performed satisfactorily in comparison to classical ones.

• When the right-removal pattern is used, the estimation of the reliability and hazard rate functions performs better than with other patterns, such as left-removal and middle-removal patterns.

Finally, making use of the previously mentioned data sets and four optimality standards, an evaluation of picking the optimal progressive censoring plan is carried out. In future work, it will be valuable to explore alternative loss functions, such as LINEX and general entropy, to investigate the Bayesian reliability estimation of the Weibull-exponential distribution using improved adaptive progressively Type-II censored data. Another area for future research is to examine the estimation problems of the model used and the scheme considered when the data involve multiple causes of failure.