Laser isotope enrichment of ¹⁶⁸Er

Abstract

This present study investigates a three-step laser isotope separation method for the enrichment of ¹⁶⁸Er isotope using 631.052 nm – 586.912 nm – 566.003 nm three-step photoionization scheme. The lineshape contours observed in three-step photoionization process have been investigated in detail. This study shows that enrichment of ¹⁶⁸Er isotope can be achieved with a relatively simple experimental configuration. With the derived system configuration, it has been shown that it is possible to produce 18 g/day of 90% enriched ¹⁶⁸Er. Using the enriched ¹⁶⁸Er isotope obtained from the laser isotope separation process, irradiation in low, medium, and high flux reactors can produce 180, 1800, and 18,000 doses per day (each with an activity of 7.4 GBq) respectively. After 24 h of irradiation and chemical separation, the radioisotopic purity of the medical isotope reaches to > 99% making it suitable for the medical applications. This is the first ever study on the laser isotope separation of ¹⁶⁸Er isotope.

Introduction

Peptide receptor radionuclide therapy (PRRT) has evolved as a very effective treatment protocol for the treatment of the non-endocrine tumours (NET). In this method, a radionuclide is tagged with an appropriate peptide or its analogue binds to the peptide receptor of the tumour cell. The radiation emitted (α or β) destroys the tumour cells thus providing an effective treatment. Among the several radioisotopes being explored for PRRT, ¹⁷⁷Lu is widely preferred for the following reasons. ¹⁷⁷Lu emits both β and γ radiation thus can be used for both therapeutics and diagnostics (known as theranostics) simultaneously. An excellent review on the available options for the production of ¹⁷⁷Lu for targeted radionuclide therapy has been published in 2015¹. ¹⁷⁷Lu can be produced by irradiation of its enriched precursors namely ¹⁷⁶Lu and ¹⁷⁶Yb. Currently, a significant shortage of these precursor isotopes is severely limiting the availability of medical isotopes for the treatment of patients in need. Several articles have been published by the Indian^{2,3,4,5,6,7,8,9}, Korean^10,11 and Russian^{12,13,14,15,16,17,18,19,20} researchers addressing the laser enrichment of Lu and Yb isotopes through atomic route.

¹⁶⁹Er is an interesting isotope having a half-life of 9.392(18) days. It releases two β^- particles with maximum energies of 342.9 keV (45%) and 351.3 keV (55%) and two low intensity γ-rays 109.8 keV (1.3 × 10^–3%) and 118.2 keV (1.4 × 10^–4%). A brief comparison of the properties of ¹⁷⁷Lu and ¹⁶⁹Er and their precursor isotopes is shown in Table 1. There are a number of reasons which make ¹⁶⁹Er a promising nuclide^21,22 for PRRT. They are as following.

Table 1 Comparison of the properties of ¹⁷⁷Lu and ¹⁶⁹Er radioisotopes and their precursor stable isotopes.

Mean energy of β^- particles (99.8 keV) released by ¹⁶⁹Er is considerably lower than mean energy of β^- particles (133.6 keV) released by ¹⁷⁷Lu. Thus, the mean penetration depth of β^- particles released by ¹⁶⁹Er is 300 μm while it is 670 μm for the β^- particles released by ¹⁷⁷Lu. The lower mean energy of β^- particles of ¹⁶⁹Er minimises dose to the adjacent healthy tissues. Further, the gamma ray yields of ¹⁶⁹Er are lower by several orders in comparison to the ¹⁷⁷Lu isotope, thus minimising the dose to the non-target body tissues. Additionally, the longer half-life of ¹⁶⁹Er isotope (9.392 days) in comparison to ¹⁷⁷Lu isotope (6.6443 days) would enable transport of the medicine to distant and remote locations. Interestingly, the ionic radius of Er³⁺ (89 pm) closely matches that of Lu³⁺ (86 pm), therefore, the chelators currently employed for ¹⁷⁷Lu can be effectively utilized for chelating ¹⁶⁹Er. Finally, higher natural abundance of the precursor isotope ¹⁶⁸Er (26.978%) facilitates increased production of the medical isotope through irradiation.

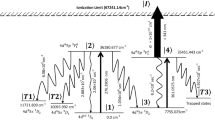
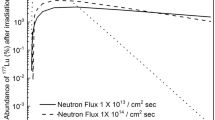
Given these aforementioned reasons, there is a need to develop efficient methods for the production of ¹⁶⁹Er. The ¹⁶⁹Er radioisotope is produced by irradiating the stable ¹⁶⁸Er isotope through the ¹⁶⁸Er(n,γ)¹⁶⁹Er nuclear reaction. The thermal neutron absorption cross-section of the reaction is 2.74 ± 0.08 b (Table 2). When natural erbium is irradiated in a nuclear reactor, the resulting stable and radioisotopes are shown in Fig. 1. The production efficiency of ¹⁶⁹Er from natural erbium (Fig. 2) in low (neutron flux 1 × 10¹³ neutrons/cm²/sec), medium (neutron flux 1 × 10¹⁴ neutrons/cm²/sec) and high (neutron flux 1 × 10¹⁵ neutrons/cm²/sec) flux reactors after 21 days of irradiation has been calculated to be 6.8 × 10^–6, 7.2 × 10^–5 and 9.7 × 10^–4 respectively. Even when irradiated in high-flux reactors, the ratio of ¹⁶⁹Er to the stable isotopes of erbium is expected to be as low as 1:1030. The presence of stable erbium isotopes during the radioisotope complexation process can be problematic. These stable isotopes compete with the radioactive ¹⁶⁹Er for binding with cancer cells, which can hinder the effective delivery of the therapeutic dose to tumour cells. Therefore, using the enriched ¹⁶⁸Er isotope is mandatory for the production of the ¹⁶⁹Er radioisotope. When an enriched ¹⁶⁸Er is irradiated in low, medium and high flux reactors for 21 days (Fig. 3), the production efficiency of ¹⁶⁹Er isotope has been calculated to be 2.5 × 10^–5, 2.5 × 10^–4 and 2.5 × 10^–3. Therefore, irradiating erbium in a high-flux reactor for 21 days can increase the ratio of ¹⁶⁹Er to ¹⁶⁸Er to 1:400.

Table 2 Atomic and nuclear data of stable erbium isotopes.

Fig. 1

Radioisotopes production and decay chain of natural erbium.

Fig. 2

Production efficiency of ¹⁶⁹Er by irradiation of natural erbium in low (neutron flux 1 × 10¹³ neutrons/cm²/sec), medium (neutron flux 1 × 10¹⁴ neutrons/cm²/sec) and high (neutron flux 1 × 10¹⁵ neutrons/cm²/sec) flux reactors. Cooling time 0 days.

Fig. 3

Production efficiency of ¹⁶⁹Er by irradiation of ¹⁶⁸Er in low (neutron flux 1 × 10¹³ neutrons/cm²/sec), medium (neutron flux 1 × 10¹⁴ neutrons/cm²/sec) and high (neutron flux 1 × 10¹⁵ neutrons/cm²/sec) flux reactors. Cooling time 0 days.

Among the available methods for isotope enrichment, three are most commonly used. They are gas centrifugation, electromagnetic isotope separation and atomic vapor laser isotope separation. The gas centrifuge isotope separation process is employed to separate isotopes of elements that readily form volatile compounds, typically fluorides, which exhibit high vapor pressures near room temperatures. Enrichment of the target isotope is achieved through cascading the high-speed centrifugation process. Gas centrifugation cannot be employed for the isotope separation process of erbium due to the high melting (1146 °C) and boiling (2200 °C) points of ErF₃. While electromagnetic isotope separation achieves high degrees of enrichment, the quantity of enriched isotopes produced through this method typically ranges from milligrams to grams²³ primarily owing to its low ionization efficiency. Therefore, this method alone is unlikely to meet the global demand for enriched ¹⁶⁸Er. Furthermore, both centrifugation and electromagnetic isotope separation methods are susceptible to the isobaric impurities originating from elemental impurities of the feedstock material, which could restrict the use of enriched isotopes in medical applications. Rubel Chakravarty et al.²⁴ have studied the production and purification of ¹⁶⁹Er for therapeutic applications particularly for the radiation synovectomy (RSV). They have observed that the co-production of ¹⁶⁹Yb (due to the presence of ¹⁶⁸Yb as an impurity) is a significant obstacle for the clinical use of ¹⁶⁹Er in radioisotope therapy, necessitating electrochemical purification.

For such applications, separation methods that are not dependent on isotope mass would be more desirable. Atomic Vapor Laser Isotope Separation (AVLIS) is a method wherein the lasers are tuned to the target isotope interact with the atoms of the isotope mixture in gas phase. Atoms in their ground state are sequentially excited to higher energy states and eventually ionized. Lasers are tuned to specific frequencies that selectively excite and ionize the target isotopes, which are collected. The advantage with AVLIS process is that its single state separation efficiency is far higher than any other known isotope separation method. Since the method is not based on isotope mass, the isobaric impurities from the feedstock material are not transferred to the enriched end product, therefore, the end product is suitable for the production of ¹⁶⁹Er medical isotope.

Previous laser isotope separation methods have typically required narrowband lasers with a bandwidth of around 100 MHz and highly collimated atomic beams to achieve the desired degree of enrichment^3,6,12,13. However, it is important to note that such experimental setups are often complex and challenging to handle. In contrast, the present work investigates the laser isotope enrichment of ¹⁶⁸Er using a simpler experimental configuration, where the excitation lasers have a bandwidth of approximately 500 MHz and the atomic beam has an angular divergence of about 30°. This considerably reduces the complexity of experimental systems. Density matrix formalism has been applied to study the laser-atom interactions in the three-step photoionization process. The effect of atomic, laser and atom source parameters on the degree of enrichment and production rate have been studied. This is the first ever study on the laser isotope separation of ¹⁶⁸Er.

Photoionization of erbium

Erbium is an element of the lanthanide series having an atomic number of 68. It has six stable isotopes (Table 2) namely; ¹⁶²Er (0.139%), ¹⁶⁴Er (1.601%), ¹⁶⁶Er (33.503%), ¹⁶⁷Er (22.869%), ¹⁶⁸Er (26.978%) and ¹⁷⁰Er (14.910%). Among all the stable isotopes, ¹⁶⁷Er is the only isotope that exhibits hyperfine structure due to its non-zero nuclear spin I = 7/2. Erbium has a melting point of 1529 °C and a boiling point of 2868 °C. The variation in vapor pressure and the number density of atoms with source temperature is shown in Fig. 4A. At 1200 °C, the vapor pressure of erbium has been calculated to be 8.1 μbar and the corresponding number density is 4 × 10¹³ atoms/cm³.

Fig. 4

(A) A plot of vapor pressure and number density of erbium with source temperature (B) Population distribution of erbium ground and meta-stable states with source temperature.

Erbium has a ground state electronic configuration of 4f¹²6s^{2 3}H₆ (0.0 cm^-1). The energy of the next low-lying metastable state is 4f¹²6s^{2 3}F₄ (5035.193 cm^-1). At this 1200˚C, the population of the ground state is 99.2% (Fig. 4B). Therefore, photoionization scheme for the laser isotope separation of erbium must originate from the 4f¹²6s^{2 3}H₆ (0.0 cm^-1) ground state. The first ionization energy²⁵ of erbium is 49,238 cm^-1 (6.105 eV). Since energy of the photons in the visible region is about 17,000 cm^-1 (2.1 eV), it requires three photons for the photoionization of erbium atoms.

A very few studies have been reported so far on the laser isotope separation of erbium^26,27,28. Among them, Karlov et al.^26,27 have used $4{f}^{12}6{s}^{2}{}^{3}{H}_{6} \left(0.0 {cm}^{-1}\right)\stackrel{582.842 nm}{\to }4{f}^{12}6s6p {\left(\text{6,1}\right)}^{o} J=7 \left(17157.307 {cm}^{-1}\right) \stackrel{mercury-lamp}{\to }{Er }^{+}$ photoionization scheme for the separation of erbium isotopes. This scheme cannot be adopted for the large scale separation of erbium isotopes due to the poor ionization efficiencies associated with non-resonance ionization using incoherent radiation (mercury lamp).

Christopher A Haynam and Earl F. Worden²⁸ have patented a three step laser isotope separation process for the separation of ¹⁶⁷Er in 1995. They have reported two possible photoionization pathways for the laser based separation. They are 582.842 nm – 635.826 nm – 566.003 nm and 631.052 nm – 586.912 nm – 566.003 nm. Among them, the transition isotope shifts of the latter photoionization scheme have been reported to be considerably larger than the former. Therefore, this photoionization scheme has been chosen for further investigations.

Photoionization scheme

$$\begin{aligned}4{f}^{12}6{s}^{2}{}^{3}{H}_{6} \left(0.0 {cm}^{-1}\right) \stackrel{631.052 nm}{\to }4{f}^{11}5d6{s}^{2} {\left[\frac{13}{2},\frac{3}{2}\right]}_{7}\left(15846.549 {cm}^{-1}\right) \stackrel{586.912 nm}{\to }4{f}^{11}5{d}^{2}6s J&=8 \left(32884.867 {cm}^{-1}\right) \stackrel{566.003 nm}{\to } J \\ &= 9 \left(50552.6 {cm}^{-1}\right) \stackrel{Autoioization}{\to }{Er }^{+}\end{aligned}$$

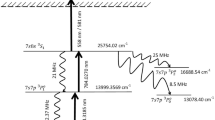
The isotope shifts of the transitions and the hyperfine structure constants of the ¹⁶⁷Er relevant to the photoionization scheme²⁸ have been shown in Tables 3 and 4 respectively. The relevant Rabi frequencies of transitions along with the decay rates have been shown in Fig. 5.

Table 3 Isotopes shifts of the transitions with reference to ¹⁶⁸Er isotope. Ref. ²⁸.

Table 4 Hyperfine structure constants of ¹⁶⁷Er. Ref. ²⁸.

Fig. 5

Schematic representation of three step photionization of erbium (not to scale). I is the intensity of laser in W/cm². Decay rates (Γ) and Rabi frequencies (Ω) have been calculated from the excitation cross-section data provided in Ref. ²⁸.

Results & discussion

In the three-step photoionization process under investigation, the atoms present in the 4f¹²6s^{2 3}H₆ (0.0 cm^-1) ground state are excited to the 4f¹¹5d6s² J = 7 (15,846.549 cm^-1) excited level using the first excitation laser tuned to the 631.052 nm transition. Atoms that are excited to the first excitation level are further excited to the 4f¹¹5d²6s J = 8 (32,884.867 cm^-1) level using a second excitation laser tuned to the 586.912 transition. These excited atoms are ionized by further exciting into an auto-ionization level present at 50,552.6 cm^-1 using a third excitation laser tuned to the 566.003 nm transition. For the present work, all the lasers have been considered to be having a pulse width of 30ns, with a pulsed repetition frequency (PRF) of 10 kHz. The lasers have been considered to be co-propagating unless stated otherwise.

The density matrix elements describing the laser-atom interactions in three-step photoionization scheme have been published previously²⁹. The density matrix elements are numerically integrated using the standard integration methods for the entire pulse duration using Gaussian temporal profiles with no temporal delay between pulses.

At the end of the laser-atom interaction, the atomic population of the auto-ionization state undergoes ionization. Therefore, population of the auto-ionization state has been considered as the ionization efficiency. From the ionization efficiency of the constituent isotopes, the degree of enrichment of the target isotope has been calculated using the equation

$$\text{Degree of enrichment }\left(\text{\%}\right)\text{ of }{}^{168}\text{Er }=\left\{\frac{{\upeta }_{{168}_{\text{Er}}}{*\text{A}}_{{168}_{\text{Er}}}}{\sum_{x}^{all isotopes}{\upeta }_{{\text{x}}_{\text{Er}}}{*\text{A}}_{{\text{x}}_{\text{Er}}}}\right\}*100$$

(1)

where, η is the ionization efficiency of an isotope and A is its fractional abundance.

Features of the ionization efficiency contours

First, ionization efficiency of natural erbium has been calculated under Doppler free conditions (i.e., ignoring the angular and velocity distribution of atoms) varying the frequency of the first and second excitation lasers for a bandwidth of 100 MHz and the intensity of 5 W/cm² for all the lasers. For these calculations the third excitation laser is set to the ¹⁶⁸Er resonance. The resultant two-dimensional contour is plotted in Fig. 6. The following observations can be drawn from the contour.

Fig. 6

Two dimensional ionization efficiency contour of natural erbium under Doppler free condition. The third excitation laser is tuned to ¹⁶⁸Er resonance. The bandwidth and intensity of all excitation lasers are 100 MHz and 5 W/cm² respectively. The weakly observed 15/2–17/2–19/2 hyperfine pathway of ¹⁶⁷Er isotope is marked with *. Additional resonance of ¹⁶²Er isotope is marked with #.

All the resonances of even isotopes have been found at the expected positions (Table 5). Since the third excitation laser is tuned to the resonance of ¹⁶⁸Er isotope, the ionization efficiency of other isotopes at their resonance frequencies positions in two-dimensional reference frame does not correspond to the respective abundances. The horizontal ridge of an isotope corresponds to the line spectra of the first excitation transition while the vertical ridge corresponds to the line spectra of the second excitation transition. The diagonal ridge observed arises due to the coherent two-photon excitation at all frequencies wherein the detuning of the two transitions are equal in magnitude and opposite in sign (i.e., Δ₁ =—Δ₂). The coherent two-photon excitation probability decreases with increase in detuning ($\left|\Delta \right|$).

Table 5 Two photon frequency positions of erbium isotopes. Frequency scale is reference to the ¹⁶⁸Er resonance.

Under the conditions described in Fig. 6, the coherent two-photon excitation is strong and extends to a few GHz. The resonance of the ¹⁶⁸Er target isotope lies on coherent two-photon excitation ridges of the non-target even isotopes. Since the degree of coherent two-photon excitation of the constituent isotopes is determined by the laser (such as bandwidth and intensity) and atom source parameters (such as Doppler broadening) a careful control of all the system parameters is important to obtain adequate degree of enrichment and production rate.

Ionization efficiency contours of even isotopes of Er

In two dimensional reference frame, ¹⁶²Er resonance appears (marked as ¹⁶²Er) when the first and second excitation lasers are tuned to the (-5981 MHz, 5270 MHz) frequencies respectively. Its ionization efficiency is lower as the third excitation laser is detuned by + 398.4 MHz in its reference frame. The net detuning of this transition Δ₁ + Δ₂ + Δ₃ is 0 MHz + 0 MHz + 398.4 MHz =  + 398.4 MHz in three-photon reference frame of ¹⁶²Er isotope. An unexpected additional resonance (marked as #) for ¹⁶²Er has been observed at frequency positions of (-5981 MHz, 4871.6 MHz). This resonance occurs due to the direct two-photon ionization of ¹⁶²Er isotope from the first excitation level. Since the third excitation is laser is detuned by + 398.4 MHz (in ¹⁶²Er reference frame) the resonance occurs at the frequency of 5270 MHz – 398.4 MHz which is equal to + 4871.6 MHz. In this case, the net detuning from the resonance is Δ₁ + Δ₂ + Δ₃ = 0 MHz – 398.4 MHz + 398.4 MHz = 0 MHz. Since the detuning in this case is smaller than the resonance at (-5981 MHz, 5270 MHz), this resonance (marked with #) is stronger. A similar but poorly resolved resonance (due to the small shift of + 187 MHz) can be for observed for ¹⁶⁴Er isotope as well. In fact, this type of resonance can also be observed for all non-target constituent isotopes, although it cannot be resolved due to the saturation broadening and small isotope shifts associated with the third excitation transition. A detailed discussion on the lineshape contours of the three-step photoionization can be found in Ref.³⁰.

Ionization efficiency contour of odd ¹⁶⁷ Er isotope

A weak resonance corresponding to the 15/2–17/2–19/2 hyperfine pathway of ¹⁶⁷Er isotope can be observed at (-1775 MHz, 348.6 MHz) frequency position (marked as * in Fig. 6). Although the natural abundance of ¹⁶⁷Er is relatively high at 22.869%, its ionization efficiency at the frequency position corresponding to the 15/2–17/2–19/2 hyperfine pathway is quite low. This is because of the large spread of the hyperfine spectrum (4378 MHz, 4370 MHz and 5760 MHz for the three excitation transitions respectively) of ¹⁶⁷Er. Furthermore, the most intense resonance of the ¹⁶⁷Er isotope, associated with the 19/2–21/2–23/2 hyperfine pathway, is not observed at the (-1401.6 MHz and -53.1 MHz) frequency position (see Table 5). This cannot be explained using the two-photon reference frame presented in Table 5; instead, a three-photon reference frame must be considered. Using the spectroscopy selection rules, it is possible to formulate 135 hyperfine pathways for the three-step photoionization of ¹⁶⁷Er (see Table 6). To further elucidate, a two-dimensional contour plot of ¹⁶⁷Er has been plotted in Fig. 7A, where the third excitation laser is tuned to the 23/2–25/2 hyperfine transition of ¹⁶⁷Er. The hyperfine pathways in Fig. 7 were marked as per the serial numbers in Table 6. Since the third excitation laser is tuned to the 23/2–25/2 hyperfine transition, the most intense hyperfine pathway 19/2–21/2–23/2–25/2 is distinctly observed (marked as 30 in Fig. 7A) at the expected frequency position of (-1401.6 MHz, -53.1 MHz, 815.9 MHz). It should be noted that when the excitation lasers are tuned to the (-1401.6 MHz, -53.1 MHz, 815.9 MHz) frequencies, ionization also occurs through hyperfine pathways 19/2–21/-23/2–23/2 and 19/2–21/-23/2–21/2 corresponding to the (-1401.6 MHz, -53.1 MHz, 2876.9 MHz) and (-1401.6 MHz, -53.1 MHz, 4481.5 MHz) frequency positions respectively. However, the contribution of ionization of ¹⁶⁷Er through these channels would be rather small as third excitation laser frequency is farther away from these hyperfine pathways of the third excitation transition. Though it is expected to observe (since the third excitation laser is tuned to 23/2–25/2 hyperfine pathway) only one resonance corresponding to 19/2–21/2–23/2–25/2 hyperfine pathway (marked as 30), it is interesting to observe several other resonances (Fig. 7A). It is possible to understand the underlying reasons for the occurrence of all the resonances, nevertheless only two cases are discussed here in detail.

Table 6 Three photon frequency positions of erbium isotopes. Frequency scale is reference to the ¹⁶⁸Er resonance.

Fig. 7

Two dimensional ionization efficiency contour of ¹⁶⁷Er under Doppler free condition. The bandwidth and intensity of all excitation lasers is 100 MHz and 5 W/cm² respectively. (A) Third excitation laser is tuned to the 23/2–25/2 hyperfine transition of ¹⁶⁷Er (B) The third excitation laser is tuned to ¹⁶⁸Er resonance. Hyperfine pathway numbers marked in the figure are as per Table 6.

A resonance marked as 22 in Fig. 7A is observed at the frequency position (-1431.9 MHz, 684.3 MHz) which in two dimensional frame corresponds to 13/2–15/2–17/2 hyperfine pathway. At the outset, this is entirely unexpected as the third excitation laser is tuned to 815.9 MHz corresponding to the 23/2–25/2 hyperfine pathway. On the closer look, one can observe that the (-1431.9 MHz, 684.3 MHz) in two-dimensional reference frame corresponds to the three hyperfine pathways 13/2–15/2–17/2–19/2, 13/2–15/2–17/2–17/2 and 13/2–15/2–17/2–15/2 (marked as 21–23 in Table 6). Among them the hyperfine pathway, 13/2–15/2–17/2–17/2 hyperfine pathway (marked as 22) corresponds to the frequency position the (-1431.9 MHz, 684.3 MHz, 690.8 MHz) in three-dimensional reference frame. Since the third excitation laser (at 815.9 MHz) is detuned to as little as 125 MHz, this resonance is observed. The contribution from the hyperfine pathways 21 and 23 is expected to be smaller because the larger detuning associated with the third hyperfine transition reduce the effective coupling.

Similarly, the resonance at (877.8 MHz, 3583.1 MHz) in two-dimensional reference frame (marked as 119 in Fig. 7A) corresponds to the 19/2–19/2–17/2 hyperfine pathway. In three dimensional reference frame this corresponds to 19/2–19/2–17/2–19/2, 19/2–19/2–17/2–17/2 and 19/2–19/2–17/2–15/2 hyperfine pathways (marked as 118–120 in Table 6) at frequency positions (877.8 MHz, 3583.1 MHz, -213.2 MHz), (877.8 MHz, 3583.1 MHz, 690.8 MHz) and (877.8 MHz, 3583.1 MHz, 1337.9 MHz) respectively. As discussed earlier, contribution from the hyperfine pathway 19/2–19/2–17/2–17/2 at (877.8 MHz, 3583.1 MHz, 690.8 MHz) would be much higher than other hyperfine pathways (118 and 120) due to the lower detuning associated with of the third step excitation.

Apart from the relative intensities of the hyperfine transitions, the contribution from the different hyperfine pathways to the ionization of ¹⁶⁷Er varies with variation in all the laser and atom source parameters. Thus, when the third excitation laser is tuned to the ¹⁶⁸Er resonance the relative contribution of all the 135 hyperfine pathways towards the ionization of ¹⁶⁷Er varies (Fig. 7B). In this, case the hyperfine pathway at (-122.9 MHz, 348.6 MHz) in two-dimensional reference frame (marked as 76 in Fig. 7B) corresponds to the hyperfine pathways 17/2–17/2–19/2–21/2, 17/2–17/2–19/2–19/2 and 17/2–17/2–19/2–17/2 (marked as 76–78 in Table 6) at frequency positions (-122.9 MHz, 348.6 MHz, 111.7 MHz), (-122.9 MHz, 348.6 MHz, 1332.6 MHz) and (-122.9 MHz, 348.6 MHz, 2236.6 MHz) respectively. Among them the contribution by the 17/2–17/2–19/2–21/2 at (-122.9 MHz, 348.6 MHz, 111.7 MHz) frequency position would be the highest due to higher intensity and lower detuning corresponding to the hyperfine pathway of the third excitation transition (19/2–21/2).

It is also important to note that when the excitation lasers are tuned to ¹⁶⁸Er, the resonance of ¹⁶⁸Er isotope lies on the vertical ridge (step-wise excitation of the second excitation transition) of hyperfine pathways (marked 76–78 in Table 6) of ¹⁶⁷Er isotope. This is in contrast to the case of even isotopes (Fig. 6), wherein the resonance of ¹⁶⁸Er isotope lies on the diagonal ridges of even isotopes (arising due to coherent two-photon excitation). Therefore, the ionization of ¹⁶⁷Er can be somewhat controlled by controlling the intensity and bandwidth of the second excitation laser. On the other hand, to reduce the ionization of non-target even isotopes, one needs to control the intensity and bandwidth of all excitation lasers.

It is not possible to qualitatively assess the effect of intensity and bandwidth of all the three excitation lasers on the ionization efficiency of target and non-target isotopes. For quantitative assessments, one needs to obtain ionization efficiencies of all constituent isotopes varying the system parameters through numerical integration of coupled differential equations²⁹.

A series of calculations have been conducted by varying the intensities of all three excitation lasers across different bandwidths, all under Doppler-free conditions. The results have been tabulated in Table 7. The table shows that it is possible to enrich the ¹⁶⁸Er isotope to up to 95% for all laser bandwidths up to 750 MHz. Therefore, laser bandwidths need to be controlled to ≤ 750 MHz. Interestingly, the content of ¹⁶⁷Er decreased with an increase in the excitation laser’s bandwidth. This can be attributed to the reduction in the intensity of the second excitation laser (please refer to the earlier discussion in this section).

Table 7 Optimum values of laser intensity, ionization efficiency of ¹⁶⁸Er and the degree of enrichment calculated under Doppler free condition for the various bandwidths of excitation lasers.

Effect of Doppler broadening

So far, the Doppler broadening of the atomic ensemble has been ignored for the computations. However, in the laser isotope separation process, the atomic ensemble exhibits Doppler broadening due to the velocity distribution of the atoms.

To include Doppler broadening of the atomic ensemble, atomic flux-velocity distribution is taken as

$$\phi \left(v\right)=2\left(\frac{{v}^{3}}{{\alpha }^{4}}\right).{e}^{-\left(\frac{{v}^{2}}{{\alpha }^{2}}\right)}dv$$

(2)

where, α is the most probable velocity; for the present calculations, the integration is carried out up to 4α, at which the relative flux had dropped to the value of ~ 10^–7 of the maximum.

At 1200 ˚C, the erbium atoms have a most probable velocity of 381.7 m/sec. When these atoms traverse with an angle of “θ” to the laser propagation axis, the Doppler shift of the resonance can be expressed by the equation

$$Doppler shift \left(MHz\right)= \frac{v Sin\left(\theta \right)}{\lambda }\times {10}^{3}$$

(3)

where v is the velocity of the atom (m/sec) and λ is the wavelength of the transition (nm) and θ is the divergence angle of the atom relative to the laser propagation axis. When an atom has a divergence angle of 10˚ with reference to the laser propagation axis, the Doppler shift of the transitions is 105.1 MHz, 113.0 MHz, 117.2 MHz. Even when all the co-propagating lasers are tuned to resonance for each excitation step, the net detuning caused by the Doppler shift totals 335.3 MHz, which is the sum of 105.1 MHz, 113.0 MHz, and 117.2 MHz. If the bandwidth of all the excitation lasers is 100 MHz or greater, the atoms will be excited and ionized, though with reduced efficiency. In a practical laser isotope separation process, the atomic ensemble exhibits a distribution of velocities Therefore, to account for Doppler broadening, ionization efficiency calculations have been performed for a range of angular divergences of the atomic ensemble. The results are summarized in Table 8, which includes the degree of enrichment for each isotope and the ionization efficiency of the target isotope. It can be observed that a degree of enrichment greater than 95% can be achieved for all laser bandwidths up to 750 MHz when the atomic ensemble’s full angular divergence is 30° or less. A laser bandwidth of 500 MHz and a full angle divergence of 30° can be considered optimal for the laser isotope separation process. Under these conditions the degree of enrichment of ¹⁶⁸Er is > 96% and the ionization efficiency is 0.2.

Table 8 Optimum values of laser intensity, ionization efficiency of ¹⁶⁸Er and the degree of enrichment calculated for various angular divergence values and bandwidths of excitation lasers.

Choice of co-propagating vs counter-propagating laser beams

In laser isotope separation, employing co-propagating laser beams ensures simpler and optimal overlap throughout the interaction zone, thereby maximizing the effectiveness of the separation process. While co-propagating beams provide the benefit of effective overlap, laser isotope separation can also be achieved using counter-propagating laser configuration. Since the resonance of the ¹⁶⁸Er target isotope lies on the coherent two-photon excitation lines of non-target even isotopes (Fig. 6), the ionization efficiency of target and non-target isotopes varies with co- and counter-propagating laser beam configurations. Consequently, calculations have been conducted to determine the ionization efficiency of the ¹⁶⁸Er isotope and the enrichment levels of all constituent isotopes across all four possible configurations (see Table 9). Data from Table 9 suggests that the direction of laser-3 propagation (relative to laser-1 or laser-2) does not influence both degree of enrichment and the ionization efficiency of the constituent isotopes. However, Table 9 also shows that when laser-2 propagates in the opposite direction (counter-propagating) relative to laser-1, the degree of enrichment of the target isotope ¹⁶⁸Er decreases by 1%. This decrease is attributed to the increased ionization efficiency of neighbouring non-target even isotopes, particularly ¹⁶⁶Er and ¹⁷⁰Er. When laser-2 counter-propagates (relative to laser-1), it cancels out the velocity-induced detunings in the two-photon reference frame, resulting in higher ionization efficiency of non-target isotopes. Therefore, the co-propagating configuration (↑↑↑) is preferred for the laser isotope separation process.

Table 9 A table of ionization efficiency of ¹⁶⁸Er and degree of enrichment of stable isotopes of erbium with variation in the laser configuration. The bandwidth of all excitation lasers is 500 MHz. Full angle divergence of the atomic ensemble is 30˚.

Charge-exchange collisions

Charge exchange collisions significantly influence the effectiveness of the laser isotope separation process. To achieve a high production rate of the enriched isotope, it is essential to operate the atomic ensemble at the highest feasible atomic number density. However, as the number density increases, the charge-exchange collisions also increase, which negatively impacts the degree of enrichment. The probability of charge-exchange collisions can be calculated using the expression.

$$\text{Probability of charge exchange} p=1-{e}^{-\sigma dN}$$

(4)

Where, σ is the resonant charge exchange cross-section (cm²), d is the distance traversed by photoions prior to collection at the ion collector (cm) and N is the number density of the atoms (atoms / cm³).

Resonant charge exchange cross-section can be calculated using the following formula³¹

$$\sigma \left(v\right)=\left(1.81\times {10}^{-14}-2.12\times {10}^{-15}{.log}_{10}v\right).{\left(\frac{IP}{13.6}\right)}^{-1.5}$$

(5)

where v is the velocity of the ion in cm/sec and IP is the ionization potential of the element in eV.

For the most probable atomic velocity of 381.7 m/sec for erbium at 1200° C, the resonant charge exchange cross-section has been calculated to be 4.2 × 10^–14 cm², which is in reasonable agreement with the value of 2.8 × 10^–14 cm² reported by Smirnov et al.³².

A series of calculations of degree of enrichment have been carried out varying the number density of the atoms in the laser-atom interaction region diameter of 5 cm and the results are plotted in Fig. 8. It can be observed from Fig. 8 that a degree of enrichment of > 90% for ¹⁶⁸Er can be achieved by controlling the number density to ≤ 7 × 10¹¹ atoms/cm³; while a degree of enrichment of 80% for ¹⁶⁸Er can be achieved at the number density of 2 × 10¹² atoms/cm³. From the data in Fig. 8, the appropriate number density value can be chosen based on the desired degree of enrichment for the target isotope. Although ¹⁶⁷Er is adjacent in mass to the target isotope, its degree of enrichment is lower than that of ¹⁶⁶Er. This is attributed to the broader hyperfine spectrum of ¹⁶⁷Er.

Fig. 8

Effect of charge-exchange collisions on the degree of enrichment of erbium isotopes. The distance traversed by photoions prior to collection at the ion collector is taken as 5 cm. The bandwidth of all excitation lasers is 500 MHz. The intensities of the excitation lasers are 800 W/cm², 1000 W/cm² and 2400 W/cm² respectively. All the excitation lasers are tuned to ¹⁶⁸Er resonance.

Production rate

Production rates can be calculated using the following equation

$$P \left(\frac{g}{hour}\right)=2.827\times {10}^{3}\times \left({b}^{2}.p.l.d.A.f.{\eta }_{i}.i.n.\frac{M}{{N}_{A}}.PRF\right)$$

(6)

where b is the laser beam diameter (cm), p is the fractional population of the ground level, l is the length of the laser-atom interaction region (cm), d is the number density of atoms in the interaction region (atoms/ cm³), A is the fractional abundance of the target isotope, f is the fractional flux (flux relative to the flux of unhindered atomic beam), η is the ionization efficiency (derived from the density matrix calculations), i is the irradiation probability, n is the number of passes of the laser beam through the laser-atom interaction region, M is the atomic mass of the target isotope (AMU), N_A is the Avogadro number (6.02214076 × 10²³) and PRF is the pulse repetition frequency of the lasers (Hz).

For the values of b = 5 cm, p = 0.992, l = 100 cm, d = 7 × 10¹¹ atoms/cm³, A = 0.26978, f = 1, η = 0.20, i = 1, n = 1, M = 168, PRF = 10 kHz, the production rate has been calculated to be 740 mg/ hour (or 18 g/day). A summary of the optimum system parameters for the separation of ¹⁶⁸Er isotope is shown in Table 10.

Table 10 A summary of the optimized system parameters for the laser isotope separation of ¹⁶⁸Er.

Table 11 compares the degree of enrichment and the production rates of precursor isotopes from previous studies with those from the current work. The production rate of the precursor isotope with the current method is one to two orders of magnitude higher than that of previously reported methods. Therefore, it is envisaged that the enriched isotopes produced by this method will meet the current demand for the enriched isotope precursors.

Table 11 A comparison of the production rates and degree of enrichment of precursor isotopes reported for the production of medical isotopes.

Irradiation of enriched isotope mixture

In this section, the utility of enriched ¹⁶⁸Er (produced through the AVLIS process) for medical applications has been studied for its suitability to medical application. When the natural erbium is irradiated in a nuclear reactor, after chemical separation erbium, it consists of five erbium radioisotopes namely., ¹⁶³Er, ¹⁶⁵Er, ¹⁶⁹Er, ¹⁷¹Er and ¹⁷²Er. (Fig. 1). On the other hand, when the enriched erbium is irradiated, after chemical separation, it consists of only three ¹⁶⁹Er, ¹⁷¹Er and ¹⁷²Er radioisotopes. The production efficiency erbium radioisotopes during the irradiation in low, medium and high-flux reactors is shown in Fig. 9. The separated radioisotopes of erbium produce decay chain nuclides which are shown in Fig. 10.

Fig. 9

Production efficiency radioisotopes of erbium produced during irradiation of enriched erbium in (A) low (B) medium and (C) high flux reactors.

Fig. 10

Radioisotopes of erbium isotopes produced during the irradiation of enriched erbium and their daughter nuclides.

Medical fraternity desires the medical isotope to be produced with highest radioisotopic purity (not to be confused with isotopic purity) possible for the optimal control of the dose to the patient. The radioisotopic purity (R_i) of an isotope “i” can be calculated using the expression:

$${R}_{i} (\%)= \frac{{S}_{i}*{f}_{i}}{\sum_{i}^{n}{S}_{i}*{f}_{i}}\times 100$$

(7)

where S_i is the carrier free specific activity of the radioisotope “i” (Bq/g), f_i is the relative fractional abundance of the isotope present in the isotope mixture, n is the number of radioisotopes in the isotope mixture.

Since the radioisotopes of the isotopic mixture have varying half-lives the radioisotopic purity of the isotope mixture varies with time. The radioisotopic purity of the ¹⁶⁹Er produced from the enriched erbium increases from 96% to 99.5% within 24 h which is adequate for the application intended (Fig. 11). Using the enriched ¹⁶⁸Er isotope obtained from the laser isotope separation process, irradiation in low, medium, and high flux reactors can produce 180, 1800, and 18,000 doses per day (each with an activity of 7.4 GBq) respectively.

Fig. 11

Change in the radioisotopic purity of ¹⁶⁹Er with cooling time. Open Circle – Natural erbium irradiated in low-flux reactor (reactor flux 1 × 10¹³ neutrons/cm²/sec) for 21 days. Closed Circle – Enriched erbium irradiated in low-flux reactor (reactor flux 1 × 10¹³ neutrons/cm²/sec) for 21 days.

Conclusions

This present study investigates a three-step laser isotope separation method for enriching ¹⁶⁸Er using 631.052 nm – 586.912 nm – 566.003 nm three-step photoionization scheme. The lineshape contours observed in three-step photoionization process have been investigated in detail. The effect of bandwidth and intensity of the excitation lasers, Doppler broadening of atomic ensemble on the degree of enrichment and the production rate have been systematically studied. It has been shown that, unlike the enrichment processes for other lanthanides such as ¹⁷⁶Lu and ¹⁷⁶Yb isotopes, enriching ¹⁶⁸Er requires a relatively simpler experimental configuration.

Based on the above investigations, an optimum system configuration for the efficient laser isotope separation of ¹⁶⁸Er has been derived. With the derived system configuration, it is possible to produce 18 g/day of 90% enriched ¹⁶⁸Er. Using the enriched ¹⁶⁸Er isotope obtained from the laser isotope separation process, irradiation in low, medium, and high flux reactors can produce 180, 1800, and 18,000 doses per day (each with an activity of 7.4 GBq) respectively. After 24 h of irradiation and chemical separation, the radioisotopic purity of the medical isotope reaches to > 99% making it suitable for the medical applications. The current method is also free from isobaric impurities, which can otherwise affect the performance of the medical isotope.

From an application standpoint, enriching the ¹⁶⁸Er isotope offers significant advantages compared to ¹⁷⁶Lu and ¹⁷⁶Yb. This is the first ever study on the laser isotope separation of ¹⁶⁸Er isotope, holds promise for filling the growing demand–supply gap for the radioisotope precursors in the coming years.