Introduction

The advent of modern transportation systems has led to an increase in the construction of roads. The elastic modulus of recoverable strain under repeated stress is called resilient modulus (MR). It is defined as the ratio of the deviator stress (σd) to the recoverable strain (εr). As one of the essential characteristics of soil, MR has been found to depend on several factors such as the weighted plasticity index (wPI), dry unit weight (γd), confining stress (σc), deviator stress (σd), moisture content (w) and the number of FT cycles (NFT)1,2,3,4. The prediction of MR is of paramount importance to the safe and sustainable design of flexible pavement systems5,6. Traditional forecasting methods for MR can be classified into three primary categories: experimental methods, regression equation methods, and principal modeling methods (as illustrated in Table 1). Owing to their complexity and time consumption, these technologies are challenging to implement in engineering.

Table 1 The traditional methods for predicting MR.
Full size table

On the other hand, developing intelligent computing technologies, including support vector machines, long-short-term neural networks, random forests, and artificial neural networks, has enabled the rapid, effective, and cost-effective resolution of some civil engineering problems36,37,38,39,40,41,42,43,44,45. As illustrated in Table 2, some researchers have employed various machine learning techniques to predict the MR, either by utilizing single or combinatorial algorithms. These studies demonstrate that machine learning methods are proficient at predicting MR.

Table 2 Application of machine learning for predicting MR.
Full size table

Research gap

However, there is room for improvement in some of these machine learning studies. The accuracy of the models presented in the article can be improved. Fewer soil types were used in the experiments, making it difficult to demonstrate the generalizability of the models. Moreover, non-computer individuals have difficulties in using the models. Therefore, there is a need for more research in machine learning for predicting MR.

Research objective

This paper aims to develop an efficient, generalizable and user-friendly MR prediction model. For that purpose, this study proposed the black-winged kite algorithm-extreme gradient boosting model (BKA-XGBOOST) and collected 12 types of soil data from multiple studies to verify the feasibility and generalizability of the model. The model was based on XGBOOST, well-suited for capturing many-to-one nonlinear relationships66,67,68,69,70. Moreover, BKA, with powerful optimization capabilities71, was employed to optimize the parameters of XGBOOST, ensuring that XGBOOST maintains optimal performance. In addition, an application program based on BKA-XGBOOST has been developed to facilitate its use by engineers.

Research significance

This study addresses the problem of MR being difficult to assess in the geotechnical field. Traditional methods for predicting MR are complex and time-consuming, and some machine learning models exhibit low accuracy and inadequate generalizability. By proposing the BKA-XGBOOST model, this study introduces a novel approach to accurately and efficiently assess various types of MR. The application developed based on the proposed model is user-friendly and can assist engineers in geotechnical engineering.

Research methodology

The BKA-XGBOOST model proposed in this paper employs BKA to search for the three best parameters of XGBOOST to improve its prediction accuracy for various soil data. The dataset utilized for the experiment was collected from Ding, Rahman, Solanki and Ren2,3,4,72, encompassing 2813 soil data points. To evaluate the performance of the proposed model, it was compared with nine single models and four hybrid models utilized in previous studies from a range of evaluation metrics. In addition, a BKA-XGBOOST-based application was developed to improve the model’s usability. Figure 1 illustrates the structure of the research methodology for this study.

Fig. 1
figure 1

The structure of the research methodology.

Full size image

Experimental environment

The training and testing were conducted using a hardware setup that consists of a 12th Gen Intel (R) Core i5-12500 H processor, 32.0 GB of RAM, and an NVIDIA GeForce RTX 3060 graphics card. The utilized software is MATLAB 2023b. Furthermore, the proposed model requires an average of 0.5247 s to predict 563 samples within the specific hardware setting.

Data analysis

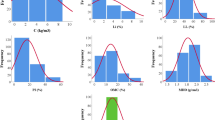
Several factors affect MR. Choosing the wrong factors as inputs to XGBOOST would lead to imprecise forecasts and unnecessary computations. Some researchers have demonstrated that the wPI, γd, σc, σd, w and NFT exert a more pronounced influence on MR1,2,3,4 ; hence, this study employs these factors as inputs. To validate the feasibility of the proposed model, this study gathered 2,813 sets of soil data from earlier studies as experimental data2,3,4,72. The dataset comprises six inputs and one output. wPI equals the plasticity index measured by the standard plasticity test multiplied by the percent passing 0.425 mm sieve; γd is the dry weight of the soil divided by the soil’s volume; σc, σd and MR are obtained from the triaxial test; w is typically calculated by determining the mass difference after drying the soil; NFT is derived from cyclic freeze-thaw experiments. Twelve soil types were included in the dataset, with two originating from China, five from the United States, and five from Canada. According to the statistical analysis in Table 3, it can be seen that the value distribution of γd is relatively concentrated, while the distribution of other inputs is relatively scattered. In particular, a larger standard deviation for σc, σd, and MR implies more significant fluctuations in their values. From Fig. 2, all the variables soil data variables exhibit a non-positive distribution, and the relationship between the two variables is complicated, encompassing negative, positive, and weak correlations. For instance, the sub-graphs in the first column of the fifth row and the second column of the fifth row illustrate that w tends to increase with wPI, contrary to γd. On the other hand, σd remains constant as σc escalates. It is essential to analyze the relationship between the variables further.

Table 3 Soil data statistics.
Full size table
Fig. 2
figure 2

Soil data statistics.

Full size image

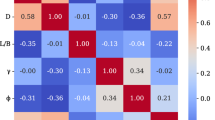
Correlation analysis was employed to investigate the relationship between these variables further. Pearson, Spearman, and Kendall are three standard methods for analyzing the correlations between two variables. The Pearson method is suitable for normally distributed continuous variables. In contrast, the Spearman method is suitable for non-normally distributed continuous variables, and the Kendall method is suitable for categorical variables. Because all variables in the data were non-normally distributed, the Spearman correlation coefficient was employed73. If the correlation coefficients between two variables range from ± 0.81 to ± 1.0, ± 0.61 to ± 0.80, ± 0.41 to ± 0.60, ± 0.21 to ± 0.40, and ± 0.00 to ± 0.20, respectively, then they may show a very strong, strong, moderate, weak, and no relationship74. From Fig. 3, it shows that γd and w present a very strong negative correlation, wPI and w exhibit a strong positive correlation, while wPI and γd, as well as w and MR, show moderate negative correlations. The remaining variables display either weak correlation or no correlation with one another. Although γd and w, as well as wPI and w, exhibit a strong correlation, the rest of the variables have a weak correlation. Consequently, it was unnecessary to assess the data for multicollinearity.

Fig. 3
figure 3

Correlations between variables.

Full size image

Soft computing approaches

Extreme gradient boosting

XGBOOST, the foundation of the proposed model, was initially introduced by Chen in 201675. It represents an improvement upon the gradient-boosting decision tree (GBDT). Compared to GBDT, XGBOOST exhibits the following principal advantages: (1) The CART tree produced by XGBOOST takes into account the intricacy of the tree. (2) XGBOOST is a second-order derivative expansion that fits the previous round of loss function. In contrast, GDBT is a first-order derivative expansion that fits the previous round of loss function. Hence, XGBOOST exhibits higher accuracy and necessitates a reduced number of iterations. (3) XGBOOST can utilize multi-threading throughout the process of selecting the optimal split point, resulting in a significant enhancement in the speed of execution. (4) XGBOOST integrates regularization terms into the loss function, which helps control the complexity of the model and prevents overfitting. (5) XGBOOST permits the utilization of custom objective functions and evaluation functions, provided that the objective function is second-order differentiable76. (6) XGBOOST can automatically learn the trend of missing feature values in sample77. Regarding regression problems, the fundamental algorithm of XGBOOST mainly involves determining expected MR and objective functions. The specific contents of this algorithm are as follows:

For soil data \(\:\left\{\left({x}_{1},{\text{y}}_{1}\right),\dots\:,\left({x}_{n},{y}_{n}\right)\right\}\), containing n samples, the predicted value of MR can be expressed as:

$$\:\begin{array}{c}{\hat{y}}_{i}=\sum\limits_{k=1}^{K}\:{f}_{k}\left({x}_{i}\right)\:{f}_{k}\in\:F,\end{array}$$
(1)

where \(\:{x}_{i}\) is the impact factor of MR containing m features, and \(\:{\hat{y}}_{i}\) is the predicted value of MR. k is the number of the classification and regression tree (CART), F is the set of regression trees, and \(\:{f}_{k}\left({x}_{i}\right)\) is the predicted value of CART.

For real values \(\:{y}_{i}\) the objective function is defined as follows:

$$\:\begin{array}{c}Obj=\sum\limits_{i=1}^{n}\:l\left({y}_{i},{\hat{y}}_{i}\right)+\sum\limits_{k=1}^{K}\:\varOmega\:\left({f}_{k}\right),\end{array}$$
(2)

where \(\:l\left({y}_{i},{\hat{y}}_{i}\right)\) is the loss function used to evaluate the accuracy of \(\:{\hat{y}}_{i}\), and \(\:{\Omega\:}\left({f}_{k}\right)\) represents the regularization term to avoid overfitting.

Substitute \(\:{\hat{y}}_{i}={\sum\limits}_{k=1}^{K}\:{f}_{k}\left({x}_{i}\right)={\hat{y}}_{i}^{(t-1)}+{f}_{t}\left({x}_{i}\right)\) into formula 2, the objective function after k iterations is defined as follows:

$$\:\begin{array}{c}Ob{j}^{\left(k\right)}=\sum\limits_{i=1}^{n}\:l\left({y}_{i},{\hat{y}}_{i}^{k-1}+{f}_{k}\left({x}_{i}\right)\right)+\varOmega\:\left({f}_{k}\right)+\text{\:}\text{c}\text{o}\text{n}\text{s}\text{t}\text{a}\text{n}\text{t}.\end{array}$$
(3)

Use the second-order Taylor expansion of Eq. 3 and delete the constant, the following formula is obtained:

$$\:\begin{array}{c}Ob{j}^{\left(k\right)}=\sum\limits_{i=1}^{n}\:\left({g}_{i}{f}_{k}\left({x}_{i}\right)+\frac{1}{2}{h}_{i}{f}_{k}^{2}\left({x}_{i}\right)\right)+\varOmega\:\left({f}_{k}\right),\end{array}$$
(4)

where \(\:{g}_{i}={l}^{{\prime\:}}\left({y}_{i},{\hat{y}}_{i}^{k-1}\right)\), and \(\:{h}_{i}={l}^{{\prime\:}{\prime\:}}\left({y}_{i},{\hat{y}}_{i}^{k-1}\right)\). \(\:{g}_{i}\) and \(\:{h}_{i}\) represent the first-order and second-order gradient statistics of the loss function respectively.

For a tree containing L leaves, which contain j sample sets, and the weight of the leaves is \(\:\omega\:\), the regularization term \(\:{\Omega\:}\left({f}_{k}\right)\) can be expressed as:

$$\:\begin{array}{c}\varOmega\:\left({f}_{k}\right)=\lambda\:L+\frac{1}{2}\mu\:\sum\limits_{j=1}^{L}\:{\omega\:}_{j}^{2},\end{array}$$
(5)

where λ and µ are constants.

Further simplify the objective function, the following formula is obtained:

$$\:\begin{array}{c}Ob{j}^{\left(k\right)}=\sum\limits_{j=1}^{L}\:\left[{G}_{i}{\omega\:}_{j}+\frac{1}{2}\left({H}_{i}+\mu\:\right){\omega\:}_{j}^{2}\right]+\lambda\:L,\end{array}$$
(6)
$$\:\text{w}\text{h}\text{e}\text{r}\text{e}\:{G}_{i}={\sum\limits}_{i\in\:{I}_{j}}\:{g}_{i}\:\text{a}\text{n}\text{d}\:{H}_{i}={\sum\:}_{i\in\:{I}_{j}}\:{h}_{i}.$$

Black-winged kite algorithm

BKA is a biologically inspired algorithm proposed by Wang in 202471. The algorithm replicates black-winged kites’ predation and migration patterns, known for their remarkable ability to adjust to environmental fluctuations in their natural habitat. This simulation strategy enables the method to efficiently adapt to dynamic optimization situations. BKA exhibits an optimal balance between global and local search, a rich population diversity, and simple computational complexity. Furthermore, it demonstrated satisfactory performance in a comparative analysis of 59 test functions with 17 optimization algorithms, including particle swarm optimization, whale optimization algorithm, grey wolf optimization, and sparrow search algorithm71. Therefore, BKA is utilized to determine the most suitable settings for XGBOOST, which allows XGBOOST to achieve its highest level of performance. The primary computation of BKA consists of three phases: initialization, predation, and migration. The specifics of this algorithm are as follows:

Initialization

As the initial stage of the algorithm, this stage mainly involves the definition of individuals and optimal positions.

Use a matrix to represent the position of black-winged kites.

$$\begin{array}{*{20}c} {BK = \left[ {\begin{array}{*{20}c} {BK_{{1,1}} } & {BK_{{1,2}} } & \ldots & \ldots & {BK_{{1,~\dim ~}} } \\ {BK_{{2,1}} } & {BK_{{2,2}} } & \ldots & \ldots & {BK_{{2,~\dim ~}} } \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {BK_{{pop,1}} } & {BK_{{pop,2}} } & \ldots & \ldots & {BK_{{pop,~\dim ~}} } \\ \end{array} } \right]}, \\ \end{array}$$
(7)

where pop is the number of individuals, dim is the dimension of the problem being asked, and BKi, j represents the i-th black-winged kite in the j-th dimension.

Use the following formula to represent the position of i-th black-winged kite:

$$\:\begin{array}{c}{X}_{i}=B{K}_{lb}+{rand}\left(B{K}_{ub}-B{K}_{lb}\right),\end{array}$$
(8)

where \(\:B{K}_{lb}\) and \(\:B{K}_{ub}\) are the lower and upper bounds of the black wing kite in the j-th dimension respectively, and rand is a random number between 0 and 1.

Use the root mean square error as the adjustment value and represent the leader (\(\:{X}_{\text{L}}\)) of the population with the individual with the smallest fitness value, and its position is expressed by the following formula:

$$\:\begin{array}{c}{X}_{L}=X\left(find\left({f}_{\text{bett\:}}==f\left({X}_{i}\right)\right)\right),\end{array}$$
(9)

where \(\:{f}_{\text{best\:}}=min\left(f\left({X}_{i}\right)\right.\).

Predation

The second stage represents the global exploration and search process of the algorithm by simulating the hunting and searching behavior of black-winged kites on small grassland mammals. The following is the mathematical expression that describes the attacking behavior of black-winged kites.

$$\:\begin{array}{c}{y}_{t+1}^{i,j}=\left\{\begin{array}{l}{y}_{t}^{i,j}+n\left(1+\text{sin}\left(r\right)\right)\times\:{y}_{t}^{i,j}p<r\\\:{y}_{t}^{i,j}+n\times\:\left(2r-1\right)\times\:{y}_{t}^{i,j}\:\text{\:else\:}\end{array}\right.,\end{array}$$
(10)
$$\:\begin{array}{c}n=0.05\times\:{e}^{-2\times\:{\left(\frac{t}{T}\right)}^{2}},\end{array}$$
(11)

where \(\:{y}_{t}^{ij}\) and \(\:{y}_{t+1}^{ij}\) respectively represent the position of the i-th black-wing kite in the j-th dimension in the t and t + 1 iterations. r is a random number between 0 and 1, and p is a constant with a value of 0.9. T is the maximum number of iterations and t is the number of iterations completed so far.

Migration

When the climate and food resources are inadequate to support black-winged kites, they will relocate to a different habitat under the direction of a leader in pursuit of more favorable living conditions and increased food availability. In this stage, the leader’s fitness value is utilized to assess their suitability for guiding the populace in migration. If the fitness value of the leader’s current position is lower than that of a randomly selected individual, the leader will relinquish its leadership. In contrast, the leader will guide the populace towards the destination. The subsequent mathematical formula delineates the migratory patterns exhibited by black-winged kites.

$$\:\begin{array}{c}{y}_{i+1}^{i,j}=\left\{\begin{array}{cc}{y}_{t}^{i,j}+C\left(\text{0,1}\right)\times\:\left({y}_{t}^{i,j}-{L}_{t}^{j}\right)&\:{F}_{i}<{F}_{ri}\\\:{y}_{t}^{i,j}+C\left(\text{0,1}\right)\times\:\left({L}_{t}^{j}-m\times\:{y}_{t}^{i,j}\right)&\:\:\text{\:else\:}\end{array}\right.,\end{array}$$
(12)
$$\:\begin{array}{c}m=2\times\:\text{sin}\left(r+\frac{\pi\:}{2}\right),\end{array}$$
(13)

where \(\:{L}_{t}^{j}\) represents the leader of the black-winged kites in the j-th dimension of the t-th iteration. \(\:{y}_{t}^{i,j}\) and \(\:{y}_{i+1}^{i,j}\) respectively represent the position of the i-th black-winged kite in the j-th dimension in the t and t+1 iterations. \(\:{F}_{i}\) represents the position of any black-winged kite in the j-th dimension in t iteration. \(\:{F}_{ri}\) represents the fitness value of a random position in the j-th dimension obtained by any black-winged kite in t iterations. \(\:C\left(\text{0,1}\right)\) represents Cauchy mutation78, and its standard formula is \(\:f\left(x\right)=\frac{1}{\pi\:}\frac{1}{{x}^{2}+1},\:-{\infty\:}<x<{\infty\:}\).

Black-winged kite algorithm-extreme gradient boosting

The BKA-XGBOOST model combines BKA and XGBOOST (Fig. 4). XGBOOST serves as the foundation of the model, processing the input and output data of the soil. Although XGBOOST is proficient in managing nonlinear many-to-one relationships, its performance is most significantly influenced by the depth of the tree, the learning rate, and the maximum number of iterations79,80. It is challenging to predict MR using XGBOOST with inappropriate parameter settings accurately81. Furthermore, manually identifying optimal parameters necessitates a certain degree of expertise, is also inherently time-consuming, and frequently yields suboptimal outcomes82. Consequently, BKA is employed here to ascertain the optimal tree depth, learning rate, and maximum number of iterations for XGBOOST, thereby contributing to the accurate prediction of MR. Upon reaching the maximum number of iterations or when the fitness value no longer decreases, BKA will provide an optimal tree depth, learning rate, and maximum number of iterations. Otherwise, BKA will continue to determine the optimal parameters.

Using raw data with disparate magnitudes and sizes along different dimensions for direct training and prediction may result in prolonged training periods and suboptimal training outcomes83. Consequently, all the data are transformed using the max-min normalization approach to ensure they fall within the range of 0 to 1. Moreover, the ratio of the training set to the test set significantly influences the predictive performance of XGBOOST. 80% of the data are randomly selected for model training and the remaining data are used for prediction67,84. Moreover, a 5-fold cross-validation procedure is employed to mitigate overfitting during training85,86. The training data are divided into five distinct subsets in the cross-validation process. One of these subsets is the validation data set, while the other four subsets are used to train the model68.

Fig. 4
figure 4

The structure of BKA-XGBOOST.

Full size image

Performance evaluation

Model performance was assessed using the mean absolute error (MAE), root mean square error (RMSE), determination coefficient (R2), mean absolute percentage error (MAPE), and relative percent deviation (RPD). The ideal values of MAE, RMSE, R2, and MAPE are 0, 0, 1, and 0, respectively, and an RPD above 1.4 indicates that the model is reliable87,88,89,90. The formulas are as follows:

$$\:\begin{array}{c}MAE=\frac{1}{n}\sum\limits_{i=1}^{n}\:\left|{y}_{i}-{\hat{y}}_{i}\right|,\end{array}$$
(14)
$$\:\begin{array}{c}RMSE=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}\:{\left({y}_{i}-{\hat{y}}_{i}\right)}^{2}},\end{array}$$
(15)
$$\:\begin{array}{c}{R}^{2}=1-\frac{\sum\:{\left({y}_{i}-{\hat{y}}_{i}\right)}^{2}}{\sum\:{\left({y}_{i}-\bar{y}\right)}^{2}},\end{array}$$
(16)
$$\:\begin{array}{*{20}c} {MAPE = \frac{1}{n}\sum\limits_{{i = 1}}^{n} {\left| {\frac{{y_{i} - \hat{y}_{i} }}{{y_{i} }}} \right|} \:,} \\ \end{array}$$
(17)
$$\:\begin{array}{c}RPD=\frac{SD}{RMSE},\end{array}$$
(18)
$$\:\begin{array}{c}SD=\sqrt{\frac{1}{n-1}\sum\:_{i=1}^{n}{\left({y}_{i}-\bar{y}\right)}^{2}},\end{array}$$
(19)

where \(\:{y}_{i}\) represents the actual value, \(\:{\hat{y}}_{i}\) represents the estimated value, and \(\:\bar{y}\) represents the average of the actual values.

Results and discussion

Predictions of the proposed model

The parameter settings of BKA-XGBOOST are primarily determined by the parameters of BKA and the optimization range. The number of populations and the maximum number of iterations of BKA are set to 10 and 20, respectively, to balance the optimization time and effect. The three critical parameters of XGBOOST optimized by BKA are the depth of CART, the learning rate, and the number of iterations of XGBOOST. BKA searches for the optimal parameter within the set range and determines whether the resulting parameter is optimal by the magnitude of the RMSE, which ultimately yields the parameter combination with the smallest RMSE after 20 iterations. The optimization ranges of the three parameters should be set moderately to avoid suboptimal solutions and waste computing resources. Based on previous studies67,80,91,92,93,94, the optimization ranges of these three parameters are set as follows: the depth of CART is set to 3 to 30, the learning rate is set to 0.001 to 0.1, and the number of iterations of XGBOOST is set to 100 to 1000.

To determine the reliability of BKA-XGBOOST, the original data were randomly and nonrepetitively reassembled ten times. BKA-XGBOOST was employed to predict ten distinct data combinations. The optimization process of BKA and the corresponding optimal parameters are illustrated in Fig. 5; Table 4, respectively. The corresponding parameter combinations obtained from Table 4 indicate that the optimal parameter settings consist of parameter combinations with different values, and there is no apparent linear trend in the parameter settings. Manually determining parameters is a challenging and time-consuming task. Furthermore, the prediction results illustrated in Fig. 6 indicate that the prediction curve aligns well with the actual value curve overall. BKA-XGBOOST, with this parameter configuration, demonstrates great predictive accuracy. This is further substantiated by the indicators shown in Table 5.

Fig. 5
figure 5

The XGBOOST parameters optimization process.

Full size image
Table 4 Optimal XGBOOST parameters.
Full size table
Fig. 6
figure 6

BKA-XGBOOST predictions.

Full size image
Table 5 BKA-XGBOOST prediction performance.
Full size table

Sensitivity analysis

Sensitivity analysis aims to determine the relative importance of inputs to outputs. Since the contributions of wPI, γd, σc, σd, w and NFT to the prediction of MR are unknown, the proposed model is still a black box model. Therefore, it is necessary to conduct sensitivity analysis to explore the impact of each variable on MR. To further explore the impact of each input on MR, the maximum information coefficient (MIC) method was employed. The notion of MIC is derived from mutual information theory and is utilized to quantify the level of mutual effect between two variables95. MIC is a method that is universally applicable and provides a fair assessment of the relationships between variables, in contrast to methods such as Pearson, Spearman, and Kendall, which lack these qualities96,97,98. As illustrated in Fig. 7, the influence of w on MR is pronounced, whereas the impacts of NFT, σd, and σc on MR are relatively modest. This suggests that MR depends heavily on w, γd, and wPI.

Fig. 7
figure 7

The degree of influence of inputs on MR.

Full size image

Comparison of various models

To ascertain the effectiveness of the proposed model, the models in Table 2 are employed for comparison, including the extreme learning machine (ELM), the K-nearest neighbor (KNN), the support vector machine (SVM), the extreme gradient boosting (XGBOOST), the random forest (RF), the least square support vector machine (LSSVM), the radial basis function neural network (RBFNN), the back propagation neural network (BPNN), and the generalized regression neural network (GRNN). Table 6 presents the parameter settings employed in the comparison models.

Table 6 Parameters of comparison models.
Full size table

The dataset used for the comparison model is the 4th dataset in Table 4 (BKA-XGBOOST’s performance on this dataset is closest to its average performance, and the feasibility of the proposed model can be fairly evaluated by comparing its performance on this dataset). Figure 8 shows the predictions of different models for the same dataset. According to Fig. 8, the prediction curve of KNN is far from the actual value curve, and the absolute prediction error for most samples is the largest. On the other hand, the prediction curve of BKA-XGBOOST is closer to the actual value, and the error is the smallest in all samples except the 407th sample. Based on the model performance comparison shown in Fig. 9, XGBOOST outperforms the other single models, indicating that using XGBOOST to predict MR is reasonable. In addition, the performance of XGBOOST optimized by BKA has improved. The proposed model accomplishes the objective of precisely forecasting MR.

Fig. 8
figure 8

Predictions from different models.

Full size image
Fig. 9
figure 9

Performance of various models.

Full size image

Score analysis

Score analyze is a method for evaluating model performance99,100. In score analysis, models are allocated scores based on various evaluation metrics, and the model with the performance metrics closest to the desired values requires the highest score101,102,103. This study evaluates ten models from five error metrics with a maximum score of 10 and a minimum score of 1. The scores obtained by the models are presented in Table 7. From Table 7, it can be seen that BKA-XGBOOST has received the highest score and is the best-performing model. XGBOOST follows.

Table 7 The models’ scores.
Full size table

Regression error characteristics curve

Regression error characteristic (REC) curve visually depicts a regression model’s predictive performance. REC curve contrasts with conventional merits by emphasizing the cumulative distribution function of the absolute error104. The area over the REC curve (AOC) represents a biased estimate of the predicted error105, with the lowest AOC value signifying the most effective model106. To evaluate the models’ performance, the REC curves were generated (Fig. 10) and the AOC was computed (Table 8). Table 8 demonstrates that the AOC of BKA-XGBOOST is the lowest, signifying it as the most effective model.

Fig. 10
figure 10

The models’ REC curves.

Full size image
Table 8 The models’ AOC.
Full size table

Anderson–Darling test

The Anderson-Darling (AD) test is a nonparametric test typically used to assess data’s normality and analyze the dispersion of predictions. If the model’s AD value is close to the AD value of the actual value, the model demonstrates a reliable capacity to evaluate the MR107. The AD test was employed to evaluate the fit of the models’ predictions to the actual value. As shown in Table 9, the P of the actual value and all predictions are below 0.005, indicating that they are non-normally distributed. Moreover, the AD value of BKA-XGBOOST is closest to the AD value of the actual value, which indicates that BKA-XGBOOST has the best performance.

Table 9 Anderson-Darling test results.
Full size table

Comparison models in the literature

Table 10 shows the comparison with previous studies using different models, including genetic algorithm-adaptive layered population structure (GA-ALPS), symbiotic organisms search-least square support vector machine (SOS-LSSVM), jellyfish swarm optimizer- extreme gradient boosting (JSO-XGBOOST) and genetic algorithm-artificial neural network (GA-ANN). As the previous research utilizes a different dataset than the one employed in this work, direct performance comparisons are unconvincing. The proposed model retains the same parameters as previously stated and predicts the dataset, including 283 data points utilized by Ghorbani (Additional data 2), and 891 data points employed by Sadik, Azam, and He (Additional data 1). According to Table 10, the proposed model demonstrated the highest level of accuracy in predicting outcomes. The RMSE of the proposed model is reduced by 13.72% and 24.82% compared to GA-ANN and JSO-XGBOOST, respectively. The proposed model improves the prediction accuracy to a certain extent, and this research contributes to the accurate prediction of MR.

Table 10 Comparison with previous studies.
Full size table

Model programing

To increase the practicality of the model, MATLAB App Designer is employed to create the MR prediction program. The program is divided into two interfaces: the login interface and the main program (illustrated in Fig. 11). Prior to accessing the main program, users are required to enter their accounts and passwords on the login interface. Upon successful verification, users are permitted to enter the main program. The main program is divided into three sections: the setting area, the functional area, and the output area. The setting area reserves the default BKA basic parameters and the optimization range of XGBOOST parameters, which users have the option to adjust. The ribbon contains Input, Analyze, Predict, Output, and Quit buttons. By clicking the Input button, the data are imported into the program, which supports files in the formats xls, csv, and xlsx. If the user wants to explore the sensitivity of different input factors to MR, the importance of the inputs calculated by the MIC method (the inputs are represented by numbers in order) will be shown by clicking the Analyze button. Subsequently, clicking the Predict button initiates the random selection of 80% of the data for training, with the objective of identifying the optimal XGBOOST parameters. The remaining data are then predicted on the basis of the obtained parameters. The prediction performance of the model is displayed in the form of a line chart, and the prediction accuracy of the model is evaluated with five evaluation indicators. In addition, the program also displays the optimal number of iterations, tree depth, and learning rate obtained through BKA. After clicking the Output button to obtain the prediction results, the user can click the Quit button to exit the program.

Fig. 11
figure 11

Soil resilient modulus prediction program.

Full size image

Summary and conclusions

Forecasting MR is an important part of assessing road safety and sustainability. Traditional methods, including experimental, regression equation, and constitutive model methods, are difficult to implement in engineering due to their time-consuming and complex characteristics. The generality and accuracy of some machine learning methods for predicting MR also need to be further improved. In this situation, this study proposes BKA-XGBOOST as a novel approach for predicting MR. The performance of the proposed model is compared with nine individual models and four literature models using several metrics. The conclusions drawn from this study are as follows:

  • Influence of geotechnical factors: Among the six geotechnical factors utilized as inputs, the one that has the most impact on MR is w, which is influenced by γd.

  • Effect of optimization algorithm: For different combinations of soil data, BKA can provide the optimal parameters to XGBOOST to ensure its outstanding performance. Moreover, the AOC of XGBOOST following BKA optimization is reduced significantly and further improved in accuracy.

  • The best performance model: Performance metrics (MAE = 0.975 MPa, RMSE = 1.7719 MPa, R2 = 0.995, RPD = 15.3902, MAPE = 0.0354), score analysis (score = 50), REC curve (AOC = 14.3497), AD test (model’s AD = 42.056, a difference of 0.232 from the AD of the actual value) indicate that BKA-XGBOOST is the best model. It also proved to be the best model in comparison with four literature models (MAE = 2.8754 MPa, RMSE = 4.1266 MPa, R2 = 0.9769 for additional dataset 1; MAE = 3.1306 MPa, RMSE = 4.4862 MPa, R2 = 0.9816 for additional dataset 2).

In conclusion, this study introduced a new model, BKA-XGBOOST, for evaluating MR. The proposed model exhibits great accuracy, generalizability, and user-friendliness. It has potential for application in geotechnical engineering. However, the soil types employed in the experiments are inadequate. Consequently, more types of soil data will be used in subsequent experiments to test the model’s generalizability and precision further.