Introduction

In general, wireless sensor networks (WSNs) and cognitive radio (CR) are reasonably combined with intelligence for constructing the cognitive radio sensor network (CRSN)1. The CRSN nodes with the potentiality of spectrum sensing have the capability of accessing the bands of the licensed spectrum more opportunistically when they don’t possess any of the primary users (PUs)2. This potentiality of spectrum sensing access prevents the problem of spectrum scarcity posed by the classical WSNs which in turn enhances the performance of the network3. In specific, clustering routing protocol refers to the category of energy-potent routing protocol in CRSN. The process of data aggregation over the cluster head (CH) during the clustering process minimizes the collision probability with PUs, mean reduced energy consumptions, fewer data transmissions, and a lower number of data transmissions in the entire network4. Moreover, cooperative spectrum sensing between the nodes of a cluster has the possibility of minimizing the collision probability with PUs due to the miss detection in spectrum sensing. The clustering routing protocol designed for CRSN is hot research area which has attracted a wide number of researchers with the view to enhance the performance of the network5.

In the design of clustering routing protocol, the three vital dimensions of reasonable channel allocation, optimal number of clusters construction and CH selection need to be considered in CRSN6. In the process of CH selection, the CHs plays an indispensable role in data transmission, data aggregation and data collection within the cluster, and in relaying the data to other clusters too7. Hence the energy consumption is identified to be generally greater than the normal nodes. Number of available channels and residual energy is considered during the process of selecting CHs. On the other hand, optimal number of constructed clusters is another challenge which need to be handled in CRSN8. This challenge of optimal number of constructed clusters results in changes in the network topology in CRSN. This challenge completely depends on change in the state of the PUs channel occupancy and deaths of the nodes due to the drain out of the energy9,10,11. Hence, the optimal number of clusters need to be adopted for dynamic CRSN characteristics12,13,14. In addition, channel allocation in a reasonable manner need to perform channel allocation with satisfied required inter-cluster communication and reduced impact on PUs15.

In this paper, HMABFOA) is proposed as an imperfect spectrum sensing approach for achieving better utilization of downlink energy harvesting and sustain maximized degree of energy between the nodes in the network. This HMABFOA scheme reduced the negative impact of imperfect spectrum sensing for extended network lifetime which sustains the capabilities of the network surveillance. It helped in constructing a distributed cluster with multi-hop routing selection between clusters depending on an energy level function that explores and exploits the factors associated with CHs selection. It specifically used the merits of Mexican axolotl optimization algorithm (MAOA) for better CH selection and cluster formation such that energy stability is sustained in the network. It further used the significance of Bitterling Fish Optimization (BFOA) for achieving optimized multi-hop route between the clusters such that energy consumption is minimized with maximized spectrum sensing that proves better channels availability in the network.

The major contributions of the proposed HMABFOA scheme-based cluster routing protocol is listed as follows.

  1. (i)

    It derived the merits of MAOA for exploring and exploiting the factors that contribute towards better clustering and optimal CHs selection which maximized network lifetime with sustained energy stability.

  2. (ii)

    It used BFOA for attaining multi-hop and reliable optimized routing between the established clusters for minimizing the unnecessary energy drain in the network with maximized packet delivery.

  3. (iii)

    It is proposed with the capability of handling the degree of high imbalance in residual energy which exists between the selected CHs that in turn negatively impacts the delivery of data packets in the networks.

  4. (iv)

    The simulation experiments of the proposed HMABFOA scheme is conducted based on throughput, spectrum utilisation rate, network lifetime and packet delay and energy consumptions with different active sensor nodes and simulation time.

The remaining section of the paper is structured as follows. Section 2 presents the comprehensive view of the existing cluster routing protocol formulated for extending network lifetime and preventing PUs collision probability with the merits and limitations. Section 3 presents a detailed view of the proposed HMABFOA scheme with the adopted system model, primitives and integration of MAOA and BFOA incorporated for attaining the clustering process. Section 4 demonstrates the results and discussion of the proposed HMABFOA scheme to network lifetime compared to the baseline approaches considered for evaluation. Section 5 concludes the paper with major contributions of the proposed work and future scope of enhancement.

Related work

In this section, the comprehensive review of the existing metaheuristic optimization algorithms-based clustering schemes that contributed to enhancing energy stability and network lifetime in CRSNs is presented with merits and limitations.

Stephan and Suresh Joseph16 initially contributed a Particle swarm optimization-based energy efficient clustering scheme which is capable of adapting to dynamic features of CRSN. It was proposed with the capability of considering the existence of available free channels during the process of CHs selection in the network. It also includes energy utilization into account for fairness improvement during the allocation of channels. It exploited the merits of PSO for selection of CHs through the exploration of free channels and residual energy with cognitive radio sensor nodes. Then the selected CHs at the start of each frame send a beacon signal using the operating model for determining the data from the cluster members to the CHs in the network. This PSO-based approach predicted the residual energy during the process of channel assignment through the support of CHs in the network. Wang et al.17 proposed a Ion motion inspired optimization-basedcentralized cluttering approach (IMIOCCA) for the process of reliably identifying the CHs and determine the optimal number of clusters in CRSNs. It was proposed with dynamic characteristics that get adopted with the attributes of the network such that information about the sink position is identified for better packet delivery. It is proposed to prevent control overhead incurred during the process of CH selection and cluster construction. This phenomenal cluster construction phenomenon aided in conserving energy to the maximized level. It determined the list of channels available at each instant for attaining potential channel allocation to the constructed channels with a maximized degree of collision probability related to the PUs.

Noor et al.18 have developed an efficient clustering scheme for CRSN called network stability-aware clustering (NSAC) protocol which deals with the defects in existing clustering schemes. They have mentioned that the metrics dealing with channel availability are not secured and have focussed on tuning parameters. They have suggested restricting the size of the cluster to a pre-determined number. They have offered an analytical framework to determine cluster size and observe performance. It considers energy consumption along with spectrum dynamics. It outperforms current scheme in terms of network stability as well as energy consumption. Metric to determine channel quality metric is varied and method for computing CS’ weight is proposed. The framework considers average idle period and likelihood of channel availability as they offer more information. Devi and Umamaheswari19 proposed a Cluster based cooperative spectrum sensing Optimization techniques-based cluttering algorithm for optimal selection of CHs in the network. It considers bi-channel connectivity for improving network lifespan. It takes clustering factors like RE, channel quality, awareness of spectrum, appearance probability of PUs, robustness of arrival of PUs and Euclidean distance amid nodes into consideration to choose hop count as well as common channels for forming clusters. The proposed scheme offers improved lifetime, number of clusters, network stability and reduces number of times re-clustering is performed.

Furthermore, Ramkumar and Vadivel20 proposed a Whale optimization routing protocol (WOAP) for minimizing energy consumption in cognitive radio wireless sensor network. This WOAP was proposed as one of the significant methods which helped in determining the best routes between the constructed clusters to enhance the network efficiency and at the same time minimizing the packet delay in the network. It was proposed with the intelligence derived from foraging behaviour of whales and their strategy of hunting. This WOAP approach considered total energy and residual energy into account during the process of route determination. It facilitated energy-aware route selection method which parallelly explored comprehensive factors of impact. Deng et al.21 proposed an intelligent resource allocation scheme depending on the clustering of nodes during the process of energy harvesting in CRSNs. The intelligent resource allocation scheme aids in determining optimal amount of clusters which form the fundamental clustering structure. It serves time-triggered traffic periodically and uses priority-based schedule with respective frame structures for efficient distribution of event-driven information. It offers a clustering framework for time-triggered traffic that does not construct clusters and selects routes following emergent events. It involves only CRSN nodes for finding emergent events, and corresponding CHs take part in transmission. Only few nodes are involved when sink is positioned at the corner. It consumes less total energy, standard deviation of RE and delay involving reduced number of nodes. It guarantees prompt delivery of event-based information along with assured performance of handling time-triggered traffic.

Wang and Ge22 proposed a multihop clustering routing protocol using radio frequency energy harvesting (MCRPRFEH) for guaranteeing better energy balance and optimized spectrum sensing and assignment in CRSNs. It was proposed with a non-linear energy harvesting model which helped in handling the issues concerned with channel assignment and energy efficiency with optimised allocation of resources. It leveraged the benefits of curve fitting for assessing the degree of accurate harvested energy. The validity of this model determined the optimal number of clusters through empirical analysis. It managed the states of the sensor node to enhance the objective of cluster construction stability. It adopted a energy inspired function as the criterion of selection for determining the link quality which determines better relays and cluster heads. Binyamin and Ragab23 proposed a clustering scheme for CRSNs using the merits of modified dwarf mongoose optimization algorithm (MDMOACA) to sustain maximized stability in the network. This MDMOACA scheme mainly targeted on self-organizing the deployed number of sensor nodes into groups termed clusters. It was proposed as an effective mechanism that handled problem of spectrum scarcity prevention. It is one among the few hierarchical cluster-related techniques contributed for CRSNs to improve the comprehensive network lifetime improvement in better energy stability and scalability in the network. It integrated the merits of oppositional-based learning (OBL) and dwarf mongoose optimization (DMO) algorithm to construct clusters which optimize network performance to the necessitated level. It also adopted a multi-objective function which mainly concentrated on the process of enhancing the network efficiency.

Sharada et al.24 proposed an adaptive ant colony distributed intelligent based clustering scheme (AACDICS) for sustaining maximized degree of energy in CRSNs. This AACDICS approach estimated optimal number of CHs using the phenomenon of distributed cluster-based sensing and connectedness. This mechanism is implemented over a system model which comprises of uncertain number of PUs and SUs in CRSNs. It adopted the strategy of multi-user clustered communication which helped in conversing the solutions by increasing the rate of balanced local and global search. It was identified to be significant in minimizing the degree of Signal-to-Noise Ratio to levels through the maximization of detection likelihood rate. It was proposed with the capability of addressing the challenges associated with multimodal optimization which helps the mechanism in attaining lowest false positive with optimized network performance. The simulation results confirmed that the changes in SNR produce a significant impact over the successful detection probability such that sensor data reliability is achieved with utmost efficiency. Wang et al.25 proposed a Imperfect Spectrum Sensing-Based multi-hop clustering routing protocol (ISSMHCRP) which helped in better energy harvesting that improved network longevity in CRSNs. This ISSMHCRP was proposed for handling the degree of imbalance in terms of residual energy possessed by the selected CHs in the network. It specifically included the merits of simultaneous wireless information and power transfer (SWIPT) for handling the problem of residual energy imbalance. It was proposed as one of the significant methodologies which targeted on the utilization of complete downlink energy harvesting such that residual energy between the sensor nodes are highly balanced in the network. It specifically concentrated on the process of resolving the negative impact of imperfect spectrum sensing over the performance of the network that aids in better energy utilization. In addition, Table 1 presents a review of the existing metatheoretic optimization algorithms-based clustering schemes that contributed to enhancing energy stability and network lifetime in CRSNs.

Table 1 Review of the existing metatheoretic optimization algorithms-based clustering schemes contributed to enhancing energy stability and network lifetime in CRSNs.
Full size table

Research gaps identified

The research gaps identified from the review of the existing literature26,27,28,29 is listed as follows.

  1. (i)

    The number of clusters constructed, is still marginal, and hence needs improvement for maximizing throughput and packet delivery rate with minimized energy consumptions in the network.

  2. (ii)

    Only a minor number of clustering approaches together handled the issues of spectrum sensing and channel assignment dynamically, hence imperfect spectrum sensing clustering approaches are essential.

  3. (iii)

    Some of the clustering approaches adopted energy efficiency as an important factor for clustering and CHs selection but need to include other impactful factors that contribute towards better cluster construction.

The above-mentioned limitations formed the basis behind the formulation and implementation of the proposed HMABFOA Scheme for better CHs selection, cluster construction, and optimal route determination between clusters in the network.

Proposed hybrid Mexican axolotl and bitterling fish optimization algorithm-based spectrum sensing multi‑hop clustering routing protocol (HMABFOA) scheme

In this section, the system model used for implementing the proposed HMABFOA scheme, the role of MAOA algorithm included for cluster formation and cluster selection, and the importance of BFOA in optimized route determination attained with established clusters.

This proposed HMABFOA scheme comprise of several rounds in which every round involves 4 phases: sensing spectrum, selection of CHs and formation of cluster, establishing multi-hop path between clusters and transmission of data. Information got from spectrum sensing phase is leveraged for computing level of detection and idle detection accuracy (IDA) of channels and aid in selecting succeeding CH and relay in the next hop. Clusters and paths among paths are employed in transmitting data.

System model

The system model used for implementing the proposed HMABFOA scheme incorporated the benefits of Semi-Markov model30 for imitating the adaptive occupancy nature of users in a licensed spectrum. User alternates amid busy as well as idle states with random durations independent of factors ‘\(\:{\text{P}}_{\text{B}\text{u}\text{s}\text{y}}\)’ and ‘\(\:{\text{P}}_{\text{I}\text{d}\text{l}\text{e}}\)’. In specific, Gaussian white noise is considered with mean of ‘\(\:0\)’ and variance ‘\(\:{\text{\S\:}}_{\text{n}}^{2}\)’, and signal from ‘\(\:{\text{U}}_{\text{j}}\)’ follows identically distributed and independent stochastic process involving a mean ‘\(\:0\)’ and a variance of ‘\(\:{\text{\S\:}}_{\text{x},\text{j}}^{2}\)’. On implementation of energy identification schemes31 sensing spectrum, false alarm as well as detection probabilities of node ‘\(\:\text{i}\)’ among ‘\(\:\text{n}\)’ nodes based on ‘\(\:{\text{U}}_{\text{j}}\)’32 are given by,

$$\:{\text{P}}_{\text{i},\text{j}}^{\text{f}}=\text{Q}\left(\frac{{\uplambda\:}-{\text{\S\:}}_{\text{n}}^{2}}{\frac{{\text{\S\:}}_{\text{n}}^{2}}{\sqrt{\frac{\text{Z}}{2}}}}\right)$$
(1)
$$\:{\text{P}}_{\text{i},\text{j}}^{\text{d}}=\text{Q}\left(\frac{{\uplambda\:}-\left({\text{\S\:}}_{\text{n}}^{2}-{\text{\S\:}}_{{\text{x}}_{\text{i},\:\text{j}}}^{2}\right)}{\frac{{\text{\S\:}}_{\text{n}}^{2}+{\text{\S\:}}_{{\text{x}}_{\text{i},\:\text{j}}}^{2}}{\sqrt{\frac{\text{Z}}{2}}}}\right)$$
(2)

Where, \(\:\text{j}\:=\text{1,2},\dots\:,\text{m}\), ‘\(\:\text{m}\)’ signifies total quantity of users in network, ‘\({\text{Q}}\left( \cdot \right)\)’ represents a ‘\(\:\text{Q}\:\)’ function.

\(\:\text{Z}={\text{T}}_{\text{s}}\times\:{\text{f}}_{\text{s}}\), where ‘\(\:\text{Z}\)’ signifies quantity of samples. ‘\(\:{\uplambda\:}\)’ denotes threshold of detection of energy. ‘\(\:{\text{T}}_{\text{s}}\)’ denotes duration of spectrum sensing while ‘\(\:{\text{f}}_{\text{s}}\)’ denotes sampling frequency. Based on Neyman-Pearson Lemma33, ‘\(\:{\uplambda\:}\)’ is computed using Eq. (5) where ‘\(\:{\text{P}}_{\text{i},\text{j}}^{\text{f}}\)’ represents a constant ‘\(\:{\stackrel{-}{\text{P}}}_{\text{i},\text{j}}^{\text{f}}\)’. ‘\(\:{\text{\S\:}}_{{\text{x}}_{\text{i},\:\text{j}}}^{2}\)’ signifies signal power obtained by node ‘\(\:\text{i}\)’ from ‘\(\:{\text{U}}_{\text{j}}\)’ as presented in Eq. (3).

$$\:{\uplambda\:}={\text{\S\:}}_{\text{n}}^{2}\times\:\left(\frac{{\text{Q}}^{-1}\times\:{\stackrel{-}{\text{P}}}_{\text{i},\text{j}}^{\text{f}}}{\sqrt{\frac{\text{Z}}{2}}+1}\right)$$
(3)
$$\:{\text{\S\:}}_{{\text{x}}_{\text{i},\:\text{j}}}^{2}\left\{\begin{array}{c}=\left|{\text{h}}_{\text{i},\text{j}}\right|\times\:{\text{\S\:}}_{\text{x},\text{j}}^{2},\:if\:{\text{d}}_{\text{t}\text{o}{\text{U}}_{\text{i},\text{j}}}\le\:IPR\\\:\approx\:0,\:Else\end{array}\right.$$
(4)

Where, ‘\(\:{\text{d}}_{\text{t}\text{o}{\text{U}}_{\text{i},\text{j}}}\)’ signifies Euclidean distance from ‘\(\:\text{i}\)’ to ‘\(\:{\text{U}}_{\text{j}}\)’. In case node ‘\(\:\text{i}\)’ is inside Interference Protection Range (IPR) of \(\:{\text{\S\:}}_{{\text{x}}_{\text{i},\:\text{j}}}^{2}=\left|{\text{h}}_{\text{i},\text{j}}\right|\times\:{\text{\S\:}}_{\text{x},\text{j}}^{2}\), else received signal power is taken as ‘0’. ‘\(\:{\text{h}}_{\text{i},\text{j}}\)’ represents power gain amid ‘\(\:\text{i}\)’ and ‘\(\:{\text{U}}_{\text{j}}\)’ ref.34 as presented in Eq. (5).

$$\:{\text{h}}_{\text{i},\text{j}}=\left\{\begin{array}{c}\frac{{\text{G}}_{\text{T}}{\text{G}}_{\text{R}}{\text{l}}^{2}}{16{{\uppi\:}}^{2}.{\text{d}}_{\text{t}\text{o}{\text{U}}_{\text{i},\text{j}}}^{2}},\:if\:{\text{d}}_{\text{t}\text{o}{\text{U}}_{\text{i},\text{j}}}\le\:{\text{d}}_{0}\\\:\frac{{\text{G}}_{\text{T}}{\text{G}}_{\text{R}}{\text{h}}_{\text{T}}^{2}{\text{h}}_{\text{R}}^{2}}{{\text{d}}_{\text{t}\text{o}{\text{U}}_{\text{i},\text{j}}}^{4}},\:Else\:\end{array}\right.$$
(5)

Where, ‘\(\:{\text{G}}_{\text{T}}\)’ and ‘\(\:{\text{G}}_{\text{R}}\)’ signify transmission and receiving antenna gains. ‘\(\:\text{l}\)’ signifies transmission signal wavelength. ‘\(\:{\text{h}}_{\text{T}}\)’ and ‘\(\:{\text{h}}_{\text{R}}\)’ signify heights of transmitting as well as receiving antenna respectively. If \(\:{\text{d}}_{\text{t}\text{o}{\text{U}}_{\text{i},\text{j}}}\le\:{\text{d}}_{0}\), attenuation of signal involves free-space path loss; else it involves multi-path loss. ‘\(\:{\text{d}}_{0}\)’ signifies distance threshold.

Based on Euclidean distance amid sink and nodes, nodes in circular region with radius ‘\(\:\text{R}\)’ are split into diverse layers for restricting hop counts and respective amount of energy consumed, while width of every layer is initialised to maximum transmission range \(\:\left({\text{R}}_{\text{M}\text{a}\text{x}}\right)\). Layer 1 (\(\:{\text{l}}_{1}\)) is close to sink, wherein number representing layer is a function (increasing) representing Euclidean distance to sink. Nodes update as well as store information along with that of neighbours, construct clusters and search for paths involving multiple hops.

The information in node ‘\(\:\text{i}\)’ includes:

  • Layer number \(\:\left({\text{l}}_{\text{i}}\right)\) which is computed based on co-ordinate \(\:\left({\text{x}}_{\text{i}},{\text{y}}_{\text{i}}\right)\) and Euclidean distance to sink \(\:\left({\text{d}}_{\text{S}\text{i}\text{n}\text{k}}^{\text{i}}\right)\)

$${\text{l}}_{{\text{i}}} = \left[ {\frac{{{\text{d}}_{{{\text{Sink}}}}^{{\text{i}}} }}{{{\text{R}}_{{{\text{Max}}}} }}} \right]$$
(6)

where, ‘\(\:\lceil\:\text{x}\rceil\:\:\)’ represents minimum integer equal to more than ‘\(\:\text{x}\)’

  • ‘\(\:{\text{E}}_{\text{R}\text{e}\text{s}}^{\text{i}}\)’ signifying residual energy

  • ‘\(\:\text{C}\text{h}\text{a}\text{n}\text{n}\text{e}{\text{l}}_{\text{i}}\)’ representing collection of available channels and ‘\(\:{\text{C}}_{\text{i}}\)’ denoting quantity of available channels

  • ‘\(\:{\text{N}\text{e}\text{i}\text{g}\text{h}}_{\text{i}}\)’ representing number of running neighbours. Neighbour of node (\(\:\text{i}\)) is given by node (\(\:\text{j}\)) that satisfies ensuing conditions: they are in same layer, \(\:{\text{l}}_{\text{i}}={\text{l}}_{\text{j}}\); ‘\(\:\text{j}\)’ is in circle positioned at ‘\(\:\text{i}\)’ with radius of ‘\(\:{\text{R}}_{\text{c}}\left({\text{l}}_{\text{i}}\right)\)’. In worst case, ‘\(\:\text{i}\)’ may not have neighbours. This will not have an impact on transferring data in several cases.

  • ‘\(\:{\text{P}}_{\text{f}}^{\text{i},\text{t}}\)’ and ‘\(\:{\text{P}}_{\text{d}}^{\text{i},\text{t}}\)’ representing False alarm and detection probabilities based on every channel ‘\(\:\text{t}\)’ (\(\:\text{t}\:=\text{1,2},\dots\:,\text{c}\), ‘\(\:\text{c}\)’ signifies quantity of channels).

Energy detection method is applied, and ‘\(\:{\text{P}}_{\text{f}}^{\text{i},\text{j}}\)’ and ‘\(\:{\text{P}}_{\text{d}}^{\text{i},\text{j}}\)’ of node ‘\(\:\text{i}\)’ based on ‘\(\:{\text{U}}_{\text{j}}\)’ are determined as shown in Eq. (1) and Eq. (2). When users are randomly distributed and several licensed channels exist, ‘\(\:{\text{P}}_{\text{f}}^{\text{i},\text{j}}\)’ and ‘\(\:{\text{P}}_{\text{d}}^{\text{i},\text{j}}\)’ of ‘\(\:\text{i}\)’ on channel ‘\(\:\text{t}\)’ are given by,

$$\:{\text{P}}_{\text{f}}^{\text{i},\text{t}}=\text{Q}\times\:\left(\frac{{\uplambda\:}\times\:{\text{\S\:}}_{\text{n}}^{2}}{\frac{{\text{\S\:}}_{\text{n}}^{2}}{\sqrt{\frac{\text{Z}}{2}}}}\right)$$
(7)
$$\:{\text{P}}_{\text{d}}^{\text{i},\text{t}}=\text{Q}\times\:\left(\frac{{\uplambda\:}\:-\:\left({\text{\S\:}}_{\text{n}}^{2}+\sum\:_{\text{j}=1}^{\text{m}}{\text{\S\:}}_{{\text{x}}_{\text{i},\:\text{j},\text{t}}}^{2}\right)}{\frac{{\text{\S\:}}_{\text{n}}^{2}+\sum\:_{\text{j}=1}^{\text{m}}{\text{\S\:}}_{{\text{x}}_{\text{i},\:\text{j},\text{t}}}^{2}}{\sqrt{\frac{\text{Z}}{2}}}}\right)$$
(8)

where, ‘\(\:{\text{\S\:}}_{{\text{x}}_{\text{i},\:\text{j},\text{t}}}^{2}\)’ represents signal power obtained by node ‘\(\:\text{i}\)’ from ‘\(\:{\text{U}}_{\text{j}}\)’ on ‘\(\:\text{t}\)’. In case ‘\(\:\text{t}\)’ is occupied by ‘\(\:{\text{U}}_{\text{j}}\)’, \(\:{\text{\S\:}}_{{\text{x}}_{\text{i},\:\text{j},\text{t}}}^{2}={\text{\S\:}}_{{\text{x}}_{\text{i},\:\text{j}}}^{2}\), else ‘\(\:\text{i}\)’ cannot obtain signal power from ‘\(\:{\text{U}}_{\text{j}}\)’ on ‘\(\:\text{t}\)’, \(\:{\text{\S\:}}_{{\text{x}}_{\text{i},\:\text{j},\text{t}}}^{2}=0\)

  • ‘\(\:{\text{P}}_{\text{O}\text{f}\text{f}}^{\text{i},\text{t}}\)’ and ‘\(\:{\text{P}}_{\text{O}\text{n}}^{\text{i},\text{t}}\)’ representing idle as well as occupancy probabilities of ‘\(\:\text{t}\)’ for detection of perfect spectrum,

‘\(\:{\text{P}}_{\text{C}\text{o}\text{n}}^{\text{j},\text{t}}\)’ and ‘\(\:{\text{P}}_{\text{C}\text{o}\text{f}\text{f}}^{\text{j},\text{t}}\)’ represent the ratio of channel utilization of ‘\(\:\text{t}\)’ based on ‘\(\:{\text{U}}_{\text{j}}\)’ and opposite ratio. They are computed using statistics showing channel occupancy. The nodes do not have control on usage of channels. Rather, they can access spectrum holes for efficiently establishing communication.

Hence, for finding idle as well as occupancy probabilities of every licensed channel, the users must be taken into consideration to adjust to numerous channel occupancy conditions. When ‘\(\:\text{i}\)’ that is in the IPR of ‘\(\:{\text{U}}_{\text{j}}\)’ performs spectrum sensing on ‘\(\:\text{t}\)’ accurately, ‘\(\:{\text{P}}_{\text{C}\text{o}\text{f}\text{f}}^{\text{j},\text{t}}\)’ and ‘\(\:{\text{P}}_{\text{C}\text{o}\text{n}}^{\text{j},\text{t}}\)’ represent probability that ‘\(\:{\text{U}}_{\text{j}}\)’ does not use channel ‘\(\:\text{t}\)’ and conflicting probability anticipated by ‘\(\:\text{i}\)’ respectively. In case ‘\(\:\text{i}\)’ is beyond IPR of ‘\(\:{\text{U}}_{\text{j}}\)’ as signal power obtained by ‘\(\:\text{i}\)’ is feeble, it is ensured that ‘\(\:{\text{U}}_{\text{j}}\)’ does not use ‘\(\:\text{t}\)’, ‘\(\:{\text{P}}_{\text{O}\text{f}\text{f}}^{\text{i},\text{j},\text{t}}=1\)’ and ‘\(\:{\text{P}}_{\text{O}\text{n}}^{\text{i},\text{j},\text{t}}=0\)’.

‘\(\:{\text{P}}_{\text{O}\text{f}\text{f}}^{\text{i},\text{j},\text{t}}\)’ and ‘\(\:{\text{P}}_{\text{O}\text{n}}^{\text{i},\text{j},\text{t}}\)’ are determined as shown below.

$$\:{\text{P}}_{\text{O}\text{f}\text{f}}^{\text{i},\text{j},\text{t}}=\left\{\begin{array}{c}{\text{P}}_{\text{C}\text{o}\text{f}\text{f}}^{\text{j},\text{t}},{\text{d}}_{\text{t}\text{o}{\text{U}}_{\text{i},\text{j}}}\:\le\:IPR\\\:1,\:Else\end{array}\right.$$
(9)
$$\:{\text{P}}_{\text{O}\text{n}}^{\text{i},\text{j},\text{t}}=\left\{\begin{array}{c}{\text{P}}_{\text{C}\text{o}\text{n}}^{\text{j},\text{t}},{\text{d}}_{\text{t}\text{o}{\text{U}}_{\text{i},\text{j}}}\:\le\:IPR\\\:0,\:Else\end{array}\right.$$
(10)

By performing spectrum detection accurately, idle as well as occupancy probabilities of ‘\(\:\text{t}\)’ observed by ‘\(\:\text{i}\)’ are given by,

$$\:{\text{P}}_{\text{O}\text{f}\text{f}}^{\text{i},\text{t}}=\prod\:_{\text{j}=1}^{\text{m}}{\text{P}}_{\text{O}\text{f}\text{f}}^{\text{i},\text{j},\text{t}}$$
(11)
$$\:{\text{P}}_{\text{O}\text{n}}^{\text{i},\text{t}}=1-{\text{P}}_{\text{O}\text{f}\text{f}}^{\text{i},\text{t}}$$
(12)

Based on ‘\(\:{\text{P}}_{\text{f}}^{\text{i},\text{t}}\)’ and ‘\(\:{\text{P}}_{\text{d}}^{\text{i},\text{t}}\)’, ‘\(\:{\text{P}}_{\text{O}\text{f}\text{f}}^{\text{i},\text{t}}\)’ and ‘\(\:{\text{P}}_{\text{O}\text{n}}^{\text{i},\text{t}}\)’ of channels, node ‘\(\:\text{i}\)’ determines detection level of channels \(\:\left({\text{P}}_{\text{C}\text{L}}^{\text{i}}\right)\) as shown below.

$$\:{\text{P}}_{\text{C}\text{L}}^{\text{i}}=\sum\:_{\text{t}\in\:\text{C}\text{h}\text{a}\text{n}\text{n}\text{e}{\text{l}}_{\text{i}}}{\text{P}}_{\text{O}\text{f}\text{f}}^{\text{i},\text{t}}\times\:\left(1-{\text{P}}_{\text{f}}^{\text{i},\text{t}}\right)-{\text{P}}_{\text{O}\text{n}}^{\text{i},\text{t}}\times\:\left(1-{\text{P}}_{\text{d}}^{\text{i},\text{t}}\right)$$
(13)

where, ‘\(\:\text{t}\)’ represents idle channel observed by ‘\(\:\text{i}\)’, \(\:\text{t}\in\:\text{C}\text{h}\text{a}\text{n}\text{n}\text{e}{\text{l}}_{\text{i}}\)

\(\:{\text{P}}_{\text{O}\text{f}\text{f}}^{\text{i},\text{t}}\times\:\left(1-{\text{P}}_{\text{f}}^{\text{i},\text{t}}\right)\) signifies probability that ‘\(\:\text{t}\)’ is free; there are no false alarms while sensing spectrum

\(\:{\text{P}}_{\text{O}\text{n}}^{\text{i},\text{t}}\times\:\left(1-{\text{P}}_{\text{d}}^{\text{i},\text{t}}\right)\) denotes probability that ‘\(\:\text{t}\)’ is engaged, but missed identification may exist while sensing spectrum

When ‘\(\:\text{t}\)’ is seen to be idle, missed ‘\(\:{\text{P}}_{\text{d}}^{\text{i},\text{t}}\)’ that is considered as penalty is deducted from accurate detection probability. ‘\(\:{\text{P}}_{\text{C}\text{L}}^{\text{i}}\)’ denotes complete detection level on free channels observed by ‘\(\:\text{i}\)’. These channels which perform better sensing contribute much to ‘\(\:{\text{P}}_{\text{C}\text{L}}^{\text{i}}\)’, while those with lesser performance contribute less to ‘\(\:{\text{P}}_{\text{C}\text{L}}^{\text{i}}\)’. Hence, by using summation in Eq. (13), a negotiation amid quantity of free channels as well as spectrum sensing is obtained.

If \(\:\text{t}\in\:\text{C}\text{h}\text{a}\text{n}\text{n}\text{e}{\text{l}}_{\text{i}}\), accuracy of idle detection of ‘\(\:\text{t}\)’ is given by,

$$\:{\text{P}}_{\text{r}}^{\text{i},\text{t}}=\frac{{\text{P}}_{\text{O}\text{f}\text{f}}^{\text{i},\text{t}}\times\:\left(1-{\text{P}}_{\text{f}}^{\text{i},\text{t}}\right)}{{\text{P}}_{\text{O}\text{f}\text{f}}^{\text{i},\text{t}}\times\:\left(1-{\text{P}}_{\text{f}}^{\text{i},\text{t}}\right)+{\text{P}}_{\text{O}\text{n}}^{\text{i},\text{t}}\times\:\left(1-{\text{P}}_{\text{d}}^{\text{i},\text{t}}\right)}$$
(14)

Where, denominator denotes total probability that ‘\(\:\text{t}\)’ is anticipated to be free.

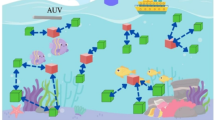
In addition, Fig. 1 presents the view of the process of spectrum sensing and data transmission in each round.

Fig. 1
figure 1

Process of spectrum sensing and data transmission in each round.

Full size image

Mexican axolotl optimization algorithm (MAOA)-based selection of CHs and formation of clusters

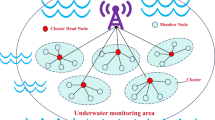
In this section, the MAOA-based Selection of CHs and Formation of Clusters is presented with the process of computing the cluster radius process of clustering.as specified in (Fig. 2).

This clustering and cluster formation phenomenon depends on the ‘\(\:{\text{P}}_{\text{C}\text{L}}^{\text{i}}\)’, in which ‘\(\:\text{i}\)’ determines value of CHs competition as presented in Eq. (15). Nodes with better detection ability, increased ‘\(\:{\text{E}}_{\text{R}\text{e}\text{s}}^{\text{i}}\)’ and increased number of neighbours may become CHs.

$$\:\text{C}\text{o}\text{m}\text{p}{\text{t}}_{\text{i}}={\text{P}}_{\text{C}\text{L}}^{\text{i}}\:\times\:{\text{E}}_{\text{R}\text{e}\text{s}}^{\text{i}}\times\:\text{N}\text{e}\text{i}\text{g}{\text{h}}_{\text{i}}$$
(15)

Running nodes in ‘\(\:{\text{l}}_{1}\)’ are grouped separately for eliminating the amount energy consumed during selection of CHs and formation of clusters. More amount of energy is preserved for relaying packets to other layers. The running nodes except the ones in ‘\(\:{\text{l}}_{1}\)’ send their information along with values of CHs competition within radius. They also obtain conforming information from neighbours seen within the range. Radius of cluster of ‘\(\:\text{i}\)’ \(\:\left({\text{R}}_{\text{c}}\left({\text{l}}_{\text{i}}\right)\right)\) is determined as shown below.

$$\frac{{{\text{R}}_{{\text{c}}} \left( {{\text{l}}_{i} } \right)}}{{{\text{R}}_{0} }} = \frac{{\zeta \times \pi \left[ {{\text{l}}_{{\text{i}}}^{{\text{2}}} - \left( {{\text{l}}_{{\text{i}}} - 1} \right)^{2} \times {\text{R}}_{{{\text{Max}}}}^{2} } \right]}}{{\zeta \times \pi \times \left[ {\left\lceil {\frac{{\text{R}}}{{{\text{R}}_{{{\text{Max}}}} }}} \right\rceil ^{2} - \left( {\left\lceil {\frac{{\text{R}}}{{{\text{R}}_{{{\text{Max}}}} }}} \right\rceil - 1} \right)^{2} } \right] \times {\text{R}}_{{{\text{Max}}}}^{2} }}$$
(16)

where, ‘\(\:{\upzeta\:}\)’ denotes node density, ‘\(\:{\text{R}}_{0}\)’ signifies range within which selection of CHs and formation of clusters in outmost layer is seen. Ratio of ‘\(\:{\text{R}}_{\text{c}}\left({\text{l}}_{\text{i}}\right)\)’ and ‘\(\:{\text{R}}_{0}\)’ is assigned proportion of nodes in ‘\(\:{\text{l}}_{\text{i}}\)’ and outmost layers to balance distribution of CHs amid diverse layers. ‘\(\:{\text{R}}_{0}\)’ is initialised to ‘\(\:{\text{R}}_{\text{M}\text{a}\text{x}}\)’, and ‘\(\:{\text{R}}_{\text{c}}\left({\text{l}}_{\text{i}}\right)\)’ becomes,

$${\text{R}}_{{\text{c}}} \left( {{\text{l}}_{{\text{i}}} } \right) = \frac{{{\text{l}}_{{\text{i}}}^{2} - \left( {{\text{l}}_{{\text{i}}} - 1} \right)^{2} }}{{\left\lceil {\frac{{\text{R}}}{{{\text{R}}_{{{\text{Max}}}} }}} \right\rceil ^{2} - \left( {\left\lceil {\frac{{\text{R}}}{{{\text{R}}_{{{\text{Max}}}} }}} \right\rceil - 1} \right)^{2} }} \times {\text{R}}_{{{\text{Max}}}}$$
(17)
Fig. 2
figure 2

System model used for CH selection and cluster formation using HMABFOA protocol.

Full size image

Radii of cluster can be analysed in 2 phases:

  • Total energy consumed in exchanging control information is dropped. Instead, broadcasting range of information is limited within radius rather than ‘\(\:{\text{R}}_{\text{M}\text{a}\text{x}}\)’. The amount of energy consumed is lessened as it is positively proportionate to range of broadcast. In contrast, neighbours are considered as nodes which are positioned within radius rather than within ‘\(\:{\text{R}}_{\text{M}\text{a}\text{x}}\)’. Drop in quantity of neighbours lead to reduced number of control packets involved. This leads to reduction in the amount of energy consumed in reception of control information.

  • The quantity of members within clusters decreases, and hence the amount of energy consumed in receiving and aggregating data within clusters at the CHs is also decreased.

In case value of CH competition of a node is less than that of a neighbour, it leaves the competition; else it becomes the CH. The process repeats until every node becomes a CH or leaves the competition.

CHs other than the ones in ‘\(\:{\text{l}}_{1}\)’ broadcast CH notification message inside radius of a cluster. Nodes which are not CHs connect to clusters by forwarding a request to CHs that have maximum competition values as well as share channels, and respective CHs get request and put them in CMs list. Nodes which do not get any notification message act as independent CHs.

While selecting cluster channels, for promoting successful packet delivery within clusters, idle channels must be precisely selected for transmitting data. CMs determine IDA of every channel available using Eq. (16). The channel available at CH with maximum ‘\(\:{\text{P}}_{\text{r}}^{\text{i},\text{t}}\)’ is taken as cluster channel. As there are chances for CMs to choose different channels, CH must switch among channels to aggregate data within clusters. For reducing channel switching to the maximum extent possible, CHs successively schedule transmission from CMs on the channel, and shift to another till CMs finish transmission.

Mexican axolotl variable optimization (MAVO)

Mexican axolotl optimization (MAO) algorithm stimulated by behaviour of axolotl is detailed below. Its birth, restoration of tissues and breeding, and way they survive in an aquatic setting are taken as inspiration. Axolotls are split into males and females. The capability of axolotl in altering its colour, colour of body parts’ for camouflaging and evading predators are taken into consideration.

In a numeric optimization problem that is given by ‘\(\:\text{O}\)’ function, parameters like vectors with dimension \(\:\left(\text{d}\right)\) are taken such that every dimension (\(\:{\text{d}}_{\text{i}}\)) is limited by \(\:[{\text{m}\text{i}\text{n}}_{\text{i}},\:{\text{m}\text{a}\text{x}}_{\text{i}}]\). There is a collection of solutions (axolotls) of size (\(\:{\text{n}}_{\text{a}}\)) for population \(\:\text{P}=\left\{{\text{A}}_{1},\dots\:{\text{A}}_{{\text{n}}_{\text{a}}}\right\}\). Every solution \(\:{\text{A}}_{\text{j}}\in\:\text{P},\text{j}\in\:[1,{\text{n}}_{\text{a}}]\) is signified as a vector, \(\:{\text{A}}_{\text{j}}=\left[{\text{a}}_{\text{j}}^{1},\dots\:{\text{a}}_{\text{j}}^{\text{D}}\right]\) with \(\:{\text{m}\text{i}\text{n}}_{\text{i}}\le\:{\text{a}}_{\text{j}}^{\text{i}}\le\:{\text{m}\text{a}\text{x}}_{\text{i}}\), \(\:\text{O}\left({\text{A}}_{\text{j}}\right)\in\:\text{R}\). Minimum value of ‘\(\:\text{O}\)’ is to be found.

Initially, population is set at random. Every member is set as male or female, owing to axolotls getting developed based on sex, thus offering 2 sub-populations. Transition to adult from larvae commences. Males transit from larvae to adult in water by regulating colour of parts toward a male which is highly adaptable to environment.

Members which are highly adapted have improved camouflage, and other members change colour accordingly. Nevertheless, the capability of axolotls to modify colour is restricted, and every member does not have to be capable of fully adapting to the best. Hence, inverse transition probability is introduced, based on which, axolotl is chosen to camouflage toward best.

‘\(\:{male}_{Best}\)’ represents male that shows better adaptation (best value of ‘\(\:O\)’), and ‘\(\:\lambda\:\:\)’ is a transition factor in the range [0, 1] for male ‘\(\:{m}_{j}\)’ that will alter parts of body as shown in Eq. (18).

$$\:{\text{m}}_{\text{j}}^{\text{i}}={\text{m}}_{\text{j}}^{\text{i}}+\left({\text{m}}_{\text{B}\text{e}\text{s}\text{t}}^{\text{i}}-{\text{m}}_{\text{j}}^{\text{i}}\right)\times\:{\uplambda\:}$$
(18)

Likewise, females alter their bodies to adults from larvae towards female with better adaptation by using Eq. (20).

$$\:{\text{f}}_{\text{j}}^{\text{i}}={\text{f}}_{\text{j}}^{\text{i}}+\left({\text{f}}_{\text{B}\text{e}\text{s}\text{t}}^{\text{i}}-{\text{f}}_{\text{j}}^{\text{i}}\right)\times\:{\uplambda\:}$$
(19)

Where ‘\(\:{f}_{Best}\)’ represents best female and ‘\(\:{f}_{j}\)’ signifies present female axolotl

Nevertheless, based on inverse transition probability, dummy members incapable of camouflaging themselves toward best with their colours are chosen. In case \(\:r\in\:\left[\text{0,1}\right]\:\)is less than inverse transition probability (‘\(\:r\)’ represents a random number), then corresponding member is chosen. In problem of minimization, for male (\(\:{m}_{j}\)) with value of optimization (\(\:{om}_{j}\)), inverse transition probability is determined as shown in Eq. (20). For female (\(\:{f}_{j}\)) with value of optimization (\(\:{of}_{j}\)), Eq. (21) is used. Worst members have increased likelihoods of random transitions.

$$\:\text{p}{\text{m}}_{\text{j}}=\frac{{\text{o}\text{m}}_{\text{j}}}{\sum\:{\text{o}\text{m}}_{\text{j}}}$$
(20)
$$\:\text{p}{\text{f}}_{\text{j}}=\frac{{\text{o}\text{f}}_{\text{j}}}{\sum\:{\text{o}\text{f}}_{\text{j}}}$$
(21)

Members change their ‘\(\:{i}^{th}\)’ body parts at random (every body part is a dimension of the function) as shown in Eqs. (22 and (23), respectively. Members which perform random transition will be chosen based on value of optimization function.

$$\:{\text{m}}_{\text{j}}^{\text{i}}={\text{m}\text{i}\text{n}}_{\text{i}}+\left({\text{m}\text{a}\text{x}}_{\text{i}}-{\text{m}\text{i}\text{n}}_{\text{i}}\right)\times\:{\text{r}}_{\text{i}}\:$$
(22)
$$\:{\text{f}}_{\text{j}}^{\text{i}}={\text{m}\text{i}\text{n}}_{\text{i}}+\left({\text{m}\text{a}\text{x}}_{\text{i}}-{\text{m}\text{i}\text{n}}_{\text{i}}\right)\times\:{\text{r}}_{\text{i}}\:$$
(23)

Where, \(\:{r}_{i}\in\:\left[\text{0,1}\right]\) signifies a random number selected for every body part (\(\:i\))

By moving in water, axolotls may get entangled in accidents and become hurt. This is taken into consideration in Injury as well as restoration stage. For every axolotl ‘\(\:{A}_{i}\)’ (male or female), in case damage probability (\(\:dp\)) is satisfied, axolotls lose some parts of the body. By using regeneration probability (\(\:rp\)) per bit, it loses ‘\(\:{j}^{th}\)’ part (bit) and substitutes it as \(\:{{f}_{j}^{i}}^{{\prime\:}}={min}_{i}+\left({max}_{i}-{min}_{i}\right)\times\:{r}_{i}\), where \(\:{r}_{i}\in\:\left[\text{0,1}\right]\) is arbitrarily selected for every part. Reproduction in population begins. For every female in population, male is chosen from which offspring is got using tournament selection.

To be simple, it is assumed that every pair of axolotls has 2 eggs. Females wait for the eggs to hatch, after which process of assortment commences. Newly formed members (larval state) contend with parents to persist in population. In case young are improved based on objective function, they substitute them.

After assortment, TIRA repeats until stopping condition is satisfied.

Stage 1

Transition to adult state from larvae.

Stage 2

Injury along with restoration.

Stage 3

Reproduction along with assortment.

Proposed MAO algorithm includes numerous aspects of life of axolotl in process of optimization like aquatic growth, capability to convert body to adult state from larvae, reproduction and ability to redevelop organs as well as body parts. The difference between evolutionary and Swarm Intelligence (SI) algorithms are discussed below.

  • Individuals are split into males and females.

  • Females are considered to be more significant based on the fact that for every female, a best male is found based on tournament selection for getting offspring.

  • An exclusive replacement method is used for including new individuals into population. Female is chosen as the best individual, while a male is chosen as the next best individual. There is a likelihood of transforming a male to a female, in case male seems to be the best.

In addition, Algorithm 1 presents the steps involved in the implementation of the proposed Mexican axolotl optimization algorithm (MAOA)-based Selection of CHs and formation of clusters.

Algorithm 1
figure a

MAOA-based selection of CHs and formation of clusters.

Full size image

The above specified algorithm helps in better CHs selection and optimized cluster construction in the network.

BFOA-based multi‑hop route establishment between clusters

In this section, the process of Multi‑hop Route Establishment between Clusters attained using the merits of BFOA algorithm is presented as follow.

In this multiple hop route determination process, the nodes positioned in ‘\(\:{\text{l}}_{1}\)’ may reach sink in one hop, and henceforward data directly to sink. Other CHs must choose appropriate relays for forwarding data until sink is reached. Value of relay competition of ‘\(\:\text{i}\)’ is given by,

$$\:\text{R}\text{e}\text{l}\text{a}\text{y}\text{c}\text{o}\text{m}\text{p}{\text{t}}_{\text{i}}={\text{P}}_{\text{C}\text{L}}^{\text{i}}\:\times\:{\text{E}}_{\text{R}\text{e}\text{s}}^{\text{i}}\times\:\frac{1}{{\text{E}}_{\text{E}\text{l}\text{e}\text{c}}+{\text{E}}_{\text{f}\text{s}}\times\:{\text{d}}_{\text{i},\:\text{S}\text{i}\text{n}\text{k}}^{2}}$$
(24)

Where, ‘\(\:{\text{E}}_{\text{E}\text{l}\text{e}\text{c}}\)’ signifies energy consumed at transceiver per bit and ‘\(\:{\text{E}}_{\text{f}\text{s}}\)’ denotes co-efficient representing energy consumption at the power amplifier. Denominator denotes the amount of energy consumed in forwarding a bit of data towards sink. Nodes which have strong capability to sense the spectrum, increased ‘\(\:{\text{E}}_{\text{R}\text{e}\text{s}}^{\text{i}}\)’ and which are at proximity to sink have increased probability of being chosen as relays in the next hop. In case the chosen relay is positioned in ‘\(\:{\text{l}}_{1}\)’, it is seen that the route is established; else selection of next-hop relay continues. CHs positioned in ‘\(\:{\text{l}}_{1}\)’ send data directly to sink those aggregates and broadcasts the received data to nodes positioned in ‘\(\:{\text{l}}_{2}\)’. The quantity of energy consumed in broadcasting information (nodes in ‘\(\:{\text{l}}_{1}\)’) and that of getting respective information (nodes in ‘\(\:{\text{l}}_{2}\)’) is lessened. Those CHs which are not in ‘\(\:{\text{l}}_{1}\)’ broadcast notification message within the radius ‘\(\:{\text{R}}_{\text{M}\text{a}\text{x}}\)’. CHs seen in the layer and neighbours in ensuing external layer get information that may be employed for selecting next-hop relays. CH in subsequent inner layer in range of communication is favoured as it shares idle channels and is at proximity to sink. In case such CHs may not be determined, CM that is close to sink and can communicate with CH in ensuing inner layer is chosen. Moreover, Algorithm 2 presents the process of route establishment adopted in the proposed approach.

Algorithm 2
figure b

Route establishment.

Full size image

In case it is not possible to find such a next hop, CH in the layer which shares channels, owns increased value of relay competition and is nearer to sink will be chosen. The process repeats until relays in ‘\(\:{l}_{i}\)’ are determined or no path may be found.

As information about next-hop are available at the relays during exchange of control information, accuracy of idle detection of every channel based on Eq. (16), and one with maximum ‘\(\:{P}_{r}^{i,t}\)’ is taken as inter-cluster channel for improving PDR amid clusters. Once cluster is formed and route is established, CHs assign time slots for scheduling transmission of data from CMs. CMs send data to the CHs in allocated time slots on channels in cluster. CHs send aggregated data to sink by relaying data between clusters.

Bitterling fish optimization (BFO)

Behaviour of bitterling fish is detailed, and algorithm is formulated. In the process of mating, male as well as female species meet and discharge sperms and eggs into water which is a huge drawback. While performing sexual selection, females select males based on colour and physical strength. Males find appropriate shells for spawning and search for bigger oysters with more space to preserve the eggs. Young fishes are open to diverse dangers and may become prey. Only few of eggs become fish, while most of the fish are taken prey by other animals. On seeing victims (oysters), the fishes resist the opponents. The cause of this male violent behaviour is that other males may employ oysters for themselves.

Modelling

Supposition is considered for modelling BFO algorithm in dealing with optimization as depicted in (Fig. 3).

  • Every solution is a complex fish.

  • Oyster acting as function of target (objective) is efficient in case objective function offers a better value.

  • Fish solutions are distributed and assessed in oysters.

  • Every oyster may expel numerous fishes that may be local or global searches.

  • Oyster laurels slay pathogens or fishes.

Initial solutions

Every solution is a bitterling egg or fish as shown in Eq. (25). Several populations of bitterling fish which are generated as arbitrary population are considered as shown in Eq. (26):

$$\:{\text{F}}_{\text{i}}=\left[{\text{F}}_{\text{i}}^{1},{\text{F}}_{\text{i}}^{2},{\text{F}}_{\text{i}}^{3},\dots\:{\text{F}}_{\text{i}}^{\text{d}}\right]$$
(25)
$${\text{F}} = \left[ {\begin{array}{*{20}c} {{\text{F}}_{1}^{1} } & {{\text{F}}_{1}^{2} } & {\begin{array}{*{20}c} \ldots & {{\text{F}}_{1}^{{\text{d}}} } \\ \end{array} } \\ {{\text{F}}_{2}^{1} } & {{\text{F}}_{2}^{2} } & {\begin{array}{*{20}c} \ldots & {{\text{F}}_{2}^{{\text{d}}} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {{\text{F}}_{{\text{n}}}^{1} } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {{\text{F}}_{{\text{n}}}^{1} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \vdots \\ \ldots \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {{\text{F}}_{2}^{{\text{d}}} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$
(26)

‘\(\:\text{d}\)’ signifies quantity of decision variables or dimensions of every solution. Value of ‘\(\:\text{i}\)’ is a problem solution. ‘\(\:\text{F}\)’ represents a matrix involving key populations of ‘\(\:\text{n}\)’. ‘\(\:{\text{F}}_{\text{i}}^{\text{j}}\)’ signifies dimension ‘\(\:\text{j}\)’ of ‘\(\:{\text{i}}^{\text{t}\text{h}}\)’ solution. The population produced in interval \(\:[\text{l},\:\text{u}]\:\)forms primary population as shown in Eq. (27).

$$\:{\text{F}}_{\text{i}}^{\text{j}}=\text{l}+\left(\text{u}-\text{l}\right)\times\:\text{r}$$
(27)

‘\(\:\text{r}\)’ represents random number in the range [0, 1]

Assess solutions

Every solution is a fish in BFO algorithm. To assess every solution, efficient selection of oyster plays a dominant role. Every fish is based on appropriate oyster it selects and entices other females. A target function (\(\:\text{f}\)) is used for assessing every solution or fish. Competency of every solution is represented as competency matrix as shown in Eq. (28):

$${\text{Fitness}} = \left[ {\begin{array}{*{20}c} {{\text{f}}\left( {{\text{F}}_{1}^{1} {\text{~F}}_{1}^{2} {\text{~}} \ldots {\text{F}}_{1}^{{\text{d}}} } \right){\text{~}}} \\ {{\text{f}}\left( {{\text{F}}_{2}^{1} {\text{~F}}_{2}^{2} {\text{~}} \ldots {\text{F}}_{2}^{{\text{d}}} } \right)} \\ {\begin{array}{*{20}c} \vdots \\ {{\text{f}}\left( {{\text{F}}_{{\text{n}}}^{1} {\text{~F}}_{{\text{n}}}^{2} {\text{~}} \ldots {\text{F}}_{{\text{n}}}^{{\text{d}}} } \right)} \\ \end{array} } \\ \end{array} } \right]$$
(28)

Search and grab oysters

Solutions search problem spaces to determine appropriate mating oysters. Every fish is positioned in a region with more ideal shells. Fishes may roam in search of an oyster wherein; it focuses on an oyster and approaches it. Target is not observed by another fish and is seized. State of possession of oyster is given in Eq. (29).

$$\:{\text{F}}_{\text{t}+1}^{\text{i}}=\left\{\begin{array}{c}J.{\text{F}}_{\text{t}}^{\text{i}}+\left({\text{F}}^{+}-\text{J}.{\text{F}}_{\text{t}}^{\text{i}}\right).\delta\:,r\le\:p\\\:J.{\text{F}}_{\text{t}}^{\text{i}}+\left({\text{F}}^{\text{*}}-\text{J}.{\text{F}}_{\text{t}}^{\text{i}}\right).\delta\:,r>p\end{array}\right.$$
(29)

‘\(\:{\text{F}}_{\text{t}}^{\text{i}}\)’ and ‘\(\:{\text{F}}_{\text{t}+1}^{\text{i}}\)’ represent present and new locations of fish in ‘\(\:\text{t}\)’ and ‘\(\:\text{t}+1\)’ iteration for ‘\(\:{\text{i}}^{\text{t}\text{h}}\)’ solution respectively. ‘\(\:{\text{F}}^{\text{*}}\)’ represents best oyster or ideal solution, while ‘\(\:{\text{F}}^{+}\)’ signifies worthies of oyster population which is arbitrarily chosen. ‘\(\:{\updelta\:}\)’ and ‘\(\:\text{r}\)’ represents a random number in the range [0, 1]. ‘\(\:\text{J}\)’ signifies quantity of steps or rate at which fishes move for escaping or approaching oyster. The factor is dropped by iterating the algorithm. The value of ‘\(\:\text{J}\)’ decreases when activity of male drops as they succeed in mating. Reduction in the value of ‘\(\:\text{J}\)’ leads to decrease of global search to local search with time. Reduction of the value of ‘\(\:\text{J}\)’ is shown in Eq. (30).

$$\:{\text{J}}_{\text{t}}=\left({\text{J}}_{1}-\frac{{\text{J}}_{1}\times\:\text{t}}{\text{M}\text{a}{\text{x}}_{\text{t}}}\right)\times\:{\text{U}}_{\text{t}}$$
(30)

‘\(\:{\text{J}}_{1}\)’ represents step of fish and value of jump in initial iterations. Values of ‘\(\:\text{t}\)’ and ‘\(\:\text{M}\text{a}{\text{x}}_{\text{t}}\)’ signify present and maximum iteration respectively. ‘\(\:{\text{J}}_{\text{t}}\)’ signifies step as well as jump of every fish to determine oyster in ‘\(\:\text{t}\)’. ‘\(\:\text{U}\)’ is a random function that uses Eq. (31) for generating random sequences.

$$\:{\text{U}}_{\text{t}+1}=\text{c}\text{o}\text{s}(\text{t}\times\:{\text{c}\text{o}\text{s}}^{-1}\left({\text{U}}_{\text{t}}\right))$$
(31)

‘\(\:{\text{U}}_{1}\)’ is equivalent to one. By combining Eq. (30)–(32) is obtained.

$$\:{\text{J}}_{\text{t}+1}=\left({\text{J}}_{1}-\frac{{\text{J}}_{1}\times\:\text{t}}{\text{M}\text{a}{\text{x}}_{\text{t}}}\right)\times\:\text{c}\text{o}\text{s}(\text{t}\times\:{\text{c}\text{o}\text{s}}^{-1}\left({\text{U}}_{\text{t}}\right))$$
(32)

Ideal solution is investigated with time based on space repetition around ideal solution. It is indispensable for reducing ‘\(\:\text{P}\)’ with time to second criterion with condition ‘\(\:\text{r}>\text{P}\)’ that is highly probable (Eq. (29)). Function resembling arctangent behavior is used for ‘\(\:\text{P}\)’ as shown in Eq. (33).

$$\:\text{P}=\left|1-\frac{\text{t}}{\sqrt{1+{\text{t}}^{2}}}\right|+\frac{\text{r}\text{a}\text{n}}{{\text{t}}^{\text{a}}}$$
(33)

‘\(\:\text{t}\)’ signifies repetition counter, ‘\(\:\text{a}\)’ represents reduction power. With reduction in power, the value of ‘\(\:\text{P}\)’ reduces with iteration. Probability of 2 kinds of searches in Eq. (29) drops with least difference.

Escape and not grab oyster

A fish considers oyster and makes fish to abstain from moving toward oyster and choosing a location. Equation (34) is used for escaping or unintentionally searching for a fish which was not successful in seizing oysters.

$$\:{\text{F}}_{\text{t}+1}^{\text{i}}=\left\{\begin{array}{c}J.{\text{F}}_{\text{t}}^{\text{i}}+\left({\text{F}}^{\text{*}}-\text{J}.\text{M}\right).\delta\:,r\le\:0.5\\\:l+\left(\text{u}-\text{l}\right).\delta\:,r>0.5\end{array}\right.$$
(34)

‘\(\:\text{M}\)’ represents mean location of fish swarm

After escaping, the fishes search the space between average and ideal or arbitrary space problems. Equation (35) is used for determining gravity point of population.

$$\:\text{M}=\frac{\sum\:_{\text{i}=1}^{\text{n}}{\text{F}}_{\text{t}}^{\text{i}}}{\text{n}}$$
(35)

Production

On finding an oyster, males attract females and lay eggs in oyster. The males fertilize eggs for creating new fishes around present fish as shown in Eq. (36):

$$\:{\text{F}}_{\text{t}+1}^{\text{i}}={\text{F}}_{\text{t}}^{\text{i}}+\text{R}\times\:\text{r}\text{a}\text{n}\left(\text{0,1}\right)$$
(36)

Where, ‘\(\:\text{R}\)’ signifies fish’s radius of distribution round about the shell within them. This radius is set a value within range of [0,2]. Typically, the value is considered to be 2, but decreases with time based on iteration of algorithm.

Fig. 3
figure 3

BFOA-based multi-hop routing established between clusters.

Full size image

Hunting fish

Oysters may hold numerous little fishes. Oysters or predators may hunt and kill some weak ones. The likelihood of dropping a solution is found to be inversely proportionate to its excellence. Suppose it is a minimization problem, the chance of dropping a fish is given in Eq. (37):

$$\:\text{d}\left({\text{F}}_{\text{t}}^{\text{i}}\right)=\frac{\text{f}\left({\text{F}}_{\text{t}}^{\text{i}}\right)}{\sum\:_{\text{i}=1}^{\text{n}}\text{f}\left({\text{F}}_{\text{t}}^{\text{i}}\right)}$$
(37)

Where, ‘\(\:\text{d}\left({\text{F}}_{\text{t}}^{\text{i}}\right)\)’ represents the likelihood of excluding solution \(\:\left({\text{F}}_{\text{t}}^{\text{i}}\right)\), while ‘\(\:\text{f}\left({\text{F}}_{\text{t}}^{\text{i}}\right)\)’ signifies value for objective function for the solution. Numerous solutions are produced in arbitrary problem space. Solutions are forwarded to optimal for achieving ideal solution. In the proposed scheme, stages comprise of generating initial population, updating factors, assessing solutions, searching as well as capturing oysters, running away from other fishes, moving to fish collection, reproduction, production as well as extinction of unwanted fishes.

In addition, Algorithm 3 presents the steps involved in the implementation of the proposed BFOA-based multi-hop routing established between clusters.

Algorithm 3
figure c

BFO-based multi-hop routing established between clusters.

Full size image

This Algorithm 3 presents the steps included in establishing the route between the selected CHs and the sink node for delivering the sensed data from the deployed cognitive sensor nodes to the sink for reactive decision making. This determination of optimal routes between the selected CHs and the sink node is attained based on the factors of energy and distance between the selected CHs and the sink node. This route determination approach explores and exploits different number of routes identified between the selected CHs and the sink node. From these identified number of feasible routes, one optimal route is determined based on the evaluation of the fitness function using the factors of energy and distance determined between the selected CHs and the sink node. This optimal route is selected with minimized number of hops such that energy utilized during the process of routing is considerably minimized in the network. It also focusses on determining the possible single hop between the selected CHs and the sink for further reduction of energy during the of data transmission. This routing approach used comprehensive number of factors which helped in determining the fitness valued routing path for identifying the optimized one from the feasible number of routes which could be confirmed from the search space of the network. Thus, the adopted BFOA algorithm helped in achieving optimized multi-hop route between the clusters such that energy consumption is minimized with maximized spectrum sensing that proves better channels availability in the network.

Results and discussion

The simulation experiments of the proposed HMABFOA scheme and the benchmarked MDMOACA23, AACDICS24 and WOAP20 approaches are achieved using MATLAB R2019. This implementation of the proposed HMABFOA scheme and the benchmarked approaches is conducted with 100 cognitive sensor nodes out of which 50 PUs are uniformly and randomly deployed in the monitoring area of the circular network. The sink node is located at the network center with the communication radius of the cognitive sensor nodes assigned to 150 m. The fixed period over which the sink node provides the amount of RF energy to the deployed cognitive sensor nodes is set to 0.2 s. During the entire monitoring period, each of the active cognitive sensor nodes need to transmit data to the sink in which the data collected from the environment under monitoring is processed for reactive decision making. In addition, the number of active cognitive sensor nodes varied from 0 to 100 with the maintained network radius of 50 m with the objective of exploring the node density impact and scalability handled by the proposed HMABFOA scheme. In addition, Table 2 presents the Simulation parameters used for implementing the proposed HMABFOA scheme and the benchmarked clustering protocol approaches used for comparative analysis.

Table 2 Simulation parameters used for implementing the proposed HMABFOA scheme.
Full size table

Initially, the proposed HMABFOA scheme and the benchmarked MDMOACA, AACDICS, and WOAP approaches are compared using mean throughput, network lifetime, mean packet latency and mean energy consumption with different number of simulation time. In specific, Figs. 4 and5 present the throughput and network lifetime attained in the network environment using the implementation of the proposed HMABFOA scheme and the benchmarked MDMOACA, AACDICS and WOAP approaches under different simulation time. It is visualized that with increase in the simulation time, the throughput achieved by the proposed HMABFOA scheme, and the benchmarked approaches also increases due to the generation of a comparatively greater number of packet than the initial starting time. But the proposed HMABFOA scheme is comparatively better in guaranteeing the reception of a greater number of packets by an individual node at any point in time. This predominance of the proposed HMABFOA scheme since it selected the only active mode with high residual node for determining the optimal route for the objective of transferring the data to the specific destination. On the other hand, the inclusion of access selection algorithm which targets on enhancing the strength of the signal also plays an indispensable role in identifying the reliable path which aids in improving the network lifetime with minimized energy utilization. These potential characteristics of the proposed HMABFOA scheme helped in improving the throughput on average by 19.32%, better than the baseline approaches. At the same time, the network lifetime sustained during the implementation of the proposed HMABFOA scheme under increasing simulation time is also realized to be extended to an average by 21.86%, better than the benchmarked schemes used for comparative investigation.

Fig. 4
figure 4

Proposed HMABFOA-mean throughput with different simulation time.

Full size image
Fig. 5
figure 5

Proposed HMABFOA-network lifetime with different simulation time.

Full size image

Then Figs. 6 and 7 demonstrate the plot of packet delay and energy consumptions incurred in the network using the deployment of the proposed HMABFOA scheme and the benchmarked MDMOACA, AACDICS and WOAP approaches under different simulation time. With an increase in the simulation time, the interaction and degree of packet forwarding, and reception increases proportionally. This proportional increase in the packet delivery process eventually incurs comparatively higher energy utilization and higher delay when the packets are propagating from one active node to another. But the proposed HMABFOA scheme is capable enough in comparatively minimizing the rate of energy consumption by selecting only the sufficient energy path sufficiently during data dissemination. This inherent significance of the proposed HMABFOA scheme prevented the number of unnecessary control packet retransmissions resulting in reduced packet delay during the process of data forwarding, this predominance also helped in utilizing minimized energy in the network such that stability of the network is maintained for an extended time. Hence the proposed HMABFOA scheme, on average minimized the packet delay and energy consumptions by 19.65 and 22.74%, better than the baseline approaches used for comparative investigation.

Fig. 6
figure 6

Proposed HMABFOA-mean packet latency with different simulation times.

Full size image
Fig. 7
figure 7

Proposed HMABFOA-mean energy consumptions with different simulation time.

Full size image

In the second part of the investigation, the proposed HMABFOA scheme and the benchmarked approaches are compared using throughput, network lifetime, packet delay and energy consumptions with different number of active sensor nodes. Figures 8 and 9 depict the results of HMABFOA scheme and the benchmarked approaches using throughput and network lifetime with different active sensor nodes. When the number of active sensor nodes is 0, then the throughput and network lifetime is also 0. It then starts steadily increasing with an increase in the number of active sensor nodes in the network. This is because when the number of active sensor nodes is 0 then the packets generated by the sensor nodes are always equal to 0. Thus, the throughput of the network is 0, and at the same time the network lifetime is determined only with respect to the active number of nodes which are operating in the network for the mentioned objective of the research. This throughput and network lifetime can be potentially investigated with a considerably greater number of active sensor nodes of the network by varying the sensor nodes from 0 to 100. The proposed HMABFOA scheme exploited and explored the possible paths in the routing path using the merits of BFOA such that optimized route is determined between the selected CHs and the sink node. This optimized route determination is also confirmed through the evaluation of factors associated with energy and distance such that minimized hops decide upon the delivery of data from the selected CHs to the sink node. Hence the proposed HMABFOA scheme, on an average improved throughput and network lifetime on an average of 17.34 and 21.45%, better than the baseline approaches used for comparative investigation.

Fig. 8
figure 8

Proposed HMABFOA-mean throughput with cognitive sensor nodes.

Full size image
Fig. 9
figure 9

Proposed HMABFOA-network lifetime with cognitive sensor nodes.

Full size image

Further Figs. 10 and 11 highlight the results of HMABFOA scheme and the benchmarked approaches using mean packet latency and mean energy consumptions with different active sensor nodes. When the number of active sensor nodes in the network are zero, the mean packet latency and mean energy consumptions are also zero. This is because when the active number of sensor nodes is 0, the mean packet latency and mean energy consumption is also 0 as there are no packets that are generated from the source sensor nodes. Since the number of packets is zero, the amount of energy incurred for data dissemination during the process of data generation, data forwarding, and data reception also becomes 0. But this pattern slowly and systematically gets changed with respective increase in the number of active sensor nodes in the network. When the active sensor nodes in the network increases, the responsibility of transmitting the generated packets and receiving the packets incurs significant amount of energy which also gets proportionally increased in the network. This generated packet incurs a significant amount of time to get generated, transmitted and received at the sink for reactive decision making. This proposed HMABFOA scheme identified optimized routes with the factors of energy and distance which eventually sustained more energy with the sensor nodes and time incurred during the process of routing in the established network. Hence the proposed HMABFOA scheme, on average minimized the packet delay and energy consumption by 17.64 and 20.32%, better than the baseline approaches used for comparative investigation.

Fig. 10
figure 10

Proposed HMABFOA-packet delay with cognitive sensor nodes.

Full size image
Fig. 11
figure 11

Proposed HMABFOA-energy consumptions with cognitive sensor nodes.

Full size image

In addition, the proposed HMABFOA scheme and the benchmarked approaches are compared using the number of resounds at which the first node death, and last node death of sensor nodes are visualized in the environment. In both the network lifetime of FND and LND as portrayed in Fig. 12, the proposed HMABFOA scheme performed remarkably well since it adopted a reactive strategy of sustaining energy in the network. This inclusion of an energy-efficient routing process helped remarkably well in exploring the factors that contribute towards better network lifetime by extending the death of sensor nodes. It also adopted an approach which comprehensively determined the impact of energy over the life of the sensor nodes which are employed over the network. In specific, the proposed HMABFOA scheme extended FND by 10.12% and prolonged LND by 8.74%, better than the benchmarked approaches used for comparison.

Fig. 12
figure 12

Performance assessment based on stability analysis with different rounds.

Full size image

Finally, Fig. 13 exemplifies the energy stability guaranteed in the network during the employment of the proposed HMABFOA scheme and baseline approaches evaluated using different active sensor nodes. The proposed HMABFOA scheme exploited and explored the factors that contribute towards better data routing between the necessitated source and the destination. Moreover, the proposed HMABFOA scheme on average sustained a maximized energy stability of 23.41%, better than the benchmarked approaches used for comparison.

Fig. 13
figure 13

Performance assessment based on stability analysis with different nodes.

Full size image

Conclusions

The proposed HMABFOA Protocol adopted an imperfect spectrum sensing approach and achieved better utilization of downlink energy harvesting and sustained maximized degree of energy between the nodes in the network. It reduced the negative impact of imperfect spectrum sensing for extended network lifetime which sustains the capabilities of the network surveillance. It helped in constructing a distributed cluster with multi-hop routing selection between clusters depending on an energy level function that explores and exploits the factors associated with CHs selection. It specifically used the merits of Mexican axolotl optimization algorithm (MAOA) for better CH selection and cluster formation such that energy stability is sustained in the network. It further used the significance of bitterling fish optimization (BFOA) for achieving an optimized multi-hop route between the clusters such that energy consumption is minimized with maximized spectrum sensing that proves better channel availability in the network. The simulation results of the proposed HMABFOA scheme, on average minimized the packet delay and energy consumption by 17.64 and 20.32%, better than the baseline approaches used for comparative investigation. Then the proposed HMABFOA scheme extended FND by 10.12% and prolonged LND by 8.74%, better than the benchmarked approaches used for comparison. Moreover, the proposed HMABFOA scheme on average sustained a maximized energy stability of 23.41%, better than the benchmarked approaches used for comparison.