A deep learning identification method of tight sandstone lithofacies integrating multilayer perceptron and multivariate time series

Abstract

Lithofacies classification and identification are of great significance in the exploration and evaluation of tight sandstone reservoirs. Existing methods of lithofacies identification in tight sandstone reservoirs face issues such as lengthy manual classification, strong subjectivity of identification, and insufficient sample datasets, which make it challenging to analyze the lithofacies characteristics of these reservoirs during oil and gas exploration. In this paper, the Fuyu oil formation in the Songliao Basin is selected as the target area, and an intelligent method for recognizing the lithophysics reservoirs in tight sandstone based on hybrid multilayer perceptron (MLP) and multivariate time series (MTS-Mixers) is proposed. Firstly, appropriate logging curve parameters are selected based on the contribution rate as the basis of the lithofacies intelligent discrimination. Second, preprocessing operations are performed on the logging dataset to ensure the quality of the experimental data. Finally, the MLP-MTS hybrid intelligent model is constructed by combining the powerful information extraction and classification recognition capabilities of the MLP and MTS models to complete the intelligent recognition of the petrography of tight sandstone reservoirs. The experimental results demonstrate that the recognition efficiency of MLP-MTS model for all kinds of lithofacies phases is more than 90%, which verifies the good applicability of deep learning model in solving the process of lithofacies phase recognition in reservoirs.

Introduction

With the continuous development of unconventional oil and gas exploration prospects, tight oil reservoirs have attracted extensive attention due to their immense industrial value¹. However, the identification of lithofacies in tight sandstone reservoirs is challenging primarily due to the complex reservoir composition, poor pore structure, and strong heterogeneity². These factors limit the scale expansion of reservoir exploration and efficient development, and reduce the efficiency of manual lithofacies division³. Therefore, achieving efficient intelligent lithofacies identification is of significant importance for the exploration and evaluation of tight sandstone reservoirs⁴.

Lithofacies typically refer to sedimentary lithofacies that reflect the lithological characteristics of certain sedimentary environments, encompassing all physical, lithological, and biological features⁵. Geophysicists and geological experts explore the correlation between lithofacies and logging data using properties such as continuity and multidimensionality. The development of lithofacies identification technology has undergone three main stages: traditional lithofacies identification⁶, shallow neural network identification⁷, and deep neural network identification⁸. Traditional lithofacies methods include the rendezvous diagram method and the logging curve superposition method. Delong et al.⁹ proposed the cross plot method for identifying reservoir lithology and fluid types, but logging curve features cannot be effectively identified by individual logging curve parameters. Wei et al.¹⁰ introduced the logging curve overlap method, which selects logging curves sensitive to shale and overlays them, but relying solely on one logging curve parameter cannot fully identify lithofacies types, necessitating a combination with other lithofacies identification methods. Although the traditional lithofacies recognition method can recognize the petrography to a certain extent, its recognition process is too dependent on manual recognition by experts in the field of lithofacies recognition, which leads to low efficiency. In the shallow neural network recognition stage: Linfu et al.¹¹ employed self-organizing neural networks for automatic lithofacies identification using logging data, but it is not suitable for regions with complex lithofacies variations. Qiangfu et al.¹² proposed the nearest neighbor algorithm, but lithofacies identification results are poor under sparse thin-section samples and suboptimal well conditions. In summary, Although the recognition accuracy of the shallow neural network method is better than that of the traditional lithofacies identification method, based on the limitations of the algorithm itself, it is unable to approximate the mapping relationship between reservoir features and lithofacies types, which leads to the accuracy of the lithofacies identification process still appears to be unsatisfactory. With the development of deep learning technology, more and more experts have started to use deep learning technology in the field of geological petrography. Yang¹³ proposed a lithofacies logging identification method based on convolutional neural networks(CNN), significantly improving accuracy compared to shallow neural networks, but this method only uses a small number of lithofacies categories and lacks uniformity. Junjie¹⁴ proposed an automatic labeling model based on deep learning LSTM for lithofacies identification, but the model’s generalization ability is weak. Liu et al.¹⁵ applied clustering algorithms to compare mud shale facies, although the proposed algorithms are usually accurate, they are limited by the amount of data in the facies samples. Dwivedi et al.¹⁶ proposed the development and testing of automated detection and identification of facies using an integrated approach of seven common classifiers, but the process has three classifiers competing with each other in terms of classification performance. To address the overall feature learning limitations of deep neural networks, Li et al.¹⁷ proposed a multivariate time series method (MTS-Mixers) to capture long-term dependencies for data classification and identification tasks. Overall, Ismail et al.¹⁸ proposed the MLP method applied to seismic reflections and lithology classifications, and it has been used in the field of geologic characterization and logging. combination of geologic features and logging plays a great role in the field of oil and gas exploration. The deep neural network discrimination method has improved the efficiency of research work in this field, but the accuracy of lithology intelligent discrimination still needs to be improved.

The deep neural network recognition method has improved the efficiency of research in this field, but the accuracy of the intelligent recognition of petrography still needs enhancement. Therefore, based on analyzing the existing methods of lithofacies recognition in tight sandstone, this paper proposes an intelligent recognition model for tight sandstone reservoirs that integrates multilayer perceptron and multivariate time series algorithms by combining the flexible feature learning ability of multilayer perceptron and the advantage of multivariate time series in processing complex time series data quickly. It makes up for the problems of long training time and low accuracy in the traditional lithofacies identification method, and provides the basis for the next reservoir evaluation and dessert prediction.

The main advantages of MLP-MTS include:

• 1. Automatic classification and identification: The deep learning method enables the automatic identification of subtle differences in dense sandstone petrography that may be overlooked in manual identification.

• 2. Powerful information extraction and classification capabilities: The integration of MLP and MTS models facilitates efficient identification, even with small sample datasets.

• 3. Selection of appropriate logging curve parameters: By utilizing contribution rates, the model achieves automatic classification and accurate identification of various lithofacies phases within the reservoir.

Preliminary work

This section elaborates on the basic overview of Fuyu Reservoir in Sanzhao Sag and the overall design concept of the intelligent lithofacies identification method for tight sandstone reservoirs, providing a basis for subsequent intelligent lithofacies identification.

Study area overview

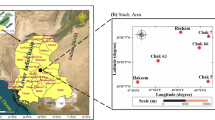
The Fuyu Reservoir in Sanzhao Sag is an important area for tight oil exploration and development in Songliao Basin¹⁹. The study area is located in Zhaozhou Oilfield of North Songliao Basin (as shown in Fig. 1). It is adjacent to Daqing Placanticline in the west, borders Chaoyanggou Terrace in the east, connects to Anda Depression in the north, and extends to Fuyu Uplift in the south, with a total area of 5575 km²²⁰. The Songliao Basin is a Mesozoic primary oil-bearing basin extending to the northeast. Dual tectonics of pressure over faults, tectonic evolution in the northern Songliao Basin The tectonic evolution of the northern Songliao Basin went through three stages (rupture, dehiscence, dehiscence, and reversal)²¹, resulting in three tectonic units (rupture tectonics, depression tectonics, and reversal tectonics).

The burial depth of the top surface of the Fuyu Reservoir ranges from − 1780 to – 1840 m, and the thickness of the formation ranges from 230 to 250 m. The overall structure exhibits a low-amplitude nose-shaped feature inclined to the northwest²². The Fuyu Reservoir belongs to a typical porous tight sandstone reservoir, mainly composed of fine sand and siltstone, with a small amount of medium and coarse sandstone²³. The average porosity in the study area is 10.9%, and the average air permeability is 0.86 mD. By analyzing indicators such as porosity and permeability of tight sandstone reservoirs, we can better classify high-quality reservoirs in the Fuyu Reservoir of Sanzhao Sag^24,25.

Fig. 1

Structure location of Sanzhao Sag of Songliao Basin (According to LiuFang (2023), modify by MapGIS)²⁶.

Design concept of MLP-MTS model

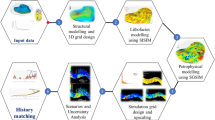
The MLP-MTS intelligent lithofacies identification method for tight sandstone reservoirs consists of four steps. Step 1: Analyze the overview of the study area, discussing the correlation between lithofacies and logging curves, classification schemes, and the selection of logging parameters as the basis for intelligent lithofacies identification. Step 2: Convert the depth-domain data of logging curves into time-domain data, preprocessing the logging curve dataset, including data cleaning, data standardization, and gaussian filter, to ensure the quality of experimental data. Step 3: Establish the MLP-MTS model and conduct training for intelligent identification of different lithofacies types in tight sandstone reservoirs. Step 4: Verify the effectiveness of the MLP-MTS intelligent lithofacies identification method through experiments, ensuring its ability to quickly and accurately complete the intelligent identification of lithofacies. The overall process of the method is shown in Fig. 2.

Fig. 2

MLP-MTS model processing method.

Lithofacies classification and logging curve data characteristics

This section elaborates on the correlation between lithofacies and logging curves, as well as the classification scheme of lithofacies. After completing the screening of logging curves for tight sandstone, the quantitative characteristics of logging data of different lithofacies types and the correlation between logging curve data and time series data are studied.

Correlation between lithofacies and logging curves

Logging curves provide crucial information about rock properties and geological features, aiding in the identification of different lithofacies. For instance, mudstone typically exhibits higher natural gamma values due to the presence of radioactive substances like potassium, thorium, and uranium. In contrast, sandstone generally has lower natural gamma values because its minerals typically contain fewer radioactive elements. Sandstone transition rocks may show natural gamma values between those of mudstone and sandstone, depending on their composition and content. In the process of intelligent lithofacies identification, various logging parameters of lithofacies are extracted for comparison to determine the correlation between geological lithofacies and logging information.

Lithofacies classification

In this paper, the lithofacies division is based on the lithological type and stratigraphic structure of the lithofacies combined with the response characteristics of the logging curves. Combined with the experiments of cast thin section, scanning electron microscope, constant velocity mercury compression, high-pressure mercury compression, CT scanning, and nuclear magnetic resonance by geologists²⁶. Lithology types in the study area are classified into three types: mudstone, sandstone and sandstone transition rock; Bedding structures are classified into five types: trough cross-bedding, tabular cross-bedding, parallel bedding, ripple bedding, and horizontal bedding. Based on conventional logging data analysis and statistics, the study reveals that the tight sandstone reservoirs in Fuyu Reservoir mainly comprise five sandstone lithofacies and one sandstone and mudstone transition lithofacies: Troughed Cross-bedding Fine Sandstone (St), Tabular Cross-stratified Fine Sandstone (Sa), Parallel Stratified Fine Sandstone Facies (Sp), Undulating Stratified Fine Sandstone Facies (Sw), Horizontal Stratified Siltstone Facies (Fh), Undulating Bedding Argillaceous Siltstone (Fw). Facies such as Climbing Bedding Siltstone Facies, Massive Bedding Siltstone Facies, Convolute Bedding Argillaceous Siltstone, Lenticular Bedding Siltstone Facies, and Horizontal Bedding Argillaceous Siltstone are less developed and collectively referred to as other mudstone lithofacies (O). Table 1 shows the porosity and permeability of seven different lithofacies types.

Table 1 Porosity and permeability table for different lithofacies types.

Based on the reservoir physical properties and lithological characteristics of different lithofacies types, the tight sandstone reservoirs of Fuyu Reservoir in Zhou-6 Block are classified into four categories from best to worst based on average porosity and permeability values: Class I reservoirs include St, Sa, and Sp lithofacies; Class II reservoirs include Sw lithofacies; Class III reservoirs include Fh and Fw lithofacies; Class IV reservoirs include O lithofacies.

Contribution rate of logging curves

Currently, the identification of lithofacies based on logging curves primarily uses data such as spontaneous potential, acoustic time difference, formation resistivity, caliper, natural gamma, and deep and shallow lateral resistivity^27,28,29. To effectively screen logging curve parameter data closely related to lithofacies types and couple lithofacies characteristics with conventional logging curve features, the Principal Components Analysis (PCA) is employed in this paper to score logging curve parameter values. k is the principal component of the main feature, and the contribution rate C refers to the proportion of a particular feature value to all feature values, calculated as shown in Eq. (1):

$$C=\frac{{{{\text{y}}_{\text{j}}}}}{{\sum\nolimits_{{{\text{k}}=1}}^{{\text{m}}} {{{\text{y}}_{\text{k}}}} }}$$

(1)

Where, ${{\text{y}}_{\text{j}}}$ is the j-th feature value and ${{\text{y}}_{\text{k}}}$ is the k-th feature value.The top five logging curve parameters with the highest comprehensive contribution rates are shown in Table 2. Therefore, natural gamma (GR), spontaneous potential (SP), caliper (CAL), Density (DEN), and acoustic time difference (AC) are chosen as input features of the sample dataset for intelligent lithofacies identification.

The five results with the highest integrated contribution of logging curve parameters are shown in Table 2; the importance feature map of logging curve parameters is more intuitively seen in Fig. 3. Therefore, in this paper, GR, SP, CAL, DEN, and AC are selected as the input features of the sample dataset for lithofacies intelligent discrimination. Due to the limitation of the modeling algorithm in this paper, adding too many logging curve parameters will lead to overfitting of the model, so only the first five items that contribute most to the logging curve parameters are added as input features for feature selection in this paper.

Fig. 3

Importance scoring of logging curves.

Table 2 Contribution rate and cumulative contribution rate of principal component analysis of logging curve.

MLP-MTS intelligent lithofacies identification method

This section provides a detailed overview of the research process for the MLP-MTS intelligent lithofacies identification method. It includes five key steps: logging data analysis, establishment of lithofacies dataset, preprocessing of logging curve data, intelligent lithofacies identification model and model training.

Logging data analysis

Logging and core analysis data provide precise lithological and lithophysics information essential for the identification of lithofacies in sedimentary environments and diagenetic processes³⁰. The logging data from 10 wells in the Fuyu Reservoir of Sanzhao Sag is analyzed. The data sources include detailed observation and description of centimeter-level core and standardized processing of logging curve (considering different logging time and different logging series), combined with key interface analysis of logging curve and core depth homing correction. Detailed information on the logging data is shown in Table 3.

Table 3 Logging curve statistics of Fuyu reservoir in Sanzhao Sag.

In this study, 25,345 sets of data from 10 core wells in the Fuyu Reservoir of Zhou-6 Block are selected. Taking Wells F188 and S55 as examples, the lithofacies distribution data of F188 and S55 are shown in Fig. 4. Wells F188 and S55 have a total of 4400 data sets of logging curve data, including St:114 sets, Sa:208 sets, Sp:548 sets, Sw:926 sets, Fh:898 sets, Fw:637 sets, O:1069 sets.

Fig. 4

Lithofacies direct view of data sample.

Establishment of lithofacies dataset

The logging curve data reflects the physical properties of formation rocks, which in turn control the properties of fluids, while fluid properties depend on diagenetic processes and sedimentary facies characteristics after sediment deposition, so there is a certain correlation between logging curve information and diagenetic processes³¹. The sedimentation time of rocks under sedimentation and diagenesis changes with depth. Therefore, this study can transform the logging curve parameters from the depth domain to the time domain, and retain as much reservoir information as possible by converting the depth domain to the time domain, The time-domain logging curves are used to interpret and invert these thin layers accurately.

For instance, Well F188 has a total of 1821 data sets across 12,741 depth nodes. All data sets are sampled and sorted at 0.05-meter depth intervals (DEPT). Key logging curve parameters including GR, SP, AC, CAL and Den are selected as input parameters for model training. To ensure flawless logging quality control, we use standard operating procedures to standardize the logging process and minimize variability in data collection.

To ensure the accuracy of logging curve data during model training, data standardization is applied to process the logging data. After data standardization, all logging data values are at the same order of magnitude, balancing the influence of logging curve values in the model^32,33. In this paper, Gaussian filtering³⁴ is used to smooth the original data, and the difference in the effect before and after the standardized processing is shown in Fig. 5, the data after standardized processing is obviously more average, and the extreme points are much smoother than before, which is due to the continuous change of logging and downhole environment during the movement of logging instruments, and the logging data initially obtained contains a large amount of noise. The cleanliness of the logging data preprocessing will directly affect the accuracy of the lithofacies discrimination model. In view of this, the data preprocessing of the logging curve dataset is carried out next.

Fig. 5

The effect difference map before and after standardization of logging data.

Data preprocessing

Before using the deep learning network model to explore the relationship between logging curve data and lithofacies, preprocessing operations need to be performed on the logging curve data to reduce noise in the dataset and thereby improve the model’s prediction accuracy. The data preprocessing workflow is illustrated in Fig. 6. First, the logging sequence is transformed from the depth domain to the time domain using the depth-time relationship, thus converting the logging sequence from the depth domain to the time domain. Next, a data cleaning method is employed to check the lithofacies dataset for abnormal values and to clean the data if necessary. Finally, data interpolation is conducted to fill in missing or sparse data points in the logging data.

Fig. 6

Logging curve pre-processing flowchart.

• 1. Depth-Time Domain Conversion: First, acoustic time different data is extracted from the logging curves to establish a velocity model. Then, the depth-to-time conversion relationship is computed using the velocity data, and a depth-time curve is generated for transforming the logging curve data. Finally, the logging data is transformed from the depth domain to the time domain using the depth-time curve.

• 2. Data Cleaning Method: The purpose of data cleaning is to remove noise from the logging data and reduce the impact of extremums on data³⁵. In this study, a regression method is employed to comprehensively analyze and observe the F188 single well dataset, and to statistically regress the abnormal yellow data in Table 4. The function values fitted through regression are then compared with the original logging curve data to eliminate noisy data, as shown in Eqs. (2)–(4):

$$y=a+bx$$

(2)

According to the principle of least squares, $\hbox{min} \sum {{{({y_i} - \bar {y})}^2}}$, the slope b and intercept of the estimated ${a_1}$ regression equation can be calculated from the well logging curve data.

$$b=\frac{{{l_{xy}}}}{{xx}}=\frac{{\sum\nolimits_{{i=1}}^{n} {({x_i} - \bar {x}} )({y_i} - \bar {y})}}{{\sum\nolimits_{{i=1}}^{n} {{{({x_i} - \bar {x})}^2}} }}$$

(3)

$${a_1}=\bar {y} - b\bar {x},\bar {x}=\frac{{\sum {{x_i}} }}{n},\bar {y}=\frac{{\sum {{y_i}} }}{n}$$

(4)

• 3. Data Interpolation Method: To address missing parameters or sparse data points in the logging data, a data interpolation method is used to enhance the completeness and quality of the logging data. The core of data interpolation is to establish a relevant mapping relationship and use predicted data for interpolation, ensuring data integrity and quality. The data interpolation method is expressed as Eq. (5):

$${Y_i}=f({X_i})+{\upvarepsilon _i}$$

(5)

Where, Y_i represents the data interpolation method, X_i denotes the independent variable feature, e is the data error, and f reflects the mapping relationship between X_i and Y_i. The preprocessed logging curve data effectively addresses issues such as data standardization, data missing, and data anomalies, enabling effective handling of data fluctuations in lithofacies identification. This enhances the accuracy and reliability of data processing.

• 4. Unbalanced data processing: Due to the small sample size of rock phases such as St and Sw, this paper considers the use of random downsampling and SMOTE to equalize the sample size. The SMOTE oversampling technique is to use a few classes of samples to control the generation and distribution of artificial samples, to achieve the purpose of dataset equalization. To construct a synthetic sample, firstly, K nearest neighbors is randomly selected, and then the difference of corresponding eigenvectors is multiplied by a random number between [0,1], whose expression can be expressed as:

$${c_{new}}={c_i}+\left( {{{\hat {c}}_i} - {c_i}} \right) \times \delta$$

(6)

Where ${c_i}$ is a minority class sample, ${\hat {c}_i}$ a k-nearest neighbor of ${c_i}$, and $\delta$ is a random number that exists between [0,1].

MLP-MTS intelligent lithofacies identification model design

The flowchart of the MLP-MTS model is shown in Fig. 7. Figure 7a represents the original data set of the five logging curves selected in this paper. The MLP-MTS combines two powerful neural network structures: MLP and MTS-Mixers, making it more advantageous in the automatic continuous identification of logging curve sequence data. Advantage 1: MLP captures the features of logging curve values through multiple computational layers and non-linear transform operations, and continuously updates the weights and bias parameters of each layer through the gradient descent algorithm to find better features in the feature extraction process. Advantage 2: Logging data is discrete time series data, and the physical properties of subsurface reservoirs have a certain continuity. The MTS-Mixers model better captures the long-term dependency relationship in the logging curve data. The combination of advantages enables MLP-MTS to fully understand the features of various parameters in the logging curve data set, handle complex dependency relationships and time series data, and more accurately predict changes in lithofacies types. It can effectively achieve low-cost, high-efficiency, high-precision, and full-section automatic continuous quantitative identification of lithofacies in strong heterogeneous tight sandstone reservoirs.

MTS-Mixers utilize the low-rank characteristics of existing logging data in time series data to obtain better accuracy and efficiency through the decomposition of time and channel mixing. This algorithm not only combines attention mechanisms to improve lithofacies prediction performance, but also solves the problem of sampling frequency and sensor influence during data acquisition. MLP provides more flexible feature learning capabilities and utilizes convolutional layers to capture logging curve information while paying attention to the nonlinear relationship between logging curves and lithofacies.

Fig. 7

MLP-MTS model flow chart.

The MLP-MTS is the core algorithm for intelligent lithofacies identification, mainly including the extraction of logging curve features, downsampling and denoising processing, model data classification identification.

• 1. Extraction of logging curve features: The MTS-Mixers model, as shown in Fig. 8, is divided into Encoder Block and Linear Layer. The Encoder undergoes 2 layers of operations, including 1 feedforward neural network layer to learn channel features, and 1 Self Attention layer. The output of the Encoder operation will continue as the input to the Linear Layer. Above the Multi-Head Attention, there is also an Add & Norm layer, where Add represents the residual connection to prevent network degradation, and Norm (Layer Normalization) normalizes the vector data containing logging curve information.

Fig. 8

Extraction of logging curve characteristics.

The source time series is divided into multiple sub-sequences, and the sub-sequences of 5-dimensional logging curve parameters are disassembled to learn the time information, and then reassembled to extract the time dependency of logging curve, as shown in Eqs. (7)–(9):

$${X_{h,1,…,}}{X_{h,s}}=Sampled(norm({X_h}))$$

(7)

$$X_{{h,i}}^{T}=Temporal({X_{h,i}}){\text{i}} \in [1,{\text{s]}}$$

(8)

$$X_{h}^{T}=M{\text{erge}}\left( {X_{{h,1,…,}}^{T}X_{{h,{\text{s}}}}^{T}} \right)$$

(9)

Specifically, $X_{h}^{{}}$ represents multivariate time series instance, and $X_{h}^{T}$ represents time dependency.

• 2. Downsampling and denoising processing: The equidistant time series is downsampled into multiple interleaved sub-sequences, and MLP is used to learn the time information of the logging curve sub-sequences. The learned information is then merged into the original time sequence, as shown in Fig. 9. The noise of the time series logging data is reduced for the redundant channel data in the channel dimension through matrix factorization, as shown in Eqs. (10) and (11).

$$\tilde {X}_{h}^{C}={X_h}+X_{h}^{T}$$

(10)

$$\tilde {X}_{h}^{C}=X_{h}^{C}+N \approx UN+N$$

(11)

Where, $X_{h}^{C}$ represents channel interaction. $N \in {R^{{\text{n}} \times {\text{c}}}}$ represents the noise value of the logging curve parameters; $X_{h}^{C} \in {R^{{\text{n}} \times {\text{c}}}}$ represents the dependency relationship between the logging curve parameters and lithofacies after denoising.

Fig. 9

Example of temporal factorization when s = 2.

• 3. Model data classification identification: An MLP model is added to the MTS-Mixers encoder Output layer. The MLP model is divided into Input Layer, Hidden Layer, and Output Layer¹⁷, as shown in Fig. 7c. The analytical formula for the Hidden Layer neuron and the Output Layer component is shown in Eq. (13):

$${\text{z}}_{j}^{1}=f\left[ {\sum\limits_{{i=1}}^{{{N_x}}} {\left( {{w_i}{,_j}{,_1}{x_i}+{b_i}{,_j}{,_1}} \right)} } \right]$$

(12)

Where, ${\text{z}}_{j}^{1}$ represents the j-th neuron on the first hidden layer; ${x_i}$ is the i-th component of the input layer; ${w_i}{,_j}{,_1}$ is the connection weight between the i-th component of the input layer and the j-th neuron on the first hidden layer. In back propagation, using ${\text{z}}_{j}^{1}$ as input, recursion is performed on Eq. (12) in turn, and the calculation formula for the hidden layer neurode is shown in Eq. (13):

$${\text{z}}_{j}^{k}=f\left[ {\sum\limits_{{i=1}}^{{{N_z}}} {\left( {{w_i}{,_j}{,_k}{\text{z}}_{i}^{{k - 1}}+{b_i}{,_j},k} \right)} } \right]$$

(13)

The MLP-MTS model shows good performance in long-term prediction of time series information and is suitable for intelligent identification of logging curve data with depth as the sequence data. It simplifies the network structure while accurately extracting features, allowing for faster processing and prediction of logging curve data set.

Training of MLP-MTS lithofacies identification model

The Adam optimization algorithm is a gradient-based stochastic optimization method³⁶ that can automatically calculate adaptive learning rates under parameter settings. In this study, the minimization of the loss function is set as the optimization goal, and the Adam optimization algorithm is used to update the model training parameter ${\theta _t}$ in the training process to complete the iterative training. The process of updating the training parameter ${\theta _t}$ is described as follows:

• 1. Gradient calculation:

Initialize matrix vectors. While ${\theta _t}$ does not converge, t = t + 1, and a new round of gradient values is obtained.In each iteration, the gradient, where${g_t}$ represents the current loss function and ${f_t}\left( \theta \right)$ is the parameter value from the previous iteration, is computed.

$${g_t}={\nabla _\theta }{f_t}\left( {{\theta _{t - 1}}} \right)$$

(14)

Where, ${g_t}$ represents the gradient information of small batch samples; $J\left( {\theta ,{X_t},{y_t}} \right)$ represents the objective function; ${X_t},{y_t}$ represents features and labels that represent a small batch of samples.

• 2. Momentum and weighted averages:

The ADAM algorithm uses first-order moment estimates ${m_t}$ and ${v_t}$ on top of the gradient to perform a weighted moving average of the gradient information.

$${m_t}={\beta _1} \cdot {m_{t - 1}}+\left( {1 - {\beta _1}} \right) \cdot {g_t}$$

(15)

$${v_t}={\beta _2} \cdot {v_{t - 1}}+\left( {1 - {\beta _2}} \right) \cdot g_{t}^{2}$$

(16)

Where, ${m_t}$ represents the first moment estimation vector; ${v_t}$ represents the second moment estimation vector; ${\beta _1}$ and ${\beta _2}$ represent the decay rate, with values of 0.9 and 0.999, respectively.

• 3. Bias calibration:

Since the momentum and weighted average may be biased at the initial stage, Adam adjusts for this by means of a bias calibration. The first matrix quantity of the calibration and the second matrix quantity of the calibration are calculated as shown in Eqs. (18) and (19) below.

$${\hat {m}_t}={m_t}/\left( {1 - \beta _{1}^{t}} \right)$$

(17)

$${\hat {v}_t}=v/\left( {1 - \beta _{2}^{t}} \right)$$

(18)

Where, $\widehat {{{m_t}}}$ and $\widehat {{{v_t}}}$ represents the first moment estimate vector and the second moment estimate vector after the bigotry correction. $\alpha$represents the learning rate. $\epsilon$ indicates a smooth item. The value is ${10^{ - 8}}$ to prevent division by 0.

• 4. Update the weight parameter${\uptheta _{\text{t}}}$:

The parameter update quantity ${\theta _{\text{t}}}$ is calculated using the learning rate $\alpha$ and the bias-corrected moments.

$${\theta _t}={\theta _{{\text{t}} - 1}} - \alpha \cdot {\hat {m}_t}/\left( {\sqrt {{{\hat {v}}_t}} + \in } \right)$$

(19)

The iteration loss process is shown in Fig. 10. The prediction step is set to 100 steps, and the iteration count is set to 2000 times. It can be observed that after approximately 1750 iterations, the model’s error gradually approaches zero, reaching the preset training accuracy. This indicates that the model in this study can fit the training data well after sufficient training.

Fig. 10

Training and iterative convergence graph.

Experimental design

The experiment is divided into five parts: Model performance evaluation experiment, Model convergence speed experiment, Execution speed evaluation experiment, Multi-Well Experiment Set Effect Experiment, Single-Well Identification Effectiveness Experiment. Specific parameters of experimental equipment : CPU is Intel Xeon Silver 4210R, the memory is 64G, GPU is RTX 6000/8000; the operating system is Ubuntu 20.04.3; the experimental framework is PyTorch 1.7.1.

Model performance evaluation experiment

The model performance evaluation experiment includes three parts: precision evaluation experiment, accuracy evaluation experiment and cluster analysis experiment.

Precision evaluation experiment: Calculate the lithofacies types of tight sandstone and select the Precision, Recall, and F1 score as the evaluation criteria for the MLP-MTS model.

Precision: It refers to the proportion of correctly identified tight sandstone lithofacies types in the total identified number, as shown in Eq. (20). Where, TP represents true positive identification results, and FP represents false positive results.

$${\text{Precision}}=TP/(TP+FP)$$

(20)

Recall: It refers to the proportion of correctly identified tight sandstone lithofacies types in the total number to be identified, as shown in Eq. (21). Where, TP represents true positive identifications, and FN represents false negative results.

$${\text{Recall}}={\text{TP}}/({\text{TP}}+{\text{FN}})$$

(21)

F1 score³⁷: The F1 score is calculated based on Precision and Recall, as shown in Eq. (22). The F1 score ranges from 0 to 1, with a higher value indicating better identification performance.

$${\text{F}}1=\frac{{2 \times \left( {{\text{Precision}} \times \operatorname{Re} {\text{call}}} \right)}}{{\left( {{\text{Precision}}+\operatorname{Re} {\text{call}}} \right)}}~$$

(22)

Accuracy comparison experiment: Construct a model confusion matrix. During the experiment, the same amount of data sets are used. The accuracy of lithofacies identification is compared using four network models: MLP-MTS, MLP, MTS-Mixers, and Transformer to demonstrate the effectiveness of the MLP-MTS algorithm. Among them, Transformer is a framework for natural language processing and other sequence-to-sequence deep learning models proposed by Vaswani et al.³⁸ in 2017, which performs well in processing sequence data.

Cluster analysis experiment: The accuracy rate of MLP-MTS model petrography is compared by cluster analysis experiment. This experiment uses the same amount of training data and test data to compare three different clustering methods, namely K-means clustering, Gaussian mixture clustering, and aggregation clustering methods, to quantitatively analyze the accuracy rate of the MLP-MTS model to assess the influence of the clustering methods on the discrimination methods.

Model convergence speed experiment

To verify the convergence speed of the automatic lithofacies sample labeling method proposed in this paper, its convergence speed and accuracy are compared with those of the manual labeling method.

Execution speed evaluation experiment

Due to the large volume of training data and long training times, this study evaluates the performance of the MLP-MTS, MLP, MTS-Mixers, and Transformer models through an execution speed experiment. The execution speed evaluation experiment tests the mean run time (MRT) of the above four models and assesses the speed at which the algorithms complete the identification task. The experiment data is selected from the F188-138 and S55 well data sets in Songliao Basin, and the data volume is 4400 sets of logging data. In the execution speed evaluation experiment, the MRT values are recorded when the data set sizes are 400, 800, 1200, 1600, 2000, 2400, 2800, 3200, 3600, 4000, and 4400. The experiment is conducted for 11 times, and the mean value of the 11 experiments is calculated.

Multi-well experiment set effect experiment

Six wells (Z11, Z22, Z43-251, B102, F29, F464) that were not included in the training set were randomly selected for lithofacies identification experiments in the state six area of the Sanzhao depression in the Songliao Basin, and the validity of the model, its generalization ability, and lithofacies discrimination were verified by means of a multi-well training set.

Single-well identification effectiveness experiment

The MLP-MTS model is applied to conduct a single well experiment on a random well (not involved in training) in the target area to compare the MLP-MTS model and manual lithofacies identification results, and obtain the accuracy of the single-well experiment.

Experimental results

Model performance evaluation experiment results

Precision evaluation experiment: To verify the accuracy of the MLP-MTS model, the Precision, Recall, and F1 score of the MLP-MTS model are compared with those of the MLP, MTS-Mixers, and Transformer models, as shown in Fig. 11.

Fig. 11

Accuracy, Recall and F1 score of 4 models in different lithofacies identification. (a) Precision calculation result (b) Recall Calculation result (c) F1 Score Calculation result.

As shown in Fig. 11a, the MLP-MTS method outperforms the MLP, MTS-Mixers, and Transformer models in Precision, Recall, and F1 score. The lower Precision of the Sa facies is mainly due to the similarity of corresponding logging curves of Sa and St facies, which leads to confusion in identification.

Figure 11b shows that all four models have a high misclassification rate for the St and Sw lithofacies, mainly due to the small sample size of St and Sw, resulting in some samples being misclassified as other lithofacies. The MLP-MTS model achieves an identification efficiency of over 90% for all lithofacies, with a Recall of over 87% for all lithofacies, indicating its good Recall performance.

Figure 11c indicates that the MLP-MTS model has the highest F1 score, all above 85%, confirming the effectiveness and robustness of the hybrid model, which can meet the accuracy requirements for identifying tight sandstone lithofacies.

Accuracy comparison experiment: To verify the accuracy of the MLP-MTS model in identifying different lithofacies of tight sandstone, confusion matrices are constructed for the MLP-MTS, MTS-Mixers, Transformer, and MLP models, and the influence of geological features on different models is analyzed, as shown in Fig. 12.

Fig. 12

Lithofacies identification results of 4 models. (a) MLP-MTS model identification results, (b) MTS-Mixers model identification results. (c) Transformer model identification results. (d) MLP model identification results.

As shown in Fig. 12a, during the identification of 7 different lithofacies, the MLP-MTS model has the best identification performance, followed by the MTS-Mixers model, then the Transformer model, and the MLP model performs the worst. This is because the MLP-MTS model combines the advantages of MLP and MTS-Mixers, effectively capturing the complex dependencies between time and channels, resulting in the highest identification accuracy.

Figure 12b shows that in the lithofacies identification process of the four models, 4.5% of St samples are misclassified as Sa and Sp, 6.2% of Sa samples are classified as Sp and Fh, 3.1% of Sp samples are classified as St and Sw, 7.3% of Sw samples are partially classified as Fh and Fw, 5.6% of Fw samples are classified as Sw and Fh, and 8.1% of O samples are classified as Sa, Sp, and Sw. The main reason for the above results is that different lithofacies exhibit different logging curve characteristics during the deposition process in geological history, leading to misclassification of lithofacies types. In summary, the MLP-MTS model achieves an identification accuracy of 90.4% for the 7 lithofacies, higher than the identification performance of the other 3 models, although there are errors, the errors are within an acceptable range for lithofacies identification in practical work.

The clustering experiment results: The results of the accuracy of three clustering methods rock relative to each other are shown in Fig. 13. The Gaussian hybrid clustering method has the highest accuracy of 87%, the aggregation clustering method has 86% accuracy, and the k-means method has only 85%. Although the aggregation clustering method and the k-means method can capture the structural information of the data, the Gaussian hybrid clustering method can better deal with the information and processing in the process of logging curve data and lithofacies discrimination.

Fig. 13

Accuracy of MLP-MTS clustering methods.

Model convergence speed experiment results

In this section, according to the principle of using one hour identification volume as the baseline for evaluation, the 1-hour manual identification method was performed on a randomly selected logging curve dataset and compared with the automatic identification method of the MLP-MTS model. Considering that this test only focuses on the lithofacies recognition results, the manual recognition efficiency is relatively high. The model iteration test table is shown in Table 4. The MLP-MTS based lithofacies intelligent recognition conveniently saves 23% time compared to the manual recognition method, and with the increase of the number of iterations; with the increase of time, the ratio of incorrect recognition in the test set is not higher than 2.5%, and there is a trend of decreasing the ratio of error in the test set after the eighth iteration.

Table 4 Iterative test table of lithofacies intelligent recognition model for MLP-MTS.

Execution speed evaluation experiment results

The execution speed evaluation experiment is conducted for the MLP-MTS, MTS-Mixers, Transformer, and MLP models, and the experimental results are shown in Table 5. The variation trend of MRT values with the increase in experimental data volume is shown in Fig. 14.

Table 5 MRT values for different datasets.

As shown in Table 5, the MRT values of the MLP-MTS model are lower than those of the MTS-Mixers, Transformer, and MLP models, indicating that the MLP-MTS model has the fastest execution speed and highest efficiency. In addition, when the experimental data set is 4400, the MRT of the MLP-MTS model is 275.83 s, proving that the execution efficiency of the MLP-MTS model can meet the practical requirements for intelligent lithofacies identification of tight sandstone.

As shown in Fig. 14, the Transformer and MLP algorithms exhibit relatively stable performance when the data set is small, but when the experimental data set is large (> 2000), the MRT values increase significantly, indicating that the two algorithms are sensitive to the size of the data set. In contrast, the MRT values of the MLP-MTS model are linearly related to the size of the data set, indicating that the execution speed of this model is relatively less affected by the size of the data set.

Fig. 14

Variation trend of MRT values with data volume in four models.

Multi-well experimental set effect experiment results

In this section, six untrained wells are randomly selected for lithofacies discrimination using the MLP-MTS method, and the accuracy of the recognition results is shown in Table 5. Through Table 6 we can draw the following conclusions:

• 1. Among these 6 random wells, St and Sa have a relatively small number of relative datasets and relatively low recognition accuracy, while Fw and O have relatively large datasets and better accuracy, indicating that as long as the dataset is sufficient the recognition accuracy of the model can be guaranteed.

• 2. The integrated accuracy of petrography of six untrained random wells in this section reaches 84.76%, which can meet the basic requirements of petrography recognition, although the integrated accuracy of petrography after training has decreased compared with that in section “Model performance evaluation experiment results”. This experiment verifies the general ability of the MLP-MTS model, and more multi-well experiments can also better determine the effectiveness of the model.

Table 6 Randomized well lithofacies identification accuracy.

Single well identification effect experiment results

To further verify the effectiveness of the MLP-MTS model, a well (not included in the training) is randomly selected from the Fuyu Reservoir in Zhao-6 Block of Sanzhao Sag of Songliao Basin for verification, and the identification results are shown in Fig. 15.

Fig. 15

Lithofacies identification results of single well.

Figure 15 compares the manually identified true lithofacies results with the MLP-MTS model’s identification results for the 7 tight sandstone lithofacies, achieving an accuracy of 87.6% in the single well identification results.

Conclusion

Based on the intersection of geological big data and artificial intelligence, an MLP-MTS method for lithofacies identification for tight sandstone reservoirs is proposed in this paper, addressing the difficulties in lithofacies identification, high time costs, and low efficiency of manual identification. The following conclusions are drawn from theoretical exposition and experimental demonstration:

• 1. The Fuyu Reservoir in Zhou-6 Block of Sanzhao Sag in Songliao Basin is a typical tight sandstone reservoir, mainly including lithofacies types such as St, Sa, Sp, Sw, Fh, Fw, and O. Based on the reservoir physical properties, porosity, and permeability of different lithofacies types, the lithofacies of the Fuyu Reservoir are classified into three reservoir categories from best to worst. St, Sa, and Sp are classified as Class I reservoirs; Sw is classified as Class II reservoirs; Fh and Fw are classified as Class III reservoirs, thus achieving lithofacies identification while evaluating reservoir performance.

• 2. By comparing the logging curve data parameters for scoring, the logging curve parameters such as GR, SP, CAL, DEN and AC have higher contribution in lithofacies discrimination. Therefore, the above five feature selection parameters are used as an important basis in the lithofacies intelligent judgment work.

• 3. In the model performance evaluation experiments, through the accuracy evaluation experiments, the accuracy evaluation experiments, and the quantitative analysis experiments of the clustering method, it is concluded that the MLP-MTS model has strong accuracy and precision in lithofacies identification compared with other models.

• 4. The mean MRT value of the MLP-MTS model is lower than that of MTS-Mixers, Transformers, MLP, and other models, indicating that the MLP-MTS model has the fastest execution speed. With an experimental dataset of 4400 sets, the MRT of the MLP-MTS model is 275.83 s, demonstrating that its operational efficiency is less affected by data volume and it can meet the practical demand for intelligent lithofacies identification of tight sandstone reservoirs.

• 5. The accuracy of the MLP-MTS model reaches 87.6% in the single-well identification results, which proves that the MLP-MTS model can achieve a better identification effect during the single-well identification process; and the accuracy of the model reaches 84.7% in the multiple-well experimental results, which proves that the model in this paper has a strong generalization ability in different datasets, and it has a wide application prospect in the field of lithofacies identification.

The limitation of the current MLP-MTS model is that it has good recognition effect only in the tight sandstone dataset, and has not been validated in other types of lithologic reservoirs. The application of deep learning technology only solves part of the problems in the evaluation of tight sandstone reservoirs, and further research should be carried out to realize the deep integration and application of deep learning technology in the field of unconventional reservoir evaluation and promote the intelligent transformation of unconventional reservoir evaluation.

In the future, leveraging the data sensitivity advantages of the MLP-MTS model, this lithology identification method can be more broadly applied to reservoir evaluation tasks involving logging curves to distinguish various lithologies, including mudstone, shale, and others. Additionally, the method may be explored in the context of diagenetic phases, focusing on the classification and identification of logging data associated with these phases.