Introduction

Antibiotics are the most widely used drugs of antibacterial agents, so developing and improving corresponding drug delivery has always been a great concern for the pharmaceutical industry. With the development of nanotechnology, the application of nano-techniques has revolutionized drug delivery methods for the past decades.

Nano-structures, such as nanoparticles (NPs), nano-micelles, dendrimers, liposomes, and nanotubes, have emerged as powerful drug carriers for biomedical applications. A literature research suggests that NPs were among the most effective drug carriers for drug delivery. Integrating drugs into NPs shows great advantages compared to other nano-structures1.

NPs usually have a core-shell structure where the drugs are encapsulated inside. The loaded drug bioactivity can be preserved for weeks, leading to a scalable production2. Previous research has shown that NP size distributions can be controlled around 100nm, which make it capable for delivering drugs through blood capillaries and allow for access into cells. In addition, NPs can deliver drugs to targeted sites precisely by modifying NPs to synthesize polymers with specific ligands3. Due to NPs’ outstanding properties, NP-base drug delivery systems are effective and versatile.

Due to the widely adoption of NP-base drug delivery systems, study of its properties has aroused great research interests. Release profiles of encapsulated drugs are an important aspect of drug delivery systems Modelling the release processes mathematically has been being an active interdisciplinary research area.

Various factors affect release profiles of drug from NPs. Among those factors, pH value of the release matrix or environments, and solubility of the encapsulated drug are the most important4.

pH plays an important role in human body. Various diseases can alternate local lesion matrix of pH, in which PLGA NP release profiles change accordingly5. Results in literature reveal that pH-values of human organs are quite different. For example, the pH-value of a health lung is maintained at 7. But cystic fibrosis causes its pH decreasing to become acidic6. Normally, the pH-value of skin surfaces is in the range of 4.1–5.8 with small variations among different parts of human body. However, inflammatory and diseases with an involvement of the epidermis can break the skin antimicrobial barriers, leading to an increase in pH-value7. The pH-value of blood and interstitial fluid is in the range of 7.35–7.45. On the other hand, a highly acidic pH value 1–1.5 can be measured in an empty stomach7.

Modelling the processes of drug release from micro-/nanoparticles has been attracting researchers from various disciplines. In 2012, Siepmann summarized empirical/semi-empirical governing equations for various NP-based drug delivery systems8. But these mathematical models described release profiles under idealized circumstances and postulations, which limited their predictability.

Recently, machine learning (ML) has become a power research tool for a wide range of scientific and engineering problems9,10 ML algorithms can handle and analyze complicated datasets and identify linear and nonlinear relationships among variables accurately and effectively10. These include the classical algorithms like linear regression and principal component analysis (PCA) and recent more advanced algorithms such as Gaussian regression process (GPR), and artificial neural networks (ANNs)9,11,12.

Compared to machine learning, the existing works on mathematical modelling of drug release based on analytical, semi-analytical, or numerical methods assume idealized conditions8 such as homogeneous matrices, perfect sink conditions, constant diffusion coefficients, degradation dynamics being neglected, and so on. The resulted models often lack predicability for further experiments and/or complicated release behaviors due to more sophisticated release mechanisms.

As a new research paradigm, machine learning provides an inexpensive and environment-friendly approach for conducting certain types of research, e.g., drug release, which previously relies on tedious and error-prone experiments13. Once a machine learning model is established, it can be readily used with various parameter values.

Since ML algorithms are data driven, idealized assumptions are not necessary. ML can potentially address limitations of the traditional mathematical models in leveraging large datasets to advanced algorithms, and leads to development of accurate and adaptive models. In addition, ML models can be updated to improve their accuracy and adaptivity once new data sets are acquired. This approach helps avoid conducting repeated experiments and saves a lot of manpower and resources.

Mechanisms for drug release from PLGA micro-/nanoparticles have been widely studied. The following four release mechanisms have been well recognized when drugs are encapsulated within PLGA nanoparticles14,15,16.

  1. (1)

    Diffusion through polymeric shells, which usually governs the early stage of release;

  2. (2)

    Convection through pores on the shells;

  3. (3)

    Osmotic Pumping: Caused by the drug concentration gradient;

  4. (4)

    Degradation: As the particles degrade in the late stage.

As for medical applications of drugs encapsulated in PLGA particles, minimum bactericidal concentration (MBC) is one of our major concerns, when applying antibiotics for bacterial infection control. MBC is the minimum concentrations of antibiotics that is bactericidal17. In addition, existing research works have shown that most MPs/NPs experienced a burst at the early stage. Therefore, quantification of the burst release profiles and determination of effects of pH-value and drug solubility becomes critical for MP/NP-based drug delivery systems because neither underdose nor overdose can control bacterial infections, without mentioning local side effects.

The goals of this paper lied on applying ML algorithms integrating with in vitro experimental results to study effects of pH and drug solubility on NP-based drug delivery system release profiles. While a variety of approaches have been conducted to study release profiles from different perspectives, this paper applied ML algorithms to reveal the relationships among pH, drug solubility, and release rates. Our objectives were establishing cognitive mathematical models, and aided by the powerful ML algorithms to generalize computational results for various circumstances. In summary, the paper focuses lies on

  1. (1)

    Study factors like pH-value of release environment/matrix, particle size, drug molecular weight, and drug solubility that affect drug release profiles;

  2. (2)

    Apply machine learning algorithms to the release data collected from literature; The data are collected from results of in vitro experiments on a variety of drugs in various conditions reported by various authors; These include data items on the release amount percentage, pH-values of the environment/matrix, particle size, drug solubility, and drug molecular weight;

  3. (3)

    Conduct our in vitro experiments with various drugs and conditions with the results of machine learning as guidelines for experiment design; Characterize release profiles;

  4. (4)

    Compare results of our new in vitro experiments with that from machine learning algorithms to check potential agreement.

The novelty of our approach lies in a synergistic combination of two research paradigms: in vitro experiments and machine learning, both are utilized for study of drug release from PLGA particles.

Machine learning algorithms

In this section, we briefly review four main algorithms for machine learning: linear regression, principal component analysis, Gaussian process regression (GPR), and artificial neural networks (ANNs). See Fig. 1 for an illustration.

Fig. 1
figure 1

Task modules of machine learning for study of drug release from PLGA particles. Data was collected from over 50 literature. Linear regression, principle component analysis, Gaussian process regression, and artificial neural networks are utilized to analyze data.

Full size image

Linear regression

Linear regression is a simple but widely used supervised machine learning model that provides a linear model for correlation among a dependent variable and one or more explanatory variables.

Mathematically, linear regression can be expressed as

$$\begin{aligned} \displaystyle y = X \beta + \epsilon , \end{aligned}$$
(1)

where \(\beta\) (as a vector) represents the coefficients that quantify the influence of each independent variable (a component of X), and \(\epsilon\) is the error term. In practical use, \(\beta\) can be approximated by \(\displaystyle {\widehat{\beta }} = (X^T X)^{-1} (X^T y)\), using the ordinary least squares (OLS).

For linear regression, Python provides has an OLS class in statsmodels.api.

Principal component analysis (PCA)

Principal component analysis (PCA) is a classical unsupervised learning method that uses patterns present in a data set to reduce the complexity of the data while retaining the most important information.

Mathematically, PCA utilizes the eigenvalues and eigenvectors of the covariance matrix of a given set of data. Let X be a data matrix with m rows (observations) and n columns (features or variables). Assume matrix X is already standardized. Then the covariance matrix C is given by

$$\begin{aligned} \displaystyle C = \frac{1}{n-1} X^{T}X. \end{aligned}$$
(2)

It is known that C is a symmetric positive semi-definite (SPD) matrix. Let \((\lambda _{i}, \textbf{v}_i), 1 \le i \le n\) be the eigenvalues and eigenvectors of C with all eigenvalues arranged in the descending order.

If V is the matrix whose columns are the eigenvectors of C, then \(\textbf{x}V\) are the Principal Components(PCs), where \(\textbf{x} = [x_{1},\ldots x_{n}]\). \(S = XV\) is the score matrix. The entries of loading matrix V represents the contribution of each original variable to the principal components, i.e.,\(v_{ij}\) stands for how much i-th feature contributes to j-th principal component.

In Python, principal component analysis is implemented using ’sklearn.decomposition,PCA’. One way to visualize PCA result is using biplot. Biplot can be seen as a combination of PC score plot and loading plot. To be seen in a 2d graph, we keep only PC1 and PC2 for example. These two PCs will be the two axis of the plot, and the vectors of features from loading matrix V are projected onto these two axis. The projected values on each PC show the influence of the original variables, and the angles between vectors show how much they correlate with each other.

Gaussian process regression (GPR)

GPR is a supervised learning technique and a non-parametric method. It is employed to handle relatively smaller datasets, providing a probabilistic output, while capturing complexities, e.g., highly nonlinearity in the data. There are some choices for the kernel function in GPR. A radial basis function (RBF) as shown below is a common choice.

$$\begin{aligned} \displaystyle k(x, x') = \exp \left( -\frac{(x - x')^2}{2\ell ^2} \right) , \end{aligned}$$
(3)

where \(\ell\) is a length scale parameter. The predictive mean function is given by

$$\begin{aligned} \displaystyle \mu (x^{*}) = k(x^*, X) \left( K(X, X) + \sigma ^2_n I \right) ^{-1} y, \quad {\text{ with } \;\; I \;\; \text{ being } \text{ the } \text{ identity } \text{ matrix }.} \end{aligned}$$
(4)

Among the popular Python packages, scikit-learn contains GaussianProcessRegressor as a GPR implementation, with common kernels like RBF, Matern, WhiteKernel, and RationalQuadratic (RQ). Matern is more flexible when smoothness of the function can vary. WhiteKernel is applied to (white) noisy data. RQ can be seen as a scale mixture of RBF.

Artificial neural networks (ANNs)

ANNs is another desired tool for data analysis18. For our study of drug release from PLGA particles, an ANN was employed to examine correlation between drug release profiles and pH-value of release matrix/environment, drug solubility, drug molecular weight, and particle size. Figure 2 shows a flow chart of this ANN with all inputs and the aimed output. There are four inputs and one output along with one hidden layer where the factors are drug solubility, drug molecular weight, release matrix pH-value, and particle size distribution.

For our study, data splitting is as follows. 70% of data is used for training, 15% for validation, and 15% for testing.

For an ANN model, the mean absolute error (MAE)19 and root mean square error (RMSE)20 are important metrics. Consider \(y_i (1 \le i \le n)\) as data for test and \({\hat{y}}_i (1 \le i \le n)\) as the values predicted by the ANN model. Then

$$\begin{aligned} \displaystyle MAE = \frac{1}{n} \sum _{i=1}^{n} |y_{i}-{\hat{y}}_{i}|, \quad \quad RMSE = \sqrt{\frac{1}{n} \sum _{i=1}^{n} (y_{i}-{\hat{y}}_{i})^2}. \end{aligned}$$
(5)

Data normalization helps, in which each feature is normalized so that the mean is 0 and the standard deviation is 1. Based on this, we use the normalized RMSE also.

Fig. 2
figure 2

An artificial neural network (ANN) with 1 hidden layer and 10 neurons designed for study of drug release from PLGA micor-/nano-particles.

Full size image

In vitro experiments (protocols and procedures)

Materials used in in vitro experiments

Poly (D, L-lactide-co-glycolic acid) (PLGA, lactide: glycolic 75:25, Mw 4000 15,000, Sigma-Aldrich) and polyvinyl alcohol (PVA, 99+%, Mw 89,000 98,000, Sigma-Aldrich) were used for PLGA NP/MP synthesis. Gentamicin (99+%, Sigma-Aldrich) and Penicillin (99+%, Sigma-Aldrich) were used as the encapsulated drugs. Deionized water (Fisher Scientific) and Dichloromethane (DCM. Mw 84.93, 99.8%, Sigma-Aldrich) were used to dissolve PLGA for NP synthesis. Buffer solutions with pH at 4, 7 10 (Reagecon, #1040525CTT, #1070525CTT, and #1100525CTT) were used for study of release profiles.

Methods for synthesis of PLGA MPs/NPs

PLGA NPs/MPs were synthesized via a double emulsion solvent evaporation method derived from2 100 mg PLGA powder dissolved in 4 ml dichloromethane (DCM) was mixed with 45 mg gentamicin in 0.5 ml water to yield a primary solution that was mixed with 75\(\mu\) L, 750\(\mu\)L, 7.5ml of 9% PVA, respectively, to get three different droplet dispersed solutions. Those solutions were sonicated at 35% amplitude for 20 minutes via a sonic dismembrator (\(\hbox {Fisherbrand}^{TM}\)) Model 505 and the obtained dispersion solutions were titrated into 50ml 3% PVA solution resulting into opaque solutions. PLGA NPs/MPs precipitated after 8-h solvent evaporation. Penicillin encapsulated PLGA NPs were synthesis with the same procedure.

Characterizations for PLGA particles

PLGA MPs/NPs size distributions were measured via the dynamic light scattering (DLS, Malvern Zetasizer Nano ZS). A comprehensive size distribution profile was derived from the collective data obtained from the DLS measurements for each PLGA MP/NP solution. PLGA MP/NP morphology exploration utilized scanning electron microscopy (SEM, JEOL JSM-6500F field emission scanning electron microscope). Drug release profiles were determined with an ultraviolet-visible spectroscopy (UV–Vis, Agilent Cary 4000). Gentamicin loaded PLGA particle release profiles were representative by the accumulative release percentage at 5 discretized time points with the drug detection wavelength at 220 nm21. A batch of PLGA NPs was well distributed into 5 test tubes at pH of 4, 7 and 10 respectively with 3 ml particle-solution for each tube. Time intervals for the release measurements were 0 h, 0.5 h, 1 h, 1.5 h, and 2 h. The experiments were conducted multiple times for gentamicin encapsulated PLGA particles with size of 800 nm, 2\(\mu\)m, and 3\(\mu\)m at different pH release conditions. Release profiles of penicillin were determined via the same procedure with the drug detection wavelength at 324 nm22.

Machine learning results and discussion

Our data are collected from literature with 97 observations. See Table 1 for a brief summary. We focus on five features: the accumulative released amount percentage of the drug, drug solubility, drug molecular weight, PLGA particle size, and pH-value of the environment or matrix.

Table 1 Summary of literature for data collection (More details can be found in the Appendix).
Full size table

Linear regression

Fig. 3
figure 3

Results by linear regression. Linear correlation cannot be established between the released amount (percentage) and other factors.

Full size image

The first step for our study of drug release from PLGA particles is to filter out parameters that can affect the release profiles. Linear regression was employed to establish roughly the correlation among release rates, release matrix pH-value, temperature, particle size distribution, drug solubility, and molecular weight. As shown in Fig. 3.

However, the results in Fig. 3 showed that most data items were highly condensed in partial areas and the correlation could be nonlinear. Therefore, more advanced machine learning models need to be explored.

Principal component analysis (PCA)

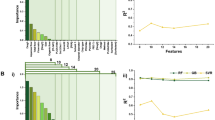
Among several factors relevant to drug release from PLGA particles, the released amount percentage, pH-value, drug solubility (mg/ml), drug molecule weight (g/mol), and particle size are important. These are treated as five features in the data we collected from literature. PCA is used to this data set (97 by 5) to identify the most important component (PC1, PC2).

Fig. 4
figure 4

Results of PCA (biplot): Five original features (release amount %, solubilty, molecular weigh (Mw), pH value, NP size) are projected onto the plane spanned by (PC1,PC2); PC scores are plotted as blue points.

Full size image

As shown in the Fig. 4, PCA results imply that pH-value is likely to have negative correlation with release, since it has the strongest positive loading on PC1 whereas the released amount percentage has a strong negative loading. Similarly, particle size and the released amount percentage might be negatively correlated also. Moreover, strong influence of pH-value on PC1 suggests that it significantly affects the properties being studied.

In summary, PCA reveals correlation among the five features, but is insufficient to reveal all important patterns in the dataset. Among these features, PC1 and PC2 could explain only about 48% of the variance. Other machine learning methods need to be explored for this topic on drug release.

Gaussian process regression (GPR)

For our study of drug release from PLGA particles, release matrix pH-value, drug solubility, and MP/NP size distribution were the three most important factors to be investigated. GPR was adopted to explore those three parameters in detail.

GPR is adopted to study release behaviors of particle-based drug delivery because of considerations in several aspects. Firstly, as a nonparametric method, GPR is good at dealing with low-dimensional and/or small datasets due to the characteristics of Gaussian processes and certain flexibility in choosing kernel functions. Secondly, GPR is capable of identifying highly nonlinear relationships even though a dataset may be small. Thirdly, GPR can handle uncertainty among data via calculations of confidence areas. The resulted models can be updated once new data become accessible, since GPR is a Bayesian method.

In the regression process, all the data were regrouped using the clustering method known as K-Nearest Neighbors (KNN). The processed data were sent to GPR resulting in 1-dim and 2-dim Gaussian distributions.

A dual-kernel, i.e., a linear combination of RBF and RQ, was adopted to predict effects of pH-values on release profiles. One kernel with a small length scale \(\ell\) enhancing the model responsiveness to rapid changes in data was combined with another kernel with a large initial length scale allowing it to capture broad and smooth trends across the dataset, resulting in a more nuanced understanding and predictions of dynamic processes governing drug release from PLGA MPs/NPs34,35. Therefore, this approach accommodate both localized variations and overarching trends within the data.

Since multiple factors have significant impacts on release profiles, it is essential to isolate pH-value from other parameters in order to gain a good understanding of the impact of pH-value. Figure 5(1) showed results for all drugs in a wide range of pH-values. We also studied release of doxorubicin (DOX) from PLGA particles with different pH-values. Figure 5(2) showed a clear parabolic shape with respect to the pH-value. In other words, the drug release rate was obviously higher in the more acid or alkaline release environment.

While most small molecule drugs have a molecular weight in the range 100–500 (Dalton or g/mol), Fig. 5(3) shows a pattern of better release efficiency for those in the range 120–200. This somehow suggests that the small molecule drugs are indeed what we should pursue, in terms of release efficiency.

The MSE and R-squared for doxorubicin only are 0.00007 and 0.61, respectively. Even though the R-squared was a bit larger, the MSE was considered as a significantly small number, and the models were still reasonable.

Fig. 5
figure 5

Results by GPR on effect of pH-values, molecular weight, and particle size. (1) Effect of pH-value 1–10 for all drugs; Release enhanced as pH-value is decreased. (2) Release of a single drug doxycycline (DOX); A clear parabolic shape reveals more acid or alkaline environment helps release. (3) Effect of molecular weight on release: Those in the range of 120–200 show a pattern of better release efficiency. (4) Effect of particle size (actually the reciprocal), release enhanced as the surface-to-volume ratio increases.

Full size image

As shown in Fig. 5(4), the release were more efficient than those with a larger size. This can also be explained mathematically. For a sphere with radius of r, the volume, surface area, and surface-to-volume ratio are, respectively,

$$\begin{aligned} \displaystyle Vol = \frac{4}{3} \pi r^3, \qquad Surf = 4 \pi r^2, \qquad R = \frac{Surf}{Vol} = \frac{4\pi r^2}{\frac{4}{3} \pi r^3} = \frac{3}{r} \end{aligned}$$
(6)

So, the smaller the particle size, the larger the surface-to-volume ratio, the more efficient release from a porous spherical shell.

Here are details of the findings from Gaussian Process Regression.

  1. (1)

    Acidic release environment favored drug release from particles. As pH-value decreased, the release efficiency increased.

  2. (2)

    When the pH-value increased from acid to alkaline in the comprehensive region, the release rates decreased.

  3. (3)

    Acidic or alkaline release environment benefited doxorubicin (DOX) released from PLGA particles, and the minimum release rates occurred at neutral pH-value.

Although GPR is applicable to small datasets, models developed from GPR do have limitations in handling data involving highly complex biological systems, in which local tissue pH values, enzyme levels, inflammatory responses vary. Such variations may lead to uncertainty beyond model capacity. In these scenarios, ML models struggle to capture complexity without using large and detailed datasets. However, high-quality biological data is often difficult to obtain, due to the invasive nature of sample collection, even sophisticated models such as deep nets may fail to generalize when unseen or rare biological conditions are involved.

Artificial neural networks (ANNs)

Figure 6 presented our artificial neural network results, in which factors of release matrix pH, drug solubility, MP/NP average size, and molecular weight against release rates were taken into consideration resulting into a 4-dimension error histogram. According to the Fig. 6, most data falling into the areas closed to the zero errors line indicating the artificial neural network model successfully predicted release rates under the effects of various factors. In addition, the error distribution was well normalized demonstrating the model was convincible and reliable. There was couple of data points having large errors which was attributed to the limited database, but the artificial neural network accuracy can be improved once more data become accessible36.

For the raw data we collected, 70% of data is used for training, 15% for validation, and 15% for testing. The corresponding MAE is 0.289797, RMSE 0.327767, Normalized RMSE 0.712538. These metrics support the reliability and efficiency of this ANN model.

Fig. 6
figure 6

Results by a 4-dim ANN: Histogram of prediction error. Most data fell into the area close to the zero-error vertical line indicating the ANN model able to predict release profiles with high accuracy.

Full size image

As one way of integrating machine learning algorithms with in vitro experiments, we conducted experiments on encapsulating penicillin (PCN) or gentamicin (GEN) into PLGA particles with average size at 3\(\mu\)m, 2\(\mu\)m, and 800 nm, respectively. Drug release was conducted at pH-value 4, 7, 10, respectively.

The loss for training was close to zero, and the cross validation loss was less than 0.1. The trained ANN model was applied to the dataset of 18 terms from real experiments.

The solubility for PCN and GEN are both 50 (mg/ml), their molecular weights are 356.37 and 477.60 (g/mol), respectively. Then the ANN model was applied to this set of 18 data items. The obtained results show that for the release amount percentage, the MAE is 0.112687 and RMSE is 0.132647. The normalized RMSE is 0.288364, which is less than 0.5 and considered to be good. Especially for GEN, the result was even better, since that feature was generally well-learnt during the training.

For more details of the release profiles from these experiments, see Section “Release Profiles of Drug from PLGA MPs/NPs” (Figs. 8 and 9).

In the neural networks, measurements of uncertainty were not provided, since no standard deviation was computed explicitly. In order to obtain confidence intervals/areas as shown in GPR, Monte Carlo dropout can be a feasible way to fulfill the expectation37. However, it was difficult to plot the errors as a 4-dimensional error histogram when multiple parameters were involved. Further study needs to be conducted to find out the ANN confidence areas.

In our current work, data were retrieved from publications with a main focus on development of particle-based drug delivery systems for human beings. Thus, temperature was well controlled around \(37^\circ\)C. In addition, antibiotics molecular weight and particle size (factors in the ANN model) further complicate with skewed pH values. Although the molecular weight parameter and its interaction with other factors have have potentially effects on release behaviors, they are hard to be isolated for further exploration. This topic will be addressed in our future work.

In summary, four major findings from for machine learning can be concluded as follows.

  • (1) An acidic or alkaline release matrix/environment may accelerate drug release;

  • (2) A higher solubility resulted in a higher release rate;

  • (3) An increase in the surface-volume ratio leads to an increase in the release rate;

  • (4) Particles synthesized with a smaller molecular weight tend to have a smaller size, leading to an increase in release efficiency.

In vitro experimental results and discussion

Morphology and size distribution of PLGA MPs/NPs

PLGA MPs/NPs were spherical shapes with pores all over the surface, and particles had a core-shell structure where the drugs were encapsulated within the core as shown in Fig. 7. When PLGA MPs/NPs were precipitated from the droplet dispersion solution, the water within the particle diffused through the particle shell causing the formulation of the porous structures, and those pores were benefit for the encapsulated drug release. When the volume of the second aqueous phase was fixed, penicillin loaded PLGA MPs/NPs had a smaller size distributions compared to those of gentamicin loaded PLGA MPs/NPs, which may be caused by the variant in the molecular weight. According to the literature penicillin has a molecular weight of 334.39g/mol while gentamicin has a molecular weight of 1390.71g/mol. The results indicated that the encapsulated drug can affect antibiotics loaded PLGA MP/NP size distributions in which a higher molecular weight of drug lead to an increase in the resulting particle size distributions.

Fig. 7
figure 7

Morphology of PLGA particles. (1) An SEM image of particles with pores on surfaces. (2) Illustration of a spherical particle.

Full size image

Release profiles of drug from PLGA MPs/NPs

According to the literature, there are four widely accepted release mechanisms which are diffusion, convection, osmotic pumping, and degradation. One or multiple release mechanisms occur from time to time, but the release rates are determined by the denominated mechanisms. Commonly, a burst release occurs when particle start to delivery encapsulated drugs, which is mainly caused by the diffusion of drugs on the surface of particles.

Gentamicin loaded PLGA MPs/NPs were synthesized via a double emulsion solvent evaporation method reported by Sun et, al. The resulting MP/NP release profiles at pH of 4, 7, and 10 were measured via UV–Vis. The acquired accumulative release percentages at different time were plotted against time, and the resulting diagrams represented the antibiotics loaded PLGA MP/NP release profiles shown in Figs. 8 and  9.

Fig. 8
figure 8

In vitro experiments: Release of gentamicin (GEN) from PLGA particles. (1) 806.22 nm-NP release profiles for pH-value 4,7,10; (2) 1.96\(\mu\)m-MP profiles for pH-value 4,7,10; (3) 3.02\(\mu\)m-MP profiles for pH-value 4,7,10; (4) Three different profiles at pH-value 4,7,10.

Full size image

In Figs. 8 and  9, the release profiles presented a linear relations at the first 1.5 h and 2 h, which indicated a burst release caused by the diffusion. Commonly, the burst effect caused by the diffusion of gentamicin and penicillin on the MP/NP surface. Once the MPs//NPs were embedded in the buffer solution to release, the antibiotics on the surface can be released immediately into the outer matrix. Each batch of MP/NP had an higher average release rate under an alkaline release environment because the alkaline release environment can accelerate the hydrolysis of ester bonds in PLGA. Since antibiotics can be easily released from degraded MPs/NPs, the higher degree of degradation of MPs/NPs lead to an increasing release rates. At pH of 7, no more than 30\(\%\) of antibiotics can be released at every batch. Compared to those acidic or alkaline release surroundings, neutral release matrix has the least impacts on release profile, which may be attributed to the tiny solubility of PLGA in water. Because of PLGA can barely be dissolved in water, PLGA MP/NP degradation processes were slowed down leading to an extent in drug release profiles.

In addition, Fig. 8(4) showed that MP/NP size distributions can affect release profiles. Those NPs with an average size of 800 nm had can release more antibiotics during the first 2 h. With the an increase in MP/NP dimension, a decrease in release rates can be observed. According to literature, size distributions can affect MP/NP release profiles due to the surface-to-volume ratios. The surface-to-volume ratios reveal the factor of relative surface areas, and a large relative surface enables a wide diffusion panel for drug diffusion resulting into an increase in diffusion flux.

The ML major findings on factors affecting drug release were integrated into in vitro experiment design and validated by experiment results. In particular, penicillin-incorporated PLGA MPs/NPs were synthesized via the same procedure to achieve designed release behaviors, as shown in Fig. 9. To reduce the release rates, increasing the particle average size is a feasible way, as shown in Fig. 9(2) and (3). Those MPs/NPs had more active release behaviors as expected, see Fig. 9(3). In addition, penicillin-loaded PLGA MPs/NPs had average release rates higher than those of gentamicin-loaded PLGA MP/NPs, as shown in Fig. 8. This was attributed to the smaller molecular weight of penicillin and hence smaller particles, compared to the gentamicin-loaded PLGA MPs/NPs. This agrees with the 4th statement in the findings stated above.

Fig. 9
figure 9

In vitro experiments: Release of penicillin (PEN) from PLGA particles. (1) 806.22 nm-NP release profiles for pH-value 4,7,10; (2) 1.96\(\mu\)m-MP profiles for pH-value 4,7,10; (3) 3.02\(\mu\)m-MP profiles for pH-value 4,7,10; (4) Three different profiles at pH-value 4,7,10.

Full size image

Conclusion

This paper presents a novel approach for study of drug release from PLGA particles that combines the traditional paradigm in vitro experiments and the recent new paradigm machine learning.

First, in vitro experimental data about drug release from PLGA particles reported in about  50 research papers were collected. Data collection was focused on released amount percentage, pH-value of release matrix or environment, drug solubility, drug molecular weight, and particle size. Such a data set is analyzed by linear regression, PCA, GPR, and ANN, respectively.

The learnt results obtained from the machine learning algorithms were used as guidelines for designing our own in vitro experiments. It is interesting to notice that the results of release profiles from these experiments agree well with that by machine learning algorithms.

Our findings indicated that ML did advance our understanding of drug release profiles, especially, for drug-incorporated MPs/NPs synthesized with different drugs, particle sizes, and release matrix pH values. Therefore, applying ML to examine drug release behaviors can help optimize MPs/NPs-based drug delivery systems when these systems are adopted in controlling of bacterial infection or similar applications.

As our work was progressing, we noticed that a recent paper38 published in this journal (Scientific Reports) elaborated on a similar topic from a different perspective. Another recent publication39 provided further insights on application of AI/ML for optimizing drug release profiles.

Finally, we want to point out that the machine learning problem presented in this paper is nontrivial. There is not much raw data on drug release from PLGA particles available in the literature. The raw data we collected from literature is heterogeneous (different types of drugs with various solubility, viscosity of PLGA, etc.). The data is also skewed, as the pH values are mostly around 7.4, which is close to that of human bodies. As such, Gaussian Process Regression still generated some useful results about the factors that affect drug release profiles. While machine learning cannot simply replace in vitro experiments yet, we will continue to develop more sophisticated machine learning models for drug release from PLGA particles.