Introduction

Sensors are essential in smart applications to detect stimuli such as mechanical, thermal, humidity, and optical. They can be used for health monitoring of the human body to prevent or diagnose disorders or diseases1,2. In recent years, the concept of manipulating structural geometry to create structures with a negative Poisson’s ratio, called auxetic, has been introduced3,4. Auxeticity has since emerged as a key feature in sensor fabrication technology, particularly for wearable sensors. Textiles, being soft and flexible, provide an ideal platform for auxetic sensors, offering enhanced sensitivity and improved mechanical and physical properties5,6.

Auxetic textile structures, known for their negative Poisson’s ratio, expand laterally when stretched, offering enhanced energy absorption, improved shear resistance, and high breathability7. These structures are commonly fabricated using methods like spinning, weaving, knitting, and braiding, and they can take the form of fibers, yarns, fabrics, and composites for applications such as personal protective equipment, medical devices, and sportswear, due to their ability to conform to surfaces and absorb impacts8,9,10. For instance, Lim developed a semi-auxetic yarn by sewing a thin inextensible cord through a fat elastic cord in a triangular pattern, creating a simplified model to describe the Poisson’s ratio in both conventional and auxetic planes. The study revealed that the Poisson’s ratio in the auxetic plane decreases with the initial half angle of the thin cord and increases with the Poisson’s ratio of the fat cord, while in the conventional plane, the Poisson’s ratio increases with both parameters, achieving a maximum positive Poisson’s ratio of 0.906 in the conventional plane and −4.82 in the auxetic plane11. Piezoresistivity, an electromechanical property where materials change resistivity in response to mechanical stimulation12, has been exploited in textile sensors fabricated using methods such as electrospinning, wet spinning, thermal drawing, melt extrusion, and coating. Electrospinning produces nanofibers with high surface area for enhanced sensitivity, wet spinning creates porous or hollow fibers via gelation control, and thermal drawing and melt extrusion enable scalable filament production. Coating methods, like dip or spray coating, deposit conductive materials onto fiber surfaces to enhance electrical properties13,14. Zhang et al. developed a silver-polymer framework (SPF) combining polyacrylonitrile (PAN) with in situ reduced silver nanoparticles, achieving high stretchability (up to 1200%), conductivity (0.076 S/m), and tensile strength (0.76 MPa), enabling applications in artificial muscles and human–machine interfaces15. The study also introduced innovative spinning techniques, such as NVIPS and PSEA, achieving over 500% stretchability, tensile strengths above 6 MPa, and conductivity of 1.82 S/m, providing sustainable solutions for wearable electronics16,17. Li et al. fabricated a wearable sensor array using graphene, polyaniline, Sb-doped SnO₂, and WO₃, with machine learning enhancing NH₃ and NO₂ detection in mining environments, achieving over 99% accuracy through a wireless bracelet for real-time monitoring18. Tian et al. developed a 3D all-fabric piezoresistive sensor using multi-wall carbon nanotubes (MWCNTs) coated on polyethylene/polypropylene (PE/PP) bicomponent nonwovens via a binder-free, in-situ welding method. The sensor exhibited high sensitivity (9.43% kPa⁻1 for 0–10 kPa and 0.076% kPa⁻1 for 20–120 kPa), a wide sensing range (0–120 kPa), and rapid response times (100 ms and 60 ms), enabling real-time monitoring of pulse, cough, and joint movements. This low-cost, scalable fabrication method created a breathable, durable sensor suitable for wearable applications, though the Poisson’s ratio was not directly relevant to this study19.

Numerous studies have focused on the fabrication of auxetic textile sensors, exploring innovative methods and applications. Wu et al.20 developed a full-fiber auxetic-interlaced yarn sensor (AIYS) using conductive silver-coated PA (polyamide) yarns and polyurethane (PU) yarns through a continuous, mass-producible computerized yarn-wrapping spinning technology. They used this method to create a sign-language translation glove with 16 AIYS sensors to detect finger joint movements. The AIYS exhibited a negative Poisson’s ratio of −1.5, robust mechanical properties, and rapid response times of 0.025 s, demonstrating its potential for real-time sign-language translation with 99.8% communication accuracy between signers and non-signers. Similarly, Zhang et al.21 fabricated braided auxetic yarn sensors (BAYs) using PU and PA coated with silver layers through a high-speed braiding method. The BAY sensors displayed pronounced auxetic behavior with a negative Poisson’s ratio exceeding −3, as well as excellent shape adaptability, structural stability, and high sensitivity, with a response time of 149.9 ms. These characteristics make BAY sensors highly promising for wearable electronics, particularly in monitoring significant human motions like joint and muscle movements.

Extensive research has focused on developing auxetic textiles for various applications. Although integrating auxetic properties into textile sensors is promising, research in this field remains limited. Furthermore, studying the electromechanical behavior of auxetic textile sensors is crucial to fully understand their potential and broaden their applications. This work aims to advance research in this area by proposing a new auxetic textile sensor. The proposed sensor’s structure draws inspiration from semi-auxetic yarn11. Entirely textile-based, the sensor provides both stretchability and flexibility. To evaluate its performance, an electromechanical model was developed.

Experimental section

Materials

A conductive nonwoven fabric (EeonTex Conductive Fabric) made of polyester/nylon 6 (70:30), with a basis weight of 170 gsm, a thickness of 0.80 mm, and a surface conductivity of 52 Ω/m2, was sourced from Core Electronics. A high-tenacity polyester monofilament yarn (linear density of 60 Tex) was used as the stitching yarn, while a metallic tack button (silvery press button) with a diameter of 1.5 cm and conductivity of 1.28 MS/m served as the electrode; both were obtained from the marketplace. An elastic band measuring 4 cm in width and 0.2 cm in thickness was purchased from Amazon. The distance between stitching points was varied from 2 to 3 cm to study its effect on the gauge factor of the semi-auxetic piezoresistive textronic material.

Fabrication methodologies

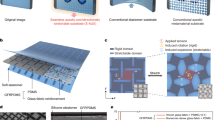
To fabricate the semi-auxetic piezoresistive textronic structure, the conductive nonwoven fabric was cut into 2.5 × 2.5 cm2 pieces and sandwiched between metallic tack buttons, as shown in Fig. 1a. Wires were soldered to the metallic tack buttons, and the sensors were stitched onto an elastic band using polyester monofilament yarn, as illustrated in Fig. 1b. To ensure secure attachment and prevent sensor malfunctions, heat-activated adhesion was applied using a heating gun. Four sensors were installed on each sample and connected in a series–parallel configuration for testing, as depicted in Fig. 1c.

Fig. 1
figure 1

(a) Schematic illustration of the piezoresistive sensor composed of conductive nonwoven fabric and metallic tack buttons, (b) schematic representation of the semi-auxetic piezoresistive textronic structure, and (c) configuration of the sensor connection arrangement.

Full size image

Characterization methodologies

An electromechanical analysis, illustrated in Fig. 2a, was performed using a digital multimeter (OWON) under quasi-static uniaxial tensile loading with elongation rates ranging from 50 to 150 mm/min. The gauge factor was calculated using Eq. (1)22.

Fig. 2
figure 2

(a) Electromechanical measurement setup and (b) tensile and Poisson’s ratio assessment of the semi-auxetic piezoresistive textronic, where the critical strain refers to the strain at which the maximum negative Poisson’s ratio is observed.

Full size image
$$Guage factor=\frac{\Delta R}{\varepsilon {R}_{0}}$$
(1)

Here, \(R\) and \(\varepsilon\) represent the resistance of the sample and the applied strain, respectively. The tensile and deformation behaviours of the samples in the thickness direction, as illustrated in Fig. 2b, were analyzed by capturing the transverse strain with a camera under quasi-static uniaxial tensile loading using an Instron 5566. The minimum Poisson’s ratio was determined using Eq. (2)23.

$${\nu }_{(i)}=\text{min}(-\frac{{T}_{\left(i\right)}-{T}_{\left(1\right)}}{{T}_{\left(i\right)}{\varepsilon }_{\left(i\right)}})$$
(2)

where \(T\) represents the thickness of the sample in the i-th image.

Results and discussion

Electromechanical behavior of semi-auxetic piezoresistive textronic

Figure 3a illustrates the tensile behaviour of the elastic band and stitching yarn. Although both components exhibit the same rupture strain, the stitching yarn undergoes plastic deformation. The stress–strain curve for the polyester monofilament (stitching yarn) displays three distinct regions: an elastic phase where the material returns to its original shape after stress, a yield point, and a plastic deformation phase where permanent stretching occurs. As the stress increases further, the material reaches its breaking point. Polyester’s moderate tensile strength and elasticity make it ideal for flexible and durable applications24. Figure 3b shows that increasing the stitching length results in a decrease in the gauge factor (GF), with the highest GF value of −4.80 achieved at a stitching length of 2 cm. Additionally, a linear electromechanical response, ideal for strain sensor applications, was observed. Figure 3c demonstrates that a reduction in Poisson’s ratio to negative values correlates with a decrease in the GF, highlighting a trade-off between auxeticity and the GF of the sensor. The sensor achieved a response time of 64 ms, reaching 80% of the peak response (Tp), as shown in Fig. 3d. The post-peak signal reduction in piezoresistive sensors is primarily attributed to stress relaxation, hysteresis, and time-dependent recovery of conductive pathways within the material, along with contributions from viscoelastic properties, material fatigue, and minor interface losses. These effects collectively reflect the nonlinear recovery dynamics typical of piezoresistive materials25.

Fig. 3
figure 3

(a) Tensile behaviour of components, (b) electromechanical performance of the developed semi-auxetic piezoresistive sensor, (c) relationship between Poisson’s ratio and gauge factor, (d) response time analysis, (e) cyclic test under varying strain with a constant strain rate, (f) cyclic test under varying strain rates with constant strain, (g) stability test over 1000 cycles.

Full size image

The electromechanical behaviour of the sensor was further analyzed under varying strains (0.15 to 0.2) at a constant strain rate, revealing that increased strain results in a greater and stable relative change in resistance (Fig. 3e). Under varying strain rates (0.1 to 0.025) at a constant strain, the sensor exhibited stability, with an increased number of peaks at higher strain rates (Fig. 3f). A stability test conducted over 1000 cycles under constant strain and strain rate showed a drift of only 0.02%, as depicted in Fig. 3g. Overall, the electromechanical analysis demonstrates the semi-auxetic piezoresistive sensor’s significant potential for health monitoring applications.

Electromechanical mechanism of semi-auxetic piezoresistive textronic

To elucidate the relationship between the piezoresistive mechanism and Poisson’s ratio in the proposed auxetic piezoresistive textronic structure, a theoretical model was developed. The model assumes that the stitching yarns behave as rigid materials, while the elastic band and sensor are deformable, complying with Hooke’s law and exhibiting a constant Poisson’s ratio.

Figure 4a presents a schematic illustration of the auxetic piezoresistive textronic structure. In this configuration, tensile loading causes the stitching yarns to straighten due to their mechanical dominance, as they possess a higher Young’s modulus compared to the elastic band. This induces tensile stress in the elastic band, which, in turn, subjects the sensors to compressive stress resulting from the transverse deformation of the elastic band. Thus, when the structure is under tensile loading, the auxetic deformation generates compressive stress on the sensor. Subsequently, the electromechanical and Poisson’s ratio models for the developed auxetic piezoresistive textronic structure will be derived based on its geometry and material properties.

Fig. 4
figure 4

(a) Schematic illustration of the auxetic piezoresistive textronic structure, (b) geometry of the unit cell under load-free and critical strain conditions, and (c) force components at critical strain.

Full size image

A unit cell of the structure is identified and illustrated in Fig. 4b, showing its geometry in two states: load-free and at critical strain. This structure is adapted from semi-auxetic yarn, termed “semi” because it exhibits auxeticity only in one plane (XZ). Critical strain is emphasized because the maximum negative Poisson’s ratio occurs at this specific strain. It refers to the point at which the unit cell’s length equals the length of the stitching yarn within the unit cell, signifying that the stitching yarn has become fully straightened. For modeling purposes, the indices eee, mmm, and sss are used to denote the elastic band, stitching yarn, and sensor, respectively, while the indices 000 and ccc represent the initial and critical states. At critical strain, the gauge factor (\({GF}_{c}\)) of the semi-auxetic piezoresistive textronic can generally be expressed as follows26.

$${GF}_{c}=\gamma {\left(\frac{\Delta R}{{R}_{0}}\right)}_{s}\frac{1}{{\varepsilon }_{c}}=\gamma {GF}_{s}\frac{{\varepsilon }_{s}}{{\varepsilon }_{c}}$$
(3)

where \(\gamma\) is an experimental constant, while the gauge factor of the sensor (\({GF}_{s}\)) and the critical strain of the semi-auxetic piezoresistive textronic (\({\varepsilon }_{c}\)) are input parameters. To calculate the strain applied to the piezoresistive sensor (\({\varepsilon }_{s}\)), Hooke’s law and the concept of engineering stress can be employed27.

$${\varepsilon }_{s}=\frac{{f}_{s}}{{E}_{s}{A}_{{s}_{0}}}$$
(4)

where \(E\), \(f\), and \(A\) represent Young’s modulus, force, and cross-sectional area, respectively. In this context, the Young’s modulus of the piezoresistive sensor (\({E}_{s}\)) and the initial cross-sectional area of the piezoresistive sensor (\({A}_{{s}_{0}}\)) are known parameters. Referring to Fig. 4c, there are two vectors of equal magnitude that result in the force \({f}_{s}\). Hence, the following expression can be derived:

$${f}_{s}=2{f}_{e}sin{\theta }_{e}$$
(5)

To calculate the angle (\({\theta }_{e}\)) between the elastic band and the central axis of the structure, we use the following equation:

$${\theta }_{e}={\mathit{tan}}^{-1}(\frac{2({T}_{e}/2+{{T}_{s}}_{0})}{\left({{L}_{e}}_{0}\left(1+{\varepsilon }_{c}\right)-{{L}_{s}}_{0}\right)})$$
(6)

where \(L\) and \(T\) represent the length and thickness, respectively. Based on this assumption, the critical strain (\({\varepsilon }_{c}\)) can be defined as follows27:

$${\varepsilon }_{c}=\frac{{{L}_{m}}_{0}-{{L}_{e}}_{0}}{{{L}_{e}}_{0}}$$
(7)

The initial length of the stitching yarn can be formulated as depicted in Fig. 4b, and is expressed as:

$${{L}_{m}}_{0}=2({{T}_{e}}_{0}/2+\sqrt{{({{L}_{e}}_{0}-{{L}_{s}}_{0})}^{2}/4+{{{T}_{s}}_{0}}^{2}})+{{L}_{s}}_{0}$$
(8)

Using the definition of Poisson’s ratio (\({\nu }_{e}\)) and the engineering strain for the elastic band, the relationship can be expressed as follows:

$${T}_{e}={{T}_{e}}_{0}(1-{\nu }_{e}\frac{{L}_{e}-{{L}_{e}}_{0}}{{{L}_{e}}_{0}})$$
(9)

To determine the length of the elastic band at critical strain, Eq. (8) can be expressed in terms of the geometry of the structure as follows:

$${L}_{e}={{L}_{s}}_{0}+2\sqrt{{\left({{L}_{e}}_{0}\left(1+{\varepsilon }_{c}\right)-{{L}_{s}}_{0}\right)}^{2}/4+{({T}_{e}/2+{{T}_{s}}_{0})}^{2}}$$
(10)

Now, the acting axial force can be estimated using the following equation:

$${f}_{e}={A}_{{e}_{0}}{E}_{e}{\varepsilon }_{e}={A}_{{e}_{0}}{E}_{e}\frac{{L}_{e}-{{L}_{e}}_{0}}{{{L}_{e}}_{0}}$$
(11)

Finally, to evaluate the Poisson’s ratio (\(\nu\)) of the structure, the following equation is used:

$$\nu =-\frac{T-{T}_{0}}{{T}_{0}{\varepsilon }_{c}}$$
(12)

where \(T\) represents the equivalent thickness of the structure. Based on the geometry, \(T\) can be expressed as:

$${T}_{0}=2({{T}_{e}}_{0}/2+{{T}_{s}}_{0})$$
(13)
$$T=2({T}_{e}+{{T}_{s}}_{0})$$
(14)

Using the proposed models, the Poisson’s ratio and the gauge factor of the semi-auxetic textronic material can be predicted at critical strain. To interpret the experimental results, the input values for these models were determined and are summarised in Table 1.

Table 1 Value of input parameters for theoretical study.
Full size table

The predicted and experimental values for both the gauge factor and Poisson’s ratio of the semi-auxetic textronic are presented in Fig. 5. The model effectively captures the overall trends of both parameters. However, discrepancies between the predicted and experimental values are observed, likely due to measurement errors and the inherent assumptions of the models. The results reveal that increasing the stitching length reduces the gauge factor while enhancing the negative Poisson’s ratio. This behaviour can be attributed to the decrease in the transverse force component with increased stitching length, leading to reduced stress applied to the sensor. Furthermore, the increase in stitching length results in a smaller critical strain at which transverse displacement occurs, thereby contributing to a more pronounced negative Poisson’s ratio. These findings highlight the need to optimise the gauge factor and auxeticity of the semi-auxetic piezoresistive textronic depending on the specific application, as a trade-off exists between these two properties.

Fig. 5
figure 5

Comparison between experimental and theoretical values for (a) the gauge factor and (b) the Poisson’s ratio of the semi-auxetic piezoresistive textronic.

Full size image

Potential applications of semi-auxetic piezoresistive textronic

Figure 6 illustrates potential applications for semi-auxetic piezoresistive textronics. The tunable auxeticity and gauge factor of these materials make them highly versatile for various applications. For instance, in yoga straps, stretchability is more critical than auxeticity, yet the gauge factor remains high due to increased transverse stress. Conversely, in vehicle safety belts, auxeticity plays a vital role in reducing injury during accidents, while a high gauge factor is less crucial. In compression bandages, a high gauge factor enhances precision in health monitoring, while improved auxeticity supports smart drug delivery. For maternity belts, both auxeticity and gauge factor are essential, as they enable precise health monitoring of the mother and fetus, stabilize the abdomen and lower back, and help distribute abdominal weight while balancing the center of gravity. Optimizing the balance between gauge factor and auxeticity is thus critical for tailoring these materials to specific applications.

Fig. 6
figure 6

A summary of potential applications of semi-auxetic piezoresistive textronic.

Full size image

It has been found that under uniaxial tensile loading conditions, a trade-off exists between auxeticity and sensitivity in semi-auxetic piezoresistive textronics. Nevertheless, in practical applications, this trade-off frequently leads to enhanced sensitivity due to the intensified contact pressure at the interface between the sensor and human skin. As a result, semi-auxetic piezoresistive textronics exhibit higher transverse stress (contact pressure) compared to sensors integrated with stretchable bands with positive Poisson’s ratio or fully stretchable sensors with positive Poisson’s ratio in similar applications. Overall, these sensors are distinguished by their high sensitivity and customisable deformation characteristics, allowing for modulation of clothing pressure.

Conclusion

In this study, a novel auxetic textile piezoresistive sensor, inspired by semi-auxetic yarn and designed in the form of a band, is presented. The structure demonstrates a negative Poisson’s ratio in the thickness direction, achieving a sensitivity of −4.8 and a negative Poisson’s ratio of −14.1. A mathematical model revealed an inverse relationship between auxeticity and sensitivity, underscoring the importance of tuning these variables to optimise the sensor’s design for specific applications. These include yoga straps, driving safety belts, compression bandages, and breathable pregnancy belly belts. By tailoring the auxetic properties and sensitivity, the sensor can be customised to enhance performance, comfort, and functionality across these diverse applications, ensuring an ideal balance between flexibility and responsiveness.