Introduction

Microtubules are crucial for key cellular processes, including cell division, morphogenesis, and intracellular transport. Structures like preprophase bands, centrosomes, spindle fibers, and phragmoplasts, which are made up of microtubules, are involved in cell division, while cortical microtubules play a role in morphogenesis.

In the current study, Ionic waves (IV) traveling through live cells' microtubules are a key biological and medical paradigm. Essentially, this model provides an accurate depiction of the feebly nonlinear shallow water wave system moving through the cells that make up human DNA and heredity. This concept was developed in refs1,2,3, they proposed that microwave energy spectra might be used by biological systems as a quantum-free source of energy in mono-phase events. This spectrum is caused by the referred semi-discrete proximity model, which describes how nonlinear dimer molecules of bimolecular dipole breathers travel along microtubules. In actuality, the cytoskeleton's empty protein polymers are what give rise to microtubules. The polymers are formed up of coupling series known as proto-filaments (PF) that are grouped in a circle to form a tube with a diameter of around 25 nm.

Moreover, the distance between avoidant parallel PF is much smaller for bonds than the distance between dimers inside PF.As a result, longitudinal waves propagating through PFs are caused by the longitudinal displacements of corresponding dimers within a single PF. The nonlinear structure of microtubules reveals that each dimer has just a single degree of freedom,\(N_{n}\), which indicates the dimer's longitudinal displacement at position \(n\).

Several academics developed techniques for determining exact solutions for fractional and non-fractional NLPDE, like unified solver method (USM)4 , Weierstrass elliptic function method (WEFM)4, generalized Kudryashov (GK) approach5, sine–Gordon expansion approach5, extended hyperbolic function (EHF) method6, extended sub-equation method (ESEM)7, improved (Υ′/Υ) expansion method8,9, expa function method9,10, new auxiliary equation method (NAEM)10, three-wave methods11,12, Kudryashov expansion method11,13, and other methods14,15,16,17,18,19,20,21,22,23,24,25,26,27,28.

In this paper the Paul-Painleve method (PPM)29 will be built in order to produce ODE of the NSIW that propagate along microtubules in living cells. Parallel to this, Auxiliary Equation Approach (AEA)30,31 and Sardar Sub Equation Approach (SSEA)32,33 have been used to construct the solutions for this model. These approaches have advantages that give many solutions compared to another method.

The rest of the paper has been arranged as follows: Sec. 2 “Forming the Problem” discusses of the modeling of the equation. Sec.3 “Extended Auxiliary Equation Approach (AEA)” provide a brief discussion of the AEA. Sec. 4 “New Solutions of Eq. (20) via (AEA)”. In Sec. 5 “Sardar Sub Equation Approach (SSEA) provides a mathematical analysis of the approach. Sec.6 “New solution of Eq. (20) by new extended (SSEA) approach”. Sec.7 provides a “Graphical depiction” of several analytical solutions. Finally, the calculations are summarized in the conclusion.

Forming the problem

In that follows34, consider the Laplace and Euler equations as defined as:

$$\Lambda_{xx} + \Lambda_{yy} = 0,0 < y < d + \delta , - \infty < x < \infty$$
(1)
$$\Lambda_{t} + \frac{1}{2}\left( {\kappa \Lambda_{y} + i\Lambda_{y} } \right)^{2} + f\delta = 0,y = d + \delta$$
(2)
$$\delta_{t} + \delta_{x} \Lambda_{x} - \Lambda_{y} = 0$$
(3)
$$\Lambda_{y} = 0,y = 0$$
(4)

Introduce

$$\nu = \frac{{\delta_{0} }}{d},\mu = \left( {\frac{d}{\rho }} \right)^{2} < 1$$
(5)

where \(\delta_{0}\) and \(\rho\) are represent the wave amplitude , the characteristic length-like wavelength respectively.

$$x = \frac{x}{\rho },y = \frac{y}{\rho },\chi = \frac{at}{\rho },\Xi = \frac{\delta }{{\delta_{0} }},\Omega = \frac{d}{{\delta_{0} \rho a}}\Lambda$$
(6)

As a result, we consider a comprehensive set of acceptable non-dimensional parameters:

where \(a = \sqrt {fd}\) and \(f\) are represent the shallow-water wave speed and the gravitational acceleration respectively.

$$\mu \Lambda_{xx} + \Lambda_{yy} = 0$$
(7)
$$\Omega_{\tau } + 0.5v\left( {\Omega_{x}^{2} + \Omega_{y}^{2} } \right) + {\rm E} = 0,y = 1 + v\Xi$$
(8)
$$\Xi_{\tau } + v\left( {\Xi_{x} \Omega_{\tau } } \right) - \frac{1}{\mu }\Omega_{y} = 0,y = 1 + v\Xi$$
(9)
$$\Lambda_{y} = 0,y = 0$$
(10)

Expand \(\Omega \left( {x,t} \right)\), admits

$$\Omega = \Omega_{0} + \mu \Omega_{1} + \mu^{2} \Omega_{2}$$
(11)

for \(s = \frac{\partial \Omega }{{\partial x}}\) and putting Eq. (11) into Eqs. (7–9) we obtain

$$\left( {\Omega_{0} } \right)_{\tau } - \frac{\mu }{2}s_{x\tau } + \Xi + \frac{{vs^{2} }}{2} = 0$$
(12)
$$\Xi_{\tau } + vs\Xi_{x} + \frac{1}{\mu }\left( {1 + v\Xi } \right)s_{x} = \frac{\mu }{6}s_{xxx}$$
(13)

By differencing Eq. (12) with regard to x and reorder Eq. (13) we have

$$s_{\tau } + vss_{x} + \Xi_{x} - \frac{\mu }{2}s_{xx\tau } = 0$$
(14)
$$\Xi_{\tau } + \left[ {s\left( {1 + v\Xi } \right)} \right]_{x} - \frac{\mu }{6}s_{xxx} = 0$$
(15)

Equation (11) become

$$r_{t} + rr_{x} + f\delta_{x} = \frac{1}{3}d^{2} s_{xxt}$$
(16)

To combine the displacement and velocity of water particles, we can utilize the function \(P(x,t)\) yield

$$r = \frac{1}{d}P_{t} ,\delta = - P_{x}$$
(17)

Which change the Eq. (16) to

$$P_{tt} - fdP_{xx} + \frac{1}{2d}\left( {P_{t}^{2} } \right)_{x} = \frac{1}{3}d^{2} P_{xxtt}$$
(18)

Substituting \(\varsigma = x - wt\) for traveling wave solutions with shifting coordinates in Eq. (18) yields

$$\left( {\eta^{2} - fd} \right)P_{\varsigma \varsigma } + \frac{{\eta^{2} }}{2d}\left( {P_{\varsigma }^{2} } \right)_{\varsigma } = \frac{1}{3}d^{2} \eta^{2} P_{\varsigma \varsigma \varsigma \varsigma }$$
(19)

By integrating Eq. (19) and placing \({\rm N} = P_{\varsigma }\) we get

$${\rm N}_{\varsigma \varsigma } - \Im_{0} {\rm N}^{2} - \Im_{1} {\rm N} - c = 0$$
(20)

Extended auxiliary equation approach (AEA)

In what follows30,31, the auxiliary equation approach is described in the following manner:

Procedure 1: Let’s utilize the transformation \(l\left( {x,y,t} \right) = {\rm N}\left( \varsigma \right)\),\(\varsigma = x + \psi_{1} y + \psi_{2} t\) to modify NLPDE

$$Z\left( {l,l_{x} ,l_{y} ,l_{z} ,l_{xx} l_{xy} ,......} \right) = 0$$
(21)

Into ODE:

$$L\left( {l,l^{\prime},l^{\prime\prime},l^{\prime\prime\prime},......} \right) = 0$$
(22)

Procedure 2: Suppose that the solution of Eq. (22) as

$$l\left( \varsigma \right) = b_{0} + b_{1} \Pi \left( \varsigma \right) + ... + b_{n} \Pi^{n} \left( \varsigma \right)$$
(23)

where \(b_{i}\) and are real constants, such that \(0 \le i \le n\).

Procedure 3: Using the homogeneous balancing basic terms, determine the balancing number \(n\) between the highest order derivative and the highest order nonlinear term in Eq. (22), and \(\Pi \left( \varsigma \right)\) indicate the solutions of ODE:

$$\left( {\frac{d\Pi }{{d\varsigma }}} \right)^{2} = k_{0} \Pi^{2} \left( \varsigma \right) + k_{1} \Pi^{3} \left( \varsigma \right) + k_{2} \Pi^{4} \left( \varsigma \right)$$
(24)

where, \(k_{0}\), \(k_{1}\) and \(k_{2}\) are real parameters.

The solutions of Eq. (24) with \(\varepsilon = \pm 1,{\mkern 1mu} \;\mathchar'26\mkern-10mu\lambda = k_{1}^{2} - 4k_{0} k_{2}\) are:

case 1: \(k_{0} > 0\)

$$\Pi_{1} \left( \varsigma \right) = \frac{{ - k_{0} k_{1} {\text{sech}}^{2} \left( {0.5\sqrt {k_{0} } \varsigma } \right)}}{{k_{1}^{2} - k_{0} k_{2} \left[ {1 + \varepsilon \tanh \left( {0.5\sqrt {k_{0} } \varsigma } \right)} \right]^{2} }}$$
(25)

case 2: \(k_{0} > 0\)

$$\Pi_{2} \left( \varsigma \right) = \frac{{k_{0} k_{1} {\text{csch}}^{2} \left( {0.5\sqrt {k_{0} } \varsigma } \right)}}{{k_{1}^{2} - k_{0} k_{2} \left[ {1 + \varepsilon \coth \left( {0.5\sqrt {k_{0} } \varsigma } \right)} \right]^{2} }}$$
(26)

case 3: \(k_{0} {\text{ }} > 0,{\mkern 1mu} \;\mathchar'26\mkern-10mu\lambda > 0\)

$$\Pi _{3} \left( \varsigma \right) = \frac{{2k_{0} \text{sech} \left( {\sqrt {k_{0} } \varsigma } \right)}}{{\varepsilon \sqrt{ \mathchar'26\mkern-10mu\lambda} - k_{1} \text{sech} \left( {\sqrt {k_{0} } \varsigma } \right)}}$$
(27)

case 4: \(k_{0} < 0{\mkern 1mu} ,\mathchar'26\mkern-10mu\lambda > 0\)

$$\Pi _{4} \left( \varsigma \right) = \frac{{2k_{0} \sec \left( {\sqrt { - k_{0} } \varsigma } \right)}}{{\varepsilon \sqrt { \mathchar'26\mkern-10mu\lambda} - k_{1} \sec \left( {\sqrt { - k_{0} } \varsigma } \right)}}$$
(28)

case 5: \(k_{0} > 0,\;\mathchar'26\mkern-10mu\lambda < 0\)

$$\Pi _{5} \left( \varsigma \right) = \frac{{2k_{0} \text{csch} \left( {\sqrt {k_{0} } \varsigma } \right)}}{{\varepsilon \sqrt { - \mathchar'26\mkern-10mu\lambda } - k_{1} \text{csch} \left( {\sqrt {k_{0} } \varsigma } \right)}}$$
(29)

case 6: \(k_{0} < 0,\;\mathchar'26\mkern-10mu\lambda < 0\)

$$\Pi _{6} \left( \varsigma \right) = \frac{{2k_{0} \csc \left( {\sqrt{ - k_{0}} \varsigma } \right)}}{{\varepsilon \sqrt{\mathchar'26\mkern-10mu\lambda} - k_{1} \csc \left( {\sqrt{ - k_{0} } \varsigma } \right)}}$$
(30)

case 7: \(k_{0} < 0,\,k_{2} > 0\)

$$\Pi_{7} \left( \varsigma \right) = \frac{{ - k_{0} {\text{sech}}^{2} \left( {0.5\sqrt {k_{0} } \varsigma } \right)}}{{k_{1} + 2\varepsilon \sqrt{k_{0} k_{2} } \tanh \left( {0.5\sqrt{k_{0} } \varsigma } \right)}}$$
(31)

case 8: \(k_{0} < 0,\,k_{2} > 0\)

$$\Pi_{8} \left( \varsigma \right) = \frac{{ - k_{0} \sec^{2} \left( {0.5\sqrt { - k_{0} } \varsigma } \right)}}{{k_{1} + 2\varepsilon \sqrt { - k_{0} k_{2} } \tan \left( {0.5\sqrt { - k_{0} } \varsigma } \right)}}$$
(32)

case 9: \(k_{0} > 0,\,k_{2} > 0\)

$$\Pi_{9} \left( \varsigma \right) = \frac{{k_{0} {\text{csch}}^{2} \left( {0.5\sqrt {k_{0} } \varsigma } \right)}}{{k_{1} + 2\varepsilon \sqrt {k_{0} k_{2} } \coth \left( {0.5\sqrt {k_{0} } \varsigma } \right)}}$$
(33)

case 10: \(k_{0} < 0,\,k_{2} > 0\)

$$\Pi_{10} \left( \varsigma \right) = \frac{{ - k_{0} \csc^{2} \left( {0.5\sqrt { - k_{0} } \varsigma } \right)}}{{k_{1} + 2\varepsilon \sqrt { - k_{0} k_{2} } \cot \left( {0.5\sqrt { - k_{0} } \varsigma } \right)}}$$
(34)

case 11: \(k_{0} > 0,\;\mathchar'26\mkern-10mu\lambda = 0\)

$$\Pi_{11} \left( \varsigma \right) = - \frac{{k_{0} }}{{k_{1} }}\left[ {1 + \varepsilon \tanh \left( {0.5\sqrt {k_{0} } \varsigma } \right)} \right]$$
(35)

case 12: \(k_{0} > 0,\;\mathchar'26\mkern-10mu\lambda = 0\)

$$\Pi_{12} \left( \varsigma \right) = - \frac{{k_{0} }}{{k_{1} }}\left[ {1 + \varepsilon \coth \left( {0.5\sqrt {k_{0} } \varsigma } \right)} \right]$$
(36)

case 13: \(k_{0} > 0\)

$$\Pi_{13} \left( \varsigma \right) = \frac{{k_{0} e^{{\varepsilon \left( {\sqrt {k_{0} } \varsigma } \right)}} }}{{0.25\left( {e^{{\varepsilon \left( {\sqrt {k_{0} } \varsigma } \right)}} - k_{1} } \right)^{2} - 4k_{0} k_{2} }}$$
(37)

case 14: \(k_{0} > 0,\,k_{1} = 0\)

$$\Pi_{14} \left( \varsigma \right) = \frac{{ \pm k_{0} \varepsilon e^{{\varepsilon \left( {\sqrt {k_{0} } \varsigma } \right)}} }}{{0.25 - k_{0} ce^{{2\varepsilon \left( {\sqrt {k_{0} } \varsigma } \right)}} }}$$
(38)

Procedure 4: Putting Eq. (23) and Eq. (24) into Eq. (22) utilizing a symbolic computing methodology, assembling all the factors of \(\left[ {\Pi \left( \varsigma \right)} \right]^{i}\)\(\left[ {\Pi^{\prime}\left( \varsigma \right)} \right]^{j}\), where \(i = 0,1,2,...\), with \(j = 0,1\) and putting them all equal to zero produces a series of algebraic formulas for \(k_{j}\)\(j = (0,1,2,...,N)\),\(k_{0}\), \(k_{1}\),\(k_{2}\),\(\nu\). Finally by entering the results of these equations into Eq. (23) along with the solutions of Eq. (24), which are Eq. (25–38), and substituting \(\varsigma = x + \psi_{1} y + \psi_{2} t\), then we get the solutions of Eq. (21).

New solutions of Eq. (20) via (AEA)

To solve Eq. (20) by auxiliary equation approach mentioned above, balancing \({\rm N}^{\prime\prime}\) and \(N^{3}\) in Eq. (20), we get N = 2.Then the solution of Eq. (20)

$${\rm N}\left( \varsigma \right) = b_{0} + b_{1} \Pi \left( \varsigma \right) + b_{2} \Pi^{2} \left( \varsigma \right)$$
(39)

Entering Eq. (39) into Eq. (20) with the help of Eq. (24) yields.

$$Set\,1:\left\{ \begin{gathered} k_{0} = \pm \sqrt {\Im_{1}^{2} - 4\Im_{0} c} ,k_{1} = \frac{2}{3}b_{1} \Im_{0} ,k_{2} = 0, \hfill \\ b_{0} = \pm \frac{1}{2}\frac{{ \pm \Im_{1} + \sqrt {\Im_{1}^{2} - 4\Im_{0} c} }}{{\Im_{0} }},b_{1} = b_{1} ,b_{2} = 0 \hfill \\ \end{gathered} \right\}$$
(40)

Substituting Eq. (40) into Eq. (39), with aid Eq. (25–38) admits

$${\rm N}_{1,i} \left( \varsigma \right) = \pm \frac{1}{2}\frac{{ \pm \Im_{1} + \sqrt {\Im_{1}^{2} - 4\Im_{0} c} }}{{\Im_{0} }} + b_{1} \Pi_{i} \left( \varsigma \right)$$
(41)
$$Set\,2:\left\{ \begin{gathered} k_{0} = \pm \sqrt {\Im_{1}^{2} - 4\Im_{0} c} ,k_{1} = \frac{1}{3}b_{1} \Im_{0} ,k_{2} = \pm \frac{1}{36}\frac{{\Im_{0}^{2} b_{1}^{2} }}{{\sqrt {\Im_{1}^{2} - 4\Im_{0} c} }}, \hfill \\ b_{0} = \pm \frac{1}{2}\frac{{ \pm \Im_{1} + \sqrt {\Im_{1}^{2} - 4\Im_{0} c} }}{{\Im_{0} }},b_{1} = b_{1} ,b_{2} = \pm \frac{1}{6}\frac{{\Im_{0} b_{1}^{2} }}{{\sqrt {\Im_{1}^{2} - 4\Im_{0} c} }} \hfill \\ \end{gathered} \right\}$$
(42)

Putting Eq. (42) into Eq. (39) with the aid of Eqs. (25–38) yield

$${\rm N}_{2,i} \left( \varsigma \right) = \pm \frac{1}{2}\frac{{ \pm \Im_{1} + \sqrt {\Im_{1}^{2} - 4\Im_{0} c} }}{{\Im_{0} }} + b_{1} \Pi \left( \varsigma \right) \pm \frac{1}{6}\frac{{\Im_{0} b_{1}^{2} }}{{\sqrt {\Im_{1}^{2} - 4\Im_{0} c} }}\Pi^{2} \left( \varsigma \right)$$
(43)

where \(i = 1,2,3,...,11\).

Sardar sub equation approach (SSEA)

In what follows17,18, consider the solution Eq. (20) as

$${\rm N}\left( \varsigma \right) = \sum\limits_{i = 0}^{n} {\vartheta_{i} \Gamma^{i} } \left( \varsigma \right)$$
(44)

where \(\vartheta_{i} = \vartheta_{1} ,\vartheta_{2} ,\vartheta_{3} ,...,\vartheta_{n}\), are coefficients will be find later with \(\left( {\vartheta_{i} \ne 0} \right)\) and \(\Gamma \left( \varsigma \right)\) fulfilled:

$$\left[ {\Gamma^{\prime}\left( \varsigma \right)} \right]^{2} = \Theta + \ell \Gamma^{2} \left( \varsigma \right) + \Gamma^{4} \left( \varsigma \right)$$
(45)

where \(\ell\) and \(\Theta\) are constants. The Eq. (45) has solutions follow as:

Case 1: \(\ell > 0,\Theta = 0\),

$$\Gamma_{1}^{ \pm } \left( \varsigma \right) = \pm \sqrt { - gh\ell } {\text{sech}}_{gh} \left( {\sqrt \ell \varsigma } \right)$$
(46)
$$\Gamma_{2}^{ \pm } \left( \varsigma \right) = \pm \sqrt { - gh\ell } {\text{csch}}_{gh} \left( {\sqrt \ell \varsigma } \right)$$
(47)

where

$${\text{sech}}_{gh} \left( \varsigma \right) = \frac{2}{{ge^{\varsigma } + he^{ - \varsigma } }},{\text{csch}}_{gh} \left( \varsigma \right) = \frac{2}{{ge^{\varsigma } - he^{ - \varsigma } }}$$
(48)

Case 2: \(\ell < 0,\Theta = 0\)

$$\Gamma_{3}^{ \pm } \left( \varsigma \right) = \pm \sqrt { - gh\ell } \sec_{gh} \left( {\sqrt { - \ell } \varsigma } \right)$$
(49)
$$\Gamma_{4}^{ \pm } \left( \varsigma \right) = \pm \sqrt { - gh\ell } \csc_{gh} \left( {\sqrt { - \ell } \varsigma } \right)$$
(50)

where

$$\sec_{gh} \left( \varsigma \right) = \frac{2}{{ge^{i\varsigma } + he^{ - i\varsigma } }},\csc_{gh} \left( \varsigma \right) = \frac{2i}{{ge^{i\varsigma } - he^{ - i\varsigma } }}$$
(51)

Case 3: if \(\ell < 0\,and\,\rho = \frac{{a^{2} }}{4b}\,\) then

$$\Gamma_{5}^{ \pm } \left( \varsigma \right) = \pm \sqrt { - \frac{\ell }{2}} \tanh_{gh} \left( {\sqrt { - \frac{\ell }{2}} \varsigma } \right)$$
(52)
$$\Gamma_{6}^{ \pm } \left( \varsigma \right) = \pm \sqrt { - \frac{\ell }{2}} \coth_{gh} \left( {\sqrt { - \frac{\ell }{2}} \varsigma } \right)$$
(53)
$$\Gamma_{7}^{ \pm } \left( \varsigma \right) = \pm \sqrt { - \frac{\ell }{2}} \left[ {\tanh_{gh} \left( {\sqrt { - 2\ell } \varsigma } \right) \pm i\sqrt {gh} {\text{sech}}_{gh} \left( {\sqrt { - 2\ell } \varsigma } \right)} \right]$$
(54)
$$\Gamma_{8}^{ \pm } \left( \varsigma \right) = \pm \sqrt { - \frac{\ell }{2}} \left[ {\tanh_{gh} \left( {\sqrt { - 2\ell } \varsigma } \right) \pm \sqrt {gh} {\text{csch}}_{gh} \left( {\sqrt { - 2\ell } \varsigma } \right)} \right]$$
(55)
$$\Gamma_{9}^{ \pm } \left( \varsigma \right) = \pm \sqrt { - \frac{\ell }{8}} \left[ {\tanh_{gh} \left( {\sqrt { - \frac{\ell }{8}} \varsigma } \right) + \coth_{gh} \left( {\sqrt { - \frac{\ell }{8}} \varsigma } \right)} \right]$$
(56)

where

$$\tanh_{gh} \left( \varsigma \right) = \frac{{ge^{\varsigma } - he^{ - \varsigma } }}{{ge^{\varsigma } + he^{ - \varsigma } }},\;\coth_{gh} \left( \varsigma \right) = \frac{{ge^{\varsigma } + he^{ - \varsigma } }}{{ge^{\varsigma } - he^{ - \varsigma } }}$$
(57)

Case 4: if \(\ell > 0\,and\,\Theta = \frac{{\ell^{2} }}{4}\) and then

$$\Gamma_{10}^{ \pm } \left( \varsigma \right) = \pm \sqrt {\frac{\ell }{2}} \tan_{gh} \left( {\sqrt {\frac{\ell }{2}} \varsigma } \right)$$
(58)
$$\Gamma_{11}^{ \pm } \left( \varsigma \right) = \pm \sqrt {\frac{\ell }{2}} \cot_{gh} \left( {\sqrt {\frac{\ell }{2}} \varsigma } \right)$$
(59)
$$\Gamma_{12}^{ \pm } \left( \varsigma \right) = \pm \sqrt {\frac{\ell }{2}} \left[ {\tan_{gh} \left( {\sqrt {2\ell } \varsigma } \right) \pm \sqrt {gh} \sec_{gh} \left( {\sqrt {2\ell } \varsigma } \right)} \right]$$
(60)
$$\Gamma_{13}^{ \pm } \left( \varsigma \right) = \pm \sqrt {\frac{\ell }{2}} \left[ {\cot_{gq} \left( {\sqrt {2\ell } \varsigma } \right) \pm \sqrt {gq} \csc_{pq} \left( {\sqrt {2\ell } \varsigma } \right)} \right]$$
(61)
$$\Gamma_{14}^{ \pm } \left( \varsigma \right) = \pm \sqrt {\frac{\ell }{8}} \left[ {\tan_{gh} \left( {\sqrt {\frac{\ell }{8}} \varsigma } \right) + \cot_{gh} \left( {\sqrt {\frac{\ell }{8}} \varsigma } \right)} \right]$$
(62)

where

$$\tan_{gh} \left( \varsigma \right) = - i\frac{{ge^{i\varsigma } - he^{ - i\varsigma } }}{{ge^{i\varsigma } + he^{ - i\varsigma } }}\,,\cot_{gh} \left( \varsigma \right) = i\frac{{ge^{i\varsigma } + he^{ - i\varsigma } }}{{ge^{i\varsigma } - he^{ - i\varsigma } }}$$
(63)

Inserting Eq. (44) with the help of Eq. (45) into Eq. (20) and gathering all the coefficient of power of \(\Gamma \left( \varsigma \right)\) are equated to zero and solve the algebraic system for \(\vartheta_{i} \, n\) and \(c\). As a result, the answer will be accomplished.

New solution of Eq. (20) by new extended (SSEA) approach

Balancing \({\rm N}^{2}\) with \(\,{\rm N}^{\prime\prime}\) in Eq. (31), we get \(n = 2\), hence, the solution of Eq. (20) as the follows as:

$${\rm N}\left( \varsigma \right) = \vartheta_{0} + \vartheta_{1} \Gamma \left( \varsigma \right) + \vartheta_{2} \Gamma^{2} \left( \varsigma \right)$$
(64)

putting Eq. (64) into Eq. (20) with along Eq. (45) and equating all the factors of \(\Gamma \left( \varsigma \right)\) zero, to zero, we determine a set of algebraic equations and following solve them, yields:

$$\left\{ {\ell = \frac{{\Im_{1} }}{4} + \frac{1}{2}\Im_{0} \vartheta_{0} ,c = \frac{{ - \Im_{1} \vartheta_{0} \Im_{0} + 12\Theta - \Im_{0}^{2} \vartheta_{0}^{2} }}{{\Im_{0} }},\vartheta_{0} = \vartheta_{0} ,\vartheta_{1} = 0,\vartheta_{2} = \frac{6}{{\Im_{0} }}} \right\}$$
(65)
$${\rm N}_{j} \left( \varsigma \right) = \vartheta_{0} + \frac{6}{{\Im_{0} }}\Gamma_{j}^{ \pm 2} \left( \varsigma \right)$$
(66)

where \(j = 1,2,3,...,14\).

Graphical depiction

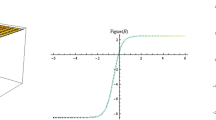
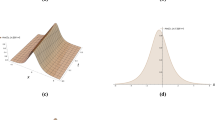
In the field of nano biosciences, transmission line models are pivotal for understanding the significance of ionic wave propagation along microtubules within living cells. These waves, resembling nanotubes, are indispensable for cellular activities such as cell motility, division, intracellular trafficking, and neuronal information processing. Furthermore, these waves are associated with higher neuronal functions like memory formation and the development of consciousness. This section focuses on visually exploring certain solutions acquired. The specific parameter values utilized for generating the graphs are provided in the caption of each corresponding figure. The Figs. 1,2,3,4,5 are generated using Matlab software. The first (i), second (ii), and third (iii) subfigures depict the absolute value, real part, and imaginary part respectively. In Fig. 1 and Fig. 2 the graphical representation of \({\rm N}_{1,1} (x,t)\) and \({\rm N}_{1,11} (x,t)\) for \(w = 0.2\),\(c = 5\), and \(\Im_{0} = \Im_{1} = b_{1} = 0.2\) depict the bright-dark, kink and anti-kink types solutions . In Fig. 3 the graphical representation of \({\rm N}_{2,1} (x,t)\) for \(w = c = \Im_{1} = 0.2\), and \(\Im_{0} = b_{1} = 2\) represent the bright-dark type solution. In Fig. (4) the graphical representation of \({\rm N}_{5} (x,t)\) for \(\vartheta_{0} = \Im_{0} = w = g = 0.2\),\(h = 0.3\) and \(\ell = 0.9\) show periodic bright and periodic kink types solutions. In Fig. (5) the graphical representation of \({\rm N}_{9} (x,t)\) for \(\vartheta_{0} = 2\),\(\Im_{0} = g = 2\),\(w = 5\),\(h = 3\) and \(\ell = 0.002\) show the bright-dark and dark types solutions .

Fig. 1
figure 1

The solution \({\rm N}_{1,1} (x,t)\) (A) 3D mesh of \({\rm N}_{1,1}\), and (B) 3D projection of \({\rm N}_{1,1}\) at \(w = 0.2\), \(c = 5\), and \(\Im_{0} = \Im_{1} = b_{1} = 0.2\).

Full size image
Fig. 2
figure 2

The solution \({\rm N}_{1,11} (x,t)\) (A) 3D mesh of \({\rm N}_{1,11}\), and (B) 3D projection of \({\rm N}_{1,11}\) at \(w = 0.2\), \(c = 5\), and \(\Im_{0} = \Im_{1} = b_{1} = 0.2\).

Full size image
Fig. 3
figure 3

The solution \({\rm N}_{2,1} (x,t)\) (A) 3D mesh of \({\rm N}_{2,1}\), and (B) 3D projection of \({\rm N}_{2,1}\) at \(w = c = \Im_{1} = 0.2\), and \(\Im_{0} = b_{1} = 2\).

Full size image
Fig. 4
figure 4

The solution \({\rm N}_{5} (x,t)\) (A) 3D mesh of \({\rm N}_{5}\), and (B) 3D projection of \({\rm N}_{5}\) at \(\vartheta_{0} = \Im_{0} = w = g = 0.2\),\(h = 0.3\) and \(\ell = 0.9\).

Full size image
Fig. 5
figure 5

The solution \({\rm N}_{9} (x,t)\) (A) 3D mesh of \({\rm N}_{9}\), and (B) 3D projection of \({\rm N}_{9}\) at \(\vartheta_{0} = 2\),\(\Im_{0} = g = 2\),\(w = 5\),\(h = 3\) and \(\ell = 0.002\).

Full size image

Conclusion and summary

In the present work, the solutions obtained here are novel and provide fresh insights into how NSIW propagates along microtubules in real cells via two novel approaches, by comparing the findings from our current study with the established results derived by other researchers through diverse methodologies34,35. They also provide a more accurate description than the prior one found in the literature34,35. No other theoretical method had previously produced the obtained theoretical solutions. The exact solutions obtained with these two suggested methods are new distinct types of the ocean solitons and agree with one another. There are new approaches that will be used in the future. This our task in future.