Introduction

Air quality forecasting is an important analytical method and aims to raise a warning when pollution concentrations surpass a certain level1,2. Precisely predicting air pollution levels is also essential for enacting efficient restrictions and protecting public health3,4. Thus, examining and forecasting air pollution has garnered significant attention from scholars5,6,7. Machine learning (ML) techniques such as Random Forest, Extra Trees, XGBoost, and LightGBM have been attractive for forecasting applications over the past decade8,9,10 since they effectively perform a range of duties; thereby, many researchers have utilised ML techniques to predict air quality around the world. For instance, Castelli et al.11 applied Support Vector Regression (SVR), a widely used ML technique, to estimate the concentration of pollutants and anticipate the air quality index (AQI) in California, USA. In another study, Liang et al.12 predicted air quality index levels in several regions of Taiwan using AdaBoost, random forests, stacking ensembles, and support vector machines (SVMs) applying an 11-year dataset. He et al.13 and Guo et al.14,15 demonstrated that the ANN is effective in predicting monthly and daily aerosol concentrations in Liaocheng, Shanghai, and Chongqing, China, by identifying nonlinear relationships between the input and output variables. Furthermore, ML-based atmospheric transport models are commonly used to predict air pollution levels with high accuracy in terms of time and location. These models are beneficial for regular air quality forecasts, typically predicting pollutant levels 1–3 days in advance16. In this context, Wang et al.17 developed an ML model that combines TROPOMI level-2 satellite observations with detailed meteorological data to forecast the levels of ground-level ozone (O3) in California. ML techniques, when combined with spatiotemporal modelling, can offer more adaptable measures related to exposure. This approach has been investigated using various model architectures18. Wong et al.19 employed a Land Use Regression (LUR) model integrated with ML algorithms to evaluate the spatial-temporal fluctuations of particles that are 2.5 microns or less in diameter (i.e., PM2.5). Their findings showed that the standard LUR model and the hybrid kriging-LUR model were able to recognise 58% and 89% of the fluctuations in PM2.5, respectively. Therefore, the geographic pattern of air pollution has been comprehensively captured using LUR. Nevertheless, linear methods may prove difficult to implement when dealing with regional contexts and non-linear relationships20. Simultaneously, enhancing the precision of conventional ML models, given the dynamic nature of pollutants and limited data availability, might pose challenges21,22.

The lack of long-term data is a significant constraint for numerous studies, considering it will be essential for addressing seasonal fluctuations as well as additional variables. ML models based on short-term data might have limited generalisation capabilities when applied to various timeframes or regions12,23. Consequently, forecasting air quality is a challenging endeavour because of the intricate characteristics, instability, and significant fluctuations in pollutants over time and location16. The effectiveness of the mathematical models is constrained by flaws in the emission inventory and biases in the beginning and boundary situations, along with shortcomings in the present physical and chemical schemes. The extent of disparity between the anticipated exposures produced by multiple models and one model that yields trustworthy projections is uncertain24. Prior investigations employed ML and statistical models to categorise and predict air pollution. Nevertheless, the intricate nature of the air pollution dataset makes these algorithms inefficient for classifying and predicting. ML-based models encounter problems such as poor data preprocessing, class inequality concerns, data splitting, and hyperparameter tuning25.

An important issue that affects the methods mentioned above is overfitting, which occurs when models achieve favourable results on training data but perform poorly in generalising their findings onto new and unseen data. The overfitting issue occurs when a model learns from noise and unrelated patterns of the training data with poor predictive performance. Lopez et al.26 described overfitting as an issue where the statistical ML model learns much about noise as well as signal, which is present in the training data. Overfitting also remains an issue even in contexts involving a few dimensions, especially when there is a failure to make a correlation between the result and predictor variables robust27.

Implementing regularisation techniques is crucial in improving model performance by decreasing overfitting. The performance of different regularisation techniques, such as the Frobenius norm, nuclear norm, and Lasso, has been explored to enhance the accuracy of air quality prediction23,28. Lasso regularisation applies a penalty to the absolute value of regression coefficients, which reduces less important feature coefficients to zero29. This process contributes to feature selection30, reduction of overfitting, and enhancement of the interpretability of the model. Several studies in Iran have shown that air pollution harmfully impacts the physical and mental health of citizens, reducing labour productivity and student academic performance31. Prolonged exposure to ambient PM2.5 and O3 significantly increased mortality in Tehran, with ischaemic heart disease being the most responsible cause32, highlighting the necessity of air pollution modelling to demonstrate its behaviour. The intention is to utilise Lasso’s capacity to improve the simplicity and reliability of models to create reliable prediction models that can estimate pollution concentrations under various scenarios. Hence, the main goal of this study is to examine the utilisation of Lasso regularisation in the context of forecasting air pollution factors in the Tehran megacity, which is the most polluted city in Iran.

The rationale for employing Lasso regression in this study is rooted in its ability to handle high-dimensional datasets and perform effective feature selection. Here, we used an extensive collection of features, including concentrations of key pollutants as well as meteorological variables from 16 sensors in Tehran, spanning 10 years (2013–2023). Given the complexity of the dataset, which includes variables with potential multicollinearity and varying degrees of importance, Lasso regression was particularly suitable due to its ability to identify the most relevant predictors. This characteristic is crucial for environmental modelling, where isolating the key factors that influence air pollutant concentrations enhances our understanding of the underlying processes. While Lasso is inherently a linear method, it serves as an essential baseline for evaluating linear relationships within the data. In the context of air pollution forecasting for Tehran, where some relationships—such as the influence of meteorological variables on pollutant dispersion—can often be approximated as linear, Lasso regression provides a robust and interpretable modelling approach.

Materials and methods

Study area

Tehran, located at coordinates 35°41′ N and 51°26′ E, serves as the political centre and largest metropolis of Iran. Tehran, with an approximate area of 730 km2, has an approximate population density of 10,555 individuals/km2. The region’s altitude varies between 900 and 1800 m above sea level. The northern area experiences a cold and arid climate, while the southern portion is characterised by a hot and dry climate. The city faces a yearly temperature range of 15° to 18 °C, with a variance of around 3° in different Sects33,34.

Data acquisition

The study dataset includes the air pollutants CO, O3, NO2, SO2, PM10, and PM2.5. The concentrations of atmospheric PM2.5 and PM10 (µg/m− 3), O3 (ppbv), NO2 (ppbv), SO2 (ppbv), and CO (ppmv) were measured using beta-attenuation (Met One BAM-1020, USA; Environment SA, MP 101 M, France), UV-spectrophotometry (Ecotech Serinus 10 Ozone Analyser, Australia), chemiluminescence (Ecotech Serinus 40 Oxides of Nitrogen Analyser, Australia), and ultraviolet fluorescence (Ecotech Serinus 40 Ox), respectively. The air pollutants’ real-time data from sensors is transmitted to the quality control unit. The weather sensors’ location is based on a number of effective factors on air pollution, such as elevation from the ground, dominant wind currents, interval to polluting sources (e.g., industrial units and high-traffic areas), and land use. Preferably, weather sensors are situated in places where precisely indicate the properties of the immediate medium. The weather sensors in the city mainly operate in areas distinguished by high traffic10. A reference laboratory at the Iran’s Sharif University of Technology is responsible for periodically checking the operational efficiency, precision, and accuracy of sensors. The sensors’ data is ceaselessly received by Tehran Air Quality Control Company (TAQCC) via optical fibre. The outputs are daily publicised, complying with the validation process. Among the 22 weather sensors in Tehran, only 16 cases have been active, and data has been collected since 2013. The dataset covers ten years (Jan 2013–Dec 2023), ensuring sufficient temporal coverage for training and testing the predictive models. A complete set of 40,172 data values pertaining to 11 parameters was gathered.

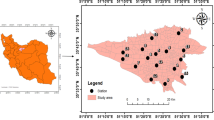
Meteorological data was obtained from the Weather Underground archive, which can be explored at https://www.wunderground.com. There are almost 6,000 automated weather gauges located at airports worldwide. These sensors report their measurements every 1, 3, and 6 h. The weather indicators included in the present research are temperature (T in ºC), relative humidity (RH in %), wind speed (WS in km/h− 1), dew point (DW in ºC), and air pressure (AP in hPa (hectopascal)). The weather indicators are collected to capture the environmental conditions that influence the dispersion and concentration of air pollutants. The international airport linked to this system is Mehrabad Airport in Tehran, located at coordinates 35°41′ N, 51°19′ E. Figure 1 represents the studied geographical region, the air quality and meteorological stations, and several gadgets used in this study.

Fig. 1
figure 1

(a): Map showing the position of the research region and monitoring locations; (b): Met One BAM-1020, USA (for PM); (c): Ozone Analyser (Ecotech Serinus 10, Australia); (d): NO2 analyser (Ecotech Serinus 40, Australia); (e): The weather station; (f): Public air quality monitors; (g): Severe air pollution in Tehran.

Full size image

Data preprocessing

To ensure optimal results, it is required to preprocess the data before applying the Lasso method. This involves handling missing values and standardising variables if necessary35. Initially, the dataset contained a limited number of missing values. We adopted an interpolation technique that predicts the missing values by estimating them based on the surrounding data points. This adjustment ensures that the data integrity is maintained without introducing significant biases while avoiding the information loss associated with the direct elimination of missing values. Then, due to the sensitivity of the Lasso method to the scale of features, we need to standardise the variables36. To do this, each feature is subtracted from the mean and divided by its standard deviation so that it has a mean of zero and unit variance. So, variables with larger scales are prevented from dominating the regularisation process37. Further, to accurately evaluate the model’s performance, it is required to split the data into training and testing sets38.

Methods

Overfitting in ML arises when a model acquires excessive knowledge about the intricacies and random fluctuations in the training data39,40, leading to detrimental effects on its performance when applied to new data (Fig. 2). Essentially, the model becomes excessively intricate and seizes the “noise” or arbitrary variations within the training data instead of the fundamental pattern. When tested on the training data, this outcome yields high accuracy, though it fails to generalise well to unseen data. We first conduct a primary prediction for the CO variable to show this issue by employing various ML techniques. In our analyses, 80% of the data were used for model training and 20% for model testing, and the trace of R-squared (R²) values was plotted for different models (Fig. 3). To ensure robust evaluation and consistency, the results in Fig. 3 were generated using a k-fold cross-validation approach—high differences between R2 in the train and test models hallmark overestimation in the prediction of CO analyses. Additionally, to illustrate the phenomenon of overfitting, we have included several evaluation metrics such as Mean Absolute Error (MAE), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and Normalised Mean Squared Error (NMSE) in Table 1. The results show lower error metrics on the training set compared to the test set, indicating the presence of overfitting to varying degrees across all the evaluated models. In this paper, the Lasso regularisation technique will be employed to counteract overfitting by incorporating a penalty equivalent to the absolute value of coefficient magnitudes into the loss function. This penalty term encourages the model to favour simpler solutions, effectively shrinking certain coefficients to zero and facilitating feature selection. By reducing model complexity, Lasso regularisation assists in mitigating overfitting and performing automatic feature selection.

Fig. 2
figure 2

Plot of fitting different models.

Full size image
Fig. 3
figure 3

Accuracy of different ML techniques, including Random Forest, LightGBM, Extra Trees Regressor, and XGBoost, in predicting CO.

Full size image
Table 1 Performance metrics of the ML models.
Full size table

Working principle of Lasso regularisation

The aim of linear regression is to minimise the loss function, generally represented by the sum of squared errors (SSE) (Eq. 1):

$$\:SSE={\sum\:}_{i=1}^{n}\:{\left({y}_{i}-{\stackrel{\prime }{y}}_{i}\right)}^{2}$$
(1)

which can be stated as Eq. 2:

$$\:SSE={\sum\:}_{i=1}^{n}\:{\left({y}_{i}-\left({\beta\:}_{0}+{\sum\:}_{j=1}^{p}\:{\beta\:}_{j}{x}_{ij}\right)\right)}^{2}$$
(2)

where \(\:n\) represents the number of observations, \(\:p\) denotes the number of variables that are available in the dataset, β0​ is the intercept or constant term, which represents the value of the dependent variable y when all the independent variables xij​ are zero; βj​ for j = 1, 2, …, p are the regression coefficients for each independent variable xij​. These coefficients indicate the magnitude and direction of the relationship between the independent variable xij and the dependent variable y, and \(\:{x}_{ij}\) represent the value of the j-th variable for the i-th observation (i = 1, 2, …, n and j = 1, 2, …, p). Lasso regularisation introduces an additional penalty term to the loss function as follows (Eq. 3):

$$\:{\sum\:}_{i=1}^{n}\:{\left({y}_{i}-\left({\beta\:}_{0}+{\sum\:}_{j=1}^{p}\:{\beta\:}_{j}{x}_{ij}\right)\right)}^{2}+\lambda\:{\sum\:}_{j=1}^{p}\:\left|{\beta\:}_{j}\right|$$
(3)

where λ (lambda) can take various values as follows:

  • λ = 0: Same coefficients as ordinary least squares linear regression.

  • λ = ∞: All coefficients are zero.

  • 0 < λ < ∞: Coefficients are between 0 and that of least squares linear regression.

The magnitude of λ determines the amount of penalty. The larger the value of λ, the more coefficients are forced to be zero to simplify the model; the smaller the value of λ, the lesser the impact, thus enabling most coefficients to remain almost as they were. An appropriate value of lambda should be chosen carefully to get the right type of sparsity. A common procedure for selecting the lambda is based on cross-validation, which is a resampling technique in which the training data are divided into multiple subsets or folds. The Lasso model is trained on a subset of the folds and evaluated on the remaining fold. This process is carried out for different values of lambda, and the lambda minimising the model’s error—e.g., mean squared error or cross-validated error—is chosen. One of the most common cross-validation techniques applied to choose lambda is k-fold cross-validation41. In k-fold cross-validation, the training data is divided into k equal-sized subsets or folds as shown in Fig. 442. In brief, the Lasso model is trained on k folds and evaluated on the remaining fold, repeated for each fold, and the average error across all folds is computed for each lambda value. The lambda value with the lowest average error is selected as the optimal lambda.

Fig. 4
figure 4

The diagram of 10-fold cross-validation, adapted from43.

Full size image

Variable selection

Not only does the Lasso method provide predictions by model fitting of regression, but it also conducts feature selection on the data, simultaneously44. The Lasso will automatically identify less important features and exclude these features from the final model by shrinking their coefficients towards zero. The variable selection property of Lasso has a number of practical implications. It provides better interpretability because the non-zero coefficients in this method indicate the most influential features for the target variable prediction. Secondly, Lasso variable selection may afford more efficient or parsimonious models. By excluding redundant or irrelevant features, the model’s complexity is reduced, which can improve its generalising performance on unseen data. Thirdly, in Lasso, the non-zero coefficients identify the most important features w.r.t. the problem at hand and yield insight into the underlying structure of the data and relationships among the subjects. The process of researching the changes in the coefficients with the change in the level of regularisation has been referred to as tracing the lambda path or regularisation path. The lambda path is a sequence of models derived by changing the regularisation parameter, lambda (λ).

Evaluation metrics

Evaluating the model’s performance to assess its predictive accuracy and generalisation capabilities is necessary while implementing the Lasso method or any other ML technique. Different evaluation metrics exist for evaluating the efficacy of the Lasso model. In this study, the most commonly used evaluation metrics, MSE, RMSE, normalised mean squared error (NMSE), and coefficient of determination (R²) are employed, similar to Doreswamy et al.45 and Guo et al.46. The MSE is one of the most frequent metrics, which accounts for the average of squared differences between predicted and actual values, hence quantifying the overall quality of the model’s predictions. To compute the MSE, the difference between each predicted value and its corresponding true value is squared first, and then the average of these squared differences is taken. MSE characterises the goodness of the fit of the Lasso model to the data, with lower values indicating better performance. NMSE is a variation of the MSE that provides a relative measure of prediction accuracy, considering the scale of the target variable. It’s particularly useful when comparing models operating on different scales or units. It is computed as the MSE divided by the variance of the true values. R2 is a metric that is commonly used for evaluating what percentage of variance in the target variable is predictable from the independent variables. It is computed as the quotient of explained variance over the total variance of the target variable. Given the Lasso method, R2 conveys the overall measure of how well-selected features explain the variation in the target variable. A low value of MSE and NMSE will indicate that this Lasso model is giving rather accurate predictions, while a high R2 will mean that the selected features describe a substantial part of the variability in the target variable.

Software and tools

Data analysis and predictive modelling were implemented using Python 3.11. The experiments were conducted on a machine equipped with an Intel Core i3-1115G4 CPU @ 3.00 GHz, 4 GB RAM, running Windows 10, and the time required to run the models ranged from 0.8397 to 1.9027 s. The Scikit-learn library is utilised for ML procedures, Pandas is used for data manipulation, and Matplotlib is used for data visualization. Using these tools, statistical analyses and cross-validation procedures were facilitated, ensuring robust and reproducible results. The study area map and location of weather stations were provided using ArcGIS version 10.3.

Results

Finding lambda

The ideal tuning parameter λ was established by 10-fold cross-validation. The optimal λ was selected based on minimising the cross-validated mean squared error (MSE) for different target variables, as shown in Fig. 5. For the Lasso model, we used the default maximum number of iterations of 1000 to ensure sufficient iterations for convergence. The convergence tolerance was set to its default value of 1 × 10− 4, which served as the stopping criterion for the optimisation process. The optimisation was performed using a cyclic coordinate descent algorithm, which iteratively updates the coefficients by cycling through each feature, one at a time, while holding the other coefficients fixed. The final Lasso model will be trained using the indicated “1 standard error rule” (λ-1se) values. The charts reveal the optimal λ for balancing model complexity and prediction accuracy. The scale of λ, shown on the x-axis, indicates that as λ grows, the adjustment impact intensifies, penalising more coefficients. The y-axis displays cross-validation average MSE values, with lower values indicating better model performance. The blue line represents the mean MSE, whereas the shaded region is the mean MSE ± 1SE, indicating estimated variability or uncertainty. In addition, the red dashed line shows the ideal λ value using the λ-1se, which picks the model with the most consistent adjustment and an error within one standard error of the minimal error. To balance model complexity and prediction accuracy and also minimise overfitting, the ideal λ (λ-1se) for all pollutants is about 0.1. SO2 had the highest mean cross-validated MSE values, while CO had narrower MSE ranges. Overall, mean cross-validated MSE values with narrow error bars around ideal λ are more reliable, whereas those with large error bars at extreme λ values reflect model uncertainty and variability.

Fig. 5
figure 5

Plots of cross-validation MSEs against λ values for air pollutants.

Full size image

Lasso regularisation and feature selection

The Lasso model coefficients of drivers affecting air pollutants, including CO, O3, NO2, SO2, PM10, and PM2.5, are presented in Table 2. Further, the coefficient trajectory for various λ values is displayed in Fig. 6, demonstrating Lasso selective feature removal as λ grows. The x-axis (λ) displays the regularisation factor λ, showing how Lasso selectively eliminates features as λ increases. The coefficient routes demonstrate how changes in characteristics occur as λ rises. The coefficients of less relevant characteristics decline to 0 as λ grows, whereas critical traits retain importance. Based on the optimal λ values (λ-1se) shown in Fig. 6 and the coefficient paths in Fig. 7, we can identify the irrelevant features in the prediction process for each dependent variable. In Fig. 6a, DW is the first feature to shrink to zero, indicating its diminishing importance in predicting CO. For PM2.5 prediction (Fig. 6b), the features T and AP can be excluded. In Fig. 6c, the prediction of PM₁₀ eliminates the features T and O₃. When predicting O₃ (Fig. 6d), PM2.5 and SO₂ are deemed irrelevant. In Fig. 6e, RH shrinks rapidly to zero, suggesting it has no impact on NO₂ prediction. Finally, Fig. 6f shows that DW and O₃ are removed from the prediction of SO₂. From a physicochemical reaction perspective, the DW can affect precipitation, thereby considerably decreasing pollutant concentrations. Increased precipitation intensities correlate with decreased levels of air pollutants, such as PM10, SO2 and NO2, varying between 15% and 35% of the decrease relative to arid conditions47. DW frequently corresponds with other meteorological factors, including T and RH. Such associations may result in its deletion from predictive models such as Lasso if considered superfluous48,49.

Fig. 6
figure 6

Plots of coefficient paths for different λ values.

Full size image
Fig. 7
figure 7

Plots of permutation feature importance for air pollutants.

Full size image

The Lasso regularisation examination across the pollutants indicates major factors associated with every forecasting model. The coefficients of selected features by the Lasso model for air pollutants are presented in Table 2. O3 was the most significant factor influencing atmospheric CO concentrations, with a strong positive coefficient (3.632). CO also had a positive coefficient with NO2 (2.917), PM2.5 (2.837), SO2 (1.801), and T (1.463). PM2.5 was most affected by PM10, with a strong positive coefficient of 17.405, followed by RH (5.283), SO2 (5.085), NO2 (4.674), and CO (2.928), respectively. The most effective factors on atmospheric PM10 concentrations were PM2.5, DW, WS, and AP, with positive coefficients of 19.422, 2.507, 1.541, and 0.154, respectively. T had the highest positive coefficient (15.004) with O3, followed by NO2 (8.031) and DW (0.393), respectively. The most important factors affecting NO2 concentration included PM2.5, O3, CO, and AP, respectively, with positive coefficients of 7.838, 6.204, 3.828, and 0.866. SO2 had positive coefficients with PM2.5 (5.241) and CO (1.751).

To better understand the significance of individual features in predicting pollutant levels, we employed permutation feature importance. This method evaluates the contribution of each feature by measuring the drop in model performance after permuting the values of that feature while keeping others constant. The importance scores were calculated as the mean decrease in performance across the number of permutations. The feature importance for each pollutant is visualised using bar charts, as shown in Fig. 8, which provides a visual confirmation of the above results. This visualisation highlights the relative contributions of the predictors to the model’s performance, providing insights into the factors most strongly associated with pollutant concentrations.

Fig. 8
figure 8

Plots of accuracy scores for different numbers of features.

Full size image
Table 2 Coefficients of selected features by the Lasso model.
Full size table

Model performance

The essential performance metrics of the Lasso model are presented in Table 3. The MAE quantifies the average absolute value of mistakes, irrespective of their direction; accordingly, O3 had the greatest discrepancy, with an MAE of 11.973, compared to SO2 with the smallest discrepancy (5.386). The average squared difference between actual and forecasted values is quantified by the MSE, making it particularly sensitive to big inaccuracies. Among the analysed variables, O3 had the largest deviation (MSE = 277.998); on the contrary, CO had the lowest deviation (MSE = 57.574). The highest and lowest RMSE, the squared MSE, belonged to O3 (16.673) and CO (7.589), respectively. The NMSE, the normalised mean squared error, which indicates the level of error in the data and among the pollutants, was the highest for SO2 (0.718) and the lowest for PM2.5 (0.165).

Table 3 The Lasso model performance metrics.
Full size table

The overfitting in the Lasso regression models (Fig. 7) was analysed by comparing the R2 trace to the number of features in the training and test data sets. To compare the model’s performance on test and training data, the features were added to the model, and then the R2 value was calculated after every addition. The model was then evaluated using experimental data. The plots show that adding features increases R2 values for both training and test data, i.e., higher values in the y-axis imply an improved fit. However, a tight alignment of values demonstrates that the model is not overfitted. The training and test scores for CO (Fig. 7a) improve with feature count and maintain around the R2 value of 0.45. Nevertheless, the CO model performance starts to drop significantly following seven features, and the modest discrepancy between training and test results suggests minor overfitting. The training and test scores rise quickly and remain at the R2 value of 0.80 for PM2.5 (Fig. 7b). Additional features do not improve the model performance significantly after adding eight features in the PM2.5 plot, and a minimal score discrepancy implies good model generalization. The training and test scores for PM10 (Fig. 7c) improve until the R2 value of 0.75, and then the model efficiency remains unchanged after adding eight features. In the PM10 plot, a modest score difference demonstrates a well-generalised model for PM10. In the SO2 plot (Fig. 7d), the training and test scores rise to the R2 range of 0.65 to 0.7 and then subsequently stabilise. Additional features cannot increase the model’s efficiency after adding six features in the SO2 plot, and a minor score difference shows that the model does not overfit. Regarding O3 (Fig. 7e), both training and test scores noticeably rise until the R2 value of 0.65, and then the performance does not improve following the addition of five features. Small gaps pointed out strong generalisation in the prediction of O3. The training and test R2 scores for NO2 (Fig. 7f) significantly rise to 0.45, and then the model performance improvements do not change after adding eight features. Moreover, a small distance indicates no overfitting for NO2. Overall, the R2 values for Tehran’s air pollutants decrease in the order of PM2.5 (0.8) > PM10 (0.75) > SO2 (0.65) > NO2 (0.55) > CO (0.45) > O3 (0.35). Hence, CO and O3 with lesser values reflect greater forecasting challenges. Decreased returns were identified across all pollutants upon integrating 7–8 features, defining them as the key drivers. A narrow training-test score gap pointed to strong generalisation and minimal overfitting. It is important to note that the above results were obtained using cross-validation during the implementation of the Lasso models. By repeatedly training and testing the model on different subsets of the data, the consistency of the model’s predictive accuracy was confirmed. The results demonstrate that the models remain robust and perform reliably under variations in the input data.

Discussion

The model efficiency

In contrast to expectations, the findings revealed major disparities in the modelling outcomes for PM and air pollutant gases. The high R2 values in the PM prediction ML models (> 0.70 for PM10 and > 0.80 for PM2.5( remarked that the model explains a large proportion of the variance in the PM concentration data (Table 3). Several factors could contribute to this high R2. First, in the context of modelling, significantly correlated characteristics may predict PM2.5 values in the model, which is frequently accomplished by feature selection or domain understanding that detects PM concentrations. The ML algorithms have the power to accurately represent intricate and non-linear interactions50 between input parameters and PM levels. The application of LGBM and other ML methodologies has demonstrated favourable outcomes in predicting surface concentrations of NO2 and O3, attaining R2 values of up to 0.91 for O3 and 0.83 for NO2 in China51,52. The Prophet forecasting model has been employed in Seoul to anticipate air pollution levels, exhibiting enhanced performance relative to conventional models53. Furthermore, deep learning models, particularly Long Short-Term Memory (LSTM) networks, have been utilised to forecast air quality by amalgamating data from several sources, encompassing meteorological and pollutant data. These models have demonstrated enhanced predictive accuracy for air pollutants such as PM2.5, CO, NO2 and O3 in Beijing54 and Shanghai55, with R2 values of up to 0.86. The high-quality, noise-free data with a lot of observations may help the algorithm train and forecast56,57. Many empirical studies have shown that the noise in the dataset dramatically leads to decreased classification accuracy and poor prediction results58. Additional data makes correlations and patterns clearer. The evaluation of the Tehran dataset indicated that PM, particularly PM2.5, was measured by a greater number of sensors. In addition, regularisation methods, such as Lasso regularisation, as applied in the present study, help prevent overfitting by penalising large coefficients and promoting simpler models and can increase generalisation to unseen data and contribute to a high R2 value in the test set59,60. Hybrid ML models were also employed by Qiao et al.61 and Cheng et al.62 to develop a highly efficient PM2.5 prediction model in China.

Moreover, as similarly concluded in this study, it has been reported that decreasing the number of features in the model and the suggested feature optimisation contribute to higher interpretability of the model and give insights into the most crucial factor influencing air quality63. However, ML-based air pollution research is associated with a gap, because of inappropriate handling and optimisation of the data25. Weather conditions, different levels of pollutants (e.g., NO2), and temporal variables (time of day, day of the week, and seasonal fluctuations) as important features might be substantially associated with PM concentrations64,65. Weather factors, including T, RH, and WS, affect PM chemical reactions, production, and dispersion, respectively66. Additionally, air pressure can reflect meteorological conditions that impact pollution levels67. Thus, it appears that the combination of the mentioned factors has been instrumental in achieving a relatively high R2 for PM.

At the same time, even after addressing overfitting and minimising the gap between training and testing data, the prediction models for gaseous chemicals, including CO, SO2, O3, and NO2 still have R2 values < 0.70 (Table 3); consequently, ML techniques still struggle to predict the majority of air pollution, as similarly reported by Mendez et al.68 and Sharma et al.69. Gaseous pollutants such as NO2, O3 and SO2 are influenced by intricate, nonlinear interactions among multiple components, complicating the correct prediction of their correlations by machine learning models. In contrast to PM, which exhibits more regular patterns, gaseous pollutants are acutely responsive to variations in atmospheric conditions, vehicular traffic, and industrial operations, resulting in swift oscillations in their concentrations. These abrupt alterations can lead to considerable fluctuations in the levels of air gaseous pollutants, thus complicating predictive accuracy relative to the more consistent trends observed in PM70,71.

The air pollution dataset may include missing values owing to equipment malfunction or servicing, reducing the precision of models72. One possible explanation for the reduction in the R2 value is that there was a higher amount of missing data in gases compared to PM in Tehran. In other word, the absence of data for PM was minimal, necessitating merely interpolation without the requirement for additional analysis. Furthermore, additional sensors for PM have been proposed as a potential factor contributing to the model’s superior performance. Top-quality information needs to be gathered routinely and at multiple places to adequately reflect pollution shifts. In Tehran, a lack of previous data limits reliable model development since the gradual establishment of stations and their subsequent deployment over ten years may result in inconsistencies in the data. It has been reported that discontinuities in air pollution data, such as gaps in spatial and temporal data, add complexity to the forecast process73. Moreso, fluctuations in weather, traffic, and manufacturing operations dramatically and promptly affect gaseous pollutants, thereby rendering real-time data processing difficult74. Furthermore, shifts in political approaches and natural calamities additionally influence the air quality, which is often hard to forecast75. Pattanayak and Kumar76 highlighted how natural calamities can significantly affect environmental conditions, including air quality, and how these impacts are intertwined with political decisions and responses. Regarding this issue, it is noteworthy to highlight the shifts in the approach towards addressing air pollution in Tehran over the years under examination. Throughout the examined years, there have been multiple updates in the rules regarding vehicular traffic, factory operations, and the temporary shutdown of schools and offices during polluted days in Tehran. Model adaptability and dependability require a thorough real-world evaluation and continual updates77 for application in various regions of Tehran because applying ML algorithms to current systems is difficult owing to compatibility and standards difficulties, and models need to adapt across areas and levels of pollution for widespread adoption. Atmospheric researchers may overlook some of these important issues when using ML in air pollution assessments78.

Air quality forecasting

It is imperative to interpret pollutant models and interactions from the viewpoint of the environment to comprehend pollutant interactions and improve the modelling process. This is because numerous ML models, including SVM and multilayer perceptron (MLP), are plagued by the black box issue, which complicates the interpretation of the physical significance of the predictions. This lack of transparency can result in problems such as overfitting and local minima79. In this context, the findings of this study demonstrated that O3 has a significant prediction error in all metrics, though its lower NMSE signals superior data variance performance. SO2 had the lowest MAE and greatest NMSE, reflecting minor mean errors except for unreliable model performance. CO, PM10, and NO2 exhibited moderate to significant errors, with varying NMSE values, highlighting various degrees of performance. Despite greater overall flaws, PM2.5 provided the most successful prediction accuracy, as similarly obtained by Zhang et al.80 and Chen et al.81, considering its lower NMSE than actual data variability.

To comprehend the interrelations between contaminants, from a chemical point of view, O3 production occurs through photochemical interactions between NO2 and volatile organic compounds (VOCs) under sunlight, and their nonlinearity and environmental sensitivity make prediction challenging82. As a secondary contaminant, O3 is created by atmospheric processes, which must be accurately modelled83. Temperature and direct sunlight affect O3 generation and breakdown. It has been demonstrated that temperature-dependent changes in local chemistry and increased emissions of NO2 in warmer conditions significantly contribute to higher O3 levels84. Moreover, O3 forecasting is complicated by NO2 catalytic cycles and interactions with other pollutants like CO and SO285,86. As a result, O3 regeneration and NO2 reactivity in the atmosphere generate a dynamic system that has proved hard to describe87,88. Different regions exhibit varying O3-temperature dynamics, influenced by local meteorological conditions and precursor emissions89. Ren et al.18 and Eslami et al.90 have demonstrated that nonlinear ML techniques, such as Random Forest and Extreme Gradient Boosting, have obtained superior prediction accuracy compared to linear models, particularly in the context of spatiotemporal modelling; however, precisely measuring peak O3 levels continues to be a major obstacle. Lasso is intended for linear correlations and may have difficulty capturing intricate, non-linear interactions commonly observed in air chemistry and pollutant dynamics. Moreover, the regularisation procedure may result in omitting potentially pertinent features, which could be especially vital for precisely predicting O3 level due to its sensitivity to various environmental conditions. Alternatively, techniques such as Thresholded Lasso (TL), Smoothly Clipped Absolute Deviation (SCAD) and Minimax Concave Penalty (MCP) may yield enhancements. These methodologies mitigate the biases and feature selection challenges associated with Lasso, rendering them more appropriate for intricate prediction tasks like O3-level modelling91. Consequently, traditional ML approaches have limitations in accuracy and interpretability for predicting these pollutants. The prediction of air pollution has preliminarily depended on physical and chemical models, thereby their efficiencies are influenced by precisely considering the intricate dynamics of air pollutant transport, consisting of the long-range transport and secondary formation of pollutants via atmospheric chemical reactions56.

Air quality forecasting and evaluation systems are efficient tools for improving air quality and public health, reducing acute air pollution episodes, especially in urban regions, and decreasing the potential effects on climate, ecosystems and agriculture. Despite that, the air pollution predictive models need a higher optimisation, knowing the best-suited combining of data and algorithms for different dependent variables sounds difficult92. Despite the admirable efforts of researchers and administrators in Tehran, the air quality of urban areas is continuously declining, influencing the quality of air, water and land in this region. On a global scale, the issue of air pollution remains a significant concern, with detrimental effects that impact residents and the environment. According to the Lancet Commission on Pollution and Health, atmospheric pollution caused nine million premature mortalities in 2015, rendering it the leading hazardous driver of illness and early mortality worldwide93. Hence, it is highly imperative to implement every potential measure to tackle air pollution.

Emerging geospatial intelligence technologies, along with big data analytics, machine learning and artificial intelligence, remarkably strengthen early warning systems for air pollution induced by climate change. Using such technologies, real-time data collection and analysis are facilitated, leading to prompt attempts at pollution incidents and thus creating more sustainability in urban media. These technologies help urban areas improve public health consequences and expand more efficient environmental policies. Moreover, integrating observations obtained from both ground sensors and satellite remote sensing instruments to air pollution is a growing necessity. Connecting low-cost sensors is significant for collecting data, although data quality obtained from these sensors is of great importance. There is still a crucial issue regarding different physical scales in air pollution modelling, in particular in cities influenced by long-range transport and localised air quality guidelines. Eventually, long-term, prospective, and interdisciplinary studies, along with international collaborations, are needed to tackle global air pollution.

Conclusions

The results of this study demonstrated how Lasso regularisation raised the accuracy and reliability of air pollution models by overcoming the challenge of overfitting. Regularisation decreased the model’s complexity on account of the addition of the penalty term, thereby enhancing performance expressed as sparsity and improving generalisation performance. The very important stride in the prediction of a wide range of pollutant variants, notably reducing overfitting and selecting the most important features for the models, was accomplished by applying Lasso on a rich dataset from Tehran over a decade. The findings highlight the capability of Lasso regularisation as a promising technique in air quality prediction that could support governments in devising successful policies on air pollution management. The closeness of the training and test set performances of the model across various contaminants highlights its durability and dependability. Despite the difficulties of forecasting specific gaseous pollutants due to their complicated behaviours and interactions, Lasso regularisation has proved advantageous in increasing model interpretability and precision. Moreover, the application of Lasso allows the identification of the most important predictors out of a large number of variables, which helps in pinpointing aspects that bear the most influence on air quality. This feature selection power is very important because simplification of the models does not come with a sacrifice in predictive strength and hence makes the models more applicable in the real world. The current study opens new avenues for future research in areas like the combination of Lasso with other advanced regularisation methods and machine learning algorithms to improve model performance. In addition, the method could be applied to other ecological data and developed to forecast diverse ecological effects. Besides, the conclusions of this study underlined how necessary it is to continuously update and monitor any kind of prediction model when the environmental conditions and behaviours of the pollutants are in variable states. Air pollution is dynamic, driven by variables such as urbanisation, industrial activity, and climate fluctuations, necessitating the use of robust and adaptable modelling techniques. With an added ability to manage very large data sets and relevant feature selection, the Lasso regularisation is one convenient method for continuous air quality evaluation and control.

The ramifications of the study extend beyond scholarly activities, providing real advantages to environmental authorities and urban planners. Using the more powerful prediction capabilities of Lasso-regularised models, policymakers may adopt more focused and successful environmental protection actions, devote budgets systematically, and create urban settings that reduce exposure to hazardous pollutants. Such higher precision in these models may additionally collaborate with early warning systems for high pollution occurrences, therefore protecting public health. Overall, including Lasso regularisation in air quality prediction models is a significant step forward in environmental assessment, as well as providing a potential route for further investigation and operational uses in air pollution control.