UAV selection for high-speed train communication using OTFS modulation

Abstract

Providing continuous wireless connectivity for high-speed trains (HSTs) is challenging due to their high speeds, making installing numerous ground base stations (BSs) along the HST route an expensive solution, particularly in rural and wilderness areas. This paper proposes using multiple unmanned aerial vehicles (UAVs) to deliver high data rate wireless connectivity for HSTs, taking advantage of their ability to fly, hover, and maneuver at low altitudes. However, autonomously selecting the optimal UAV by the HST is challenging. The chosen UAV should maximize the HST’s achievable data rate and provide an extended HST coverage period to minimize frequent UAV handovers constrained by the UAV’s limited battery capacity. The optimization challenge arises from accurately estimating each UAV’s expected coverage period for the HST, given both are moving at high speeds and the UAV’s flying altitude is unknown to the HST. This paper utilizes the estimated HST-UAV channel parameters in the delay-doppler (DD) domain, employing orthogonal time frequency space (OTFS) modulation, to estimate the relative speeds between the HST and UAVs, as well as the UAVs’ flying altitudes. Based on these estimates, HST can predict the maximum coverage period each UAV provides, allowing for selecting the best UAV while considering their remaining battery capacities. Numerical analysis demonstrates the effectiveness of the proposed approach compared to other benchmarks in various scenarios.

Introduction

Background

High-speed trains (HSTs) are an advanced mode of transportation known for their ability to operate at significantly higher speeds than traditional rail systems¹. These trains achieve remarkable speeds, often exceeding 250 kilometers per hour (km/h), by employing cutting-edge technology such as streamlined aerodynamics, robust electric propulsion systems, and sophisticated signaling systems. HSTs efficiently connect distant urban centers, reducing travel times, enhancing regional and international connectivity, lowering reliance on fossil fuels, and alleviating congestion on roads and at airports^1,2. However, providing continuous wireless connectivity for HSTs for both control and management and offering high-speed data connectivity for passengers presents a significant challenge². The wireless communication channel between the serving base station (BS) and the HST is highly variable due to excessive doppler frequency shifts. To maintain continuous gigabit (Gbit) data rate connectivity using high-frequency bands, a substantial number of ground BSs must be deployed alongside the HST route. This is costly, particularly in remote areas between cities and rural regions. Additionally, satellite communications, such as those using low earth orbit (LEO) satellites, cannot provide the necessary ultra-high-speed data connectivity due to their low operating frequencies and the high propagation loss coming from their high altitude of thousands of kilometers³. This paper proposes using unmanned aerial vehicles (UAVs) to ensure continuous wireless connectivity for HST, especially in rural and wilderness areas. UAVs will be deployed above the HST route to relay their information to the nearest ground BS, leveraging their flying, hovering, and maneuvering capabilities. This approach offers a cost-effective, ultra-high wireless platform for the HSTs using high-frequency band communications at low altitudes. Additionally, delay-tolerant data can be buffered in the UAVs and later offloaded to the BS after the HST has passed, then BS relays it to the subsequent UAVs along the HST route. Due to their remarkable features and low installation costs, UAVs have recently been employed in various wireless communication applications. For instance, they provide efficient solutions for disaster relief operations by acting as ad hoc wireless connection points for rescue workers and victims^4,5. They also function as flying BS to deliver connectivity in remote and rural areas and advanced applications like Metaverse⁶. Reconfigurable intelligent surfaces (RIS) can be mounted on UAVs to enhance wireless coverage in densely populated hotspots, as proposed in^7,8. Despite the rich research on UAV-based wireless communication and its various applications, there has been a limited focus on their use in HST systems, which is the primary motivation of this paper^{9,10,11,12,13}.

A key challenge in designing the multi-UAV HST system is the autonomous dynamic selection by the HST of the optimal UAV from its covering UAVs at any given time t. The selected UAV should maximize the achievable HST-UAV data rate while ensuring an extended HST coverage period to minimize frequent UAVs handovers. Additionally, since UAVs are battery feed, the selection process must consider the remaining battery capacities of the UAVs to avoid depleting them during HST coverage. A fundamental difficulty in this optimization problem is how to accurately predict the UAVs’ coverage periods, as the HST has no prior information about the UAVs’ speeds or their flying altitudes. In this paper, to address this challenge, we will utilize the estimated channel parameters in the delay-doppler (DD) domain by employing orthogonal time frequency space (OTFS) modulation^14,15,16. Unlike the global positioning system (GPS) localization, the DD channel provides detailed information about doppler frequency shifts and delay spreads, leading to more accurate sensing information than GPS positioning¹⁷.

In 2017, OTFS was introduced as an alternative to orthogonal frequency division multiplexing (OFDM), aiming to mitigate inter-carrier interference (ICI) caused by high doppler shifts^14,15. Unlike OFDM, which operates in the frequency-time (FT) domain, OTFS distributes symbols across the DD domain, maintaining orthogonality in both time and frequency domains. This enhances resilience to time-varying channels and doppler shifts^14,15. By transforming signals into a 2D representation, the DD domain allows for the estimation of channel gains, doppler frequency shifts, and delay spreads¹⁶.

Key contributions

This paper delves into utilizing the estimated DD channel parameters for HST-based UAV selection in UAV-HST communication. Therefore, the main contributions of this paper can be summarized as follows:

• Multiple UAVs are proposed to provide continuous high-data-rate connectivity for HSTs. In the proposed system model, UAVs will serve as relays between the HST and the nearest ground BS, leveraging their flying, hovering, and maneuvering capabilities. The optimal UAV selection autonomously done by the HST will be formulated as an optimization problem aimed at maximizing the HST-UAV transmitted data via maximizing both the HST-UAV achievable data rate and the HST coverage period while considering the UAVs’ remaining battery lifetimes.

• To address this optimization problem, we will utilize OTFS modulation to estimate the DD channel parameters, including the maximum doppler shift and the line of sight (LoS) delay spread. Accordingly, HST can accurately estimate the UAVs’ speeds and their flying altitudes, which is mandatory information facilitating the precise prediction of the HST coverage period offered by each covering UAV, enabling the HST to select the best among them.

• Extensive numerical analysis demonstrates the superior performance of the proposed UAV selection scheme for UAV-HST applications compared to other benchmarks relying on maximum data rate or random selection

Paper organization

The rest of this paper is structured as follows: Section “Existing Work” explores the research works within the paper’s scope. Section “Proposed UAV-HST System Model” presents the proposed system model, including UAV’s channel modeling, the optimization problem formulation, and the fundamentals of OTFS modulation. Section “Proposed OTFS Based UAV Selection in UAV-HST System” gives the proposed OTFS-based UAV selection scheme. Section “Simulation Results” highlights the conducted numerical simulations, and Section “Conclusions” concludes this paper.

Existing work

Recent research on HST operation and management covers various aspects, including speed trajectory control¹⁸, train-to-train (T2T) communications¹⁹, re-scheduling control under unavoidable disruptions²⁰, resource allocation among HSTs²¹, and fault-tolerant control²². A comprehensive survey on HST communications is also presented in¹. However, only a limited number of studies have explored UAV-assisted HST communications. In⁹, UAVs equipped with free space optical (FSO) communication terminals are employed to establish backhaul connections for HSTs, addressing challenges like atmospheric turbulence and pointing errors. However, the study did not account for the relative speeds of HSTs and UAVs and their impact on backhaul link construction. Also, no multiple UAV scenarios or optimal UAV selection were considered. In¹⁰, utilizing FSO and visible light communication (VLC) links, a novel all-optical triple-hop HST-UAV communication system for providing broadband internet access for HSTs was proposed. This study deduced closed-form expressions for the average bit error rate (BER) and outage probability while considering the influence of various environmental and system parameters. Still, the authors did not consider the optimal UAV selection problem in the rapidly changing UAV-HST environment. In¹¹, a UAV relaying for HST broadband wireless communication was proposed for meeting certain quality of service (QoS) requirements by mitigating link blockage and maximizing transmission flows. The study overlooked the crucial issue of dynamic UAV selection by only considering a static environment with UAVs hovering above the HST. In¹², a dual-band UAV-HST wireless network architecture was introduced by integrating sub-6 GHz and millimeter wave (mmWave) bands. The proposed system model used the sub-6 GHz band to establish reliable ground BS to UAV transmissions with high-capacity communication links between UAV and HST. However, the issue related to the optimal UAV selection in multi-UAV scenarios was not considered. In¹³, two mmWave links were utilized to relay flows from BS to HST via UAV, focusing on scheduling to maximize flow while meeting QoS requirements. This study enhanced the completed flow and system throughput compared to baseline schemes but only considered UAVs hovering above the HST without considering the optimal UAV selection problem in the dynamic multi-UAV-HST environment. In²³, an automatic framework for detecting potential safety hazards along high-speed railroads using UAV imagery was proposed for enhancing safety and efficiency compared to manual inspections. By leveraging multi-scale feature representation, a lightweight feature pyramid network, and a hazard level evaluation method achieved precise hazard detection and quantification, demonstrating high accuracy and processing speed in experiments with UAV datasets. In²⁴, a UAV equipped with RIS was proposed to enhance HST communication, addressing challenges such as obstructed links in mountainous regions. By comparing co-located and distributed antenna layouts on HST, the study shows that while the co-located layout maximizes average cell capacity, the distributed layout provides a more uniform capacity distribution, with the optimal choice depending on deployment needs. In²⁵, an adaptive joint communication and computation resource allocation scheme for energy optimization in a dual-band UAV and mobile relay-assisted HST offloading system was proposed. Using a deep reinforcement learning-based parameterized deep Q-network algorithm, the approach achieved lower energy consumption and high task completion rates through efficient resource allocation and offloading decisions. Despite the efficient UAV-HST proposals presented in^23,24,25, neither multi-UAV scenario nor optimal UAV selection was considered.

For OTFS-based UAV-HST communications, the only paper that exists in literature is proposed by the authors of this paper in²⁶. This paper proposes a UAV with OTFS modulation to provide continuous high-data-rate connectivity for an HST, overcoming the challenges posed by their extreme speeds and the limitations of ground BSs and satellites. By estimating relative velocities and separation distances using DD channel parameters, the method enables proactive UAV positioning, optimizing coverage time and transmission rates, as validated through analytical and numerical analysis. However, the problem of optimal UAV selection was not investigated.

To the best of our knowledge, no existing research on UAV-HST systems has tackled the critical problem of optimal UAV selection to maximize the UAV-HST transmission rate while ensuring extended HST coverage, considering the limited battery budget of UAVs in this highly dynamic environment. This study aims to address this research gap effectively.

Fig. 1

Proposed UAV-HST system model.

Proposed UAV-HST system model

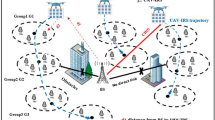
In the proposed system model, multiple UAVs are deployed above the HST route to relay information between the nearest ground BS and HST, as shown in Fig. 1. The UAVs fly at different altitudes with different speeds. This is considered an efficient and cost-effective solution for continuous HST coverage, especially in remote and rural areas among cities. Given its ultra-high speed, establishing several ground BSs alongside the HST route to achieve full coverage in these regions will be difficult and too expensive. Alternatively, the high-altitude LEO-Sats cannot provide the massive data rates needed for HST applications. In the proposed multi-UAV-HST system is shown in Fig. 1, mobile relays (MRs) are mounted on the top of HST to establish wireless connections with the UAVs using high-bandwidth communication links. Thanks to UAV buffering and to compensate for the high train speed, time-tolerant data can be stored and relayed to the ground BS even after the HST exits UAV coverage. In contrast, time-sensitive data will be immediately forwarded to the BS. To maintain continuous coverage, the HST will smoothly transition between UAVs along its path. One major challenge of this system is the dynamic optimal UAV selection from those currently covering the HST to maximize the HST-UAV transmitted data subject to UAVs’ remaining battery capacities. The HST should autonomously manage this due to the challenges of maintaining a continuous direct communication link between the BS and the HST, which stems from the limited number of BSs and the train’s ultra-high speed. These factors withstand the applicability of centralized control through the BS.

For the rest of this section, the used UAV to ground channel modeling will be presented, the optimization problem will be formulated, and the fundamentals of OTFS modulation/demodulation, including its mathematical foundation, will be given.

Air to ground channel modeling

Due to the lack of a dedicated UAV-HST channel modeling in literature, we utilized that presented in²⁷ for aerial-to-ground (A2G) channel modeling designed for hilly and mountainous environments. This will not lose the generalization of the proposed approach as it applies to any UAV channel modeling. The authors in²⁷ developed their A2G channel model through a conducted field measurements campaign in various hilly and mountainous settings. A fixed-wing UAV flying at an average altitude of 542 meters communicating with a ground BS was used to perform channel measurements using various flight paths. The measured frequency bands are L (0.9–1.2 GHz) and C (5.03–5.09 GHz) bands. In this paper, we adopted the hilly Latrobe model as it is the most appropriate to our study²⁷. The detailed structures of the sounder system used for transmitter (Tx) and receiver (Rx) are given in²⁷. The complex delay-time (DT) channel impulse response (CIR) using this modeling is stated as²⁷:

$$\begin{aligned} h_{DT}\left( \alpha ,t\right) =\sum _{i=1}^{P}{h_{i,t}e^{-j2\pi \beta _{i,t}t}}\delta (\alpha -\alpha _{i,t}), \end{aligned}$$

(1)

Here, $h_{i,t}$ represents the complex amplitude of path i at time t, while $\alpha _{i,t}$ and $\beta _{i,t}$ indicate its delay spread and doppler shift, respectively. LoS path is represented by $i=1$, where P is the total number of paths and $\delta (\cdot )$ is the Dirac delta function. Large-scale path loss is used to evaluate the relative power of the LoS path $h_{1,t}$ in dB as follows:

$$\begin{aligned} {PL}_{h_{1,t}}[dB]=PL_0+10nlog(d/d_0)+\rho +\xi C_0, \end{aligned}$$

(2)

where d denotes the separation distance between Tx and Rx, and ${PL}_0$ signifies the reference path loss at the reference distance $d_0$. The log-normal shadowing term is represented by $\rho \sim \mathcal {N}(0,\sigma _\rho ^2)$ with zero mean and standard deviation of $\sigma _\rho$. $C_o$ acts as a correction factor in dB, where the parameter $\xi$ denotes the UAV flight direction, taking a value of $-1$ if the UAV flies towards the MR and 1 otherwise. The relative power of $h_{i,t}^2/h_{1,t}^2, 2\le i\le P$, comes from Gaussian distribution with mean and standard deviation values of ($-30$.8 dB, 3.9 dB) for the hilly Latrobe model employed in this paper²⁷.

For $\alpha _{i,t}$ modeling, $\alpha _{1,t}=d/\epsilon$ in seconds is attributed to the LoS path where $\epsilon$ represents the speed of light. The remaining delay taps $\alpha _{i,t}, 2\le i\le P$, are derived using this empirical equation:

$$\begin{aligned} {log}_{10}(\alpha _{i,t})=A_{\alpha _i}+n_{\alpha _i}\left( d-d_0\right) +\rho _{\alpha _i}, \end{aligned}$$

(3)

The constant $A_{\alpha _i}$ represents the linear correlation between the extra delay of path i and the link distance d in kilometers, as outlined in²⁷. $n_{\alpha _i}$ indicates the gradient of this relationship, while $\rho _{\alpha _i}\sim \mathcal {N}(0,\sigma _{\alpha _i}^2)$ signifies a Gaussian random variable with a mean of zero and a standard deviation of $\sigma _{\alpha _i}$. The specific numerical values for these parameters can be found in²⁷. For path 2 in the hilly Latrobe model, the average values of these parameters are $A_{\alpha _2}=2.664$ ns, $n_{\alpha _2}=-0.0029$ ns, and $\sigma _{\alpha _2}=0.0645$ ns, which are employed to calculate $\alpha _{2,t}$.

Jackes spectrum model is used to evaluate $\beta _{i,t}$ as given in²⁸:

$$\begin{aligned} \beta _{i,t}=\beta _{max}\cos {\left( \varphi _{i,t}\right) } \end{aligned}$$

(4)

where, the maximum doppler frequency is expressed by $\beta _{max}$ which is equal to $v_Uf/\epsilon$, where $v_U$ is the speed of the UAV, and f represents the operating frequency. $\varphi _{i,t}$ represents the angle of arrival of path i at time t coming from a uniform distribution in the range of $[-\pi ,\pi ]$²⁸. Comprehensive information about the Jackes spectrum model, including the derivation of the probability density function of the doppler frequencies and the doppler power spectrum efficiency, can be found in Appendix A of reference²⁸.

Fig. 2

Schematic diagram of UAV-HST coverage.

Optimization problem formulation

From Fig. 1, we assumed that both HST and UAVs are located on the same Y plan, and HST is traveling along the X-axis at a velocity of $v_{S,t}$ m/s at time t. Also, the number of UAVs is Q, $1\le q\le Q$, and each UAV q flies horizontally along the X-direction with a different velocity of $v_{q,t}$ m/s and at a different altitude of $Z_{q,t}$. A schematic diagram of HST coverage using a UAV q at time t is presented in Fig. 2. In this figure, the farthest MR of the HST is located at $X_{S,t}$, while UAV q is located at $X_{q,t}$ and $Z_{q,t}$ with an elevation angle $\theta _q$. $d_{C_q,t}=Z_{q,t}/\cos {(\theta _q)}$ represents the coverage distance of the UAV when flying at altitude $Z_{q,t}$, and $d_{q,t}$ indicates the actual distance between UAV q and the farthest MR. In this context, $\theta _q$ is the sector angle of the UAV antenna pattern, which is defined by manufacturer beforehand. Thus, it can be fixed for the UAV-HST system modeling during installations. Thus, $d_{q,t}\le d_{C_q,t}$, is an essential condition for HST coverage using UAV q. Among $Q_t\subset Q$, which is the subset of UAVs that cover the HST at time t satisfying $d_{q,t}\le d_{C_q,t}$, the HST should autonomously select the optimal UAV maximizing the total HST-UAV transmitted data. This implies maximizing the HST-UAV achievable data rate $\psi _{q,t}$ and the HST coverage period $\tau _{q,t}$ provided by UAV q. This should be subject to the UAVs’ remaining battery capacities. In mathematical representation, this can be formulated as follows:

$$\begin{aligned}&\max _{q\in Q_t} \left( \psi _{q,t}\tau _{q,t}\right) \nonumber \\&\text {Subject to} \end{aligned}$$

(5)

$$\begin{aligned}&Z_{q,t}\in \left\{ Z_{Umin},\ Z_{Umax}\right\} \end{aligned}$$

(5a)

$$\begin{aligned}&d_{q,t}\le d_{C_q,t} \end{aligned}$$

(5b)

$$\begin{aligned}&P_{U_q}\tau _{q,t}<E_{R_q,t} \end{aligned}$$

(5c)

$$\begin{aligned}&v_{S,t}\le v_{Smax}, \end{aligned}$$

(5d)

$$\begin{aligned}&v_{q,t}\le v_{Umax}, \end{aligned}$$

(5e)

where

$$\begin{aligned} \psi _{q,t}={Blog}_2\left( 1+\frac{P_{t_q}\left| h_{DT,q}\left( \alpha ,t\right) \right| ^2}{\ \sigma _g^2}\right) , \end{aligned}$$

(6)

B indicates the available bandwidth, $P_{t_q}$ is the UAV Tx power (assuming downlink without loss of generalization), and $\sigma _g^2$ is the additive white gaussian noise (AWGN) power. $\left| h_{DT,q}\left( \alpha ,t\right) \right| ^2$ is the DT channel power between UAV q and the HST at time t as stated in Eq. (1). Also, $\tau _{q,t}$ is upper bounded by:

$$\begin{aligned} \tau _{q,t}\le \frac{Z_{q,t} tan(\theta _q)-\Delta X_{S,q}}{(v_{S,t}-v_{q,t})}, \end{aligned}$$

(7)

where $\Delta X_{S,q}$ indicates the offset in the start X position between HST and UAV q. This comes from the second constraint of Eq.(5), which can be re-written as:

$$\begin{aligned} \left( X_{S,t}-X_{q,t}\right) \le Z_{q,t}tan(\theta _q), \end{aligned}$$

(8)

Considering HST and UAV speeds, Eq. (8) can be formulated as:

$$\begin{aligned} \tau _{q,t}\left( v_{S,t}-v_{q,t}\right) +\Delta X_{S,q} \le Z_{q,t} tan(\theta _q), \end{aligned}$$

(9)

which gives Eq. (7). If UAV q starts flying horizontally as soon as HST becomes under its coverage, then both will start from the same X-position, implying $\Delta X_{S,q}=0$.

The first constraint in (5) indicates that the flying altitude of UAV q should lie between its minimum allowable altitude $Z_{Umin}$ and the maximum altitude $Z_{Umax}$. In this regard, $Z_{Umin}=L_S/2\tan (\theta _q)$, where $L_S$ refers to the whole HST length, indicates the minimum UAV flying altitude satisfying the full HST coverage. $Z_{Umax}=d_{C_qmax}\cos {(\theta _q)}$, where $d_{C_qmax}$ is the maximum UAV coverage distance corresponding to the maximum allowable path loss as given in Eq. (2), $\left( i.e.,\ d_{C_qmax}={d_0\times 10}^{\left( \frac{{PL}_{Max}-{PL}_0-\xi C_o}{10n}\right) }\right)$. The second constraint means that all MRs should be covered by UAV q. The third constraint indicates that the UAV energy consumed in HST coverage should be less than its remaining battery capacity $E_{R_q,t}$. Actually, there are eight sources of UAV power consumption, as given in detail in²⁹. However, the flying, $P_f$, and the hovering, $P_h$, including thrust power consumption are the most dominant ones, as shown in²⁹, with flying consumes more energy than hovering²⁹. Both $P_f$ and $P_h$ are related to the mass of the UAV, the gravitational force, the radius of the propeller, and the air density. In addition, $P_f$ depends on the deviation angle between the UAV vertical axis and the Z axis, as shown in²⁹. For more details about various sources of UAV power consumptions and their mathematical details, interested readers are advised to check²⁹. Herein, $P_{U_q}$ is equal to:

$$\begin{aligned} P_{U_q}=P_{f_q}+P_{h_q}+P_{t_q}, \end{aligned}$$

(10)

where $P_{f_q}$ and $P_{t_q}$ are the flying and Tx powers of UAV q, while $P_{h_q}$ is its hovering power including the thrust power. Finally, the fourth and fifth constraints ensure that the UAV and HST speeds did not exceed their maximum allowable values, i.e., $v_{Smax}$ and $v_{Umax}$, respectively. The optimization problem presented in Eq. (5) constitutes a highly dynamic non-linear programming challenge. Furthermore, the HST has no prior information about the upper bound of $\tau _{q,t}$ provided by each UAV as it has no information about their flying speeds or altitudes at time t as given in Eq. (7). Nevertheless, the selection process should be bounded by the UAVs remaining battery capacities at time t, $E_{R_q,t}$. This renders the optimal exhaustive search solution impractical due to the absence of this information in this autonomous decision-making environment.

Fig. 3

OTFS Baseband Modulation/Demodulation.

OTFS modulation/demodulation

In this subsection, we will explain the principles of OTFS modulation and demodulation, including its mathematical foundations. Figure 3 represents the basic block diagram of the OTFS baseband communication system. The complex modulation symbols, e.g., quadrature amplitude modulation (QAM) symbols, $s_{DD}[l,k]\in C^{M\times N}$ are arranged in a two-dimensional matrix of size $M \times N$, where $0\le l\le M-1$ and $0\le k\le N-1$, denoting the delay and doppler dimensions in the DD grid, respectively. The total duration of the OTFS symbol is equal to NT seconds. It occupies a $B=M\Delta f$ Hz bandwidth, where T and $\Delta f$ represent the duration of the modulation symbol and the subcarrier spacing, respectively, with $\Delta fT=1$. The Doppler and delay resolutions are $\frac{1}{NT}$ and $\frac{1}{M\Delta f}$, respectively. In the following, we will review the mathematical foundations of OTFS modulation/demodulation.

OTFS modulation

Inverse symplectic Fourier transform (ISSFT) is the first stage in the OTFS modulation, which is used to convert $s_{DD}[l,k]$ from the DD domain into $s_{FT}[m,n]\in C^{M\times N}$ in the FT domain. In ISFFT, fast Fourier transform (FFT) is applied across the delay domain of $s_{DD}$, while inverse FFT (IFFT) is applied across its doppler domain, as follows¹⁴:

$$\begin{aligned} s_{FT}[m,n]= \sum _{l=0}^{M-1}{\sum _{k=0}^{N-1}{s_{DD}[l,k] e^{j2\pi \left( \frac{nk}{N}-\frac{ml}{M}\right) },}} \end{aligned}$$

(11)

The one-dimensional Tx signal, $x_{DT}(t)]\in C^{MN \times 1}$, in the DT domain, is generated using the Heisenberg transform, see Fig. 1, employing a windowing function $b_{TX}(t)$ as follows¹⁴:

$$\begin{aligned} x_{DT}(t)= \sum _{l=0}^{M-1}{\sum _{k=0}^{N-1}{s_{FT}[m,n]b_{Tx}(t-nT) e^{j2\pi m \Delta f(t-nT)},}} \end{aligned}$$

(12)

DD channel

The signal $x_{DT}(t)$ is transmitted through the DD channel $h_{DD}(\alpha ,\beta )$, which is expressed as:

$$\begin{aligned} h_{DD}(\alpha ,\beta )=\sum _{i=1}^{P}{h_i\delta (\alpha -\alpha _i)\delta (\beta -\beta _i)} \end{aligned}$$

(13)

where $\alpha$ and $\beta$ denote the continuous delay and doppler shift, respectively. In addition, the parameters of the DD channel P, $h_i$, $\alpha _i$, and $\beta _i$ are defined in Eq. (1), where their given values are specified in Section III-A of the measurement campaign given in²⁷. As we are concerned with the duration of an OTFS symbol, we have omitted the subscript t in Eq. (13) as it indicates one OTFS symbol. In discrete form, the DD channel can be represented as:

$$\begin{aligned} h_{DD}[l,k]= \sum _{i=1}^{P}{h_i\delta (l-l_i)\delta (k-k_i)}, \end{aligned}$$

(14)

where the indices $l_i$ and $k_i$ denote the normalized delay and Doppler taps corresponding to the continuous values $\alpha _i$ and $\beta _i$ defined as:

$$\begin{aligned} \alpha _i=\frac{l_i}{M\Delta f}< \frac{lmax}{M\Delta f}=\alpha _{max}, \beta _i=\frac{k_i}{NT}<\frac{k_{max}}{NT}=\beta _{max}, \end{aligned}$$

(15)

In this context, the maximum indices $l_{max}<M$ and $\left| k_{max}\right| <N/2$ are related to the maximum delay spread $\alpha _{max}$ and doppler shift $\beta _{max}$ as given in Eq. (15).

OTFS demodulation

At the receiver side, the received DT signal $r_{DT}(t)$ shown in Fig. 3 is expressed as¹⁴:

$$\begin{aligned} \hspace{-3mm}r_{DT}(t)=\iint {h_{DD}(\alpha ,\beta )x_{DT}(t-\alpha )e^{j2\pi \beta (t-\alpha )}}d\alpha d\beta +g_{DT}(t) \end{aligned}$$

(16)

where, $g_{DT}(t)\sim \mathcal {N}(0,\sigma _g^2)$ is the AWGN noise term with zero mean and standard deviation of $\sigma _g$. Wigner transform is applied on $r_{DT}(t)$ to inverse the ISFFT operation, performed on the Tx side, by representing $r_{DT}(t)$ back into the FT domain, using the received pulse $b_{Rx}(t)$, as follows¹⁴:

$$\begin{aligned} y(f,t)=\int {b_{Rx}^*(t^\prime -t)r_{DT}(t^\prime )e^{j2\pi f(t^\prime -t)}dt^\prime } \end{aligned}$$

(17)

In discrete representation, y(f, t) is sampled at $f=m \Delta f$ and $t=nT$ to produce $y_{FT}[m,n]$ in the FT domain¹⁴:

$$\begin{aligned} y_{FT}\left[ m,n\right] =y(f,t)f=m\Delta f,t=nT \end{aligned}$$

(18)

In¹⁵, it is proved that the input-output relationship in the FT domain between $y_{FT}\left[ m,n\right]$ and $s_{FT}[m,n]$ given in Eq. (11) is as follows:

$$\begin{aligned} y_{FT}[m,n] =H_{FT}[m,n]s_{FT}[m,n]+G_{FT}[m,n], \end{aligned}$$

(19)

where $G_{FT}[m,n]$is the sampled AWGN in the FT domain and $H_{FT}[m,n]$ indicates the FT channel response, formulated as¹⁵:

$$\begin{aligned} H_{FT}\left[ m,n\right] = \iint h_{DD}(\alpha ,\beta )e^{j2\pi \beta nT}e^{-j2\pi (\beta +m\Delta f)\alpha } d\alpha d\beta \end{aligned}$$

(20)

To retrieve the Rx signal in the DD domain, $y_{DD}[l,k]$, SFFT is applied on $y_{FT}[m,n]$ as follows¹⁴:

$$\begin{aligned} y_{DD}[l,k]= \frac{1}{MN} \sum _{m=0}^{M-1}{\sum _{n=0}^{N-1}{y_{FT}[m,n]e^{-j2\pi (\frac{nk}{N}-\frac{ml}{M})}}} \end{aligned}$$

(21)

Thus, the overall input–output relationship in the DD domain between $s_{DD}[l,k]$ and $y_{DD}[l,k]$ can be deduced by substituting Eqs. (11) and (20) into Eq. (19), then substitute the results into Eq. (21) assuming bi-orthogonal pulses¹⁴:

$$\begin{aligned} y_{DD}\left[ l,k\right] = \frac{1}{MN} \sum _{l'=0}^{M-1}{\sum _{k'=0}^{N-1}{s_{DD}[l',k']h_{DD}^w[l-l',k-k']+G_{DD}[l,k]}} \end{aligned}$$

(22)

where $G_{DD}[l,k]$ is the AWGN in the DD domain, and $h_{DD}^w[{{l-l}^\prime ,k-k}^\prime ]$ denotes the windowed CIR in DD domain, where $h_{DD}^w[l,k]$ is given by¹⁵:

$$\begin{aligned} h_{DD}^w[l,k]=\sum _{i=1}^{P}h_i e^{-j2\pi \left( \frac{l_ik_i}{NM}\right) }w[l-l_i,k-k_i], \end{aligned}$$

(23)

As described in¹⁵, $h_{DD}^w[l,k]$ is obtained by the circular convolution of the CIR with the SFFT of a rectangular window function w[l, k], defined as:

$$\begin{aligned} w[l,k]= \sum _{m=0}^{M-1}{\sum _{n=0}^{N-1} {1.e^{-j2 \pi \left( \frac{nk}{N}-\frac{ml}{M}\right) }}} \end{aligned}$$

(24)

Proposed OTFS based UAV selection in UAV-HST system

In this section, to efficiently address the optimization problem given in Eq. (5), we propose to use OTFS modulation to estimate the DD channel parameters between HST and all Q UAVs at time t. By utilizing these DD channel estimates, the HST can predict $Q_t$ as well as the upper bound of $\tau _{q,t} \forall q\in Q_t$. Then, HST can select the best UAV among $Q_t$, which maximizes Eq. (5). To do that, the HST should estimate DD channel parameters, ${\hat{\alpha }}_{1_q,t}$ and ${\hat{\beta }}_{{max}_q,t} \forall q\in Q$. This can be accomplished using the scheme given in¹⁶. In this approach, techniques for DD channel estimation using embedded pilot-aided methods were introduced. Within each OTFS frame, pilot, guard, and data symbols are carefully placed in the DD domain to accommodate both integer and fractional doppler shifts. A single pilot symbol is transmitted within guard symbols in the DD grid. At the Rx, the pilot symbol spreads throughout the DD grid due to circular convolution with the CIR in the DD domain. DD taps are detected based on specific signal-to-noise ratio (SNR) thresholds at the Rx. When the SNR at a particular location in the DD grid exceeds the threshold, it indicates the presence of a path at that location with certain $l_i$ and $k_i$ values. From the received symbols, the DD channel parameters, such as channel gains $h_{i,t}$, delay taps $l_{i,t}$, and doppler taps $k_{i,t}$ are estimated for all UAV-HST channels. Subsequently, the maximum ${\hat{\alpha }}_{1_q,t}$ corresponding to the farthest MR and ${\hat{\beta }}_{{max}_q,t}$ between the HST and UAV q are derived from their respective $l_{1_q,t}$ and $k_{{max}_q,t}$ values using Eq. (15). We considered the impact of DD channel estimation errors to utilize OTFS-estimated DD channel parameters for HST-based UAV selection. Following the method outlined in³⁰, the channel estimation error is modeled as Gaussian random variables. Thus, accounting for estimation errors, ${\hat{\alpha }}_{1_q,t}$ and ${\hat{\beta }}_{{max}_q,t}$ can be expressed as³⁰:

$$\begin{aligned} {\hat{\beta }}_{{max}_q,t}=\beta _{{max}_q,t}+\Delta \beta , {\hat{\alpha }}_{1_q,t}=\alpha _{1_q,t}+\Delta \alpha , \end{aligned}$$

(25)

where the exact values of the LoS delay spread and the maximum doppler shift are represented by $\alpha _{1_q,t}$ and $\beta _{{max}_q,t}$, and $\Delta _{\beta }=\mathcal {N}(0,\sigma _{\beta }^2)$ and $\Delta _{\alpha }=\mathcal {N}(0,\sigma _{\alpha }^2)$ are two normal random variables with zero means and standard deviations of $\sigma _\beta$ and $\sigma _\alpha$, respectively³⁰.

Based on ${\hat{\beta }}_{{max}_q,t}$, HST can estimate the relative velocity between it and UAV q, ${\hat{v}}_{qS,t}$, and then the current speed of UAV q, ${\hat{v}}_{q,t}$, as follows:

$$\begin{aligned} {\hat{v}}_{qS,t}={\hat{\beta }}_{{max}_q,t}\epsilon /f,\ {\ \hat{v}}_{q,t}=v_{S,t}-{\hat{v}}_{qS,t},\ \forall q\in Q, v_{S,t}\le v_{Smax}, {\hat{v}}_{q,t}\le v_{Umax} \end{aligned}$$

(26)

The HST will check if the condition ${\hat{v}}_{q,t}\le v_{Umax}$ is satisfied or not, and if it is not satisfied, it will put ${\hat{v}}_{q,t}=v_{Umax}$. Based on ${\hat{v}}_{q,t}$ and by assuming that the HST awares by its current location ${X}_{S,t}$, the HST can estimate the X-positions of all UAVs as follows:

$$\begin{aligned} {\hat{X}}_{q,t}={{X}}_{S,t}{\hat{v}}_{q,t}/v_{S,t}, \forall q\in Q \end{aligned}$$

(27)

From ${\hat{\alpha }}_{1_q,t}$ and by referring to Fig. 2, HST can estimate the separation distance, ${\hat{d}}_{q,t}$, between it and all UAVs:

$$\begin{aligned} {\hat{d}}_{q,t}={\hat{\alpha }}_{1_q,t}\epsilon , \forall q\in Q \end{aligned}$$

(28)

Then, it can estimate the flying altitudes of all UAVs:

$$\begin{aligned} {\hat{Z}}_{q,t}=\sqrt{{{\hat{d}}_{q,t}}^2-\left( X_{s,t}-{\hat{X}}_{q,t}\right) ^2} \forall q\in Q \end{aligned}$$

(29)

The HST will estimate ${\hat{d}}_{C_q,t}={\hat{Z}}_{q,t}/\cos {(\theta _q)}$, and then it will check if condition ${\hat{d}}_{q,t}\le {\hat{d}}_{C_q,t}$ is satisfied or not. If this is satisfied, then UAV q will be considered as a candidate UAV for HST coverage at time t, i.e., $q\in Q_t$; otherwise, it will be considered as an uncovering UAV at time t. Suppose the UAV is considered as a candidate covering UAV. In that case, its upper bound of $\tau _{q,t}$ will be estimated using Eq. (7) for its pre-designed $\theta _q$ value while assuming all UAVs start flying horizontally as soon as HST becomes under their coverage, and then $\Delta X_{S,q}=0 \forall q\in Q_t$ as follows:

$$\begin{aligned} {\hat{\tau }}_{q,t}^{UP}=\frac{{\hat{Z}}_{q,t}tan(\theta _q)}{\left( v_{S,t}-{\hat{v}}_{q,t}\right) }\, \forall q\in Q_t \end{aligned}$$

(30)

As given by Eq. (7), $\Delta X_{S,q}$ is just a constant indicating the initial distance offset value, and it is not the main factor affecting $\tau _{q,t}$, where $Z_{q,t}$, $v_{S,t}$, and $v_{q,t}$ represent the dominant factors belong to the UAV and HST characteristics including their speeds and UAV flying altitudes. So, for simplicity and fair comparisons among candidate UAVs, we relaxed this initial offset to be equal 0 for all candidate UAVs in Eq. (30) without affecting the solution of the optimization problem by any means. This assumption ensures that UAVs can provide uninterrupted coverage as soon as the HST enters their operational range. This maximizes both $\psi _{q,t}$ and $\tau _{q,t}$. If $\Delta X_{S,q}\ne 0$, the UAV would require additional time and energy to align with the HST, potentially reducing the efficiency of the system. Thus, $\Delta X_{S,q}=0$ assumption represents a boundary condition for optimal performance. From a practical perspective, modern UAV systems are typically deployed from pre-determined points, such as ground-based stations, mobile platforms, or launch systems, that can be strategically synchronized with the movement of an HST. The pre-planned HST trajectories allow UAV deployment to be coordinated with near-zero offsets, where advanced technologies such as GPS and automated dispatch systems enable this precise alignment, making $\Delta X_{S,q}=0$ a realistic assumption under controlled operational conditions.

The UAV coverage time is constrained by $E_{R_q,t}, \forall q\in Q_t$, as given in the third constraint in Eq. (5). Thus, the estimated coverage time of UAV q should be the minimum between ${\hat{\tau }}_{q,t}^{UP}$ and its remaining battery lifetime, which is evaluated as:

$$\begin{aligned} {\hat{\tau }}_{q,t}=\min {\left( {\hat{\tau }}_{q,t}^{UP},E_{R_q,t}/P_{U_q}\ \right) ,\ \ \ \ \ \forall q\in Q_t} \end{aligned}$$

(31)

After estimating ${\hat{\tau }}_{q,t}$, the HST will select the best UAV $q_t^*$ among $Q_t$, which maximizes $\left( \psi _{q,t}{\hat{\tau }}_{q,t}\right)$ as the objective of Eq. (5). Algorithm 1 summarizes the proposed OTFS-based UAV selection in a multi-UAV-HST system. This algorithm will be implemented in the HST for the autonomous UAV selection process. The algorithm output is the best UAV $q_t^*$ for covering the HST at time t, while the inputs are t, Q, $\epsilon$, f, and $\theta$, $E_{R_q,t}$, $v_{S,t}$, $X_{S,t}$. In this context, all UAVs are assumed to have the same value of $\theta$ pre-known by the HST as it is fixed by manufacturer beforehand. At first, the HST will estimate ${\hat{l}}_{1_q,t}$ and ${\hat{k}}_{{max}_q,t}\ \forall q\in Q$ using OTFS DD channel estimation techniques similar to the one given in¹⁶, and then the values of ${\hat{\alpha }}_{1_q,t}$ and ${\hat{\beta }}_{{max}_q,t} \forall q\in Q$ can be estimated using Eq. (15). Afterward, the value of ${\hat{v}}_{q,t}$ is evaluated using Eq. (26), and if the condition ${\hat{v}}_{q,t}\le v_{Umax}$ is not satisfied, then ${\hat{v}}_{q,t}=v_{Umax}$. The value of ${\hat{X}}_{q,t} \forall q\in Q$ is evaluated using Eq. (27). Then, the values of ${\hat{d}}_{q,t}$ and ${\hat{Z}}_{q,t} \forall q\in Q$ are calculated using Eqs. (28) and (29), respectively. The subset of UAVs $Q_t\subset Q$, satisfying the condition ${\hat{d}}_{q,t}\le {\hat{d}}_{C_q,t}$, is enumerated. Then after calculating ${\hat{\tau }}_{q,t}^{UP}$ and ${\hat{\tau }}_{q,t}$ using Eqs. (30) and (31), the HST can select the best UAV at time t, i.e., $q_t^*$ ,from $Q_t$ as given in Algorithm 1.

Although DD channel information between UAVs and HST is used to facilitate the selection of the best UAV, it can be used to prevent physical collisions among UAVs, as well. In this procedure, UAVs can share their estimated positions and velocities derived from their inter-DD channel information via a centralized or distributed network. Then, a minimum separation-distance threshold is defined to ensure safety among UAVs. This shared data along with the predefined minimum distance allows joint proactive trajectory planning for UAVs while preventing their physical collisions. However, this point needs more investigations, including network design and orchestrations, optimization problem formulation, minimum separation distance adjustment, OTFS based joint collision free proactive UAVs trajectory planning, which is left for future investigations.

Algorithm 1

OTFS-based UAV selection

Simulation results

In this section, comprehensive numerical analyses are conducted to validate the effectiveness of the proposed algorithm. Multiple numbers of UAVs are randomly distributed above the HST with random altitudes in the range of $\left\{ Z_{Umin},\ Z_{Umax}\right\}$ where $Z_{Umin}\approx 10m$ corresponding to HST length $L_S$ of 230 m while $Z_{Umax}=351m$ corresponding to ${PL}_{Max}$ of 120 dB. UAVs’ speeds are randomly allocated in the range of $\left\{ 10,\ 60\right\}$ km/h. $P_{t_q}=10$ mWatt, $P_{f_q}=4$ Watt³¹, $P_{h_q}=2$ Watt³¹ and $\theta _q = 85^\circ$; other simulation parameters are listed in Table 1 unless otherwise stated. As this study represents the first research effort to address the problem of UAV selection specifically tailored to HST scenarios, we employed fundamental benchmarks for performance comparisons, including optimal, maximum-rate, and random UAV selection schemes. In the optimal approach, HST is assumed to have precise prior knowledge of the expected coverage durations and achievable data rates of all UAVs. This information is then used to select the optimal UAV that maximizes the objective function at each time instant t through exhaustive search. While this scheme is practically infeasible-earning its characterization as an oracle algorithm-its performance serves as an upper bound for the objective function and thus provides a valuable benchmark. The maximum-rate scheme, a baseline approach in wireless communications, selects the UAV offering the highest instantaneous data rate without regard to its coverage duration. This method is included as a reference point for comparison. Finally, the random selection scheme, in which the HST arbitrarily selects a UAV, is considered to highlight the performance gains achieved by more systematic selection strategies. Compared to these benchmarks, the proposed scheme leveraged OTFS to extract high-resolution DD channel information, which is particularly effective in high-mobility scenarios, such as UAV-HST communications under consideration. Also, it incorporates UAVs mobility constraints including their velocities, coverage periods, and remaining battery capacities, ensuring practical feasibility. These mobility constraints are overlooked by benchmarks leading to inefficient UAV selections. Finally, the proposed framework balances coverage time, data rate, and mobility constraints, outperforming traditional utility-based methods that focus on a single metric. For performance assessment, we are interested in measuring the average HST- UAV achievable data rate $\overline{\psi _{q,t}}$ in Mbps, the average HST coverage time $\bar{\tau }_{q,t}$ in sec, and the average transmitted data $\overline{(\psi _{q,t}\tau _{q,t})}$ in Gbits. Additionally, average energy efficiency $\overline{(\psi _{q,t}\tau _{q,t})/E_{R_q,t}}$ in MbpJ will be assessed.

Table 1 Simulation parameters.

Against the number of UAVs

In this part of numerical simulations, we evaluate the performance of the schemes involved in the comparisons against varying the number of UAVs. At the same time, HST maintains a constant speed of $v_{Smax}=120$ km/h. Figures 4, 5, 6 and 7 show the performances of the compared schemes against the number of UAVs, while assuming perfect DD channel estimation, i.e., $\sigma _\alpha =\sigma _\beta =0$.

Figure 4 illustrates the average data rate performance in Mbps of the compared schemes as a function of the number of UAVs. All schemes, except for the “Random” scheme, demonstrate an upward trend with an increasing number of UAVs. This improvement is attributed to the higher probability of identifying a UAV with lower altitude and higher data rate. Additionally, assuming no DD channel estimation error, the proposed scheme aligns precisely with the optimal performance, as both select the UAV that maximizes Eq. (5). However, the proposed scheme differs from the optimal one in that it does not have prior information about the UAVs’ coverage times. Instead, it estimates these times using OTFS modulation as detailed in Section IV. The “Maximum Rate” scheme achieves the highest data rate performance by selecting the UAV that maximizes the achievable data rate at each time t, irrespective of its coverage duration. In contrast, the “Random” selection scheme maintains constant performance regardless of the number of UAVs, as it randomly selects a UAV at each time t. When the number of UAVs is set to 10, both the proposed and optimal schemes achieve a data rate that is 84% of that of the “Maximum Rate” scheme, and 1.33 times higher than the “Random” scheme. These values increase to 89% and 1.72 times, respectively, as the number of UAVs reaches 100.

Fig. 4

Average data rate against number of UAVs using fixed train speed of 120 km/h.

Fig. 5

Average HST coverage time against number of UAVs using fixed train speed of 120 km/h.

Fig. 6

Average transmitted data against number of UAVs using fixed train speed of 120 km/h.

Fig. 7

Average energy efficiency against number of UAVs using fixed train speed of 120 km/h.

Figure 5 presents the average HST coverage time performance in sec as a function of the number of UAVs, with a fixed train speed of 120 km/h. Without channel estimation error, the proposed scheme precisely matches the optimal performance. Both schemes exhibit improved performance with increasing the number of UAVs. This enhancement is due to the selection of the UAV that maximizes both the achievable HST-UAV data rate and the HST coverage time. The “Random” scheme maintains constant performance regardless of the number of deployed UAVs, as it arbitrarily selects the covering UAV at each time t. Notably, the HST coverage time performance of the “Maximum Rate” scheme is lower than that of the “Random” scheme and decreases as the number of UAVs increases. This is because the “Maximum Rate” scheme selects the UAV with the highest data rate, which typically has the lowest altitude, thereby reducing the upper bound of the HST coverage time as described by Eq. (30). From Fig. 5, when the number of UAVs is set to 10, the proposed and optimal schemes achieve HST coverage times that are 4.45 and 1.88 times higher than those of the “Maximum Rate” and “Random” schemes, respectively. When the number of UAVs is increased to 100, these values rise to 12.47 and 2.44 times, respectively.

Figure 6 presents the average transmitted data performance in Gbits, aligned with the objective of Eq. (5), for the compared schemes as a function of the number of UAVs. Both the proposed and optimal schemes select the UAV that maximizes Eq. (5) at each time t, thereby exhibiting the highest performance levels. In the absence of channel estimation error, the proposed scheme precisely matches the optimal performance. The “Random” scheme maintains a constant performance, influenced by its data rate and HST coverage time metrics. For the “Maximum Rate” scheme, the predominant impact of HST coverage time over achievable data rate results in decreasing transmitted data performance with increasing the number of UAVs. As illustrated in Fig. 6, when the number of UAVs is set to 10, the proposed and optimal schemes achieve transmitted data performances that are 3.7 and 2.5 times higher than those of the “Maximum Rate” and “Random” schemes, respectively. When the number of UAVs is increased to 100, these values escalate to 11.09 and 4.2 times, respectively.

Figure 7 depicts the average energy efficiency performances in MbpJ of the compared schemes against the number of UAVs. The proposed scheme selects the UAV that maximizes the HST achievable data, constrained by UAVs’ remaining battery capacities, resulting in the highest energy efficiency performance. This exactly matches the optimal scheme as no channel estimation error is assumed. In contrast, the “Maximum Rate” scheme experiences a significant decline in performance with an increasing number of UAVs. This decline occurs because the “Maximum Rate” scheme prioritizes selecting the UAV that maximizes the HST-UAV data rate without considering its expected HST coverage time or remaining battery capacity, thereby reducing its energy efficiency. From Fig. 7, with 10 UAVs, the proposed scheme achieves energy efficiency that is 2.47 and 1.62 times higher than that of the “Maximum Rate” and “Random” schemes, respectively. These values change to 2.45 and 1.61 when the number of UAVs is increased to 100, respectively.

Against HST speed

In this part of numerical simulations, we examine the performances of the compared schemes against changing the HST speed. Figures 8, 9, 10 and 11 show the average data rate, the average HST coverage time, the average transmitted data, and the average energy efficiency against changing the HST speed using 50 UAVs, respectively.

Fig. 8

Average data rate against train speed using 50 UAVs.

Figure 8 shows the average data rate in Mbps of the compared schemes against the train speed using 50 UAVs. Generally, the performance of all compared schemes decreases when increasing the train speed. This is due to the decrease in the channel gain resulting from the high doppler shift coming from the high-speed difference between HST and UAVs. The performance of the proposed scheme exactly matches the optimal performance as no channel estimation error was considered. This is done without the need to pre-know the HST coverage times provided by each UAV as in the optimal performance thanks to the use of DD channel estimating by

Fig. 9

Average HST coverage time against train speed using 50 UAVs.

Fig. 10

Average transmitted data against train speed using 50 UAVs.

employing OTFS modulation. Also, both schemes have lower performance than the “Maximum Rate” scheme as they maximize the data rate and the HST coverage time simultaneously. As the “Maximum Rate” scheme selects the UAV with the highest data rate, it shows the best data rate performance, while the “Random” selection shows the worst performance as it selects the UAV at random. When the train speed is set to 120 km/h, the proposed and the optimal schemes achieve a data rate performance of 91.24% of the “Maximum Rate” scheme, while it attains 1.68 times higher than the “Random” scheme. These values become 91.3% and 1.51 times, respectively.

Figure 9 illustrates the average HST coverage time in sec of the compared schemes against the train speed using 50 UAVs. Generally, the performance of all schemes declines as the train speed increases. This reduction is attributed to the decrease in $\tau _{q,t}$ given in Eq. (7) caused by the increase in $v_{S,t}$ in its denominator. The proposed scheme achieves performance identical to the optimal scheme, assuming no channel estimation error. Unlike the impractical assumptions of the optimal scheme, the proposed approach does not require any prior knowledge about the HST coverage times provided by each UAV, thanks to its use of DD channel estimation with OTFS modulation. Both the proposed and optimal schemes exhibit higher performance than the “Maximum Rate” and the “Random” schemes, as both has no functionalities to maximize the HST coverage time. Also, the “Random” scheme provides higher HST coverage time than that provided by the “Maximum Rate” scheme due to the aforementioned reasons. At a train speed of 120 km/h, the proposed and optimal schemes achieve HST coverage time higher than “Maximum Rate” and “Random” schemes by 10.13 and 2.33 times, respectively. These values become 3.362 and 1.812 times, respectively when HST speed reaches 600 km/h.

Figure 10 displays the average transmitted data in Gbps against the train speed using 50 UAVs. Across all compared schemes, performance declines with increasing train speed, reflecting decreases in both average data rate and HST coverage time as depicted in Figs. 8 and 9. The proposed scheme demonstrates superior performance, matching the optimal scheme by maximizing achievable data rate and HST coverage time without assuming channel estimation error. In contrast, the “Maximum Rate” scheme exhibits the poorest performance, which falls below that of the “Random” scheme. This outcome arises because the HST coverage time exerts a more dominant effect than the achievable data rate in the “Maximum Rate” scheme’s selection criteria. From Fig. 10, at a train speed of 120 km/h, the proposed and optimal schemes achieve transmitted data performances that are 9.186 and 3.9 times higher than those of the “Maximum Rate” and “Random” schemes, respectively. As the train speed decreases to 600 km/h, these values reduce to 2.7 and 2.5 times higher, respectively.

Fig. 11

Energy efficiency against train speed using 50 UAVs.

Figure 11 presents the average energy efficiency of the compared schemes against the train speed using 50 UAVs. As observed in Fig. 10, where transmitted data decreases with increasing train speed, average energy efficiency similarly declines. The proposed scheme exhibits the highest performance, matching the optimal scheme because it maximizes both achievable data rate and HST coverage time without assuming channel estimation error. In contrast, the “Maximum Rate” scheme displays the lowest performance, even below the “Random” scheme. This is influenced by its transmitted data performance, as shown in Fig. 10, and its selection criteria favoring UAVs that maximize achievable data rates without consideration of HST coverage time. From Fig. 11, at a train speed of 120 km/h, the proposed scheme achieves higher energy efficiency than the “Maximum Rate” and “Random” schemes by factors of 2.26 and 1.52, respectively. As the train speed increases to 600 km/h, these values reduce to 1.6 and 1.7 times higher, respectively.

Fig. 12

Transmitted data of the proposed scheme against channel estimation error.

Fig. 13

Energy efficiency of the proposed scheme against channel estimation error.

Effect of DD channel estimation errors

In this part of the numerical simulation, we examine the performance of the proposed scheme under different channel estimation errors, i.e., $\sigma _\alpha$ and $\sigma _\beta$ settings. Figures 12 and 13 show the transmitted data in Gbits and the energy efficiency in MbpJ of the proposed scheme against the normalized DD channel estimation errors, $\left( i.e.,\sigma _\alpha /\alpha _{(1,t)}\ and\ \sigma _\beta /\beta _{max}\right)$ ranging from 0 to 100%, under various HST speed, $v_{Smax}$, while fixing the maximum UAVs speed, $v_{Umax}$ to 60 Km/h. From these figures, as the channel estimation error increases, the performance of the proposed scheme decreases in all tested scenarios. Also, when increasing the discrepancy between $v_{Smax}$ and $v_{Umax}$, i.e., when increasing $v_{Smax}$, the performance degradation in the proposed scheme slightly increases. This is because when increasing $v_{Smax}$, the error in the estimated relative velocity between the HST and UAVs, ${\hat{v}}_{qS,t}$ will increase when increasing the channel estimation error. This results in increasing the error in the estimated UAVs’ speed ${\hat{v}}_{q,t}$, and in their estimated coverage periods in consequence. This increases the error in selecting the best UAV at each time t, and the overall performance in consequence as given in Figs. 12 and 13. For instance, with $v_{Smax}=120$ km/h and $v_{Umax}=60$ km/h, $\left( i.e., v_{Smax}=2v_{Umax}\right)$, the performance decline when increasing,$\sigma _\alpha /\alpha _{(1,t)}$ and $\sigma _\beta /\beta _{max}$ from 0 to 100% is equal to 52% and 49% for the transmitted data and the energy efficiency, respectively. These values become 48% and 39%, respectively, when $v_{Smax}=240$ km/h and $v_{Umax}=60$ km/h , $\left( i.e.,\ v_{Smax}=4\ v_{Umax}\right)$. Also, when $v_{Smax}=360$ km/h and $v_{Umax}=60$ km/h, $\left( i.e.,\ v_{Smax}=6\ v_{Umax}\right)$, these values become 44.5% and 33.4%, respectively. When $v_{Smax}$ is further increased to 480 km/h, $\left( i.e., v_{Smax}=8\ v_{Umax}\right)$, these values become 42% and 30%, respectively. Finally, these values reach 41% and 29.5% respectively, when $v_{Smax}=600$ km/h and $v_{Umax}=60$ km/h, $\left( i.e.,\ v_{Smax}=10\ v_{Umax}\right)$.

From these results, two approaches can be considered to mitigate the degradation in the performance of the proposed approach caused by channel estimation errors. The first is to reduce the channel estimation error itself, and the second is to enhance the UAV selection methodology. In the first approach, advanced estimation techniques, such as Bayesian filtering or Kalman filtering, can refine DD channel estimates ($\hat{\alpha }_{1_q,t}$and $\hat{\beta }_{max_q,t}$) by incorporating historical data and dynamically adapting to changing channel conditions. Also, employing multiple pilot symbols in the DD grid for redundancy could enhance estimation accuracy, particularly under high-speed scenarios. For the second approach, after estimating the candidate UAVs’ speed, the UAV with a speed nearly matches that of HST should be selected. This is because as the speed difference between the HST and the selected UAV is decreased, better compensation against channel estimation error is obtained as revealed by the results in Figs. 12 and 13. Also, a machine learning-based approach could be employed to predict UAV-HST link quality, leveraging prior knowledge of channel characteristics and UAV mobility patterns. Such models could learn to compensate for estimation errors and improve decision-making robustness. While the current study evaluates performance under various estimation error levels and speed conditions, future research will focus on integrating the suggested mitigation strategies to quantify their effectiveness. By addressing estimation errors through these strategies, the resilience of the proposed scheme can be significantly enhanced, ensuring its applicability to real-world high-speed scenarios.

Complexity analysis

In this subsection, we give the computational complexity of the schemes involved in the comparisons. For the proposed scheme, its computational complexity comes from (1) Channel parameters estimation: The estimation of $l_{1_q,t}$ and $k_{max_q,t}$ involves the computation of DD profiles for each UAV, with computational complexity of O(QNM). (2) Distance and velocity evaluation: Computing $\hat{d}_{q,t}$, $\hat{Z}_{q,t}$, and $\hat{v}_{q,t}$ for Q UAVs involves O(Q) operations. (3) Candidate filtering: Checking the condition $\hat{d}_{q,t}\le \hat{d}_{C,t}$ has a computational complexity of O(Q). (4) UAV selection: Evaluating the utility function for $Q_t$ candidates and selecting the best UAV involves $O(Q_t)$. Thus, the overall computational complexity of the proposed Algorithm will be the maximum among those complexities, i.e., O(QNM), which is scalable for practical deployments with a moderate number of UAVs and DD resolution.

For the optimal scheme, besides it is impractical, it involves a computational complexity of $O(Q\eta )$, where $\eta$ is the computational complexity of estimating the data rate and the coverage period of each UAV $q\in Q$. For the maximum rate scheme, its computational complexity is $O(Q\zeta )$, where $\zeta$ is the computational complexity of estimating the data rate of each UAV UAV $\forall {q}\in Q$. For the random scheme, its computational complexity is O(1) as it selects a one UAV at random. Thus, we can conclude that the proposed scheme has a comparable computational complexity to the impractical optimal scheme, while obtaining the same performance.

The computational complexity analysis of the proposed algorithm reveals that its complexity increases with the DD grid resolution (M $\times$ N) and the number of deployed UAVs Q. Therefore, a tradeoff arises between improving the DD resolution to enhance DD channel parameter estimation and overall scheme performance, and the associated increase in computational complexity, which presents a limitation to the proposed approach. Additionally, HST should estimate DD channel parameters for all UAVs, which introduces challenges related to synchronization and communication overhead. Consequently, the proposed scheme is most suitable for scenarios with a moderate DD resolution and a manageable number of UAVs.

Conclusions

In this paper, we addressed the challenge of UAV selection in multi-UAV-HST communications, where the HST should autonomously choose the optimal UAV from those covering it at any given time. The selected UAV should maximize the HST’s data transmission, maximizing its achievable data rate and coverage duration. To tackle this issue efficiently, we employed the estimated DD channel parameters using OTFS modulation, allowing the HST to autonomously estimate the speeds and flying altitudes of the UAVs covering it. This enables the HST to estimate their coverage periods and select the best UAV to maximize its total transmitted data. Numerical analysis demonstrated the effectiveness of our proposed approach, showing that it precisely matches the optimal performance when no channel estimation error is present. Additionally, we examined the impact of channel estimation errors on the proposed scheme under varying HST speeds. We observed a performance degradation in the proposed scheme ranging from 52% to 29.5% as the normalized channel estimation error increased from 0 to 100%, and the speed difference between the HST and UAVs increased from 2 to 10 times, respectively.