Introduction

Safety helmets are crucial tools for protecting the heads of construction workers in various industries such as construction, electric power, and chemicals. They play a vital role in ensuring the personal safety of workers. Research data reveals that over 60% of accidents can be attributed to a lack of safety awareness among construction site workers who fail to wear helmets in accordance with the relevant rules and regulations1. Currently, safety management heavily relies on conventional video surveillance systems and manual supervision. However, various approaches suffer from limitations such as inadequate real-time detection, subpar detection performance, and high costs. Therefore, there is a pressing necessity to explore feasible methods for enabling real-time helmet detection.

In recent years, with the rapid development of deep learning technology, convolutional neural networks have achieved remarkable success in various computer vision recognition tasks. Currently, target detection algorithms are mainly classified into two mainstream directions2. One is the single-stage detection algorithm based on regression strategy, such as SSD3, YOLO series4,5,6,7, RetinaNet8. The core theory of these algorithms is to input the image into the model and directly return the bounding box, position and category information of the target. The other is direction involves two-stage detection algorithms that optimize the candidate region. Although these algorithms exhibit relatively high detection accuracy, they require more time for processing. Some representative algorithms in this category include R-CNN9, Fast R-CNN10 Faster R-CNN11 and R-FCN12, etc. At present, many researchers at home and abroad have applied deep learning methods to the field of helmet detection. For instance, Sun et al.13 improved the Faster R-CNN algorithm by incorporating the attention mechanism, thus improving the problems of helmet detection difficulty and high leakage rate in different scenes, but the detection rate of the algorithm is low. Additionally, Dai et al.14 designed R-FCN, a region-based fully convolutional network, which is suitable for the study of helmet-wearing detection in dense crowds complex scenes. Chen et al.15 replaced the additional VGG16 layer in the original SSD with the Inception module released by Google, resulting in improved performance for recognizing small targets in real application scenarios for helmet-wearing detection. Song16 proposed the RSSE module with compressed excitation, based on YOLOv3, to bolster feature extraction, which utilizes four-scale feature prediction, an enhancement over three-scale feature measurement, and refines the CIOU loss function, thereby enhancing detection accuracy and speed. However, its efficacy in detecting small objects requires further improvement. In order to improve detection accuracy and reduce the leakage rate of small helmet objects, Sun et al.17 implemented the MCA attention mechanism to YOLOv5s. In addition, Jung et al.18 conducted a comparative analysis of the target detection performance of YOLOv7 and YOLOv8, highlighting the superior accuracy and speed of YOLOv8. Luo et al.19 proposed a lightweight real-time detection method based on YOLOv8, optimizing the model to strike a balance between performance and computational efficiency, thus providing an effective solution for target detection tasks. However, in the field of helmet-wearing detection, challenges such as task complexity and small target sizes persist. While the aforementioned detection methods have led to improvements in accuracy, there still exist algorithms characterized by complexity, extensive computation, and demanding hardware requirements.

Therefore, in order to address the aforementioned issues, this paper optimizes the model based on YOLOv8n and proposes a helmet-wearing detection algorithm YOLOv8n_H, with the following main contributions:

  1. 1.

    Aiming at the redundant parameter count of the current helmet wear detection algorithm, the SCConv (Spatial and Channel Reconstruction Convolution) module is introduced20. Additionally, a new module, SC_C2f, is designed to reduce redundant features within the model.

  2. 2.

    To expand the sensory field, emphasize the essential details of helmet-wearing identification and strengthen the network’s capacity for feature extraction, the Coordinate Attention (CA) module is embedded after the SC_C2f module of the backbone network21.

  3. 3.

    Subsequently, to further minimize the amount of floating-point computation and model parameters, a lightweight decoupling head (PC-Head) based on the PConv module is designed to replace the original Detect structure.

  4. 4.

    In order to speed up network convergence and enhance the bounding box regression performance of the model, the WIoU_ Loss22 loss function to replace the CIoU_Loss in the original model23 loss function in the original model.

Related works

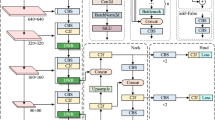
YOLOv8, the most recent version of the YOLO paradigm, is versatile for various computer vision tasks such as object detection, image classification, and instance segmentation. In this paper, we focus on target detection tasks using YOLOv8. According to the network depth and width, YOLOv8 is divided into YOLOv8n, YOLOv8s, YOLOv8m, YOLOv8l, and YOLOv8x. Considering model size and computational complexity, we opt for the YOLOv8n network due to its compact size and high accuracy. The YOLOv8n model detection network is mainly composed of three parts (shown in Fig. 1): Backbone, Neck, and Head.

The Backbone comprises the C2f, SPPF, and CBS (Conv + BN + SiLU) modules. The Backbone Neck network draws inspiration from the YOLOv724 ELAN structure, where the C3 structure of YOLOv5 is replaced by the C2f structure with enhanced gradient flow. Moreover, the number of channels is tailored to different scale models, significantly enhancing model performance. YOLOv8 retains the SPPF module from the YOLOv5 architecture, also known as spatial pyramid pooling. This module enables the creation of a fixed-size feature vector from feature maps of any dimension, facilitating both local and global feature fusion, thereby enhancing feature richness.

The primary modification to the head component involves transitioning from the connected head to the decoupled head. This alteration separates the classification and detection heads, replacing Anchor-Based YOLOv5 with Anchor-Free. Concerning the loss function, the BCE Loss remains employed in the classification branch, while the regression branch necessitates integration with the Distribution Focal Loss. BCE Loss remains utilized for the categorization branch, while the regression branch adheres to the integral form representation proposed in Distribution Focal Loss, employing both Distribution Focal Loss and CIoU Loss.In terms of sample matching, the previous methods of IOU matching or unilateral proportion allocation are abandoned in favor of Task-Aligned Assigner positive and negative sample allocation techniques.

Fig. 1
figure 1

YOLOv8n network architecture.

Full size image

YOLOv8n algorithm improvement strategy

The current traditional network for helmet target detection suffers from slow inference, excessive model parameters, large model size, and other issues. To address these challenges, this study proposes a helmet wear detection approach based on YOLOv8n_H. The network structure of the proposed YOLOv8n_H algorithmic model, featuring four main improvement components, is depicted in Fig. 2.

Fig. 2
figure 2

YOLOv8n_H network structure.

Full size image

The performance of the network model detection is enhanced by incorporating the SCConv module and introducing the new SC_C2f module, which significantly reduce the number of parameters and computational volume of the network. Furthermore, integrating the CA module into the backbone network improves the extraction of feature-rich regions, thereby enhancing the algorithm’s detection accuracy. Furthermore, the design of the PC-Head detector head, replacing the original Detect structure, substantially reduces the parameter count of the detector head, resulting in a lightweight network. Moreover, the introduction of the WIoU loss function enhances the bounding box regression performance of the model. And, the subsequent subsections will delve into the working principles and technical details of each module.

SC_C2f module

Convolutional neural networks, or CNNs, are now often used for a variety of computer vision applications. However, their efficacy has been largely reliant on substantial computational and storage resources, partly due to the extraction of redundant features by convolutional layers. Various model compression strategies and network designs used to improve network efficiency in the past25,26,27, including network pruning28,29, weight quantization30, low-rank decomposition31, and knowledge distillation32,33, etc. However, these methods are all considered as post-processing steps, and thus their performance is usually bounded by the upper bound of a given initial model. To solve the above problems, Li et al. attempted to improve efficiency by lowering feature redundancy in terms of space and channel and proposed an efficient reconstruction convolution module, SCConv. The module consists of two components: the Spatial Reconstruction Unit (SRU) and the Channel Reconstruction Unit (CRU), which aim to suppress feature redundancy from spatial and channel perspectives, respectively. SCConv is interchangeable with ordinary convolution and seamlessly integrates into any convolutional model. As shown in Fig. 320, these two units are sequentially arranged: input features traverse the spatial reconstruction unit to obtain spatial refinement features, then proceed through the channel reconstruction unit for channel refinement, and finally undergo a 1 × 1 convolution to produce the final output feature map with adjusted channel dimensions.

Fig. 3
figure 3

SCConv module.

Full size image

The SRU addresses spatial redundancy through weight separation-reconstruction operations, as shown in Fig. 4. First, SRU employs the learnable parameter γ from Group Normalization (GN) to evaluate the information content of feature maps along the spatial dimension. The γ parameter in GN reflects the richness of spatial information across different channels, with higher values indicating more spatially informative features. By normalizing the γ values of various feature maps and applying a threshold, SRU categorizes the feature maps into two types: information-rich (W1) and less informative (W2). Subsequently, SRU performs a cross-reconstruction operation, integrating the information from both types of feature maps to optimize the information flow. Through this approach, SRU generates spatially refined feature maps, reducing spatial redundancy while enhancing feature representation.

Fig. 4
figure 4

SRU structure.

Full size image

The CRU mitigates channel redundancy via the split-transform-fusion strategy as illustrated in Fig. 5. CRU first splits the input feature map along the channel dimension into two parts, containing αC and (1 − α)C channels, respectively, where α represents the split ratio. Each part undergoes a 1 × 1 convolution to reduce computation and improve the efficiency of subsequent operations. In the transformation step, CRU combines Group Convolution (GWC) and Pointwise Convolution (PWC) to efficiently extract high-level features for the upper portion of the split channels. For the lower portion, CRU applies 1 × 1 pointwise convolution to generate feature maps, reusing the upper portion’s features to provide additional detail without extra computation. Finally, CRU adaptively fuses the two parts using a simplified Selective Kernel Networks (SKNet) method, yielding the final channel-refined feature map through weighted fusion. This design effectively compresses and suppresses channel redundancy, significantly reducing parameters and computation while preserving feature integrity.

Fig. 5
figure 5

CRU structure.

Full size image

In order to deal with the high model complexity challenges and a large number of FLOPs in the current helmet-wearing detection algorithm, this study incorporates SCConv to restructure the C2f network within the YOLOv8 algorithm. This adjustment aims to mitigate intrinsic redundancy in the network model parameters, thus enhancing detection performance. As illustrated in Fig. 6, the SC_Bottleneck initially augments the channel count via the first SCConv as an extension layer, followed by batch normalization and activation using the SiLU function. Subsequently, to align the output feature maps with the input channels via the second SCConv, the channel count is reduced. Finally, it overlays the input feature maps to generate the output results.

Fig. 6
figure 6

SC_Bottleneck structure.

Full size image

As shown in Fig. 7, the newly designed module, SC_C2f, is produced by replacing each and every Bottleneck module with SC_Bottleneck in the C2f module of the original network. This adjustment not only enhances feature diversity across various network layers through cross-stage feature fusion and truncated gradient streaming but also accelerates the processing of redundant gradient information. Moreover, it ensures network detection accuracy while achieving lightweight network architecture.

Fig. 7
figure 7

SC_C2f module.

Full size image

CA attention mechanisms introduced

Considering that the number of small targets within helmet images, which occupy a minimal portion of the image and contain few pixels, and their susceptibility to background factors such as lighting, this study aims to enhance the correlation between location information and helmet features within images. To enrich the representation of crucial location information within the network, we incorporate an attention mechanism into the YOLOv8 architecture. This enables the network to assimilate global information, selectively emphasizing features rich in information while filtering out irrelevant data. Channel attention, spatial attention, and their combinations constitute the two primary categories of attention mechanisms. However, conventional methods like the Convolutional Block Attention Module (CBAM) and Squeeze-and-Excite (SE) have limitations. For example, SE primarily enhances channel interdependencies at the expense of spatial details, while CBAM struggles with addressing long-range dependencies despite employing large convolutional kernels for spatial feature extraction. While alternative attention mechanisms have made strides in overcoming these challenges, they introduce an excessive number of parameters, compromising their deployment efficiency. To address these issues, as depicted in Fig. 8, this study introduces a Coordinate Attention (CA) mechanism that integrates coordinate and channel information.

The Coordinate Attention (CA) module enhances the model’s ability to accurately detect and identify relevant regions, serving as a lightweight attention technique. In contrast to the channel attention mechanism, which utilizes 2-dimensional global pooling to convert the feature tensor into individual feature vectors, the CA attention mechanism divides channel attention into two distinct 1-dimensional feature encoding processes. The input dimensions of the feature map X are C × W × H. This technique involves independently encoding each channel along the horizontal and vertical axes using 1-dimensional pooling kernels of dimensions (H, 1) and (1, W), respectively. Subsequently, as demonstrated by Eqs. (1) and (2), the outputs of the cth channel with height h and the cth channel with width w are combined along the two spatial directions. This approach enables the capture of distant dependencies along one spatial direction, while preserving precise positional information along the other. The resulting feature maps are encoded to be direction-aware and location-sensitive, complementing the input feature maps to enhance the representation of the focal object. This underscores the essence of the CA attention mechanism, which considers both channel information and direction-dependent location information.

$${\text{Z}}_{{\text{c}}}^{h} \left( h \right) = \frac{1}{{\text{W}}}\sum\limits_{{0 \le {\text{i}} \le {\text{W}}}} {{\text{X}}_{{\text{c}}} (h,{\text{i}})}$$
(1)
$${\text{Z}}_{{\text{c}}}^{{\text{w}}} \left( {\text{w}} \right) = \frac{1}{{\text{H}}}\sum\limits_{{0 \le {\text{j}} \le {\text{H}}}} {{\text{X}}_{{\text{c}}} ({\text{j}},{\text{w}})}$$
(2)

Where, in Eq. (1), \(\:{\text{Z}}_{\text{c}}^{h}\left(h\right)\) represents the aggregated feature value of channel c at height h, computed by averaging the pixel values across all width dimensions at that height. Specifically, \(\:{\text{X}}_{\text{c}}(h,\text{i})\) denotes the pixel value at height h, width i, and channel c, while W indicates the total width of the feature map. In Eq. (2), \(\:{\text{Z}}_{\text{c}}^{\text{w}}\left(\text{w}\right)\) represents the aggregated feature value of channel c at width w, computed by averaging the pixel values across all height dimensions at that width. Here, \(\:{\text{X}}_{\text{c}}(\text{j},\text{w})\) denotes the pixel value at height j, width w, and channel c, while H indicates the total height of the feature map.

Fig. 8
figure 8

CA attention mechanism network structure.

Full size image

PConv module based lightweight decoupling header

The PConv (Partial Convolution) module is a component within the most recent lightweight backbone network, FasterNet. It serves as a substitute for conventional convolution and reduces computational complexity. PConv introduces the concept of partial convolution, applying standard convolution only on a subset of input channels to extract spatial features, while keeping the remaining channels unchanged and directly passing them through an identity mapping. This design not only minimizes computational redundancy but also effectively improves floating-point operation speed, achieving lightweight performance without significantly compromising accuracy, as shown in Fig. 934.

In this structure, the continuous cp channels are treated as representatives of the feature map for computation. To maintain generality, it can be assumed that the input and output feature maps have the same number of channels. The floating-point operation count (FLOPs) for PConv can be expressed as:

$$\:{\text{F}\text{L}\text{O}\text{P}\text{s}}_{\text{P}\text{C}\text{o}\text{n}\text{v}\:}=\text{h}\times\:\text{w}\times\:{\text{k}}^{2}\times\:{{\text{c}}_{\text{p}}}^{2}$$
(3)

In contrast, the FLOPs for standard convolution are given by:

$$\:{\text{F}\text{L}\text{O}\text{P}\text{s}}_{\text{C}\text{o}\text{n}\text{v}}=\text{h}\times\:\text{w}\times\:{\text{k}}^{2}\times\:{\text{c}}^{2}$$
(4)

where h and w are the height and width of the feature map, k is the size of the convolution kernel, and cp denotes the number of channels actually involved in the convolution. When the ratio of participating channels \(\:\text{r}=\frac{{\text{c}}_{\text{p}}}{\text{c}}=\frac{1}{4}\), the FLOPs of PConv is approximately \(\:\frac{1}{16}\) that of standard convolution.

Additionally, the memory usage for PConv can be calculated as:

$$\:{\text{m}\text{e}\text{m}}_{\text{P}\text{C}\text{o}\text{n}\text{v}\:}=\text{h}\times\:\text{w}\times\:2{\text{c}}_{\text{p}}+{\text{k}}^{2}\times\:{\text{c}}_{\text{p}}^{2}\approx\:\text{h}\times\:\text{w}\times\:2{\text{c}}_{\text{p}}$$
(5)

In comparison, the memory usage for standard convolution is:

$$\:{\:\text{m}\text{e}\text{m}}_{\text{C}\text{o}\text{n}\text{v}}=\text{h}\times\:\text{w}\times\:2\text{c}+{\text{k}}^{2}\times\:{\text{c}}^{2}\approx\:\text{h}\times\:\text{w}\times\:2\text{c}$$
(6)

In the above formulas, c represents the number of channels in standard convolution. By comparison, it is evident that the memory usage of PConv is approximately \(\:\frac{1}{4}\) that of standard convolution. PConv utilizes identity mapping to directly pass through the channel information that does not participate in the convolution, allowing subsequent standard convolutions to continue extracting complete features. This design allows PConv to significantly reduce computational redundancy and memory usage while preserving feature integrity, resulting in a lightweight model architecture.

Fig. 9
figure 9

PConv module.

Full size image

Building upon the RetinaNet network and the shared parameter detection head proposed in prior research, this study endeavors to develop a shared convolutional structure to supplant the computationally intensive convolution operation within the original detection head. In YOLOv8, the Head section employs a decoupled design. Initially, it utilizes 3 × 3 convolutions to partition the channel count of the three distinct feature layers (denoted as C) generated by the Neck section, segregating them into C1 and C2 based on their roles in positioning and classification tasks. Subsequently, the convolutional module continues to extract features. Finally, the output channels for the localization task amount to 4×reg_max, representing the coordinates of the prediction box’s center point and the adjustment parameters for width and height information. Meanwhile, the output channels for the classification task are denoted as CN, representing the number of categories for the identified helmet target, and Fig. 10 displays the particular structure.

Fig. 10
figure 10

YOLOv8-head.

Full size image

However, the preceding process relies solely on stacked convolutional layers for feature extraction. Although it enhances the model’s detection accuracy to some degree, it still encounters challenges related to low computational efficiency and a more complex structure. To mitigate these issues, this study, utilizing the YOLOv8 detection head as its foundation, proposes a PC-Head decoupling approach. This approach introduces a novel shared convolution module to substitute the initial four 3 × 3 convolutions in the Head section. The new shared convolution module comprises two subunits: a 3 × 3 PConv, which selectively chooses input channels for convolution to diminish redundant information in the feature maps and alleviate computational load; and a 1 × 1 standard convolution, primarily utilized to adjust the number of channels in the input feature maps and enhance the extraction of pertinent feature information. This amalgamation of sub-units seeks to optimize feature representation, minimize computational resource utilization, and enhance detection performance. As the YOLOv8 detection head comprises solely decoupled classification and regression branches, it is imperative to output features in a decoupled manner. The final improved detection head is shown in Fig. 11.

Fig. 11
figure 11

PC-head.

Full size image

WIoU loss function

The YOLOv8 loss function comprises three components: classification loss (cls_loss), distribution focal loss (dfl_loss), and bounding box regression loss (box_loss). This paper maintains the original network architecture for YOLOv8 and retains the first two types of loss functions unchanged, namely, the original binary cross-entropy loss function. As for the bounding box regression loss, the original YOLOv8 uses CIoU Loss, and the complete calculation is shown in Eq. (7):

$$\:{L}_{CIoU}=1-IoU+\frac{{\rho\:}^{2}(b,{b}^{gt})}{{c}^{2}}+\alpha\:v$$
(7)

Where α is the weight function, and v is used to measure the consistency of the aspect ratio, defined as in Eqs. (8) and (9). The intersection and concurrency ratio of the anticipated and real frames are indicated by IoU, the Euclidean distance is represented by ρ, b, and bgt are the boundaries of the predicted frame and the real frame respectively centroid, and c denotes the diagonal length of the smallest outer rectangle of the predicted and real frames degree.

$$\:\alpha\:=\frac{v}{(1-IoU)+v}$$
(8)
$$v = \frac{4}{{\pi ^{2} }}\left( {arctan\frac{{w^{{gt}} }}{{h^{{gt}} }} - arctan\frac{w}{h}} \right)^{2}$$
(9)

where the anticipated and real frames’ width and height are denoted by the variables w, h, wgt, and hgt, respectively.

Although CIoU Loss considers the overlapping area, center point distance, and aspect ratio in bounding box regression, thereby addressing the issue that DIoU Loss cannot distinguish cases when the center points overlap, the variable “v” in the formula only reflects the difference in aspect ratio, failing to capture the true differences in width and height relative to their confidence scores. When the aspect ratios of the predicted box and the target box are identical, the penalty term associated with the aspect ratio becomes ineffective, rendering it unable to accurately represent the actual relationship between the predicted box and the target box. Moreover, CIoU Loss primarily focuses on enhancing the fitting capability of the bounding box loss without considering the detrimental impact of low-quality data on model performance, leading to slow and inefficient network convergence.

To address these issues, we present WIoUv3 Loss as the bounding box loss function. WIoUv3 Loss utilizes a dynamic non-monotonic focusing mechanism, defining outlier degree instead of IoU to characterize anchor box quality, where a low outlier degree suggests high-quality anchors. Additionally, it implements a wise gradient gain allocation strategy to mitigate the competitiveness of high-quality anchor boxes and alleviate the detrimental impact of low-quality anchors. By mitigating harmful gradients from low-quality anchor frames, the model can prioritize ordinary quality anchor frames, thereby enhancing overall performance. The WIoUv3 Loss is shown by Eqs. (10) to (13):

$$\:{\text{L}}_{\text{W}\text{I}\text{o}\text{U}}={\upgamma\:}{\text{R}}_{\text{W}\text{I}\text{o}\text{U}}{\text{L}}_{\text{I}\text{o}\text{U}}$$
(10)
$$\:{\upgamma\:}=\frac{{\upbeta\:}}{{\updelta\:}{{\upalpha\:}}^{{\upbeta\:}-{\updelta\:}}}$$
(11)
$$\upbeta = \frac{{{\text{L}}_{{{\text{IoU}}}}^{{\text{*}}} }}{{\overline{{{\text{L}}_{{{\text{IoU}}}} }} }} \in [0, + \infty )$$
(12)
$$\:{\text{R}}_{\text{W}\text{I}\text{o}\text{U}}=\text{e}\text{x}\text{p}\left(\frac{{(\text{x}-{\text{x}}_{\text{g}\text{t}})}^{2}+{(\text{y}-{\text{y}}_{\text{g}\text{t}})}^{2}}{{({\text{W}}_{\text{g}}^{2}+{\text{H}}_{\text{g}}^{2})}^{\text{*}}}\right)$$
(13)

where\(\:{\upbeta\:}\) is the outlier of the anchor frame, and \(\:{\text{L}}_{\text{I}\text{o}\text{U}}^{\text{*}}\) is the variable \(\overline{{{\text{L}}_{{{\text{IoU}}}} }}\) converted to a constant, and \(\overline{{{\text{L}}_{{{\text{IoU}}}} }}\) is the running mean of momentum m, γ denotes the non-monotonic focusing coefficient, and \(\:{\upalpha\:}\) and\(\:\:{\updelta\:}\) are the hyperparameters, the width and height of the minimum enclosing frame are represented by Wg and Hg, respectively, while the horizontal and vertical coordinates of the center points of the predicted and real frames are represented by x, y, xgt, and ygt, respectively, and R WIoU\(\:\in\:\:\) [1,e), which will significantly amplify the normal mass anchor box\(\:{\text{L}}_{\text{I}\text{o}\text{U}}\). Since \(\overline{{{\text{L}}_{{{\text{IoU}}}} }}\)h is dynamic, the quality division of anchor frames is also dynamic, which allows WIoU to make the gradient gain assignment strategy that best fits the current situation at each moment.

Experimental results and analyses

Experimental environment

This experiment was conducted on the Windows 10 operating system with a CPU model of 8vCPU Intel Xeon Processor (Skylake, IBRS) and a GPU model of Tesla T4 with 16G graphics memory. The compilation environment is Python 3.8, using Pytorch version 1.11.0, and the GPU is accelerated by CUDA 11.3.

Experimental datasets

This study utilizes a combined helmet dataset comprising the SHWD dataset (Safety Helmet Wearing Dataset) and select images from the Safety Helmet Detection dataset. The SHWD dataset comprises 7,581 images, encompassing 9,044 instances of helmet-wearing objects and 11,514 instances of non-helmet wearing objects. However, due to the uneven distribution of labels and the limited number of images in the SHWD dataset, there is a risk of model overfitting. To address this issue, we intend to augment the SHWD dataset by incorporating 2,419 high-quality images from the Safety Helmet Detection dataset and re-labeling them, categorizing the original class named “head” into the “person” class, representing the non-helmet-wearing category. Ultimately, the labeled dataset contains only two classes: “hat” and “person,” consistent with the labels in the SHWD dataset. Subsequently, we merge the two datasets to construct a safety helmet dataset containing 10,000 images. Additionally, the Pascal VOC format within the dataset is batch-converted to YOLO format using a Python script, facilitating training with the YOLOv8n model. The dataset is divided in a 7:2:1 ratio into separate training, validation, and test sets of 7,000, 2,000, and 1,000 images respectively.

Evaluation indicators

To accurately assess the effectiveness of the model in detecting helmet-wearing, the evaluation indexes used in the experiments of this paper are divided into detection precision and model complexity, where the detection precision is mainly reflected by the model’s accuracy P (precision), recall R (recall), and mean average precision mAP (mean average precision).

$$\:P=\frac{TP}{TP+FP}$$
(14)
$$\:R=\frac{TP}{TP+FN}$$
(15)
$$\:AP={\int\:}_{0}^{1}P\left(R\right)dR$$
(16)
$$mAP = \frac{1}{N}\sum\limits_{{j = 1}}^{N} {AP_{j} }$$
(17)

where TP (True Positive) denotes the number of positive samples classified as positive samples; FP (False Positive) is the number of negative samples classified as positive samples; FN (False Negative) denotes the number of positive samples classified as negative samples; n denotes the number of detection target categories.

Model complexity is gauged by factors such as parameter count, floating-point operations (FLOPs), and model size, where larger metrics indicate greater complexity.

Model training and validation

In this paper, we analyzed the performance of the YOLOv8n model before and after improvements under identical hardware conditions and parameters. The trained loss curves, along with the validation loss curves, were used as representative indicators of the experimental results, comparing various loss values, including box_loss, dfl_loss, and cls_loss, before and after the enhancements, as shown in Fig. 12. The comparison clearly shows that the improved algorithm outperforms the original one across all loss functions. In particular, the significant reduction in box_loss indicates that WIoU Loss effectively improves bounding box regression accuracy, thereby accelerating the overall convergence speed.

Specifically, box_loss measures the precision of bounding box regression, and in this study, we replaced the original box_loss (based on CIoU Loss) with WIoU Loss. This new loss function introduces additional geometric features, such as aspect ratio and angle, making it more effective in complex scenes, especially when dealing with small and irregularly shaped targets. The dfl_loss focuses on improving the regression quality for small and hard-to-detect objects, while cls_loss evaluates the accuracy of class predictions. The combination of WIoU Loss, dfl_loss, and cls_loss works together to further optimize bounding box positioning, classification accuracy, and overall regression performance. From the figure below, it is evident that the enhanced algorithm exhibits a lower loss value compared to the original algorithm, indicating faster convergence speed and superior performance.

Fig. 12
figure 12

Comparison of Loss Values by Category. (a) train/box_loss diagram; (b) train/dfl_loss plot; (c) train/cls_loss charts; (d) val/box_loss diagram; (e) val/dfl_loss plot; (f) val/cls_loss charts.

Full size image

Impact of different attention mechanisms on network performance

The experiment also used some other attention mechanism modules such as the SE Attention Module, CBAM Attention Module, and EMA Attention Module. The results of the experiment are shown in Table 1. From Table 1, it can be seen that the addition of the CA module does not result in a significant reduction in speed while accuracy is improved compared to other studied attention mechanism modules, such as the SE, CBAM, and EMA modules. Therefore, this paper chooses to add the CA attention mechanism after the C2f module of the backbone network, which achieves a better balance between speed and accuracy.

Table 1 Comparison results of multiple attention mechanisms.
Full size table

Ablation experiments

In this paper, the algorithm takes into account that there are a few tiny targets in the helmet image that are vulnerable to the background and other elements. It integrates the CA attention module into the backbone network, introduces the SC_C2f module, and devises the PC-Head lightweight decoupling head to streamline model processing. Eventually, the WIoU metric is employed as the loss function. Ablation experiments are conducted in this paper to assess the impact of each module on the algorithm, as shown in Table 2.

Table 2 Ablation experiments.
Full size table

The mAP value in YOLOv8n is increased by 0.6% when the CA module is the only one included, according to an analysis of the experimental findings in the table, with negligible changes to the number of parameters and computational volume. Sequential addition of the SC_C2f module and PC-Head results in a 46.63% reduction in model volume, a decrease of 1.33 M parameters, and a decrease of 4.5GFLOPs in computational volume, significantly reducing model complexity. However, this also impacts the average accuracy of the model, leading to a 0.4% decrease in mAP value. Incorporating the WIoU loss function leads to a 0.1% improvement in the model’s mAP value, slightly surpassing that of the original YOLOv8n detection algorithm. This algorithm notably decreases model size, parameter count, and computational load, achieving an average accuracy of 93.8%, facilitating its deployment on hardware devices.

Comparative experiments

To practically demonstrate the effectiveness of the algorithm proposed in this study for detecting helmet wear, in comparison to the most recent detection techniques, including Faster-RCNN11, SSD3, RetinaNet35, EfficientDet36, DETR37, YOLOv438, YOLOv5s39, YOLOX40, YOLOv7-Tiny41, and YOLOv8n42, employing identical hardware setups for consistency. The comparison results are detailed in Table 3.

Table 3 Comparative experiments.
Full size table

The comparative results indicate that the average accuracy of the proposed algorithm, following enhancements, surpasses that of current mainstream detection algorithms, with improvements of 2.9%, 10.4%, and 7%, corresponding to accuracy gains of 3%, 1.2%, and 0.1%, respectively. While DETR demonstrates superior average accuracy, its complexity may hinder real-time performance. In contrast, the proposed algorithm exhibits a significant advantage in model complexity compared to other existing detection algorithms. Furthermore, the enhanced algorithm has achieved a modest improvement in detection speed, reaching 145 frames per second. Compared to the widely adopted YOLOv8 algorithm, the proposed method maintains robust performance. A comprehensive analysis reveals that the enhanced model significantly outperforms other network models, striking a more favorable balance between accuracy and complexity, thus making it more suitable for practical applications.

Analysis of detection effects

To further comprehend the algorithm’s detection performance pre and post-enhancement, this study chooses part of scenes featuring individuals wearing helmets. The comparison between the YOLOv8n detection before and after improvement is illustrated in Fig. 13, with the enhanced algorithm’s detection effect shown on the bottom and the original approach’s effect on the top. The results indicate that the proposed approach in this paper is lightweight, demonstrates strong detection performance, exhibits robust generalization capabilities, and adeptly addresses concerns regarding model leakage and false detections.

Fig. 13
figure 13

Comparison of YOLOv8n and YOLOv8n_H detection effect. (a–c) YOLOv8n Algorithm detection result graph; (d–f) YOLOv8n_H Algorithm detection result graph.

Full size image

Conclusion

To facilitate helmet detection, this study introduces an enhanced lightweight YOLOv8n detection method. Initially, the original C2f module of the network is replaced with the SC_C2f module, leading to an overall improvement in the model’s detection performance by minimizing redundant computation. Furthermore, to enhance the algorithm’s detection accuracy, the CA attention mechanism is integrated into the backbone network. Following this, the PC-Head decoupling head is developed, substantially reducing the number of model parameters and floating-point computations. Lastly, the WIoU loss function is employed during training to augment the model’s generalization capability.

The experimental results on the SHWD dataset after integration and expansion demonstrate that the algorithm proposed in this paper achieves a model volume reduction to 3.17 MB, parameter volume reduction to 1.68 M, and computational volume reduction to 3.7GFLOPs. Additionally, it achieves high accuracy, recall, and average precision rates of 91.7%, 86.8%, and 93.8%, respectively. These reductions significantly reduce the model’s complexity while maintaining a high detection efficacy. Compared with other mainstream detection algorithms, the algorithm in this paper is more suitable for helmet-wearing target detection.