Analyzing disease control through testing game approach embedded with treatment and vaccination strategies

Abstract

This research introduces an expanded SEIR (Susceptible-Exposed-Infected-Recovered) model that incorporates the components of testing, treatment, and vaccination. The study utilizes an evolutionary game theory (EGT) framework to investigate the impact of human behavior on the acceptance and implementation of these interventions. The choice to undergo testing and vaccination is considered a strategic decision influenced by perceived risks and benefits. Regarding disease dynamics, adherence to vaccination and testing protocols is seen as a behavioral factor. The present study employs a finite difference method to numerically examine the impact of proactive vaccination and retroactive treatment policies on human behavior. The investigation focuses on these policies’ individual and combined effects, considering various factors, including vaccination and testing costs, vaccine efficacy, awareness level, and infection rates. The findings indicate that the integration of heightened awareness and enhanced vaccination efficacy can successfully alleviate the transmission of diseases, even in situations where the expenses associated with testing and vaccination are substantial. Reducing infections in situations characterized by low or moderate awareness or vaccination effectiveness is contingent upon low testing costs. The final epidemic size (FES) negatively correlates with testing and vaccine costs, indicating that lower costs are linked to a lower FES. Optimal vaccine coverage (VC) occurs when vaccine costs are minimal and vaccine efficiency is efficient, whereas treatment coverage (TC) reaches its peak when testing costs are minimal. This research underscores the significance of considering human behavior and the intricate relationship between vaccination, testing, and treatment approaches in managing the transmission of contagious illnesses. It offers valuable perspectives for policymakers to mitigate the consequences of epidemics.

Introduction

The present study brings forth an expanded SEIR (Susceptible-Exposed-Infected-Recovered) model that integrates the processes of testing, treatment, and vaccination, employing an evolutionary game theory (EGT) approach to examine the influence of human behavior on the adoption of these interventions. The decision to undergo testing and vaccination is conceptualized as a strategic decision, considering its perceived risks and benefits. Additionally, adherence to vaccination and testing protocols is considered a behavioral factor that impacts the dynamics of the disease. The COVID-19 pandemic has brought attention to the significance of implementing efficient intervention strategies in managing the transmission of contagious diseases. Mathematical modeling has been pivotal in comprehending the dynamics of diseases and providing guidance for public health policies^1,2,3. In conjunction with pharmacological interventions such as vaccination, non-pharmacological strategies such as testing, contact tracing, and isolation have demonstrated their indispensability in combating epidemics^4,5,6. Using EGT has become a prominent framework in examining the intricate relationship between human behavior and the dynamics of diseases^7,8,9,10. The EGT framework examines the strategic interactions between individuals and the subsequent evolution of their decisions, which are influenced by their perceptions of risks and benefits. The concept has been utilized in diverse settings, including the examination of vaccination patterns^11,12,13,14, the implementation of social distancing measures¹⁵, and the adoption of non-pharmaceutical interventions¹⁶.

Numerous scholarly investigations have been conducted to examine the effects of testing strategies on epidemic control through mathematical models. Grassly et al.¹⁷ conducted a study that provided evidence of the efficacy of mass testing and isolation measures in mitigating the transmission of COVID-19 within the United Kingdom. The study conducted by Aleta et al.¹⁸demonstrated that implementing testing, contact tracing, and isolation strategies effectively managed the epidemic while mitigating the economic consequences. Nevertheless, these studies frequently assume flawless adherence to testing and follow-up treatment or isolation protocols, which may not consistently hold in practical situations. The success of intervention strategies is heavily influenced by human behavior. Individuals can either comply with or decline testing and isolation due to various factors, including the perceived risk of infection, the financial and logistical burden associated with testing, and the socio-economic implications of isolation^19,20. EGT offers a theoretical framework for capturing behavioral aspects and examining their influence on the dynamics of diseases.

The importance of individual decision-making cannot be overstated in the context of infectious disease control strategies in practical scenarios. The field of behavioral epidemiology, which combines game theory and psychology with epidemiology, has attracted significant attention in recent years^21,22,23. In contrast to conventional methodologies, behavioral epidemiology emphasizes examining individuals’ dynamic behavioral changes, thereby establishing a conducive environment for the emerging field of social dynamics²⁴. The study employs various methodologies, including evolutionary game theory and statistical physics, to elucidate human behavior^21,24. Evolutionary game theory (EGT) is often considered a complex topic across various domains. Its inherent characteristics offer a suitable scientific framework for modeling and advancing cooperative behavior^25,26. This demonstrates an individual’s behavior over time during an epidemic, as predicted by Bauch and Bhattacharyya²⁷, based on the overall magnitude of the epidemic. Tori and Tanimoto²⁸ conducted a study using evolutionary game theory to investigate the prosocial behaviors of wearing a mask and self-quarantining to prevent disease spread. The compromises between self-quarantine and imposed quarantine measures to contain an outbreak were investigated by Khan et al.²⁹using the EGT approach. Recent works by Kabir et al. have further advanced the application of EGT in epidemic modeling. Kabir and Tanimoto³⁰developed an evolutionary vaccination game to study behavioral dynamics during economic shutdowns and shield immunity during the COVID-19 pandemic. They also proposed a cyclic epidemic vaccination model incorporating individual attitudes towards vaccination through social interactions³¹. Furthermore, Kabir³² investigated behavioral vaccination policies considering game-environment feedback in epidemic dynamics. These studies highlight the importance of integrating human behavior into epidemic models for more realistic predictions and policy insights. Nevertheless, there is a dearth of research investigating the impact of testing and diagnosis under EGT framework.

This study’s primary contribution is an extended SEIR model incorporating testing, treatment, and vaccination as intervention strategies. The model is enhanced by integrating human behavior through an EGT framework, wherein the decision to undergo testing and vaccination is considered strategic. We examine how behavioral factors, such as adherence to vaccination and testing protocols, affect the progression of diseases and the effectiveness of interventions. We offer valuable insights regarding the most effective combination of intervention strategies and behavioral incentives to control the epidemic effectively.

Model and methods

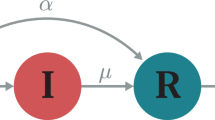
The population is categorized into seven compartments: susceptible ($\:S$), vaccinated ($\:V$), exposed ($\:E$), detected infectious ($\:{I}^{d}$), undetected infectious ($\:{I}^{nd}$), treatment ($\:T$), and recovered ($\:R$) (Fig. 1). Vulnerable individuals receive vaccinations at a rate of $\:{x}_{v}\left(t\right)$ based on behavioral game dynamics. Individuals who are susceptible and vaccinated become infected when they encounter infectious individuals at rates of $\:\beta\:$ and $\:\left(1-\eta\:\right)\beta\:$, respectively, without considering detection where $\:\eta\:$ represents the vaccination efficiency. After an incubation period of $\:\frac{1}{\alpha\:}$ day, infected individuals become contagious. During this period, individuals are tested at a rate $\:p\left(t\right)$ determined by behavioral game dynamics. Detected people move to the $\:{I}^{d}$ compartment, while undetected people move to the $\:{I}^{nd}$ compartment. Individuals who are identified receive treatment with a probability of $\:\tau\:$. The natural cure rate is represented by $\:\gamma\:$, and the treatment cure rate is represented by $\:\delta\:$. The system’s differential equations are as follows, incorporating the total birth rate $\:\lambda\:$ and per capita death rate $\:\mu\:$.

$$\:{S}^{{\prime\:}}\left(t\right)=\lambda\:-\beta\:S\left(t\right)\left[{I}^{d}\left(t\right)+{I}^{nd}\left(t\right)\right]-{x}_{v}\left(t\right)S\left(t\right)-\mu\:S\left(t\right)$$

(1.1)

$$\:{V}^{{\prime\:}}\left(t\right)={x}_{v}\left(t\right)S\left(t\right)-\left(1-\eta\:\right)\beta\:V\left(t\right)\left[{I}^{d}\left(t\right)+{I}^{nd}\left(t\right)\right]-\mu\:V\left(t\right)$$

(1.2)

$$\:{E}^{{\prime\:}}\left(t\right)=\beta\:\left[S\left(t\right)+\left(1-\eta\:\right)V\left(t\right)\right]\left[{I}^{d}\left(t\right)+{I}^{nd}\left(t\right)\right]-\alpha\:E\left(t\right)-\mu\:E\left(t\right)$$

(1.3)

$$\:{{I}^{d}}^{{\prime\:}}\left(t\right)=p\alpha\:E\left(t\right)-\left(\tau\:+\gamma\:\right){I}^{d}\left(t\right)-\mu\:{I}^{d}\left(t\right)$$

(1.4)

$$\:{{I}^{nd}}^{{\prime\:}}\left(t\right)=\left(1-p\right)\alpha\:E\left(t\right)-\gamma\:{I}^{nd}\left(t\right)-\mu\:{I}^{nd}\left(t\right)$$

(1.5)

$$\:{T}^{{\prime\:}}\left(t\right)=\tau\:{I}^{d}\left(t\right)-\delta\:T\left(t\right)-\mu\:T\left(t\right)$$

(1.6)

$$\:{R}^{{\prime\:}}\left(t\right)=\gamma\:\left[{I}^{d}\left(t\right)+{I}^{nd}\left(t\right)\right]+\delta\:T\left(t\right)-\mu\:R\left(t\right)$$

(1.7)

Fig. 1

The seven Compartments are Susceptible ($\:S$), Exposed ($\:E$), Vaccinated ($\:V$), Detected Individuals (I^d), Non-detected Individuals (I^nd), Treatment (T), and Recovered (R). Without the vaccine, susceptible individuals may become exposed. After some duration of 1/α, exposed individuals turn infected. Who tests they go to the detected individuals at a p testing rate. Those who do not test also go to non-detected individuals at a 1-p rate. The detected individuals are taking treatment at τ rate. They are also recovering naturally at γ rate. After taking treatment, they are getting recover at δ rate. Non-detected individuals are also recovering naturally at γ rate.

Positivity and boundedness

It is necessary to have the sum of all populations in all the compartments equal to the total population $\:N\left(t\right)$ at all times $\:t\ge\:0$ to comply with the principle of mass conservation.

$$\:S\left(t\right)+V\left(t\right)+E\left(t\right)+{I}^{d}\left(t\right)+{I}^{nd}\left(t\right)+T\left(t\right)+R\left(t\right)=N\left(t\right)$$

(2)

Differentiating Eq. (2) and substituting values from Eq. (1.1) to (1.7), it follows,

$$\:\lambda\:-\mu\:N\left(t\right)={N}^{{\prime\:}}\left(t\right)$$

(3)

For a constant population, regardless of time, we can assume $\:N\left(t\right)=N=1$, which gives the following results based on Eqs. (2) and (3).

$$\:\lambda\:=\mu\:$$

(4.1)

$$\:{S}^{{\prime\:}}\left(t\right)+{V}^{{\prime\:}}\left(t\right)+{E}^{{\prime\:}}\left(t\right)+{{I}^{d}}^{{\prime\:}}\left(t\right)+{{I}^{nd}}^{{\prime\:}}\left(t\right)+{T}^{{\prime\:}}\left(t\right)+{R}^{{\prime\:}}\left(t\right)=0$$

(4.2)

For a non-constant population, solving Eq. (3) for $\:N\left(t\right)$ gives us

$$\:N\left(t\right)=\frac{\lambda\:}{\mu\:}+\left(N\left(0\right)-\frac{\lambda\:}{\mu\:}\right){e}^{-\mu\:t}$$

(5)

Therefore, for all $\:t\ge\:0$, we have $\:0\le\:N\left(t\right)\le\:\frac{\lambda\:}{\mu\:}$ as long as $\:N\left(0\right)\in\:\left[0,\frac{\lambda\:}{\mu\:}\right]$. Furthermore, consider any compartment $\:X\left(t\right)$ from the model and its corresponding equation. Evidently, $\:X\left(t\right)\le\:N\left(t\right)$ and $\:{X}^{{\prime\:}}\left(t\right)\ge\:\mu\:X\left(t\right)$ for all $\:X\left(t\right)$ with $\:t\ge\:0$. Therefore,

$$\:X\left(t\right)\ge\:X\left(0\right){e}^{-\mu\:t}$$

(6)

From Eqs. (5) and (6), it can be concluded that $\:X\left(t\right)\in\:\left[X\left(0\right){e}^{-\mu\:t},\frac{\lambda\:}{\mu\:}+\left(N\left(0\right)-\frac{\lambda\:}{\mu\:}\right){e}^{-\mu\:t}\right]$ for all $\:t\ge\:0$. As long as $\:X\left(0\right)$ and $\:N\left(0\right)$ are finitely bounded, any compartment $\:X$ of the model is always finitely bounded and positive.

Disease free equilibrium

The disease-free equilibrium (DFE) is obtained by setting the right-hand side of Eq. (1.1) to (1.7) equal to zero alongside $\:{I}^{d}=0$ and $\:{I}^{nd}=0$. It yields that the DFE of the system is $\:{E}_{0}=\left({S}^{*},{V}^{*},{E}^{*},{\left({I}^{d}\right)}^{*},{\left({I}^{nd}\right)}^{*},{T}^{*},{R}^{*}\right)=\left(\frac{\lambda\:}{{x}_{v}^{*}+\mu\:},\frac{\lambda\:{x}_{v}^{*}}{\mu\:\left({x}_{v}^{*}+\mu\:\right)},\text{0,0},\text{0,0},0\right)$ where $\:{x}_{v}^{*}$ is the vaccination rate at the disease-free equilibrium.

Basic Reproduction Number

The next-generation operator method³³ is used at DFE to calculate the number of new cases generated by a single infected individual for the epidemic model. The basic reproduction number $\:{\mathcal{R}}_{0}$ corresponding to the model is obtained as follows.

$$\:{\mathcal{R}}_{0}\left(t\right)=\rho\:\left(F{V}^{-1}\right)=\beta\:{s}_{0}\left[\frac{\alpha\:p\left(t\right)}{\left(\alpha\:+\mu\:\right)\left(\gamma\:+\tau\:+\mu\:\right)}+\frac{\alpha\:\left(1-p\left(t\right)\right)}{\left(\alpha\:+\mu\:\right)\left(\gamma\:+\mu\:\right)}\right]$$

(7)

Here, $\:{s}_{0}={S}^{*}+\left(1-\eta\:\right){V}^{*}$ is the total susceptible population at DFE, including both unvaccinated and vaccinated individuals. $\:\rho\:\left(X\right)$ is the spectral radius of $\:X$, and $\:F$ and $\:V$ are the new infection matrix and transition matrix, respectively, defined as follows.

$$\:F=\left[\begin{array}{ccc}0&\:\beta\:{s}_{0}&\:\beta\:{s}_{0}\\\:0&\:0&\:0\\\:0&\:0&\:0\end{array}\right]$$

(8.1)

$$\:V=\left[\begin{array}{ccc}\alpha\:+\mu\:&\:0&\:0\\\:-\alpha\:p\left(t\right)&\:\gamma\:+\tau\:+\mu\:&\:0\\\:-\alpha\:\left(1-p\left(t\right)\right)&\:0&\:\gamma\:+\mu\:\end{array}\right]$$

(8.2)

Ignoring the demographic terms, the basic reproduction number becomes

$$\:{\mathcal{R}}_{0}\left(t\right)=\beta\:{s}_{0}\left[\frac{p\left(t\right)}{\gamma\:+\tau\:}+\frac{1-p\left(t\right)}{\gamma\:}\right]$$

(9)

Since $\:p$ changes with time, the basic reproduction number also changes with time. The first term is associated with detected individuals, whereas the second is for undetected individuals. They can be rewritten as follows.

$$\:{\mathcal{R}}_{0,d}\left(t\right)=\beta\:{s}_{0}\frac{p\left(t\right)}{\gamma\:+\tau\:}$$

(10.1)

$$\:{\mathcal{R}}_{0,nd}\left(t\right)=\:\beta\:{s}_{0}\frac{1-p\left(t\right)}{\gamma\:}$$

(10.2)

The DFE is globally asymptotically stable in $\:{\mathcal{R}}_{0}<1$. When $\:{\mathcal{R}}_{0}>1$, the DFE is unstable, and a unique endemic equilibrium exists, which is stable as long as $\:{I}^{d}\left(0\right)+{I}^{nd}\left(0\right)>0$³⁴.

Stability analysis

We employ the Lyapunov function approach to analyze the DFE stability of the model. A suitable Lyapunov function is constructed, showing that the DFE is globally asymptotically stable in $\:{\mathbb{R}}^{7}$ when the basic reproduction number $\:{\mathcal{R}}_{0}$ is less than or equal to unity. Consider the following Lyapunov function:

$$\:\mathcal{L}={a}_{1}E+{a}_{2}{I}^{d}+{a}_{3}{I}^{nd}+{a}_{4}T$$

(11.1)

where $\:{a}_{1}$, $\:{a}_{2}$, $\:{a}_{3}$ and $\:{a}_{4}$ are positive constants to be determined. The derivative of the Lyapunov function along the differential equations of the model is given by:

$$\:\dot{\mathcal{L}}={a}_{1}\left[\beta\:\left(S+\left(1-\eta\:\right)V\right)\left({I}^{d}+{I}^{nd}\right)-\alpha\:E-\mu\:E\right]+{a}_{2}\left[p\alpha\:E-\left(\tau\:+\gamma\:\right){I}^{d}-\mu\:{I}^{d}\right]+{a}_{3}\left[\left(1-p\right)\alpha\:E-\gamma\:{I}^{nd}-\mu\:{I}^{nd}\right]+{a}_{4}\left[\tau\:{I}^{d}-\delta\:T-\mu\:T\right]$$

(11.2)

Let $\:{s}_{0}={S}^{*}+\left(1-\eta\:\right){V}^{*}$ be the total susceptible (vaccinated and unvaccinated) population at the DFE. Since $\:S\left(t\right)\le\:{S}^{*}$ and $\:V\left(t\right)\le\:{V}^{*}$ for all $\:t\ge\:0$, we have

$$\:\dot{\mathcal{L}}\le\:\:{a}_{1}\left[\beta\:{s}_{0}\left({I}^{d}+{I}^{nd}\right)-\alpha\:E\right]+{a}_{2}\left[p\alpha\:E-\left(\tau\:+\gamma\:\right){I}^{d}\right]+{a}_{3}\left[\left(1-p\right)\alpha\:E-\gamma\:{I}^{nd}\right]+{a}_{4}\left[\tau\:{I}^{d}-\delta\:T\right]$$

(11.3)

Choosing $\:{a}_{1}=1$, $\:{a}_{2}=\frac{{a}_{1}\beta\:{s}_{0}}{p\alpha\:}$, $\:{a}_{3}=\frac{{a}_{1}\beta\:{s}_{0}}{\left(1-p\right)\alpha\:}$, and $\:{a}_{4}=\frac{{a}_{2}\tau\:}{\delta\:}$, we obtain

$$\:\dot{\mathcal{L}}\le\:\left({\mathcal{R}}_{0}-1\right)\left[p\alpha\:{I}^{d}+\left(1-p\right)\alpha\:{I}^{nd}\right]$$

(11.4)

where $\:{\mathcal{R}}_{0}$ is the basic reproduction number given by Eq. (7). If $\:{\mathcal{R}}_{0}\le\:1$, then $\:\dot{\mathcal{L}}\le\:0$ for all $\:E,\:{I}^{d},\:{I}^{nd},\:T\ge\:0$. Furthermore, $\:\dot{\mathcal{L}}=0$ if and only if $\:E={I}^{d}={I}^{nd}=T=0$. By LaSalle’s invariance principle³⁵, the DFE $\:{E}_{0}$ is globally asymptotically stable in $\:{\mathbb{R}}^{7}$ when $\:{\mathcal{R}}_{0}\le\:1$. This implies that the disease will be effectively controlled and eventually eliminated if $\:{\mathcal{R}}_{0}$ can be maintained below unity through appropriate testing, treatment, and vaccination strategies.

Evolutionary game dynamics

In the context of evolutionary game theory, individuals in the population can choose their strategies based on their perceived risks, benefits, and the behavior of others. In this study, we consider two main strategies: vaccination and testing. The decision to get vaccinated and get tested depends on the individual’s perception of the benefits and costs of testing. We model the vaccination behavior using simple imitation dynamics^{9,10,11,36,37}. Let $\:{x}_{v}\left(t\right)$ denote the fraction of the population that chooses to get vaccinated at time $\:t$. The following differential equation governs the evolution of $\:{x}_{v}\left(t\right)$.

$$\:{x}_{v}^{{\prime\:}}\left(t\right)=m{x}_{v}\left(t\right)\left[1-{x}_{v}\left(t\right)\right]\left[{I}^{d}\left(t\right)+{I}^{nd}\left(t\right)-{C}_{v}V\left(t\right)\right]$$

(12)

where $\:m>0$ is the imitation rate, and $\:{C}_{v}$ represents the relative cost of vaccination. Equation (12) implies that individuals imitate others’ vaccination strategies based on the perceived prevalence of the disease ($\:{I}^{d}+{I}^{nd}$) and the cost of vaccination. More individuals are likely to choose vaccination when the prevalence is high, and the cost is low.

The testing behavior is modeled using similar imitation dynamics but with an additional term representing the awareness or willingness to get tested. Let $\:p\left(t\right)$ denote the fraction of the population that chooses to get tested at time $\:t$. The evolution of $\:p$ is given by

$$\:{p}^{{\prime\:}}\left(t\right)=mp\left(t\right)\left[1-p\left(t\right)\right]\left[{I}^{d}\left(t\right)+{I}^{nd}\left(t\right)+A-{C}_{t}\varphi\:\right]$$

(13)

where $\:A$ represents the awareness or willingness to get tested, $\:{C}_{t}$ is the relative cost of testing, and $\:\varphi\:$ is a parameter that scales the cost term. The awareness term $\:A$ captures the effect of public health campaigns, media coverage, and individual perceptions of the importance of testing. A higher value of $\:A$indicates a greater willingness to get tested, even without a high disease prevalence. The coupling between the epidemic dynamics and the evolutionary game dynamics is achieved through the dependence of the vaccination and testing rates on the disease prevalence. As the number of infected individuals increases, more people are likely to choose vaccination and testing, affecting the spread of the disease. This feedback loop between behavior and disease dynamics can lead to complex and non-trivial outcomes^13,38,39,40.

Result and discussion

The study offers an extensive examination of the interplay between testing, treatment, and vaccination strategies and human behavior in shaping epidemic dynamics. We investigate the temporal evolution and phase-space characteristics of the $\:SVE{I}^{d}{I}^{nd}TR$ model through numerical exploration using finite difference methods, focusing on the influence of evolutionary game theory on intervention outcomes.

Impact of vaccination and treatment without behavioral dynamics

The preliminary analysis concentrated on the baseline scenario in which vaccination and treatment rates are constant and unaffected by behavioral dynamics (Fig. 2). Increased vaccination rates $\:{x}_{v}$ consistently resulted in diminished infection levels. The public’s confidence in vaccination, is pivotal in determining $\:{x}_{v}$ and subsequent disease transmission. Likewise, treatment adherence, indicated by the treatment rate $\:\tau\:$, aids in epidemic control. Analysis of Panels (a-i) and (a-ii) indicates that elevated testing rates significantly diminish disease transmission by enhancing detection and facilitating timely treatment.

Fig. 2

. The change in the number of infected people with respect to time is presented in Panel (a-*) for different vaccine rates x_v= 0.01 (black), 0.1 (green), and 0.3 (red), respectively, in terms of different treatment rate τ = 0.1 and 0.9. The remaining parameter values are β=1.0,α=0.2,η=0.5,γ=0.1,p=0.1,0.9, and δ=0.01,0.5.

Role of testing behavior and awareness

When testing rates are influenced by behavioral dynamics (Figs. 3 and 4), the interaction between testing costs $\:{C}_{t}$ and awareness levels $\:A$ is essential. At minimal awareness ($\:A\:=\:0.1$), infection rates persist at elevated levels (35–40%) irrespective of testing cost, demonstrating that mere cost reduction is inadequate when public health awareness is low. This underscores the essential significance of health education and risk communication in epidemic management.

Fig. 3

Testing game and without Vaccination game. The change in the number of infected people with respect to time is presented in Panel (a-*) for different testing costs C_t= 0.1 (blue), 0.5 (green), and 0.9 (red), respectively, in terms of different awareness values A = 0.1, 0.5, and 0.9. Panel (b-*) also displays distinct awareness values A = 0.1 (red), 0.5 (green), and 0.9 (blue), respectively, in terms of different testing costs C_t= 0.1, 0.5, and 0.9. The remaining parameter values are β=1.0,γ=0.1,m=0.2,δ=0.2,τ=0.8,α=0.2.

Fig. 4

Testing game and without Vaccination game. The change in the number of treated people with respect to time is presented in Panel (a-*) for different testing costs C_t= 0.1 (blue), 0.5 (green), and 0.9 (red), respectively, in terms of different awareness values A = 0.1, 0.5, and 0.9. Panel (b-*) also displays distinct awareness values A = 0.1 (red), 0.5 (green), and 0.9 (blue), respectively, in terms of different testing costs C_t= 0.1, 0.5, and 0.9. The remaining parameter values are β=1.0,γ=0.1,m=0.2,δ=0.2,τ=0.8,α=0.2.

The influence on treatment-seeking behavior is notably significant. Limited awareness yields negligible treatment uptake (approximately 5% of the population), whereas elevated awareness ($\:A\:=\:0.9$) facilitates extensive treatment coverage irrespective of cost. This illustrates how public health awareness can surmount financial obstacles to the adoption of interventions. An intriguing phenomenon arises at intermediate awareness levels ($\:A\:=\:0.5$), where treatment rates exhibit significant sensitivity to testing costs, varying from 13% coverage at low costs to reduced rates at high costs.

Vaccination game dynamics

The examination of vaccination behavior (Figs. 5 and 6) underscores the pivotal influence of vaccine efficacy ($\:\eta\:$) on public reaction. Low efficacy ($\:\eta\:=0.1$) leads to vaccination rates under 70%, with maximum coverage reached approximately on day fifteen, subsequently followed by a gradual decrease. This pattern illustrates how perceived ineffectiveness can jeopardize vaccination initiatives. Conversely, moderate efficacy ($\:\eta\:\:=\:0.5$) attains roughly 80% coverage, peaking around day twenty with enhanced sustained participation.

The correlation between vaccine expenses and effectiveness reveals significant threshold effects. When efficacy is diminished, fluctuations in costs exert negligible influence on infection rates, as the inherent ineffectiveness eclipses issues of accessibility. At elevated efficacy levels, cost emerges as a critical determinant of vaccination rates and, consequently, infection control.

Fig. 5

Vaccination game and without the Testing game. The change in the number of infected people with respect to time is presented in Panel (a-*) for different vaccine costs C_v= 0.1 (blue), 0.5 (green), and 0.9 (red), respectively, in terms of different vaccine efficiency η=0.1, 0.5, and 0.9, respectively. Panel (b-*) also displays distinct vaccine efficiency η=0.1 (red), 0.5 (green), and 0.9 (blue), respectively, in terms of different vaccine costs C_v=0.1, 0.5, and 0.9. The remaining parameter values are β=1.0,γ=0.1,m=0.2,δ=0.2,τ=0.8,α=0.2.

Fig. 6

Vaccination game and without the Testing game. The change in the number of vaccinated people with respect to time is presented in Panel (a-*) for different vaccine costs C_v= 0.1 (blue), 0.5 (green), and 0.9 (red), respectively, in terms of different vaccine efficiency η=0.1, 0.5, and 0.9, respectively. Panel (b-*) also displays distinct vaccine efficiency η=0.1 (red), 0.5 (green), and 0.9 (blue), respectively, in terms of different vaccine costs C_v= 0.1, 0.5, and 0.9. The remaining parameter values are β=1.0,γ=0.1,m=0.2,δ=0.2,τ=0.8,α=0.2.

Synergistic effects of combined interventions

The most critical insights arise from examining the concurrent execution of vaccination and testing strategies (Figs. 7 and 8). Elevated awareness coupled with significant vaccine efficacy can proficiently manage disease transmission, even in the presence of considerable testing and vaccination costs. This finding indicates that effective public health communication and superior vaccines can surmount specific financial obstacles to the adoption of interventions.

Fig. 7

Together with the Testing game and Vaccination game. The change in the number of infected people with respect to time is being presented in Panel (a-*) for different testing costs C_t= 0.1 (blue), 0.5 (green), 0.9 (red), and together with different vaccine costs C_v=0.9 (blue), 0.5 (green), 0.1 (red) respectively in terms of different vaccine efficiency η=0.1, 0.5, and 0.9 respectively. Also, different government force values A=0.1, 0.5, and 0.9, respectively. Panel (b-*) also displays distinct awareness efficiency A=0.1 (blue), 0.5 (red), 0.9 (green) and together with distinct vaccine values η=0.9 (blue), 0.5 (red), 0.1 (green), respectively in terms of different vaccine costs C_v=0.1, 0.5, and 0.9 respectively and also different vaccine costs C_v= 0.1, 0.5, and 0.9 respectively. The remaining parameter values are β=1.0,γ=0.1,m=0.2,δ=0.2,τ=0.8,α=0.2.

Fig. 8

Together with the Testing and Vaccination games. The change in the number of treated people with respect to time is being presented in Panel (a-*) for different testing costs C_t= 0.1 (blue), 0.5 (green), 0.9 (red) and together with different vaccine costs C_v= 0.9 (blue), 0.5 (green), 0.1 (red) respectively in terms of different vaccine efficiency η=0.1, 0.5, and 0.9 respectively and also different awareness values A=0.1, 0.5, and 0.9 respectively. Panel (b-*) also shows the change in the number of vaccinated people with respect to time is being presented in Panel (b-*) for different testing costs C_t= 0.1 (blue), 0.5 (green), 0.9 (red), and together with different vaccine costs C_v=0.9 (blue), 0.5 (green), 0.1 (red) respectively in terms of different vaccine efficiency η=0.1, 0.5, and 0.9 respectively and also different awareness values A=0.1, 0.5, and 0.9 respectively. The remaining parameter values are β=1.0,γ=0.1,m=0.2,δ=0.2,τ=0.8,α=0.2.

Fig. 9

Together with the Testing and Vaccination games. The change in the number of treated people with respect to time is being presented in Panel (a-*) for different awareness values A=0.1 (blue), 0.5 (green), 0.9 (red), and together with different vaccine efficiency η=0.9 (blue), 0.5 (green), 0.1 (red) respectively in terms of different testing costs C_t=0.1, 0.5, and 0.9 respectively and also different awareness values A=0.1, 0.5, and 0.9 respectively. Panel (b-*) also shows the change in the number of vaccinated people with respect to time being presented for different awareness values A=0.1 (blue), 0.5 (green), 0.9 (red) and together with different vaccine efficiency η=0.9 (blue), 0.5 (green), 0.1 (red) respectively in terms of different testing costs C_t=0.1, 0.5, and 0.9 respectively and also different awareness values A=0.1, 0.5, and 0.9 respectively. The remaining parameter values are β=1.0,γ=0.1,m=0.2,δ=0.2,τ=0.8,α=0.2.

An important observation arises concerning the timing of intervention preferences. Figure 8(a) illustrates a critical threshold time point at which the relative benefits of vaccination compared to treatment change. Prior to this threshold, reduced treatment costs result in increased vaccination rates; conversely, beyond the threshold, the relationship reverses. This transition point signifies a critical factor for the timing and sequencing of public health interventions.

Cost effects on final outcomes

Analysis of the final epidemic size (FES) through two-dimensional heatmaps (Figs. 9 and 10) reveals consistent negative correlations with both testing and vaccine costs. Low costs for both interventions ($\:{C}_{t}=\:0.1$, $\:{C}_{v}=\:0.1$) minimize FES by improving accessibility and increasing population-level participation. This effect is amplified by high awareness and vaccine efficacy, demonstrating how behavioral and technological factors can work together to optimize outcomes.

Fig. 10

The final epidemic size (FES) is depicted as a 2D heatmap via changing two factors: the transmission rate (β) on the x-axis and the vaccine efficiency (p) on the y-axis. First row (a-*) shows only vaccine effect for without behavioral dynamics. 1st and 2nd columns in second row (b-*) show only treatment effect. And third column (b-iii) shows combined effect of vaccination and treatment. The remaining parameters are γ= 0.1,α=0.2,δ=0.2.

Fig. 11

The final epidemic size (FES) is depicted as a 2D heatmap via changing two factors: the awareness (A) on the x-axis and the vaccine efficiency (η) on the y-axis. The first, second, and third rows in this figure indicate the outcome of changing the testing costs for (a-*) C_t=0.1, (b-*) C_t=0.5, and (c-*) C_t=0.9. Along with that, the first, second, and third columns indicate the outcomes of adjusting the vaccine cost rate: (*-i) C_v=0.1, (*-ii) C_v=0.5, and (*-iii) C_v=0.9. The treatment coverage reaches its peak level when testing costs are low. On the contrary, the ultimate level of treatment coverage is reduced when testing cost is high. The remaining parameters are: ϕ=0.5,β=1.0,γ= 0.1,m=0.2.

Fig. 12

The final vaccine coverage (VC) is depicted as a 2D heatmap via changing two factors: the awareness (A) on the x-axis and the vaccine efficiency (η) on the y-axis. The first, second, and third rows in this figure indicate the outcome of changing the testing costs for (a-*) C_t=0.1, (b-*) C_t=0.5, and (c-*) C_t=0.9. Along with that, the first, second, and third columns indicate the outcomes of adjusting the vaccine cost rate: (*-i) C_v=0.1, (*-ii) C_v=0.5, and (*-iii) C_v=0.9. The treatment coverage reaches its peak level when testing costs are low. On the contrary, the ultimate level of treatment coverage is reduced when testing cost is high. The remaining parameters are: ϕ=0.5,β=1.0,γ= 0.1,m=0.2.

Fig. 13

The treatment coverage (TC) is depicted as a 2D heatmap via changing two factors: the awareness (A) on the x-axis and the vaccine efficiency (η) on the y-axis. The first, second, and third rows in this figure indicate the outcome of changing the testing costs for (a-*) C_t=0.1, (b-*) C_t=0.5, and (c-*) C_t=0.9. Along with that, the first, second, and third columns indicate the outcomes of adjusting the vaccine cost rate: (*-i) C_v=0.1, (*-ii) C_v=0.5, and (*-iii) C_v=0.9. The treatment coverage reaches its peak level when testing costs are low. On the contrary, the ultimate level of treatment coverage is reduced when testing cost is high. The remaining parameters are: ϕ=0.5,β=1.0,γ= 0.1,m=0.2.

Vaccine coverage (VC) shows similar cost sensitivity but with important nuances (Fig. 11). Peak VC occurs under conditions of low vaccine costs and high efficacy, reflecting rational decision-making by individuals weighing costs against benefits. Treatment coverage (TC) exhibits strongest dependence on testing costs (Fig. 12), with maximum coverage achieved when testing is both affordable and supported by high awareness levels.

Conclusion

This research enhances our comprehension of epidemic management by innovatively combining behavioral dynamics with conventional epidemiological modeling. By augmenting the SEIR framework to include testing, treatment, and vaccination elements, and utilizing evolutionary game theory (EGT), we uncover significant insights into the influence of human behavior on the efficacy of interventions. Our findings indicate that effective epidemic control necessitates a sophisticated comprehension of three fundamental dynamics: relationship between awareness and the effectiveness of interventions; correlation between expenses and participation rates; and the temporal progression of behavioral reactions to interventions.

A notable finding of the study is that elevated awareness levels, when paired with effective vaccines, can surmount cost obstacles to the adoption of interventions. This indicates that investment in public health education and vaccine development may provide superior returns compared to direct cost subsidies in certain contexts. In scenarios of moderate awareness or vaccine effectiveness, it is essential to keep testing costs low for efficient disease management. The correlation between intervention expenses and epidemic results demonstrated consistent significance across various metrics. Reduced testing and vaccination expenses are associated with a diminished final epidemic size (FES), whereas optimal vaccine coverage (VC) is achieved under circumstances of low vaccine costs and high efficacy. Treatment coverage (TC) exhibits notable sensitivity to testing expenses, underscoring the significance of accessible diagnostic services.

Our findings suggest multiple strategies for epidemic control. Public health education must be prioritized via awareness campaigns that highlight the individual and communal advantages of testing and vaccination, as elevated awareness can mitigate cost barriers to the adoption of interventions. Policymakers ought to adopt dynamic pricing strategies by modifying intervention costs according to the current epidemic phase and public awareness levels, while ensuring low initial costs to facilitate the adoption of interventions. The establishment of early detection infrastructure is essential, prioritizing accessible and cost-effective testing facilities, as early detection markedly affects treatment adoption and overall epidemic results. Authorities should meticulously evaluate the temporal dynamics of behavioral responses when implementing interventions, as the efficacy of various measures fluctuates during the epidemic cycle. In resource-constrained scenarios, policymakers must judiciously allocate investments to enhance both intervention effectiveness and accessibility, contingent upon the existing awareness levels within the target demographic.

This study presents multiple promising directions for future research in epidemic management and behavioral dynamics. Examining network effects may elucidate the impact of social structures on the dissemination of disease and intervention behaviors, potentially integrating more advanced game-theoretic models. Models that incorporate economic feedback loops between the effects of epidemics and the availability of intervention resources would yield significant insights into system sustainability. The existing framework may be expanded to incorporate population heterogeneity in risk perception and decision-making, providing a more nuanced understanding of intervention efficacy across various demographic groups. Investigating multi-pathogen dynamics may examine how behavioral reactions to one pathogen affect the adoption of interventions for others, especially in scenarios with multiple simultaneous health threats. The creation of frameworks for real-time modification of intervention strategies based on observed behavioral responses would improve the adaptability of public health measures. Furthermore, examining how epidemic experiences alter long-term health behaviors and the acceptance of interventions in populations could enhance future public health planning and preparedness initiatives.

The incorporation of behavioral dynamics via evolutionary game theory is especially beneficial for comprehending how individual choices culminate in population-level results. This indicates that forthcoming public health initiatives must explicitly incorporate behavioral factors in their design and execution, transcending solely medical or epidemiological considerations.