Based on model randomization and adaptive defense for federated learning schemes

Abstract

Federated Learning (FL) is a privacy-enhancing technique that enables multiple participants to collaboratively train machine learning models without sharing their local data. While FL is a promising paradigm, it is vulnerable to attacks targeting model updates and malicious behavior from clients. To address these challenges, we propose a Privacy-Preserving and High-Secure FL (PPHSFL) scheme, incorporating Models Randomization and Compensation (MRC) and Adaptive Defensive Rewards (ADR). MRC involves using a randomized discrete loss function in FL training to prevent gradient backward inference, enhancing model security. ADR counters dishonest client attacks through adaptive client selection and dynamic rewards. Our suggested technique ensures customer privacy preservation and mitigates threats during FL processing. Numerical analysis and performance evaluation demonstrate the efficacy of our approach compared to existing methods. The PPHSFL method has an average accuracy improvement of 3.0% for the cutting-edge method.

Introduction

In recent years, the topic of distributed machine learning has become popular among scholars and is widely applied in many fields^1,2,3,4. The massive edge devices are producing vast amounts of data⁵. But, the thorny question is that private owners of sensitive data are reluctant to expose and share their data entirely, which forms a large number of islands⁶.

In the conventional Federated Learning (FL)⁷ system model, FL allows multiple participants to generate a global model in a privacy-preserving manner. The traditional FL scheme consists of three processes⁸: (1) the global server distributes the model parameters to local clients; (2) each local client trains its own model and uploads the value of the gradient change rather than raw data; (3) The trusted server will aggregate local owners’ parameters to update global model. Although traditional FL is a tremendous modern shift in distributed machine learning, its privacy preservation is not yet fully guaranteed. Some methods can recover some data information by mimicking the learning process or referring to gradient inversely, which achieves better performance^9,10. Additionally, in the conventional FL, the trustworthiness of participants is not taken into account. It’s possible that several local clients are offline for valid reasons or that local devices have compromised the tradeoff by providing unreliable or malicious models¹¹.

Existing research studies have explored several solutions to partial challenges related to FL using different technologies from multiple directions¹². To enhance the privacy-preserving level of participants, many scholars design some schemes that add noise to the model parameters when uploading. Their methods are based on the theory of Differential Privacy (DP)^13,14, for instance, Hierarchical FL with Local DP (HFL-LDP)¹⁵, Sparsified Model Perturbation in FL (Fed-SMP)¹⁶. Of course, some scholars also have elaborated on some FL models with privacy protection using cryptographic tools such as Homomorphic Encryption (HE) and Secure Multiparty Computation (SMC)¹⁷. Common methods include FL based on Additively Symmetric and HE (named FLASHE by authors)¹⁸, as well as privacy-protected FL using SMC¹⁹.

However, the key problem with DP-FL is that adding considerable amounts of additional random noise significantly reduces the model accuracy, especially for Deep Neural Networks (DNN) with massive parameters²⁰. At the same time, encrypted FL also faces the following challenges²¹: (1) local devices need to be equipped with high computational performance; (2) communication costs have risen significantly; (3) the increase in data transmission volume leads to long training times. The common advantage of the above methods is to prevent information leakage during the training process, but they do not take into account the FL model being broken by dishonest or malicious participants. This is unacceptable in practical applications.

In addition, there is a widespread phenomenon that clients maliciously or unintentionally may destroy the training of the global model, thereby degrading the model’s performance in the target task. For example, when processing image classification, a Malicious Client (MC) can re-label cars as birds, thus causing the learned model to think that a car is a bird²². Driven by this motivation, science researchers have designed and proposed various security protection strategies for FL, such as a blockchain-FL-based intrusion detection scheme^23,24, a conditional variational automatic encoder to detect malicious model updates (named Fedcvae)²⁵, and an ensemble FL immune to MCs²⁶. The central idea of these approaches is to alleviate the impact of statistical anomalies in local model updates. However, they do not take into account strict privacy protection, and are quite complex in threshold definition. Systematically ensuring that local clients’ privacy is not compromised, and that poisoned clients do not attack the global model, will be an interesting and challenging proposition.

Although recent research has explored the privacy preservation in local data and the anti-attack ability of server-side in FL, there is currently no unified approach that tackles both challenges simultaneously^27,28,29,30. However, in large-scale distributed computing, these two issues often need to be considered together, and the absence of either defense can be extremely fatal to a system. In summary, the major contributions of this article are:

• 1. Firstly, we propose a privacy protection method that focuses on enhancing client data security. This method utilizes process randomization by adding process noise during local training. Furthermore, to compensate for the loss of accuracy caused by the noise, we designed a client compensation strategy to improve the model’s accuracy. Our MRC can effectively overcome the issue of low accuracy in DP-FL.

• 2. Secondly, to address the possibility of dishonest or semi-honest attacks from clients, we design an adaptive defensive rewards policy (i.e., ADR) to strengthen the global model’s defense against attacks, ultimately forming a more secure system.

• 3. We conducted comprehensive experiments to test the effectiveness of our privacy protection and anti-attack methods. We evaluated its performance on various datasets and compared the results with the accuracy and convergence of existing methods.

The structure of the rest of the paper is outlined as follows. In “Related work”, related works are discussed. “Preliminaries” presents some preliminaries utilized by PPHSFL. In “Observation and motivation”, our observations regarding FL are outlined. “Threat model and problem statement” introduce some assumptions and threat model considered in this article. “System design” presents the algorithm design of PPHSFL that consists of MRC and ADR. “Performance evaluation” presents performance evaluation results. “Conclusion” concludes the paper with future work.

Related work

This section presents an overview of previous and noteworthy studies regarding privacy-preserving techniques and client attacks in the field of FL.

Privacy-Preservation in FL. The issue of preserving privacy in FL has garnered significant attention in recent years. The state-of-the-art solution to mitigate client privacy leakages is through the use of DP in FL. Building upon the cloud-edge-client hierarchical architecture and using LDP, Shi et al.¹⁵ proposed a novel privacy-preserving scheme called HFL-LDP. This approach introduces the concept of moment accounting, which allows for monitoring of cumulative privacy losses. The article demonstrates that the proposed algorithm satisfies LDP requirements with a suitable level of perturbation and strikes a balance between privacy and utility, providing a higher level of privacy with improved performance. The literature¹⁶ proposed a privacy-persevering paradigm of FL with Sparsified Model Perturbation (Fed-SMP), which employs DP at the client level to maintain model accuracy. The Fed-SMP strategy effectively combines random sparsification with top-k sparsification in local models. Meanwhile, this paper also enhances the privacy-accuracy tradeoff, showcases the effectiveness of Fed-SMP, and reduces communication costs. The literature¹⁸ introduced the FLASHE scheme, which masks local gradient updates through the use of HE and modular addition operations. The authors abandon the asymmetric-key design to optimize computation efficiency, but FLASHE adapts to cross-silo FL rather than various types of FL. Compared literature¹⁵ and¹⁶, Mou et al.¹⁹ proposed an extraordinary privacy-preserving FL scheme based on SMC and DP. The addition of SMC reduces noise introduced by DP, resulting in improved model accuracy compared to DP-based FL, while still having the ability to protect client privacy during the FL process. However, SMC-based FL increases computation cost and communication overhead due to the use of encryption.

Dishonest Client’s Attack (DCA). In FL, there are several types of DCAs that can occur, including physical offline attacks, attacks from poisoned clients, and attacks from the model centralizer, among others. Hei et al.²³ proposed a blockchain-FL-based cloud intrusion detection system (BFL-CIDS) to address malicious attacks in a distributed environment. The solution introduces the use of a cloud computer center, which stores the training process parameters and behavior information using blockchain technology. This approach reduces the likelihood of false alarms and improves the accuracy of FL. Considering defending against targeted model poisoning attacks, the literature²⁵ proposes a strategy called Fedcvae. In this approach, the central server employs a conditional Variational AutoEncoder (VAE) to detect and eliminate malicious models in an unsupervised FL system. The Fedcvae surmounts a few weaknesses of the VAE model but only adopts specific malicious attacks, e.g., the same-value attack. During the same year, Cao et al.²⁶ developed a secure FL approach to defend against MCs by utilizing a randomly selected subset of clients. This approach is robust against a limited number of NCs in certain scenarios. The authors also introduce a Monte Carlo algorithm to calculate certified security levels and achieve improved performance in defending against MCs³¹. In practical applications, Abubaker et al. (published in 2022)²⁴ propose a solution for detecting and removing malicious nodes in the Internet of Things (IoT) using blockchain technology based on Beyond fifth-Generation (B5G). This solution is important in building trust among all entities and the innovation of the paper is the implementation of a combined digital signature with cascading encryption to ensure non-repudiation of both the global server and local client.

Preliminaries

In “Preliminaries”, we introduce the concept of the method used and generate several discussion assumptions over the FL.

FL system

FL is a scenario where many clients collaboratively build high-quality machine learning models, which has drawn attention recently. Considering traditional FL⁸, it consists of a centralized server (i.e., global model) and n clients (i.e., local models) whose mathematical index-set is $\left\{ {1,2, \ldots , i, \ldots , n} \right\}$. Simultaneously, we could suppose that client-i has a local dataset ${D_i} = \{ x_i,y_i\}$, where $x_i$ is data input and $y_i$ is truth label of $x_i$. Thus, the total samples of participating clients can be defined as $D = \sum \limits _{i = 1}^n {{D_i}}$ in FL, where the sample size is enormous. For client side, the local loss function $F_i\left( \omega \right)$ is formulated as follows:

$$\begin{aligned} F_i\left( \omega _i \right) = \frac{1}{{{b}}} \sum \limits _{i = 1}^n {{F_b}\left( \omega _i; \xi _i\right) }, \end{aligned}$$

(1)

where b represents the length of the local dataset over mini-batch ${\xi _i}$, ${F_b}\left( \omega _i; \xi _i\right)$ is the empirical loss function computed over mini-batch ${\xi _i}$ at i-th client and local model is $\omega _i$. The FL aims to minimize the averaged sum of loss functions among the distributed and scattered data samples and explore a set of model parameters. Thus, model training can be formally described as optimizing the following objective function³², as Eq. (2).

$$\begin{aligned} \arg \min \limits _{\omega _g} {F_g}\left( \omega _g \right) = \frac{1}{{{n}}}\sum \limits _{i = 1}^{{n}} {{F_i}((\omega _i;{x_i}),{y_i})}, \end{aligned}$$

(2)

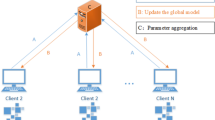
where $\omega _g$ represents the global model parameter of the FL networks, ${F_i}((\omega _i;{x_i}),{y_i})$ represents the loss function at i-th client. The iterative optimization is used for the FL training process, a general approach, as shown in Fig. 1. The ultimate result is that we get the desired global model parameters for the target task (i.e., Eq. (2) corresponds to step-4 in Fig. 1).

Figure 1

Schematic representation of the FL process.

What cannot be ignored in this iterative process is the process of updating the local model by the local client (i.e., step-2 in Fig. 1). The model will be updated by applying the Stochastic Gradient Descent (SGD) algorithm^8,33, which provides an effective way to optimize the loss function. For the mini-batch SGD, a gradient descent step over a mini-batch on each client is regarded as a local iteration (or a local update). After performing one or multiple local iterations, each client exchanges local models or gradients with its neighbors and aggregates these models. Such a training process is regarded as a communication round. Defining iteration set $T = \{ 0,1, \ldots ,t, \ldots ,\tau \}$, the local client performs a partial derivation of its loss function ${F_i}\left( \omega _i \right)$ to get a targeted local gradient $g_i({\omega _i})$ with SGD as Eq. (3) updating at t round.

$$\begin{aligned} {\omega _i}(t) = {\omega _i}(t - 1) - \eta g_i\left( {{\omega _i}(t - 1)} \right) , \end{aligned}$$

(3)

where $\eta$ is the local learning rate. Of course, there are various ways of aggregation, and the simplest method is called FedAvg³⁴ as Eq. (4).

$$\begin{aligned} {\omega _g}(t) = \frac{1}{n}\sum \limits _{i = 1}^{{n}} {{\omega _i}(t)}. \end{aligned}$$

(4)

The stopping conditions for this optimization process are that the global model convergences to a sure accuracy or the iteration number exceeds the upper limit $\tau$.

DP mechanism

DP¹³, the most popular privacy measure, is a formal notion of privacy that provides safeguards against identifying private data.In DP, D and $D'$ are denoted as being distinguishing datasets and ${\left\| {D' - D} \right\| _1} < \mu$, given constant $\mu > 0$^13,14, which means that you can make D into $D'$ by changing just a few records.

Definition 1 Differential Privacy. A randomization algorithm or a mechanism $\Psi$ is called $\varepsilon$-differential private if for all adjacent datasets D and $D'$, we always have:

$$\begin{aligned} Pr[\Psi (D) \in S] \le {e^\varepsilon }Pr[\Psi (D') \in S], \end{aligned}$$

(5)

where S is any subset of possible output. This definition demonstrates that people cannot separate D and $D'$ by inspecting the output of $\Psi$, thus protecting individual data in D from being detected. Due to its effectiveness for privacy preservation, DP and its variants are popular in mitigating privacy leaks in FL. Variants of the privacy method are generally implemented by adding ambiguous noise to the results of a query to protect sensitive information. A simple way to achieve $\varepsilon$-DP is to inject appropriate Gaussian noise. For a clearer and more straightforward description, we summarize the DP-based FL algorithm in the form of Eq. (6).

$$\begin{aligned} \omega _i(t) = \omega _i(t) + \Psi (D_i, \Phi (0,{\sigma _i}^2) ), \end{aligned}$$

(6)

where $\Psi (\cdot )$ is the result matrix after adding noise, $\Phi (0, {\sigma _i}^2)$ is the Gaussian function, where its mean is 0 and its standard deviation is $\sigma _i$. With an understanding of the detailed DP principles, we can borrow the idea of its added noise and make innovative designs for its related parameters.

Observation and motivation

In “Observation and motivation”, we introduce some observation experiments to illustrate the security problems caused by some attacks^9,10. These small tests guide designing better algorithms. The local model uses a Convolutional Neural Network (CNN) consisting of an input layer, two convolutional layers, three fully connected layers, one pool layer, and an output layer, which is more representative in image classification tasks^33,35. In addition, the learning rate $\eta$ was 0.01 in subsequent experiments.

The datasets used in these studies are [Due to laboratory data privacy requirements, datasets generated and/or analyzed during the current study are not publicly available, but may be obtained from the corresponding author upon reasonable request.]:

MNIST dataset³¹ contains 70,000 examples divided into 10 classes. In each class, there are 7000 examples, with 6,000 used for training and 1000 for testing. Each example in the dataset is a binary image of size 28$\times$28, and is labeled according to its corresponding class.

CIFAR-10 dataset³⁵ comprises 60,000 examples spread across 10 classes. Within each class, there are 6000 examples, with 5000 used for training and 1000 for testing. Each example in the dataset is a color image of dimension 32$\times$32 and is associated with a label reflecting its specific class.

Observation 1: privacy-preservation of pure FL

The core idea of FL is to co-train a neural network on a central server. In this process, each participating client receives the current global model weights from the server, and after processing its local data, sends the gradient back to the server. Nevertheless, how much privacy preservation does FL have? We answer this question through a small experiment. We can mathematically derive the actual image data from CIFAR-10 dataset by inverting gradients via the referring method of literature³³. The testing result is shown in Fig. 2, where we randomly select the three images for visual display. The top three images are the original and the bottom three images are the reconstructed. It is clear from the results that three random images prove that reconstructing input data from gradient information is extremely possible. This also shows that pure FL is not secure in terms of privacy protection.

Figure 2

Reconstruction images from the gradient information in CNN network. The objects in Fig.2 are Sheepdog, Wolfhound, and Water-ouze, respectively.

To assess the similarity level (i.e., degree of privacy leakage) between the original image and the reconstructed image, we employ two professional image evaluation indicators, Peak Signal to Noise Ratio (PSNR) and Structural SIMilarity (SSIM)³⁶. PSNR and SSIM describe the similarity of images in terms of content and structure, respectively. When two images are not related, their PSNR and SSIM should be 0. Regarding content and structure, Fig. 3 expresses the more remarkable similarity between the raw image and the image reconstructed after the invasion. SSIM values are all existed and the indicators of PSNR are all relatively high, both of which were much greater than 0. This observation strongly indicates that partial information about the original data can be obtained by the gradient backward inference invasion, and shows that FL must be supplemented with other privacy-preserving methods.

Figure 3

PSNR and SSIM evaluation.

Observation 2: DP-FL evaluation

DP is the most popular privacy measure to enhance the privacy of FL models^13,14. However, the DP essentially adds some incorrect biases resulting in a severe reduction of accuracy, the consequence of applying DP to FL would be a tremendous challenge. The parameter $\varepsilon$ in DP defines the level of privacy preservation, with smaller values indicating stronger privacy preservation. To realize the tradeoff test between privacy and utility, we tested the relationship between accuracy and parameter $\varepsilon$. The results are shown in Fig. 4. It can be observed from Fig. 4 that, in general, the stronger the privacy preservation, the worse the accuracy. When the privacy-preserving ability of FL is enhanced, the model accuracy drops sharply and may even lead to non-convergence of the model, as shown in Fig. 4a. When $\varepsilon$ approaches a specific interval (eg. [0.3, 0.5].), DP weakens its ability to protect privacy, but with more desirable accuracy, as shown in Fig. 4b. Overall, adding noise seems to have a favorable effect on privacy protection, but it should never be added to the training results, which will lose some accuracy.

Figure 4

Observing the tradeoff between privacy and accuracy in DP.

Observation 3: Client selection

In each iteration of FL, all local users stay online and upload their parameters to a server for aggregation. In actual scenarios, FL clients exhibit significant heterogeneity in terms of data statistics and system configurations, which can degrade FL performance if they all participate in global aggregation³⁷. Thus, FL client selection (also known as participant selection or device sampling) is an emerging topic. An effective FL client selection scheme can significantly improve model accuracy, strengthen robustness³⁸, and reduce training overheads³⁹. And currently there are essentially two types of client selection, a constant certain selection and a random selection in all clients³⁷. Therefore we tested what kind of selection method has improved FL performance. First, variables ${N_c}$ and ${N_r}$ are denoted as the number of clients based on two client selection methods, i.e., constant and random, respectively. Then we test the FL accuracy under multiple variants of ${N_c}$ and ${N_r}$, and the results are shown in Fig. 5a. This small experiment shows that the client selection methods in different quantities and by different methods play different roles in the global model. It can be seen that the random number of clients is significantly high accurate than the constant value in Fig. 5a. The fewer randomly selected clients, the higher the accuracy of the model. A random value that varies in the interval time also does not perform well. This finding suggests that randomly selecting a diverse group of clients can help to improve the generalization ability of the global model. After this discovery, we urgently needed to understand whether these two client selection methods had any impact on training time, as FL training efficiency is something we also focus on more than anything else. We specifically compared the training time for different client numbers to achieve the same rounds by random and constant methods, and the results are shown in Fig. 5b, It is almost no difference in their training time under random and constant ways. This suggests that we can confidently go about randomly selecting clients and designing the number of clients which is selected.

The two small tests illustrate that it is not optimal for all clients to participate in FL training, but rather to choose a randomly selected group of local participants. It is important to evaluate the impact of different numbers of randomly selected clients on the FL performance and choose the optimal number for each scenario. This discovery provides novel ideas for dealing with DCA and improving model accuracy.

Figure 5

The impact of the number of clients and being selected way on the global model. The dataset is MNIST and the number of total clients is 50.

Threat model and problem statement

Our focus is on a cross-device FL system, where both clients and the server are assumed to be honest and curious. The server will adhere to the FL protocol while showing interest in individual model updates, and clients will use LDP to safeguard their model updates. Our proposed method aims to minimize performance loss due to LDP in cross-device FL, while ensuring ample security protection for participating clients. We assume that clients will not disclose their private data to others, a common practice in systems with DP protection^4,27,28. Protection against malicious activities like cloud-client collusion, poisoning attacks, or backdoor attacks is not the primary focus of this work, and we refer to existing methods for additional privacy measures^29,30. Given the design objective and security assumptions, we define the research issue as follows: given the subpar performance of existing FL with LDP, how can we adaptively determine the appropriate level of noise and enhancements in performance while ensuring a sufficiently high level of security?

System design

Benefiting from the observations in “Observation and motivation”, we designed a Privacy-Preserving and High-Secure FL (i.e., PPHSFL). Figure 6 shows the framework of our proposed approach, which consists of the following stages:

1. Privacy-Preservation in Client-Side (“Privacy-preservation method: MRC”). The privacy-preserving implementation consists of three steps. First, the local client generates a list of models by performing multiple rounds of local training without uploading model parameters to the server. Second, the client randomly selects a group from the model parameter list. Finally, the client computes the compensation values of the local model parameters and uploads them to the server. Overall, MRC provides a promising DP alternative to address privacy threats while retaining useful information. Section “Privacy-preservation method: MRC” is a detailed description of the MRC.

2. Defense DCA in Server-Side (“Solution for DCA: ADR”). DCA pose a complex and challenging problem that cannot be completely solved directly. Such attacks may be launched actively by participating nodes or passively manipulated by malicious actors. To mitigate the risk of attacks, we propose an optimized solution based on Adaptive Reward with Randomization (ADR) in this article. The ADR algorithm randomly generates d client subsets and chooses one subset to reduce the probability of being attacked by dishonest clients. Then, considering the contribution of each client’s model accuracy in the selected subset, we actively update the list generated by the incentive function. The ADR algorithm selects safer clients by analyzing the impact on the model’s accuracy each time and uses incentives to increase the aggregation weight of high-quality and secure clients. In summary, this approach reduces the likelihood of attacks by actively defending against them and selecting high-quality clients.

Figure 6

System overview of the PPHSFL.

Privacy-preservation method: MRC

This section describes the detailed principle or process of MRC, primarily based on locally trained randomized models that unintentionally create noise during the training process.

To the best of our knowledge, to speed up FL training, more work^38,40,41 used a simple processing method. That is, the local client performs some training epochs and then uploads the local model of the last epoch to the server for aggregation. Based on these works, we denoted k as the number of local training epochs in one full FL round. During the round t of local training, the client saves k model parameters generated under the local disk to form the model sequence $\tilde{\omega }_i^k(t)$, as in Eq. (7).

$$\begin{aligned} \tilde{\omega }_i^k(t) = \{\omega _i^0(t),\omega _i^1(t), \cdot \cdot \cdot ,\omega _i^k(t)\}, \end{aligned}$$

(7)

where $i \in N$ and represents the i-th client. Where we differ is that when FL goes to round $t+1$, the whole system training pattern becomes a traditional FL training pattern^7,8. That is, the client has to upload model parameters to the server after each local training. Next we perform the first-in-first-out principle on $\tilde{\omega }_i^k(t)$. The client deleted $\tilde{\omega }_i^0(t)$ and obtained the newest model sequence $\tilde{\omega }_i^{k+1}(t+1)$, as in Eq. (8).

$$\begin{aligned} \tilde{\omega }_i^{k+1}(t+1) = \{\omega _i^1(t+1),\omega _i^2(t+1), \cdot \cdot \cdot ,\omega _i^{k+1}(t+1)\}. \end{aligned}$$

(8)

The sequential length of $\tilde{\omega }_i^k$ is always constant k throughout the FL training process. Only then the model is guaranteed to converge globally.

The core of our MRC approach is that each client will randomly select a random model parameter from $\tilde{\omega }_i^k$ to upload. The advantage of this operation is that we clutter the direction of the SGD, which also makes it difficult for an attacker to perform gradient backward inference. As an example, in five consecutive FL training rounds, there is a high probability that Client-i has always uploaded $\omega _i^3$ or $\omega _i^5$. Of course, this method has a high degree of randomness. Within a limited range of k values, convergence can be ensured, but it is difficult to guarantee the convergence speed. Therefore, we need to make model corrections based on this and upload the optimized results to the server. The optimized results are an unbiased estimate compared to the true values.

Next, define a random constant s that $t \le s \le k$, we assume a randomly chosen model parameter $\omega _i^s(t)$ at t round. Our compensation mechanism for the pending upload model is shown in Eq. (9).

$$\begin{aligned} \omega _i^s(t) = \omega _i^s(t) + \left[ {({\omega _g}(t) - \frac{1}{{s - k + 1}}\sum \limits _{s = s + 1}^k {\omega _i^s(t)} } \right] \end{aligned}$$

(9)

We abbreviate the compensation mechanism ${({\omega _g}(t) - \frac{1}{{s - k + 1}}\sum \nolimits _{s = s + 1}^k {\omega _i^s(t)} }$ as $C_i^s(t)$. Due to the presence of two random variables in $C_i^s(t)$ here, it provides FL with sufficient privacy protection capabilities. In each local round of updates, an external attacker would need to spend a significant amount of time to attempt to determine the true direction of gradient changes. Meanwhile, we also define $\xi$ as the privacy-preserving level of FL, where $\xi =s/k$ and $\xi \in (0,1]$. If $\xi$ is equal to 1, our method loses its effect and becomes traditional FedAvg^7,8. The smaller the value of A, the greater the privacy-preserving ability of FL. Overall, our method does not require adding additional noise to enhance privacy. We innovatively utilize the sequence of locally trained models to increase the difficulty for attackers to crack the training process. However, this approach also results in certain model performance losses.

Proof of DP for MRC methods. Suppose there are two input datasets D and $D'$, which differ by only one element, i.e., the elements of D and $D'$ are x and $x'$, respectively, and $\left| {x - x'} \right| = 1$. The procedure of the MRC method is as follows. A random number r is chosen at random and r obeys the Laplace distribution. Compute the MRC output according to the following equation: $MRC(D)\, = x + r \times MRC(D') = x' + r$. To prove that the MRC method is $\epsilon$-DP, we need to show that the following inequality holds for any input datasets D and $D'$, and for any output value y:

$$\begin{aligned} \Pr [MRC(D) = y\,] \leqslant \exp (\varepsilon ) * \Pr [MRC(D') = y]. \end{aligned}$$

(10)

Based on the way the output of the MRC method is calculated, we can get the following inequality:

$$\begin{aligned} \begin{aligned} \Pr [MRC(D) = y\,] = \Pr [x + r = y] = \Pr [r = y - x] \\ \Pr [MRC(D) = y\,] = \Pr [x' + r = y] = \Pr [r = y - x'] \\ \end{aligned}. \end{aligned}$$

(11)

Since r obeys the Laplace distribution and $\left| {x - x'} \right| = 1$, we have: The difference in absolute values of $\Pr [r = y - x] = \Pr [r = y - x']$ is limited by the parameters of the Laplace distribution. Therefore, by comparing the probabilities, it can be shown that the MRC method satisfies the definition of $\epsilon$-DP, thus ensuring data privacy.

Solution for DCA: ADR

Some existing research suggests that the biggest threat to FL comes from attacks launched by dishonest members, mainly due to the uncontrollability and dependency of the server-side on the client⁴². To combat DCA threats, an excellent solution is to reduce the probability of participation and the dependency of the client side, ensuring that the model is not attacked. Therefore, based on observation 4.3, we have designed a client selection scheme that integrates ADR to detect intrusions and achieve high security while staying within a limited computation budget.

The fundamental idea of the ADR scheme we have designed is to select m clients from N clients to aggregate the model and minimize the risk of DCA. For this selected subset, we can minimize the subset risk of DCA and formulate this objective as follows:

$$\begin{aligned} \mathop {argmax}\limits _{{M_{sub}}} \,\Theta ,\,\,\,\,s.t.\,\, m = \left| {\{M_{sub}\}} \right| \le n, \end{aligned}$$

(12)

where m is the number of a random subset ${M_{sub}}$ in n clients and $\Theta$ is the most secure level under computational budget.

First, we need to build a list $R=[{R_1},{R_2}, \ldots ,{R_n}]$ to store the incentive values of all clients in the training of FL, and all elements will be initialized with zero by the server when $t=0$.

To abstract the most valuable information that makes the most sense to improve the accuracy of the model, so we will denote a(t) to characterize the contribution degree in the accuracy impact of each candidate client of FL at t-round. Inspired by literature⁴³, we constructed the Sigmod function to describe participants’ contributions to the model. The advantage of the Sigmod function is that it is a threshold function, and the output does not overflow as the iterations change. To prevent redundant calculations, we choose to calculate all clients at once, as in Eq. (13)

$$\begin{aligned} \left\{ \begin{array}{l} {p_i}(t) = \exp ({\ell _i}(t))/\sum \nolimits _1^{n} {\exp ({\ell _i}(t))},\\ {a_i(t)} = 1/(1 + \exp ( - \vartheta \cdot {p_i}(t))), \end{array} \right. \end{aligned}$$

(13)

where $\vartheta$ is a constant, $\ell _i (t)$ represents Kullback-Leibler (KL) divergence⁴³ between local model and global model at t-round. The $p_i(t)$ is denoted as the divergence percentage of the i-th client across all clients.

Next, we will randomly pick up d client-subsets from all participants with replacement, and the size of each subset ${M_{sub}}$ is both m. Once the contribution capacity a(t) of each client on accuracy is obtained, we can sum theirs and define it as the convergence ability of the client subset ${M_{sub}}$ to the global model. The result is that the server side will get a convergence degree sequence ${A_d(t)}$ of all client subsets that can be selected, as Eq. (14).

$$\begin{aligned} {A_d(t)} = \left\{ \sum {{a_1}(t),\sum {{a_2}(t), \ldots ,\sum {{a_d}(t)} } }\right\} . \end{aligned}$$

(14)

Following the maximization strategy, the client’s subset ${M_{sub}}$ corresponding to the largest in ${A_d}(t)$ will be chosen to aggregate the model on the server side.

At each round t, the update of the ${R_i}$ is the most important part in client selection and will be calculated using Eq. (15) to get weights of clients.

$$\begin{aligned} {R_i}(t) = {R_i}(t - 1) + {\theta ^{{a_i(t - 1)} - 1}} + B,t \in T, \end{aligned}$$

(15)

where $\theta$ is a constant and B is defined as the client’s selection and abandonment, represented by “1” and “0” respectively. The motivation of parameter ${{a_i(t)}}$ is to reward the selective clients and filter out non-credible or dishonest clients. Meanwhile, setting B ensures the selected number of clients is not higher than the budget. The final step in the ADR approach is that the server performs parameter aggregation as Eq. (16).

$$\begin{aligned} {w_g}(t) = \frac{1}{{{m}}}\sum \limits _{i = 1}^{m} {{\omega _i}(t)}. \end{aligned}$$

(16)

The whole ADR algorithm will be performed with iterations of traditional FL. The ADR is based on random selection and active defense. After random selection and grouping, even if malicious or dishonest clients are selected, their incentive factors will be minimal over several iterations, which means that these clients will have little effect on the model. Combining learning rewards with random fading effects on the client gives FL high-level security. To better understand the process of the proposed PPHSFL, we give the algorithm pseudocode in Table 1.

Table 1 Pseudo-code for the PPHSFL algorithm.

Performance evaluation

This section performs some experiments on the evaluation of the performance of the algorithm. Section “Experimental setting” describes the environment and parameters of the relevant tests, and “Experimental evaluation” implements some results on the PPSHFL and gives a detailed explanation and discussion of them.

Experimental setting

FL Datasets. The experiments are driven by the datasets introduced in “Observation and motivation”. The experimental datasets in this paper are MNIST³¹, CIFAR-10³⁵, and Fashion-MNIST³¹, which are three classic datasets built for image classification. Following the common practice, we take 50,000 samples as the training dataset and 10,000 as the test dataset for all 10 classes.

Models. The local model uses a CNN, which is more representative in image classification tasks^33,35. The structure of the model is as follows: The input layer has an image size of 32 $\times$ 32 and a channel count of 3 (RGB image). Three consecutive convolutional layers were added, each followed by a batch normalization layer. The convolution kernel size is 3 $\times$ 3 with 64, 128 and 256 convolution kernels. The activation function is ReLU. A maximum pooling layer (2 $\times$ 2 pooling window) is added between each convolutional layer to reduce the size of the feature map. After each maximum pooling layer, Dropout layer is added to prevent overfitting. Finally, there is a fully connected layer section that includes a Flatten layer for spreading the 2D feature maps to 1D, followed by a fully connected layer containing 512 neurons with an activation function of ReLU and following the batch normalization and Dropout layers. The last fully connected layer consists of 10 neurons and uses a softmax activation function for multi-classification output. The model uses the Adam optimizer with a loss function of sparse classification cross entropy and an evaluation metric of accuracy. The learning rate is 0.01. The mini-batch size is 64.

Implementation. We conduct evaluations on a Linux server with 2 GeForce RTX 3090 GPUs, 1 Intel Xeon CPU, and 256 GB memory. We implement our framework with PyTorch, and utilize PySyft⁴⁴ to transmit model parameters.

Evaluation metrics. The metrics we measure are the accuracy of image classification. Accuracy is the most commonly used metric and refers to the number of correctly classified samples as a percentage of the total number of samples, with the following formula:

$$\begin{aligned} Accuracy = \frac{{TP + TN}}{{TP + FN + FP + TN}}, \end{aligned}$$

(17)

where: TP (True Positive): Number of positive samples and classified as positive, FN (False Negative): Number of positive samples labeled and classified as negative, FP (False Positive): Number of samples whose label is negative and classified as positive, TN (True Negative): Number of samples labeled negative and classified as negative.

Experimental evaluation

1). Testing for convergence. For machine learning, convergence is an essential consideration for any solution. As we disrupt the standard training process in the local training step, the convergence of the entire algorithm is the most critical test. Since no factors diverge learning in the aggregation process, we first do not introduce the ADR method in this experiment to exclude irrelevant variables. This experiment only tests the convergence of the MRC algorithm, and the averaging method is used for the global model in the server. The convergence testing is proof of the reasonableness and correctness of the MRC method in the paper. In our experiments, we design local rounds to be k = 5⁴⁵ without losing generality. Meanwhile, we chose the FedAvg and DP-FL ($\varepsilon$ = 0.6) on IID datasets as reference methods. We tested the MRC ($\xi$ = 0.6) method on both the Non-IID and IID datasets shown in Fig. 7.

Figure 7

Convergence is tested on two datasets. The local model is CNN, and the total sum of clients is 100.

The experimental results show that the method in this paper is fully used on the IID dataset and the test accuracy is better than DP. It can also be found that if the original FedAvg is tested with better accuracy on the dataset, the MRC method will also give excellent results in terms of test accuracy. But unfortunately, it does not perform well for the Non-IID dataset, mainly because the heterogeneity of the Non-IID dataset violates Assumption 2. In conclusion, the MRC method is applicable to replace DP in specific situations in the FL Framework. This experiment group demonstrates the rationality and convergence of the algorithm in this paper.

2). Privacy-Preserving Ability of MRC. DP algorithm is designed to enhance the privacy-preserving capabilities of FL, but it loses much of the model’s accuracy. We have shown that the MRC algorithm outperforms DP in terms of accuracy under certain conditions in the above experiments. Nevertheless, how efficient it is in privacy preservation is an urgent testing problem. Therefore, we will test the privacy-preserving ability of both methods at the same convergence accuracy (Acc = 20% and Acc = 25%). Here we have chosen the algorithm Deep Leakage from Gradients (DLG) proposed by Zhu et al⁴⁶. The main reason is that the DLG method consistently outperforms the previous approach by a large margin⁴⁶. We measured PSNR and SSIM of 200 images on the CIFAR-10 dataset. The result of the experience is shown in Fig. 8.

Figure 8

Privacy-preserving ability on public dataset.

From this experimental result, we can derive that the traditional FedAvg has almost no defense against the inverted gradient inference attack. Our MRC approach can be compared with DP in terms of privacy-preserving ability and shows a slight advantage in the SSIM evaluation. This result is because our approach disrupts the descent direction of the original gradient and increases the structural loss. In conclusion, our MRC method can replace the DP method in FL and perform better.

3). Ability to Defend Against DCA. In real FL implementations, clients could have different dishonest data caused by various causes. Therefore, the DCA in this paper includes any local type of attack without making any assumptions. For example, DCA contains physical offline attacks, data manipulation attacks, and data cleaning attacks. In this experiment, we will test the anti-attack capability of ADR-FL and PPHSFL under Continuous DCA (named ADR-DCA and PPHS-DCA, respectively) and compare it with FedAvg (abbreviated as FedAvg-C), and the results are shown in Fig. 9.

Figure 9

The anti-attack capability of ADR and PPHSFL is tested with a total of 100 clients. The number of malicious or dishonest clients is 5 (10 % of total). Parameter $M_s$ is 20 and K is 3, respectively.

From the experimental results, we can easily see that traditional FL already suffers from a significant loss of accuracy for a one-time DCA. When a continuous DCA occurs in the training process, the unprotected FedAvd is destroyed and shows a non-converging outcome. In sharp contrast, whether the ADR method is without privacy protection or the PPHSFL method with privacy protection, our methods substantially outperform the anti-attack capabilities in the presence of continuous attacks. Meanwhile, from the image curves of ADR-DCA and PPHS-DCA, the ADR method has an extremely strong ability to hold accuracy, which is mainly because the ADR method is equipped with a rewarding instrument. In general, the ADR method does not lose too much model accuracy and provides perfect anti-DCA capability.

4). Ablation Study of Parameters. Since the novel algorithm proposed in this paper involves in three significant parameters, namely, length $\gamma$ of local gradient sequence, K skip-steps, and random $M_s$ clients, we need to explore the mode in which these three parameters are mixed , and analyze their influence on the accuracy of the algorithm. Here we take the final convergence accuracy as the evaluation index and set the number of the client is 10 which would launch various attacks. The testing is conducting in three public datasets, i.e., MNIST, CIFAR-10, Fashion-MNIST. The detailed experimental results are shown in the following Table 2. After we analyze the data, we find that the accuracy decreases as K increases, but it is not a fatal loss and is a state that is acceptable in practice. The $M_s$ value changes have almost no effect on the accuracy. Therefore, to lower the probability of being attacked, we could choose a smaller $M_s$-value. Defining the ratio of K and $\gamma$, it represents the ability for the FL to protect data privacy. Therefore, we would like this value to be as large as possible, but this causes some loss of accuracy. By observing the experimental results, here the ratio exceeds 0.5 in a total of three groups, namely group-(6), group-(9) and group-(10), but the accuracy of group-(9) and group-(10) is much less than that of group-(6). Hence we can choose group-(6), i.e., $\gamma$=5, K=3, $M_s$=20, which is a set of parameters to ensure the complete privacy-preserving and high-secure function of the algorithm and make the experiment achieve the desirable performance.

Table 2 Convergence accuracy with different parameters.

5). Comparison with State-of-the-Art Methods. To validate the effectiveness of the method in this paper, we compare the method in this paper with existing methods under the same setting. The comparison methods selected are several attack-resistant methods recently proposed in the machine learning community (e.g., Krum, Trimmed mean, and Median)⁴⁷, which aim to be robust to Byzantine faults but do not have privacy protection. Also, we selected the Reinforcement Learning-based Defense Strategy (DPRLDS)⁴⁸ and the cutting-edge method (RMCS)⁴⁹, both of which are privacy-preserving and counter-attacking approach. Thus, the HSFL and PPHSFL methods in this paper will be tested based on the above four methods in three public datasets using two local models. In this section, the basic experimental parameters are set as follows: $\gamma$=5, K=3, $M_s$=20, the testing is conducted in three public datasets, i.e., MNIST, CIFAR-10, Fashion-MNIST (F-MNIST), the local models are Multilayer Perceptron (MLP) and CNN. And here the number $N_p$ of poisoned clients is 5, 10, and 15, respectively. Tables 3 and 4 are the testing results of maximum convergence accuracy.

Table 3 Performance comparison via MLP networks.

Table 4 Performance comparison via CNN networks.

The experiments demonstrate that our proposed method outperforms the existing strategies under various dataset settings. Of all the methods, the Median is the least effective method, so it is no longer considered for comparison. As the number of poisoned clients rises from 5 to 15, it can be seen that the average test accuracy of Krum and Trimmed mean drops significantly, by 3.6% for Krum and 8.9% for Trimmed mean on MNIST, and by 2.7% for Krum and 0.9% for Trimmed mean on CIFAR-10. As for HSFL, it performs almost the same as Krum on the MNIST and CIFAR-10 datasets, while on Fashion-MNIST, HSFL outperforms Krum. The above can prove that our proposed solution is robust against different DCAs.

We compare PPHSFL with the state-of-the-art FL method under data privacy protection and attack prevention, demonstrating that it can perform comparably to existing federated algorithms. On the MNIST dataset, the PPHSFL method outperforms the other methods with accuracies of 89.2%, 87.3%, and 86.6%, respectively. In contrast, other methods such as Krum, Trimmed mean, and Median have accuracy rates of 85.1%, 75.7%, and 68.3%, respectively, which are significantly behind the PPHSFL method in terms of accuracy. Specifically, compared to the RMCS method, the accuracy of our method is improved by 1.9%, 2.7%, and 3.6% on the MNIST datasets, respectively. Combining the average accuracy difference for the three datasets, the PPHSFL method has an average accuracy difference of 3.0% for the RMCS method, indicating that the PPHSFL method outperforms the RMCS method on these datasets.

In summary, the PPHSFL method performs the best on all datasets and has the highest accuracy rate, which is a clear advantage over other methods. Therefore, it can be concluded that the PPHSFL method is a more reliable and efficient choice for model training using CNN networks.

Conclusion

Although recent works explored the privacy-preservation in local data and the anti-attack ability of servers in FL, such methods are fatal to the accuracy or computational cost. Currently, there is no unified approach for tackling both challenges simultaneously in FL. To tackle this challenge, we have refined FL by designing MRC and ADR. We have innovated FL with privacy protection and high security. We have conducted several tests on both datasets. The experiments show that our method has excellent performance compared to other existing methods. Unfortunately, our method does not perform well on the Non-IID dataset, which will motivate us to conduct subsequent research and improvements.