Introduction

Due to fewer components and simple electronic circuits, DC/DC buck converter is extensively used at high, medium, and low power levels. Its state-space model based on differential equations is a nonlinear and time-varying function. These equations need to linearized around the stable equilibrium point before being exploited using a linear controller with linearization techniques. A significant disturbance might cause a typical DC/DC buck converter to deviate significantly from its regular operating point, making it challenging to attain total stability1. Given this position, the DC/DC buck converter design based on nonlinear controllers is presented. In the last few years, numerous nonlinear control strategies, such as the sliding mode method, have attracted the interest of numerous scientists. This control system has been extensively utilized in industrial applications, including DC/DC buck converter voltage control, because of its powerful characteristics2.

Difficulties associated with SMC include chatter, steady-state errors caused by high-frequency operations, and the requirement for large frequency ranges in the regulator, making applying these digital control techniques very difficult3.

Fuzzy neural control is the most popular approach among many artificial intelligence based nonlinear control strategies for voltage regulation in DC/DC buck converters. In recent years, neuro-fuzzy control has emerged as one of the realistic solutions for complex control challenges. However, the design of an efficient neuro-fuzzy controller relies on the system predictions of the expert4.

Fuzzy logic control (FLC) is another important non-linear control strategy. Remarkable results have been demonstrated in the control of linear and angular positions of inverted pendulum on cart systems using FLC as mentioned in reference5.

To address the voltage control issues of the DC/DC buck converter and enhance its operating performance, many algorithms and controllers have been developed in the literature. These strategies are divided into many types, especially: adaptive fast terminal synergetic controller based on dual RBF neural networks6, adaptive fuzzy-neural fast terminal synergetic controller7, adaptive fuzzy fast terminal synergetic control8, fuzzy-tree adaptive synergetic control9, and fractional-order terminal sliding mode control10.

This study suggests a synergetic control (SC) algorithm based on the simplified state space average model of DC/DC buck converter to regulate the output voltage. SC algorithm is a state space technique based on modern synergistic and mathematics. It was proposed by the Russian researcher11 based on the SCT, which is used to analyze and evaluate the complex and highly nonlinear system consisting of many subsystems. Additionally, the SC algorithm is a powerful control method based on the analytical design of aggregated regulators (ADAR) approach12 to regulate a nonlinear system and guaranteeing that it satisfies the dynamic response requirements. Moreover, it is a computational approach that can generate the control laws directly via the nonlinear DC/DC buck converter model without the need for linearization.

Further, this control method has many benefits, including low bandwidth requirements and good suppression of high-frequency noise, making it appropriate for digital applications13. It also operates at a low frequency, hence decreasing filter design costs, is noise-free, and has the inherent characteristics of the variable structure method14.

However, the flexibility of the SC technique remains intact up to the transient stage, during which the system state trajectories do not reach the attractor. To avoid the intrinsic complexity of the SC technique, a new fast terminal synergistic control scheme is developed, eliminating the reaching stage15. Nevertheless, fast terminal synergetic control is limited, as it cannot be applied when the system’s nonlinearity is unknown. The global estimation feature of the T1-FLS makes it helpful in estimating nonlinear functions that are not entirely known.

Applications of T1-FLS in adaptive fast terminal synergetic controllers (AF-TSCs) are relatively recent. While it has been widely used in many adaptive strategies to control uncertain nonlinear systems, only a limited number of such applications have been reported in the literature16,17,18.

As far as the authors know, the applications of adaptive fuzzy fast terminal synergetic controllers for uncertain nonlinear DC/DC buck converters have not received much attention in the open control literature17,18. Based on the above comments and remarks, the present study introduces an innovative digital regulator for uncertain DC/DC buck converters, which is based on AF-FTSC so that it does not have the problems mentioned above.

In the proposed controller, the unknown nonlinear dynamics of the considered converter are estimated by a T1-FLS-based on the universal approximation theory to ensure finite-time convergence to the attractor in the existence of internal or external disturbance. This makes the control law design robust and simpler to implement. The convergence of the tracking and estimation errors can be guaranteed by way of Lyapunov synthesis. The effectiveness of the considered AF-FTSC regulator is indicated by its utilization in trajectory tracking of a DC/DC buck converter in an experimental study under severe operating situations. The following is a summary of the primary contributions of the article:

  • It is the first time that T1-FLS is implemented for an uncertain DC/DC buck converter based on FTSC algorithm;

  • Unlike previous related studies in this area, the suggested synergetic adaptive regulator is created using the macro-variable to shorten the time required for convergence, facilitate the expression of the regulator, guarantee quick dynamic response and low steady-state error, as well as excellent accuracy in tracking output voltage;

  • The system’s overall stability is demonstrated using the theory of Lyapunov, which also generates updated laws for unknown fuzzy parameters.

  • Avoid the need to obtain an exact dynamic model using T1-FLS approximator to estimate unknown converter functions;

  • This article decreases the computational burden;

  • Experiments are performed using the studied control algorithm on a DC/DC buck converter;

The following structure applies to the rest of the work. The second section presents some fundamental related to SCT and fuzzy logic approximator. The third section provides the required DC/DC buck converter representation. The fourth section presents the design of the AF-FTSC strategy for the DC/DC buck converter. The fifth section presents laboratory tests on a DC/DC buck converter to validate the applicability and effectiveness of the studied AF-FTSC approach. A summary of the obtained results is presented in section six of the article.

Principles of SC method

The SC strategy is generally based on the nonlinear control methodology using the characteristics of regular nonlinear dynamic system and the philosophy of directed self-organization theories. Here are the basic concepts of the regular SC strategy:

  • In the state-space of the regulated system, a uniform manifold is formed. Ensure that the attractor (manifold) has the necessary static and dynamic properties for the system under control. The design of this attractor provides evidence for the theory of directed self-organization.

  • The concept of compression and decompression of phase flow of controlled variables is the most significant rule in SC method.

  • Designer requirements are introduced as a set of constants that characterize the required operating modes of the controlled system.

To present some concepts of synergetic theory, like stability and control design, let us take care of a class of affine nonlinear control system of order n-degree defined by Eq. (1):

$$\dot{x} = g\left( {x,\,\tau ,\,t} \right)$$
(1)

where τ ∈ Rm, and x ∈ Rn, represent the control system and state variables, respectively. The g(.) represents a continuous nonlinear function. Generally, the state variables x are used to define the macro-variable υ in the design process of the SC algorithm19:

$$v = v\left( {x,\,\,t} \right)$$
(2)

The key objective the SC algorithm is to force the converter to operate on predefined manifold υ = 0.

Developing a synergetic controller that can drive the states of the converter to reach the preferred manifold exponentially can be written as follows:

$$m\,\dot{v}\, + \,v = 0,\,\,\,\,m > 0$$
(3)

where \(\dot{\upsilon }\) is the derivative of the considered macro-variable over time, and m is a positive coefficient that allows the author to determine the time of convergence to the pre-specified attractor. After solving Eq. (3), the expression for υ(t) is as follows:

$$v\left( t \right) = v_{0} \,e^{ - t/m}$$
(4)

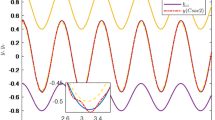
The curves plotted in Fig. 1 indicate that \(\upsilon\)(t) → 0 at t → ∞, implying that \(\upsilon\)(t) is attracted to \(\upsilon\) = 0 from any starting point \(\upsilon\) 0 (Fig. 1). Given a temporal constant greater than 0, the macro-variable \(\upsilon\) will experience an exponential increase at a rate determined by the factor. Since the system remains stable, the minimum value is of m, the faster the macro-variable decays. When \(\upsilon\) attains 0, the system goes to the manifold and then works on the attractor without leave.

Fig. 1
figure 1

Convergence of multiple macro-variables to the attractor from different beginning at υ = 0.

Full size image

Suppose the following equation gives the derivative of Eq. (2):

$$\dot{v}\, = \frac{{dv\left( {x,\,\,t} \right)}}{dt} = \frac{{\partial v\left( {x,\,\,t} \right)}}{\partial x}.\frac{dx\left( t \right)}{{dx}}$$
(5)

By substituting (1) and (3) in (5), we have (6):

$$m.\frac{{\partial v\left( {x,\,\,t} \right)}}{\partial x}.g\left( {x,\,\tau ,\,t} \right) + v\left( {x,t} \right) = 0$$
(6)

The final formula for SC law is given by resolving Eq. (6):

$$\tau = g\left( {x,\,v\left( {x,\,\,t} \right),\,m,\,t} \right) = 0$$
(7)

The SC algorithm Eq. (7) forces state trajectories to meet condition (3). A correct choice of \(\upsilon\)(t) and m guarantees optimal performance and intended stability20. SC law Eq. (7) can be reconstituted as a solution of the Kolesnikov function Eq. (8). Select the next performance indicator21:

$$J_{\sum } = \int_{0}^{\infty } {F\left( {\dot{v},v} \right)\,dt = \int_{0}^{\infty } {\left( {\sum\nolimits_{k = 1}^{n} {m_{k}^{2} \,\dot{v}_{k}^{2} + v_{k}^{2} } } \right)} } \,dt$$
(8)

Using the Lyapunov function allows to achieve global stability:

$$V\left( t \right) = \frac{1}{2}v\left( {x,\,t} \right)^{2}$$
(9)

As long as m > 0, the following inequality is satisfied:

$$\dot{V}\left( t \right) = \dot{v}\left( {x,\,t} \right)v\left( {x,\,t} \right) = - \frac{1}{m}v\left( {x,\,t} \right)^{2} < 0$$
(10)

Figure 2 bottom displays the SC method’s phase plane and stability properties as indicated by the convergence to the manifold. The point of stability is the origin, when the error approaches zero. Equation (3) represents a linear curve with a slope of (−1/m) that traverses the origin. The system’s operating point moves towards the inclined straight line before continuing along it in the direction of the origin.

Fig. 2
figure 2

The phase plane for Eq. (3).

Full size image

The graphical illustration, presenting the numerical computations of the designed SC method is presented in (Fig. 3).

Fig. 3
figure 3

A graphical illustration of the suggested SC method.

Full size image

The basis of fuzzy logic approximator

It’s recognized that FLS is universal approximator and has various applications in the identification and design of controllers. Typically, T1-FLS consists of 04 main elements: the fuzzifier, the fuzzy rules base, the fuzzy inference model and the defuzzifier, as illustrated in (Fig. 4).

Fig. 4
figure 4

Basic structure of T1-FLS.

Full size image

The main feature of T1-FLS is its capability to use conditional fuzzy logic to represent human-like thought processes and respond appropriately to experiences. The expression for creating a mapping from a collection of inputs (x) to a set of collection (y) using If–Then rules is as follows:

$$\begin{gathered} R^{l} :\,If\,x_{1} \,is\,A_{1}^{i} (x_{1} \,),\,x_{2} \,is\,A_{2}^{i} (x_{2} \,),...,\,x_{n} \,is\,A_{n}^{i} (x_{n} \,), \hfill \\ \,\,Then\,y_{1} \,is\,B_{1}^{i} (x_{1} \,),\,y_{2} \,is\,B_{2}^{i} (x_{2} \,)...,\,y_{m} \,is\,B_{m}^{i} (x_{m} \,)\,\,\,\, \hfill \\ \end{gathered}$$
(11)

where l = 1, 2,…, L, with L indicates the total number of rules, x = [x1, x2,…, xn]T and y = [y1, y2,…, ym]T symbolize the input and output variable vectors of T1-FLS. Ail and Bjl are the linguistic components of the fuzzy groups, represented by their membership functions (MFs) \({\mu }_{{A}_{i}^{l}}\), and \({\mu }_{{B}_{i}^{l}}\). Both the input and output variables of T1-FLS have the same type of MFs, which are Gaussian member MFs expressed as:

$$\mu_{{A_{i}^{l} }}^{{}} \left( {x_{i} } \right) = \mu_{{B_{i}^{l} }}^{{}} \left( {y_{i} } \right) = \,exp\left( { - \frac{{\left( {x_{i} - m_{i} } \right)^{T} \left( {x_{i} - m_{i} } \right)}}{{2.\,c_{i}^{2} }}} \right)$$
(12)

where ci and mi are the width and center vector of the ith fuzzy set Ail and Bjl, respectively. Utilizing the singleton fuzzifier, product inference concept, and center-average defuzzifier, the final output of the T1-FLS can be defined as22:

$$y_{j} (x) = \,\frac{{\sum\nolimits_{l = 1}^{L} {\left( {\prod\nolimits_{i = 1}^{n} {\mu_{{A_{i}^{l} }} \left( {x_{i} } \right)} } \right)\overline{y}_{j}^{l} } }}{{\sum\nolimits_{l = 1}^{L} {\left( {\prod\nolimits_{i = 1}^{n} {\mu_{{A_{i}^{l} }} \left( {x_{i} } \right)} } \right)\overline{y}_{j}^{l} } }}$$
(13)

where \({\overline{y} }_{j}^{l}\) represents the point in \({y}_{j}\) at which \({\mu }_{{B}_{i}^{l}}\left({y}_{j}\right)\) reaches its finest value (taking into account that \({\mu }_{{B}_{i}^{l}}\left({y}_{j}\right)=1\)). An adaptive T1-FLS is created when is \({\overline{y} }_{j}^{l}\) selected as the independent variable in (12). Hence, the following compact structural representation becomes possible:

$$y_{j} (x) = \,\sum\nolimits_{l = 1}^{L} {\overline{y}_{j}^{l} } = v_{j}^{T} o_{j} \left( x \right)$$
(14)

where \({v}_{j}={\left[{\overline{y} }_{j}^{1}, {\overline{y} }_{j}^{2},\dots , {\overline{y} }_{j}^{L} \right]}^{T}\in {R}^{L}\) is named the regulating gain vector, and \({o}_{j}(x)={\left[{o}_{1}(x), {o}_{2}(x),\dots , {o}_{L}(x) \right]}^{T}\in {R}^{L}\) is the fuzzy basis function (FBFs) is given by:

$$o_{j} \left( x \right) = \frac{{\sum\nolimits_{i = 1}^{n} {\mu_{{A_{i}^{l} }} \left( {x_{i} } \right)} }}{{\sum\nolimits_{j = 1}^{L} {\left( {\prod\nolimits_{i = 1}^{n} {\mu_{{A_{i}^{l} }} \left( {x_{i} } \right)} } \right)} }}$$
(15)

Remark

The compact form Eq. (14) is commonly utilized in fuzzy regularization research23. We should mention that the FBFs, οj(x), must be calculated correctly in advance. The vector νj(x) can be calculated online using certain update rules.

Modelling of the DC-DC buck converter

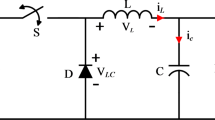
The basic configuration of the controlled PWM DC/DC buck converter is illustrated in (Fig. 5). It comprises of a DC-load resistance Ro, an inductance L, a capacitance C, a power diode D, an input DC voltage Vin, a DC output voltage Vo, a power transistor Q.

Fig. 5
figure 5

The basic circuit of a DC/DC buck converter.

Full size image

Following is a description of state-space equations for a DC/DC buck converter operating in steady-state24:

$$\left\{ {\begin{array}{*{20}c} {\frac{{di_{L} }}{dt} = - \frac{1}{L}V_{o} + \frac{{V_{in} }}{L}\tau \,\,\,\,\,} \\ {\frac{{dV_{o} }}{dt} = - \frac{1}{C}i_{L} + \frac{1}{RC}V_{o} } \\ \end{array} } \right.$$
(16)

where iL represents the current flowing through inductance L and τ denotes the On/Off ratio of the converter. Given the assumption that the output voltage (Vo) and its corresponding derivative (\({\dot{V}}_{o}\)) are the state variables, we can write the following equation:

$$\left\{ {\begin{array}{*{20}c} {x_{1} = V_{o} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \\ {x_{2} = \dot{x}_{1} - \frac{{dV_{o} }}{dt}} \\ \end{array} } \right.$$
(17)

Consequently, the state equations of the converter can be given in the structure of Eq. (18):

$$\left\{ {\begin{array}{*{20}c} {\dot{x}_{1} = x_{2} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} \\ {\dot{x}_{2} = - \frac{{x_{1} \,}}{LC} - \frac{{x_{2} }}{RC} + \frac{{V_{in} }}{LC}\tau } \\ \end{array} } \right.$$
(18)

Work’s goal

This research paper aims to develop a suitable AF-FTSC algorithm τ for converter model (16) as a function of state-variables (x1, x2), which delivers the appropriate output voltage x1 = x1_ref without prior knowledge of the converter model and under the restriction that the tracking error rapidly approaches the origin in a limited amount of time tr, which leads to:

$$\mathop {lim}\limits_{{t \to t_{r} }} \left\| e \right\| = \mathop {lim}\limits_{{t \to t_{r} }} \left\| {x_{1} - x_{1\_ref} } \right\| \to 0$$
(19)

Design of the suggested AF-FTSC method

Assuming that Vref is the reference output voltage for x1_ref. Hence, the tracking error and its derivative have the following definitions:

$$e = x_{1} - V_{ref}$$
(20)
$$\dot{e} = x_{2} - \dot{V}_{ref}$$
(21)

To enable the implementation of AF-FTSC technique on a DC/DC buck converter, it is important to define a specific function referred as the macro variable which is selected as a nonlinear set of state variables25:

$$v = \dot{e} + \rho \,e + \sigma \,e^{\alpha /\beta }$$
(22)

where ρ and ρ represent the control gains. The gains α and β are both positive numbers. In this case, the α and β condition is described as follows: 1 < α/β < 2. The following constraint can be utilized to impose a desired dynamic on the macro variable:

$$m\,\dot{v} + v = 0$$
(23)

where m is a positive value that helps the designer determine the rate of convergence to the designed manifold υ = 0. Consequently, Eq. (22) for υ = 0 can be expressed mathematically in the following manner:

$$\dot{e} + \rho \,e + \sigma \,e^{\alpha /\beta } = 0$$
(24)

The convergence speed of the suggested system from any given starting point e(0) ≠ 0 to the manifold υ = 0 is a limited time tr ≥ 0 and is calculated by integrating Eq. (22), and by specifying the accurate parameters ρ, σ, α, and β as follows:

$$t_{r} = \frac{\alpha }{{\rho \left( {\alpha - \beta } \right)}}Ln\left[ {\frac{{\rho \left| {e\left( 0 \right)} \right|^{{1 - \left( {\frac{\alpha }{\beta }} \right) + \sigma }} }}{\sigma }} \right]$$
(25)

We can now derive υ, which gives:

$$\dot{v} = \ddot{e} + \rho \,\dot{e} + \sigma \frac{\alpha }{\beta }\,e^{{\left( {\alpha /\beta } \right) - 1}} \dot{e}$$
(26)

Combining (23) and (26), leads to (27):

$$\ddot{e} + \rho \,\dot{e} + \sigma \frac{\alpha }{\beta }\,e^{{\left( {\alpha /\beta } \right) - 1}} \dot{e} = - \frac{1}{m}v$$
(27)

Rearranging Eq. (18), \(\ddot{e}\) becomes:

$$\ddot{e} = - \frac{{x_{1} }}{LC} - \frac{{x{}_{2}}}{RC} + \frac{{V_{in} }}{LC}\tau - \ddot{V}_{ref}$$
(28)

When developing the suggested FTSC algorithm, we utilize the following simplifications:

\(g\left( x \right) = \frac{{V_{in} }}{LC}\) and \(f\left( x \right) = - \frac{{x_{1} }}{LC} - \frac{{x{}_{2}}}{RC}\).

Simplifying the FTSC algorithm, leads to (29):

$$\tau_{FTSC} = \frac{1}{g\left( x \right)}\left[ {\ddot{V}_{ref} - f\left( x \right) + \frac{1}{m}v - \rho \,\dot{e} + \sigma \,\frac{\alpha }{\beta }e^{{\left( {\alpha /\beta } \right) - 1}} \dot{e}} \right]$$
(29)

Stability confirmation

The Lyapunov function can be applied to check the overall stability of the system:

$$V_{1} = \frac{1}{2}v^{T} \,v$$
(30)

Differentiating V1 and substituting Eq. (26) into it, then one can have:

$$V_{1} = v\left( { - \frac{1}{m}v} \right) = - \frac{1}{m}v^{2} \le 0$$
(31)

Thus, the regulator (29) can satisfy the overall stability criterion of the system. Nevertheless, in practical implementation, the nonlinear system components f(x) as well as g(x) are unknown and hard to calculate precisely. Hence, it is not possible to apply the control law (29). To deal with this challenge, a FLS with the universal estimation method is exploited in this article to estimate online the unknown nonlinear components f(x) and g(x) in Eq. (29). Suppose \(\widehat{f}(\left.x\right|{v}_{f})\) and \(\widehat{g}(\left.x\right|{v}_{g})\) be approximate values of f(x) and g(x). These functions are formulated as:

$$\hat{f}\left( {x\left| {v_{f} } \right.} \right) = v_{f}^{T} \,o_{f} \left( x \right)$$
(32)
$$\hat{g}\left( {x\left| {v_{g} } \right.} \right) = v_{g}^{T} \,o_{g} \left( x \right)$$
(33)

where \({o}_{f}(x)\) and \({o}_{g}\left(x\right)\) denote the fuzzy basis functions, \({v}_{f}\) and \({v}_{g}\) represent the factors of the FLS. Using the approximated functions (32) and (33), the overall algorithm of AF-FTSC can be defined as follows:

$$\tau_{AF - FTSC} = \frac{1}{{\hat{g}\left( {x\left| {v_{g} } \right.} \right)}}\left[ {\ddot{V}_{ref} - \hat{f}\left( {x\left| {v_{f} } \right.} \right) + \frac{1}{m}v - \rho \,\dot{e} + \sigma \,\frac{\alpha }{\beta }e^{{\left( {\alpha /\beta } \right) - 1}} \dot{e}} \right]$$
(34)

Lemma 1

Suppose the given nonlinear system (18) with the command input (34), if the fuzzy-based adaptive rules are formed as:

$$\dot{v}_{f} = - d_{1} \,v\,\,o_{f} \left( x \right)$$
(35)
$$\dot{v}_{g} = - d_{2} \,v\,\,o_{g} \left( x \right)$$
(36)

where d1, and d2 are arbitrary positive parameters and all variants in the closed-loop system are limited, then the considered adaptation method guarantees the total stability of the system, which implies that the tracking error approaches the zero in a limited-time.

Assumption 1

Let x exist in compressed space Rn = {x ∈ Rn:∣x∣ ≤ Hx <  +  ∞}, Where Hx is a constant. The optimal parameters νf* and νg* belongs in the following convex group:

$$M_{f} = \left\{ {v_{f} \in R^{n} :\left| {v_{f} } \right| \le H_{f} } \right\}$$
(37)
$$M_{g} = \left\{ {v_{g} \in R^{n} :\left| {v_{g} } \right| \le H_{g} } \right\}$$
(38)

where Hf and Hg are designed coefficients, and the radius Mf and Mg are restriction sets for νf and νg.

Assuming that there are ideal parameter approximations of type-1 FLS variables νf* and νg*, which can be expressed in the following format without losing generality:

$$v_{f}^{*} = \mathop {v_{f} \in M_{f} }\limits^{arg\,min} \left\{ {sup\left| {\hat{f}\left( {x\left| {v_{f} } \right.} \right) - f\left( x \right)} \right|} \right\}$$
(39)
$$v_{g}^{*} = \mathop {v_{g} \in M_{g} }\limits^{arg\,min} \left\{ {sup\left| {\hat{g}\left( {x\left| {v_{g} } \right.} \right) - g\left( x \right)} \right|} \right\}$$
(40)

Thus, f(x) and g(x) are estimated to arbitrary precision by the FLS estimators (32) and (33) as in reference14.

Lemma 2

See26, for any specified smooth functions f(x) and g(x) in a compressed space x ∈ Rn and any random lf > 0, and lg > 0, there exists a fuzzy estimator and in the form of Eqs. ( 41) and (42) such that:

$$\mathop {Sup}\limits_{{x \in R^{n} }} \left| {\hat{f}\left( {x\left| {v_{f} } \right.} \right) - f\left( x \right)} \right| < l_{f}$$
(41)
$$\mathop {Sup}\limits_{{x \in R^{n} }} \left| {\hat{g}\left( {x\left| {v_{g} } \right.} \right) - g\left( x \right)} \right| < l_{g}$$
(42)

The design of T1-FLS approximator is explained in detail as follows:

figure a

Remark

Depending on the variation of x1 and x2, the controller parameters οf(x) and οg(x) can be adaptively calculated using fuzzy rules by employing the T1-FLS approximator developed previously. Thus, the following formula can be used to obtain the minimum estimation error:

$$\hat{e} = \left[ {\hat{f}\left( {x\left| {v_{f}^{*} } \right.} \right) - f\left( x \right)} \right] + \left[ {\hat{g}\left( {x\left| {v_{g}^{*} } \right.} \right) - g\left( x \right)} \right]\tau$$
(43)

where \(\widehat{e}\) is limited by a positive constant \(\widehat{e}\) ≤\({\widehat{e}}_{max}\).

Substituting (43) into (23), the dynamic of macro-variable can be computed by Eq. (44):

$$\dot{v} = \left[ {\hat{f}\left( {x\left| {v_{f}^{*} } \right.} \right) - f\left( x \right)} \right] + \left[ {\hat{g}\left( {x\left| {v_{g}^{*} } \right.} \right) - g\left( x \right)} \right]\tau + \frac{1}{m}v + \hat{e}$$
(44)

Following a few straightforward adjustments, we obtain:

$$\dot{v} = \left( {v_{f}^{*T} - v_{f}^{T} } \right)\,o\left( x \right) + \left( {v_{g}^{*T} - v_{g}^{T} } \right)\,o\left( x \right)\tau + \frac{1}{m}v + \hat{e}$$
(45)

Using the given equation, it is possible to write:

$$\dot{v} = \hat{v}_{f}^{T} \,o\left( x \right) + \hat{v}_{g}^{T} \,o\left( x \right)\tau + \frac{1}{m}v + \hat{e}$$
(46)

where \({\widehat{v}}_{f}={v}_{f}^{*}-{v}_{f}\) and \({\widehat{v}}_{g}={v}_{g}^{*}-{v}_{g}\)

Stability confirmation

Let’s use the following formula for the Lyapunov function:

$$V = \frac{1}{2}\left( {v^{2} + \frac{1}{{d_{1} }}\hat{v}_{f}^{T} \,\hat{v}_{f} + \frac{1}{{d_{2} }}\hat{v}_{g}^{T} \,\hat{v}_{g} } \right)$$
(47)

Upon calculating the time derivative of Eq. (47), we arrive at (48):

$$\dot{V} = v\dot{v} + \frac{1}{{d_{1} }}\hat{v}_{f}^{T} \,\dot{\hat{v}}_{f} + \frac{1}{{d_{2} }}\hat{v}_{g}^{T} \,\dot{\hat{v}}_{g}$$
(48)

By replacing (46) into (48), we can obtain (49):

$$\dot{V} = v\left( {\hat{v}_{f}^{T} \,o\left( x \right) + \hat{v}_{g}^{T} o\left( x \right)\tau - \frac{1}{m}v + \phi } \right)\frac{1}{{d_{1} }}\hat{v}_{f}^{T} \,\dot{\hat{v}}_{f} + \frac{1}{{d_{2} }}\hat{v}_{g}^{T} \,\dot{\hat{v}}_{g}$$
(49)

That we use:

$$\,\dot{\hat{v}}_{f} = \dot{v}_{f}$$
(50)

And

$$\,\dot{\hat{v}}_{g} = \dot{v}_{g}$$
(51)

Replacing (50) and (51) in (49) gives (52):

$$\dot{V} = - \frac{1}{m}v^{2} + v\phi + \frac{1}{{d_{1} }}\hat{v}_{f}^{T} \,\left( {d_{1} \left( x \right)\,v\,o\left( x \right) + \dot{v}_{f} } \right) + \frac{1}{{d_{2} }}\hat{v}_{g}^{T} \left( {d_{2} \,\left( x \right)v\,o\left( x \right)\tau + \dot{v}_{g} } \right)$$
(52)

The variables \({\dot{v}}_{f}\) and \({\dot{v}}_{g}\) are adjusted using the rules (50) and (51). Substituting, Eqs. (35) and (36) into (52), leading to:

$$\dot{V} = - \frac{1}{m}v^{2} + v\phi$$
(53)

Using an appropriate number of fuzzy bases to approximate f(x) and g(x) will guarantee a very small estimation error, resulting in (54):

$$\dot{V} \le - \frac{1}{m}v^{2} \le 0$$
(54)

The fact that the error in \(\widehat{e}\) (46) is the optimal result that can be obtained will lead us to guarantee that all variables are strictly limited. Clearly, if \(\widehat{e}\left(0\right)\) is limited, then \(\widehat{e}\left(t\right)\) is also limited. The desired signal xref is limited, consequently the converter state x(t) is as well. To complete the proof and create asymptotic convergence for the tracking error, it’s better to prove that υ → 0 as t → ∞. In addition, assume that ∥ψ∥ ≤ μ. Hence, the following new formulation of Eq. (53) is possible:

$$\dot{V} \le - \frac{1}{m}\mu \left| \psi \right| + \mu \left| \phi \right|$$
(55)

Integrating on both sides of Eq. (55) provides:

$$\int_{0}^{t} {\left| v \right|\,} dt \le \frac{m}{\mu }\left( {V\left( 0 \right) - V\left( t \right)} \right) + m\int\limits_{0}^{t} {\left| \phi \right|} \,dt$$
(56)

Equation (55) means that all variables are uniformly limited. Subsequent to this, υ ∈ L1. We can conclude from (54) that the macro-variable is bounded and all terms in (55) have limits, thus \(\left(\upsilon ,\dot{\upsilon }\right)\in {L}_{\infty }\), making exploit of Barbalat theory27. Hence, we can deduce that the tracking error asymptotically approaches zero, which meets the stability requirement. Therefore, it is possible to ensure the stable control operation of the buck converter without the need for system information. Figure 6 depicts the general diagram representation of the considered AF-FTSC method.

Fig. 6
figure 6

Schematic representation for suggested AF-FTSC regulator.

Full size image

Simulation results

Simulation results are provided in this part to illustrate the applicability and efficacy of the suggested AF-FTSC regulator. The design coefficients of the AF-FTSC control law for the simulation and experimental implementation are as follows: ρ = 100, σ = 150, α = 7, β = 9, Ts = 0.005, d1 = 2000, d2 = 1500. In the T1-FLS estimator, we can construct a group of 7 MFs distributed equally over a universe of discourse [−1, 1], according to the following model:

$$\mu_{f}^{k} = \mu_{g}^{k} = exp\left[ { - \left( {x + 4 - 1.6\left( {n - 1} \right)^{2} } \right)} \right],\,n = 1,...,7$$
(57)

n = 7, indicates that there are 49 fuzzy rules to approximate the uncertain functions. The 49 fuzzy rules can include the whole space and estimate any non-linear function. The MFs degree is depicted in (Fig. 7). The adaptive fuzzy parameters are chosen according to the following formula:

$$\left[ {\begin{array}{*{20}c} {v_{f} } \\ {v_{g} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {v_{f}^{1} } & {v_{f}^{2} } & {\begin{array}{*{20}c} {v_{f}^{3} } & {v_{f}^{4} } & {\begin{array}{*{20}c} {v_{f}^{5} } & {v_{f}^{6} } & {v_{f}^{7} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {v_{g}^{1} } & {v_{g}^{2} } & {\begin{array}{*{20}c} {v_{g}^{3} } & {v_{g}^{4} } & {\begin{array}{*{20}c} {v_{g}^{5} } & {v_{g}^{6} } & {v_{g}^{7} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$
(58)
Fig. 7
figure 7

Membership function of variable x.

Full size image

The starting values for the adaptive fuzzy parameters are set arbitrary, and the vector of fuzzy basis functions was formulated by (13).

Table 1 contains a list of the values of the components necessary to build the systems under consideration.

Table 1 Details of the studied system.
Full size table

The dynamic performance of the output voltage achieved by the suggested AF-FTSC regulator during start-up test is displayed in (Fig. 8). It can be observed that the output voltage takes only 10 ms to follow the new DC voltage value of 30 V.

Fig. 8
figure 8

Start-up voltage tracking response of AF-FTSC regulator.

Full size image

To further evaluate the effectiveness of the recommended AF-FTSC voltage regulator, the DC/DC converter is tested against to rapid changes in load resistor value from 36 Ω to 82 Ω and vice versa. The response obtained during the occurrence of mismatch uncertainty is depicted in (Fig. 9). The output voltage demonstrates no variation in its profile for load perturbation. During this event of load variation, the inductor current profile changed smoothly with little fluctuation.

Fig. 9
figure 9

Steady‐state response of AF-FTSC regulator under load transients.

Full size image

Figure 10 illustrates the reference trajectory tracking from 30 to 50 V for the closed loop DC–DC buck converter. The tracking objective is achieved in 3.55 ms time. Similarly, the tracking level Vref is decreased suddenly from 50 to 30 V and it can be observed in Fig. 10 that the suggested AF-FTSC regulator takes only 0.51 ms to track, despite displaying some undershoot in the amplitude of inductor current.

Fig. 10
figure 10

Response of AF-FTSC regulator under reference trajectory tracking.

Full size image

Figure 11 illustrates the dynamic behavior of Vo and iL of the suggested AF-FTSC regulator with triangular-wave tracking. By analyzing this figure, it can be concluded that the suggested AF-FTSC regulator provides quicker transient and better steady-state performance in the output voltage.

Fig. 11
figure 11

Response of AF-FTSC regulator under triangular-wave tracking.

Full size image

An additional simulation test is performed for the sine wave tracking condition. The converter outcomes are presented in (Fig. 12). It is evident from the results that the recommended AF-FTSC regulator has excellent response regardless of changes in the output voltage.

Fig. 12
figure 12

Steady‐state response of AF-FTSC regulator under sinusoidal-wave tracking.

Full size image

To determine the performance indicator of the suggested AF-FTSC regulator, the output voltage profile for settling time (ts), peak overshoot (Po) and peak undershoot (Pu) under various perturbations are reported in (Table 2).

Table 2 Performance indicator for output voltage regulation using the suggested AF-FTSC regulator.
Full size table

Experimental testing

A series of laboratory tests were conducted to verify that the suggested AF-FTSC regulator can effectively regulate the output voltage under certain common operating conditions. The proposed AF-FTSC algorithm was built and implemented using MATLAB software, dSPACE Blocksets, MATLAB-to-DSP Interface Libraries, Real-Time Interface (RTI) to Simulink and Real-Time Workshop (RTW) on a host PC. After that, the AF-FTSC algorithm was downloaded and tested at a sampling rate of 10 µs on a dSPACE DS1103 control board. The inputs to the DS1103 are the output voltage (Vo) provided by the LV-25P voltage transducer coupled to the output capacitor and the inductor current (iL) detected by the LEM LTS-15-NP Hall effect sensor. The outputs of the DS1103 are PWM signal inputs to the IGBT. A voltage amplification circuit is built to increase the PWM signal’s voltage to obtain the IGBT driver’s input voltage. Experiment results are collected by Agilent DSO X3034A oscilloscope. The laboratory configuration of the converter under study is presented in (Fig. 13).

Fig. 13
figure 13

Laboratory setup of the converter under study.

Full size image

The tests for the proposed control law include the start-up transient test, followed by the step-load variation test and then the reference trajectory-tracking test with different reference voltages. These tests were done to compare the permanence of the designed AF-FTSC method with the Global Fast Terminal Sliding Mode Control (GFTSMC) method developed in reference28, and the Non-Singular Terminal Sliding Mode Control (NTSMC) proposed in reference29. The experimental results are displayed in (Figs. 14–18). The start-up transient reaction of Vo, iL and control law τ pending variations in the reference voltage Vref from 0 to 30 V is illustrated in (Fig. 14). It should be noted that Vo asymptotically tracks the preferred output voltage in a limited-time (tr = 0.56 ms), while the time of the GFTSMC and NTSMC algorithms is about 20 and 16 ms, respectively. Furthermore, as seen in Fig. 14, the tracking by the suggested AF-FTSC control law exhibits an overshoot that reaches up to 5 V. Hence, the AF-FTSC algorithm guarantees the stability of the system and facilitates a rapid reaction during the transient startup response.

Fig. 14
figure 14

Comparison between: (a) AF-FTSC, (b) GFTSMC, (c) NTSMC under Startup response.

Full size image

Figure 15 displays the experimental responses of Vo, iL and τ when loading resistor (Ro) steps from 82 Ω to 36 Ω and vice-versa. As can be seen in this figure, since the AF-FTSC algorithm is independent of Ro, the considered regulator demonstrates good control performance for severe changes of Ro.

Fig. 15
figure 15

Comparison between: (a) AF-FTSC method, (b) GFTMC, (c) NTSMC under Step-load response.

Full size image

The robustness of the step variation in Vo was verified by varying Vo from 20 to 30 V and vice-versa. The experimental outcomes are presented in Fig. 16, which displays that Vo precisely follows the preferred reference voltage with reduced overshoot and settling time when applying the proposed AF-FTSC method, resulting in the convergence of tracking voltage errors to zero within a limited time. Thus, the experimental results demonstrate that the proposed AF-FTSC approach can transition to a stable value and respond faster than the GFTMC and NTSMC algorithms.

Fig. 16
figure 16

Comparison between: (a) AF-FTSC method, (b) GFTSMC, (c) NTSMC under reference trajectory tracking.

Full size image

Figure 17 displays the experimental responses of Vo and iL for the considered AF-FTSC, GFTSMC and NTSMC methods, respectively, during triangular-wave tracking; the three designed controllers exhibited comparable response voltages, although the voltage regulation achieved with the suggested AF-FTSC technique was smoother and more stable, resulting in reduced voltage error.

Fig. 17
figure 17

Comparison between: (a) AF-FTSC method, (b) GFTSMC, (c) NTSMC under triangular-wave tracking.

Full size image

The experimental outcomes with sine wave tracking in the reference voltage are presented in (Fig. 18). Again, the proposed AF-FTSC and GFTSMC methods showed similar voltage response during sine wave tracking, while the NTSMC method had the highest current and voltage fluctuation.

Fig. 18
figure 18

Comparison between: (a) AF-FTSC method, (b) GFTSMC, (c) NTSMC under sinusoidal-wave tracking.

Full size image

The performance indicators during start-up, reference trajectory tracking and load disturbances have been presented in (Table 3). In contrast to the GFTSMC and NTSMC strategy, the suggested AF-FTSC strategy has the advantage of faster response time and shows superior performance in load variation and start-up response.

Table 3 Experimental output voltage performance under suggested AF-FTSC and GFTSMC method.
Full size table

To effectively compare the three designed algorithms, qualitative performance criteria are essential. They are widely utilized in the literature for comparative analysis. This article emphasizes three key criteria, namely: rise-time (tr), maximum error (emax), and maximum overshoot or undershoot (Mp-o). Table 4 provides a summary of the comparison regarding the qualitative performances of the three constructed algorithms.

Table 4 Comparison between the NTSMC, FO-NTSMC and AFFO-NTSM controllers.
Full size table

The above qualitative comparison confirmed that the suggested AF-FTSC algorithm has the optimal performance on DC-DC buck converter.

Conclusion

A new AF-FTSC algorithm is proposed and tested in this article to address the output voltage-tracking problem of uncertain DC/DC buck converter. The suggested controller has been computed using STC and terminal attractor methods, which ensure finite-time convergence of the output voltage to the reference voltage. In addition, T1-FLS can be used in combination with appropriate adaptive laws to accurately estimate unknown nonlinear functions in the designed controller. Under certain assumptions, the direct Lyapunov technique has been used to check the convergence of voltage errors and stability of the system. Some experimental tests have been performed to prove the validity of the considered AF-FTSC algorithm. Experimental results from the test prototype prove the validity of the recommended AF-FTSC algorithm and show that the AF-FTSC method has superior transient and steady state properties than the GFTSMC and the NTSMC algorithms.

The following are the significant results obtained from using the AF-FTSC algorithm to control the DC/DC buck converter:

  • Easy and quick implementation of the suggested AF-FTSC algorithm;

  • Fast tracking of the desired values during output voltage changes with significant minimization of overshoots and undershoots;

  • Effective rejection of disturbances affecting the load resistance of the DC/DC buck converter.

The next step is to incorporate nature-inspired optimization methods into the AF-FTSC algorithm to find the best gains parameter, and at the same time, apply the AF-FTSC algorithm to other DC-DC converters.