Introduction

Strong coupling happens when spontaneous emission between two photonic cavities can be reversed, leading to the re-absorption and re-emission of the emitted photon, and the coupling strength g exceeds the decay rate γ of both cavities1,2. This phenomenon is widely used for applications such as single-molecule sensing3,4,5, single photon emitters6, and low-threshold solid state lasers7. The investigation of strong coupling is fundamental to cavity quantum electrodynamics8,9 (cavity QED). Meta material (MM), is an efficient method for achieving strong light-matter interaction, with various applications in integrated optical devices, such as active modulators and detectors10, and active manipulation of the band structure of the photon molecules11.

MMs can realize the impedance matching conditions through structural design in the Terahertz (THz) band (typically ranging from 0.1 to 10 THz),which allows for the control of THz wave transmittance, such as creating perfect absorption devices of THz band12, selecting filters of THz wave13 and regulating the polarization of THz waves through mode coupling14. THz MMs also have good applications in regulating strong coupling15,16,17,18, especially as a biomedical sensor19. Near-field nano-spectroscopy yet enables direct investigation of nanoscale systems, such as nanoscale dielectric properties of materials20, test carrier concentration21, extracting optical parameters22, high-resolution penetration imaging23, MM near-field characteristic response24,25. However, THz MM’s strong coupling spectral features has not yet been investigated in the near-field THz time domain spectroscopy.

In this study, we design an angle-controlled coupling strength tunable photon molecules system which consists of the base waveguide layer and a single ribbon structure above it. It can transform two modes’ strong and weak coupling by changing ribbon’s angle. We use our scattering-type scanning near-field microscopy (s-SNOM) system to image and extract spectral information from a single nano-resonator. Subsequent experiments and simulations also prove that changing the corresponding parameters, such as the ribbon’s length and the substrate’s thickness or permittivity, can change the hybrid states of the system. Compared with traditional coupling strength control MM devices, our photon molecules system only needs to adjust the angle of the single ribbon to achieve coupling strength tuning without changing its own structure. At the same time, different from the traditional in-plane coupling, our system belongs to the longitudinal coupling of ribbon and base waveguide, both of which can be regulated separately, and the regulation mode is more flexible, which has a good application scenario in the sensing field.

Results and discussion

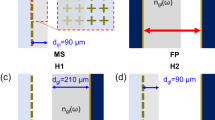
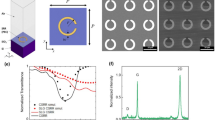
We lay a single ribbon structure on the waveguide substrate with the thickness of 20 um (see the methods section for specific structural parameters). The base waveguide layer and the angle variable ribbon structure form a coupling strength tunable photon molecules system. We use a metallic nanotip to excite individual ribbon to obtain near-field spectra, as illustrated in Fig. 1a. In order to accurately analyze the microscopic near field, a single structure is used to avoid the influence of periodic arrays, and each ribbon structure is separated by ~300 um (The optical image is shown in Fig. 1b). The ribbons of each length rotates from 0 to 90° with a step of 10 degrees. The ribbons with the length L ranging from 38 to 70 um, and the corresponding resonant frequency ranging from ~0.65 to 0.95 THz. As shown in Fig. 1c and d, measured near-field real and imaginary part spectra Indicates the hybridization caused by the interaction between ribbon and waveguide. We find that when L is about 52 um, the ribbon resonant frequency and the waveguide frequency are both at 0.85 THz. Strong coupling occurs between them. At the same time, we set up a model in CST simulation software (see the methods section for specific simulation models and parameters). L is set from 38 to 70 um, and the waveguide layer uses the same substrate as the experiment. The specific parameters are consistent with those described in the Method. The results are shown in Fig. 1e and f. Both the simulation and the experimental results show that as L changes, the waveguide coupling to ribbon produces hybrid states 26.

Fig. 1
figure 1

(a) Schematic diagram of near-field measurement. (b) The optical image of the ribbon. (c, d) Experimental results of real and imaginary parts of near-field spectra with L from 38 to 70 um. (e, f) Simulation results of real and imaginary parts of near-field spectra with L from 38 to 70 um.

Full size image

We choose the ribbon with the length of 52 um whose resonant frequency is consistent with the waveguide frequency for analysis. It is used to design a system to control the coupling strength of the photon cavity by changing the in-plane angle (θ) from 0° to 90° with a step of 10 degrees between ribbon and incidence as shown in Fig. 2a. The near-field real and imaginary spectra are obtained simultaneously, as shown in Fig. 2b and c, where the solid line represents the experimental results and the dashed line represents the fitting. When θ is very small, corresponding to incidence polarization aligning to ribbon dipole, the ribbon resonance is mainly be excited at about 0.85 THz, whilst the resonance of the waveguide mode is relatively weak, causing no apparent coupling between two modes. However, as the angle gradually increases, the incident polarization corresponds to the weakening of the ribbon dipole, decreasing the ribbon’s resonance as well. At this time, the waveguide mode gradually becomes more robust. The photon molecules system enters the strong coupling region, thus two hybrid states arise at ~ 0.75 THz and ~ 0.91 THz, respectively. At the same time, according to the fitting results of coupled mode theory (CMT) theory, the coupling strength (g) corresponding to θ changing from 0° (g = 0.03 THz) to 90° (g = 0.08 THz) is shown in Fig. 2d (\({\upgamma }_{\text{a}}\)=\({\upgamma }_{\text{b}}\)=0.05 THz, \({\upomega }_{\text{a}}\)=\({\upomega }_{\text{b}}\)=0.85 THz), as well as the phasor fluctuating with θ. By increasing θ, the ribbon is thus weakly excited, causing the circles in phasor diagram decrease, while intersecting circles emerging in the middle. The larger the intersecting circles, the stronger the coupling between ribbon and waveguide27,28. According to the fitting results, as θ gradually ascends, the coupling strength (g) of the two modes gradually increases from 0.03 THz (weak coupling, < 0.05 THz ) to about 0.08 THz (strong coupling, > 0.05 THz29). We finally conclude that the active control of coupling strength can be achieved by angle.

Fig. 2
figure 2

(a) Schematic diagram of near-field measurement. (b) Experimental and fitting results of real part of near-field spectra from 0° to 90°. (c) Experimental and fitting results of imaginary part of near-field spectrum from 0° to 90°. (d) 0°-90° corresponding modeled coupling strength. The illustration represents the corresponding phasor.

Full size image

In order to further extend the conclusion, we set up the same model in CST software, fixed ribbon length 52 um unchanged, changing the angle θ. By changing θ to 20° and 70°, the near-field real and imaginary parts spectra are obtained as shown in Fig. 3a and b. Similar with the experimental results, the simulated spectra show a strong resonance mode of ribbon at about 0.83 THz, when θ is as small as 20°. When θ increases to 70°, the strongly coupled photon molecules system produces two new hybridized states at 0.78 and 0.93 THz. The spectra show that the ribbon and waveguide transition from weak coupling to strong coupling with the angle changing. However, the coupling of simulation results is weaker than the experimental results, mainly because the experimental probe enhances more local fields and the coupling excitation is stronger30.

Fig. 3
figure 3

(a, b) Simulation results of the real and imaginary parts of the 20° and 70° spectra (Solid line represents real part and dashed line represents imaginary part). (c) Electric field distribution along ribbon cross section at 20°, 0.83 THz. (d, e) Electric field distribution along ribbon cross section at 70°, 0.78 and 0.93 THz.

Full size image

The electric field distribution at different frequencies is shown in Fig. 3c–e. The dashed box represents the waveguide layer. Electric field counter diagram is drawn along ribbon cross section. It can be seen that at 20°, the ribbon at 0.83 THz has a solid dipole resonance. As the angle increases to 70°, the dipole resonance of the ribbon decreases at the frequencies of two hybrid states as expected.

We then keep the length L= 52 um, and change the thickness (Z) of the substrate from 12-30 um. Figure 4a and b show that no significant strong coupling occurs at θ= 20°, no matter how the thickness of the dielectric layer is changed. Yet, as shown in Fig. 4c and d, when the angle increases to θ= 70°, with the thickness climbed to about 20 um, two hybrid states are generated in this photon molecules system. Therefore, changing substrate’s thickness Z will alter the waveguide frequency accordingly. When the resonant frequency of the ribbon and the waveguide frequency are close to each other, the hybrid states can be generated by controlling the angle. On this basis, in order to further explore the regulation effect of dielectric layer permittivity on the coupling strength of the system, we keep L = 52 um, Z = 20 um, θ = 70° unchanged and change the dielectric layer permittivity (ε) from 7 to 16, as shown in Fig. 4e and f. It is found that changing the permittivity of the dielectric layer can also change the hybrid states of the ribbon and the base waveguide to achieve the effect of regulating the coupling strength.

Fig. 4
figure 4

(a, b) Simulation results of the real and imaginary parts of the near-field spectra with the thickness Z from 12 to 30 um at 20°. (c, d) Simulation results of the real and imaginary parts of the near-field spectra with the thickness Z from 12 to 30 um at 70°. (e, f) Simulation results of the real and imaginary parts of the near-field spectra with ε from 7 to 16 at 70°.

Full size image

Conclusion

We use scattering-type scanning near field microscopy (s-SNOM) to demonstrate an angle-controlled coupling strength tunable photon molecules system. By changing the in-plane angle between ribbon and the incidence, the transformation of ribbon resonance mode and base waveguide mode from weak to strong coupling can be performed. To quantitatively explain the variation of coupling strength with the changing angle, we set up a numerical model with CMT. The fitted results show good agreements with the measured curves. Furthermore, we set up the ribbon model in simulation software according to the actual size. By changing the parameters such as the length of the ribbon and the thickness or permittivity of the substrate, we can change the hybrid states of the system. Our angle-controlled coupling system provides new solutions to manipulate and extend the optical response of nano-cavities, to control light-matter interaction, and corresponding applications in designing integrated THz optical devices such as modulators, sensors, etc.

Methods

Experimental equipment

Our THz s-SNOM platform is engineered based on a commercial AFM platform (Neaspec, attocube systems AG) and TDS THz source (TeraSmart, menlosystems TERA15-TX-FC). After collimating, the THz wave is gathered at the tip of the probe through the off-axis paraboloid mirror, and the probe works in the tapping mode. The near-field signal at the tip of the probe is modulated and scattered to the free space, and finally received by the receiving optical antenna. By demodulation of the higher-order harmonics of the tapping frequency of the probe, relatively pure THz near-field information can be obtained. Specifically, the probe we used was 25PtIr600B-H100 produced by RMN Company. The probe resonant frequency Ω = 15.5 kHz and amplitude near 100 nm were demodulated for 2Ω and 3Ω. The imaging resolution is determined by the size of the probe tip rather than the wavelength, which allows the diffraction limits to be surpassed and enables nanoscale imaging.

Sample structure

We have designed a MM structure of individual ribbon with a length of 38–70 um. The thickness of gold is about 100 nm. At the same time, the commercial SOI wafer is used as the substrate, and the substrate is 675 um low-resistance silicon, 2 um silicon dioxide and 20 um high-resistance silicon from bottom to top, in which the resistance value of low-resistance silicon is about 0.01 Ω*cm, and the resistance value of high-resistance silicon is greater than 1000 Ω*cm.

Simulation parameters

We built the simulation model in CST software. The base three layers of medium, from bottom to top, are successively Si layer with permittivity of 11.36, oxide layer with permittivity of 4, and dielectric layer with permittivity of 7–16. The thickness of the dielectric layer is set to 12–30 um. The size of the three layers of media is 150*150 um. The top layer is placed with a gold ribbon with the thickness of 100 nm and the length of 38–70 um. The angle between the gold ribbon and the electric field direction is \(\uptheta\), varying from 0 to 90°. The excitation source is the excitation waveguide port incident, standard Gaussian beam, frequency range is 0.1–1.5 THz. The boundary condition is set to the open boundaries.

Theory

Coupled mode theory (CMT) 31,32,33 can deal with transmission spectra with a coupling configuration. However, the biggest defect of CMT is the required fitting process, and the coupling strength of the MM should be obtained by the fitting process. For two separate MM structures, it is assumed that the resonant frequencies are ω1 and ω2, the loss are γ1and γ2, and the phases are φ1 and φ2. The coupling strength g is derived from the physical configuration of the two MM structures. The resonance frequencies, the loss and the phases can be obtained by the spectrum of each signal MM structure, and coupling strength describes the connection of two MM structures. The linear superposition has a very close relationship with energies in each MM structure. The complete CMT can be given by

$$\left[ {\begin{array}{*{20}c} {\omega - \omega_{{\text{a}}} - {\text{i}}\gamma_{{\text{a}}} } & {{\text{g}} - {\text{i}}\sqrt {\gamma_{{\text{a}}} \gamma_{{\text{b}}} } } \\ {{\text{g}} - {\text{i}}\sqrt {\gamma_{{\text{a}}} \gamma_{{\text{b}}} } } & {\omega - \omega_{{\text{b}}} - {\text{i}}\gamma_{{\text{b}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\text{a}} \\ {\text{b}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sqrt {\gamma_{{\text{a}}} } {\text{E}}} \\ {\sqrt {\gamma_{{\text{b}}} } {\text{e}}^{{{\text{i}}\varphi }} {\text{E}}} \\ \end{array} } \right]$$

where |a|2 and |b|2 are the energies in each MM structure.\(\upomega\) is the frequency of the input THz wave. \({\upomega }_{\text{a}}\) and \({\upomega }_{\text{b}}\) represent the resonant frequencies of structures A and B (\({\upomega }_{\text{a}}\)=\({\upomega }_{1}\); \({\upomega }_{\text{b}}\)=\({\upomega }_{2}\)). \(\text{i}\sqrt{{\upgamma }_{\text{a}}{\upgamma }_{\text{b}}}\) is the coupling strength with loss between the two structures. \({\upgamma }_{\text{a}}\) and \({\upgamma }_{\text{b}}\) are the loss terms of metamaterial structures, which are closely to \({\upgamma }_{1}\),\({\upgamma }_{2}\) for each single MM structure and φ is the phase between them. E is the amplitude of the externally excited THz wave.