Multi-user joint task offloading and resource allocation based on mobile edge computing in mining scenarios

Abstract

With the development of the industrial internet of things, an increasing number of intelligent terminal devices are being deployed in mining operations. However, due to the surge in network traffic and the limited availability of computational resources, these terminal devices face challenges in meeting high-performance requirements such as low transmission latency and low energy consumption. To address this issue, this paper proposes a method that combines partial offloading with collaborative mobile edge computing (MEC). This approach leverages device-to-device communication to partition computational tasks into multiple subtasks, offloading some of them to collaborative devices or MEC servers for execution. This not only alleviates the computational burden on MEC servers but also makes full use of the idle computing resources of terminal devices, thereby enhancing resource utilization efficiency. Given the limited computational capacity of terminal devices, this paper optimizes the offloading decision-making process between terminal devices and MEC servers. By introducing weighted coefficients for latency and energy consumption, the proposed method ensures that task completion latency does not exceed a predefined threshold while minimizing the overall system cost. The problem is formulated as a multi-objective optimization problem, which is solved using a two-layer alternating optimization framework. In the upper layer, an improved genetic algorithm (IGA) based on heuristic rules is employed to generate an offloading decision population, while the lower layer utilizes the deep deterministic policy gradient (DDPG) algorithm to optimize the offloading strategy and the weighted coefficients for latency and energy consumption. To evaluate the effectiveness of the proposed method, we compare it with five baseline algorithms: the improved grey wolf optimizer metaheuristic algorithm, the traditional genetic algorithm, the binary offloading decision mechanism, the partial non-cooperative mechanism, and the fully local execution mechanism. Simulation results demonstrate that the proposed IGA-DDPG algorithm achieves significant improvements over these baseline methods. Specifically, under various experimental scenarios, IGA-DDPG reduces latency by an average of 24.5%, decreases energy consumption by 26.3%, and lowers overall system cost by 44.6%. Moreover, the algorithm consistently ensures a 100% task completion rate under different system configurations.

Introduction

In recent years, with the acceleration of global intelligence, various smart devices and applications have been widely integrated into multiple domains, driving the development of the digital industry through information and communication technologies and playing a vital role in industrial production¹. To effectively meet the stringent requirements for completion time and system resources of delay-sensitive and computation-intensive tasks in the Internet of Things (IoT), the computing paradigm has gradually shifted from traditional cloud computing to edge computing, which is closer to end users^2,3. The smart mining system integrates IoT, edge computing, big data, and modern mining technologies, enabling proactive sensing, intelligent analysis, rapid processing, and optimized decision-making in mining production, safety monitoring, technical support, logistics, and other areas. Edge computing technology plays a crucial role in the mining IoT, providing core technological support, especially when handling complex tasks that require low latency and high energy efficiency⁴.

Task offloading is a fundamental technique in Mobile Edge Computing (MEC) that enables mobile devices to delegate computationally intensive tasks to external computing resources, thereby improving performance and reducing energy consumption. Depending on the extent of offloading, task offloading can be categorized into three main types: fully local execution⁵, full offloading⁶, and partial offloading⁷. Fully local execution means that the task is entirely processed on the mobile device without offloading, which avoids network transmission delays but may lead to high energy consumption and prolonged processing time, particularly for computation-intensive applications. Full offloading, on the other hand, transmits the entire computational workload to an MEC server for execution, significantly reducing the computational burden on mobile devices but introducing high communication latency and network congestion, especially when bandwidth resources are limited. Partial offloading divides the task into multiple subtasks, with some executed locally while others are offloaded to the MEC server or collaborative edge devices. This hybrid approach balances computation efficiency and communication overhead, making it particularly suitable for dynamic and resource-constrained environments.

With the increasing number of devices in mining operations, competition for computational resources on Mobile Edge Computing (MEC) servers has intensified, which may result in server overload. Meanwhile, the CPU utilization of most mobile terminal devices is only about one-third of their capacity⁸, leaving a substantial portion of computational resources underutilized. To address this issue, this paper proposes an optimization framework that integrates partial task offloading with collaborative MEC servers. Partial offloading refers to dividing computational tasks into multiple independent subtasks, enabling parallel execution across different computational units. In a traditional MEC architecture, partial offloading enables a portion of the task to be executed locally, while the rest is offloaded to the MEC server for computation. By enabling collaborative execution between terminal devices and edge servers, this approach effectively mitigates server workload while maintaining computational efficiency. Collaborative MEC relies on device-to-device (D2D) communication, allowing mobile terminals to establish direct connections via technologies such as LTE, Wi-Fi, and Bluetooth^9,10,11. This mechanism enables task offloading to nearby available devices, referred to as collaborative computing devices. Extensive research has demonstrated the feasibility of offloading tasks to neighboring devices via D2D communication to utilize their available computational resources efficiently. By integrating partial offloading with collaborative MEC strategies, when local or surrounding devices have idle computing resources, part of the task can be executed locally, while the remaining portion is offloaded via D2D communication to either the MEC server or neighboring devices^{12,13,14,15,16,17}. This not only alleviates server congestion but also improves computational resource utilization in mobile terminal devices. Due to the physical and economic constraints of mobile terminal devices, their energy supply remains limited, posing a challenge to computational efficiency. Therefore, a key challenge lies in optimizing the total system cost while meeting task latency constraints. To achieve this goal, this paper aims to optimize task offloading strategies by adjusting the weighting coefficients of latency and energy consumption to achieve overall system cost minimization.

Assuming that the MEC server and the base station (BS) are co-located, multiple mining mobile devices process a portion of their computational tasks locally while offloading the rest to the edge server or collaborative devices. As a result, both device-to-device (D2D) and device-to-edge (D2E) communication links coexist within the system. To reduce communication interference among devices, it is further assumed that D2D and D2E communications operate on separate spectrum channels. Additionally, D2D links employ Orthogonal Frequency Division Multiple Access (OFDMA) for spectrum sharing, dividing the available bandwidth into multiple independent subcarriers, each assigned to a dedicated D2D connection. In contrast, D2E links utilize Non-Orthogonal Multiple Access (NOMA), allowing multiple devices to share the same frequency band, with the base station employing Successive Interference Cancellation (SIC) to decode individual signals. The core challenge lies in the interdependence of task offloading decisions, latency-energy weighting factors, and their collective impact on device energy consumption and task completion delay. This paper models these interdependent factors as a multi-objective optimization problem. To solve this problem, we propose a hierarchical optimization strategy that divides the problem into two subproblems and applies an alternating optimization approach based on a heuristic-driven Improved Genetic Algorithm (IGA)¹⁸ and a Deep Reinforcement Learning (DRL) method. Specifically, the IGA algorithm generates offloading decisions, whereas the DRL algorithm refines task allocation ratios and adjusts latency-energy weighting factors based on the given decisions to enhance overall system performance.

The main contributions of this paper are summarized as follows:

• This study proposes a novel task offloading optimization framework that integrates partial task offloading with collaborative mobile edge computing (MEC) and establishes a multi-objective optimization model. The model aims to minimize the overall system cost while ensuring that computational tasks meet latency constraints and improving the utilization of computational resources. Unlike traditional MEC task offloading methods, this framework not only considers device-to-device (D2D) communication but also introduces dynamically adjustable latency-energy weighting coefficients, providing a more flexible offloading strategy to adapt to different mining computing environments.

• To address the proposed multi-objective optimization problem, this study designs a two-level alternating optimization approach for task offloading decision-making and task allocation optimization. At the upper level, an improved genetic algorithm (IGA) is employed to generate optimized task offloading strategies. At the lower level, the deep deterministic policy gradient (DDPG) algorithm is utilized to further optimize task allocation ratios and dynamically adjust latency-energy weighting coefficients, making the offloading scheme more adaptable to various mining environment requirements.

• Extensive simulation experiments were conducted under various system configurations to evaluate the effectiveness of the proposed method. The results demonstrate that the IGA-DDPG algorithm not only exhibits good convergence performance but also outperforms five baseline algorithms, including the improved grey Wolf Optimizer metaheuristic algorithm(IGWO),the Traditional Genetic Algorithm (TGA), Binary Offloading Decision Mechanism (BODM), Partially Non-Cooperative Mechanism (PNCM), and Fully Local Execution Mechanism (FLEM), in terms of latency, energy consumption, and total system cost.

The structure of this paper is as follows: “Related work” section reviews related work; “System model and problem statement” section presents the system model and formulates the optimization problem; “Problem solution” section provides a detailed description of the proposed method; “Results and discussion” section presents the simulation results; and “Conclusion” section concludes the paper.

Related work

To effectively alleviate the computational burden on MEC servers, existing studies have proposed strategies that integrate partial offloading with collaborative MEC. This section provides an overview of related research in these two directions, with a particular focus on analyzing their relationship to this work. Specifically, we first review the research progress on partial offloading within the traditional MEC framework. Then, based on whether tasks are divisible, we categorize collaborative MEC into binary offloading and partial offloading approaches. Finally, we explicitly highlight the distinctions between the proposed method and existing studies, while discussing the background and motivation of this research.

Partial offloading in traditional MEC architectures

In traditional MEC task offloading architectures, extensive research has been conducted on binary offloading problems. The optimization variables in such problems are typically binary (0 or 1), simplifying computation and decision-making. In contrast, partial offloading introduces continuous variables, which significantly increase problem-solving complexity. Extensive research aims to optimize system performance by minimizing energy consumption and latency. These studies fall into three categories: single-user single-server^19,20, multi-user single-server^21,22,23, and multi-user multi-server^24,25.For instance, Mao et al.²⁰ developed an optimization framework for a single-user MEC network to minimize task execution delay. This framework uses a heuristic algorithm to optimize computing and communication resource allocation, improving energy efficiency and ensuring load balancing. You et al.²¹ proposed a mode selection strategy for local and edge computing, allowing devices to offload tasks to edge servers, thus reducing both latency and energy consumption. Wang et al.²⁴ studied the optimization of computation offloading and resource allocation in wireless MEC systems. The primary objective was to improve mobile device performance and energy efficiency by offloading intensive computations to nearby edge servers powered by wireless energy transfer.Tang et al.²⁵ developed a pre-allocation algorithm for task offloading to mitigate service interruptions due to the limited coverage of Roadside Units (RSUs). Yang et al.²⁶ proposed a coalitional game-based cooperative computation offloading model, where mobile users dynamically form coalitions to share computational resources, enhancing system efficiency while reducing task execution time. Roostaei et al.²⁷ developed a game-theoretic joint pricing and resource allocation model for MEC in NOMA-based 5G networks, balancing pricing strategies and resource allocation between MEC servers and mobile users.

Binary offloading in collaborative MEC

To fully utilize the idle computational resources among user equipment (UE), the collaborative MEC problem has become a central focus of numerous studies. In the binary offloading scenario, some UEs are specifically configured as computation servers^28,29,30,31, while others serve as both task generators and computation servers simultaneously^31,32, requiring task execution under specific constraints. Li et al²⁸.integrated Intelligent Reflecting Surface (IRS) and Non-Orthogonal Multiple Access (NOMA) technologies, along with Wireless Power Transfer (WPT) for IoT devices, to effectively address the challenge of reducing latency in MEC systems. Mahmood et al²⁹. proposed a weighted utility-aware resource allocation and task scheduling method to optimize the problem of minimizing computational overhead in wireless mobile edge cloud systems. Zhao et al³². investigated service deployment and load distribution in MEC environments, with the objective of minimizing the average response time. The authors introduced a heuristic strategy designed to select hosting nodes with the lowest average response time across all requests for each application, thereby optimizing application hosting and request processing. Yang et al³³. conducted a joint optimization study on service deployment and load distribution in static scenarios. The authors designed a two-step heuristic approach to minimize the average latency of all application requests while ensuring node capacity constraints.Furthermore, Chen et al.³⁴ proposed a matching-theory-based low-latency scheme for multitask federated learning in MEC networks, which optimally assigns computational tasks among edge nodes while considering both latency and resource constraints. Similarly, Su et al.³⁵ developed a contract-theory and Bayesian matching game-based computation offloading model, enabling hierarchical multi-access edge computing environments to efficiently allocate resources among users and servers, ensuring fairness and computational efficiency.

Partial offloading in collaborative MEC

In addition to binary offloading, partial offloading has also received significant attention in the field of collaborative MEC. Most studies assume that collaborative user equipment (UE) acts as dedicated computational nodes^13,14,36, while relatively few works explore scenarios where UEs not only execute their own computational tasks but also serve as collaborative computing devices^37,38.Liu et al¹³. investigated communication overhead and data privacy issues and proposed a method called FedCPF. This method includes a customized local training strategy, a partial client participation mechanism to mitigate uplink congestion, and a flexible aggregation strategy to optimize communication overhead management.Shuai et al¹⁴. proposed a latency optimization scheme, where an optimal flow-based routing algorithm was first employed to minimize transmission delay. Subsequently, a deep Q-learning-based task offloading strategy was introduced to achieve adaptive task allocation based on the MEC load status.Yao et al³⁶. introduced a Twin Delayed Deep Deterministic Policy Gradient (TD3)-based computation offloading method. The problem was first modeled as a Markov Decision Process (MDP), and the TD3 algorithm was then applied to determine the optimal offloading strategy under minimum latency and energy consumption constraints.Wang et al³⁷. proposed a Quantum-inspired Reinforcement Learning (QRL)-based task offloading approach. Initially, resource management was formulated as a latency optimization problem, which was then transformed into an MDP and solved using QRL to determine the optimal resource allocation strategy.Zhang et al³⁸. developed a Reinforcement Learning (RL)-based task offloading algorithm to optimize throughput and reduce both computation and communication latency across Sub-6 GHz and 28 GHz frequency bands.Panda et al³⁹.proposed EDP-TO, a multi-objective task offloading algorithm for IoT-Fog-Cloud systems, improving energy efficiency, delay, and fairness compared to FTO.Additionally, Picano et al.⁴⁰ proposed a method combining stochastic network calculus and matching theory to optimize heterogeneous MEC task offloading. By modeling network uncertainties and incorporating queuing delay and computational constraints, this approach enhances system reliability and computational efficiency.

Brief summary

Task offloading in MEC systems can be categorized into traditional MEC architectures and collaborative MEC, each with binary offloading and partial offloading approaches. Despite their distinct implementations, these methods share a common objective: optimizing computational efficiency, reducing latency, and minimizing energy consumption. Both traditional and collaborative MEC leverage offloading strategies to dynamically allocate computational resources, improving system performance under varying workloads. However, key differences exist in resource management, task execution scope, and communication models.

In traditional MEC architectures, task offloading primarily occurs between mobile devices and MEC servers. Binary offloading simplifies decision-making but lacks flexibility, while partial offloading introduces continuous optimization variables, increasing computational complexity. Existing solutions, such as game-theoretic models and heuristic algorithms, optimize task allocation by balancing energy consumption and execution delay.

Conversely, collaborative MEC expands the traditional model by incorporating user devices (UEs) as computing nodes, allowing for more dynamic resource sharing. Binary offloading in collaborative MEC enables UEs to either serve as task generators or computation servers, relying on matching theory and contract-based mechanisms to optimize resource allocation. Partial offloading in collaborative MEC, on the other hand, enhances computational flexibility, enabling UEs to execute their own tasks while assisting others. Techniques like reinforcement learning (RL) and multi-objective optimization have been proposed to manage this complexity and improve offloading efficiency.

Comparison of the related work is illustrated in Table 1. Despite significant advancements, existing approaches often assume that collaborative devices act solely as computational servers, neglecting the dynamic balance between self-computation and collaborative task execution. Our proposed IGA-DDPG bi-layer optimization framework addresses this gap by combining an improved genetic algorithm (IGA) and deep deterministic policy gradient (DDPG). The upper-layer IGA optimizes offloading decisions, while the lower-layer DDPG refines task allocation ratios and dynamically adjusts latency-energy weighting coefficients. Compared to existing methods, our approach enhances adaptability, optimizes resource utilization, and ensures efficient task scheduling in complex MEC environments, making it particularly suitable for industrial applications.

Table 1 Contribution comparison of related works.

System model and problem statement

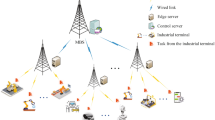
As illustrated in Fig. 1, this study models task offloading in collaborative edge computing for mining scenarios. The mining user equipment (UEs) is represented by the set $S = \{ s_1, s_2, \dots , s_m \}$, with the MEC server separately denoted as $S_0$. Each device $s_i \in S$ generates a computational task $\xi _i$, characterized by the tuple $\{ \phi _i, \delta _i, T_i^{\text {max}} \}$, where $\phi _i$ represents the task size, $\delta _i$ denotes the number of CPU cycles required per unit of the task, and $T_i^{\text {max}}$ indicates the latency constraint. The MEC server communicates with user devices through a base station (BS) and facilitates resource information sharing among devices.The task $\xi _i$ generated by each device $s_i$ can be divided into several independent subtasks for either local or offloaded computation. The offloading modes include sending subtasks to neighboring collaborative devices or the MEC server for processing. The actual task partitioning depends on the inherent properties of the task and the available computational resources.Existing studies have explored various mechanisms for task partitioning. When the input data of a task is known and exhibits bitwise independence, the task can be partitioned at an arbitrary rate⁴¹. Additionally, tasks can be decomposed into multiple subtasks, which are scheduled for parallel execution across different computational devices^42,43,44.

Fig. 1

The architecture of mine edge computing.

Let $F = S \cup \{ s_0 \}$ represent the set of target destinations available for task offloading. To describe the offloading decisions of each user equipment (UE), a matrix $\mathscr {A} = \{ a_{i,j} \mid \forall i \in S, j \in F \}$ is introduced, where $a_{i,j} \in [0, 1]$ and $\sum _{j=0}^m a_{i,j} = 1$. Here, $a_{i,j}$ indicates the proportion of the computational task $\xi _i$ generated by device $s_i$ that is allocated to target $j \in F$.

Based on different task allocation strategies, the task offloading methods for all UEs can be categorized into the following three types:

• 1. When $0 \leqslant a_{i,i} \leqslant 1$, $s_i$ executes its task locally with a proportion of $a_{i,i}$.

• 2. When $0 \leqslant a_{i,j} \leqslant 1$ and $j \notin \{ 0, i \}$, $s_i$ offloads a proportion $a_{i,j}$ of its task to the collaborative device $s_j$ for computation.

• 3. When $0 \leqslant a_{i,0} \leqslant 1$, $s_i$ offloads a proportion $a_{i,0}$ of its task to the MEC server $s_0$ for computation.

During the collaborative offloading process among UEs, the OFDMA protocol is adopted to avoid mutual interference. However, when tasks are offloaded to the MEC server, UEs cause uplink interference to each other. To describe this process, the subchannel set $C = \{ c_1, c_2, \dots , c_n \}$ is defined, representing all spectrum resources available for use by the UEs.The notations used in this paper are summarized in Table 2.

Table 2 Notations.

Local computation offloading model

When the mining user equipment $s_i$ executes its computational task locally with a task allocation proportion of $a_{i,i}$, the corresponding computation time depends on the local computational capability $f_i$ and the task size allocated for local execution, $a_{i,i}\delta _i$. Therefore, the time required for local task execution can be expressed as:

$$\begin{aligned} T_{s_i}=\frac{a_{i,i}\delta _i}{f_i} \end{aligned}$$

(1)

The energy consumption of the mining user equipment for local execution is given by⁴⁵:

$$\begin{aligned} E_{s_i}=a_{i,i}k_i\left( f_i \right) ^2\delta _i \end{aligned}$$

(2)

Here, $k$ represents the effective capacitance coefficient of the user equipment, and in this study, it is set as $k = 10^{-11}$⁴⁶. Based on the above formula, the total cost of executing computational tasks locally can be expressed as:

$$\begin{aligned} Q_{s_i}=\mu _{s_i}T_{s_i}+v_{s_i}E_{s_i} \end{aligned}$$

(3)

Here, $\mu _{s_i}$ and $v_{s_i}$ represent the weighting coefficients for the time and energy consumption of executing computational tasks locally, respectively. The relationship between these two coefficients is as follows:

$$\begin{aligned} \begin{aligned} \mu _{s_i}+\upsilon _{s_i}=1\\ 0\leqslant \mu _{s_i}\leqslant 1\\ 0\leqslant v_{s_i}\leqslant 1 \end{aligned} \end{aligned}$$

(4)

The total cost of executing computational tasks locally can be influenced by adjusting the weighting coefficients $\mu _{i}^{\text {local}}$ and $v_{i}^{\text {local}}$. A larger $\mu _{i}^{\text {local}}$ indicates that the user equipment prioritizes latency, while a larger $v_{i}^{\text {local}}$ reflects a greater emphasis on energy consumption⁴⁷. By dynamically adjusting these coefficients, the requirements of user equipment under different environmental conditions can be met.

Collaborative device computation offloading model

Assume that the system operates over a block fading channel, where the transmission power and channel gain remain constant during each transmission process. Let $H\triangleq \left\{ h_{i,j}|i\in S,j\in F-\left\{ i \right\} \right\}$ denote the channel gain matrix of the system, where $h_{i,j}$ represent the channel gain from the mining user equipment $s_i$ to the target server $s_j$. Typically, the size of the computation results is negligible, and the time and energy consumption for returning the results can be ignored.

During the process of task offloading through collaborative devices, the mining user equipment $s_i$ transmits a proportion $a_{i,j}$ of its task to the target collaborative device $s_j$. According to Shannon’s theorem, the corresponding task transmission rate is expressed as:

$$\begin{aligned} R_{i,j}=B\log _2\left( \frac{1+h_{i,j}P_{i,j}}{\delta ^2} \right) ,\forall i\in N,j\in F-\left\{ 0,i \right\} \end{aligned}$$

(5)

Here, $P_{i,j}$ represents the transmission power of the mining user equipment $s_i$ to the collaborative device $s_j$ over the channel, and $\delta ^2$ denotes the noise power. Based on the above formula, the total time for the mining user equipment $s_i$ to offload the computational task to the collaborative device $s_j$ and for the task to be executed is expressed as follows:

$$\begin{aligned} T_{s_j}=\frac{a_{i,j}\phi _i}{R_{i,j}}+T_{i,j}^{wait}+\frac{a_{i,j}\delta _i}{f_j} \end{aligned}$$

(6)

In the formula: $\frac{a_{i,j}\phi _i}{R_{i,j}}$ represents the time required for task transmission; $T_{i,j}^{\text {wait}}$ denotes the waiting time when the collaborative device has its own computational tasks to process⁴⁸; $\frac{a_{i,j}\delta _i}{f_j}$ represents the time required to execute the computational task.

The energy consumption of the mining user equipment $s_i$ for offloading its computational task to the collaborative device $s_j$ and executing the computation is expressed as:

$$\begin{aligned} E_{s_j}=P_{i,j}\left( \frac{a_{i,j}\phi _i}{R_{i,j}}+T_{i,j}^{wait} \right) +a_{i,j}k_j\left( f_j \right) ^2\delta _i \end{aligned}$$

(7)

Based on the above formula, the total cost of executing computational tasks on the collaborative device can be expressed as:

$$\begin{aligned} Q_{s_j}=\mu _{s_j}T_{s_j}+v_{s_j}E_{s_j} \end{aligned}$$

(8)

MEC server computation offloading model

When the mining user equipment offloads its computational task to the MEC server with an allocation proportion of $a_{i,0}$, channel interference occurs among user devices. Let $C = \{ c_1, c_2, \dots , c_n \}$ represent the set of subchannels available to the user devices. To simplify computation, the bandwidth $B$ is divided into $c_n$ parts, with each subchannel represented as $\frac{B}{c_n}$. According to Shannon’s theorem, the transmission rate of the task uploaded to the MEC server can be expressed as:

$$\begin{aligned} r_{i,0}^{ch}=\varphi _{s_i}^{ch}\frac{B}{c_n}\log _2\left( 1+SINR_{s_i}^{ch} \right) \end{aligned}$$

(9)

$SINR_{s_i}^{ch}$ represents the signal-to-interference-plus-noise ratio (SINR) of the task transmission.

$$\begin{aligned} SINR_{s_i}^{ch}=\frac{p_{s_i}^{ch}g_{s_i}^{ch}}{N_0+\sum _{s_i=1,s_i\ne s_j}^S{p_{s_j}^{ch}g_{s_i,s_j}^{ch}}} \end{aligned}$$

(10)

Here, $N_0$ represents the background noise, while $p_{s_i}^{ch}$ and $p_{s_j}^{ch}$ denote the channel transmission power of mining user equipment $s_i$ and $s_j$, respectively. $g_{s_i}^{ch}$ is the channel gain between mining user equipment $s_i$ and the MEC edge server $s_0$. Similarly, $g_{s_i,s_j}^{ch}$ represents the channel gain between mining user equipment $s_i$ and $s_j$⁴⁹. $\varphi _{s_i}^{ch}$ indicates whether subchannel $c_n$ is allocated to mining user equipment $s_i$: if $\varphi _{s_i}^{ch} = 1$, the subchannel is allocated to $s_i$; otherwise, if $\varphi _{s_i}^{ch} \ne 1$, the subchannel is not allocated to $s_i$.Based on the above descriptions, the total task transmission rate when mining user equipment $s_i$ offloads its task to the MEC server $s_0$ can be expressed as:

$$\begin{aligned} R_{i,0}^{ch}=\sum _{c_n=1}^C{r_{i,0}^{ch}} \end{aligned}$$

(11)

Based on the above formula, the time required for mining user equipment $s_i$ to offload its computational task to the MEC server $s_0$ and execute the task is as follows:

$$\begin{aligned} T_{s_0}=\frac{a_{i,0}\phi _i}{R_{i,0}^{ch}}+\frac{a_{i,0}\delta _i}{f_0} \end{aligned}$$

(12)

The energy consumption of the mining user equipment for offloading its computational task to the MEC server and executing the computation is as follows:

$$\begin{aligned} E_{s_0}=\frac{p_{s_i}^{ch}a_{i,0}\phi _i}{R_{i,0}^{ch}}+a_{i,o}k_0\left( f_0 \right) ^2\delta _i \end{aligned}$$

(13)

Based on the above formula, the total cost of executing computational tasks on the MEC server is given as:

$$\begin{aligned} Q_{s_0}=\mu _{s_0}T_{s_0}+v_{s_0}E_{s_0} \end{aligned}$$

(14)

Delay and energy consumption model

The delay and energy consumption during the task offloading process depend on the selected offloading mode and the proportion of the task being offloaded. The specific model is as follows:

• When the computational task $\xi _i$ generated by mining user equipment $s_i$ is executed entirely locally, $a_{i,i} = 1$, $T = T_{s_i}$, and $E = E_{s_i}$.

• When the mining user equipment $s_i$ offloads a proportion $a_{i,0}$ of its task to the MEC server $s_0$ for computation, the local and MEC server can execute the tasks in parallel. The formula for calculating $T_i$ is as follows:

  $$\begin{aligned} T_i=\max \left\{ T_{s_0},T_{s_i} \right\} \end{aligned}$$

  (15)

  The total energy consumption includes the energy consumed by the mining user equipment $s_i$ for local computation and the energy consumed by the MEC server $s_0$ for executing the computational tasks. Therefore, the formula for calculating the total energy consumption $E_i$ is as follows:

  $$\begin{aligned} E_i=E_{s_0}+E_{s_i} \end{aligned}$$

  (16)

• When the mining user equipment $s_i$ offloads a proportion $a_{i,j}$ of its task to the collaborative device $s_j$ for computation, the collaborative device $s_j$ must first complete its own computational tasks before executing the offloaded task from $s_i$, if necessary. When the computation time for $s_j$’s own task $T_{i,j}^{\text {wait}} > \frac{a_{i,j}\phi _i}{R_{i,j}}$, the offloaded task from $s_i$ must be delayed until $s_j$ completes its own computation. However, if $T_{i,j}^{\text {wait}} \leqslant \frac{a_{i,j}\phi _i}{R_{i,j}}$, the offloaded task from $s_i$ can be directly transmitted to $s_j$ for computation. Therefore, the formula for calculating $T_i$ is as follows:

  $$\begin{aligned} T_i= & \max \left\{ T_{s_i}, T_{s_j} \right\} , j \in F- \left\{ 0, i \right\} \ \end{aligned}$$

  (17)
  $$\begin{aligned} T_{s_j}= & {\left\{ \begin{array}{ll} \displaystyle \frac{a_{i,j} \phi _i}{R_{i,j}} + T_{i,j}^{\text {wait}} + \frac{a_{i,j} \delta _i}{f_j}, & \text {if } T_{i,j}^{\text {wait}} > \frac{a_{i,j} \phi _i}{R_{i,j}} \\ \displaystyle \frac{a_{i,j} \phi _i}{R_{i,j}} + \frac{a_{i,j} \delta _i}{f_j}, & \text {if } T_{i,j}^{\text {wait}} \le \frac{a_{i,j} \phi _i}{R_{i,j}} \end{array}\right. } \end{aligned}$$

  (18)

  The energy consumption $E$ includes the energy consumed by the mining user equipment for local computation, as well as the energy consumed for transmitting the task to the collaborative device $s_j$ and for the computation executed by $s_j$. Therefore, the formula for calculating the energy consumption $E$ is as follows:

  $$\begin{aligned} E_i=E_{s_i}+E_{s_j}\text {,} j\in F-\left\{ 0,i \right\} \end{aligned}$$

  (19)

Thus, for any mining user equipment $s_i \in S$, the following expression is obtained by summarizing the above formulas:

$$\begin{aligned} T= & \max \left\{ T_{s_i},T_{s_j}^{\max },T_{s_0} \right\} \text {,}j\in F-\left\{ 0,i \right\} \end{aligned}$$

(20)

$$\begin{aligned} E= & E_{s_i}+\sum _{j=1,j\ne i}^S{E_{s_j}+E_{s_0}} \end{aligned}$$

(21)

$$\begin{aligned} Q= & \mu T+\upsilon E \end{aligned}$$

(22)

Problem statement

Our objective is to minimize the total system cost by jointly considering system delay and energy consumption, while ensuring that tasks are completed within the latency constraints. This is achieved by introducing weighting coefficients $\mu$ and $\nu$, and optimizing the task offloading ratio $\alpha$, as well as the weighting coefficients $\mu$ and $\nu$. Therefore, the problem is formulated as follows:

$$\begin{aligned}&P:\underset{a,\mu ,\upsilon }{\min }\ \quad Q^{total} = \sum _{i=0}^S Q_i & \nonumber \\&\text {s.t.} \quad 0 \leqslant a_i \leqslant 1, \forall i \in S, & \quad \text {(C1)} \nonumber \\&\quad \sum _{j=0}^m a_{i,j} = 1, & \quad \text {(C2)} \nonumber \\&\quad \mu + \upsilon = 1, & \quad \text {(C3)} \nonumber \\&\quad 0 \leqslant \mu \leqslant 1, & \quad \text {(C4)} \nonumber \\&\quad 0 \leqslant \upsilon \leqslant 1, & \quad \text {(C5)} \nonumber \\&\quad T_i \leqslant T_i^{\max }, \forall i \in S, & \quad \text {(C6)} \end{aligned}$$

(23)

Here, constraint C1 restricts the task offloading ratio to values within $[0, 1]$; constraint C2 ensures that the sum of the task offloading ratios equals 1; constraint C3 indicates that the sum of the weighting coefficients $\mu$ and $\nu$ is equal to 1; constraints C4 and C5 specify that the values of the weighting coefficients $\mu$ and $\nu$ must lie within $[0, 1]$; finally, constraint C6 ensures the latency constraint for each task.

Problem solution

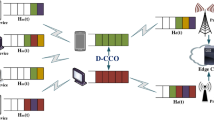
The decision variables of Problem $P$ consist of the task offloading ratio $\alpha$ and the weighting coefficients $\mu$ and $\nu$. Among them, $\alpha$ is a discrete variable, while $\mu$ and $\nu$ are continuous. This leads to a hybrid discrete-continuous action space, which poses challenges for traditional optimization methods. Conventional mathematical programming approaches (e.g., integer linear programming) struggle with scalability due to the combinatorial nature of discrete variables, while heuristic-based algorithms (e.g., genetic algorithms) may suffer from slow convergence and difficulty in dynamically adapting to real-time system variations. To efficiently handle this complexity, Problem $P$ is reformulated into a two-level optimization model. The upper-level problem focuses on generating feasible task offloading decisions, where a heuristic-based Improved Genetic Algorithm (IGA) is employed to explore the discrete decision space efficiently. The lower-level problem is modeled as a Markov Decision Process (MDP), where Deep Reinforcement Learning (DRL) is applied to optimize both the task offloading ratio $\alpha$ and the weighting coefficients $\mu$ and $\nu$ under given offloading decisions. Specifically, the Deep Deterministic Policy Gradient (DDPG) algorithm is adopted to handle the continuous variables while simultaneously learning an optimal policy for discrete decisions. The advantage of DRL lies in its ability to adapt to dynamic environments, optimize high-dimensional hybrid action spaces, and improve computational efficiency in large-scale MEC systems. Moreover, DDPG leverages experience replay and target networks to enhance stability and convergence, making it particularly suitable for complex resource allocation problems involving both discrete and continuous decision variables.

Problem transformation

The initial problem $P$ has two key characteristics. First, the task offloading allocation ratio $\alpha$ varies in response to changes in the system’s offloading decisions. Second, the total system cost fluctuates based on variations in the weighting coefficients $\mu$ and $\nu$ for delay and energy consumption. Due to the interdependence of variables in problem $P$, a bi-level optimization approach is implemented to decompose problem $P$ into an upper-level and a lower-level problem. Solving the lower-level problem relies on the task offloading decisions obtained from the upper-level problem, while its solution further refines the task offloading strategy determined by the upper-level problem⁵⁰. By iteratively solving these two subproblems, the globally optimal solution is achieved.

In this research scenario, the task offloading ratio $\alpha$ for mining user equipment $s_i$ is determined by solving the upper-level problem, while the optimal weighting coefficients $\mu$ and $\nu$ for $s_i$ are derived from the lower-level problem. Although deterministic methods, such as exhaustive search, can be used to solve the upper-level problem and determine the task offloading decisions and offloading ratio, their prohibitive computational complexity limits their feasibility for large-scale applications. Therefore, a heuristic-based improved genetic algorithm is proposed, applying genetic operations such as mutation to generate a population of task offloading ratios $\alpha = \{ a_1, \dots , a_i \}$. Thus, the upper-level problem $P1$ is formulated as follows:

$$\begin{aligned} \begin{aligned} P1:\underset{\alpha }{\min }Q^{total}\\s.t.C1\sim C6 \end{aligned} \end{aligned}$$

(24)

In the lower-level problem, given the population of task offloading ratios $\alpha$, we employ the Deep Deterministic Policy Gradient (DDPG) algorithm to identify the optimal chromosome encoding $\alpha ^*$ and determine the optimal weighting coefficients $\mu ^*$ and $\nu ^*$. Thus, the lower-level problem is formulated as follows:

$$\begin{aligned} \begin{aligned} P2:\underset{\alpha ^*,\mu ^*,\upsilon ^*}{\min }\ Q^{\text {total}} \\ \text {s.t. } C1 \sim C6 \end{aligned} \end{aligned}$$

(25)

Upper-level optimization

The task allocation problem in Mobile Edge Computing (MEC) systems involves both discrete and continuous decision variables, making it an NP-hard problem that is difficult to solve optimally with traditional mathematical programming approaches. To efficiently explore the solution space, we employ a combination of the Genetic Algorithm (GA) and Simulated Annealing (SA).An improved GA incorporating heuristic rules is employed to solve the upper-level optimization problem, which primarily consists of three stages: chromosome encoding, neighborhood search, and chromosome decoding. GA is particularly well-suited for combinatorial optimization problems due to its strong global search capability. By employing selection, crossover, and mutation operations, it can explore multiple possible task allocation strategies in parallel, making it effective for handling large-scale MEC environments. However, it may sometimes converge prematurely to local optima.To further refine the solution quality, we integrate SA as a post-processing step. Its probabilistic acceptance mechanism enables it to escape local optima, ensuring a more optimized allocation of tasks and resources. The combined GA-SA approach balances exploration and exploitation, achieving high-quality solutions within reasonable computational costs.While alternative methods such as Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), and Deep Reinforcement Learning (DRL) exist, they either struggle with discrete task allocation or require extensive training costs. Compared to Integer Linear Programming (ILP), which guarantees optimality but suffers from high computational complexity.

Chromosome encoding

A chromosome represents a task allocation ratio scheme, which specifies how the computational task of mining user equipment $s_i$ is allocated to collaborative devices $s_j$ and the MEC server $s_0$ for computation, with the task allocation ratio denoted as $\alpha = \{ a_1, \dots , a_i \}$. Based on the characteristics of mining edge computing, the chromosome encoding adopts a natural number encoding method. Here, $d_{i,j}, j \in F - \{ i \}$, represents the availability of collaborative devices $s_j$ and the MEC server $s_0$ for mining user equipment $s_i$. The specific steps for chromosome encoding are as follows:

• (1) During the initial stage of chromosome encoding, the computational task of mining user equipment $s_i$ is allocated according to the initial task allocation ratio scheme $\alpha = \{ a_1, \dots , a_i \}$. For example, if $d_{i,j} = 1$, where $j \in F - \{ i \}$, then the task $\xi _i$ is allocated to the service device $s_j$ for computation with the offloading ratio $a_{i,j}$.

• (2) The task allocation corresponding to the service node numbers is arranged into a sequence, which serves as the initial chromosome.

Neighborhood search

For a given chromosome, new neighborhoods are generated using genetic operations such as gene mutation. Gene mutation refers to changing the position of a specific gene in the chromosome by modifying its value, which corresponds to migrating a task from one service node (the source node) to another (the destination node). However, generating neighborhoods through random transformations can lead to excessive unreasonable task migrations, reducing algorithmic search efficiency.To address this issue, neighborhoods are constructed by assigning selection probabilities to each service node as a source or destination and integrating heuristic rules to improve the sampling of feasible neighborhoods.

For a given task allocation scheme, a higher-cost service node presents greater optimization potential when transferring tasks to other nodes. Transferring tasks from a high-cost service node to a low-cost service node is more effective for optimization than transferring in the opposite direction or between nodes with similar costs. Based on this intuition, a heuristic neighborhood construction method is proposed.The neighborhood search follows these steps:

• (1) Calculate the total cost $Q_j$ for each service node $s_j$, where $j \in F - \{ i \}$.

• (2) Calculate the probability of each service node $s_j$ being selected as the source node for task transfer, denoted as $p_{j}^{\text {out}}$:

  $$\begin{aligned} p_{j}^{\text {out}} = \frac{Q_j}{\sum _{j=0}^s Q_j} \end{aligned}$$

  (24)

• (3) Based on the probabilities calculated in step 2), use the roulette wheel selection method to choose a service node as the source node, denoted as $\Bbbk$. From the task set of the source node $\Bbbk$, randomly select a task, denoted as $\psi$. Calculate the total cost $Q_{j}^{\psi }$ when each service node $s_j$ processes task $\psi$.

• (4) Compute the optimization potential $Q_{j}^{*}$ of the scheme when transferring task $\psi$ to each service node $s_j$.

  $$\begin{aligned} Q_{j}^{*}=\left( Q_{j}^{\psi }-Q_{\Bbbk }^{\psi } \right) ^+ \end{aligned}$$

  (26)

  If the optimization potential $Q^{*} = 0$, return to step 3).

• (5) Calculate the probability of each service node being selected as the destination node, denoted as $p_{j}^{\text {in}}$.

  $$\begin{aligned} p_{j}^{in}=\frac{Q^*}{\sum _{j=0}^s{Q_{j}^{*}}} \end{aligned}$$

  (27)

  And use the roulette wheel selection method to choose a service node, denoted as the destination node $\mathbb {X}$.

• (6) Modify the gene value of task $\psi$ in the chromosome from $\Bbbk$ to $\mathbb {X}$ to obtain the neighborhood chromosome.

Chromosome decoding

The chromosome specifies the service nodes corresponding to the offloaded tasks, allowing the total execution cost to be derived. However, except for the initial chromosome, it is not necessary to model subproblems and solve them for all service nodes during each decoding process. By proving two key properties, it is sufficient to analyze only partial information in the chromosome during decoding.

Property 1：

For a given upper-level optimization problem, let $\varPsi _{A}^{*}$ represent an optimal offloading scheme under encoding $A$. If there exists another encoding $B$, where the set of offloaded tasks assigned to service nodes $s_{m_1}, s_{m_2}, \dots , s_{m_j}, j \in F - \{ i \}$ under encoding $B$ is identical to that under encoding $A$, then at least one optimal offloading scheme $\varPsi _{B}^{**}$ exists under encoding $B$, in which the offloading scheme assigned to service nodes $s_{m_1}, s_{m_2}, \dots , s_{m_j}$ is the same as that in $\varPsi _{A}^{*}$.

Proof：

Let $\varPsi _{B}^{*}$ represent an optimal offloading scheme under encoding $B$. In the task offloading schemes $\varPsi _{A}^{*}$ and $\varPsi _{B}^{*}$, the task offloading sets for the service node $s_{m_j}$ are denoted as $V_{As_j}$ and $V_{Bs_j}$, respectively, with the total execution costs denoted as $Q_{As_j}^{*}$ and $Q_{Bs_j}^{*}$. Since $\varPsi _{A}^{*}$ and $\varPsi _{B}^{*}$ are both optimal offloading schemes, $Q_{As_j}^{*}$ and $Q_{Bs_j}^{*}$ represent the minimum total costs under the task offloading set $V_{Bs_j}$. When $V_{As_j} = V_{Bs_j}$, it follows that $Q_{As_j}^{*} = Q_{Bs_j}^{*}$.

By replacing the task offloading scheme of the service nodes $s_{m_1}, s_{m_2}, \dots , s_{m_j}$ in scheme $\varPsi _{B}^{*}$ with the corresponding task offloading scheme in $\varPsi _{A}^{*}$, a feasible offloading scheme $\varPsi _{B}^{**}$ under encoding $B$ is obtained. According to the above inference, the total cost of each service node in scheme $\varPsi _{B}^{**}$ is the same as that in scheme $\varPsi _{B}^{*}$. Moreover, since both $\varPsi _{B}^{**}$ and $\varPsi _{B}^{*}$ are offloading schemes under encoding $B$, the total costs for each service node must be identical. Consequently, the total offloading cost for both schemes is the same, which implies that $\varPsi _{B}^{**}$ is also an optimal offloading scheme. Clearly, the task offloading scheme for the service nodes $s_{m_1}, s_{m_2}, \dots , s_{m_j}$ in $\varPsi _{B}^{**}$ is identical to the task offloading scheme for the same nodes in $\varPsi _{A}^{*}$. $\square$

Property 2：

For a given upper-level optimization problem, let $\varPsi _{A}^{*}$ represent an optimal task offloading scheme under encoding $A$. Encodings $A$ and $B$ assign offloaded task sets $V_{As_j}$ and $V_{Bs_j}$, respectively, to service node $s_j$, where $j \in F - \{ i \}$. If: (1) $V_{As_j} \subset V_{Bs_j}$; and (2) there exists a feasible offloading scheme $\varPsi _{B}^{\prime }$ under encoding $B$, in which the start times of tasks belonging to $V_{As_j}$ are identical to those in $\varPsi _{A}^{*}$, and the tasks belonging to $V_{Bs_j} \setminus V_{As_j}$ can be completed within the expected time; then there exists at least one optimal offloading scheme $\varPsi _{B}^{**}$ under encoding $B$, in which the task offloading scheme for service node $s_j$ is identical to that in $\varPsi _{B}^{\prime }$.

Proof：

Let $\varPsi _{B}^{*}$ represent an optimal task offloading scheme under encoding $B$. In the schemes $\varPsi _{A}^{*}$ and $\varPsi _{B}^{*}$, the total cost for service node $s_j$ is denoted as $Q_{Aj}^{*}$ and $Q_{Bj}^{*}$, respectively. In the scheme $\varPsi _{B}^{\prime }$, the total cost for service node $s_j$ is denoted as $Q_{Bj}^{\prime }$. The following conclusions are proven separately: (1) $Q_{Bj}^{\prime } \leqslant Q_{Bj}^{*}$;(2) $Q_{Bj}^{\prime } \geqslant Q_{Bj}^{*}$.

• (1) In scheme $\varPsi _{B}^{\prime }$, the offloaded task set for service node $s_j$ is also $V_{Bs_j}$. Since $V_{As_j} \subset V_{Bs_j}$, there are two types of tasks in $V_{Bs_j}$: tasks belonging to $V_{As_j}$ and tasks belonging to $V_{Bs_j} \setminus V_{As_j}$. For the first type of tasks, their start times are the same as those in scheme $\varPsi _{A}^{*}$, and their execution times are also the same as those in $\varPsi _{A}^{*}$. Consequently, their total cost is identical to that in $\varPsi _{A}^{*}$. In scheme $\varPsi _{B}^{\prime }$, the total cost of tasks belonging to $V_{Bs_j}$ equals the total cost of tasks belonging to $V_{As_j}$ in scheme $\varPsi _{A}^{*}$, i.e., $Q_{Bj}^{\prime } = Q_{Aj}^{*}$. Given the condition $V_{As_j} \subset V_{Bs_j}$, it follows that $Q_{Aj}^{*} \leqslant Q_{Bj}^{*}$. Therefore, $Q_{Bj}^{\prime } \leqslant Q_{Bj}^{*}$.

• (2) $\varPsi _{B}^{\prime }$ is a feasible offloading scheme under encoding $B$, while $\varPsi _{B}^{*}$ is the optimal offloading scheme under encoding $B$. Clearly, $Q_{Bj}^{\prime } \geqslant Q_{Bj}^{*}$.

From conclusions (1) and (2), it follows that $Q_{Bj}^{\prime } = Q_{Bj}^{*}$.

By replacing the task offloading scheme of service node $s_j$ in $\varPsi _{B}^{*}$ with the task offloading scheme of service node $s_j$ in $\varPsi _{B}^{\prime }$, a feasible offloading scheme $\varPsi _{B}^{**}$ under encoding $B$ is obtained. Based on the above inference, the total cost of each service node in $\varPsi _{B}^{**}$ is the same as that in $\varPsi _{B}^{*}$. Moreover, since $\varPsi _{B}^{**}$ and $\varPsi _{B}^{*}$ are both task offloading schemes under encoding $B$, the total execution cost of all service nodes must be identical. As the total costs of the two schemes are the same, $\varPsi _{B}^{**}$ is also an optimal offloading scheme. Clearly, the task offloading scheme for service node $s_j$ in $\varPsi _{B}^{**}$ is identical to that in $\varPsi _{B}^{\prime }$.

Based on the proofs of the two properties above, the specific steps for chromosome decoding are as follows:

1) During each neighborhood search process, only the task sets of two service nodes change: the source node $\Bbbk$ and the destination node $\mathbb {X}$. According to Property 1, it is only necessary to recompute the task offloading schemes for these two service nodes, while the task offloading schemes for other service nodes can be directly inherited from the decoding results of the previous chromosome.

2) Obtain the task scheduling scheme for the source node $\Bbbk$:

2.1) If the source node $\Bbbk$ is the service node $s_j$, remove task $\psi$ from its task set.

2.2) If the source node $\Bbbk$ is not $s_j$, solve the corresponding subproblem using the branch-and-bound method⁵¹.

3) Obtain the task offloading scheme for the destination node $\mathbb {X}$:

3.1) If the destination node $\mathbb {X}$ is the service node $s_j$, add task $\psi$ to its task set.

3.2) If the destination node $\mathbb {X}$ is not $s_j$, construct its time-node plane based on the decoding results of the previous chromosome. Determine whether a feasible position exists on the plane to place task $\psi$ such that it can be completed within the delay constraint.

3.2.1) If a feasible position exists, place the task rectangle in that position. According to Property 2, the updated time-node plane represents the task offloading scheme for the destination node $\mathbb {X}$.

3.2.2) If no feasible position exists, solve the subproblem corresponding to the destination node $\mathbb {X}$ using the branch-and-bound method. $\square$

Simulated annealing selection

In the simulated annealing selection operation, the offspring chromosome replaces the parent chromosome with a certain probability. Let $A$ represent the parent chromosome, $B$ represent the offspring chromosome, and $T$ represent the temperature. The replacement probability $p$ is given by the following formula:

$$\begin{aligned} p=\left\{ \begin{array}{c} 1,f\left( B \right) \leqslant f\left( A \right) \\ \exp \left( \frac{f\left( A \right) -f\left( B \right) }{T} \right) ,f\left( B \right) \geqslant f\left( A \right) \\ \end{array} \right. \end{aligned}$$

(28)

At the beginning of the algorithm, an initial temperature $T$ is set, and the temperature is adjusted during the iterative process using $T \leftarrow \kappa T$, where $\alpha$ is the temperature decay coefficient, $0< \kappa < 1$. Clearly, as the number of iterations increases, the temperature gradually decreases, and the replacement probability under the second condition also decreases accordingly. In the later stages of the iteration, the probability of a suboptimal offspring chromosome replacing the parent chromosome becomes nearly zero.

Algorithm 1 summarizes our algorithm for generating offloading decisions based on the improved genetic algorithm.

Algorithm 1

Offloading Decision Generation Algorithm Based on the Improved Genetic Algorithm

Lower-level optimization

After obtaining the offloading decision population from the upper-level problem, this section utilizes a deep reinforcement learning (DRL) approach to determine the optimal offloading decision $\alpha ^*$ and the optimal weighting coefficients $\mu ^*$ and $\nu ^*$. Finally, the total system energy consumption is computed and returned to the upper level for optimization. Before introducing the specific algorithm design, Problem $P2$ is formulated as a Markov Decision Process (MDP) with three components: state space, action space, and reward space, as detailed below.

State space: Each state consists of task offloading decisions and their corresponding total cost, with the offloading decision population from the upper level forming part of the state space. Specifically, $s_l = \{ s_{l,1}, s_{l,2}, \dots , s_{l,N}, Q_{l}^{\text {total}} \}$, where $s_{l,i}$ represents an offloading decision, and $Q_{l}^{\text {total}}$ denotes the corresponding total cost.

Action space: Each action is defined as $a_l = \{ a_{l,1}, \dots , a_{l,N}; \mu _{l,1}, \dots , \mu _{l,N}; \nu _{l,1}, \dots , \nu _{l,N} \}$, where $a_{l,i}$ represents the offloading ratio of task $\xi _i$ under action $a_l$, and $\mu _{l,i}$ and $\nu _{l,i}$ denote the weighting coefficients for delay and energy consumption, respectively.

Reward space: When the agent takes action $a_l$ in state $s_l$, it receives an immediate reward $r_l$ and transitions to state $s_{l+1}$. To optimize the total system cost, if action $a_l$ satisfies the constraints, the reward $r_l$ is set to the negative total cost in state $s_{l+1}$, i.e., $r_l = -Q_{l+1}^{\text {total}}$. Otherwise, if action $a_l$ violates any constraints of Problem $P2$, a fixed penalty value is assigned.

Since the action space is continuous, the DDPG algorithm is well-suited for solving Problem $P2$. The DDPG framework consists of a primary actor network $\mu \left( s_l | \theta ^{\mu } \right)$, a primary critic network $\eta \left( s_l, a_l | \theta ^{\eta } \right)$, a target actor network $\mu ^{\prime }\left( s_l | \theta ^{\mu ^{\prime }} \right)$, a target critic network $\eta ^{\prime }\left( s_l, a_l | \theta ^{\eta ^{\prime }} \right)$, and an experience replay buffer that stores system state transition data⁵². Each experience is stored as the tuple $\left( s_l, a_l, r_l, s_{l+1} \right)$. During the training phase, experience replay allows the DDPG algorithm to randomly sample experiences from the buffer for network parameter updates. Based on the current state and action, the critic network computes the current and target Q-values and refines them by minimizing the loss function. Subsequently, the primary actor network updates the policy using the policy gradient method while synchronizing the parameters of the target networks.

Primary critic network

The effectiveness of the selected actions is assessed by the primary critic network, and the primary actor network is optimized using the approximate action-value function $Q\left( s_l, a_l | \theta ^Q \right)$. Under the deterministic policy $\mu$, the value function $Q\left( s_l, a_l | \theta ^Q \right)$ is expressed using the Bellman equation as follows:

$$\begin{aligned} y_l=r_l+\gamma Q^{\prime }\left( s_{l+1},\mu ^{\prime }\left( s_{l+1}|\theta ^{\mu ^{\prime }} \right) |\theta ^{Q^{\prime }} \right) \end{aligned}$$

(29)

Here, $\gamma$ is the discount factor, with a value range of $[0, 1]$. In each iteration, a mini-batch containing $N_b$ samples is selected from the experience replay buffer. The primary critic network updates the parameters $\theta ^Q$ using the Time Difference (TD) Error method by minimizing the following loss function:

$$\begin{aligned} L={\frac{1}{N_b}}\sum _l{\left[ \left( Q\left( s_l,a_l|\theta ^Q \right) -y_l \right) ^2 \right] } \end{aligned}$$

(30)

This loss function measures the difference between the current Q-value and the target Q-value.

Primary actor network

The policy is optimized using the gradient ascent method to gradually converge to the optimal solution. The gradient expression for the policy update is as follows:

$$\begin{aligned} \nabla _{\theta ^{\mu }J}\approx \frac{1}{N_b}\sum _l{\nabla _aQ}\left( s_l,a_l|\theta ^Q \right) \nabla _{\theta ^{\mu }}\mu \left( s_l|\theta ^{\mu } \right) \end{aligned}$$

(31)

Here, $\theta ^{\mu }$ represents the reference information provided by the primary critic network. $\nabla _a Q\left( s_l, a_l | \theta _Q \right)$ denotes the gradient of the Q-value with respect to the action $a_l$, while $\nabla _{\theta ^{\mu }} \mu \left( s_l | \theta ^{\mu } \right)$ corresponds to the gradient of the actor network’s policy. Through this update process, the actor network gradually optimizes its policy to achieve optimal performance.

Target networks

The target Actor network selects the optimal action $a_{l+1} = \mu ^{\prime }\left( s_{l+1} \mid \theta ^{\mu ^{\prime }} \right)$ according to the subsequent system state $s_{l+1}$. Its network parameters are periodically updated as follows:

$$\begin{aligned} \theta ^{\mu ^{\prime }}=\tau \theta ^{\mu }+\left( 1-\tau \right) \theta ^{\mu ^{\prime }} \end{aligned}$$

(32)

Here, $0< \tau < 1$ ensures stable updates. The target Critic network computes the loss function $L$. Its parameter update process is similar to that of the target Actor network, as shown below:

$$\begin{aligned} \theta ^{Q^{\prime }}=\tau \theta ^Q+\left( 1-\tau \right) \theta ^{Q^{\prime }} \end{aligned}$$

(33)

Algorithm 2

IGA-DDPG Algorithm

Results and discussion

In this section, we present experimental validation and discussion of the proposed IGA-DDPG algorithm. Consider a mining edge computing scenario with a mining working face area of 600$\times$600 square meters. In this area, an MEC server and a communication base station are deployed, with mobile terminal devices randomly distributed throughout the mine. The available bandwidth resources are divided into 90 subchannel bands. Based on the described physical interference model, the channel gain is set as $h = d^{-4}$, where $d$ represents the propagation distance⁵³. Experiments were conducted on the MATLAB 2020b simulation platform to verify the effectiveness of the proposed IGA-DDPG algorithm. The key parameters for system simulation are listed in Table 3.

Table 3 Parameter settings table.

We compare the IGA-DDPG proposed in this paper with the following five task offloading benchmark schemes:

• IGWO ( Improved Grey Wolf Optimizer metaheuristic algorithm): This algorithm is an enhanced version of the Grey Wolf Optimizer (GWO) that incorporates a nonlinear convergence factor and dynamic weighting. It is selected because it represents a swarm intelligence-based heuristic optimization approach that has been widely applied in task scheduling and resource allocation problems. Comparing IGA-DDPG with IGWO helps evaluate the effectiveness of reinforcement learning (RL) in optimizing offloading strategies.

• TGA (Traditional Genetic Algorithm Optimization): The traditionalThe genetic algorithm is a widely used evolutionary optimization technique. TGA is chosen as a baseline because, like IGA-DDPG, it is an evolutionary optimization method, albeit without reinforcement learning integration. This comparison allows us to assess the advantages of combining genetic algorithms with deep reinforcement learning in complex offloading scenarios.

• BODM (Binary Offloading Decision Mechanism): This method follows a binary offloading approach, where tasks are either fully executed locally or offloaded to an MEC server. BODM is included as a baseline to compare against methods that allow more flexible task partitioning and collaborative computing, such as IGA-DDPG, which enables fine-grained offloading decisions.

• PNCM (Partially Non-Cooperative Mechanism): In this scheme, tasks can be executed locally or offloaded to the MEC server, but they cannot be offloaded to other service terminals. PNCM represents a semi-collaborative offloading model, making it an appropriate baseline to compare against the cooperative task execution capabilities of IGA-DDPG.

• FLEM (Fully Local Execution Mechanism): This scheme represents the most basic execution strategy, where all computational tasks are performed locally on the user device. FLEM serves as an essential baseline to highlight the benefits of offloading strategies, particularly in terms of reduced computation time and system cost.

Time complexity and space complexity evaluation

In Table 4,By comparing the time and space complexity, IGA-DDPG demonstrates optimal computational efficiency and storage requirements, with a time complexity of $O(GPN) + O(EBN)$ and a space complexity of $O(GP + EB)$. This enables efficient resource scheduling and dynamic optimization in large-scale MEC task offloading scenarios. In contrast, IGWO is suitable for medium-scale task offloading; however, due to its broader optimization search space, its computational complexity, $O(IN^2)$, remains higher than that of IGA-DDPG. TGA has the highest computational complexity, reaching $O(GPN)$. Due to its population evolution mechanism, its optimization speed is relatively slow, making it unsuitable for large-scale MEC tasks. BODM and PNCM exhibit relatively lower computational complexity, with $O(N\log N)$ and $O(N^2)$, respectively, making them suitable for small-scale task offloading scenarios. However, they still have limitations in dynamic resource optimization. FLEM, which relies entirely on local computation, has the lowest time complexity of $O(N)$, but suffers from poor task processing efficiency, making it inadequate for MEC computing demands. Overall, IGA-DDPG integrates genetic algorithms and deep reinforcement learning, achieving efficient task scheduling optimization while maintaining low computational complexity. Compared to traditional algorithms, IGA-DDPG outperforms in terms of computational complexity, storage consumption, and task scheduling efficiency.

Table 4 Parameter settings table.

Comparative analysis of IGA-DDPG, IGA, and DDPG

This section compares the performance of the IGA-DDPG, IGA, and DDPG algorithms based on total cost reduction, task completion time, and energy consumption. The experimental results are presented in Fig. 2. As shown in Fig. 2a, IGA-DDPG achieves the highest total cost reduction, significantly outperforming both IGA and DDPG. The total cost reduction for IGA-DDPG is 45%, whereas IGA and DDPG achieve only 30% and 35%, respectively. This indicates that IGA-DDPG provides a more effective trade-off between energy efficiency and computational performance, demonstrating its superior optimization capabilities in complex task offloading environments.

Fig. 2

Comparative analysis of IGA-DDPG, IGA, and DDPG.

Figure 2b illustrates the task completion time for the three algorithms. The IGA-DDPG algorithm achieves the lowest task completion time of 2.1 seconds, significantly outperforming DDPG (2.5 s) and IGA (3.0 s). The shorter completion time indicates that IGA-DDPG effectively optimizes task scheduling and resource allocation, reducing system latency while maintaining a balanced computational load. In contrast, IGA and DDPG experience higher delays due to suboptimal exploration-exploitation balancing and less efficient convergence behavior.

Figure 2c presents the energy consumption of each algorithm. IGA-DDPG consumes the least energy at 15J, while DDPG and IGA consume 18J and 20J, respectively. The lower energy consumption of IGA-DDPG highlights its enhanced power efficiency, which is critical for resource-constrained edge computing environments. The higher energy consumption of IGA and DDPG indicates less efficient decision-making, leading to increased computational overhead and unnecessary processing cycles.

Figure 2d shows the loss function value over iterations. The IGA-DDPG algorithm achieves the fastest and most stable convergence, with the lowest loss values across all iterations. The improved convergence speed of IGA-DDPG compared to IGA and DDPG indicates its ability to rapidly learn optimal task offloading policies, leading to more efficient and adaptive performance. IGA and DDPG exhibit slower convergence and higher loss fluctuations, suggesting greater instability and suboptimal parameter updates during the training process.

Impact analysis of the number of mining terminals

This section compares the performance of the proposed IGA-DDPG algorithm with five baseline algorithms under different numbers of mining mobile terminals. The number of terminals is gradually increased from 10 to 40, and the evaluation focuses on total system delay, energy consumption, and total system cost.

Figure 3a presents the total system delay of different algorithms. When the number of terminals is fewer than 15, system delay remains nearly zero across all algorithms. This is because most tasks are executed locally, reducing the need for task offloading, which would otherwise introduce additional transmission and computation delays. However, as the number of terminals increases beyond 20, offloading becomes necessary due to resource limitations, causing a significant rise in system delay across all algorithms.Among the tested algorithms, IGA-DDPG exhibits the lowest system delay across all terminal sizes due to its optimized task allocation and dynamic offloading strategy. FLEM consistently shows the highest system delay, as it lacks offloading capabilities, resulting in severe local resource congestion. BODM and PNCM perform better than FLEM but experience sharp increases in delay when the number of terminals exceeds 25, indicating poor scalability. IGWO and TGA achieve moderate results, but their delay values still significantly exceed those of IGA-DDPG. On average, IGA-DDPG reduces system delay by 67.7%, 63.0%, 56.6%, 33.5%, and 29.5% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.

Fig. 3

Performance comparison of task offloading strategies under different numbers of terminals.

Figure 3b illustrates the total energy consumption for task offloading. Regardless of terminal scale-whether small-scale (10-20 terminals) or high-load (30-40 terminals)-IGA-DDPG consistently achieves the lowest energy consumption among all algorithms. As the number of terminals increases, the energy consumption of other algorithms rises significantly, whereas IGA-DDPG demonstrates a more stable growth trend, ensuring both lower absolute energy consumption and a smaller growth rate.Although TGA exhibits relatively low energy consumption for small-scale scenarios (10-15 terminals), its energy consumption increases rapidly when the number of terminals reaches 35 or 40, becoming one of the highest among all algorithms. FLEM incurs the highest energy consumption due to inefficient local execution, followed by BODM and PNCM, which also exhibit steep energy growth due to suboptimal task allocation strategies. IGWO performs better than BODM and PNCM but still lags behind IGA-DDPG in terms of energy efficiency. On average, IGA-DDPG reduces system energy consumption by 39.9%, 34.5%, 29.7%, 24.9%, and 18.1% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.

Figure 3c presents the total system cost across different numbers of mining terminals. The total system cost is calculated based on a weighted combination of system delay and energy consumption, providing a comprehensive assessment of the efficiency of each algorithm. Across all tested terminal sizes, IGA-DDPG consistently achieves the lowest system cost, demonstrating its superiority in balancing multiple objectives. As the number of terminals increases, FLEM exhibits the highest total cost, primarily due to its high system delay and excessive energy consumption. **BODM and PNCM initially perform well but experience rapid cost escalation beyond 25 terminals, indicating that they are less effective in large-scale deployment scenarios. TGA and IGWO demonstrate relatively moderate cost increases, but they still accumulate significantly higher costs than IGA-DDPG as terminal numbers grow. Overall, IGA-DDPG achieves a more effective global trade-off in multi-objective optimization scheduling, making it the most cost-efficient solution among all tested algorithms. On average, IGA-DDPG reduces total system cost by 67.7%, 63.6%, 57.0%, 48.1%, and 29.8% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.

Impact analysis of task data size

This section compares the performance of the proposed IGA-DDPG algorithm with five baseline algorithms under different computational task models. The input data size is gradually increased from 2 Mb to 7 Mb, and the evaluation focuses on system delay, energy consumption, and total system cost.

Figure 4a presents the total system delay for different input task data sizes. As the task data size increases from 2 Mb to 7 Mb, the system delay of all algorithms gradually increases, indicating that task data size is a direct influencing factor on system delay. The performance differences between the algorithms are significant. IGA-DDPG consistently outperforms all other algorithms with the lowest system delay, demonstrating its superior task offloading and scheduling efficiency. FLEM performs the worst, as all tasks are executed locally, leading to a severe increase in processing time and congestion. BODM and PNCM show better performance than FLEM but experience sharp increases in delay for larger task sizes, revealing their limitations in large-scale task handling. IGWO and TGA achieve moderate results, but their delay values remain significantly higher than those of IGA-DDPG. On average, IGA-DDPG reduces system delay by 64.6%, 59.1%, 49.4%, 38.2%, and 26.1% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.

Fig. 4

Performance of task offloading strategies under different input data sizes.

Figure 4b illustrates the total energy consumption for task offloading. As the input task data size increases from 2 Mb to 7 Mb, the energy consumption of all algorithms rises accordingly. However, IGA-DDPG consistently maintains the lowest energy consumption, with a relatively controlled increase even at high data sizes. This demonstrates the adaptive and global optimization capabilities of IGA-DDPG, making it more competitive in mining edge computing systems under surging traffic. It provides an efficient solution for achieving low energy consumption under high loads.Although TGA exhibits relatively low energy consumption for smaller task sizes, it undergoes a sharp increase when the task data size exceeds 5 Mb, making it one of the least energy-efficient algorithms. FLEM has the highest energy consumption, due to its inefficiency in local task execution, followed by BODM and PNCM, which also show steep energy growth due to suboptimal task allocation strategies. IGWO performs better than BODM and PNCM but remains less energy-efficient compared to IGA-DDPG.On average, IGA-DDPG reduces system energy consumption by 18.8%, 14.7%, 9.9%, 7.2%, and 5.4% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.

Figure 4c presents the total system cost for different input task data sizes. The total system cost is calculated based on a weighted combination of system delay and energy consumption, providing a comprehensive evaluation of overall system efficiency. Across all tested task data sizes, IGA-DDPG consistently achieves the lowest total cost, demonstrating its effectiveness in balancing multiple optimization objectives.As the task data size increases, FLEM incurs the highest total cost, primarily due to its high system delay and excessive energy consumption. BODM and PNCM initially perform well but experience rapid cost escalation when the task data size exceeds 5 Mb, indicating their poor scalability. TGA and IGWO demonstrate relatively moderate cost increases, but their total cost still remains significantly higher than that of IGA-DDPG.Overall, IGA-DDPG achieves the most controlled growth in total system cost, proving its efficiency in reducing overall operational expenses. On average, IGA-DDPG reduces total system cost by 82.9%, 66.0%, 49.3%, 47.1%, and 33.6% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.

Impact analysis of the task computation load model

This section compares the performance of the proposed IGA-DDPG algorithm with five baseline algorithms under different computational task models. The task computation load is gradually increased from 4 GHz to 9 GHz, and the evaluation focuses on system delay, energy consumption, and total system cost.

Figure 5a presents the total system delay for different task computation loads. It can be observed that as the computation load increases from 4 GHz to 9 GHz, IGA-DDPG consistently achieves the lowest system delay and exhibits the most gradual increase among all algorithms.At the highest load of 9 GHz, the delay of IGA-DDPG is only approximately 1.98 seconds, whereas the delays of other algorithms range from 2.7 to 4.8 seconds, indicating that IGA-DDPG maintains superior efficiency under increasing workloads. FLEM exhibits the highest system delay, as it lacks offloading capabilities, leading to severe local computation congestion. BODM and PNCM show better performance than FLEM but experience sharp increases in delay as computation load increases, indicating their poor scalability. IGWO and TGA perform moderately well, but their delays remain significantly higher than those of IGA-DDPG. On average, IGA-DDPG reduces total system delay by 67.8%, 58.8%, 50.3%, 33.6%, and 17.4% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.

Fig. 5

Performance of task offloading strategies under different computational loads.

Figure 5b illustrates the total energy consumption for task offloading. As the computation load increases from 4 GHz to 9 GHz, the energy consumption of all algorithms rises significantly. This corresponds to the increased resource consumption, higher network communication, and heavier processing loads associated with greater computational demands.As the computation load increases, the performance advantage of IGA-DDPG becomes increasingly pronounced compared to traditional algorithms such as FLEM and BODM. Moreover, IGA-DDPG maintains a stable low-energy consumption gap compared to TGA and PNCM, ensuring energy-efficient performance across different computation loads.On average, IGA-DDPG reduces total system energy consumption by 21.3%, 15.3%, 11.6%, 6.8%, and 4.1% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.

Figure 5c presents the total system cost for different task computation loads. From 4 GHz to 9 GHz, the total system cost for all algorithms increases monotonically. However, IGA-DDPG consistently maintains the lowest total cost across all computation loads, demonstrating its effectiveness in balancing energy efficiency and task delay optimization.As computation load increases, the total cost curves for BODM and PNCM become steeper, indicating their poor adaptability to higher workloads. Although TGA performs relatively well among traditional methods, its delay results suggest that IGA-DDPG maintains a significant advantage across all computation loads. IGWO also performs better than BODM and PNCM but remains suboptimal compared to IGA-DDPG.On average, IGA-DDPG reduces the total system cost by 21.4%, 17.6%, 12.8%, 6.3%, and 3.9% compared to FLEM, BODM, PNCM, TGA, and IGWO, respectively.

Performance analysis in large-scale scenarios

This section compares the performance of the proposed IGA-DDPG algorithm with five benchmark algorithms under different task scales. The task scale increases from 100 to 500, and the evaluation metrics include computation time, task completion rate, and total system cost.

Figure 6a illustrates the computation time of different algorithms. As the task scale increases, the computation time for all algorithms grows, indicating that task complexity directly affects computational overhead. IGA-DDPG consistently maintains the lowest computation time across all task scales, demonstrating superior computational efficiency. IGWO and TGA exhibit moderate computation time but are significantly higher than IGA-DDPG. In contrast, BODM and PNCM experience the fastest increase in computation time due to their exhaustive search strategies, leading to a sharp rise in computational burden for large-scale tasks. FLEM has the highest computation time, as all tasks are executed locally, resulting in severe computational bottlenecks. On average, IGA-DDPG reduces computation time by 49.2%, 43.9%, 35.2%, 28.1%, and 21.4% compared to FLEM, PNCM, BODM, TGA, and IGWO, respectively.

Fig. 6

Performance of task offloading strategies in large-scale scenarios.

Figure 6b presents the task completion rate of different algorithms. As the task scale increases, the task completion rate of all algorithms declines due to resource constraints. However, IGA-DDPG consistently achieves the highest task completion rate, ranging from 98.5% to 92.5%, ensuring reliable task execution even under high computational loads. IGWO and TGA exhibit slightly lower task completion rates, ranging from 96.1% to 89.8% and 93.4% to 83.2%, respectively. In contrast, BODM and PNCM experience a more rapid decline, dropping to 78.7% and 73.2% at the largest task scale, indicating weaker adaptability under high-load scenarios. FLEM has the lowest task completion rate, reaching only 60.7%, as it fully relies on local computation, resulting in excessive task processing delays and an increased task failure rate. On average, IGA-DDPG improves the task completion rate by 52.2%, 47.1%, 36.2%, 27.4%, and 19.7% compared to FLEM, PNCM, BODM, TGA, and IGWO, respectively.

Figure 6c illustrates the total system cost, which includes computational resource consumption and execution latency. As the task scale increases, the total system cost rises for all algorithms. Due to its adaptive optimization strategy, IGA-DDPG achieves the lowest total cost across all task scales. IGWO and TGA exhibit moderate system costs, but their costs increase more rapidly as the task scale grows. BODM and PNCM experience a sharp rise in system cost when the task scale exceeds 300, reflecting their high computational overhead in large-scale task environments. FLEM consistently incurs the highest system cost, as all tasks are executed locally, leading to excessive computational resource consumption and a lower task completion rate, which further increases the overall system cost. On average, IGA-DDPG reduces the total system cost by 31.5%, 28.9%, 23.7%, 18.5%, and 12.3% compared to FLEM, PNCM, BODM, TGA, and IGWO, respectively.

Analysis of variance (ANOVA)

To assess whether the performance differences among the compared algorithms are statistically significant, we adopted the ANOVA-based experimental methodology employed in⁵³.

Based on the results of one-way analysis of variance (ANOVA), we conducted significance tests on three key performance indicators: latency, energy consumption, and total cost. As shown in Table 5, the p-values for all three metrics are significantly lower than the significance level of $\alpha = 0.05$, specifically $9.0100 \times 10^{-5}$, 0.0194, and $7.6803 \times 10^{-8}$, respectively. These results indicate that there are statistically significant differences in the performance of different algorithms across all evaluated metrics.

Table 5 Analysis of variance.

Conclusion

This paper addresses the problem of multi-user collaborative task offloading and resource allocation in mining mobile edge computing scenarios. The objective is to minimize the total system cost while satisfying task delay constraints by jointly optimizing task offloading decisions and the weighting coefficients for delay and energy consumption. To solve this multi-objective optimization problem, a two-level alternating optimization framework is proposed. The upper level employs an improved genetic algorithm (IGA) to generate a population of offloading decisions, while the lower level applies the Deep Deterministic Policy Gradient (DDPG) algorithm to obtain the optimal offloading decisions and weighting coefficients for delay and energy consumption.

Simulation results indicate that the proposed IGA-DDPG algorithm exhibits high adaptability and significantly outperforms various baseline methods, including local computation, non-collaborative partial offloading, and binary offloading, in terms of delay, energy consumption, and system cost. This solution demonstrates promising potential in reducing the computational burden on edge servers and optimally utilizing the computational resources of terminal devices.

Although the proposed IGA-DDPG algorithm effectively optimizes task offloading in MEC systems, there are several potential research directions for future exploration. First, optimizing the computational efficiency of the algorithm remains an important challenge, and incorporating techniques such as parallel computing or accelerated reinforcement learning methods (e.g., PPO, SAC) could be beneficial. Second, extending the model to a heterogeneous MEC environment, where servers have different computational capabilities, bandwidth constraints, and energy consumption characteristics, would provide a more realistic deployment scenario. Additionally, considering task dependency structures in complex applications, such as deep learning inference or distributed computing, could further enhance system performance. Moreover, integrating online learning and federated learning could allow for real-time adaptive decision-making and privacy-preserving optimization. Finally, future work should focus on real-world deployment and testing on actual MEC hardware platforms, such as edge computing devices and 5G/6G networks, to validate the effectiveness of the proposed method in practical environments.