Abstract
The thermo-physiological and tactile properties of socks were analysed by using hybrid yarns which were made by Polyethylene (PE) fibre with different fibres in variable ratios, using full-factorial experimental design. Socks samples were designed using hybrid yarns made with three blend ratios of polyethylene filament with cotton (Co), polyester (PET), polypropylene (PP), modal (Mo) and viscose (Vis) spun yarns. Statistical analysis was carried out according to response surface regression analysis (RSM). Among various analytical tools, RSM is adopted for prediction of multiple responses and response optimizer (RO) was used to optimize the thermo-physiological and tactile comfort i.e. softness and smoothness properties of socks by using the desirability function approach. It was inferred that the combination of cotton with polyethylene was most influencing for thermal conductivity and softness properties. Experimental validation confirmed that predicted variables can be used to design knitted socks fabric with desired thermo-physiological and tactile comfort properties.
Similar content being viewed by others
Introduction
Comfort is the main characteristics of clothing which affect the liberty to choose product in addition to aesthetics1. Mankind is constantly struggling to improve their lifestyle by improving the comfort level. Researchers classify three categories for discomfort; physiological sensations of discomfort, like sensorial discomfort that said what fabric is worn next to skin feeling, garment fit and thermos-physiological discomfort2. Researchers described tactile discomfort and suggested that it could also be considered as the termo-sensorial discomfort since the pressure and thermal sensations can also be remarked as sensorial. The fitting of garment may be regarded and taken as pressures imposed by the garments on body3. Knitted fabrics that not only possess stretch but also give freedom of movement, with a subtle hand and appearance which leads to comfort. This is the reason they are an outright choice for sportswear, socks, underwear and casualwear. The clothing comfort depends on many factors like fibre type, yarn properties, fabric structure and the finishing treatments affects the thermo-physiological comfort4,5,6,7,8,9,10,11,12,13,14,15.
Human body rely thermo-physiologically on overall thermal comfort. Humans are homoeothermic, which can be described as the inner (core) temperature should be maintained at a constant level. According to some physiological studies, the survival temperature for a person under extended temperature exposure is 37 ± 0.5 °C. The tolerance of the inner temperature is about 2 °C from its normal level. It is necessary to maintain skin outer temperature under extended environmental conditions to remain thermally comfort2.
Human body temperature management is very important for living, which is done naturally to make the body temperature maintained at 37 °C by balancing heat loss and heat production. To retain this outstanding function, clothing plays a vital role in this regard and gives a comfortable thermal microclimate between skin and clothing4. Thermo-physiological comfort of clothing is absolutely determined by the thermal insulation, water vapour transport and moisture permeability of clothing2.
Clothing comfort is complex and multidimensional according to researchers5,6,7. There are various physiological buffer zones in a broader spectrum in which human body operates and quantification of discomfort e.g. cold, hot, scratchy, snuggy, etc. is possible16. Researchers have investigated the comfort properties of soybean, chitosan, modal, micro modal and bamboo fibres after incorporating in socks and comfort related objective measurements were evaluated such as air permeability, wicking, wetting, water vapour and heat transfer properties. Comparative studies of cotton and viscose were also conducted17.
It has been established that moisture build-up within a shoe environment is primarily due to high perspiration rate of the feet and warm or humid environment generated in enclosed shoe. Sweat from the body will vaporise into the atmosphere much quicker compared to the sweat accumulated within an enclosed shoe environment. Due to which sock fabric is accumulated with the moisture and hence frictional forces increased which obviously would introduce discomfort to the wearer18. Sports socks were checked for the influence of sensorial, textile and physiological parameters on sock’s comfort. Parameters for comfort were evaluated in two different exercises by an un-trained panel. Sensory evaluation criteria were foot temperature, fabric dampness, and pain19. It was concluded that fibre, yarn and fabric properties are the factors that affect coolness. Cool feeling to touch of fabrics is largely associated with thermal sorption and desorption phenomenon of fibres, thermal conductivity as well and also depend on the cross-section of a fibre20. Warm or cool feelings are assessed initially when the fabric is first touched by fingers. Generally, loose arrangements and surface hairiness of fabric layers are airy and create a warmer feeling21. In a study the fabrics made from bulked or fluffy yarn showed lower thermal conductivity than 100% cotton ring spun fabric, which is due to the insulation medium provided by the very bulky structure of yarns. The entrapped air did not allow heat to conduct from inner layer to outer layer as air is the insulator22. Multiple fabric layers were evaluated for the thermal contact properties and it was summarised that the inner and outer fabric interlining increases the thermal absorptivity if they place together which makes the fabric cooler to the touch23.
Normally polypropylene is the main polyolefin used in yarn manufacturing and has applications in textiles due to its resistance to humidity and light, low retention of smog, smells, or fat, and low chemical reactivity24. Polyethylene was reported as the highest thermal conductive polymer as compared to other regular polymer materiel used in textiles i.e. 340 mW/mK. Other researchers also studied about polyethylene thermal properties21,25,26,27,28. A body cools in two distinct ways, one through perspiration, this happened when sweat is evaporated through material and through infrared radiation (IR), which is wave of light which all materials emits. Normally common clothing traps IR emission while PE allows theses waves to escape. It means PE has high IR transparency. For an indoor scenario, IR radiative heat dissipation contributes to more than 50% of the total body heat loss29,30. In a study conducted by Po-Chun dual made textile was composed of a bilayer emitter embedded inside an infrared-transparent nano porous polyethylene layer, that can perform both passive radiative cooling and heating by using the same textile pieces regardless of any energy unit31.
A study showed that the polymer material for textiles must have an IR reflectance of 0.2 and transmittance of 0.644 to make a wearer It was also reported that polyethylene have an intrinsically high IR transmittance because in the IR range they do not possess vibrational modes, and their IR transmittance or transparency can be increased by reducing the diameter of yarn by reducing either fibril tows or fibre denier32. Study carried out also reported the potential of polyethylene as new generation cooling material for engineered fabrics33.
Problem with clothes in hot weather was that they kept warm by preventing IR. Despite the numerous publications published about thermo-physiological comfort properties by using different types of yarns, their blends but, the scientific literature lacks information concerning Polyethylene with reference to use in textiles to bring its thermal properties upfront.
The overall aim of this research is to optimize the knitted socks with improved thermo-physiological and sensorial comfort by using hybrid yarn. Polyethylene filament yarn (PE) which has high thermal conductive properties in combination with the conventional spun yarns such as cotton (Co), polyester (PET), polypropylene (PP), modal (Mo) and viscose (Vis) in different blend ratios were manufactured. Socks were developed by using five groups of yarns w.r.t material type and varying blend ratio sequentially. In addition, validation is done of predicted response with experimental results.
Materials and methods
The Polyethylene (PE) filament yarns were taken in three linear densities i.e. 15.5 Tex (48 filaments), 31.1 Tex (96 filament) and 61.1Tex (192 filaments) which were obtained from CTA High Tech Co. Ltd, China. The linear density of individual filament in all PE filament yarns was 1.45 denier. The different linear densities were used to obtain constant blend ratios of hybrid yarns.
The staple spun yarns of Cotton, Polyester, Modal, Polypropylene and Viscose yarns were obtained in two linear densities i.e., 29.5 Tex and 36.8 Tex from Interloop spinning Ltd., Pakistan (given in Table 1).
Twist multiplier was set at 3.7 and 3.9 for both the selected linear densities for the spun yarns. Theses yarns (Sr.No.2 to 6) were then ply twisted with polyethylene (PE) yarn to make three different blend combinations as per Design of experiments (DOE).
A full factorial design was developed and analysed through Response Surface Analysis (RSA) to examine the relative effects of material type and their blend ratios. The factors and their levels are shown in Table 2. The total number of hybrid yarn samples prepared were 15 in number.
Combination of different fibres is done to improve certain properties, and it can be done by various methods such as homogeneous blending of different spun fibres in spinning, using different yarns during weaving, plying/twisting of staple and filaments yarns34. Hybrid yarns were made by twisting low density polyethylene (PE) filament yarn (fully drawn) with five different staple spun yarns, out of which three are cellulosic and two are synthetic materials. The yarns were twisted on AGTEKS Directwist 2C6 Cone-to-cone multi-function twisting machine to make hybrid yarns of three linear densities i.e., 52 Tex, 60 Tex and 91 Tex for PE composition of 30%, 50% and 70% respectively as mentioned in Table 3.
Five sets of yarns were prepared on twisting machine. Per set of yarns includes three compositions which made total 15 sample yarns. Fibre analysis by quantitative method as per AATCC-20A: 2018 standard was performed to verify the composition % of all yarns. All the results are in the range of ± 5.
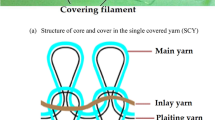
Yarn used on face side of socks is called main yarn and yarn used on back side is called plaiting yarn. The developed hybrid yarns were used as main yarn while for plaiting yarn, 70 Denier Nylon (24 filaments) covered 20 Denier elastane was used in socks which was kept constants for all developed socks.
Manufacturing of socks
Fifteen high pile terry socks samples were produced on 168 Needles 3.75 inches SC, GK616DF3 Lonati Socks Knitting Machine. All the machine parameters/settings were kept constant for all developed sock samples. Tension matched as closely as possible across the different hybrid yarns. Stitch length was also kept constant i.e. 2.5 mm during knitting process. However, it slightly changed after relaxation of the samples.
Socks were then washed to ensure stability/pre-shrunk in Tupesa RS-Basic Plus 5C Ecostar 2012 lab scale model. In this research, socks were dip washed for 5 min at 40 °C and hydro extracted in hydro extractor at 40 °C for 20 min to remove any moisture in fabric. The samples were boarded and pressed on Ghibli Tecnopea automatic machine. Boarding process is a very essential step to make socks presentable as per specifications and layouts. Socks were conditioned for 24 h prior to testing in the standard environment and tested in accordance with EN ISO 139:2005 (i.e. 20.0 ± 2.0 °C, 65.0 ± 4.0% RH).
Testing
Thermal comfort is related primarily to the efficiency of heat dissipation from a clothed human body. On the other hand, tactile comfort is related to sensory feeling such as softness and smoothness.
Thermo-physiological comfort
Thermal conductivity
Thermal conductivity is the rate at which heat transferred is measured per unit area and unit thickness of fabric at specific temperature gradient. It is the reciprocal of thermal resistance with known thickness of fabric sample. Thermal resistance is measured by test method EN ISO 11092:2014 via Alambata instrument. All the samples were tested three times for taking mean value and standard deviation (S.D). Thermal resistance (R) is noted in units m2K/W, which is directly proportional to the thickness (h) and inversely proportional to the thermal conductivity (\({\varvec{\lambda}}\)) as described in Eq. (1):
Air permeability
Air permeability (AP) is an expression describing the properties of a fabric that permit the passage of air through the fabric’s interstices. All the socks samples were tested for air permeability by the standard test method BN ISO 9237 on SDL Air Permeability tester M201. The constant air pressure used for testing samples was 100 Pascal. All the samples were tested five times for taking mean and S.D. values.
Moisture management
AATCC 195-2009 was used to measure moisture management characteristics of all develop socks samples by using moisture management tester (MMT) of SDL Atlas. The MMT is designed to sense, measure, and record the liquid moisture transport behaviours in multiple directions. The apparatus is based on the principle that electrical resistance of a fabric changes with the spread of moisture within sample (stimulate sweating). All the samples were tested thrice for calculating mean and SD (standard deviation) values.
Sensorial comfort
All objective evaluation of sensory responses to fabrics play a role in providing data to assess the appropriateness of fabrics for various end uses. PhabrOmeter testing equipment was used to check tactile comfort properties as per standard test method AATCC 202-2012, Relative Hand Value of Textiles. PhabrOmeter performs test procedures that believed to simulate hand feeling process. Two hand properties were studied in present investigation i.e. Smoothness and Softness.
Data analysis
The statistical analyses were performed using Response surface methodology (RSM) and optimization of parameters was done using Response optimizer (RO) with the statistical software Minitab ver. 14.0 for analysing the statistical relationships of measured properties of the socks.
Prior to analysis, data were tested to ensure the assumptions of normality (using Normality test/plot) were met. In order to understand the statistical importance of material type and PE blend ratio for sock’s comfort related properties, response surface analysis was performed. Response surface regression analysis is used to analyse quadratic and non-linear interactions between predictor and response parameters. This method is mostly employed after detection of vital few variables that influence the response variable and need to find the factor settings that optimize the response. RSM is an empirical modelization method, used for evaluation of experimental factors and observed results. Response surface regression analysis is used to determine and solve multi-variant equations from the quantitative data obtained from experiments. This method is also used to evaluate relationship between a set of factors and a response35,36. A regression equation was also developed to calculate the response using the input variables theoretically. Regression analysis of variance (ANOVA) is useful in determining the significance of each linear, quadratic and interaction terms in the models through probability value (p-value). The terms with p-value less than α-level (0.05) were considered as having significant effect on response while the terms having p-value more than 0.05 and less than 0.1 were considered as likely to be significant. Interaction plots are drawn to evaluate the two factor interaction in a design.
In the fitted regression equations only the regression coefficients which are significant at 95% confidence limits are considered. The accuracy of the regression equation was measured thorough R-square value which was the representative of data fitting in terms of percentage in the statistical analysis. Higher the R-square value of a model better will be its possible performance and data fitting with validation data set.
Response optimizer (RO) is often useful in product development when one need to determine operating conditions that will result in a product with desirable properties. A desirability function is defined individually for each response parameter including targets and boundaries for present study. The overall desirability for combine response is also calculated and analysed as per targets. The maximum overall desirability value can be ‘1’ and the minimum can be zero37. In this study, RO was also employed for optimization of thermal conductivity, softness, air permeability and moisture management at desired settings as maximum for former two and minimum for rest of the two latter responses were achieved. The desirability value explains the achievement of predicted response to the desired value. The closer predicted response was achieved where the values approach to 1.
Results and discussion
Physical properties
Physical properties of all developed sock samples are presented in Table 4. As it can be seen that with the increase in Tex (coarser linear density), areal density (g/m2) of socks sample increases. Similar observation was observed in thickness. The difference of yarn counts from finer to coarser has led to increase in areal density and thickness.
Thermo-physiological comfort related properties
The mean values of thermo-physiological comfort parameters along with the standard deviation (SD) are provided in Table 5.
Tactile comfort characteristics
The mean values of tactile comfort characteristics along with the standard deviations (SD) are given in Table 6.
Correlation analysis
A Pearson correlation analysis was performed to analyse the correlation effect between the predictor and response factors. The results are given in Table 7. The p-values less than α-level (0.05) are considered as statistically significant results. Ignoring the non-significant terms, the results have shown that material type have direct correlation with thermal conductivity and an inverse correlation effect has been observed with OMMC values. Blend ratios have direct correlation with air permeability and OMMC values while an inverse correlation has been observed with thermal conductivity and smoothness.
Analysis of variance (ANOVA)
Thermal conductivity
ANOVA results for thermal conductivity are given in Table 8. In this, DF, SS, and MS, represent the degree of freedom, sum of squares, and mean squares values respectively. F value is calculated by taking the MS for the variable divided by the MS of the error. After removing non-significant terms from the analysis, linear terms were only found to be statistically significant in the results.
It can be observed that material type and blend ratio have significant effect on thermal conductivity of samples. From the Fig. 1 it can be observed that by increasing content of constituent fibre other than polyethylene, thermal conductivity decreases. In other words, thermal conductivity increases by increasing polyethylene content. The results suggested that highest thermal conductivity was obtained for modal fabric followed by viscose, cotton, polypropylene and polyester structures. The thermal conductivity of dry fabric depends on properties of yarn and fabric structure. The thermal conductivity of fabric is highly influenced with air trapped inside the fabric while for thermal resistance fabric thickness has strong influence38. Air has lowest thermal conductivity 0.024 W/mK (entrapped air in fabric) than any other polymers/fibres. The impact of porosity generated with intra-yarn as well as inter-yarn spacing due to fibre and yarn linear densities may also have an impact. Yarns developed with micro filaments have fewer micro pores inside yarn structure as compared with yarn developed with macro filaments. Cotton fibre has higher thermal conductivity as compared with viscose fibre as per literature, but the convolutions on cotton fibre as well as coarser fibre diameter may result in reduced thermal conductivity results as obtained in our study. The same impact was observed with polypropylene and polyester structures. Thus socks samples made of more PE blend ratio (comparatively finer filaments) has higher thermal conductivity. The macro porosity reduces due to flat surface and non-crimpy structure of filament by increasing percentage content of PE filament and therefore makes the fabric compact. Moreover, thermal conductivity of polyethylene is higher than other constituent fibres, which also plays its role. Thus socks made with more composition of PE have higher thermal conductivity. In addition, yarn linear density also have an impact on thermal conductivity of the fabric. Fabric structures developed with coarser yarns have more macro pores which reduces its thermal conductivity39.
The thermal absorptivity i.e. cool/ warm feeling value depends on the thermal conductivity of the fabric as well as on the contact area of the skin and surface. Yarn characteristics play a significant role on thermal absorptivity. Similar to the thermal conductivity, the thermal absorptivity of samples increases with the growth of linear density and the fabric density. Thermal absorptivity has a direct relation with thermal conductivity as shown in Eq. (2)39.
where b = thermal absorptivity (W s1/2 m−2 K−1), λ = thermal conductivity (W m−1 K−1), ρ = fabric density (kg m−3), c = specific heat capacity (J Kg−1 K−1).
The lower specific heat of material indicates conductive behaviour of that material. Therefore, for increase in thermal comfort, it is suggested that the fibres used should have higher thermal conductivity. In this particular case, polyester and polypropylene fibres had lower thermal conductivity than cotton, modal and viscose fibre; therefore, the thermal conductivity of fabrics will be lower hypothetically with the addition of polyester and polypropylene content40,41,42,43,44.
Response surface methodology (RSM) analysis was done for developing a statistical model in which only significant values are considered. The regression coefficients, t-value and p-values of all the terms for thermal conductivity are given in Table 9. Coefficient of determination (R2) of value 90.34% indicates that more than 90% variation in the experimental data is explained by the terms that are included in the model. Higher R2 indicates the implication of model is more accurate which suggests that data will surely predict new observations nearly as well as it fits the existing data.
The response surface equations of thermal conductivity are shown in Table 10 and can be used directly for the prediction of thermal conductivity for sock knitted fabrics.
Air permeability
ANOVA results for air permeability (AP) are given in Table 11. The terms having p-values more than alpha level are considered as statistically non-significant and therefore removed from the analysis. It is observed that material type and blend ratio are significant factors effecting the air permeability of the socks.
The main effect plot for material type and blend ratio w.r.t air permeability is shown in Fig. 2.
The results have suggested that air permeability increases with the increase in constituent fibre content (blend ratio). Therefore, an inverse relationship has been observed with polyethylene fibre content for air permeability of socks. At lower blend ratio of constituent fibre, linear density of the yarn is coarser and thickness of the fabric is resultantly higher which hinders the flow of air through them. Interstices or pore characteristics have strong influence on airflow through textiles. PE filaments are relatively smooth and non-crimpy in structure with respect to spun fibres, therefore filament part of hybrid yarn tends to become flat/ribbon like upon application of forces. The conversion of round to flat/ribbon like cross-sectional shape enhances the cover factor and ultimately reduces the air gaps of fabric structure. These spaces and gaps are distributed throughout the fabric that makes its structure or geometry45. Therefore, with the increase of PE content, the yarn cross-sectional shape may varies which resultantly reduces the air permeability value. Similar trends were observed by other researchers46. Air permeability is a function of the fabric thickness, tightness factor and porosity of the knitted fabrics. Physical properties i.e. fabric areal density and thickness has an inverse relationship with air permeability. This situation can be explained by the amount of fibre per unit area. The amount of fibres increases, the fabric become more tightly packed. Therefore, air permeability values will be lower for heavier and thicker fabrics47.
It is observed that air permeability is highest in samples made with PE blend with polyester followed by cotton, modal, viscose and polypropylene. This is because spun polyester yarn have highest crimp/cm i.e. 7.8 while 6.9, 5.8, 5.7 and 5.5 for polypropylene, cotton, modal and viscose, respectively. Since crimp of the textile fibres is very critical to determine its physical properties and voluminosity. Crimpier structure of polyester fibre has led to the yarn became more porous; hence, it provides more gap and air space than those of other fibres. Therefore, air permeability of sock samples is high in which PET content is high48. While in case of polypropylene, the number of fibres in fibre cross-section increases due to low density of the material which make the yarn bulkier and ultimately reduces the air gaps inside the fabric structure and causes resistance for air flow. Cotton as natural fibre has high crimpiness and provides good air passages for air flow followed by regenerated fibre modal and viscose. The interaction plot of Air Permeability with respect to material type and blend ratio is shown in Fig. 3.
It was observed that blend ratio and material type have statistically significant interaction for air permeability of socks.
RSM analysis was done for developing prediction model for AP. Linear as well as interaction terms were found to be statistically significant for the development of regression model for air permeability of socks. The regression coefficients are provided in Table 12. It is observed from the results that interaction effect of modal and polypropylene is statistically significant. The regression coefficient values of interaction of blend ratio with modal was found inversely proportional while with polypropylene it was directly proportional with air permeability values. More than 97% variation in the experimental data is explained by the terms that are included in the model.
The regression equations of AP are shown in Table 13 and can be used directly for the prediction of AP for sock knitted fabrics.
Moisture management
Overall moisture management capacity (OMMC) is an index for the fabric’s overall ability to transport liquid moisture. The larger the OMMC value, the higher the overall moisture management ability of fabric. The overall moisture management capacity (OMMC) values are evaluated to investigate the comparison of overall moisture management properties of socks samples. All the samples are in fair to good range of an index as per grading scale due to terry structure (0–0.2: very poor, 0.2–0.4: fair, 0.4–0.6: good, 0.6–0.8: very good, > 0.8: excellent)49. ANOVA results for OMMC are given in Table 14. The linear as well as interaction terms of blend ratio and material type were found to be statistically significant for moisture management of socks.
Moisture management properties are effected by fibre type, yarn linear density and knit structures50. The main effect plot of input parameters verses OMMC has been shown in Fig. 4. It was observed from the results that OMMC value increases with increase in blend ratio of constituent fibre. Therefore an inverse relationship with polyethylene content with OMMC values has been observed. This might be due to packing of filaments in polyethylene yarn leading to lower gaps for moisture transportation through them. In addition, it was observed that highest OMMC values were obtained for polyester blend followed by cotton, polypropylene, modal and viscose. The reason lies on the fact that polyester has comparatively highest crimpiness in its structure as well as hydrophobic in nature which resultantly supports for moisture transportation across fabric layers as well as spreading of moisture. Cotton as natural fibre and being hydroscopic in nature, supports moisture transportation and absorption of water. In case of polypropylene, due to bulkier and crimpy structure with hydrophilic nature makes it a moderate moisture transporter. Owing to crimpy structure, capillaries may support the moisture for spreading. Modal and viscose fibres are regenerated fibres with less crimpiness and hydroscopic nature make them almost of same type with inferior OMMC property than cotton.
As the areal density increases, porosity in fabric decreases; thus, there is less rate of flow of liquid from the surface to the inside of fabric capillaries which is according to previous research51,52. The interaction plot for material type and blend ratio verses OMMC is shown in Fig. 5.
RSM analysis was done for developing prediction model in which statistically significant values are considered. More than 96% variation in the experimental data is explained by the terms that are included in the model. The results depicted that blend ratio interaction with polyester and polypropylene are statistically significant. The blend ratio and polyester interaction with OMMC was found indirectly proportional whereas polypropylene interaction was in direct proportion. The regression analysis of OMMC of socks is given in Table 15.
The regression equations are shown in Table 16 and hence can be used directly for the prediction of OMMC values of sock knitted fabrics.
Softness
In the fabric hand attributes, softness is more related to socks so effect of material types and blend ratio on softness is studied. From the ANOVA Table 17, it was observed that linear as well as square terms were found to have statistically significant effect on softness of socks.
According to objective measurement, it was found that there was a significant relationship between softness and blend ratio. The higher the values of softness, the better the fabric hand performance. The main effect plot has been shown in Fig. 6. The results show that softness values increases by increase in blend ratio up till 50% followed by decrease in values. This result explains that softness is lowest, in which PE content is high. Fabric areal density have inverse relationship with softness. High mass per unit area of the fabric is due to the closely packing of yarns due to which it is difficult to compress the fabric and hence softness is compromised. The blend ratio in all of the samples in which PE content is high has high GSM. As we mentioned in the above section that PE yarn have high number of filaments i.e. 196, which make it denser structure, that might be the reason of less softness. Experimental results revealed that areal density and thickness both contributed significant effects on hand properties measured objectively53.
The highest values were obtained for viscose followed by modal, polyester, polypropylene and cotton in turn. This attribute of softness of viscose and modal come with the inherent characteristics of wood-based cellulosic fibres54. The regression analysis of softness of socks is given in Table 18.
RSM analysis for softness was done for developing the prediction model. The R2 value obtained is 88.80% which means than 88% variation in the experimental data is explained by the terms that are included in the model.
The regression equations are shown in Table 19 which can be used directly for the prediction of relative hand value (softness) of sock knitted fabrics.
Smoothness
Fabric surface characters greatly influences the sensation. Fabric having regular/smooth surface, provide large area of contact to the contacting surface (human skin) and increase instantaneous heat flow thereby creating a cooler feeling44. Fabric smoothness has been analysed and ANOVA results are reported in Table 20. The terms having p-values more than alpha level were removed from the analysis. It is observed from the results that linear as well square terms have statistically significant effect on smoothness of socks.
The main effect plot has been shown in Fig. 7. It is observed that with the increase of blend ratio of constituent fibres, the smoothness reduces. Therefore, polyethylene content is directly proportional with smoothness of the socks. The highest smoothness values were obtained with cotton followed by polypropylene, polyester, modal and viscose. These results are almost in opposite of softness.
The regression equations for smoothness of socks are given in Table 21.
The regression equations shown in Table 21 can be used directly for the prediction of relative hand value (smoothness) of sock knitted fabrics.
Optimized response solution
The response surface optimizer has been used to define predictor levels with optimized response. The parameters used for the optimization are shown in Table 22.
The weight (importance) of the parameters were judged as per usage of the socks. In regard of sportswear for summer usage, thermal conductivity needs to be of highest importance followed by softness, air permeability, OMMC and smoothness values. These are objective evaluation and can be varied; therefore, different optimized solutions can be prepared using the above developed equations (Eq. 3–Eq. 27). The optimized factor levels are given in Table 23.
In present study, goal is to remain all of the response variables as maximum for a better thermo-physiological and tactile comfort. Limit values exhibit the available minimum and maximum values for process and response variables of present study. The weight explains the desirability of response results. Higher the weight, higher will be the importance to get maximum/target result of particular factor. Results of numerical optimization process were given in Table 23 with optimum blend ratio and material type. In this case, the predicted optimum combination variables were blend ratio of PE:Co of 58:42. Table 24 shows the obtained response levels of thermal conductivity, air permeability, moisture management, smoothness and softness values for individual desirability value.
Table 24 comprised of multiple response prediction of all the output variables, by showing confidence level (CI) and predication level (PI). Predicted response can also be validated via response optimization plot shown in Fig. 8. The predicted responses communicate that, according to the fitted models socks produced using the PE and Co with blend ratio 58:42 will exhibit the mean thermal conductivity of 0.05987 W/mK, mean air permeability of 387 mm/s, mean OMMC of 0.43, mean softness value of 87 and smoothness of 64. All these comfort values fall within the acceptable boundaries.
Validation
Table 25 shows actual and optimum predicted values of thermal conductivity, air permeability, OMMC, softness and smoothness for sock sample. It is evident that the mean error % is less than 5% for results.
Conclusions
This paper presented a quantitative study of thermo-physiological and tactile comfort properties of sock knitted fabric. The socks were manufactured with blend of Polyethylene with cotton, modal, viscose, polypropylene and polyester fibres in different blend ratios for summer application. It is concluded that the material type and blend ratio significantly affect the thermos-physiological and tactile comfort properties of socks. The results have concluded that blend ratio of constituent fibres were directly proportional to air permeability, moisture management properties and softness attributes while indirectly proportional to thermal conductivity and smoothness characteristics of socks. Therefore, with an increase of polyethylene content in fabric enhances the thermal conductivity and smoothness characteristics of fabric structure. Whereas, influence of modal has been found proportional to thermal conductivity; while, air permeability and moisture management properties were compromised with the addition of modal fibre. Cotton has been found as a good substitute to be a constituent part with polypropylene having good properties of air permeability, moisture management and smoothness. Optimization of best model is done by using response optimization tool. It was concluded that the fabric PE/Co 58:42 blend ratio was more suitable to be used as summer socks because of its optimized thermo-physiological and sensorial comfort properties. This will help to produce socks, which may provide better thermo-physiological properties associated with breathability and tactile comfort.
Data availability
Data is provided within the manuscript.
References
Čiukas, R., Abramavičiute, J. & Kerpauskas, P. Investigation of the thermal properties of socks knitted from yarns with peculiar properties. Part II: Thermal resistance of socks knitted from natural and stretch yarns. Fibre Text. East. Eur. 19, 64–68 (2011).
Fan, J. & Hunter, L. Engineering Apparel Fabrics and Garments 49–78 (Woodhead Publishing, 2009).
Arumugam, V., Militky, J. & Tunak, M. In-plane shear behavior of 3D spacer knitted fabrics. J. Ind. Text. 46, 868–886 (2016).
Čiukas, R., Abramavičiūtė, J. & Kerpauskas, P. Investigation of the thermal properties of socks knitted from yarns with peculiar properties. Part I. Thermal conductivity coefficient of socks knitted from natural and synthetic textured yarns. Fibre Text. East. Eur. 18, 89–93 (2010).
Shaker, K. et al. Effect of fabric structural design on the thermal properties of woven fabrics. Therm. Sci. 23, 3059–3066 (2019).
Nazir, A. et al. Prediction and correlation of air permeability and light transmission properties of woven cotton fabrics. Autex Res. J. 17, 61–66 (2017).
Afzal, A. et al. Influence of fabric parameters on thermal comfort performance of double layer knitted interlock fabrics. Autex Res. J. 17, 61–66 (2017).
Afzal, A. et al. Characterization and statistical modeling of thermal resistance of cottom/polyester blended double layer interlock knitted fabrics. Therm. Sci. 21(6A), 2393–2403 (2017).
Ahmad, S. et al. Effect of weave structure on thermo-physiological properties of cotton fabrics. Autex Res. J. 15, 30–34 (2015).
Nazir, A., Hussain, T., Zia, Q. & Afzal Muhammad, A. Improving thermo-physiological comfort of polyester/cotton knits by caustic and cellulases treatments. Autex Res. J. 14, 200–204 (2014).
Afzal, A. et al. Investigation and modeling of air permeability of cotton/polyester blended double layer interlock knitted fabrics. Fibers Polym. 15, 1539–1547 (2014).
Afzal, A., Hussain, T., Mohsin, M., Rasheed, A. & Ahmad, S. Statistical models for predicting the thermal resistance of polyester/cotton blended interlock knitted fabrics. Int. J. Therm. Sci. 85, 40–46 (2014).
Afzal, A., Hussain, T., Malik, M. H. & Javed, Z. Statistical model for predicting the air permeability of polyester/cotton-blended interlock knitted fabrics. J. Text. I I05, 214–222 (2014).
Özdil, N., Marmaralı, A. & Kretzschmar, S. D. Effect of yarn properties on thermal comfort of knitted fabrics. Int. J. Therm. Sci. 46, 1318–1322 (2007).
Majumdar, A., Mukhopadhyay, S. & Yadav, R. Thermal properties of knitted fabrics made from cotton and regenerated bamboo cellulosic fibres. Int. J. Therm. Sci. 49, 2042–2048 (2010).
Behera, B. K. & Mishra, R. Artificial neural network-based prediction of aesthetic and functional properties of worsted suiting fabrics. Int. J. Cloth. Sci. Technol. 19, 259–276 (2007).
Cimilli, S., Nergis, B. U., Candan, C. & Özdemir, M. A comparative study of some comfort-related properties of socks of different fiber types. Text. Res. J. 80, 948–957 (2010).
Tasron, D., Nasir, S., Troynikov, O., Lewis, R. & Carré, M. Thermo-physiological comfort and frictional characteristics of running socks in different moisture conditions. In Conference paper, IAT Malaysia, pp 778–783 (2016)
Bertaux, E. et al. Textile, physiological, and sensorial parameters in sock comfort. Text. Res. J. 80, 1803–1810 (2010).
Park, J., Yoo, H.-S., Hong, K. H. & Kim, E. Knitted fabric properties influencing coolness to the touch and the relationship between subjective and objective coolness measurements. Text. Res. J. 88, 1931–1942 (2018).
Pan, N. & Gibson, P. Thermal and Moisture Transport in Fibrous Materials 124–145 (Woodhead Publishing, 2006).
Das, A. & Alagirusamy, R. Thermal transmission. In Science in Clothing Comfort (eds Das, A. & Alagirusamy, R.) 79–105 (Woodhead Publishing, 2010).
Hes, L., De Araujo, M. & Djulay, V. V. Effect of mutual bonding of textile layers on thermal insulation and thermal contact properties of fabric assemblies. Text. Res. J. 66, 245–250 (1996).
de Rezende, C. A., Schuchardt, U. F. & Gonçalves, Md. C. Use of nylon 6/polyethylene blends in the preparation of textile yarns. J. Appl. Polym. Sci. 102, 2142–2148 (2006).
Hearle, J. W. S. & Morton, W. E. Physical Properties of Textile Fibres 4th edn, 78–127 (Woodhead Publishing, 2008).
Yamanaka, A. & Takao, T. Thermal conductivity of high-strength polyethylene fiber and applications for cryogenic use. ISRN Mater. Sci. 2011, 718761 (2011).
Henry, A. & Chen, G. High thermal conductivity of single polyethylene chains using molecular dynamics simulations. Phy. Review Lett. 101, 235502 (2008).
Shen, S., Henry, A., Tong, J., Zheng, R. & Chen, G. Polyethylene nanofibres with very high thermal conductivities. Nat. Nanotechnol. 5, 251–255 (2010).
Hardy, J. D. & Dubois, E. F. Regulation of heat loss from the human body. Proc. Natl. Acad. Sci. U.S.A. 23, 624–631 (1937).
Winslow, C.-E., Gagge, A. & Herrington, L. The influence of air movement upon heat losses from the clothed human body. Am. Physiol. Soc. J. 127, 505–518 (1939).
Hsu, P.-C. et al. A dual-mode textile for human body radiative heating and cooling. Sci. Adv. 3, e1700895 (2017).
Ball, P. Could polythene clothes be cool?. Nat. Mater. 14, 865–865 (2015).
Alberghini, M. et al. Sustainable polyethylene fabrics with engineered moisture transport for passive cooling. Nat. Sustain. 4, 715–724 (2021).
Bhaduri, S. N. Blending. In Technical Seminar on Blending, (Textile Association, New Delhi, India, 1965), pp. 35–41.
Achour, S., Khelifi, E., Ayed, L., Helal, A. N. & Bakhrouf, A. Response surface methodology for textile wastewater decolourization and biodegradation by a novel mixed bacterial consortium developed via mixture design. Desalin. Water Trea. 52, 1539–1549 (2014).
Kandar, M. I. M. & Akil, H. M. Application of design of experiment (DoE) for parameters optimization in compression moulding for flax reinforced biocomposites. Proc. Chem. 19, 433–440 (2016).
Behera, B. K. & Pattanayak, A. K. Prediction of fabric drape behaviour using finite element method. J. Text. Eng. 54, 103–110 (2008).
Rengasamy, R. S., Das, B. R. & Patil, Y. B. Thermo-physiological comfort characteristics of polyester air-jet-textured and cotton-yarn fabrics. J. Text. I 100, 507–511 (2009).
Onofrei, E., Rocha, A. M. & Catarino, A. The influence of knitted fabrics’ structure on the thermal and moisture management properties. J. Eng. Fiber Fab. 6, 10–22 (2011).
Xiong, X., Yang, T. & Mishra, R. Transport properties of aerogel-based nanofibrous nonwoven fabrics. Fibers Polym. 17, 1709–1714 (2016).
Gun, A. D. & Bodur, A. Thermo-physiological comfort properties of double-face knitted fabrics made from different types of polyester yarns and cotton yarn. J. Text. I I08, 1518–1527 (2017).
Gun, A. Dimensional, physical and thermal properties of plain knitted fabrics made from 50/50 blend of modal viscose fiber in microfiber form with cotton fiber. Fibers Polym. 12, 1083–1090 (2011).
Yang, T., Xiong, X., Venkataraman, M. & Novák, J. Investigation on sound absorption properties of aerogel/polymer nonwovens. J. Text. I I10, 196–201 (2019).
Kaynak, H. K. & Babaarslan, O. Effects of filament linear density on the comfort related properties of polyester knitted fabrics. Fibres Text. East. Eur. 24, 89–94 (2016).
Bhattacharya, S. & Ajmeri, J. Factors affecting air permeability of viscose & excel single jersey fabric. Int. J. Sci. Eng. Res. 5, 48–54 (2013).
Hassan, T., Jamshaid, H., Khan, M. Q., Petru, M. & Tichy, M. Factors affecting acoustic properties of natural-fiber-based materials and composites: A review. Textiles 1, 55–85 (2021).
Čiukas, R. & Abramavičiūtė, J. Investigation of the air permeability of socks knitted from yarns with peculiar properties. Fibres Text. East. Eur. 18, 84–88 (2010).
Maity, S. Characteristics and effects of fibre crimp in nonwoven structure. J. Text. Assoc. India. 76, 360–366 (2014).
Hu, J., Li, Y., Yeung, K.-W., Wong, A. S. W. & Xu, W. Moisture management tester: A method to characterize fabric liquid moisture management properties. Text. Res. J. 75, 57–62 (2005).
Buhai, C., Blaga, M. & Luminita, V. Comfort properties of functional weft knitted spacer fabrics. J. Text. App. 23, 220–227 (2013).
Choudhary, A. K. & Ramratan,. The influence of yarn and knit structure on moisture management properties of sportswear fabric. J. Inst. Eng. (India) Series E. 101, 77–90 (2020).
Venkataraman, M., Jasikova, D. & Kotresh, T. M. Thermodynamics of aerogel-treated nonwoven fabrics at subzero temperatures. J. Ind. Text. 45, 387–404 (2015).
Manshahia, M. & Das, A. Moisture management of high active sportswear. Fibers Polym. 15, 1221–1229 (2014).
Yim, K.-Y. & Kan, C.-W. A comparison study of fabric objective measurement (FOM) using KES-FB and PhabrOmeter system on warp knitted fabrics handle-smoothness, stiffness and softness. Int. J. Chem. Mol. Nucl. Mater. Metallur. Eng. 8, 791–794 (2014).
Acknowledgements
The authors are grateful to the Internal grant agency of Faculty of Engineering, Czech University of Life Sciences Prague, grant no.s 2024:31140/1312/3102: “Research of factors affecting ecological processing and use of polymer composite materials based on natural fillers” and 2025:31140/1312/3104: “Research into the production of composite polymer materials with a focus on improving performance”.
Funding
The authors are grateful to the Internal grant agency of Faculty of Engineering, Czech University of Life Sciences Prague, Grant Nos. 2024:31140/1312/3102: “Research of factors affecting ecological processing and use of polymer composite materials based on natural fillers” and 2025:31140/1312/3104: “Research into the production of composite polymer materials with a focus on improving performance”.
Author information
Authors and Affiliations
Contributions
Conceptualization: Ali Afzal, Talha Salman, Hafsa Jamshaid, Rajesh Kumar Mishra and Miroslav Muller; methodology: Ali Afzal, Talha Salman, Hafsa Jamshaid, Rajesh Kumar Mishra and Miroslav Muller; software: Ali Afzal, Talha Salman, Hafsa Jamshaid, Rajesh Kumar Mishra and Miroslav Muller; data analysis: Ali Afzal, Talha Salman, Hafsa Jamshaid, Rajesh Kumar Mishra and Miroslav Muller; writing—original draft preparation: Ali Afzal, Talha Salman, Hafsa Jamshaid, Rajesh Kumar Mishra and Miroslav Muller; resources: Ali Afzal, Talha Salman, Hafsa Jamshaid, Rajesh Kumar Mishra and Miroslav Muller; supervision: Ali Afzal, Hafsa Jamshaid, Rajesh Kumar Mishra and Miroslav Muller. All authors agreed to the submitted version of the article.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Afzal, A., Salman, T., Jamshaid, H. et al. Statistical modelling and optimization of thermophysiological and tactile comfort properties of sports socks. Sci Rep 15, 17528 (2025). https://doi.org/10.1038/s41598-025-01000-7
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41598-025-01000-7