Introduction

With the support of national policies and the improvement of ‘een travel, traditional fuel vehicles are gradually replaced by electric vehicles (EV)1. However, the disorderly charging of large-scale EV will produce a large random load, which will lead to the aggravation of load peak-valley difference and poor power quality, and increase the operating pressure of power grid2. The Vehicle-to-grid (V2G) technology, which has been popularized in recent years, aims to make electric vehicles participate in the operation and scheduling of microgrid3. As a small power distribution system, microgrid has a good complementarity with the use of EV, which can play a regulatory role between EV and power grid and effectively reduce the adverse effects caused by EV random access to the grid. So how to optimize the operation of microgrid considering the influence of EV in order to reduce the operation cost of microgrid and the peak-valley difference of load has become an urgent problem to be solved.

At present, many scholars at home and abroad have conducted in-depth research on the influence of electric vehicle access to the network (including the influence on power quality and load fluctuation) and achieved some results. For example, In terms of the influence on power quality, reference4 studied the change of power quality after EV was connected to microgrid from overload and harmonic. Reference5 analyzed through an example that when the charging demand of EV was relatively large or the distribution of charging time is relatively discrete, the harmonic interference caused to the microgrid was more significant. In terms of the influence on load fluctuation, reference6 used the Monte Carlo simulation method (MCSM) to demonstrate that the disorderly charging of EV would bring violent fluctuation to the load of microgrid and bring pressure to the peak regulation of power system. However, most of these documents do not carefully consider the actual travel and charging habits of electric vehicle users. For example, the charging model is not fully combined with the uncertainty of users’ daily driving mileage and home time, which leads to the gap between the model and the reality.

In addition, in the study of interaction between EV and microgrid, the randomness of EV accessing microgrid is a problem that cannot be ignored. In recent years, the operation optimization of microgrid with EV has attracted extensive attention of scholars at home and abroad. Reference7 optimized the operation of EV in microgrid by considering the time-of-use price, and used particle swarm optimization to solve the model, but the demand response characteristics of EV were not fully considered in this study. Reference8 considered EV into microgrid, and realized the organic integration of EV and microgrid. The results showed that this method could realize the economic operation of microgrid, but the objective function in this model was relatively simple. By optimizing the charging time and charging and discharging rules of EV, Reference \* MERGEFORMAT9 suppressed the fluctuation of new energy generation and system load, and realized the reliable and economical operation of microgrid. In Reference10, a complete response behavior model of large-scale EV connected to microgrid was established, and a comprehensive benefit operation optimization method based on economic cost weight was proposed, which could reduce the economic cost of microgrid operation. Reference11 proposed an optimization method of microgrid operation based on multi-objective genetic algorithm, which used high time resolution data processing method to determine the optimization level of the system. Reference12 put forward an operation optimization strategy for microgrid including EV switching station, which balanced the load of the system by adjusting the switching station to work in different charging and discharging States, and enhanced the stability of microgrid operation.

Therefore, in this paper, aiming at the problem of microgrid operation optimization considering the influence of EV, taking 24 h a day as the optimization cycle, firstly, MCSM is used to establish the load model of EV disorderly charging and orderly charging and discharging, and a multi-objective operation optimization method of microgrid considering the influence of EV is proposed, which comprehensively considers the two objective functions of minimum total operating cost and minimum peak-valley difference of load, and takes into account various constraints. Then, the multi-objective is transformed into a single objective by comprehensive evaluation model method, and the model is solved by particle swarm optimization algorithm. Finally, the effectiveness of the proposed model is verified by a practical example. The main contributions of this paper are summarized as follows:

  • Based on MCSM, the load models of disorderly charging and orderly charging and discharging of EV are established, and the effects of two access modes of EV on microgrid load are analyzed.

  • The multiple objective operation optimization (MOOO) model of microgrid considering the influence of EV is established, and many constraints are considered, which can be more in line with the actual operation of microgrid;

  • Based on the proposed MOOO method of microgrid considering the influence of EV, it can effectively reduce the operating cost of microgrid, reduce the peak-valley difference of load, and solve practical problems well, thus ensuring the economic and stable operation of microgrid.

Microgrid structure and EV load mathematical model

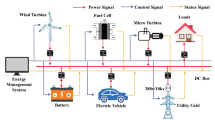
System structure

The basic structure of microgrid system with EV is shown in Fig. 1.

Fig. 1
figure 1

Micro-grid system structure with EV.

Full size image

EV behavior characteristic load model

In order to study the influence of private EV connected to microgrid, the daily driving situation of EV is obtained by probability density function method. According to statistics, it can be considered that the daily mileage of EV is approximately close to the normal distribution13, which can be expressed by the following equation:

$$f(L) = \frac{1}{{L\sigma_{L} \sqrt {2\pi } }}\exp \left( { - \frac{{(\ln L - \mu_{L} )^{2} }}{{2\sigma_{L}^{2} }}} \right)$$
(1)

where: \(\sigma_{L}\) = 3.1, \(\mu_{L}\) = 8.9.

According to the statistics of private EV travel characteristics, the probability density function of the last return time of EV users on the same day approximately satisfies the normal distribution14, assuming that this time is the EV start charging time, its expression is as follows:

$$f(t) = \left\{ \begin{gathered} \frac{1}{{\sigma_{t} \sqrt {2\pi } }}\exp \left( { - \frac{{(t - \mu_{t} )^{2} }}{{2\sigma_{t}^{2} }}} \right),(\mu_{t} - 12) < t \le 24 \hfill \\ \frac{1}{{\sigma_{t} \sqrt {2\pi } }}\exp \left( { - \frac{{(t + 24 - \mu_{t} )^{2} }}{{2\sigma_{t}^{2} }}} \right),0 < t \le (\mu_{t} - 12) \hfill \\ \end{gathered} \right.$$
(2)

where: \(\sigma_{t}\) = 3.5, \(\mu_{t}\) = 17.5.

EV disorderly charging load model

The disorderly charging behavior of EV usually means that the driver charges EV according to his own travel needs and habits without time and space restrictions, and there is no unified plan.

Taking the time when the EV user returned home for the last time on the same day as the starting charging time of EV, and combining with the daily mileage of EV, the continuous charging time of EV can be obtained, and the charging end time of EV can be calculated. The calculation formula is as follows:

$$T_{end}^{ch,i} = \left\{ \begin{gathered} T_{start}^{ch,i} + \frac{{L_{i} W_{100,i} }}{{100P_{ev,i}^{ch} \eta_{ev}^{ch} }},T_{end}^{ch,i} < 24 \hfill \\ T_{start}^{ch,i} + \frac{{L_{i} W_{100,i} }}{{100P_{ev,i}^{ch} \eta_{ev}^{ch} }} - 24,T_{end}^{ch,i} \ge 24 \hfill \\ \end{gathered} \right.$$
(3)

where: \(T_{end}^{ch,i}\) is the charging end time for the ith EV; \(L_{i}\) is the kilometers traveled by the ith EV; \(W_{100,i}\) is the power consumption for the ith EV per 100 km; \(P_{ev,i}^{ch}\) is the charging power for the ith EV; \(\eta_{ev}^{ch}\) is the charging efficiency of EV.

In this paper, the Monte Carlo simulation method (MCSM) is used to simulate each EV charged out of order15, and the load data of each EV can be obtained. By accumulating the load data of EVs in each time period, the load data of all EVs charged out of order in this time period can be obtained, and the calculation equation is as follows:

$$P_{evload} (t) = \sum\limits_{i = 1}^{N} {P_{ev,i}^{ch} (t)}$$
(4)

where: \(P_{evload} (t)\) is the total load of disorderly charging of all EVs at tth time; \(t = 1,2, \cdot \cdot \cdot ,24\); \(i = 1,2, \cdot \cdot \cdot ,N\).

Taking the typical daily load of microgrid in a certain area as an example, the relevant parameters of EV are shown in Table 1. Set the number of EVs connected to the network as 100, 200 and 300, and get the EV disorderly charging load curves of different scales respectively. Then, the load curves of EVs in three cases are superimposed with the initial load curves of microgrid, and the overall load curves of EVs with different scales connected to microgrid can be obtained, as shown in Fig. 2.

Table 1 Relevant parameters of EV.
Full size table
Fig. 2
figure 2

Load curve and overall load curve of EV disorderly charging with different scales.

Full size image

From the simulation results, it can be seen that 17:00 to 20:00 is generally the off-duty time of EV users, and most people will choose to connect EV to the micro-grid during this time to meet their own travel needs the next day, which will produce a cluster effect at the peak of system load, resulting in a sharp increase in EV charging load. With the gradual increase of EV access scale, the disorderly charging load will also increase, which will have a certain load impact on the system. At the same time, it will just overlap with the peak load at night, so that the overall peak load of the system will increase together, and there will be a situation of"peak-to-peak", which will lead to an increasing difference between peak and valley load of microgrid.

EV orderly charge-discharge load model

In order to alleviate the negative impact of disorderly charging of EV on microgrid, it is an effective solution to arrange orderly charging and discharging of EV under the premise of meeting the travel needs of EV users and giving full play to its two-way property of charging and discharging.

In the model of EV orderly charging and discharging, the starting time of night load peak in the system is set as the time \(T_{start}^{dis,i}\) when EV starts to discharge backward to the system, and the specific expression is:

$$T_{start}^{dis,i} = \left\{ \begin{gathered} T_{p} ,T_{b,i} < T_{p} \hfill \\ T_{b,i} ,T_{b,i} \ge T_{p} \hfill \\ \end{gathered} \right.$$
(5)

where: \(T_{p}\) is the starting time of the evening peak; \(T_{b,i}\) is the time when the ith EV returns home on the same day.

The end time of EV reverse discharge to the system is determined by the maximum discharge time of vehicle-mounted battery, so the expressions of the maximum discharge time of vehicle-mounted battery \(T_{\max }^{dis,i}\) and the end time of reverse discharge \(T_{end}^{dis,i}\) are as follows:

$$T_{\max }^{dis,i} = \frac{{E_{ev,i}^{\max } - E_{ev,i}^{\min } }}{{P_{ev,i}^{dis} }} - \frac{{L_{i} W_{100,i} }}{{100P_{ev,i}^{dis} }}$$
(6)

where: \(E_{ev,i}^{\max }\) and \(E_{ev,i}^{\min }\) are respectively the maximum capacity and minimum capacity of the EV vehicle-mounted battery; \(P_{ev,i}^{dis}\) is the discharge power of the ith EV.

$$T_{end}^{dis,i} = \left\{ \begin{gathered} T_{start}^{dis,i} + T_{\max }^{dis,i} ,T_{start}^{dis,i} + T_{\max }^{dis,i} < 24 \hfill \\ 24,T_{start}^{dis,i} + T_{\max }^{dis,i} \ge 24 \hfill \\ \end{gathered} \right.$$
(7)

The power required on the day of EV access to the network includes the power consumed by EV as a travel tool and the power delivered to the system in the opposite direction during the peak load period, so the required charging amount of the ith EV on that day \(W_{ev,i}\) is expressed as:

$$W_{ev,i} = \frac{{L_{i} W_{100,i} }}{100} + (P_{ev,i}^{dis} T_{end}^{dis,i} - P_{ev,i}^{dis} T_{start}^{dis,i} )$$
(8)

It can be obtained that the charging time required for the ith EV \(T_{ch,i}\), which is calculated by Eq. (9):

$$T_{ch,i} = \frac{{W_{ev,i} }}{{p_{ev,i}^{ch} \eta_{ev}^{ch} }}$$
(9)

As with the disorderly charging of EVs, the 24-h cycle is used to accumulate the load data of orderly charging and discharging of all EVs in each time period to obtain the total load of all EVs in this time period \(P_{evload} (t)\):

$$P_{ecload} (t) = \sum\limits_{i = 1}^{N} {P_{ev}^{i} (t)}$$
(10)

where: \(P_{evload} (t)\) is the total load of orderly charging and discharging of all EVs at tth time; \(P_{ev}^{i} (t)\) is the charge and discharge power for the ith EV, where \(P_{ev}^{i} (t)\) > 0 means orderly charging and \(P_{ev}^{i} (t)\) < 0 means orderly discharging.

Similarly, the orderly charge and discharge load curves under different scales and the overall load curve superimposed with the initial load curve of the microgrid are obtained, as shown in Fig. 3.

Fig. 3
figure 3

Load curve and overall load curve of EV disorderly charging and discharging with different scales.

Full size image

From the simulation results, it can be seen that during the late peak hours of load power consumption from 17:00 to 22:00, users arrange EV to be connected to the network, and transmit the remaining power of EV on that day to the system load, which plays the role of“peak cutting”; In addition, in order to ensure the next day’s travel demand, EV will switch to charging mode during the low-load electricity consumption period from 00:00 to 07:00, and the electric energy will flow from the system to EV, playing a role of"filling the valley". With the increasing number of EV access in microgrid, the original peak-valley difference gradually becomes smaller, which greatly relieves the operating pressure of the system.

Multi-objective operation optimization model of microgrid with EV

The operation optimization of EV connected to microgrid is an optimization problem including multiple objectives and multiple constraints. This paper will optimize the operation of microgrid from two aspects: economy and stability. Equation (12) is a mathematical model of multi-objective function16.

$$\left\{ \begin{gathered} \min F = \left\{ {q_{1} ,q_{2} ,...\left. {,q_{n} } \right\}} \right. \hfill \\ s.t.:g_{i} = 0,i = 1,2,...,m \hfill \\ h_{j} \le 0,j = 1,2,...,z \hfill \\ \end{gathered} \right.$$
(11)

where: \(q_{1} ,q_{2} ,...,q_{n}\) is multiple objective functions; \(g_{i}\) and \(h_{j}\) are constraint condition of equality and inequality respectively.

Charging and discharging strategy of EV connected to microgrid

Strategy one: The first trip of EV users is usually arranged at 8:00 in the morning, and the last return trip is usually at 17:00 in the evening. Because of the great uncertainty of users’ travel during the period from 8:00 to 17:00, it is difficult to reach an agreement, so EV access is not considered during this period.

Strategy two: After the last return of EV users on the same day, the microgrid is working at the peak of electricity consumption. Under the premise of meeting their own travel needs the next day, users connect EV to the microgrid to deliver electricity to the system, which plays a role of “peak clipping”, reducing the operating burden of the system and reducing the power purchase of the microgrid.

Strategy three: During the period from 0:00 to 7:00 the next day, the microgrid works in the low power consumption period, and the system can arrange EV to access the grid and use the off-peak electricity price for orderly charging, so as to play the role of “filling the valley” for the system to use during the peak load, and also improve the utilization rate of wind turbine generator (WTG) output at night.

Objective function

In the case that EV is connected to the microgrid for orderly charging and discharging, this paper takes the lowest total operating cost and the minimum peak-valley difference of load as the optimization goal to realize the MOOO of the microgrid, thus improving the economy, safety and stability of the microgrid during its operation.

• objective function \(q_{1}\): the total operating cost \(C_{total}\) is the lowest, that is:

$$\min q_{1} = C_{total} = C_{fd} + C_{wh} + C_{{_{zj} }} + C_{ex} + C_{env} + C_{ev}$$
(12)

where: \(C_{fd}\) is the power generation cost of DGU in the system, yuan; \(C_{wh}\) is the operation and maintenance cost, yuan; \(C_{zj}\) is the operating depreciation cost of energy storage unit (ESU), yuan; \(C_{ex}\) is the cost of power exchange between microgrid and external large power grid, yuan; \(C_{env}\) is the Cost for GTG pollutant emission control, yuan.

The cost of each part is analyzed as follows:

① Power generation cost of each DGU \(C_{fd}\).

Because solar energy and wind energy are renewable energy, its power generation cost \(C_{fd}\) is zero. Therefore, the power generation cost is only the cost generated by the micro gas turbine, and the formula is as follows17:

$$C_{fd} (t) = C_{mt} (t) = \sum\limits_{0}^{t} {\rho F(t)}$$
(13)

where: \(\rho\) is the fuel cost consumed for GTG power generation, yuan/m3; \(F(t)\) is the total fuel consumed for GTG power generation, m3.

The total amount of fuel consumed during GTG power generation \(F(t)\) is expressed by the following formula:

$$F(t) = \frac{{(\tau + 3600)P_{mt} (t)}}{{\xi Q_{f} }}$$
(14)

where: \(\tau\) is the thermoelectric conversion ratio of GTG; \(P_{mt} (t)\) is the contribution to GTG, kW; \(\xi\) is the heat conversion ratio of the fuel; \(Q_{f}\) is the calorific value of the fuel itself, kW/m3.

② Operation and maintenance cost \(C_{wh}\)

$$C_{wh} (t) = C_{wh - pv} (t) + C_{wh - wind} (t) + C_{wh - mt} (t) + C_{wh - bat} (t) = \sum\limits_{j = 1}^{4} {\sum\limits_{t = 1}^{T} {\left( {k_{j} P_{j} (t)\Delta t} \right)} }$$
(15)

where: \(C_{wh - pv} (t)\), \(C_{wh - wind} (t)\), \(C_{wh - mt} (t)\),and \(C_{wh - bat} (t)\) are respectively the operation and maintenance cost of photovoltaic generator (PVG), WTG, GTG and ESU, yuan.; \(j\) is the type of four units., j = 1 is PVG, j = 2 is WTG, j = 3 is GTG, and j = 4 is ESU; \(k_{j}\) is the unit operation and maintenance cost coefficient.; \(P_{j} (t)\) is the output of Class \(j\) unit., kW.

③ ESU operating depreciation cost \(C_{zj}\).

For ESU, frequent actions will accelerate the battery loss, resulting in the decline of the rated capacity of ESU, which will affect the effect of energy storage. Therefore, the operating depreciation cost of ESU must be considered. The calculation formula is as follows18:

$$C_{zj} = \frac{1}{{P_{bat - N} \times T_{bat - \max } }} \times C_{bat} \times \frac{{r(1 + r)^{n} }}{{(1 + r)^{n} - 1}} \times \sum\limits_{t = 1}^{T} {\left| {\left. {P_{bat} (t)} \right|} \right.}$$
(16)

where: \(P_{bat - N}\) is the rated output of ESU, kW; \(T_{bat - \max }\) is the maximum annual operation time of ESU, h; \(C_{bat}\) is the investment cost of ESU, yuan; \(r\) is the annual interest rate; \(n\) is the service life of ESU, year; \(P_{bat} (t)\) is the contribute to ESU, kW.

④ Power exchange cost between microgrid and external power grid \(C_{ex}\)

$$C_{ex} (t) = \sum\limits_{t = 1}^{T} {\left[ {C_{buy} (t) \times P_{ex}^{buy} (t) - C_{sell} (t) \times P_{ex}^{sell} (t)} \right]}$$
(17)

where: \(C_{buy} (t)\), \(P_{ex}^{buy} (t)\) are respectively the price (yuan/kW) and the quantity (kW) of electricity purchased from the grid for the microgrid; \(C_{sell} (t)\), \(P_{ex}^{sell} (t)\) are respectively the price (yuan/kW) and electric quantity (kW) of electricity sold to the grid for the microgrid.

⑤ GTG emission pollutant treatment cost \(C_{env}\).

The waste gas generated during GTG operation will have a negative impact on the environment, so the waste gas discharged during GTG operation must be treated reasonably. The calculation formula of \(C_{env}\) is as follows:

$$C_{env} (t) = \sum\limits_{t = 1}^{n} {d \times \lambda \times P_{mt} (t)}$$
(18)

where: \(d\) is the exhaust emission cost coefficient, yuan/kg; \(\lambda\) is the discharge of waste gas for treatment, kg/kW.

⑥ Subsidies for EV users. \(C_{ev}\).

When EV is involved in the operation of microgrid for orderly discharge, the subsidy fee that driving users can get can be expressed by the following formula:

$$C_{ev} = \left\{ \begin{gathered} \sum\limits_{t = 1}^{T} {R_{bt} (t)\sum\limits_{i = 1}^{N} {P_{ev}^{i} (t);P_{ev}^{i} (t) < 0} } \hfill \\ 0;P_{ev}^{i} (t) \ge 0 \hfill \\ \end{gathered} \right.$$
(19)

where: \(R_{bt} (t)\) is the economic subsidy electricity price when EV discharges to the microgrid, and it is taken as 0.5 yuan/kW h; \(P_{ev}^{i} (t) \ge 0\) means that EV is discharged and \(P_{ev}^{i} (t) \ge 0\) means that EV is charged.

• Objective function \(q_{2}\): EV charging and discharging load, ESU charging load, electricity sales and initial load are superimposed, and the peak-valley difference of the superimposed load curve is the smallest, that is:

$$\min q_{2} = P_{dj - \max } - P_{dj - \min }$$
(20)

where: \(P_{dj - \max }\) and \(P_{{dj - m{\text{in}}}}\) are respectively the maximum and minimum value of \(P_{dj}\), kW, \(P_{dj}\) is the power after the initial load is superimposed with EV charging and discharging load, ESU charging load and electricity sales, and its calculation formula is as follows:

$$P_{dj} = P_{0} + P_{ev} + P_{bat}^{ch} + P_{ex}^{sell}$$
(21)

where: \(P_{0}\) is the initial load of the system, kW; \(P_{ev}\) is the charge and discharge load for EV, kW; \(P_{bat}^{ch}\) is the charging load for ESU, kW; \(P_{ex}^{sell}\) is the electric power sold by microgrid to external power grid, kW.

Constraints

In order to make the microgrid meet the requirements of economy and reliability during operation, a series of constraints that the whole system and various devices in the system must meet are considered.

  • • Power balance constraint

    $$P_{pv} (t) + P_{wind} (t) + P_{mt} (t) + P_{bat}^{dis} (t) + P_{ev}^{dis} (t) + P_{ex}^{buy} (t) = P_{Load} (t) + P_{bat}^{ch} (t) + P_{ev}^{ch} (t) + P_{ex}^{sell} (t)$$
    (22)

where: \(P_{pv} (t)\) is the contribute to PVG, kW; \(P_{wind} (t)\) is the contribute to WTG, kW; \(P_{mt} (t)\) is the contribute to GTG, kW; \(P_{bat}^{ch} (t)\) and \(P_{bat}^{dis} (t)\) are respectively the charging power and discharging power for ESU, kW; \(P_{ev}^{ch} (t)\) and \(P_{ev}^{dis} (t)\) are respectively the charging power and discharging power for EV, kW; \(P_{ex}^{buy} (t)\) and \(P_{ex}^{sell} (t)\) are respectively the purchase power, sales power, kW; \(P_{Load} (t)\) is the total load of microgrid, kW.

  • • Output constraint of each DGU

    $$\left\{ {\begin{array}{*{20}c} {P_{pv - \min } \le P_{pv} (t) \le P_{pv - \max } } \\ {P_{wind - \min } \le P_{wind} (t) \le P_{wind - \max } } \\ {P_{mt - \min } \le P_{mt} (t) \le P_{mt - \max } } \\ \end{array} } \right.$$
    (23)

    where: \(P_{pv - \max }\) and \(P_{pv - \min }\) are respectively the maximum and minimum value of PVG output, kW; \(P_{wind - \max }\) and \(P_{wind - \min }\) are respectively the the maximum and minimum output for WTG, kW; \(P_{mt - \max }\) and \(P_{mt - \min }\) are respectively the maximum and minimum output for GTG, kW.

  • • ESU charging and discharging constraints

  • $$\left\{ {\begin{array}{*{20}c} {P_{bat - \min }^{ch} \le P_{bat}^{ch} (t) \le P_{bat - \max }^{ch} } \\ \begin{gathered} P_{bat - \min }^{dis} \le P_{bat}^{dis} (t) \le P_{bat - \max }^{dis} \\ SOC_{bat} (t) = (1 - \gamma )SOC_{0} + \sum\nolimits_{t = 1}^{T} {P_{bat} (t)\Delta t} \\ \end{gathered} \\ {SOC_{bat - \min } \le SOC_{bat} (t) \le {\text{S}}OC_{bat - \max } } \\ \end{array} } \right.$$
    (24)

    where: \(P_{bat - \max }^{ch}\) and \(P_{bat - \min }^{ch}\) are respectively the maximum and minimum charging power of ESU, kW; \(P_{bat - \max }^{dis}\) and \(P_{bat - \min }^{dis}\) are respectively the maximum and minimum discharge power of ESU, kW; \(\gamma\) is the self-discharge rate of electric energy storage; \(SOC_{{0}}\) is the initial value of SOC; \(SOC_{bat - \max }\) and \(SOC_{bat - \min }\) are respectively the maximum and minimum value of the state of charge of ESU, kW h.

  • • EV charging and discharging constraints

  • $$\left\{ \begin{gathered} \hfill 0 \le P_{ev}^{ch} (t) \le P_{ev - \max }^{ch} (t);00:00 \le t \le 07:00 \\ \hfill 0;08:00 \le t \le 17:00 \\ \hfill 0 \le P_{ev}^{dis} (t) \le P_{ev - \max }^{dis} (t);18:00 \le t \le 23:00 \\ \hfill SOC_{ev - \min } \le SOC_{ev} (t) \le SOC_{ev - \max } \\ \end{gathered} \right.$$
    (25)

    where: \(P_{ev - \max }^{ch}\) is the maximum charging power of EV, kW; \(P_{ev - \max }^{dis}\) is the maximum discharge power of EV, kW; \({\text{SOC}}_{ev - \max }\) and \({\text{SOC}}_{ev - \min }\) respectively represent the maximum state of charge and the minimum state of charge of the vehicle-mounted battery., kVA.

  • • Power exchange constraints between microgrid and external power grid

    $$\left\{ {\begin{array}{*{20}c} {0 \le P_{ex}^{buy} (t) \le P_{ex - \max }^{buy} } \\ {0 \le P_{ex}^{sell} (t) \le P_{ex - \max }^{sell} } \\ \end{array} } \right.$$
    (26)

    where: \(P_{ex - \max }^{buy}\) is the maximum power for purchasing electricity from external power grid, kW; \(P_{ex - \max }^{sell}\) is the maximum power for selling electricity to external power grid, kW.

Comprehensive evaluation mathematical model

In this paper, the most extensive linear weighted comprehensive evaluation model is adopted, so the multi-objective optimization problem can be simplified to a single-objective optimization problem for unified planning19:

$$\left\{ {\begin{array}{*{20}c} {\min F = \theta_{1} \left( {\frac{{q_{1} }}{{q_{1,\max } }}} \right) + \theta_{2} \left( {\frac{{q_{2} }}{{q_{2,\max } }}} \right)} \\ {\theta_{1} + \theta_{2} = 1,\theta_{1} \ge 0,\theta_{2} \ge 0} \\ \end{array} } \right.$$
(27)

where: \(q_{1,\max }\) is the maximum value of the total operation and maintenance cost; \(q_{2,\max }\) is the maximum value of the load peak-valley difference; \(\theta_{1}\), \(\theta_{2}\) are the weight coefficients of \(q_{1}\) and \(q_{2}\) respectively.

Model solving method

In this paper, PSO algorithm is used to solve the model. PSO is initialized as a group of random particles, and then the optimal solution is found through iteration. In each iteration, the particle updates itself by tracking two extreme values; The first one is the optimal solution found by the particle itself, which is called individual extremum; The other is the optimal solution found by the whole population at present, that is, the global extremum. Assuming that the total number of particles is N, when these two optimal values are found, the formulas for updating the velocity and position of the nth particle in the s dimension in the \((t + 1)\) iteration are shown in Eq. (28) and Eq. (29) respectively20.

$$v_{n,s} (t + 1) = \omega v_{n,s} (t) + c_{1} r_{1} (P_{n,s} (t) - x_{n,s} (t)) + c_{2} r_{2} (P_{g,s} (t) - x_{n,s} (t))$$
(28)
$$x_{n,s} (t + 1) = x_{n,s} (t) + v_{n,s} (t + 1)$$
(29)

where: \(n = 1,2, \cdots ,N\); \(s = 1,2, \cdots ,d\); \(\omega\) is the inertia weight; \(c_{1}\) and \(c_{2}\) are learning factors; \(r_{1}\) and \(r_{2}\) is a random number in the interval [0,1]; \(P_{n,s} (t)\) and \(P_{g,s} (t)\) are respectively the individual optimal solution and the global optimal solution in the process of tth iteration.

The particle position is updated as shown in Fig. 4.

Fig. 4
figure 4

Update mode of particle position of each generation.

Full size image

In order to solve the problem that PSO is easy to fall into local optimum, this paper uses the linear decreasing inertia weight method to improve the inertia weight, and the improved inertia weight is related to the number of iterations. The calculation formula is as follows:

$$\omega = \omega_{\min } + (\omega_{\max } - \omega_{\min } ) \times \frac{\tau }{T}$$
(30)

where: \(\omega_{\max }\) and \(\omega_{{{\text{min}}}}\) are the maximum and minimum values of \(\omega\) respectively; \(\tau\) is the current iteration number; T is the total number of iterations.

The asymmetric learning factor method is used to improve the learning factor. The calculation equation is as follows:

$$c_{1} = c_{1,\min } + (c_{1,\max } - c_{1,\min } ) \times \frac{\tau }{T}$$
(31)
$$c_{2} = c_{2,\min } + (c_{2,\max } - c_{2,\min } ) \times \frac{\tau }{T}$$
(32)

where: \(c_{1,\max }\) and \(c_{{1,{\text{min}}}}\) are the maximum and minimum values of \(c_{1}\); \(c_{2,\max }\) and \(c_{{2,{\text{min}}}}\) are the maximum and minimum values of \(c_{2}\).

Example analysis

Parameter setting

In this paper, a typical microgrid day in a certain area is taken as an example, and the operation optimization time is set to 24 h a day. The DGU in the system mainly includes PVG, WTG, GTG, ESU and EV, and the number of EVs is set to 100. The electricity price of power interaction between microgrid and external power grid adopts time-of-use electricity price, and the solution method of the model adopts PSO algorithm. In PSO, the values of \(\omega_{\max }\) and \(\omega_{{{\text{min}}}}\) are 1.0 and 0.6, the values of \(c_{1,\max }\) and \(c_{{1,{\text{min}}}}\) are 2.0 and 1.0, the values of \(c_{2,\max }\) and \(c_{{2,{\text{min}}}}\) are 2.0 and 1.0, and the population size is 50, and the maximum number of iterations does not exceed 200.

(1) Select the typical daily load curve of microgrid (namely the initial load mentioned later) as shown in Fig. 5.

Fig. 5
figure 5

Typical daily load curve.

Full size image

The output curves of PVG and WTG in typical days are shown in Fig. 6.

Fig. 6
figure 6

Typical daily load curves of PVG and WTG.

Full size image

(2) The relevant parameters of PVG, WTG, GTG and ESU in microgrid are shown in Table 2 Table 3 Table 4 Table 5 respectively. Among them, the operation and maintenance cost coefficients of PVG and WTG come from reference21, other parameters of WTG come from reference22, and ESU parameters come from reference23.

Table 2 PVG related parameters.
Full size table
Table 3 WTG related parameters.
Full size table
Table 4 GTG related parameters.
Full size table
Table 5 ESU related parameters.
Full size table

(3) See Table 6 for the time-of-use electricity price parameters setting.

Table 6 Time-of-use electricity price parameter setting.
Full size table

(4) See Table 7 for the setting of pollution gas emission control cost coefficient.

Table 7 Pollution gas emission and treatment cost coefficient.
Full size table

Analysis of operation optimization results

The PSO algorithm is used to solve the model established in this paper, and the iterative objective function curve and the output results of each power generation unit can be obtained. In this paper, the following three scenarios are set up(see Table 8), and the following three different scenarios are analyzed respectively.

Table 8 Scenario settings.
Full size table

Iterative results of each scenario

After PSO, the objective function value is effectively reduced, and the iterative curves of each scene are shown in Fig. 7. It can be seen that in each scenario, with the increase of PSO iterations (horizontal axis), the objective function value (vertical axis) shows a downward trend.

Fig. 7
figure 7

Iterative curve of each scenario.

Full size image

Power balance results of each scene

Scenario 1 is only optimized for micro-grid without EV access, and the power balance diagram of the system is drawn in the Fig. 8(a), where“superimposed load”is the total load after the initial load is superimposed with ESU charging load and the electric power sold by the system, that is, the optimized load; Scenario 2 only considers the disorderly charging of EV connected to microgrid, adopts the EV disorderly charging load model, and simulates EV by MCSM method. The power balance result of the system is shown in the Fig. 8(b), where“superimposed load”is the total load after the initial load is superimposed with ESU charging load, EV charging load and electric power sold by the system, that is, the optimized load; Scenario 3 is the case that EV is connected to the microgrid for orderly charging and discharging. The EV orderly charging and discharging load model is adopted and the MCSM method is used for simulation. The power balance results of the system are shown in the Fig. 8(c), where“superimposed load”is the total load after the initial load is superimposed with ESU charging load, EV charging and discharging load and electric power sold by the system, that is, the optimized load.

Fig. 8
figure 8

Power balance diagram of three scenarios.

Full size image

According to the Fig. 8(a), it can be seen that during the operation of microgrid, the system is in a low load period from 00:00 to 07: 00, during which time the microgrid can charge the ESU with surplus electric energy, and also sell electricity to the external power grid to obtain a certain profit, thus reducing the operating cost of the system; In addition, the system is in the peak load period from 18: 00 to 22: 00, and at this time, the system needs to buy some electric energy from the external power grid to meet the load demand, which will cause the operating cost of the microgrid to increase greatly because the electricity purchase price at peak time is much higher than the electricity sale price at valley time. As can be seen from the Fig. 8(b), when the microgrid operates during the late peak load period, a large number of EVs will be connected to the microgrid for disorderly charging during the peak load period, resulting in the problem of"adding peak to peak", which leads to the microgrid being unable to meet the power balance of the system by its own output and needing to purchase a large amount of electric energy from the external power grid, resulting in a great increase in operating cost. According to the Fig. 8(c), it can be seen that the microgrid is in the peak period of power consumption from 18:00 to 22:00. If electricity is directly purchased from the external power grid, the operating cost of the system will be greatly increased, so at this time, EV needs to be connected to the grid to discharge, so as to relieve the operating pressure of the microgrid and reduce the power purchase. In addition, from 00:00 to 07:00, the microgrid is in the low load period. Due to the low power purchase price and the high output of WTG units in the system, EV can be arranged to be connected to the grid in a staggered load peak period to make full use of the electric energy generated by DGU in the system.

Specific cost results of each scenario

See the Table 9 for the cost of each part (unit: yuan) before and after the operation optimization of microgrid.

Table 9 Comparison of various costs before and after optimization of various scenarios.
Full size table

From the Table 9, it can be found that the power generation cost, depreciation cost, pollutant treatment cost and EV user subsidy fee before optimization are all zero, because EV is not connected before optimization, and GTG and ESU are not arranged to contribute. The total cost of Scenario 1, Scenario 2 and Scenario 3 decreased by 12.63%, 3.58% and 16.58% respectively. Comparing scenario 2 with scenario 1, the operating cost is obviously increased, which shows that the operating economy of the system will be worse when EV is connected to microgrid for disorderly charging. Scenario 3 has the lowest operating cost, which shows that the orderly charging and discharging scenario of EV will reduce the operating cost of the system and improve the operating economy.

Load curve results of each scene

Compare the optimized load curve of each scenario with the initial load curve of the system, as shown in Fig. 9.

Fig. 9
figure 9

Comparison of load curves before and after optimization of three scenarios.

Full size image

From the analysis of Fig. 9, it can be seen that the peak-valley difference of load in Scenario 1 before optimization is 980 kW, and the peak-valley difference of load after optimization is effectively reduced to 688 kW, a decrease of 29.8%; The peak-valley difference of the optimized load in Scenario 2 is smaller than that in Scenario 1, which is 818.20 kW, which is reduced by 16.51%. Although it can be effectively optimized, its optimization effect is not as good as that in scenario 1. This shows that the disorderly charging of EV will lead to the deterioration of the system load curve, resulting in the problem of"peak on peak"; The peak-valley difference of Scenario 3 after optimization is 586 kW, which is the largest reduction compared with Scenario 1 and Scenario 2, and the optimization effect is the best, with a reduction of 37.44%, which shows that EV orderly charging and discharging will make the load curve smooth, and verifies the effectiveness of EV orderly charging and discharging model and solution method.

Comparison results of three scenarios

The cost and load of each period before and after the optimization of the three scenarios are shown in the Fig. 10.

Fig. 10
figure 10

Comparison of cost and load of three scenarios.

Full size image

By analyzing Fig. 10(a), it can be found that in Scenario 2, the economic cost of the microgrid will reach the highest after the EV is charged in disorder, while in Scenario 3, the cost of the microgrid will reach the lowest through the orderly charging and discharging of the EV, and the operation optimization effect is the best, which shows that the microgrid can effectively reduce the cost under the orderly charging and discharging mode of EV, thus achieving the purpose of improving the system operation economy; By analyzing Fig. 10(b), it can be found that the orderly charging and discharging behavior after EV access in Scenario 3 can minimize the peak-valley difference of system load of microgrid, achieve the best operation optimization effect, and improve the stability of microgrid operation.

Conclusion

In order to improve the economy and stability of microgrid operation, the charging and discharging behavior of EV is studied, and a multi-objective operation optimization method of microgrid considering the influence of EV is proposed. The main research conclusions are as follows:

  • A large number of EVs connected to the grid for disorderly charging causes the phenomenon of"peak-on-peak"in the microgrid during peak load periods, which increases the operating burden of the system. Conversely, the orderly charging and discharging behavior of EVs plays a role of"peak clipping and valley filling"on the overall load in the microgrid, improving the system’s stable operation capability.

  • A MOOO model of the microgrid was established, which took the minimum total operating cost and the minimum peak-valley load difference as the objective functions. The model considered the influence of EVs and multiple constraints, such as power balance constraints, EV and energy storage unit (ESU) charging/discharging power constraints, making it more consistent with the actual operation of the microgrid.

  • The proposed MOOO method effectively reduced the operating cost and load peak-valley difference of the microgrid. In three scenarios, the microgrid’s operating cost was reduced by 12.63%, 3.58%, and 16.58%, respectively, and the load peak-valley difference was reduced by 29.80%, 16.51%, and 37.44%, respectively. This solved practical problems well and ensured the economic and stable operation of the microgrid.