A hybrid model based on learning automata and cuckoo search for optimizing test item selection in computerized adaptive testing

Abstract

Computerized adaptive testing (CAT) has become one of the most effective methods of providing a customized approach to assessment. Nevertheless, the identification of student ability and the choice of appropriate test items is still a problem. In this paper, a new design of CAT strategy is proposed based on reinforcement learning, machine learning, and multi-objective optimization. A learning automaton is used to feed a neural network with the ability to predict a student’s ability based on their response history. A multi-objective cuckoo search algorithm then decides the test strategy, between content coverage and level compliance. Compared with the traditional CAT methods, our approach gives better ability estimates and selects test items that are most appropriate for each student. The findings of the study show that the efficiency, accuracy and fairness of the tests have improved through experimentation.

Introduction

Computerized adaptive testing (CAT) is a significant issue in educational resource search and educational measurement in the age of information explosion¹. The use of CAT to assess student competency on standardized examinations (like the GMAT and GRE) has grown in popularity because to its ability to adaptively seek for the questions that are most suited to each individual student. CAT is a type of personalized testing that, in contrast to standard testing/assessment systems, adaptively chooses the next question depending on students’ responses to previous questions to successfully shorten the test length^2,3,4. A CAT system typically consists of the following components: a response model that assesses the probability that a student will correctly respond to a question based on the question characteristics and the knowledge level estimate; a question selection method that selects the next most instructive question founded on the response model’s results; and a knowledge degree estimator that assesses a student’s current knowledge degree based on the answers to the prior questions⁵. Although CAT has been widely applied to real-world assessments, most existing question selection methods are static, meaning that they cannot be enhanced over time as more and more students take tests. Recently, many conceptual theories for mastering a data-driven question selection algorithm were put forth by researchers⁶. According to Lan et al.⁷, such adaptive exams require fewer questions to achieve the same measurement accuracy than traditional paper-and-pencil tests. Additionally, shorter exams lighten the stress on the system and benefit the students, who may become bored or frustrated if they have to provide too many answers^8,9.

And nowadays, artificial intelligence (AI) is being used more and more to give students and workers effective and individualized support in e-learning, job searching, and career development. To assist student learners in navigating the vast array of available learning resources and internships, for instance, recommendation systems have been developed^10,11. Because they are regularly used to characterize unique knowledge, skills, talents, interests, and values of students and jobseekers, assessments offer an essential tool for aiding personalization. Organizations now use CAT, a computer-assisted evaluation that assigns questions according on a test-takers or participant’s aptitude. In order to evaluate proficiency with regard to a latent trait dimension, represented by, that is not immediately observable (such as general intelligence, knowledge, skills, abilities, and personality traits), the answers to these questions are employed¹².

Nowadays, the existing CAT systems primarily use pre-selected set of items, which may not be best for all students. The research proposed uses a mixture of reinforcement learning and machine learning techniques for the purpose of estimating the student ability, in addition to a multi-objective optimization model for test items selection. The purpose of this research is to define if a combination of reinforcement learning and machine learning techniques can effectively predict student ability within a CAT system. Also, investigating the possibility of improving the efficiency and effectiveness of test item selection in CAT using multi-objective optimization is the second research question that this study aims to answer. For this purpose, we utilize a novel and innovative method that combines learning automata and artificial neural networks. By looking at their past and getting answers to questions, this combination can figure out a person’s performance level. The test method is chosen using an optimization model based on multi-objective cuckoo search after the user’s level has been predicted. This optimization model simultaneously follows two objectives of content coverage and level matching. In summary, the following is a list of our major contributions:

• Using the artificial neural network and learning automata model together to precisely estimate the subject’s level.

• Determining a test strategy using an optimization model based on multi-objective cuckoo search.

• estimating and evaluating the test subject’s level.

The paper unfolds as follows: In “Related work”, we review the related works. The proposed method in “Proposed method”, followed by experimental results in “Experiments” and conclusions in “Conclusions”.

Related work

The cognitive diagnostic model (CDM) and selection algorithm make up CAT. These two work in alternation until the exam is finished (in accordance with specific stopping conditions), at which point they output the student’s projected skill level and provide visual feedback to her or her teachers in order to promote further learning. By asking as few questions as feasible, the CAT seeks to precisely gauge pupils’ proficiency¹³.

Methods available

The selection algorithm is CAT’s main building block. The majority of methods, including the Kullback-Leibler Information Index (KLI)¹⁴, Maximum Fisher Information (MFI)¹⁵, and their multivariate expansions¹⁶, were initially created specifically for IRT models. Recently, the algorithms MAAT¹⁷ and BOBCAT¹⁸ that demonstrate good performance and flexibility in deep neural network-based¹⁹ have been developed using active learning and bilevel optimization in it learning, respectively. NCAT²⁰ is a reinforcement learning-based technique that picks questions based on attention. By selecting samples from the Boltzmann distribution, NCAT further regulates the question exposure²¹. RAT²² helps the selection algorithm by capturing many characteristics of the student’s aptitude. More data-driven and deep learning-based algorithms have since been developed.

Multi-objective optimization

Reaching Pareto Optimality while simultaneously optimizing many objectives is the goal of multi-objective optimization. Numerous approaches, including genetic algorithms²³, Particle Swarm Optimization²⁴, Firefly Algorithm²⁵, evolutionary algorithms²⁶, multi-objective fuzzy algorithm²⁷ and multi-objective RL algorithms²⁸, can be used to address multi-objective issues. In²⁶ suggested using a multi-objective evolutionary algorithm to optimize test length and accuracy in CAT. In²⁹ applied Scalarized Multi-Objective policy gradient method to maintain mutual independence of objectives. In the second phase, we determine the test strategy using the cuckoo search algorithm’s multi-objective method.

Proposed method

The core challenge in CAT lies in accurately estimating student ability and selecting test items that provide optimal coverage and difficulty level. Thus, the research problem can be divided into two sub-problems (i.e., estimating the individual’s level and determining a strategy for selecting test items based on the predicted level). In this section, a new strategy for solving these problems is presented. The proposed method for determining the test strategy in CAT includes the following main steps:

• Prediction of the individual’s level based on a combination of reinforcement learning and machine learning.

• Determination of a test strategy based on multi-objective optimization search.

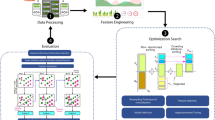
The steps of the proposed method are illustrated in a diagram in Fig. 1. In the first step of the proposed method, utilizes a unique combination of reinforcement learning and machine learning for ability estimation. An ANN estimates performance based on the student’s response history. Additionally, a learning automaton analyzes this history and influences the ANN training by evaluating the accuracy of previous estimates. This ensures the ANN considers the long-term effects of past decisions in its ability estimation. After predicting the user’s level, an optimization model based on multi-objective search is used to determine the test strategy based on the estimated level. This optimization model simultaneously pursues two objectives, “content coverage” and “level compliance,” and determines the test strategy based on this structure. The selected test items are sent to the individual, and the results of the current test step are described in the form of a logical vector. This vector is processed through a feature description model to obtain the necessary features for describing the individual’s history of responding to questions. This set of features constitutes part of the input to the proposed artificial neural network. The mentioned steps are repeated iteratively to achieve a more accurate estimation of the individual’s level and to perform a more comprehensive test based on it.

Fig. 1

Diagram of the stages of the proposed method.

Prediction of individual’s level based on a combination of reinforcement learning and machine learning

The first step of the proposed method for determining the test strategy involves estimating the individual’s level using an artificial neural network. This neural network describes the individual’s level as a numerical variable by analyzing the characteristics of test items and the individual’s history of responding to these items. The structure of the proposed neural network is shown in Fig. 2. According to Fig. 2, the proposed neural network for predicting the individual’s level consists of an input layer, two hidden layers, and an output layer. The input layer is fed through features extracted by the feature description component and actions selected by a learning automaton, which will be explained further. The received features from the input layer are processed by two hidden layers in the neural network. In this structure, the first hidden layer consists of 17 neurons, and the second hidden layer consists of 10 neurons. The activation function for the first hidden layer is chosen as the hyperbolic tangent sigmoid, and the activation function for the second hidden layer is chosen as ReLU. Finally, the individual’s level is determined through the output layer of the neural network, which contains a single neuron representing the output variable as a real number.

Fig. 2

Structure of the proposed neural network for level estimation.

To train the proposed neural network, the Levenberg-Marquardt algorithm has been used. Details of this optimization algorithm are described in³⁰, so we will not delve into the computational steps of this training algorithm. During training ANN, Mean Squared Error (MSE) was defined as the loss function and maximum number of training epochs was considered as 1000. As mentioned, the proposed neural network for estimating the individual’s level is fed through two sets of features: “Response Statistics” and “Learning Automaton Actions.” The set of features related to Response Statistics represents statistical information from the individual’s history of responding to questions in previous sessions, extracted by a feature description component. Conversely, the second set of features is described by a learning automaton model, which will be explained further.

Description of response statistics features

In the proposed method, the first part of the input features for the neural network to estimate individuals’ levels is provided by a feature description component. This component generates a numerical feature vector by analyzing the individual’s response history to questions in previous sessions, which forms part of the required input for the neural network. This component requires two inputs to extract response statistics features (Fig. 1): a logical vector indicating the response status (correct or incorrect) to questions by the individual in recent sessions, denoted as R, and a corresponding real-valued vector representing the score or difficulty level of each posed question in recent sessions, denoted as S. The set R is collected through individual feedback, and the set S is gathered from the database. Based on these two sets, the feature description component generates a feature vector that includes the following characteristics:

• 1. Average Score of Recent Session Questions: This feature is represented as a real number and is calculated by averaging the values in the vector S.

• 2. Average Score of All Questions: Using this feature, the average score of all questions posed from the beginning of the test to the current session is described.

• 3. Recent Session Correct Response Rate: This feature is described as T/|R|, where T represents the number of True values in the vector R, and | | denotes the length of the vector.

• 4. Overall Correct Response Rate from the Beginning: Using this feature, the individual’s correct response rate to all questions posed from the beginning of the test to the current session is described.

• 5. Minimum and Maximum Scores of Recent Session Questions: These two features describe the minimum and maximum values in the vector S, respectively.

• 6. Response Status to Questions with Minimum and Maximum Scores in the Recent Session, described as two logical features.

• 7. Estimated Level from the Previous Session: This feature retains the output of the neural network for the previous assessment session.

• 8. Number of Assessment Sessions: This feature describes the number of times the test has been administered, including level estimation, up to the current moment.

In this way, the feature description component generates a numerical vector with a length of 10 based on the above criteria, which forms part of the input for the neural network for learning the level estimation pattern.

Quality assessment of Estimation by the learning automaton

The second set of input features for the artificial neural network is provided through a reinforcement learning-based model using a learning automaton. The goal of employing this model in the proposed method is to provide a set of features that allow the neural network to correct its estimation error in fewer cycles. A learning automaton model consists of two sets of actions and the corresponding probabilities associated with these actions, denoted as A and P, respectively. In standard learning automaton models, action selection is performed by the automaton, and this action is directly applied to the environment. Furthermore, the prioritization of actions for selection is based on the probability vector P. In this case, after selecting an action, the learning automaton examines the effect of its choice on the environment and adjusts its probability vector (for future corrections) using reward and penalty operators. In the proposed method, the set of actions of the learning automaton is organized based on the estimations made by the artificial neural network. Thus, the set A in the proposed learning automaton model is described as $\:A=\left\{inc,same,dec\right\}.\:$If we denote the estimated level by the artificial neural network for the test-taker in cycle i as $\:{L}_{i}$, then in the action set A, the action “inc” represents the condition $\:{L}_{i}>{L}_{i-1}$, “dec” represents the condition $\:{L}_{i}<{L}_{i-1}$, and “same” represents the condition $\:{L}_{i}={L}_{i-1}.\:$

In other words, the employed learning automaton adjusts its actions based on the outputs of the neural network in the last two cycles to provide inputs corresponding to the quality assessment of its own actions. If the estimated value for the individual’s level in the recent cycle has increased compared to the previous one, the learning automaton assumes that the action applied to the environment is “inc.” Two other actions are interpreted in a similar manner. It’s worth noting that in the initial cycle of the algorithm, the action vector of the learning automaton is defined as $\:P=\left\{\frac{1}{3},\frac{1}{3},\frac{1}{3}\right\}.$

After determining the test scenario in the new cycle and receiving the response vector R from the test-taker, the results of this test are used to assess the quality of the selected action. To do this, the rate of correct responses to questions in the recent cycle compared to the cycle before it is compared, leading to one of the following probable scenarios:

(A) Reward: If the rate of correct responses to questions in the recent cycle has increased compared to the previous one, the recent action selected is rewarded using the following relationship³¹:

$$\:{p}_{j}^{\left(k+1\right)}=\:\left\{\begin{array}{c}{p}_{j}^{\left(k\right)}+\:a\left[1-{p}_{j}^{\left(k\right)}\right]\:\:\:\:\:\:\:\:if\:j\:is\:rewarded\\\:\left(1-a\right){p}_{j}^{\left(k\right)}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:otherwise\end{array}\right.$$

(1)

In the above relationship, $\:{p}_{j}^{\left(k\right)}\:$represents the probability corresponding to the j-th action of the learning automaton in iteration k. Additionally, ‘a’ denotes the reward parameter for the learning automaton.

B) Penalty: If the rate of correct responses to questions in the recent cycle has decreased compared to the previous one, the recent action selected is penalized using the following relationship³¹:

$$\:{p}_{j}^{\left(k+1\right)}=\:\left\{\begin{array}{c}\left(1-b\right){p}_{j}^{\left(k\right)}\:\:\:\:\:\:\:\:\:\:if\:j\:is\:penaltized\\\:\left(\frac{b}{2}\right)+\left(1-b\right){p}_{j}^{\left(k\right)}\:\:\:\:\:\:\:\:\:\:\:\:otherwise\end{array}\right.$$

(2)

In the proposed model, the parameters for reward and punishment are set to a = 0.5 and b = 0.5. It should be noted that if the accuracy rate of responses to questions in the recent period remains unchanged compared to the previous period, none of the aforementioned reward/punishment operators will be applied to the probability vector of the learning automaton.

After applying the reward/punishment operators and updating the probability vector of the learning automaton, the values of vector P will be used as the second set of features on the input layer of the artificial neural network. These probability values can provide a suitable pattern for correctly adjusting the target variable of the level within the artificial neural network.

Determining the multi-objective optimization-based test strategy

After estimating individuals’ levels using the proposed artificial neural network, in the second step of the proposed method, the multi-objective combinatorial search optimization (MOCS) algorithm is utilized to determine the optimal test strategy. It is assumed that the estimated level in the previous step is denoted as L. Therefore, the goal of the second step is to select an optimal subset of test items corresponding to level L in a way that maximizes the coverage of test items. To achieve this goal, initially, from the database of test items, a set of all unselected test items that have scores in the range $\:\left[L-\epsilon,L+\epsilon \right]$ is selected as the candidate set C. Then, the MOCS algorithm is employed to choose an optimal subset from C. In the following, the structure of the solution vector and the objectives of congruence are explained, followed by the steps for determining the optimal test strategy based on MOCS.

In the optimization problem discussed in this section, we consider K = |C| candidate test cases that need to have their selection status determined in the current testing strategy using the MOCS algorithm. The goal is to define an optimal test scenario based on C in a way that not only maximizes the test coverage rate but also selects test cases that have the highest alignment with level L. In this algorithm, after initializing the population randomly and calculating the fitness of each solution in the population, the search operation continues to find the optimal solution until one of the termination conditions is met.

In the proposed algorithm, the length of each solution vector is equal to the number of candidate test cases, K. Each solution vector is represented as a binary array, where the number in each position determines whether a test case is selected or not in the test scenario generated by the solution vector. Figure 3 provides an example of the structure of a solution vector for searching the optimal testing strategy in MOCS.

Fig. 3

An example solution vector for searching the optimal testing strategy in MOCS.

According to Fig. 3, if the number of K candidate test cases is identified at the beginning of this step, then the length of each solution vector will be equal to K. Each position in this vector corresponds to one of the candidate test cases. Also, the search range for all optimization variables is {0,1}. Thus, the MOCS optimization algorithm organizes solution vectors in a binary format. If a position in the vector has a value of zero, then the corresponding test case will not be selected in the scenario generated by the response vector, otherwise, that test case will be selected in the current scenario.

The fitness objectives are the most fundamental part of optimization algorithms. The goal of the fitness function in an optimization algorithm is to determine the optimality of the solution. In the proposed method, we intend to select responses that have the highest coverage rate and compliance with the tester’s level. Therefore, the proposed algorithm uses two objective criteria simultaneously to evaluate the optimality of the response.

• 1. Level compliance.

• 2. Test coverage rate.

Therefore, in the multi-objective algorithm used in the proposed method, each of the criteria, level compliance, and test coverage rate, is considered as optimization objectives. As a result, the proposed method will be capable of determining the optimal state of the test scenario based on these objectives. With these explanations, the optimization objectives in the proposed method are formulated as follows:

1. Level Compliance: The level compliance criterion indicates the alignment of the test content presented in the test with the estimated skill level of the tester. An appropriate test scenario should have the highest possible alignment with the tester’s actual skill level. This objective can be formulated as minimizing the following relationship:

$$\:Level\left(x\right)=\frac{\sum\:_{\forall\:p\in\:x}{|C}_{p}-L|}{\text{m}\text{a}\text{x}\left(C\right)}$$

(3)

In the above formula, the statement $\:\forall\:p\in\:x$ represents the set of test cases selected by response x in the test scenario. Additionally, $\:{C}_{p}\:$denotes the score corresponding to question p, and L indicates the estimated level for the tester, determined through an artificial neural network in the first phase of the proposed method. Finally, $\:\text{max}C\:$represents the maximum score among the test cases.

2. Test Coverage Rate: This objective criterion represents the set of sections of content evaluated by the test scenario. The optimization algorithm’s goal is to maximize the test coverage rate. It’s worth noting that in this criterion, covering sections that have not been evaluated in previous rounds is of significance. Therefore, maximizing the test coverage rate is equivalent to minimizing the following relationship:

$$\:coverage\left(x\right)=\frac{\left|S\right|}{\left|\bigcup\:_{\forall\:p\in\:x}P\:\cap\:S\right|}$$

(4)

In the above formula, P represents the set of content under test, and S indicates the sections for which content has not been previously introduced in previous test scenarios. Thus, the statement $\:\left|\bigcup\:_{\forall\:p\in\:x}P\:\cap\:S\right|\:$in the above formula represents the number of content elements requiring testing in the scenario resulting from response x. In other words, the formula indicates which new sections of content will be tested in the test scenario resulting from response x.

Taking into account the structure of the solution vector and the described fitting objectives, the pseudo-code for the MOCS algorithm to determine the optimal testing strategy in the proposed method will be as follows³²:

Algorithm 1 Multi-objective cuckoo search.

Based on the above pseudo-code, the algorithm starts by generating a random set of solutions for cuckoos’ nests. Then, in each iterative cycle, it randomly selects a cuckoo i and calculates its fitness based on the light intensity. In the next step, it randomly chooses another cuckoo j (another set of solutions) and compares its fitness with cuckoo i. If cuckoo j dominates cuckoo i, then the set of solutions in cuckoo j is considered as the better optimal set of solutions compared to cuckoo i, and the set of solutions in j replaces i.

In the next step of this algorithm, a fraction $\:{P}_{a}$ of the worst-performing cuckoo is abandoned, and new sets of solutions are generated randomly. At the end of each cycle, the best sets of solutions are preserved. These steps are repeated until the number of algorithm iterations reaches the predefined value T. For the implemented MOCS in this research, population size was considered as 150. Also, maximum number of iterations was 300 and $\:{P}_{a}=0.25$. These values were determined experimentally.

Experiments

In this section, we perform a series of tests on the dataset we utilized. The major question we want to answer is if the strategy we suggested can make learning more effective and prediction accuracy can be increased. As shown in Fig. 1, we have two main phases in this article: in phase 1, we predicted the test taker’s level based on the combination of machine learning techniques, and in phase 2, we determined the test strategy based on multi-objective optimization using we have developed the cuckoo search algorithm. The root mean square error (RMSE), mean absolute error (MAE) and concordance correlation coefficient (CCC) parameters are determined using the cross validation method with 10-folds for each iteration in the proposed method. In the following, we focus on examining the results. We compare proposed method with the other algorithms:

Proposed (without LA): outlines a situation in which the inputs of artificial neural networks that employ learning automata are ignored.

NCAT: The neural computerized adaptive testing (NCAT) framework, which explicitly redefines CAT as a reinforcement learning issue and directly trains selection algorithm from real-world data, is a completely adaptive testing method.

BOBCAT: We choose questions using a fully-connected structure (with 2256 hidden layers, Tanh nonlinear behavior, and a softmax output layer) that is independent of the underlying CDM, as per their specifications. It is a recently proposed technique that uses meta-reinforcement learning to enhance CAT by recasting it as a bilevel optimization problem.

MAAT: Using an active learning approach, it calculates the Expected Model Change (EMC) of CDM, which is the change in CDM that each candidate question causes, to determine the level of uncertainty for each student. It doesn’t care about the underlying CDM.

Experimental settings

The research team used EXAM dataset; a pool of student performance records retrieved from a web-based education platform²⁰ which enables students to reach a wide range of learning materials. This platform provides students with assignments, practice tests, and formal assessments. The EXAM dataset, in particular, sets forth the results of the junior high school students on mathematics exercises in web-based environments. It encompasses student responses to question types like multiple-choice questions, open-ended problems, and any other task type provided by the computer system.

Based on Fig. 4 (a, b), lower prediction error is the desired state for this metric, which is confirmed by analyzing RMSE variations and boxplots. The proposed method consistently yields lower squared error and achieves higher accuracy with lower RMSE compared to other scenarios. The results suggest a higher likelihood of correctness in the outputs of the proposed method due to the lower level of prediction error and narrower range of error variations.

Fig. 4

The amount of RMSE in the examiner’s level estimation.

The MAE values for each iteration are shown in Fig. 5a, which shows that the suggested strategy can forecast the target parameter with a lower MAE. Furthermore, as the image illustrates, the suggested approach has a lower range of absolute error changes over several repetitions, which is beneficial for algorithm reliability. The box plot of MAE after ten iterations is shown in Fig. 5b. The upper and lower bounds of the fluctuations in the algorithm’s absolute error over different iterations are represented by the solid lines in each box. The suggested method has a smaller range of absolute error fluctuations and a lower MAE than previous methods. In addition, compared to alternative ways, the suggested method has a greater average accuracy. Higher reliability is indicated by the proposed method’s reduced range of absolute error fluctuations. In conclusion, the recommended approach predicts the target variable more accurately and consistently than the other approaches. Smaller absolute error variability range of the proposed approach increases its reliability.

Fig. 5

The amount of MAE in the examiner’s level estimation.

Figure 6 in this paper plots the projected values for each approach on the vertical axis and contrasts them with the intended variable. The regression points for the suggested technique are centered on the Y = T axis, indicating a better fit with the actual values, and the proposed method has a higher correlation with the target variable with a value of R = 0.8243. Additionally, compared to previous possibilities, the proposed method’s regression line has a slope close to 1 and less displacement. The integration of learning automata and machine learning algorithms, as well as the usage of multi-objective optimization with the cuckoo search algorithm, are what have improved the accuracy of the suggested method. The purpose of each strategy is to reduce the discrepancy between expected and actual results.

The proposed model’s Pearson’s correlation coefficients, standard deviations, and RMSE are all displayed simultaneously on Taylor’s diagram. According to Fig. 7, we can see how closely each method’s detections match the actual data in terms of accuracy. The model predictions and examiner’s level are plotted on a graph along with the Pearson correlation coefficients, standard deviations, and RMSE (Root Mean Square Error). This graph offers a thorough explanation of how accurately each approach predicts the examiner’s level. The stronger correlation seen in the proposed method’s outputs further suggests that the optimization model’s capacity to predict the examiner’s level appropriately is quite great.

Fig. 6

Linear regression chart to estimate the examiner’s level.

Fig. 7

Taylor diagram displaying the effectiveness of the evaluated proposed method.

In Figs. 8 and 9, respectively, the horizontal axis represents test cycles and the vertical axis represents MAE to estimate the examinee’s level, and the vertical value in Fig. 9 represents the coverage level of the questions sent for the test. In fact, we have been able to reach the real level of the test taker in fewer courses and reduce the MAE value, and we can also choose the test items in such a way that the amount of content coverage is higher. That our proposed method performs well in both forms compared to comparative methods. In general, our method required fewer cycles to obtain a more precise estimate of the examiner’s actual level.

Fig. 8

The MAE level of several test cycles.

Fig. 9

The concept coverage rate level of several test cycles.

The more thorough outcomes of this diagram are presented in Table 1, and Fig. 10 presents an example of the optimization mode, which takes into account the ideal response or approach for testing both aspects of the aim. The NCAT, BOBCAT and MAAT methods all have higher RMSE, MAE, and lower CCC values compared to the proposed method, indicating that they have a larger average difference between predicted and actual values and a weaker correlation between predicted and actual values.

Fig. 10

Pareto front of the optimum solution points.

Table 1 Pareto front results from optimum solution points.

Computational complexity and efficiency

The following segment is devoted to the computational complexity of the method proposed and to its efficiency for practical applications of CAT. The proposed method involves two main stages: choice of test strategy and test level estimation.

• Level Estimation: Thus, the ANN is the main determinant of processing speed in this step. The complexity of ANNs is built upon the number of layers, neurons per layer, and the size of the training data. Normally, training time is allied with them. The training process of ANN could be described as O(D×N×E) where D means the number of training data points. N is the number of neurons in the network and E stands for number of epochs of training. The training process complexity poses a major performance challenge for large-scale applications. Therefore, optimization strategies are crucial.

• Test Strategy Selection: The multi-objective cuckoo search optimization model is adopted. However, the exact complexity of such algorithms may vary, but they are normally polynomial in time. In our case, the complexity is around O(P×log(P)) where P represents the number of test items in the pool.

Notwithstanding the leading factor, the overall complexity of the suggested solution is determined by the ANN training time which is O (D×N×E). This implies that the processing time will be affected by the size of the training data or the complexity of the network as it grows accordingly.

The running time of the suggested method goes up with the question size pool and the training data, used by the ANN. For the applications of CAT with limited questions and students where the value of P and D is smaller, processing time might be reasonable. Yet, for the purposeful testing with the great variety of questions, the ANN training period could turn into the obstacle. The ANN training process requires parallel execution together with GPU acceleration to overcome this challenge. The training data can be divided among multiple GPUs through data parallelism while model parallelism enables distribution of the ANN model itself. The implementation of these methods results in substantial decreases of training duration for extensive datasets. Researchers in³³ presented parallel DenseNet architecture that underscores successful parallelization methods in deep learning models which remains important for our forthcoming study. The proposed model can potentially adopt comparable parallelization methods for its implementation. The training processes become faster through the utilization of CUDA and TensorFlow which support GPU processing frameworks.

This proposed method represents a simple and efficient technique for CAT. Although most of the complexity is related to the training of the ANN, it is still applicable for small-scale usage as well. Transfer learning and alternative optimization algorithms are other techniques that should be researched further for large-scale implementations. They are needed to ensure practicable efficiency.

System deployment and user feedback

The successful implementation of our adaptive testing system hinges on a positive user experience for both students and instructors. This section delivers an in-depth examination of the methods through which our system intends to improve user experience.

(A) Integration with learning management systems (LMS):

Users will experience a smooth transition through our system because it integrates with current LMS platforms. Students would find their personalized assessments inside their current learning portals which eliminates the necessity to learn new interface systems.

For example, students taking mathematics exams can reach their LMS and choose the adaptive test function to receive assessments created according to their prior results. The immediate feedback system would display their strengths and weaknesses to help them direct their study activities.

The automated test delivery system along with detailed performance analytics would help instructors make the most out of their assessments. The system would reveal student-specific advancement data together with collective class performance data which instructors would use for modifying their educational approaches.

API standards could be implemented to address potential data exchange compatibility problems between the Learning Management System and Computerized Adaptive Testing platform.

(B) Standalone Adaptive Testing Platform:

A standalone platform provides better customization options to fulfill particular testing requirements. The platform would provide capabilities for student enrollment and test delivery together with detailed assessment results. By using a standalone platform testers would achieve better control of their testing domain while creating personalized user interface designs.

(C) User Feedback and Iterative Improvement:

The development of user-centered design will begin by obtaining feedback from students and instructors. User satisfaction and interface usability together with perceived difficulty will be measured through post-test surveys that collect quantitative and qualitative data. The think-aloud protocol methodology will show how students think while testing so researchers can identify usability challenges and necessary system improvements.

The gathered feedback will guide multiple rounds of system updates to guarantee the system satisfies each user requirement. User feedback regarding confusing question designs will prompt developers to modify their question formats. Recurring assimilation of user feedback will optimize system performance in terms of accessibility and usability and interface transparency therefore developing superior testing encounters.

Practical implications

The proposed CAT strategy has a number of practical benefits. First, it increases the efficiency of the assessment since it cuts down the time taken in testing and at the same time improves the satisfaction of the students. Consequently, if test items are chosen such that they are best suited to a student’s ability, it means that the testing process can be shortened and will be much more enjoyable for students. Second, it increases the efficiency of the assessment since it offers better ability estimates and increases the validity of the measurement. The integration of reinforcement learning and machine learning is effective in providing better ability estimation and the use of proper items for testing and assessment guarantees validity and reliability of the results. Third, the CAT strategy ensures that bias is eliminated and equal opportunities are provided hence fairness and equity. The adaptive characteristic of the test can reduce some of the biases that are associated with the fixed-form test while the nature of the assessment provides every student with a fair chance to showcase his or her potential.

However, the proposed CAT strategy is not restricted to educational contexts only; it can be implemented in other contexts. It can be used in human resources for selection and appraisal of employees, in psychological assessment for measuring intelligence and personality, and in medical assessment for measuring patient’s performance. The flexibility of the assessment approach is useful in various settings, which call for accurate and time-sensitive evaluation.

In conclusion, it can be pointed out that the practical implications of this study are of interest not only for understanding the peculiarities of educational assessment. In this paper, the proposed CAT strategy of enhancing the efficiency, accuracy and fairness of testing is likely to benefit students, educators and practitioners in various disciplines.

Limitations and future works

The research used EXAM dataset for testing the approach under consideration. The CAT method examination of the EXAM system dataset may be a great deal, however using one system does not allow for the generalization of our findings. In order to determine the efficiency of the suggested method, it is of utmost importance to analyze its performance on the different datasets comprising different educational spheres and various skill level of students. The next step for the research should be to evaluate the method’s applicability on a bigger dataset to check its robustness and effectiveness in several educational setups. Specifically, future research will seek to evaluate the model using datasets from higher education contexts, datasets encompassing diverse subject areas such as science and humanities, and multilingual datasets to assess cross cultural applicability.

The current implementation of the proposed approach involves a large data set of the past student responses required to train the neural network accurately. However, despite the fact that this approach shows good results, we understand that it may not be always possible to use such extensive data in the real-world testing process, especially when dealing with small datasets. To address this limitation and improve the generalization capacity of our model, we plan to explore the following future research directions:

• Transfer Learning: Transfer learning techniques will be explored in depth. Such an approach entails pre-training the neural network using a sizeable, multi-purpose dataset associated with educational evaluations. Then, the network can be re-trained using a smaller amount of data that relates to the target domain. Consequently, the proposed method can perform well even in the test environment where only a little data is available thanks to this ability of reducing the necessary data. For example, we will investigate pre-training the ANN on large, publicly available educational datasets and then fine-tuning it on smaller, domain-specific datasets.

• Data Augmentation: We will look at the data augmentation methods that can be used to artificially expand the existing data set. Such strategies might include, for example, producing fabricated data with the same characteristics as the actual student feedback. This may contribute to the feasibility of the model to generalize from scarce data. Specifically, we will explore techniques such as generating synthetic student response data based on statistical properties of the existing dataset, or using techniques to augment existing student response data.

Through the examination of these methods, we hope to improve the soundness and realizability of the suggested procedure, which may then be used where data is not in abundance.

The current implementation of the multi-objective optimization model focuses on two primary objectives: unit test level, coverage and conformance. On the one hand, such an approach supplies a sturdy foundation for adaptive test choice, but on the other hand, there are additional benefits of being more ambitious and of optimizing the selection process on the basis of a broader set of objectives. the fact that the consequences of these possibilities should be studied in future research is emphasized. Here are some potential areas for future investigation:

• Multi-Objective Optimization with Additional Constraints: Our future research will incorporate supplementary constraints which involve test duration, question repetition rate, and individual learning styles to our multi-objective optimization structure. The research will establish mathematical frameworks to limit test duration so tests stay within acceptable time boundaries. The objective function could include a penalty term that increases when a question appears multiple times during assessment. The research will explore methods to incorporate student learning styles (visual, auditory, kinesthetic) into the objective function through question type weight assignments based on preferred learning styles. The model performance will improve for creating customized adaptive tests through these implementation constraints.

• Exploration of Different Optimization Techniques: Whether the complexity is enhanced by the introduction of other goals or not, we should investigate some different optimization algorithms that can not only handle a great number of goals but also can do it with high efficiency.

Therefore, we are determined to do further investigation in order to fine tune the multi-objective optimization approach and develop a more holistic CAT system which uses a wider range of parameters for selection of test questions.

The suggested method so far has concentrated on the core functions of student ability estimation and test item selection. Although the approach gives us a glimpse of what is to come, it still has a great potential to improve the system by introducing context of student performance and interest into the practice. one of the ways to represent the model would be to include contextual information. This could be characterized by, for example, student demographic, preferred learning styles, anxiety of tests and previous performance of the questions. Context-awareness can individualize testing process, ensure an accurate measuring of the abilities, and increase learning outcomes. We consider the value of the further exploration of these considerations in future studies. Here are some potential areas for future investigation:

• Feature Engineering for Contextual Data: One of the approaches that we will discuss is the way to integrate the proper contextual details into the model. This might imply the use of the feature engineering methods to get the significant representation of student demographics, learning styles and previous performance data.

• Integration with External Data Sources: The strategy of integration of the proposed approach with external data sources providing contextual information about students is going to be the next item on our research. For this purpose, the connection with LMS or student information systems (SIS) may be established to acquire relevant data elements.

• Development of Context-Aware Objective Functions: Besides, the multi-objective optimization model will be extended with the incorporation of contextual information. This may entail the creation of objective functions which are constructed by considering the factors like a student’s interest and his learning style when selecting test items.

Through exploring these directions, we strive to enhance the system of CAT thereby building contextual awareness that would make testing personalized and the learning outcomes better for all students.

User experience and real-world validation is another aspect which needs further investigation in future works. Future research will focus on designing and evaluating the system from a user perspective to guarantee its effectiveness and usability for educational environments. Our research includes preparing usability studies with the purpose of learning student and instructor opinions regarding the system’s operability and user experience and interface design aspects. The evaluation process includes think-aloud protocols and post-test surveys and interviews to measure complete user satisfaction and recognize enhancement opportunities. We will perform controlled experiments to assess both student learning results and instructor operational efficiency when using the system. Real classroom experiments will test the outcomes of the proposed adaptive testing system examined against established assessment methods. The experience of users will be evaluated through a mixture of numerical statistics as well as personal opinions and technical indicators which will include measurement points for task completion times and error rates together with usability perception metrics and participant feedback. Study results will guide multiple rounds of system improvement to satisfy each stakeholder group’s requirements. The design and development process will have a feedback loop to sustain user input which makes the adaptive testing system better and user-friendly.

Conclusions

This paper presented a computerized adaptive testing (CAT) system that uses data-driven methods to select questions based on individual student abilities. CAT uses large datasets to learn from patterns and trends, enhancing the assessment process’s precision. The system uses learning automata and artificial neural networks to estimate a person’s level, which is then used in a multi-objective cuckoo search optimization model to determine the test strategy. This proposed method has several advantages over traditional testing methods, including increased efficiency, as well as predicting the examiner’s level. Overall, this paper presents a promising approach to computerized adaptive testing that has the potential to improve the assessment process in various contexts. And the outcomes demonstrate that our proposed strategy has the lowest reduction rates in RMSE and MAE with the corresponding values of 1.5379 and 1.2139, as well as a higher efficiency in the CCC parameter with a value of 0.8229.