An improved RIME optimization algorithm based maximum power point tracking method for photovoltaic system under partially shading condition

Abstract

Maximum power point tracking (MPPT) is a pivotal technology for photovoltaic (PV) systems. Due to variations in light intensity and temperature, the output characteristic curve of the photovoltaic system exhibits multi-peak phenomena, and traditional MPPT algorithms perform poorly in complex and changing environments. Therefore, this paper proposes an MPPT method grounded on an improved RIME optimization algorithm (IRIME). This approach enhances the algorithm’s exploratory capabilities by incorporating logistic mapping during the initialization stage. Furthermore, it optimizes the algorithm’s parameters through sequences generated by piecewise mapping, thereby realizing a harmonious balance between global exploration and local exploitation. Additionally, the introduction of an adaptive inertia weight dynamically adjusts the search strategy, thereby increasing the adaptability, convergence speed, and search efficiency of algorithm. Compared to PSO-MPPT and RIME-MPPT, the proposed method reduced the average tracking time by 0.085 s and 0.425 s, respectively. Additionally, in terms of maximum output power, the proposed method achieved an average improvement of 0.97% and 3.48% over the aforementioned methods, respectively. Particularly in PV system simulations under varying irradiance and temperature conditions, the proposed method consistently achieves the best results, verifying its efficient, stable, and fast-converging characteristics in MPPT strategies for PV systems.

Introduction

As global energy requirements continue to increase¹, the depletion of traditional energy resources, and the exacerbation of environmental issues, renewable energy is becoming a focal point on a global scale². Solar power ranks among the most extensively utilized renewable energy forms, converting sunlight into heat or electricity through the radiation of the sun^3,4. Photovoltaic (PV) power generation is a power generation technology that uses solar energy as its energy source^5,6. Due to zero emissions during operation, PV power generation is a greatly low-carbon and eco-friendly energy source that can remarkably decrease carbon emissions in the electricity production process. However, despite ongoing technological progress, the transformation efficiency of PV power generation continues to be relatively low, which limits its overall efficiency of electricity generation⁷. On account of this, the maximum power point tracking (MPPT) technique is proposed to fully utilize the output of PV cells and maximize their performance^8,9.

Literature review on MPPT methods

MPPT technology in PV systems is a crucial technique for ensuring that PV panels continuously output the maximum electrical energy. MPPT algorithms are mainly classified into two types: traditional algorithms and artificial intelligence algorithms^10,11. Common traditional MPPT algorithms include the perturb and observe (P&O) method, the constant voltage (CV) tracking method and incremental conductance (INC). Traditional MPPT algorithms are simple, reliable and relatively easy to implement, making them dominant in applications where economic considerations are paramount^12,13. Elgendy et al.¹⁴ proposed a P&O method that periodically increases or decreases the voltage during the operation of the PV array to achieve power output variations. The essence of the algorithm involves continuously introducing minor “perturbations” to ascertain whether the peak power point has been reached. Once the system reaches its maximum, it will continue to oscillate around the MPP, thereby engendering instability and resulting in power losses. Salameh et al.¹⁵ proposed the CV tracking method, which achieves MPPT by maintaining the operating voltage at a specific percentage of the open-circuit voltage. The INC method, evolved from the P&O method, has a core improvement in that it adjusts the basis for determining the perturbation direction from “power change” to “conductance change”¹⁶. It should be noted that these traditional methods are unable to cope with rapidly changing weather conditions and are subject to oscillations or false tracking, resulting in poor tracking accuracy.

In fact, the output change of the PV system is a complex process influenced by a combination of factors^17,18. For example, the PV arrays are exposed to their external environment, where their output power is directly influenced by factors such as sunlight intensity, windblown sand and dust, shading from trees, bird droppings. These elements have the potential to obstruct a portion of the PV panels, thereby hindering the output characteristics of the PV cells and resulting in multiple local peak points, which adds complexity to the task of tracking the global maximum power point (GMPP).

Artificial intelligence optimization algorithms have been widely applied in the MPPT field due to their global optimization capabilities^19,20,21.The particle swarm optimization (PSO) algorithm achieves optimization by simulating the feeding mannerism of bird groups, which is widely used in the field of MPPT due to its simplicity and ease of carrying out^22,23,24. The butterfly optimization algorithm (BOA) finds the optimal solution by simulating the flight actions of butterfly populations when searching for a food source, and can find a high-quality solution within a reasonable time^25,26,27. The particle swarm-butterfly optimization algorithm (PSO-BOA) incorporates the advantages of the PSO algorithm while addressing the slow convergence issue in BOA algorithm, achieving better optimization result in MPPT system^28,29. However, these intelligent algorithms may be affected by deviations in the search range, affecting the tracking accuracy of the population. Additionally, due to their relatively slow convergence speed, they may fail to adapt swiftly to rapidly changing environmental conditions, thereby affecting the maximum power output.

In addition, many scholars have optimized the algorithms to achieve more precise maximum power point tracking. Reference³⁰ investigated various metaheuristic optimization-based MPPT methods to address the nonlinear power output problem of proton exchange membrane fuel cell stacks (PEMFS). Simulation results showed that the cuckoo search method with continuous slope values (CDSV with CSM) exhibited the best performance in terms of efficiency and output power. Reference³¹ analyzed the performance of a single-diode solar PV system under different conditions through simulation and compared MPPT strategies based on PSO, genetic algorithm (GA), bat optimization, and grey wolf optimization (GWO). The results indicated that the GWO model achieved the MPPT efficiency of 98%, significantly outperforming other optimization techniques. Reference³² studied MPPT optimization algorithms for solar PV systems under partial shading conditions, and the results showed that the salp swarm optimization algorithm (SSOA) had the highest tracking efficiency, reaching 98.38%. Additionally, this study used a convolutional neural network (CNN) model to classify PV system faults, achieving an accuracy rate of 94.11%. Reference³³examined MPPT algorithms for solar PV systems under partial shading conditions, and the results indicated that the moth flame optimization algorithm (MFOA) had the highest tracking efficiency, reaching 97.39%, and achieved an MPPT power of 749.48 watts and a maximum power of 769.62 watts. Reference³⁴ used Matlab Simulink to simulate the performance of four different MPPT algorithms (GA, PSO, Bat Optimization, and GWO) on a single-diode model solar PV system under varying solar irradiance conditions. The results showed that the MPPT algorithm based on GWO performed the best in terms of both maximum power and MPPT power.

At the end of the literature review section, we added a comparison table to contrast the existing research findings, as shown in Table 1.

Table 1 Literature review on MPPT methods.

Research objective

The rime optimization algorithm (RIME)³⁵, proposed by H Su et al. in 2023, imitates the developmental course of hoarfrost in nature and introduces an innovative step-by-step search and exploitation. The RIME optimization algorithm features certain global exploration capabilities and the ability to escape local optima, enabling it to toggle between extensive exploration and intensive exploitation, thereby ensuring both scope and depth during the search process. Due to its flexibility, accuracy, and high speed, the algorithm performs well in various fields. Ismaeel et al.³⁶ applied the RIME algorithm for calculating the parameter identification of a proton exchange membrane fuel cell. Findings from the experiment manifested a good consistency between the experimental data and the voltage-current curve. He et al.³⁷applied the RIME algorithm to the detection of low voltage AC series arc fault. The optimized model demonstrates excellent efficiency and accuracy, fully reflecting the substantial advantages and robustness of the RIME algorithm.

Motivated by the aforementioned methods, this paper proposes an improved RIME (IRIME) optimization algorithm for MPPT in photovoltaic systems. This algorithm effectively solves the deficiencies of existing MPPT algorithms, realizing global tracking with high accuracy and fast convergence, thus markedly elevating the efficiency of solar power generation. Here are the contributions and innovative elements of this article:

• (1) As a relatively new heuristic optimization algorithm, the RIME algorithm has been widely applied in different fields. So far, there is a significant lack of research exploring the potential application of the RIME into the MPPT of PV system.

• (2) This study proposes an IRIME algorithm based on three optimization tactics to mitigate the inherent deficiencies of the original algorithms. Firstly, the population of the algorithm is initialized using logistic chaos, which alters the original algorithm’s way of generating random numbers with uniform distribution, thereby enhancing the randomness and ergodicity of the initial population. Secondly, the piecewise mapping strategy is employed to achieve optimal adjustment by perturbing the positions of local solutions, which enhances the global search capabilities. Lastly, with the help of inertia weighting idea, a non-linear decrease is applied in the later stages of iteration to balance the overall local exploitation capability during the optimization process.

• (3) The study of IRIME-MPPT provides new solutions for the optimal operation of PV systems. The proposed method swiftly adapts to environmental fluctuations and identifies the MPP in a short time. It exhibits adaptive regulatory attributes, promptly stabilizing its state and significantly mitigating fluctuations in the vicinity of the MPP within PV systems, thereby enhancing the steadiness of the system. Besides, the algorithm possesses strong global and local search capabilities, which can accurately locate the maximum power in complex environments. According to the simulation results, the proposed method demonstrates multiple advantages including stability, rapid convergence, and global search capability, ensuring the efficient operation of the system.

The succeeding parts of the paper are arranged as follows: Sect. "Analysis on output characteristics of PV system" outlines the PV MPPT modeling methodology and the MPPT of PV arrays under various shading conditions; Sect. "Maximum power point tracking based on IRIME" describes the IRIME optimization algorithm used to control the PV system; Sect. "Simulation analysis based on IRME in MPPT control" separately analyzes the simulation results of the IRIME, RIME, and PSO-BOA based MPPT techniques. Finally, the conclusion of this paper is given.

Analysis on output characteristics of PV system

Modeling of PV module

The PV module, as a key component, can directly convert solar energy into electrical energy and is a core part of PV power generation system. Its operational mechanism primarily relies on the absorption of photon energy, which causes electrons in the semiconductor material to transition and charge separation. Ultimately, these charges flow through an external circuit, forming a current, thereby achieving efficient conversion of light energy into electrical energy. In the ideal case, the equivalent model of a PV module can be simplified as a combination of a constant current source and an ideal diode, with its specific structure illustrated in Fig. 1.

Fig. 1

The equivalent circuit for single diode model.

In the diagram above, $\:{I}_{sc}$ represents the photonic excitation current, $\:{I}_{D}$ represents the reverse current of the diode, $\:{R}_{s}$ represents the series resistance, $\:{R}_{sh}$ represents the shunt resistance, $\:{R}_{load}$ represents the external load of the photovoltaic panel. According to Kirchhoff’s Law, $\:{I}_{pv}$ and $\:{U}_{pv}$ are found by Eq. (1) and Eq. (2), respectively represent the photovoltaic output current and output voltage.

$$\:\begin{array}{c}{I}_{pv}={I}_{sc}-{I}_{D}-{I}_{sh}\end{array}$$

(1)

$$\:\begin{array}{c}{U}_{pv}={U}_{D}-{I}_{pv}\times\:{R}_{s}\end{array}$$

(2)

Wherein $\:{I}_{sh}$ is the leakage current in parallel (the current through $\:{R}_{sh}$, flowing from top to bottom), $\:{U}_{D}$ is reverse voltage. The reverse current of the diode $\:{I}_{D}$ represents as Eq. (3):

$$\:\begin{array}{c}{I}_{D}={I}_{0}\times\:\left[exp\left(\frac{{U}_{D}}{{U}_{T}}\right)-1\right]={I}_{0}\times\:\left[exp\left(\frac{q\left({U}_{pv}+{I}_{pv}{R}_{s}\right)}{nkT}\right)-1\right]\end{array}$$

(3)

where $\:{I}_{0}$ represents the reverse saturation current of the diode, $\:{U}_{T}=knT/q$ is thermoelectric potential, $\:q$ is the charge of an electron (1.6 × 10⁻¹⁹ C), $\:n$ is the diode exponent, typically ranging between 1 and 2. $\:K$ is the Boltzmann constant (1.38 × 10^-23 J/K), and $\:T$ is absolute temperature of the PV system. By substituting these values into the original formula (1), Eq. (4) can be obtained as follows:

$$\:\begin{array}{c}{I}_{pv}={I}_{sc}-{I}_{0}\times\:\left[exp\left(\frac{q\left({U}_{pv}+{I}_{pv}{R}_{s}\right)}{nkT}\right)-1\right]-\frac{{U}_{pv}+{I}_{pv}{R}_{s}}{{R}_{sh}}\end{array}$$

(4)

Characteristic curves of photovoltaic arrays under different conditions

PV arrays are susceptible to external light, temperature, and other environmental factors, exhibiting nonlinear output characteristics. Figure 2 illustrates the I-V and P-V characteristic curves of PV arrays under the conditions of different irradiance and temperature. It is evident that as the temperature rises, the open-circuit voltage gradually decreases. Moreover, the change in open-circuit voltage with increasing irradiance is minor, while the short-circuit current increases significantly. Hence, the overall maximum power output typically decreases with rising temperature and increases with increasing irradiance. Given the significant impact of temperature and irradiance changes caused by external environments, it is essential to fully consider these two conditions when analyzing and using PV arrays.

Fig. 2

I-V and P-V curves of the PV module.

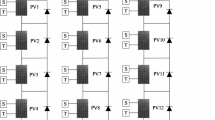
In the actual operation process, PV arrays inevitably experience partial shading due to the external environment, which leads to lower output voltage and current from the shaded PV modules. Meanwhile, the potential at the two ends of the output ports decreases, causing them to act as loads in the entire circuit. Prolonged operation under such conditions can cause a large amount of heat to accumulate on the shaded PV modules, which can lead to the destruction of PV components. To prevent this issue, many scholars recommend the solution of using parallel diodes. When a PV module is shaded, the current bypasses through the diode, thereby protecting the PV module from damage. Additionally, each PV module should be connected in series to enhance the voltage output. Multiple series-connected modules form strings, which should then be connected in parallel to increase the total current output of the system. By adopting this method, not only is the PV array effectively protected, but the overall system efficiency is also significantly improved, leading to increased power output.

Under uniform illumination conditions (UIC), as shown in Fig. 4(a), the photovoltaic array operates under standard conditions, with the ambient temperature set at 25 °C and the illumination intensity maintained at 1,000 lx. In this standard condition, the output characteristics of the photovoltaic system exhibit a unimodal feature, showing only one maximum power point (MPP), P1, which is clearly presented in case 1 of Fig.5.

Fig. 3

A schematic diagram of a photovoltaic array structure with five series modules.

Fig. 4

Photovoltaic array output P-V characteristic curve.

During the actual operation of the system, due to the differences in irradiance experienced by each PV module, the output P-V characteristic curves exhibit multiple peaks features. Under partial shading conditions (PSC), as illustrated in Fig. 3 (b), where the first and second photovoltaic panels are subjected to uniform illumination, while the remaining three panels are shaded to varying degrees, the specific operating conditions are shown in Table 2. In case 2 of Fig. 4, it can be clearly observed that P3 is the GMPP, whereas P2 and P4 are local maximum power points (LMPP). For such P-V characteristics, traditional MPPT methods are unable to effectively distinguish between P3 and P4, and are prone to getting stuck at the local maximum P4, leading to power loss. Moreover, the global tracking performance of traditional methods may further deteriorate with an increase in the number of LMPPs. Therefore, the development of an effective and efficient global maximum power point tracking (GMPPT) technology is particularly necessary.

Table 2 Different operating conditions of PV panels.

Maximum power point tracking based on IRIME

The RIME optimization algorithm, as an advanced optimization tool, integrates the characteristics of traditional and intelligent algorithms. With its excellent global search capabilities and adaptive adjustment mechanisms, it is capable of achieving high precision and rapid response objectives.

RIME optimization algorithm

The formation of frost ice under different conditions can be classed as two categories: soft frost and hard frost. The RIME draws inspiration from the growth mechanism to achieve exploration and exploitation capabilities in the optimization algorithm. The growth process of rime ice is constrained by environmental factors such as airflow and wind speed. Once the stable conditions are reached, the growth will cease. As shown in Fig. 5, soft rime forms in a light breeze environment, where low wind speed and frequent changes in wind direction result in slow growth and a random structure. In contrast, in a windy environment, due to high wind velocity and consistent wind direction within the same planar area, hard rime formed, distinguished by rapid formation and a growth direction that remains roughly consistent.

Fig. 5

The formation processes of soft rime and hard rime across various circumstances.

Combining all mechanisms, the RIME is divided into four stages: rime cluster initialization, soft rime search strategy (SRS), hard rime puncture mechanism (HRP), and positive greedy selection mechanism.

RIME cluster initialization

In RIME³⁵, the initial positions of particles are set to be randomly generated. The entire “rime-population” (denoted as $\:R$) consists of multiple “rime-agents” (denoted as $\:{S}_{m}$), where $\:m$ represents the sequential number of the rime agent, indicating the m-th agent. Each “rime-agent” $\:{S}_{m}$ is composed of multiple “rime-particles” (denoted as $\:{x}_{mn}$), where $\:n$ represents the sequential number of the rime particle, indicating the n-th particle. Firstly, the entire population of frost $\:R$ is initialized, specifically expressed as shown in Eq. (5):

$$\:\begin{array}{c}R=\left[\begin{array}{c}\begin{array}{ccc}{x}_{11}&\:{x}_{12}&\:\begin{array}{cc}\dots\:&\:{x}_{1n}\end{array}\end{array}\\\:\begin{array}{cc}{x}_{21}&\:\begin{array}{ccc}{x}_{22}&\:\dots\:&\:{x}_{2n}\end{array}\end{array}\\\:\begin{array}{ccc}\begin{array}{c}\vdots\\\:{x}_{m1}\end{array}&\:\begin{array}{c}\vdots\\\:{x}_{i2}\end{array}&\:\begin{array}{cc}\begin{array}{c}\ddots\:\\\:\dots\:\end{array}&\:\begin{array}{c}\vdots\\\:{x}_{mn}\end{array}\end{array}\end{array}\end{array}\right]\end{array}$$

(5)

Each row of the matrix represents a “rime-agent”, and each column represents a “rime-particle.”

$\:F\left({S}_{m}\right)$ serves to signify the growing status of each “rime-agent” $\:{S}_{m}$, which corresponds to the fitness value in the meta-heuristic algorithm. This fitness value $\:F\left({S}_{m}\right)$ is used to evaluate the performance of each agent, which is shown in the following Eq. (6):

$$\:\begin{array}{c}F\left({S}_{m}\right)=\left[\begin{array}{c}f\left(\left[\begin{array}{ccc}{x}_{11}&\:{x}_{12}&\:\begin{array}{cc}\dots\:&\:{x}_{1n}\end{array}\end{array}\right]\right)\\\:f\left(\left[\begin{array}{ccc}{x}_{21}&\:{x}_{22}&\:\begin{array}{cc}\dots\:&\:{x}_{2n}\end{array}\end{array}\right]\right)\\\:\begin{array}{c}\begin{array}{ccc}\vdots&\:\vdots&\:\begin{array}{cc}\ddots\:&\:\vdots\end{array}\end{array}\\\:f\left(\left[\begin{array}{ccc}{x}_{m1}&\:{x}_{m2}&\:\begin{array}{cc}\dots\:&\:{x}_{mn}\end{array}\end{array}\right]\right)\end{array}\end{array}\right]\end{array}$$

(6)

Soft-rime search strategy

The soft frost search strategy is achieved by utilizing the high degree of randomicity and spreadability of frost particles in a slight breeze environment, ensuring that they can promptly traverse the entire search area in the initial iterations and are less likely to fall into local optima. Calculating $\:\theta\:$ through Eq. (7) influences the movement direction of the particles.

$$\:\begin{array}{c}\theta\:=\pi\:\cdot\:\frac{t}{10\cdot\:T}\end{array}$$

(7)

where $\:t$ represents the present iteration count, and $\:T$ denotes the maximal number of iterations for the algorithm. $\:\beta\:$ is the environmental factor, which emulates the impact of exterior circumstances and ensures the convergence of the algorithm, as specified in Eq. (8).

$$\:\begin{array}{c}\beta\:=1-\frac{\left[\frac{\gamma\:\bullet\:t}{T}\right]}{\gamma\:}\end{array}$$

(8)

where $\:\gamma\:$ functions to control the segment quantity of the step function, [·] denotes rounding. The attachment coefficient $\:E$ influences the clustering possibility of individuals and rises as the number of iterations, as evidenced in Eq. (9):

$$\:\begin{array}{c}E=\sqrt{\left(\frac{t}{T}\right)}\end{array}$$

(9)

For the movement features of frost ice particles, the position is shown in Eq. (10):

$${R_{new}} = {R_{best}} + {r_1} \cdot {\rm{cos}}\theta \: \cdot \beta \: \cdot \left( {h \cdot \left( {Ub - Lb} \right) + Lb} \right),if\:{r_2} < E$$

(10)

where $\:{R}_{new}$ represents the new location of the particle subsequent to the update, and $\:{R}_{best}$ is the best agent in the frost body population $\:R$. The parameter $\:{r}_{1}$ is a random number in the range of $\:\left(-1,\:1\right)$, controlling the direction of the particle’s motion along with $\:\text{cos}\theta\:$ and changing with the number of iterations. $\:h$ is the viscosity, a random number in the range of $\:\left(0,\:1\right)$, governing the distance between the centers of two frost particles. $\:Ub$ and $\:Lb$ represent the up and down edges of the motion space of particles, respectively. $\:{r}_{2}$ is a random number within the range of (0,51), which plays a role in deciding whether the common control particles undergo condensation and whether their positions are updated.

Hard rime puncture mechanism

Owing to the impact of external environmental elements, hard frost condenses in a certain direction. Inevitably, intersections between hard frosts occur, which implements the dimension swapping between ordinary particles and the best particles, promoting information exchange among agents and enhancing convergence, as detailed below:

$$\:\begin{array}{c}{R}_{new}=\left\{\begin{array}{c}{R}_{best\:}\:\:\:\:\:\:\:{r}_{3}<{F}^{nor}\left({S}_{m}\right)\\\:{R}_{new}\:\:\:\:\:\:\:\:\:\:\:\:otherwise\end{array}\right.\end{array}$$

(11)

In this context, $\:{F}^{nor}\left({S}_{m}\right)$ represents the standardized fitness value of the current agent, which indicates the probability of the i-th particle being chosen. $\:{r}_{3}$ represents a random number within the interval $\:\left(-1,\:1\right)$.

Positive greedy selection mechanism

The positive greedy selection mechanism adopts a more proactive agent replacement strategy to boost the comprehensive level of the population and effectively avoid the potential negative impact of inferior agents on the iteration process, thus promoting the algorithm’s global search proficiency. Specifically, whenever a new agent is generated, the system immediately evaluates whether its fitness value surpasses that of the current agent. If the new agent demonstrates superior performance, the system immediately performs the replacement. Additionally, the global best agent is updated in real-time to ensure that the algorithm can efficiently identify the global optimum.

Improved RIME optimization algorithm

In this section, this study elaborates on the improvements to the RIME optimization algorithm in three aspects. First, the initial population is generated by using a logical mapping approach, which ensures that individuals are uniformly distributed in the solution domain, thereby effectively enhancing the diversity of the population. Second, by designing piecewise mapping rules, the algorithm’s dependence on parameters is reduced, thereby improving its robustness. Finally, the concept of inertia weight is introduced, where the weight is dynamically adjusted in accordance with the iteration count, to enhance the convergence velocity and stability of the algorithm.

Logistic mapping

In the course of the initialization procedure, the logistic chaos is introduced. Chaotic initialization exhibits the characteristics of randomness, ergodicity, and regularity.

First, a column vector Z is generated, where Z is a random number drawn from the uniform distribution [0, 1]. This value serves as the initial condition for the Logistic map.

Then, a chaotic sequence is generated using the logistic map. Its mathematical expression is Eq. (12):

$$\:\begin{array}{c}Z\left(i+1\right)=r*Z\left(i\right)*\left(1-Z\left(i\right)\right)\end{array}$$

(12)

Experiment outcomes show, as illustrated in Fig. 6, that the closer the control parameter r of the Logistic map is to 4, the more uniformly $\:Z\left(i+1\right)$ is distributed over the interval [0, 1]. When the parameter $\:r$ is equal to 4, the system enters a fully chaotic state. Therefore, setting the control parameter $\:r$ to 4 maintains the system’s chaotic behavior.

Fig. 6

Logistics chaos map under different parameters.

Piecewise mapping

Since the random numbers $\:{r}_{1}$、$\:{r}_{2}$、$\:{r}_{3}$ generated by RIME are based on uniform distribution, which can lead to uneven values and affect the global searching capacity. To heighten the randomness and traversal properties of the algorithm, chaos theory is introduced, and the piecewise mapping is used to generate chaotic sequences for $\:{r}_{1}$、$\:{r}_{2}$、$\:{r}_{3}$ parameters. This is done by perturbing the positions of local solutions, thereby minimizing the likelihood of RIME falling into local optima. The piecewise chaotic mapping is a segmented mapping function, and the chaotic mapping formula is Eq. (13):

$$\:\begin{array}{c}{x}_{i+1}=\left\{\begin{array}{c}\frac{{x}_{i}}{P}\:\:\:\:\:\:\:\:\:\:0\le\:{x}_{i} < P\\\:\frac{{x}_{i}-P}{0.5-P}\:\:\:\:\:\:\:P\le\:{x}_{i}<0.5\\\:\begin{array}{c}\:\:\:\:\frac{1-P-{x}_{i}}{0.5-P}\:\:\:\:0.5\le\:{x}_{i}<1-P\\\:\:\:\:\:\frac{1-{x}_{i}}{P}\:\:\:\:\:\:1-P\le\:{x}_{i}<1\end{array}\end{array}\right.\end{array}$$

(13)

Among them, $\:{x}_{i}$ represents the randomly iterated values, and $\:P$ acts as a piecewise control factor, dividing the piecewise function into four distinct sub-functions. Experimental results have shown that the optimal performance is achieved when $\:P$ is set to 0.3. Consequently, in this paper, the value of $\:P$ is set to 0.3.

A random number within the interval [0, 1) is generated as the initial value $\:{x}_{1}$ using the random number function. Subsequently, three iterations are performed. In each iteration, the value of $\:{x}_{i+1}$ is determined based on the current value of $\:{x}_{i}$. The result of the second iteration is assigned to $\:{r}_{1}$, the result of the third iteration is assigned to $\:{r}_{2}$, and the result of the fourth iteration is assigned to $\:{r}_{3}$.

Inertia weight of adaptive change

To enhance global optimization capabilities, the concept of inertia weight in PSO is leveraged, and an adaptive cosine-exponential function inertia weight $\:\omega\:$ is introduced. By combining the oscillatory characteristics of the cosine function and the dynamic adjustment mechanism of the exponential function, the inertia weight w within the algorithm is dynamically optimized according to the iteration process, greatly elevating the algorithm’s overall performance. The expression is shown below Eq. (14):

$$\:\begin{array}{c}\omega\:\left(t\right)=\frac{\left({\omega\:}_{2}-{\omega\:}_{1}\right)*a*\text{cos}\left(\pi\:*exp\left(b*\left(\frac{t}{T}-1\right)\right)\right)}{2}+\frac{\left({\omega\:}_{1}+{\omega\:}_{2}\right)}{2}\end{array}$$

(14)

where: $\:{\omega\:}_{1}$ is the upper limit of the target inertia weight, $\:{\omega\:}_{2}$ is the lower limit of the target inertia weight; $\:a$ is the amplitude modulation factor of the cosine function, and $\:b$ is the adjustment factor of the exponential function, used to control the sensitivity of the inertia weight variation.

In Eq. (14), the exponential function changes rapidly as the number of iterations increases, causing the value inside the cosine function to fluctuate dramatically. The periodic variation of the cosine function, combined with the fluctuations of the exponential function, results in a dynamic change in the weight w during the iteration process.

Finally, the position update formula is the modified Eq. (15):

$${R_{new}} = \omega \:\left( t \right)*{R_{best}} + {r_1} \cdot {\rm{cos}}\theta \: \cdot \beta \: \cdot \left( {h \cdot \left( {Ub - Lb} \right) + Lb} \right),if\:{r_2} < E$$

(15)

In the initial iteration stage, larger inertia weights cause $\:{R}_{new}$ to rely more on the global best position $\:{R}_{best}$, thereby conducting extensive exploration in the search space and avoiding getting stuck in local optima. In the later stages of iteration, smaller inertia weights make the new position $\:{R}_{new}$ depend more on randomly generated local positions, combined with other factors to further refine the search, thus enhancing local exploitation capabilities and improving the accuracy of the solution.

MPPT based on IRIME

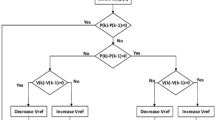
IRIME-MPPT leverages the strong global search capacity of the RIME algorithm, combined with various improvement strategies, to efficiently, accurately, and stably achieve MPPT for PV systems. The flowchart of IRME-MPPT is shown in Fig. 7, and the detailed algorithm steps are as follows:

• (1) Firstly, the parameters of the RIME algorithm are initialized using Logistic chaotic mapping. This method effectively avoids the concentration of the initial population in local regions, thereby significantly enhancing the algorithm’s global search capability. Then the global optimal power and duty cycle are continuously updated.

• (2) Secondly, depending on the motion features of frost particles, the positions of the frost particles are continuously updated. By introducing the chaotic characteristics from the $\:{r}_{1}$ sequence generated through piecewise mapping, the diversity of the search process can be significantly enhanced, effectively preventing the algorithm from falling into local optima. Meanwhile, the generated $\:{r}_{2}$ sequence is used to conduct fine searches in the neighborhood of the current optimal solution, in order to further explore potentially better solutions. Additionally, the adaptive variable inertia weight introduced dynamically adjusts the search strategy according to the optimization process, achieving an effective balance between global and local searches, thereby significantly enhancing the performance and robustness of the optimization algorithm.

• (3) Subsequently, the algorithm is updated through the frostbite penetration mechanism within it to facilitate the exchange of particles. The $\:{r}_{3}\:$sequence generated by segmented mapping further reinforces the strategy of the current optimal solution, thereby helping the algorithm converge faster to the global optimum.

• (4) Finally, the aggressive greedy selection mechanism is used to compare the updated fitness values with the pre-update values, continuously selecting the optimal results.

Fig. 7

Flowchart of the IRIME-MPPT.

Simulation analysis based on IRME in MPPT control

To thoroughly validate the availability of the proposed IRIME optimization algorithm in MPPT, a simulation model is constructed. The model is designed with four distinct environmental conditions: uniform illumination, shading condition, sudden change in illumination, and sudden changes both in illumination and temperature. Under these settings, simulation experiments are conducted to compare and analyze the performance differences among the IRIME optimization algorithm, the original RIME algorithm, and the PSO-BOA optimization algorithm³¹.

The specific parameter settings for each algorithm are shown in Table 3 below:

Table 3 Related parameters of algorithm.

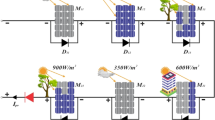
The simulation model is established as shown in Fig. 8. To achieve MPPT control of the PV system, a PV cell model is first established to accurately reflect the electrical characteristics of the actual PV cells. In this study, five PV panels linked in sequence in this module. The system collects the generated voltage and current and delivers them to the MPPT controller, where the IRIME algorithm proposed in this paper is utilized to control the duty cycle. The PWM modulator outputs a PWM waveform, which dynamically controls the conduction and cutoff of the switch in the Boost circuit. In combination with hardware circuits such as DC-DC converters, the closed-loop control design of the entire system is completed. The equivalent load resistance is adjusted to match the internal resistance of the PV array, thereby achieving the maximum power output of the system. The following are the experimental setups utilized in this paper: Operating System: Windows 10; Memory: 8GB; Processor: Intel(R) Core (TM) i7-9750 H CPU @ 2.60 GHz, 2.59 GHz; Simulation Software: MATLAB 2022a.

Fig. 8

MPPT block diagram of PV system.

This study selected a certain model of photovoltaic cell, with parameters as shown in Table 4. Tests are conducted by simulating both static and dynamic lighting conditions.

Table 4 Solar cells manufacturing specifications.

MPPT simulation optimization results under uniform illumination

The simulation experiment is conducted under uniform illumination, setting the irradiance to $\:\text{1,000}w/{m}^{2}$ and the temperature to 25℃, and comparing and analyzing the three algorithms mentioned above. As shown in Fig. 9, under these conditions, the P-V characteristic curve output is a unimodal curve, with a maximum power of approximately 8517 W.

Fig. 9

P-V characteristic curve of photovoltaic under uniform illumination.

The GMPP is tracked using the above three algorithms, with the simulation time set to 2 s, and the experimental simulation results are shown in Fig. 10:

Fig. 10

Simulation results of three algorithms under uniform lighting conditions.

From the three sets of simulations, it can be clearly seen that the IRIME algorithm achieves very desirable results in both tracking accuracy and tracking speed. The tracking accuracy of IRIME reaches 100%, which is improved by 0.36% and 1.37% compared to IRIME and PSO-BOA, respectively. The convergence time of IRIME is only 0.14 s, which is 63.63% of that of the RIME algorithm, and only 27.45% of that of the PSO-BOA algorithm. As specifically shown in Table 5.

Table 5 Tracking performance metrics of three algorithms under condition 1.

MPPT simulation optimization results under shading conditions

The simulation experiment is conducted under partial shading conditions, where the irradiance of five PV panels is set to $\:800w/{m}^{2}$、$\:800w/{m}^{2}$、$\:600w/{m}^{2}$、$\:600w/{m}^{2}$、$\:400w/{m}^{2}$, and $\:400w/{m}^{2}$, respectively, with a temperature of 25℃. Under these conditions, the three algorithms mentioned above are compared and analyzed. As is demonstrated in Fig. 11, the P-V characteristic curve under these conditions is multi-peaked, characterized by several local maximum values, and the overall maximum power is 4374 W.

Fig. 11

P-V curve of photovoltaic under shading conditions.

The above three algorithms are used to track the GMPP, and the simulation time is set to 2 s. The simulation results are shown in Fig. 12:

Fig. 12

Simulation results of three algorithms under shading conditions.

According to the simulation results, the tracking time of IRIME is only 0.17 s, which is 0.06 s less than RIME and 0.37 s less than PSO-BOA, respectively. As for the tracking accuracy, the three algorithms can all reach a high level, but IRIME still has the highest tracking efficiency. The IRIME algorithm achieves speedy and precise tracking of the GMPP, as summarized in Table 6.

Table 6 Tracking performance metrics of three algorithms under condition 2.

MPPT simulation optimization results under sudden change in illumination

The simulation experiment is conducted under conditions of sudden changes in illumination, where the irradiance of five PV panels is set to $\:\text{1,000}w/{m}^{2}$、$\:\text{1,000}w/{m}^{2}$、$\:800w/{m}^{2}$、$\:800w/{m}^{2}$、$\:600w/{m}^{2}$,before 0.6 s. At 0.6 s, the irradiance suddenly changes to $\:800w/{m}^{2}$、$\:800w/{m}^{2}$、$\:600w/{m}^{2}$、$\:600w/{m}^{2}$、$\:500w/{m}^{2}$, respectively, while the temperature remains constant at 25℃. The three algorithms mentioned above are compared and analyzed. As shown in Fig. 13, the maximum power before the mutation is 5804 W, and the maximum power after the mutation is 4786 W.

Fig. 13

P-V curve under sudden lighting change conditions.

Figure 14 shows the simulation results of following the GMPP under the condition of sudden change in illumination using the above three algorithms. The simulation time is set to 2 s.

Fig. 14

Simulation results of three algorithms under conditions of sudden illumination change.

By observation, it is apparent that the IRIME algorithm achieves tracking accuracies of 99.85% and 100% before and after the sudden illumination change, respectively. Compared to RIME and PSO-BOA, the improvements are 1.14% and 1.36% before the change, and 1.32% and 13.22% after the change. Additionally, the improved IRIME algorithm significantly reduces tracking time compared to RIME and PSO-BOA, taking only 0.09 s before the change, and stabilizing by 0.72 s after the change. Detailed analysis is shown in Table 7.

Table 7 Tracking performance metrics of three algorithms under condition 3.

Simulation optimization results under sudden changes both in illumination and temperature

The simulation experiment is conducted under conditions of sudden changes in both illumination and temperature, the initial irradiance of five PV panels is set to $\:\text{1,000}w/{m}^{2}$、$\:\text{1,000}w/{m}^{2}$、$\:800w/{m}^{2}$、$\:800w/{m}^{2}$、$\:600w/{m}^{2}$, respectively, with a temperature of 35℃. At 0.6 s, the irradiance suddenly changed to $\:800w/{m}^{2}$、$\:800w/{m}^{2}$、$\:600w/{m}^{2}$、$\:600w/{m}^{2}$、$\:400w/{m}^{2}$, respectively, with the temperature changing to 25 °C. The three mentioned algorithms are compared and analyzed. As shown in Fig. 15, the maximum power before the change is 5601 W, and after the change, it is 4374 W.

Fig. 15

P-V curve under sudden changes in illumination and temperature.

The three algorithms mentioned above are applied to track the GMPP, and the simulation time is set to 2 s. The results of experiment are given in Fig. 16:

Fig. 16

Tracking results of three algorithms under conditions of sudden changes in illumination and temperature.

Upon analysis, it is found that the average tracking accuracy of IRIME before and after tracking can reach 99.03%. Compared to the other two algorithms, it is an improvement of 1.26% and 2.9% respectively. Before the mutation, the tracking time of the IRIME algorithm is decreased by 0.1 s compared to RIME and by 0.43 s compared to PSO-BOA. After the mutation, the tracking time of the IRIME algorithm is decreased by 0.06 s compared to RIME and by 0.39 s compared to PSO-BOA. Specific analysis is shown in Table 8:

Table 8 Tracking performance metrics of three algorithms under condition 4.

The IRIME optimization algorithm demonstrates excellent characteristics in the MPPT of PV systems. Compared to the RIME and PSO-BOA optimization algorithms, the IRIME algorithm can always track the MPP with the highest precision under various environmental conditions. As the simulation results demonstrate that the waveform of the IRIME algorithm has smaller oscillations and converges quickly, enabling the system to efficiently and stably track the GMPP.

Conclusion

This study is the first to apply the RIME optimization algorithm for MPPT technology in partially shading conditions, aiming to achieve effective tracking of the GMPP when the power output characteristic curve exhibits multiple peaks. To avoid the issues of the conventional RIME algorithm, including prematurely converging to local optima and slow convergence, a logistic mapping initialization method is introduced which makes the original algorithm gain traversability, enabling wider exploration in the search space. Additionally, piecewise mapping is employed to adjust algorithm parameters and optimize the generated sequences, thereby enhancing the algorithm’s flexibility and adaptability. Moreover, an adaptively varying inertia weight is introduced, which is dynamically adjusted on the strength of the iteration process, effectively reducing the time spent in blind search and significantly enhancing the algorithm’s convergence speed. The improved algorithm achieves a better equilibrium of overall exploration and local exploitation, thereby reducing the runtime and enhancing the overall efficiency of the algorithm.

Building on this, the improved IRIME optimization algorithm is applied to the MPPT technology of PV systems, with a simulation model is established and four different environmental conditions are simulated. By comparing the IRIME algorithm with the RIME and PSO-BOA optimization algorithms, simulation outcomes indicate that the tracking accuracy of the IRIME optimization algorithm is above 98.88%, and convergence can be achieved within 0.17 s, significantly outperforming the other two optimization algorithms. Therefore, the proposed IRIME optimization algorithm enhances tracking accuracy and system adaptability, enabling the system to achieve smooth, fast, and efficient performance.

Despite the significant achievements of this study, there are still several areas that warrant further investigation and improvement.

• (1) Firstly, the potential for combining the IRIME algorithm with other optimization algorithms should be explored to further improve the performance of the algorithm.

• (2) Secondly, further research is needed to enhance the robustness of the algorithm under varying light conditions and temperature changes, particularly in extreme weather conditions.

• (3) Finally, the current research is primarily based on simulation models, and future work should include testing and validation in actual PV systems to ensure the reliability and effectiveness of the algorithm in real environments.