Introduction

Due to its high stability, long lifespan, excellent precision, and strong adaptability to various environments, strapdown inertial navigation systems are widely applied in fields such as aerospace, aviation, weaponry, maritime vessels, and automotive technologies1. Currently, these systems primarily employ dithered ring laser gyroscopes (DRLG) as core sensing components. Through the application of dithering and frequency biasing techniques, the DRLG effectively mitigates the impact of lock-in effects, significantly enhancing measurement accuracy2. However, during operation, factors such as uneven internal heat source distribution and fluctuations in external environmental temperature can lead to changes in the temperature field, causing thermal deformation of the gyroscope. This thermal deformation not only affects the gyroscope’s output accuracy but may also adversely impact its frequency stability and overall performance3.

As requirements for navigation and guidance accuracy continue to rise, the measurement accuracy of the DRLG also faces increasingly stringent demands. However, DRLGs are prone to output drift with temperature changes, which may significantly impact the alignment and navigation accuracy of strapdown inertial navigation systems4. In airborne applications, the zero-bias stability of the DRLG must be maintained within 0.008°/h, while more stringent requirements apply in maritime vessels and mid-to-long-range missile systems, where it must be controlled within 0.003°/h. To meet these high-precision application demands, it is essential to effectively reduce the zero-bias error of the DRLG and minimize the impact of temperature fluctuations on its output, thereby enhancing the navigation accuracy of strapdown inertial navigation systems5. This underscores the significant engineering value in studying the temperature field distribution characteristics of the DRLG and implementing optimized designs to mitigate the effect of temperature on its performance.

In the field of temperature field research for laser gyroscopes, B.G. Fidric identified that temperature gradients significantly affect gyroscope accuracy, and by improving the optical path channel, minimized the impact of temperature gradients on laser gyroscope operation6. Chechile et al.7 noted that differences in the thermal expansion coefficients of assembly structures result in non-uniform deformation of components during temperature increases, causing misalignment between the structure and the laser gyroscope. To address this, they designed a symmetrically positioned frame structure and re-optimized the thermal expansion coefficients of each structural component. When temperature changes occurred, the deformation of the inner and outer frames moved in opposite directions, thereby maintaining overall parameter stability7. Wu et al.8 successfully simulated the internal temperature field distribution of the laser gyroscope during startup by establishing a finite element model of the gyroscope cavity and applying two-step calculation method. Yu et al.9 used finite element analysis software to develop a temperature field model for the dithered ring laser gyroscope, incorporating the housing to deepen the understanding of its thermal field distribution. Yu et al.9 similarly utilized finite element analysis software to simulate and analyze the temperature field, thermal stress, and thermal deformation of laser-based strapdown inertial components. Jin et al.10 designed novel grooved pieces and a control mirror for optical path length to counteract high and low temperature impacts, while Zapotyl’ko et al.11 investigated the effects of temperature variations on optical resonator glass. Zubarev et al.12 simulated the temperature-induced drift of the resonator path length in a Zeeman laser gyroscope, providing an analytical tool for material evaluation and structural optimization. Their work enhances gyroscope stability through active perimeter adjustment and passive thermal compensation, improving performance in varying thermal conditions. Petrukhin and Bessonov13 developed a method to measure coupling coefficients in a laser gyroscope’s resonator, enabling the prediction of lock-in thresholds and nonlinear distortions. Their approach aids in optimizing mirror coatings and reducing assembly-induced errors, which is relevant to improving resonator stability under thermal effects. Ezhilarasi et al.14 developed a deep learning-based method for predicting temperature variations in ring laser gyroscopes, improving bias compensation and thermal adaptability in inertial navigation systems. Although these studies provide various solutions, they do not deeply explore the impact of temperature field variations on gyroscope output performance, nor do they propose effective measures to mitigate thermally induced gyroscope deformation and zero-bias error.

Building on existing research, this paper explores in depth the impact of temperature field variations on the output performance of the DRLG, clarifying how thermally induced deformations affect the gyroscope’s accuracy and stability. Utilizing finite element simulation techniques and temperature testing experiments, we verify the accuracy of temperature field distributions under various environmental conditions and their effects on DRLG structure. Unlike previous studies that focus primarily on temperature field simulations and structural optimization, this work introduces a novel approach by combining temperature field simulation, a three-point mounted dither mechanism, and multi-parameter optimization. The proposed optimized parametric design aims to reduce gyroscope deformation and zero-bias error caused by temperature fluctuations, thereby enhancing thermal stability in complex environments. Through temperature cycling experiments, we compare the zero-bias stability of the optimized and original DRLGs, revealing that the optimized DRLG exhibits a lower zero-bias Allan deviation under varying temperature conditions, validating the effectiveness of the optimized design. These research outcomes provide crucial theoretical and engineering support for the application of DRLGs in high-precision inertial navigation systems and advance related technologies.

The structure of this paper is organized as follows: Section “Theoretical basis” analyzes the impact of temperature on the output of the DRLG. Section “Temperature field analysis of a specific DRLG model” presents a simulation and experimental analysis of the temperature field of a specific DRLG model. Section “DRLG optimization design” proposes an optimized parametric design for the dither mechanism, comparing and analyzing the simulation results of the temperature field for both the optimized and original DRLG, along with a comparative analysis from temperature cycling experiments. Section “Experiment and discussion” summarizes the main conclusions of this study.

Theoretical basis

As a high-precision inertial navigation device, the performance of the DRLG is influenced by various factors, with temperature fluctuations being a critical one. The impact of temperature on the DRLG encompasses several components, including the frequency stabilization mechanism, dither mechanism, optical components, and gas physical properties. This section analyzes the influence of temperature changes on each of these components and their interrelationships, thereby exploring their effects on the output performance of the gyroscope.

Effect of temperature on the frequency stabilization mechanism

The frequency stabilization mechanism of the DRLG comprises components such as the ring resonator cavity, gain medium, mirrors, and piezoelectric ceramics, all working in unison to ensure laser frequency stability. In particular, the piezoelectric actuator fine-tunes the mirrors during cavity length adjustment to maintain the longitudinal mode frequency at the center frequency of the gain region15. The fundamental equation governing the principle of the laser gyroscope is as follows:

$$\Delta v = \frac{4S}{{\lambda L}}\Omega$$
(1)

where \(\Delta v\) denotes the frequency difference of laser, \(\Omega\) represents the angular velocity. \(S\) represents the area enclosed by the ring light path, \(\lambda\) denotes the vacuum wavelength of He–Ne laser, and \(L\) represents the length of the laser gain chamber.

Integrating both sides of (1) with respect to time t

$$\int_{0}^{t} {\Delta vdt} = \frac{4S}{{\lambda L}}\int_{0}^{t} {\Omega dt}$$
(2)

The (1) can be rewritten as follows:

$$N = \frac{4S}{{\lambda L}}\theta$$
(3)

where \(N = \int_{0}^{t} {\Delta vdt}\) is the accumulated number of periods within time interval \(t\) due to a frequency difference, \(\theta = \int_{0}^{t} {\Omega dt}\) is the total rotation angular during time interval \(t\). The total angular input and the corresponding output signal \(N\) exhibit a proportional relationship defined by the scale factor (\(4S/\lambda L\)). Under ideal conditions, the scale factor remains constant, allowing for precise angular velocity measurements through accurate calibration. However, in practical applications, thermal variations within the gyroscope and fluctuations in the surrounding environment can induce changes in the scaling factor, leading to deviations and measurement errors.

Assuming that the ring optical path area \(S\) and the wavelength \(\lambda\) remain constant, Eq. (3) indicates that the stability of the scale factor primarily depends on the cavity length \(L\). The relative error \(\eta\) induced by temperature variations affecting the cavity length can be expressed as:

$$\eta = \frac{\Delta L}{L} = \frac{\Delta T \cdot L \cdot \rho }{L} = \rho \cdot \Delta L$$
(4)

In this equation, \(\Delta L\) represents the cavity length variation, \(\Delta T\) denotes the temperature change, and \(\rho\) is the thermal expansion coefficient. The resonator is made of microcrystalline glass, with a thermal expansion coefficient of \(\rho = 5.{5} \times 10^{{ - {7}}} /^{ \circ } {\text{C}}\). When the temperature increases from − 40 to 70 °C, the corresponding temperature variation \(\Delta T = {110}\;^{ \circ } {\text{C}}\) leads to an error of 60 ppm. Such an error level is unacceptable for high-precision laser gyroscopes16.

Furthermore, during DRLG operation, rapid heating of the anode and cathode in the gain region due to discharge affects the uniformity of the internal temperature field. The small diameter (2–3 mm) and length (approximately 300 mm) of the optical path bore make it sensitive to manufacturing tolerances, potentially causing structural asymmetry. With temperature changes, the straightness and parallelism of the optical path bore may deteriorate, leading to laser path deviations and increased optical losses. This, in turn, reduces the output light intensity, negatively impacting the gyroscope’s accuracy and zero-bias stability.

Finally, in ring lasers, the direct current discharge used to excite the gaseous gain medium inevitably induces gas flow, known as Langmuir flow17. During operation, heat generated by the gyroscope and fluctuations in environmental temperature intensify gas flow within the gain region, exacerbating zero-drift errors. Although DRLGs typically employ a single-cathode, dual-anode design to maintain symmetry, achieving complete symmetry in practical applications is challenging. This asymmetry leads to Langmuir flow frequency drift, affecting frequency output. The formula for the frequency difference in the resonant cavity \(\Delta v_{L}\) caused by the Langmuir effect is as follows18:

$$\Delta v_{L} = \frac{{2\left( {G_{1} V_{1} - G_{2} V_{2} } \right)}}{{\lambda G_{0} }}A$$
(5)

where \(G_{1}\) and \(G_{2}\) denote the gains of the discharge tubes at each end; \(V_{1}\) and \(V_{2}\) are the atomic flow velocities in the discharge tubes at each end; \(\lambda\) is the laser wavelength; \(G_{0}\) is the total gain within the gas discharge tube; and \(A\) is a proportional correction factor. According to Eq. (5), ideally, to eliminate the zero drift caused by the Langmuir flow effect, complete symmetry (i.e., \(V_{1} { = }V_{2}\) and \(G_{1} = G_{2}\), should be achieved. However, in practical applications, this condition is difficult to fulfill due to factors such as varying atomic flow velocities and environmental influences. Additionally, as \(\Delta v_{L}\) and the atomic flow velocities \(V_{1}\) and \(V_{2}\) increase, the frequency difference \(\Delta v_{L}\) induced by Langmuir flow also rises. This component of the frequency difference adds to the frequency difference signal of the measured rotation, resulting in significant zero drift.

Effect of temperature on the dither mechanism

The dither mechanism of the DRLG consists of a metal dithering wheel, piezoelectric ceramics, and adhesive materials. Temperature variations affect the Young’s modulus of the metal dithering wheel, causing drift in the resonant frequency of the dither mechanism. This drift directly influences dithering sensitivity; if the dither frequency does not match the resonant frequency, the effectiveness of the dithering is reduced. The dither bias frequency represents the maximum dither angular velocity and is expressed as follows:

$$g = 2\pi \cdot f_{d} \cdot K_{d} \cdot V_{d}$$
(6)

where \(g\) is the dither bias frequency, \(f_{d}\) is the dither frequency, \(K_{d}\) is the dithering sensitivity, and \(V_{d}\) is the dither excitation voltage amplitude.

Dithering sensitivity \(K_{d}\) is maximized when the dither frequency \(f_{d}\) matches the resonant frequency of the mechanism. However, temperature fluctuations cause the resonant frequency \(f_{n}\) to drift. If the dither frequency remains fixed, sensitivity decreases, and a constant excitation amplitude \(V_{d}\) leads to a reduction in dither bias frequency \(g\). Additionally, temperature-dependent variations in the piezoelectric constant affect maximum dithering sensitivity, reducing both dither amplitude and bias frequency, which increases lock-in errors. Resonant frequency instability further causes inconsistencies in the lock-in threshold, leading to zero drift in the gyroscope’s output.

Effect of temperature on structure

Thermal deformation caused by temperature variations can impact the overall structure of the DRLG. Due to differences in material properties and an uneven temperature field, components such as the gyroscope’s mounting housing, dither wheel supports, and cavity undergo varying degrees of thermal deformation. This deformation generates torque due to interactions between components, which leads to misalignment of the optical axis, introducing output signal errors19.

Effect of optical components

The four mirrors of the ring laser gyroscope, made of fused silica, expand more than the microcrystalline glass cavity as temperature rises. This mismatch induces stress at the interface, leading to mirror deformation, optical path bending, increased losses, and weakened light intensity, ultimately causing output errors.Additionally, temperature changes affect peripheral components. The photodetector may shift or rotate, altering signal amplitude and phase, reducing accuracy, and increasing zero-bias drift. The perimeter adjuster, composed of elastic elements and piezoelectric ceramics, undergoes thermal expansion and tilting, disturbing the optical path and triggering the Langmuir flow effect, further increasing zero-bias drift.

Effect of physical characteristics

Temperature variations affect the refractive index of gases, the thermal conductivity of materials, and the optical properties of components, leading to pressure changes in the helium–neon gas within the ring resonator. These pressure variations cause refractive index inhomogeneity, impacting laser propagation20. If the refractive index fluctuations are minor and gradual, their effect on the gyroscope’s zero bias is negligible. However, abrupt changes induce reflection, refraction, and scattering, introducing optical losses. Backscattering can transfer energy between counter-propagating waves, leading to frequency shifts or even transforming traveling waves into standing waves.

Temperature field analysis of a specific DRLG model

Structural characteristics and thermal properties

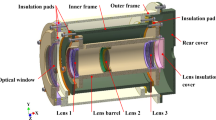
The DRLG is an inertial device based on the Sagnac effect, utilizing mechanical dithering to eliminate lock-in effects, with its core component being a ring laser. A specific DRLG model constructed using Solidworks is shown in Fig. 1. The ring resonator cavity is adhesively fixed onto the dither mechanism, which is mounted onto the base using four screws. The dither mechanism periodically drives the optical cavity of the laser gyroscope to perform angular vibrations along its dither axis. As the only moving component within the DRLG, the dither mechanism rigidly connects the optical cavity to the mounting base, and it is generally assumed that the spatial position of the dither axis relative to the base remains fixed.

Fig. 1
figure 1

(a) Schematic diagram of a specific DRLG (without top cover); (b) front and top views of the dithering mechanism.

Full size image

From a thermal perspective, the structure is sealed, lacking an internal temperature control system or forced ventilation, with the surrounding medium being air at atmospheric pressure. During DRLG operation, the primary heat sources applied to the gyroscope stem from the uneven distribution of heat within the environment and internal sources. The surfaces in contact with the surrounding air exchange heat with the external environment through convective heat transfer, while internal components transfer heat through thermal conduction.

Temperature field simulation and analysis

Temperature field analysis was performed for the DRLG system, where material parameters were specified, a finite element model was established, and thermal boundary conditions along with heat source models were implemented3. Both steady-state and transient temperature fields were simulated. To validate the accuracy of the results, experimental measurements were conducted to compare with the simulation outcomes.

Platinum resistance thermometers were placed at the corresponding positions of the cathode and anode within the gyroscope cavity. The steady-state temperatures at various points were measured in a temperature chamber set to 70 °C, and these measurements were compared with the simulation results at the corresponding points. The comparison results are presented in Table 1, indicating that the relative error is within 1%.

Table 1 Comparison of steady-state analysis simulation data and measured data at temperature measurement points.
Full size table

Transient thermal simulation analysis of the gyroscope was conducted with an initial temperature set to the current room temperature of 25 °C and an environmental temperature of 70 °C. The total simulation duration was 20 h, with a time step of 180 s. Subsequently, transient temperature values at various measurement points (anode and cathode) were obtained through experimental measurements. The experimental setup and environment are illustrated in Fig. 2. The results of the experiment were then compared with the simulation results, as shown in Fig. 3. The figure indicates that during the heating process, the maximum deviation between the experimental results from four trials and the simulation results is 2.89 °C. This discrepancy can be attributed to unavoidable variations in material properties, slight structural inconsistencies, minor fluctuations in environmental conditions, and sensor accuracy, with the temperature sensors having an accuracy of \(\pm {0}{\text{.1}}\)°C.

Fig. 2
figure 2

Experimental setup and environment.

Full size image
Fig. 3
figure 3

Simulation versus experiment: temperature variation and error analysis of cathode and anode in four test cases.

Full size image

To investigate the temperature field distribution of the gyroscope under different operating environments, multiple steady-state temperature field simulations were conducted with environmental temperatures set at − 40 °C, − 30 °C, − 20 °C, − 10 °C, 0 °C, 10 °C, 20 °C, 30 °C, 40 °C, 50 °C, 60 °C, and 70 °C. Figure 4 display the simulation results of the steady-state temperature field when the environmental temperature is set to 20 °C.

Fig. 4
figure 4

Temperature field distribution. (a) Overall structure; (b) enclosure; (c) cavity.

Full size image

The overall temperature field distribution is shown in Fig. 4a. Due to the symmetry of the structure and heat sources, the temperature exhibits a symmetrical distribution, with the highest temperature at 23.414 °C and the lowest at 20.111 °C. The highest temperature is found in the cavity’s gain area near the anode, where gas heat exchange occurs, and heat dissipation is hindered due to the small structure. The lowest temperature occurs at the upper edge of the gyroscope enclosure, away from the discharge circuit.

Figure 4b shows that the gyroscope enclosure’s temperature ranges from 20.111 to 20.14 °C, with the highest point located near the front discharge circuit (the heat source), and the lowest near the enclosure’s edge, in direct contact with the environment. The temperature difference within the enclosure is 0.029 °C, reflecting a relatively uniform distribution, which is attributed to the enclosure’s high thermal conductivity (121 W/mK).

As shown in Fig. 4c, at an environmental temperature of 20 °C, the highest temperature within the gyroscope cavity reaches 23.414 °C, while the lowest is 20.325 °C, yielding a temperature difference of 3.089 °C. This significant variation is due to the uneven distribution of internal heat sources and the cavity’s low thermal conductivity, which leads to poor heat conduction. Such non-uniformity can distort the cavity, impacting gyroscope stability, jitter performance, and optical characteristics.

Steady-state thermal analysis indicates that the cavity’s internal temperature remains relatively stable across different environmental conditions. Figure 5 shows that the gyroscope’s steady-state temperature has an approximately linear relationship with the environmental temperature. As the ambient temperature increases, so do the maximum temperatures of the gyroscope, cavity, and enclosure. Specifically, the maximum temperature of the enclosure is about 0.2 °C higher than the environmental temperature, while the maximum temperatures of the gyroscope and cavity are approximately 3 °C higher.

Fig. 5
figure 5

Relationship between steady-state maximum temperature and environmental temperature.

Full size image

Temperature-induced thermal deformation in DRLG components can lead to uneven deformation and thermal stresses. These stresses, if non-uniform or constrained, can cause cavity distortion, misalignment of mirrors, and laser path deviation, all of which significantly impact the performance of high-precision DRLGs. Therefore, analyzing thermal stress and strain is essential.

Since thermal strain is driven by the temperature field and structural strain does not affect temperature distribution, a one-way coupling approach is used for thermal stress and strain analysis. This eliminates the need for iterative calculations, allowing the temperature field results to be directly applied as loads on the structure. The three mounting reference planes of the gyroscope are fixed, and the steady-state thermal analysis results are used as temperature loads. The thermal deformation of the cavity at an environmental temperature of − 40 °C is shown in Fig. 6.

Fig. 6
figure 6

Thermal deformation of the cavity.

Full size image

Due to the non-uniformity of the temperature field and structural constraints, the cavity undergoes torsional deformation, with the maximum thermal deformation occurring at the upper edge of the cavity near the anode. The region with the smallest deformation is located at the contact point between the cavity and the dither wheel, due to the dither wheel’s restriction on cavity deformation.

As environmental temperature changes, the steady-state temperature and thermal deformation of the gyroscope also vary accordingly. Figure 7 shows the relationship between maximum cavity deformation and environmental temperature, where the maximum deformation follows a "V" pattern, increasing significantly at − 40 °C and 70 °C. Greater cavity deformation results in more pronounced effects on the gyroscope’s output.

Fig. 7
figure 7

Relationship between maximum thermal deformation of the cavity and environmental temperature.

Full size image

DRLG optimization design

Optimization analysis

This section proposes an optimized design for the dither mechanism to reduce the impact of temperature on gyroscope deformation. First, a three-point mounting structure is adopted for connecting the dither mechanism to the mounting enclosure, where three bolts connect the dither mechanism to the enclosure, as opposed to the previous four-point mounting structure that uses four bolts.

Additionally, a parametric design of the dithering mechanism was conducted using finite element analysis methods. Parameter scanning method is used to optimize the parameters of the dithering mechanism, each parameter changes systematically within a predetermined range, and the target parameters are adjusted based on iterative simulation analysis. By identifying trends and determining parameter combinations, the structural deformation is minimized while maintaining stability. The parameters include the central hole diameter \(D\), the height \(H\) of the contact surface with the inner wall of the cavity, the outer wall thickness \(h\), the support spoke width \(b_{p}\), and the depth \(l_{c}\), width \(b_{c}\), and distance \(l_{p}\) from the center point of the spoke grooves, as shown in Supplementary Fig. S1.

A detailed analysis of these geometric features of the dithering mechanism was performed to assess their impact on the thermal deformation and thermal stress of the cavity’s inner optical path wall across an environmental temperature range of − 40 °C to 70 °C, as illustrated in Supplementary Figs. S2 and S3.

Supplementary Fig. S2 shows that thermal deformation of the cavity optical path inner wall increases significantly under extreme temperatures, while it remains minimal at room temperature, indicating that temperature is a key factor affecting optical path stability. Additionally, various geometric characteristics of the dither mechanism have different levels of impact on thermal deformation, exhibiting clear patterns that highlight the crucial role of geometric design in regulating thermal conduction pathways and stress distribution amid temperature variations. Supplementary Fig. S3 demonstrates that increasing environmental temperatures generally lead to higher thermal stress on the cavity optical path inner wall, underscoring temperature as a primary driver of thermal stress. The varying degrees of influence of the dither mechanism’s geometric characteristics on thermal stress also suggest that optimizing the geometric design of the dither mechanism, particularly the grooves on the support spokes and the dimensions of the dither wheel’s outer wall, can effectively control thermal stress distribution. This enhances the temperature adaptability and structural stability of the DRLG.

Subsequently, the influence of each geometric parameter on the deformation of the cavity optical path inner wall was analyzed individually at room temperature (25 °C), as shown in Supplementary Fig. S4. The results reveal a nonlinear impact of these geometric parameters on the thermal stress distribution and structural rigidity of the cavity. Each parameter was found to have an optimal value that minimizes thermal deformation of the optical path inner wall. These optimal parameter values represent a balance point between structural rigidity and thermal stress, helping to reduce deformation of the DRLG in complex thermal environments and thereby enhancing system accuracy.

Analysis of the figure yields the following insights:

  1. a.

    Relationship between central hole diameter and thermal deformation:

    The deformation of the dither wheel shows a non-linear trend with the diameter of its central hole, decreasing initially and then increasing, with an optimal diameter at 1.75 mm. A smaller hole diameter concentrates the supporting structure, causing localized stress and increased deformation, while a larger diameter reduces structural rigidity, weakening resistance to thermal stress. The optimal diameter balances rigidity and thermal stress distribution, minimizing thermal deformation effectively.

  2. b.

    Relationship between contact surface height and thermal deformation:

    The deformation of the cavity varies with the height of the contact surface between the dither wheel and the cavity inner wall, initially decreasing and then increasing. At smaller heights, improved thermal conduction and enhanced structural support reduce deformation. However, excessive heights lead to stress accumulation, increasing deformation. The optimal contact surface height is 4.33 mm, effectively minimizing thermal deformation.

  3. c.

    Relationship between outer wall thickness and thermal deformation:

    The deformation of the cavity varies with the dither wheel’s outer wall thickness, showing an initial decrease followed by an increase. Thinner walls lack structural rigidity, leading to uneven thermal stress and greater deformation. Increasing the thickness enhances rigidity and evenly distributes thermal stress, reducing deformation. However, overly thick walls create new stress concentration areas, increasing deformation. The optimal thickness of 2.5 mm minimizes thermal deformation.

  4. d.

    Relationship between support spoke width and thermal deformation:

    Thermal deformation decreases linearly with increasing support spoke width. Wider spokes enhance the dither wheel’s structural rigidity, improving resistance to thermal stress and reducing cavity deformation by distributing thermal strain more uniformly and minimizing localized stress. The optimal width, limited by structural constraints, is 1.4 mm.

  5. e.

    Relationship between groove depth and thermal deformation:

    Thermal deformation varies with groove depth, decreasing initially and then increasing, with a minimum at 3.625 mm. Shallower grooves improve rigidity and distribute thermal stress effectively, reducing deformation, while deeper grooves weaken rigidity and concentrate stress, increasing optical path deformation. The optimal depth balances thermal stress distribution and structural rigidity.

  6. f.

    Relationship between groove width and thermal deformation:

    Groove width variations cause periodic fluctuations in thermal deformation due to interactions between thermal stress distribution and structural resonance. Different widths create localized stress concentrations or alleviations, leading to these fluctuations. An optimal width of 0.6 mm balances stress distribution and resonance effects, minimizing thermal deformation.

  7. g.

    Relationship between groove distance from center and thermal deformation:

    Thermal deformation increases linearly with the groove’s distance from the center. Greater distances weaken the groove’s support for the dither wheel, causing thermal stress concentrations at the edges and higher deformation. This linear trend highlights the consistent impact of groove position on thermal stress distribution and deformation.

Comparison and analysis of temperature field simulations

In this section, thermal deformation simulations were conducted for both the optimized and original DRLG models under environmental temperatures ranging from − 40 °C to 70 °C, with results shown in Supplementary Fig. S5. These figures illustrate the relationship between average total deformation of the gyroscope as a whole, the enclosure, and the cavity under different mounting configurations as temperature varies.

The average total deformation of the DRLG as a whole follows a “V” shape, reaching a minimum around 0 °C and peaking at − 40 °C and 70 °C. The deformation magnitude of the original DRLG is significantly higher than that of the optimized DRLG across the entire temperature range, particularly under extreme temperatures, indicating poorer stability under thermal stress, which may impact measurement accuracy.

The deformation trend of the enclosure is similar to that of the overall structure, also forming a “V” shape. The optimized DRLG exhibits smaller deformations in the enclosure over most temperature ranges, whereas the original DRLG shows noticeably larger deformation under extreme temperatures, reflecting a higher sensitivity of the original enclosure to temperature changes, potentially leading to structural instability.

The thermal deformation trend of the cavity resembles those of the overall structure and enclosure, also displaying a “V” shape. The original DRLG’s cavity shows more pronounced deformation at both high and low temperatures, especially under extreme conditions, which may result in optical path deviations and affect the output accuracy of the laser gyroscope.

In summary, the optimized DRLG demonstrates superior thermal stability compared to the original DRLG, showing reduced temperature-related deformation. The larger deformations observed in the original DRLG under extreme temperatures could lead to optical alignment errors and performance degradation. Therefore, for DRLG designs with high thermal stability requirements, the optimized three-point mounted dither mechanism with parametric design is more suitable.

Experiment and discussion

To verify the performance advantages of the optimized DRLG under complex temperature conditions, a temperature cycling experiment was conducted on both the optimized DRLG and the original DRLG (both developed in-house by our team).

The experimental setup included a self-developed Type 50 DRLG for high-precision inertial measurement, a PT1000 sensor for accurate temperature monitoring, and self-developed acquisition boards for reliable data collection and processing. To assess the impact of temperature variations, experiments were conducted in a controlled thermal environment using the KWGD601 temperature chamber from Chongqing Yinhe Experimental Equipment Company Ltd. This setup ensured precise measurement and validation of the thermal effects on the DRLG’s performance.

The experiment protocol was as follows: After maintaining power at room temperature for 2 h, the temperature was decreased to − 40 °C at a rate of 1 °C/min, held for 3 h, then increased to 65 °C at 1 °C/min and held for another 3 h. Finally, the temperature was decreased to 25 °C at 1 °C/min, held at 25 °C for 2 h, and then powered off to conclude the test. The entire experiment strictly controlled the temperature ramp rate at 1 °C/min to ensure a uniform temperature gradient, minimizing the impact of sudden temperature changes on the test results.

During the low-temperature (− 40 °C) and high-temperature (65 °C) holding stages of the temperature cycle, we analyzed the zero-bias stability and temperature sensitivity of the DRLG to further validate the optimized DRLG’s resistance to thermal stress and deformation. The total experiment duration was 48,600 s, with two repetitions of the temperature cycling experiment for both the optimized and original DRLG. The results are shown in Supplementary Fig. S6.

Based on the experimental results in Supplementary Fig. S6 and the data in Supplementary Table S1., the optimized DRLG shows zero-bias Allan deviations of 0.018508°/h and 0.020710°/h in the two experimental runs, significantly lower than the 0.064183°/h and 0.068918°/h observed in the original DRLG. This indicates that the optimized DRLG exhibits lower sensitivity to temperature field variations under identical conditions, demonstrating superior thermal stability.

The results reveal that the structural design of the optimized DRLG effectively reduces the impact of temperature gradients on gyroscope accuracy by optimizing stress distribution and simplifying the structure. Throughout the full temperature cycling test, the optimized DRLG exhibited more stable zero-bias characteristics, which is crucial for enhancing the reliability of high-precision inertial navigation systems.

Conclusion

This paper presents an in-depth analysis of the temperature field characteristics of the DRLG in strapdown inertial navigation systems and their impact on output performance. An optimized design approach is proposed to mitigate gyroscope deformation induced by temperature variations. Distinct from prior research focused on temperature field simulations and structural optimization, this work introduces a novel approach by integrating temperature field simulation, a three-point mounted dither mechanism, and multi-parameter optimization to enhance performance and stability. Finite element simulations and temperature testing experiments verified the temperature field distribution under different environmental conditions, revealing that temperature field non-uniformity significantly affects gyroscope output accuracy and stability. To enhance DRLG performance in complex environments, an optimized three-point mounted dither mechanism with a parametric design was introduced. Simulation and experimental results demonstrated that this optimized design effectively reduces zero-bias error, enhances thermal stability, and significantly improves the reliability and accuracy of the DRLG. This work has substantial engineering application value, providing a solid theoretical foundation for DRLG design and application and advancing the development of high-precision inertial navigation technology.