Introduction

A brain tumor refers to an abnormal cells within the brain, which disrupts both its structural and functional integrity. MRI is a widely used non-invasive method for diagnosing and treating brain tumor1. Accurate and reliable automatic segmentation of brain tumor is of critical clinical importance. Recently, with the rapid advancement of deep learning in medical analysis, methods based on deep learning have become the predominant approach for brain tumor segmentation2.

The U-Net3, featuring a simple encoder-decoder structure with lateral connections, is the most renowned method for enhanced feature extraction and superior segmentation results. However, the limited availability of medical image datasets with high-quality annotations substantially constrains the capacity of networks to achieve optimal performance through training. To further enhance segmentation performance, researchers have integrated U-Net with other deep learning techniques, such as Generative Adversarial Networks (GAN)4, which have proven effective in various medical segmentation tasks5,6,7. Using the GAN architecture, Xue et al.8 employ U-Net as a generator to achieve dynamic equilibrium in brain tumor segmentation, yielding commendable results. Building on this, Nema et al.9 proposed RescueNet, based on CycleGAN, using multiple generators and discriminators to ensure the generated image corresponds to the original. However, existing methods need further improvement to enhance the generator’s feature extraction capability. To improve the generator, one can draw on a variety of advanced modules introduced in the U-Net architecture, including dilated convolution10, separable convolution11, and the attention mechanism12. Especially, to capture the overall voxel information of brain tumor, researchers incorporate Transformers13, which excel in establishing long-range dependencies in visual images for segmentation tasks14,15,16. As a pioneering work, Wang et al.17 propose TransBTS by embedding Vision Transformer (ViT) into the bottleneck of U-Net, proving the effectiveness of Transformers for brain segmentation. Additionally, Roy et al.15 develop MedNeXt by embedding a Transformer into ConvNeXt, validating its effectiveness on organ, kidney, and brain tumor segmentation tasks. Chen et al.18 propose a dual-pathway Transformer module integrated into the bottleneck layer of U-Net to capture long-range interactions and global spatial dependencies. These methods described above direct integration of Transformer blocks into convolutional architectures, this way frequently induces notable disjointedness between global and local feature representations. Consequently, existing methods still need improvement in balancing global and local feature extraction for brain tumor segmentation.

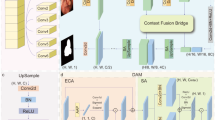
In this work, we utilize the GAN architecture to build a robust brain tumor segmentation network. Such a design can solve the problem of limited accuracy improvement by training. Furthermore, to better balance global and local information of brain tumor, we introduce a new Transformer module, the Dilated Attention Convolution Transformer (DacFormer), into the generator. DacFormer comprises multi-scale dilated attention and a next convolutional block (NCB) with a Transformer construct. Leveraging these modules, we propose a novel generative adversarial transformer network (GDacFormer), as shown in Fig. 1. This network integrates adversarial learning and an improved Transformer to enhance segmentation performance. This combination captures both global and local information while using adversarial learning to enable the network to learn more effective information with limited training data. GDacFormer is extensively evaluated on the publicly available BraTS2019-2021 brain tumor segmentation datasets, and the results demonstrate its effectiveness. The main contributions are as follows:

  • We propose GDacFormer, a novel approach that integrates adversarial learning and an improved transformer module for MRI brain tumor segmentation. This network enhances the interaction of features between tumor regions while balancing global and local information, resulting in more accurate segmentation results.

  • We develop an improved Transformer module called DacFormer by introducing NCB and MSDA to enhance the brain tumor segmentation network. NCB enhances local feature extraction and complements global interactions. MSDA captures multi-scale feature representation and models long-range dependency. They collectively contribute to the enhanced performance of the GDacFormer.

  • GDacFormer is extensively evaluated on the BraTS2019-2021 brain tumor segmentation datasets and achieves highly competitive results compared to state-of-the-art methods.

Materials and method

Overall architecture of GDacFormer

The GDacFormer architecture, shown in Fig. 1, adopts a GAN framework with two main components: the generator and the discriminator. The generator, a cascaded U-Net, produces brain tumor images progressively from coarse to fine, evaluated by the discriminator.

Fig. 1
figure 1

The overall architecture of GDacFormer for brain tumor segmentation.

Full size image

The generator’s cascaded U-Net starts with a 3D U-Net for coarse segmentation, followed by a fine segmentation stage using an improved 3D U-Net. Input size for the coarse segmentation is \(5\times 128\times 128\times 128\), outputting \(3\times 128\times 128\times 128\). It is then concatenated with the original input and passed through the fine segmentation network for further processing. Additionally, to capture both global and local features of brain tumor, GDacFormer embeds three DacFormer layers in the generator’s bottleneck. In DacFormer, the multi-scale dilated attention module focuses on capturing contextual semantic dependencies at different scales, while the NCB enhances local feature extraction, thereby improving segmentation performance.

DacFormer layer

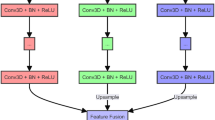
The DacFormer layer, shown in Fig. 2, enhances GDacFormer by balancing global and local feature extraction in MRI brain tumor segmentation. Embedded in the generator’s bottleneck, it integrates advanced attention mechanisms and convolutional operations. Comprising the Next Convolution Block (NCB) and Multi-Scale Dilated Attention (MSDA) module, it captures long-range dependencies and local features, providing a comprehensive approach to feature extraction.

As shown in Fig. 2, the input brain tumor image first passes through the NCB module, introduced in Sec. DacFormer layer and Fig. 4, where localized features are extracted using convolutional attention mechanisms. The processed image is then divided into 3D volumetric chunks, which are flattened and fed into the MSDA module, as shown in Fig. 4 of Sec. DacFormer layer. Here, multi-scale self-attention is applied to capture long-range dependencies and global details. The output from the MSDA module undergoes further transformation through a 2-layer MLP with GELU activation, introducing non-linear capabilities. The S-MSDA module enables the network to capture global features efficiently by enabling semantic information in different windows to interact to obtain cross-window links. Finally, the spatial information is reconstructed to form a 3D brain tumor image, integrating both detailed local features and broad contextual insights.

Fig. 2
figure 2

The structure of DacFormer Layer.

Full size image

Next convolution block (NCB)

The NCB module, depicted in Fig. 3, retains the advantages of convolutional operations, such as capturing local features, while complementing the transformer’s ability to model global interactions. The NCB includes a Multi-Head Convolutional Attention (MHCA) module, which serves as a token mixer, allowing information to be attended from different representational subspaces simultaneously(local and global). Eq. (1) detail the mathematical formulation of the NCB module, showing how the input is processed through MHCA and refined through a MLP with GELU activation. The formulations are as follow:

$$\begin{aligned} \begin{aligned} \tilde{X}^l&=\operatorname {MHCA}\left( X^{l-1}\right) +X^{l-1},\\ X^l&=\operatorname {MLP}\left( \tilde{X}^l\right) +\tilde{X}^l \end{aligned} \end{aligned}$$
(1)

where \(X^{l-1}\) denotes the input of \((l-1)\)th layer, and \(\tilde{X}^{l}\) and \(X^{l}\) are the outputs of MHCA and NCB.

Fig. 3
figure 3

The structure of Next Convolution Block (NCB).

Full size image

Feature extraction is performed in the MHCA module through the Convolutional Attention (CA) module, which achieves efficient localized feature learning by means of a multi-head form in order to simultaneously attend to information from different representational subspaces at different locations, as shown in Eq. (2):

$$\begin{aligned} \operatorname {MHCA}(X)=\operatorname {Concat}\left( \textrm{CA}_1\left( X_1\right) , \ldots , \textrm{CA}_h\left( X_h\right) \right) W. \end{aligned}$$
(2)

Here, MHCA captures information from h parallel representation subspaces. \(X=\left[ X_1, X_2, \ldots , X_h\right]\) denotes the partitioning of the input feature X into multiple heads in the channel dimension. W represents the projection layer equipped for MHCA to facilitate multi-head information interaction across. CA is the single-head convolutional attention, defined in Eq. (3):

$$\begin{aligned} \textrm{CA}(X)=\textrm{O}\left( W,\left( T_m, T_n\right) \right) , \text{ where } T_{\{m, n\}} \in X, \end{aligned}$$
(3)

where \(T_m\) and \(T_n\) are two tokens adjacent to the feature input X. O is an inner product operation with trainable parametes W and input tokens \(T_{\{m, n\}}\). By independently computing attention maps on each subspace through CA, MHCA is able to capture diverse channel-specific dependencies. These multiple attention are then aggregated, enabling the model to integrate complementary information across subspaces, thus providing richer and more discriminative feature. The MHCA is carried out with a group convolution (multi-head convolution), a point-wise convolution (conv 1x1x1 in Fig. 3), BatchNorm (BN) and ReLU are used for normalization and nonlinear activation. The ability of the DacFormer to extract local features is enhanced by adding the NCB module.

Multi-scale dilated attention (MSDA)

To leverage sparse tumor region information in brain tumor images, we construct the MSDA module to extract global, multi-scale fine semantic dependencies. The MSDA exploits the sparsity at different scales of the self-attention mechanism and models long-range dependencies using dilated attention (DA) in various feature subspaces. Besides self-attention computation, DA also increases the receptive field of the filters while maintaining the same number of parameters, making them efficient for capturing multi-scale features. Its structure is shown in Fig. 4. First, keys and values are sparsely selected in sliding windows centered on the query patch, and then self-attention is computed on the query patch. The detailed operation formula for a single DA is shown in Eq. (4):

$$\begin{aligned} {X_{DA}=\mathrm {{DA}}(Q,K,V,r), } \end{aligned}$$
(4)

where Q, K, and V represent the query, key, and value matrices, respectively, derived from the input feature, with each row of these matrices representing a query, key, or value vector. MSDA performs the self-attention computation within a sliding window centered on a region of size \(w \times w \times w\) and w is set to 7. Additionally, the sparsity in the self-attention process is controlled by defining \(r\in \mathbb {N}^{+}\). The computation of DA is given in Eq. (5):

$$\begin{aligned} \begin{aligned} x_{i j l}&=\operatorname {Attention}\left( q_{i j l}, K_r, V_r\right) , \\&=\operatorname {Softmax}\left( \frac{q_{i j l} K_r^T}{\sqrt{d_k}}\right) V_r, \\&\quad 1 \le i \le W, 1 \le j \le H, 1 \le l \le D, \end{aligned} \end{aligned}$$
(5)

where H, W, and D represent the height, width, and depth. \(k_r\) and \(V_r\) denote the keys and values selected from the feature maps K and V. \(d_k\) is the dimensionality of the keys. By sparsely selecting keys and values centered on queries, DA explicitly satisfies the properties of locality and sparsity, effectively and efficiently modeling long-range dependencies.

Fig. 4
figure 4

The structure of Multi-Scale Dilated Attention (MSDA).

Full size image

Similar to the NCB and vanilla vision transformer19, MSDA also employs multi-head DA, where each head performs DA (Eqs. 4–5) using vary dilation rates, it integrates multi-scale semantic information. We divide the channels of the feature map to n different heads and perform DA in each heads with different dilation rates. The MSDA is formulated in Eqs. (6):

$$\begin{aligned} \begin{aligned} h_i=\operatorname {DA}\left( Q_i, K_i, V_i, r_i\right) , \quad 1 \le i \le n,\\ X_{MSDA}=\operatorname {Linear}\left( \text{ Concat }\left[ h_1, \ldots , h_n\right] \right) , \end{aligned} \end{aligned}$$
(6)

where \(r_i\) is the expansion rate of the i-th head, and \(Q_i\), \(K_i\), and \(V_i\) are slices of the feature map fed into the i-th head. The outputs of all n heads \(\left\{ h_{i}\right\} _{i=1}^{n}\) are then concatenated and passed through a linear layer for feature aggregation. By this structural design, MSDA accurately combines semantic information at various scales within the receptive field and effectively reduces self-attention computation in background regions of brain tumor images.

Discriminator

The discriminator, shown in Figure 5, consists of four four convolutional blocks, each consisting of a 3D convolutional layer with a kernel size of \(1\times 1\times 1\), batch normalization (BN) layer and a LeakyReLU activation function. The \(1\times 1\times 1\) convolution kernel acts as a fully connected layer to maintain the accuracy of the discriminator’s judgment. The input to the discriminator is an image of size \(3\times 128\times 128\times 128\). The image generated by the generator module, along with the ground truth (GT), is fed into the discriminator.

Fig. 5
figure 5

The structure of the Discriminator.

Full size image

Loss function

To supervise and optimize tumor segmentation results, we use a hybrid loss function comprising three parts: adversarial loss (\(L_{adv}\))4, Dice loss (\(L_{Dice}\))20 and Cross-Entropy loss (\(L_{CE}\)). The adversarial loss ensures that the generated image is closer to the real image. Dice loss, frequently used alongside Cross-Entropy loss, is a common choice in medical image analysis to tackle class imbalance.

The hybrid loss is calculated as follows:

$$\begin{aligned} L_{{adv}} (\theta _{G} ;\theta _{C} ;y) = & E_{{(X,Y)}} \\ & \sim y\left[ { - \sum\limits_{{a \in H}} {\sum\limits_{{b \in W}} {\left\{ {\left( {1 - \eta } \right)\log \left( {\psi \left( Y \right)\left[ {a,b} \right]} \right) + \eta \log \left( {\psi 1 - \left( {\hat{Y}} \right)\left[ {a,b} \right]} \right)} \right\}} } } \right] \\ \end{aligned}$$
(7)

where y denotes the truth image, \(\theta _G\) denotes the generated image, \(\theta _c\) is used to discriminate the authenticity of the sample, \(\hat{y}\) denotes the segmentation result.

$$\begin{aligned} & {L_{Dice}=1-\frac{2\sum \nolimits _{l\in L} \sum \nolimits _{i\in N} y_i^{(l)} \hat{y}_i^{(l)}+\varepsilon }{\sum \nolimits _{l\in L} \sum \nolimits _{i\in N} (y_i^{(l)}+\hat{y}_i^{(l)})+\varepsilon }, } \end{aligned}$$
(8)
$$\begin{aligned} & {L_{CE}=-\sum _{i\in E}\sum _{l\in L} y_i^{(l)}log \hat{y}_i^{(l)},} \end{aligned}$$
(9)

where N is the set of all samples, L represents the set of all labels of the sample, \(y_i^{(l)}\) is the one-hot coding (0 or 1) of the ith sample, labeled l, and \(\hat{y}_i^{(l)}\) denotes the size of the predicted probability of the same sample i, labeled l. \(\varepsilon\) is the minima set to prevent the division by 0 condition from occurring in the computation and is set to \(1\times 10^{-5}\).

To maximize the convergence speed, the adversarial loss is multiplied by a coefficient \(\alpha\), set to 0.3 in this paper. The three components of the loss function are summed, and the complete loss function is expressed as:

$$\begin{aligned} {Loss=\alpha \times L_{adv}+L_{Dice}+L_{CE}} \end{aligned}$$
(10)

With such a hybrid Loss Function design, \(L_{Dice}\) can effectively alleviate the common category imbalance problem in medical images by optimizing the spatial overlap between the predicted segmentation and the real labels, and enhance the segmentation effect on small targets such as ET. \(L_{CE}\) aims at pixel-level accuracy and provides stable and strong gradient information at the early stage of training, which helps the model to converge quickly and improve accuracy. \(L_{adv}\) is used to improve the structural realism and boundary coherence of the segmentation map output by the generator, which can further reduce the artifacts and unreasonable boundaries in the prediction map and make the segmentation results closer to GT.

Experiments

Experimental details

Experimental setup

The experiments are performed using the PyTorch deep learning framework, with the network trained for 1000 epochs, a batch size of 1, and the Adam optimizer. Exponential decay is applied to the learning rate, with an initial learning rate is \(1\times 10^{-3}\), and the weight decay coefficient is \(1\times 10^{-4}\). The hardware environment of the experiments is configured with 1 Intel(R) Xeon(R) Gold 5222 CPU @3.80GHZ and 1 Nvidia RTX3090 GPU graphics card (24GB).

Datasets and data processing

To thoroughly assess the performance of the proposed method on the MRI brain tumor segmentation task, we utilize the publicly available BraTS 2019-2021 brain tumor segmentation dataset21,22. These datasets include both a training set and a validation set. The training set images are accompanied by ground truth (GT), manually annotated by a professional physician, and consist of four categories: healthy site (label 0), necrotic region (label 1), edematous region (label 2), and enhanced tumor (label 4). The GT labels of the validation set are not disclosed. The specific composition of the dataset is shown below: (1) BraTS 2019: 259 high-grade glioma(Hgg) cases and 76 low-grade glioma(Lgg) cases in the training set and 125 unknown tumor samples in the validation set. (2) BraTS 2020: 293 Hgg cases and 76 Lgg cases in the training set and 125 unknown tumor samples in the validation set. (3) BraTS 2021: 993 Hgg cases and 258 Lgg cases in the training set and 219 unknown tumor samples in the validation set.

As shown in Figure 6, each brain tumor data sample consists of images from four modalities: T1, T1ce, T2, and Flair. An image size of \(240 \times 240 \times 155\) for each modality and all of them co-registered to a common anatomical template (\(SRI^{45}\)) and are resampled to 1\(mm^3\). In addition, the three regions used to evaluate MRI brain tumor segmentation are Whole Tumor (WT), Tumor Core (TC), and Enhancing Tumor (ET), where WT contains labels 1, 2, and 4, TC contains labels 1 and 4, and ET contains label 4. By uploading the segmented image results of the validation set to the CBICA online platform, we can receive the evaluated results.

Fig. 6
figure 6

MRI maps of brain tumor across four modalities, along with ground truth images. From left to right: Flari, T1, T1ce, T2 and Ground Truth. Each color corresponds to a tumor class (label): red (label 4) for necrosis and non-enhancing, green (label 2) for edema, and yellow (label 1) for enhancing tumor.

Full size image

Evaluation criterion

Model performance is assessed using Dice Similarity Coefficient (DSC) and Hausdorff distance, following15,17,23,24. DSC measures the overlap between model segmentation and ground truth (GT) segmentation. The Dice Similarity Coefficient is calculated as in Eq. (11):

$$\begin{aligned} {DSC=\frac{2TP}{FP+2TP+FN}} \end{aligned}$$
(11)

where TP, FP, and FN represent the number of voxels correctly predicted to be tumor, the number of voxels incorrectly predicted to be tumor, and the number of voxels incorrectly predicted to be non-tumor, respectively.

Hausdorff distance is employed to measure the maximum distance between two image boundaries. The calculated results are generally multiplied by 95%, i.e., the formula is shown in Eq. (12).

$$\begin{aligned} HD\left( T,P\right) =\max \left\{ \begin{array}{ll} sup_{i\in T}inf_{p\in P}d\left( t,p\right) ,\\ sup_{p\in P}inf_{i\in T}d\left( t,p\right) \end{array}\right\} \end{aligned}$$
(12)

where T and P represent the GT and prediction region, respectively, and t and p are points in the two regions. d(t, p) denotes the distance function between point t and point p.

Results

Ablation study

To show the effectiveness of our network model, ablation experiments are conducted on the BraTS2020 validation set. The U-Net is used as the baseline approach. Based on the baseline network, GU-Net is constructed by incorporating GANs to verify the effectiveness of the adversarial learning approach. GU-Net+MHSA, GU-Net+MSDA and GDacFormer are used to evaluate the effectiveness of the MSDA module and NCB module in brain tumor segmentation. Where MHSA stands for multi-head self-attention in the ViT19.

Table 1 Ablation study (%) on BraTS2020 Validation set. The ET, WT, and TC metrics are presented as the mean across all samples, while MEAN represents the average of ET, WT, and TC results.
Full size table

Table 1 presents a detailed comparison of the performance of different models using the DSC and HD95 metrics on brain tumor segmentation tasks. Bold in all tables represents the highest value. Furthermore, the p-values presented in Table 1 are calculated using the Wilcoxon signed-rank test, comparing the GDacFormer with each ablated version of the model. Our main goal is to statistically demonstrate that GDacFormer performs significantly better than the versions marked with an asterisk. This provides evidence for the effectiveness of each component in our model. The baseline model, U-Net, achieves a mean DSC of 82.4% and a mean HD95 of 19.89 mm. Incorporating adversarial learning into the U-Net, resulting in the GU-Net, improves the mean DSC to 84.0% and reduces the mean HD95 to 14.26 mm, demonstrating the effectiveness of adversarial learning in enhancing segmentation accuracy and boundary alignment. Further to visualise the role of the MSDA module we introduce the traditional MHSA module in GU-Net and MSDA module in GU-Net respectively. These model achieves a mean DSC of 84.2%/84.8% and a mean HD95 of 13.82/13.43 mm. The results of GU-Net+MSDA model are better than GU-Net+MHSA model, benefiting from the long-term modeling capabilities and aggregates semantic multi-scale information of the MSDA, which enhances both the overlap and boundary metrics. Our proposed model, GDacFormer, which incorporates the NCB module in addition to the adversarial learning and MSDA, achieves the highest performance among all models. It records a mean DSC of 85.3% and a mean HD95 of 11.76 mm. This indicates that GDacFormer effectively balances global and local feature extraction, leading to superior segmentation accuracy and boundary precision. The improvements in both metrics highlight the robustness and competitiveness of GDacFormer in MRI brain tumor segmentation tasks, demonstrating its potential for clinical application.

Comparison with state-of-the-art

To better demonstrate the competitiveness of GDacFormer, we also compare it with the existing state-of-the-art brain tumor segmentation methods on the BraTS2019-2020 Validation sets and BraTS2021 Training set, and the comparative results on the three sets under DSC and HD95 metrics are reported in Tables 2, 3 and 4. In Tables 2, 3 and 4, the p-values were computed between GDacFormer and all compared methods based on the DSC and HD95. These values are used to highlight statistically significant improvements in each column of the results. This addition further supports the effectiveness of GDacFormer.

Table 2 Comparison results of DSC (%) and HD95 (mm) metrics on the BraTS2019 Validation set.
Full size table
Table 3 Comparison results of DSC (%) and HD95 (mm) metrics on the BraTS2020 Validation set.
Full size table
Table 4 Comparison results of DSC (%) and HD95 (mm) metrics on the BraTS2021 Training set.
Full size table

Table 2 showcases the performance of different models on the BraTS2019 validation set. GDacFormer demonstrates performance with a mean DSC of 84.5% and a mean HD95 of 4.61 mm. These results indicate that our model excels in both segmentation accuracy and boundary precision. Compared to CNN-based methods such as MBANet, SMRAU-Net, AMMGS, and SPA-Net, GDacFormer leads the DSC by 0.8%, 3.3%, 2.1% and 1.2%, showing clear improvements. This is due to the fact that GDacFormer uses both adversarial training and introduces global information compared to the above networks. Additionally, it outperforms Transformer-based approaches such as TransBTS, IncompleteMriSeg, and GMetaNet. GDacFormer leads the DSC by 0.9%, 0.6% and 0.8%. This is due to the fact that GDacFormer further enhances the ability of model global information to interact with local information. The performance is also better than GAN-based methods like GAU-Net(2.7%) and GVAT-Net(2.3%), highlighting the robustness and efficacy of GDacFormer in handling complex segmentation tasks. This is due to the fact that GDacFormer embeds the DacFormer layer on top of the adversarial training, which improves the model’s ability to capture global information.

The evaluation results on the BraTS2020 validation set, as shown in Table 3, further validate the effectiveness of GDacFormer. The model achieves the highest mean DSC of 85.3% and a mean HD95 of 11.76 mm. Compared to CNN-based methods like dResU-Net, SMRAU-Net, AMMGS, SPA-Net, and Residual U-Net, our model leads the DSC by 1.9%, 4.7%, 2.6%, 1.4% and 5.2%. This is due to the fact that GDacFormer uses both adversarial training and introduces global information substantial enhancements in segmentation performance. GDacFormer also outperforms Transformer-based models such as TransBTS, IncompleteMriSeg, U-Netr, and MedNeXt. GDacFormer leads the DSC by 1.8%, 0.5%, 6.8% and 0.5%. Demonstrates its superior ability to balance and integrate global context and local detail extraction. Furthermore, GDacFormer leads DSC the DSC by 3.7%, 2.9% and 4.4% than GAN-based methods such as SRAU-Net, GVAT-Net, and GATransU-Net, indicating that the integration of adversarial learning, MSDA, and NCB modules significantly increases segmentation accuracy and boundary precision.

Table 4 shows the results of the models on the BraTS2021 training set using 5-fold cross-validation. GDacFormer achieves an impressive mean DSC of 91.2% and a mean HD95 of 6.29 mm, reflecting excellent performance in segmentation tasks. This performance is notably higher than that of CNN-based methods like dResU-Net, nnU-Net, MMEF-nnUNet, SPA-Net and Residual U-Net. GDacFormer leads the DSC by 7.1%, 2.4%, 1.1%, 3.5% and 7.0%. Among transformer-based models, GDacFormer shows better DSC values than TransBTS, U-Netr, nnFormer and SSCFormer by 2. 6%, 1. 0%, 0. 7% and 0.8%. And outperforms MedNeXt in HD95 by 0.67mm. Furthermore, our model outperforms GAN-based methods such as SRAU-Net (by 1.5%) and GVAT-Net (by 5.3%), further demonstrating the effectiveness and robustness of GDacFormer in brain tumor segmentation. The experimental results demonstrate that GDacFormer exhibits strong competitiveness.

The combined analysis of Tables 2, 3 and 4 clearly demonstrates that GDacFormer consistently outperforms state-of-the-art models in different datasets and evaluation metrics. The model’s integration of adversarial learning, MSDA, and NCB modules significantly enhances its capability to accurately segment brain tumor while maintaining precise boundary alignment. These comprehensive improvements highlight GDacFormer as a highly effective and competitive solution for MRI brain tumor segmentation. Consistent performance gains across different datasets emphasize the robustness and generalizability of our proposed model, making it a valuable tool for clinical applications in brain tumor segmentation.

Visualization results

We compare visualization results with state-of-the-art methods in the BraTS2021, shown in Figs. 7, 8 and 9. Each visualized result highlights three distinct regions within the brain tumor: edema (green), enhanced tumor (yellow), and necrotic (red).

Fig. 7
figure 7

Visualization of comparison with state-of-the-art methods on the BraTS2021 Training set. The visualized results contain green, yellow, and red regions, representing the edema region, enhanced tumor region, and necrotic region, respectively. (Transverse section).

Full size image
Fig. 8
figure 8

Visualization of comparison with state-of-the-art methods on the BraTS2021 Training set. (Coronal section).

Full size image
Fig. 9
figure 9

Visualization of comparison with state-of-the-art methods on the BraTS2021 Training set. (Median sagittal section).

Full size image

First, as shown in Fig. 7, we show the transverse section visualization results. In the first case, the GDacFormer’s segmentation results closely resemble the ground truth, particularly in the red region within the blue box. This indicates that GDacFormer accurately captures the necrotic regions of the tumor, providing a clear advantage over other models. Accurate detection and delineation of the necrotic region are critical to effective treatment planning and prognosis. In the second case, the segmentation results show the distribution of small pieces of the red region. GDacFormer demonstrates a clear advantage in accurately segmenting these small, scattered necrotic areas. This capability is vital to ensure that even the smallest tumor regions are identified and treated appropriately, which can significantly impact patient outcomes. The third case focuses on the green region within the blue box, which represents edema. GDacFormer outperforms other models by providing a more precise segmentation of the edema regions. Precise segmentation of the edema is vital to assess the extent of tumor-induced swelling and to plan appropriate surgical or therapeutic interventions.

Second, as shown in Fig. 8, we show the visualization results of the coronal section. The area in the blue box clearly shows the advantage of GDacFormer’s segmentation, in the first case only GDacFormer has no incorrectly segmented red regions. In the second case, only the green region segmented by GDacFormer is coherent and closest to GT. In the third case, again focusing on the red region, all networks incorrectly segment a certain amount of the red region, but GDacFormer is the network with the smallest incorrectly segmented region.

Third, we show the visualization results of the Median sagittal section in Fig. 9. In the first and second cases, where we focus on the red region, the error region of the GDacFormer segmentation is clearly the smallest. In the third case, focusing on the green region of the segmentation, GDacFormer is the closest to GT.

In general, Figs. 7, 8 and 9 demonstrates the superior performance of GDacFormer, effectively capturing all tumor regions with high precision. This visual evidence supports the comparison results, confirming GDacFormer as a reliable method for MRI brain tumor segmentation.

Discussion

According to the evaluation experiments, it can be seen that the GAN-based segmentation method combines well the advantages of the U-Net semantic segmentation model and the adversarial learning architecture, thus achieving good segmentation results in the MRI brain tumor segmentation application. Meanwhile, after DacFormer is embedded, additional segmentation accuracy can be gained, which shows the importance of capturing both local and global feature information for segmentation.

Additionally, compared with state-of-the-art works, by well integrating adversarial learning as well as transformer mechanism, GDacFormer gains satisfactory results on three brain tumor datasets. Specifically, it achieves the optimal mean DSC values on both of BraTS2019 and BraTS2020 Validation sets. Although it is slightly worse than MedNeXt in the mean DSC value in the BraTS2021 training set, it outperforms MedNeXt on the WT and TC segmentation. These experimental results demonstrate the good competitiveness of the proposed GDacFormer on brain tumor segmentation task.

Finally, it should also be noted that although GDacFormer achieves the optimal mean DSC results on BraTS2019 and BraTS2020 Validation sets, the corresponding results are only 84.5% and 85.3%, respectively. Even on the BraTS2021 training set, MedNeXt only can achieve the highest mean DSC value of 91.4. These results also indicate that MRI brain tumor segmentation remains a very challenging medical task due to the small percentage of brain tissue, as well as various shapes and sizes of brain tumors.

Conclusion

This work proposes a novel MRI brain tumor segmentation method called GDacFormer, which integrates advanced Transformers with adversarial learning into a single network. The generator incorporates a new transformer module called DacFormer, which consists of Multi-Scale Dilated Attention (MSDA) and Next Convolution Block (NCB) modules. These components work synergistically to capture long-range dependencies at various scales and enhance local feature representations, offering a comprehensive approach to feature extraction. The discriminator ensures that the generated segmentation maps are as close to the ground truth as possible by distinguishing between real and generated images. Extensive experimental results on three brain tumor segmentation datasets demonstrate its effectiveness and competitiveness. In the future, we plan to evaluate the model in other medical image segmentation tasks to demonstrate its generalize ability. In addition, exploring other learning strategies within the adversarial learning or unsupervised38 framework for brain tumor segmentation is a future research interest.