Introduction

With the development of society and economy, a large number of underground structural engineering projects have emerged worldwide, such as railways, highway tunnels, hydraulic tunnels and underground factories, urban subways, municipal pipelines, river crossing tunnels, building basements and underground commercial streets. For example, the Montreal Underground, after decades of development, has become the largest urban underground space utilization project in the world, with an area of 36 square kilometers, equivalent to 1/10 of the total urban area. According to data, as of the end of 2022, the cumulative construction area of underground space in Chinese cities was 2.962 billion square meters. However, at the same time, underground structural problems around the world are becoming increasingly severe.

Buried below the surface, underground structures are difficult to observe and test for durability. They are often subject to complex and variable loading conditions and are influenced by groundwater. The heterogeneity, non-linearity and rheological properties of the geological materials also greatly affect the durability of underground structures. It is therefore challenging to simulate the actual damage patterns of these structures.

Since Kaplan1 first applied fracture mechanics to concrete materials, extensive research has been carried out in this field, resulting in many significant findings. However, the application of fracture mechanics to concrete materials is not without its limitations. The main challenges include studying the behavior of concrete prior to the appearance of macroscopic cracks and obtaining stable values of mechanical indicators that represent concrete fracture criteria, such as the fracture toughness value KIC, under laboratory conditions.

Since the late 1970s, researchers have developed methods to study the meso-mechanics of concrete in order to establish the relationship between the inhomogeneity of various defects in concrete and their characteristics in macro-mechanical properties. As a result, damage mechanics emerged as an essential development and important complement to fracture mechanics. Dougill2 first introduced the concept of damage into the study of concrete mechanics, studying the failure problem of concrete based on the concept of progressive fracture, and applying damage mechanics, disturbance states, and multi yield surface theory to the development of solid material mechanics. Subsequently, many researchers have proposed various damage models and damage evolution equations for concrete to explain the damage and failure phenomena.

Researchers have proposed various constitutive theories and evolution equations for damaged materials. Overall, current research in damage mechanics focuses mainly on macroscopic isotropic damage, anisotropic damage, and meso-damage theories. Macroscopic damage mechanics studies material damage and failure based on continuum damage mechanics, while meso-damage mechanics theories analyze the mechanical behavior of materials based on their micro- and mesoscopic constituents and structures and establish macroscopic constitutive relationships taking damage into account. For isotropic damage theory, Bellis et al.3 presented a low-order virtual element formulation for modelling the strain-softening response of quasi-brittle materials. For anisotropic damage theory, Desmorat4 studied a damage-induced anisotropic model of concrete-like materials. For meso-damage theory, Gurson5 presented a relatively complete set of constitutive equations and established a micro-void cell model on finite domains. This model has been widely accepted and continues to be developed and improved.

Modern concrete tests have shown that the macroscopic mechanical properties of concrete are related to the development of internal cracks. The macroscopic mechanical properties of concrete materials are controlled by their microscopic structure, and the macroscopic failure behavior is the result of the accumulation and development of damage and fracture behavior at the microscopic scale. Starting from the microstructure of concrete, using the research methods of meso-mechanics, grasping the non-uniformity of concrete materials and their mechanical properties, and combining theoretical and experimental results, establishing numerical models to study the mechanical properties and failure process of concrete materials is the most reliable and valuable research method.

In the field of underground concrete structures, Zuo and Zhan6 proposed a new method for damage detection in underground structures based on back-propagation neural network. This method takes the curvature change rate of the structure as the input scalar of the BP neural network, and uses the method of reducing the unit elastic modulus E to simulate the damage location and degree of the structure. The results indicate that the use of BP neural network can accurately identify the degree of damage to underground engineering structures, and can conveniently and effectively solve the problem of damage identification for underground engineering structures. Zhang7 investigated the effects of lining strength and thickness on the damage and failure modes of the vertical shaft lining under horizontal seismic action. The results showed that the axial force, shear force and bending moment of vertical shafts all experienced sudden changes at the rock–soil interface. The damage in the vertical shaft is located at the rock–soil interface and the failure mode is axial tensile failure, and the failure mode is axial tensile damage, with axial tensile stress playing a controlling role in its damage. Therefore, measures should be taken in the design to reduce the axial tensile force at the interface between the structure and the soil. Wang et al.8 defined a double scalar damage variable and established a stochastic damage constitutive model for concrete structures in high-speed railway tunnels by introducing a hardening function and revising the elastoplastic Helmholtz free energy. Jiang et al.9 established seismic fragility curves for underground metro stations by considering inter-story displacement angles as structural damage indicators and peak ground acceleration (PGA) as seismic intensity indicators. They used both the cloud map method and incremental dynamic analysis to calculate the results. The results showed that the post-earthquake probability of functional failure for underground structures assessed by both methods is essentially equivalent. Compared to the cloud map method, seismic fragility analysis based on incremental dynamic analysis can provide the failure probability of an underground structure under any seismic intensity. Gong et al.10 conducted corrosion tests on specimens under bending and sulfate attack, and investigated the reduction of residual flexural strength and relative dynamic modulus of elasticity of concrete. The results showed that the coupling effect of long-term bending and sulphate attack accelerated the reduction of material properties of concrete. Blikharskyy et al.11 measured the mechanical properties, fatigue characteristics, and corrosion cracking sensitivity of reinforced St3GPF steel samples. Under the action of static tension, experimental tests on samples in corrosive environments have shown that corrosion damage has little effect on strength characteristics. In addition, the cyclic loading in corrosive environments significantly reduces the fatigue limit to 20% to 24% of the original sample yield strength, which is 2–3 times lower than the fatigue limit of undamaged samples. Additional, Blikharskyy et al.12 also presents experimental studies of concrete prisms under the simultaneous action of an aggressive environment and a constant level of compressive force. In total, 32 prisms under different loading conditions and in different aggressive medium were tested. Samples were divided in series, for which different load levels were chosen (0.25fck, 0.35fck, 0.45fck). Additionally, control samples in the air and immersed in water were tested. Results of the study showed that destruction occurred due to the presence of corrosion damages of concrete and a reduction of the cross-sectional area. The stresses in the concrete at the destruction stage were less than the value of the prism strength by 10–12%. Additionally, experimental and theoretical diagrams of concrete with corrosion damages were obtained and compared. The ultimate deformations of concrete with corrosion damage, which correspond to the prismatic strength of concrete, in comparison with undamaged concrete were lower by 11–18%. The research conducted in the aforementioned literature fully demonstrates that the combined effect of long-term loading and aggressive environments may have the synergistic influence on the material durability, in particular for composite materials like concrete or reinforced concrete, where individual components may reveal different behaviors under the aggressive attack. To study the performance degradation and incremental damage of underground structures under earthquakes, Wang et al.13 established a soil-underground structure interaction model based on a two-story and three-span subway station. They selected 85 sets of natural earthquake records and corresponding main and aftershock sequences from 14 earthquakes as inputs to compare and study the seismic response characteristics of the underground structure. The results showed that the seismic damage to the underground structure tended to be more severe in general when the effects of the main and aftershocks were considered, compared to the main shock alone. However, the magnitude and extent of the incremental damage depends on factors such as the peak ground acceleration ratio of the main and aftershock sequences, the seismic motion characteristics, and the polarity of the main and aftershocks. Ma et al.14 conducted seismic performance tests on carbon fibre reinforced polymer (CFRP) reinforced concrete columns and analyzed the influence of CFRP on the lateral stiffness and deformation capacity of reinforced concrete columns. Based on the improved Park-Ang model, they evaluated the seismic damage levels of reinforced and unreinforced columns. The results showed that when the seismic PGA ranges from 0.3 g to 0.4 g, the lower level reinforced columns of the metro station structure are in a state of easy to repair or repairable. Many scholars’ studies have also shown that the use of CFRP reinforcement schemes has a good improvement effect on the ductility of various engineering structures (and components), and can thereby increase the ability of the structure to resist deformation and failure, as well as enhance the durability of the structure under various degradation factors. In order to study the physical and chemical properties of CFRP materials and their application methods and construction details in steel frame reinforcement, Liu15 comprehensively quantified the improvement effect of carbon fiber reinforcement on the strength, ductility, and durability of steel structures through static loading testing, dynamic response analysis, and long-term durability testing. The research results indicate that CFRP significantly improves the performance of steel frame structures, including significant improvements in strength, ductility, and durability.

Based on the above literature review, the application of damage mechanics theory in the study of the durability of underground concrete structures is still very limited and there is a lack of systematic and in-depth studies of theoretical and practical methods. Existing research has mainly focused on the material level, and there is a lack of sufficient investigations at the structure level. In addition, existing durability studies have mainly used single factor analysis with minimal consideration of the interactions between different factors, which does not reflect real world conditions16.

This paper focuses on the durability of underground concrete structures. Durability degradation of reinforced concrete materials is an accumulation of damage formed under external loads and environmental factors, which seriously threatens the safety, serviceability and durability of reinforced concrete structures. Thus, damage and durability are inextricably linked and all forms of durability degradation can ultimately be converted into physical or chemical forms of damage. Therefore, it is reasonable to use damage theories and methods to study the durability of underground structures. Although significant research has been conducted in this field, it is still far from sufficient for practical engineering applications. Moreover, most of the research results have been obtained for two-dimensional problems. The application of three-dimensional damage theory to practical problems is still rare, especially in the study of the durability of underground structures. Existing research mainly adopts macroscopic damage mechanics theories. Considering that actual underground engineering structures often suffer from long-term combined effects of water and soil pressure and various corrosive substances, where the magnitude of pressure and its different states of tension or compression have different impacts on structural durability damage, this paper applies the micro damage theory to the three-dimensional analysis of durability damage of underground reinforced concrete structures under external loads, carbonization, and ion corrosion to evaluate and analyze their durability life. Here, durability life refers to the time during which an engineering structure can be used or put into service normally due to long-term damage and deterioration caused by various durability factors.

Deterioration degree and its function

In order to better quantify the durability degradation of concrete structures, in this paper the degree of deterioration is defined as the extent to which a structure is damaged and degraded due to the influence of the external environment, mechanical or physical durability factors. Deterioration generally begins with the development of micro-pores and voids within the structure. The degree of deterioration is mainly manifested in two aspects, namely the degree of corrosion caused by environmental factors and the corresponding damage conditions such as reduction in load carrying capacity, cracking or deformation of the structures. The factors influencing durability can be categorized into mechanical, environmental, material and operational time factor, and their effects on the degree of structural deterioration can be expressed mathematically as follows:

$$L = \varphi (f,c,I,t)$$
(1)

where, \(\varphi \left( \cdot \right)\) is the deterioration function, L is the deterioration degree of the structure, f, c, I, and t represent the mechanical factor, environmental factor, inner factor of materials, and operational time factor, respectively.

When the degree of corrosion caused by environmental factors is taken as the evaluation index of structural deterioration, the corrosion depth X can be used as a quantitative indicator of deterioration. When the condition of structural damage is considered as the evaluation index of deterioration, the structural damage variable D or the volume percentage of micro-voids in the structure f* can be used to characterize the degree of deterioration. In addition, other indices such as crack width, compressive strength, bearing capacity, section loss rate, etc. can be used to represent the degree of deterioration of a structure. For example, if the corrosion depth of concrete X is taken as the deterioration evaluation index, and the influence of different loading conditions and concrete mixes is considered, then Eq. (1) can be written as follows:

$$L = X = \varphi (\sigma ,h,w/c,t)$$
(2)

where, X is the corrosion depth of concrete, σ is the stress in the structure, \(h\) is the concentration of aggressive agents in the environment and \(w/c\) represents water-cement ratio of concrete.

In fact, in addition to the concentration of corrosive agents h mentioned in formula (2), the external environmental factors that affect the deterioration of concrete also have a significant impact on the deterioration of the structure, including the temperature and humidity of the environment. Kopiika et al.17 studied the process of deterioration caused by increased corrosion rate of concrete structures and the decrease in durability performance in response to global climate change and the increase in carbon dioxide emissions. A study was conducted on the existing carbonisation-induced numerical models, taking into account the changes in diffusion coefficient due to temperature and humidity over time, as well as increased CO2 levels in urban environment. The model was further modified and applied to practical engineering case studies. Results demonstrate the criticality of structural deterioration in conditions of global climatic change and this highlights the need to account for environmental changes in design and practice. Stewart et al.18 used the Australian region as an example to describe a probabilistic and reliability-based approach that predicts the probability of corrosion initiation and damage (severe cracking) for concrete infrastructure subjected to carbonation and chloride-induced corrosion resulting from elevated CO2 levels and temperatures. It was found that carbonation-induced damage risks can increase by over 400% over a time period to 2100 for some regions in Australia. Damage risks for chloride-induced corrosion increase by no more than 15% over the same time period due to temperature increase, but without consideration of ocean acidity change in marine exposure.

This paper only takes one typical specific factor respectively from mechanics, environment, and internal material factors as an example to study the durability of underground structures. The impact of other factors such as temperature and humidity will be discussed separately in other papers.

Damage analysis of concrete structures

Meso-damage model for concrete

In the last decades, many meso-mechanical models have been proposed by researchers to study the damage and fracture processes in concrete. Among these models, the most typical and representative ones are the Gurson meso-damage model and its improved version. In addition, Yue et al.19 used the meso finite element method to simulate the crack propagation and damage processes of recycled aggregate concrete (RAC) specimens under uniaxial tension and compression. Vasiukov et al.20 presented a mesoscale material model for fiber reinforced composites based on coupled anisotropic viscoelasticity–viscoplasticity and anisotropic continuous damage mechanics. Wang et al.21 developed a mesoscale concrete model in which spherical coarse aggregates and voids were considered to be randomly packed without overlap. The modelled stress–strain curves and crack patterns showed excellent agreement with those from experiments in both tension and compression. Liu and Li22 developed a micro-damage model based on nonlocal theory and stochastic damage mechanics to investigate the plastic slip effect on damage and the strain evolution and damage evolution. Li et al.23 developed a finite element model for a concrete structure in which concrete members are subjected to localized tension and compression to study concrete fracture and the associated mesh sensitivity. Yang et al.24 developed a practical algorithm based on the Gurson damage model. The improved Gurson model and its application to the analysis of concrete damage in underground structures are discussed next.

The Gurson model5 consists of a relatively complete set of constitutive equations that can describe the effect of micro-void damage on the plastic deformation of materials. This model allows the use of numerical calculations to handle void interactions. The damage variable of the Gurson model, the void percentage, has a clear geometric meaning and an explicit physical meaning, allowing the simultaneous consideration of micro-void nucleation and its growth process. Tvergaard and Needleman25 improved the Gurson model by considering the interactions between voids and the evolution of micro-voids. In their study, the material is no longer considered to be plastically incompressible. The improved Gurson model is known as the G-T-N model and has a wide range of applications. For example, the G-T-N model has been widely used in simulating damage and fracture of metal materials, analyzing damage and brittle fracture of concrete structures (components), predicting necking and fracture of steel pipes and plates, and other fields.

For the cell micro-element within a finite size domain containing a spherical void, the stress, strain and displacement within the domain can be represented by σ, ε and u respectively, and the macroscopic stress and strain of the element are denoted by Σ and E respectively. For a material according to the Drucker–Prager (D–P) criterion, the damage yield surface equation is expressed as follows

$$F(\sigma ) = \mu \sigma_{m} (\sigma ) + \sigma {}_{e}(\sigma ) - \sigma_{s} = 0$$
(3)

where, \(\sigma_{m}\) is the spherical stress of the material and μ is a material constant, and \(\sigma_{e}\) is the equivalent stress of the matrix material,\(\sigma_{s}\) represents the yield stress of the matrix.

For the cell element of the D–P matrix material, the evolution equation of porosity can be expressed as follows:

$$\dot{f} = (1 - f)(\dot{E}_{kk}^{p} - \dot{\varepsilon }_{kk}^{p} ) + A\dot{\varepsilon }_{e}^{p} + B\dot{\Sigma }_{m}$$
(4)

where, \(\dot{E}_{{{\text{kk}}}}^{{\text{p}}}\) and \(\dot{\sum }_{{\text{m}}}^{{}}\) are the mean values of the macroscopic plastic volume strain and stress of the element, respectively, \(\dot{\varepsilon }_{{{\text{kk}}}}^{{\text{p}}}\) and \(\dot{\varepsilon }_{{\text{e}}}^{{\text{p}}}\) are mean values of plastic volume strain and plastic strain of the matrix, respectively. In Eq. (4), the first and the last two items on the right represent the porosity increment due to voids growth and voids nucleation, respectively.

When \(\Sigma {}_{m} \ge 0\) and \(\Sigma {}_{m}\) takes the maximum value, we can get the following:

$$A = 0, B = \frac{{f_{N} }}{{S\sigma_{S} \sqrt {2\pi } }}\exp \left[ { - \frac{1}{2}\left( {\frac{{\Sigma_{m} - \sigma {}_{N}}}{{S\sigma_{S} }}} \right)^{2} } \right]$$
(5)

When \(\Sigma {}_{m} < 0\) and \(\varepsilon_{e}^{p}\) takes the maximum value, we have the following:

$$A = \frac{{f_{N} }}{{S\sqrt {2\pi } }}\exp \left[ { - \frac{1}{2}\left( {\frac{{\varepsilon_{e}^{p} - \varepsilon {}_{N}}}{S}} \right)^{2} } \right], B=0$$
(6)

where, \(f_{N}\) is the volume percentage of void nucleation, \(\sigma_{N}\) and \(\varepsilon_{N}\) represent the stress and strain of void nucleation, respectively, and S is the variance of the random nucleation.

The formation of voids is accompanied by deformation of the material. The existing voids gradually grow, and new voids are constantly generated26, which increases the total volume of voids:

$$\dot{f} = \dot{f}_{growth} + \dot{f}_{nucleation}$$
(7)

where, \(\dot{f}\) is the total volume increment of voids, \(\dot{f}_{growth}\) and \(\dot{f}_{nucleation}\) are the increments resulting from void growth and void nucleation, respectively.

$$\dot{f}_{growth} = (1 - \dot{f})\dot{\varepsilon }_{m}^{p}$$
(8)

where, \(\dot{\varepsilon }_{m}^{p} = (\dot{\varepsilon }_{11}^{p} + \dot{\varepsilon }_{22}^{p} + \dot{\varepsilon }_{33}^{p} )/3\) is the plastic part of the volume strain component.

Strain dominated nucleation theory can be further used to deal with the problem of void nucleation:

$$\dot{f}_{nucleation} = F\dot{\varepsilon }_{eq}^{p}$$
(9)
$$F = \frac{{f_{N} }}{{S\sqrt {2\pi } }}\exp \left[ { - \frac{1}{2}\left( {\frac{{\varepsilon_{eq}^{p} - \varepsilon {}_{N}}}{S}} \right)^{2} } \right]$$
(10)

where, F is the strength function of void nucleation, \(\varepsilon_{eq}^{p}\) is the corresponding plastic strain and \(\varepsilon_{N}\) is the mean strain of void nucleation.

Next, the application of finite element method in damage analysis will be discussed. Damage mechanics analysis of structures is similar to elastoplastic analysis in terms of basic principles and methods. However, when considering damage analysis, an additional damage variable, D, should be considered compared to the elastoplastic analysis of undamaged structures. Therefore, the governing equations together with the initial and boundary conditions used in undamaged structures can be used to analyze damaged structures. Combined with the constitutive and evolution equations of damaged concrete materials, this provides the solution to the structural damage mechanics analysis. Equations can be established for various types of practical engineering structures. Finite element software is then used to determine the internal forces and damage states in any part of the structure. For a damaged concrete material, the constitutive equation can be expressed as follows:

$$\sigma = c(D)\varepsilon$$
(11)

In the case of non-linear elastic and elastoplastic problems with small deformations, the governing equilibrium equation can be expressed in the following way:

$$\sigma_{i,j} + f_{i} = 0$$
(12)

where, \(\sigma_{i,j}\) represents the stress tensor, and fi represents the physical force exerted on the structure.

The strain–displacement relationship is represented as follows:

$$\varepsilon_{ij} = \frac{1}{2}(u_{i,j} + u_{j,i} )$$
(13)

where, \(\varepsilon_{i,j}\) is the strain component, ui,j and uj,i is the displacement component.

The displacement boundary conditions are expressed as follows:

$$\left. u \right|_{{s = s_{u} }} = \overline{u}$$
(14)

where, Su represents the displacement boundary, and \(u = \overline{u}\) indicates that the displacement value on the boundary is a known value.

The traction boundary conditions are as follows:

$$\sigma_{ij} n_{j} = \overline{T}_{i}$$
(15)

where, is the feature vector, and \(\mathop T\limits^{\_}_{i}\) is the stress vector.

For the damage variable D, the initial condition is denoted as \(D_{{0}}\) and the critical condition of damage fracture is represented by \(D_{c}\).

The solution equation for damage structures using the finite element method is established based on the principle of minimum potential energy as follows:

$$\left[ {K(D)} \right]\left\{ \delta \right\} = \left\{ P \right\}$$
(16)

where, [K(D)] is the unit stiffness matrix, and \(\left\{ \delta \right\}\) represents the displacement matrix, \(\left\{ P \right\}\) is the node force vector.

The equation in an incremental form can be obtained by adopting a stepwise increment in the initial load and initial displacement as follows:

$$\left[ {K(D)} \right]\left\{ {\Delta \delta } \right\} = \left\{ {\Delta P} \right\}$$
(17)

Using the above equation, the solution is obtained through an iterative process. The solution process involves dividing the loads or displacements into a certain number of levels, thereby obtaining the damage field, stress field and strain field of the structure at any given load or displacement level. Based on this, the damage and failure conditions of the structure are determined according to the material damage and failure criteria.

Application of the damage model for underground structures

Based on the actual environment and engineering characteristics of underground structures, the factors influencing the degradation of the structures are identified, mainly including concrete carbonation, steel corrosion, coupled forces between groundwater seepage and soil, corrosive media, concrete material mix proportion and performance, etc.. Experimental analysis is used to evaluate the effect of these factors on the damage indices of a selected structure27.

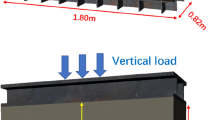
In order to demonstrate the application of the above damage model in underground structures, this article uses a specific engineering example to illustrate. This example is an experimental study conducted on underground continuous wall drill cores extracted from an underground station on Shanghai Metro Line 4. By establishing geometric models and degradation assumptions of underground structures (components) under external loads and typical environments (such as carbonization environments), the damage evolution law of underground structures is analyzed. In the experimental tests, the accelerated carbonation method was adopted, and the specimens were fabricated as corbel type for easy loading (Fig. 1). The experiment mainly simulated the carbonation conditions of the structure under bending moment, which also reflected the actual situation where the most dangerous sections (high stress areas) are often formed at the arched waist, arched foot and other parts of the underground structure when subjected to tension or compression. Based on the experimental results, a mathematical model was developed using the method of regression analysis for the carbonation depth in the underground structure under tension and/or compression. (Note: Regression analysis is an analytical method that uses statistical principles to mathematically process a large amount of statistical data, in order to determine the correlation between the dependent variable and certain independent variables, and establish a regression equation (or function expression) with good correlation. The non-linear regression method is used here because the carbonization depth has a non-linear relationship with the influencing factors.). At the same time, an elliptical trajectory model for steel corrosion propagation and a mathematical equation reflecting the evolution law of the model were established (Fig. 2).

Fig. 1
figure 1

The design method of corbel type specimen.

Full size image
Fig. 2
figure 2

Schematic diagram of elliptical profile of steel corrosion.

Full size image

The specimen has a 16 mm diameter steel bar embedded in it. In the horizontal section of the weak connection between the corbel and the specimen, a series of three 10 mm diameter steel bars was embedded to ensure safety under the applied stresses. On the basis of the experimental tests, a mathematical model was constructed to reflect the variation in carbonation depth over time. The tests showed that the trajectory of steel corrosion expansion is elliptical, and the trajectory model shown in Fig. 2 is expressed mathematically as follows:

For the upper parabola,

$$y = m\left( {\frac{{l^{2} }}{4} - x^{2} } \right) \quad x \in \left( { - \frac{l}{2},\frac{l}{2}} \right)$$
(18)

For the bottom parabola,

$$y = n\left( {x^{2} - \frac{{l^{2} }}{4}} \right) \quad x \in \left( { - \frac{l}{2},\frac{l}{2}} \right)$$
(19)

The equation for the circumference of steel can be shown as below,

$$y = \pm \sqrt {\frac{{d^{2} }}{4} - x^{2} }$$
(20)

where, d takes a value of 16 mm, and the parameters l, m and n can be determined by analyzing the relationship between the area (volume) of the corrosion trajectory (profile curve) and the quantity of steel corrosion. The result shows that the values of l, m and n are only dependent on time.

Then, based on the experiments, the finite element method was used to simulate the behavior of the specimen. Meso-damage theory was adopted for the analysis. The influence of steel corrosion expansion on concrete cracking was analyzed to predict the service life of the structure.

Damage analysis using numerical simulations

In order to analyze and describe the corrosion process of steel under stress and corrosive media, as well as the resulting structural damage and failure process, commercial finite element software MSC.MARC was used for numerical simulation of reinforced concrete specimens.

For the above corbel-type specimen, the reinforcement and concrete were modelled separately and different mechanical parameters (mainly refering to the elastic modulus, Poisson’s ratio, yield stress, fracture strain of steel and concrete) were given. Eight-node isoparametric elements were used and rigid connections were used for the interface between steel and concrete. Figure 3 shows the finite element mesh for the specimen.

Fig. 3
figure 3

Finite element mesh of the specimen.

Full size image

The basic parameters of concrete and reinforcing steel and the ultimate strain values of concrete were selected. Equations (18) and (19) were used to determine the profile curve of the corrosion-expansion material, which indicates different expansion displacements with time. Boundary displacements were incrementally applied at selected nodes around the circumference of the steel bar as initial conditions for the calculation. The initial damage \(D_{0}\) of the concrete was set at 0.001, the average nucleation strain at 0.03, the critical void volume percentage fc at 0.25, the failure void volume percentage fF at 0.4, the variance S at 0.15 and the void nucleation volume percentage fN at 0.05. When a load of 2.0 kN was applied for analysis, the numerical results showed that the specimen had reached the critical point of cracking at the 16th displacement step. At this point, the corresponding age of carbonation t was 51.2 years. The strain contour map of the specimen is shown in Fig. 4. From the above analysis, a service life of 51.2 years was estimated for the specimen.

Fig. 4
figure 4

Plastic strain contour map of the specimen.

Full size image

Conclusion and discussion

This paper has provided a detailed discussion of the method and procedure for applying the Gurson meso-damage model to study the durability of underground lining structures. Several conclusions can be drawn from this study:

  1. (1)

    The coupled effects of various influencing factors, such as the corrosive media in the environment, the stress fields of the underground rock (soil) and the groundwater seepage fields, etc., should generally be considered when investigating the durability of underground lining structures. Based on experimental results and theoretical studies, a quantitative analysis of the damage and durability of the structures can be performed by establishing degradation levels and functions. Subsequently, the service life of the structures can be further evaluated.

  2. (2)

    This paper has discussed the application of the improved Gurson meso-damage model to analyse the degree of damage (deterioration) and remaining service life of underground concrete lining structures. Satisfactory results were obtained. From the engineering examples in this article, it can be seen that by applying Gurson’s microscopic damage theory to analyze the durability damage status of underground structures, their durability life and remaining service life can be obtained. Moreover, through actual testing, it was found that the actual carbonization depth and degree of corrosion of the underground engineering structure were close to the theoretical analysis results. Based on the calculation of structural damage (deterioration) indicators, this method can effectively describe the damage accumulation process of underground concrete structures under applied loads, rock-soil stresses and the combined effects of various aggressive agents. The application process of this method has been detailed in the paper.

  3. (3)

    The application of damage mechanics in durability studies reflects the continuous accumulation of performance degradation in concrete structures, which is scientifically reasonable. Furthermore, damage mechanics is a good method to study the relationship between micro damage and macroscopic performance degradation. However, more research is needed in this area.

  4. (4)

    It is of great significance to study the durability of underground structures reinforced with CFRP materials under the combined action of various degradation factors, such as bending moment tensile stress and corrosive ions, and it is also an important research direction in the future.