TOPSIS driven complex picture fuzzy approach for speech matching and sports training feature recognition

Abstract

Speech matching and sports training feature recognition have become increasingly significant in artificial intelligence and sports science, necessitating robust decision-making frameworks to address inherent uncertainty, hesitation, and cyclic behaviors in these domains. Current approaches to multi-criteria decision-making (MCDM) often fail to address uncertainties and interactions adequately. To overcome these limitations, this paper proposes the incorporation of complex picture fuzzy information measures (CPF-IM) to boost the accuracy of TOPSIS-based decision-making. Particularly, novel similarity measures (SMs) and distance measures (DMs) have been developed to cover real and imaginary components assigned to membership degree (MD), abstinence degree (AD), and non-membership degree (NDM) within a complex picture fuzzy set (CPFS). The evaluation method employs a real-world scenario in which four domain experts rated five speaker profiles under ten relevant criteria. Result outcomes indicate that the proposed model achieves consistent alternative rankings by detecting the interdependent relationships between acoustic and biomechanical parameters. The proposed CPF-TOPSIS approach surpasses other techniques in terms of accuracy and reliability, as evidenced by the results of comparative studies. The research establishes a new decision framework for speech and sports sciences, which enhances expert assessment decisions by accurately handling uncertain data, cyclical patterns, and evaluation hesitations.

Introduction

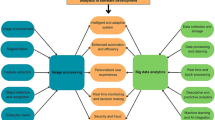
Speech matching and sports training feature recognition¹ are the focal areas in artificial intelligence, human–computer interaction as well as sports training applications as shown in Fig. 1. More specifically, speech matching aims at matching the vocal characteristics including pitch, tone, and rhythm, which could help improve the voice authentication techniques, translation of languages, or recognizing the emotion. On the other hand, sports training feature recognition involves identifying movements, posture, and coordination of the body to enhance sports performance. As will be seen, like many applications of data analysis and modeling, both domains are characterized by decision processes that are typically dynamic, uncertain, and multidimensional, making the need for sound decision-making tools paramount. As this necessity for accurate decision-making suggests, possibilities of other computational frameworks are sought, defined in the context of fuzzy logic and MCDM.

Fig. 1

Speech matching and sports training feature recognition.

The incorporation of fuzzy logic into MCDM provides a powerful tool to address numerous challenges associated with speech and sports evaluations. Core MCDM techniques are suitable for more strictly defined problems, but they often fail to provide adequate results in uncertain environments where fluctuations between choices or shifts are prevalent. Thus, the integration of MCDM with fuzzy frameworks means that vagueness and ambiguity are incorporated into the models to enhance the evaluations. Fuzzy logic, in turn, fills the gap left by conventional approaches to pave the way for the use of other advanced fuzzy frameworks, which enhance the modeling of uncertainty.

Mathematical morphology was established through the foundation of Fuzzy Sets (FS) by Zadeh² in 1965, which represents a mathematical description of a morphological domain (MD). However, an inability to describe NMD existed for FS that prompted Atanassov² in 1986 to create Intuitionistic Fuzzy Sets (IFS). As observed, although IFS extended NMD, the addition of MD and NMD confined within it sufficed for its power in handling the complexity of data. To address such constraints, extensions such as Pythagorean fuzzy sets (PyFS)³ and q-rung orthopair fuzzy sets (q-ROFS)⁴. Additional progress was made with picture fuzzy sets (PFS)⁵ that developed AD, providing more flexible approaches to managing contradictory information. The recent addition of CPFS⁶ incorporated real as well as imaginary components into MD, AD, and NMD, making it possible to represent cyclic uncertainty shown in speech and training data about sports. Complex picture fuzzy values (CPFVs) compose the MD, AD, and NMD values of CPFS through their real and imaginary number components. The real components convey the decision-maker’s fixed, certain beliefs, whereas the imaginary components provide unique measures for describing hesitation, cyclicity, and ambiguity. The imaginary components used in practical applications help model phase shifts and recurring patterns, as well as expert opinions, which vary between certain points, enabling the mathematical modeling of these phenomena. The phoneme in speech data occasionally reflects different phoneme candidates, which leads to repeated uncertainty. The expertise of evaluating physical movement manifests as oscillatory behavior, resulting in hesitation between “high” and “very high” assessments, and is therefore effectively represented through the imaginary parts.

Some fuzzy frameworks used in this work for speech matching and sports training feature recognition have given promising results. FS and IFS were introduced as the primary methods for analyzing initial simple and fundamental types of vocal and physical patterns and uncertainties. PFS and CPFS built upon these by incorporating hesitation and more complex uncertainties. However, to the authors’ knowledge, there is no systematic strategy to incorporate CPFS into MCDM frameworks to tackle these problems simultaneously. This underlines the importance of approaches that not only accommodate volatility into the model but also employ sophisticated measures of fuzzy information to sharpen the decision-making. To fill this gap in the literature, this paper introduces the CPF-TOPSIS model, which utilizes the complex picture fuzzy information measure (CPF-IM) for decision-making in speech matching and feature identification used for training in sports athletics. To this end, this paper introduces new SM and DM for CPFS that incorporate concepts of proximity and resemblance to the ideal solution, thereby producing a reliable evaluation. The paper provides a concrete example of how the proposed methodology works, demonstrating its high efficiency and adaptability in providing solutions to decision-making problems in these important fields, based on a general and flexible approach.

Research gap and motivation

The fields of Speech Matching and Sports Training Feature Recognition have progressed a lot specifically; however, there is a lack of effective methods to organize both fields under a common decision-making system. All current investigations follow the idea of evaluation of speech matching or sports training independently, whereas their combined assessment can be highly useful for adaptive sports coaching or multimodal biometric systems. Moreover, conventional approaches employ only crisp data or very simple forms of fuzzy models for modeling which are insufficient to model such complex and uncertain domains. For instance, in the case of speech signals, the effects of noise and speaker variability and dynamic environments are a challenge to signal processing where the goal is to decode speech information from signals collected in sports training recognition, problems arise on how to accurately determine attributes such as agility, balance and movement precision. Secondly, while the use of MCDM methods in other fields is gradually advancing, its use with speech and sports recognition is still quite limited. It also identifies a major gap in current models; namely, the absence of models that can cope with conflict of criteria, combine different forms of expertise, and model vagueness and changes in vagueness, in the form of hesitations and cyclic oscillations. In particular, more progressive approaches such as CPFS which can represent cyclic and ambiguous data are still unexplored. Filling these gaps with the inclusion of CPFS with MCDM approaches like TOPSIS provides an enhanced method to improve the decision-making accuracy and reliability of these essential fields.

This study is motivated by the need to bridge this gap by proposing IM which includes both SM and DM for CPFS and integrating them into the TOPSIS approach to enhance the decision-making process in speech matching and sports training feature recognition. This research aims to address the deficits in existing fuzzy MCDM approaches when dealing with multidimensional uncertain data patterns found in real-world fields such as speech and sports training. This research develops CPF-IM as a new MCDM framework by enhancing SM and DM, making it suitable for CPFS to address deficiencies in conventional MCDM approaches related to the analysis of expert opinions. The combination of real and imaginary components within these measures provides enhanced treatment of uncertainty for dealing with MD, AD, and NMD phenomena. This specialized version of SM and DM, developed to sense cyclic uncertainty components combined with human decision-making hesitation, serves as the basis for uncertainty treatment in human-evaluated and sensor-driven environments. The proposed measures combine the AD for indicating hesitation with the imaginary part for representing cyclic behaviors, while traditional distance measures process information either in a linear fashion or dismiss partial truth conditions. These constructs mathematically match complex detail behavior patterns, thereby making the proposed CPFS-based measures better suited for realistic scenarios. The paper presents both derivations and various examples that demonstrate that SM and DM retain their discriminatory abilities and ranking accuracy in situations involving contradictory and hesitant inputs while surpassing conventional fuzzy measures. The proposed measures reveal distinctive aspects between two nearly similar alternatives, as they possess equivalent MDs yet exhibit marked variations in abstinence attributes. Classical approaches would overlook these differences. The proposed method offers valuable benefits when applied to domains such as sports training and voice recognition, particularly for systems with unclear input data.

The implementation of these new CPFS-based measures in the TOPSIS framework leads to enhanced decision-making accuracy and stability when dealing with scenarios involving expert conflicts, cyclic behaviors, and multi-source evaluations that commonly occur in speech matching and sports training feature recognition. Shifting this research into its position as one of the pioneering studies that merges these two fields into an integrated fuzzy decision-making system creates opportunities in biometric technology and customized sporting training solutions. CPFS exists only in theory with minimal practical application in MCDM frameworks, especially when dealing with dynamic speech and physical movement data types. This study bridges theory and practice through domain-specific and executable approaches to SM and DM for CPFS, aiming to enhance the MCDM literature on handling realistic uncertainty in a meaningful manner. The primary objective of this research is to develop an advanced framework that enhances decision science theories regarding CPFS while delivering specific benefits through its implementation in uncertain environments, such as AI speech analysis and human biomechanics in sports.

Objectives and contribution

This study’s objectives aim to contribute to developing decision-making approaches by extending CPFS with the TOPSIS method and new measures.

• Development of novel measures: Given this, it is possible to propose and develop SM and DM for CPFS to manage multi-dimensional and cyclic uncertainties.

• Integration with CPF-TOPSIS: To incorporate the proposed SM and DM into the CPF-TOPSIS approach to extensively apply it in MCDM environments.

• Application in speech matching: To propose the methodology to improve the accuracy of decisions about speech and match them to speakers which involves issues such as noise, variability in speakers, and hesitating speech.

• Application in sports training feature recognition: For the purpose of illustrating the applicability of the methodology, it is used in the analysis of identifying key features in the sports training context – agility, precision, and movement pattern while exercising under uncertainty and cyclic conditions.

• Validation of effectiveness: To ensure the credibility of the suggested measures and approach, more real-life problems involving multiple criteria, different alternatives, and opinions of specialists will be examined.

The following are the contributions of this study, which seek to improve several decision-making systems and consider shortcomings in managing uncertainty, ambiguity, and hesitation in real-world conditions.

• Novel SM and DM: In the paper, new SM and DM for CPFS are developed which involve both real and imaginary parts of MD, AD, and NMD.

• Advanced CPF-TOPSIS framework: It expands upon the TOPSIS method by including several novel CPFS-based metrics that would enable MCDM to be more detailed and comprehensive in comparison with conflicting criteria as well as experts’ hesitation.

• First application in speech matching: The methodology is applied to speech matching for the first time The results offer an understanding of enhancing speaker recognition, voice authentication, and noise robust systems.

• Sports training feature recognition: This paper adapts and implements CPFS-TOPSIS to analyze and sort out the identification of options on sports training features, which are agility, balance, and movement precision contributing to both, sports science and training techniques.

• Unified framework for decision-making: The proposed approach offers a unified framework that is able to handle multi-dimensional uncertainty and hesitation as well as periodicity so as to offer a practical platform for bridging the gap between theory and practice in decision-making.

• Enhanced computational insights: Hence, the paper has applied and proven the proposed CPFS on real problems of speech and sports data and illustrated the workability of the approach in realistic MCDM situations.

Organization of study

This paper is organized as follows: Section “Literature review” presents the literature review and potential contributions of MCDM problems based on sports training and speech recognition, IMs, and the TOPSIS approach. Section “Preliminaries” serves the information on CPFS, SMs, and DMs. Section “Novel information measures” presents the novel IM, which includes both SM and DM for CPFS. The research methodology is presented in Section “Novel information measures”, which illustrates the use of the CPF-TOPSIS approach based on IMs and addresses the decision-making problem further evaluated by the proposed framework presented in Section “Speech matching and sports training feature recognition”. Moreover, a comparison and sensitive analysis is conducted to explore the effects of various linguistic expressions and weight values on the outcome. Finally, in section “Conclusion”, the study’s results, advantages, and limitations are discussed, and the conversation is concluded by giving future direction.

Literature review

In this section, we will discuss the existing literature on speech matching and sports training feature recognition, information measures that include both SM and DM and the MCDM TOPSIS approach.

MCDM in speech matching and sports training feature recognition

The extant research in sports training has also underlined the radical change brought by modern technology in SST, especially through wearable sensors and IoT equipment. Such applications enable athletes to improve their techniques and provide trainers with feedback in real-time. At the same time, these technologies help ease the burden of trainers without compromising the efficiency of training programs. This is especially so given that many athletes may not afford to hire professional trainers and therefore, SST comes in handy with this given that it is relatively cheaper, as noted by⁷. In addition, more attention has been paid to the psychological processes such as personal beliefs, desires, goals, motivation and concentration, and control of stress and anxiety as essential factors for success in training and further sporting activity. Many research show that these mental skills enhance an athlete’s prospects of delivering on performance outcomes⁸. Furthermore, athletes with disabilities pay significant attention to the social context and the knowledge of the coaches regarding rehabilitation and safety issues⁹. A few exercises and training schemes that are necessary should be flexibility, balance, accessibility, and cardiovascular endurance training activities for these athletes¹⁰. Automatic speech recognition has been developed for more than half a century, starting from the 1950s, initially as isolated word recognition in a noiseless environment¹¹. Previous systems also failed to operate in noisy environments and required model enhancement and system updating to enhance the recognitional capability in various conditions. Recent advancements have focused on integrating speech recognition with other branches of sciences, including physiology and psychology, to increase the reliability of the systems and to advance its applicability to the commercial level¹². Signal analysis and processing are also crucial for enhancing recognition during difficult circumstances which involves the creation of new algorithms and techniques¹³. Moreover, researchers are working towards the adaptation of speech recognition technology in fields such as sports training operations, as the former can observe the respiratory frequency and energy expenditure of athletes¹⁴. The integration of speech recognition and intelligent systems opens new possibilities for highly developed interaction between the user and the computer and real-time decision-making.

MCDM in information measure

Information measures (IM), including SM and DM, are fundamental components in fuzzy systems for analyzing uncertainty, dissimilarity, and resemblance between fuzzy elements. SM¹⁵ quantifies the degree of similarity between two objects and computes a measure of how similar the elements are, usually ranging from $0$ to $1$. These measures are widespread in decision-making, pattern recognition, clustering, and intelligent computations¹⁶. DM¹⁷ quantifies the distance or difference between fuzzy sets (FS) or probability distributions as a real number to measure the degree of separation between objects or data points for characteristics. DM has been used extensively in other tasks like classification, clustering, and data analysis¹⁸. Likewise, both SM and DM are paramount in managing uncertainty and fuzziness seen in most decisions and arising from the variability in decision-making across systems while ensuring that both similarity and difference to the chosen options are also balanced. These measures have been further developed for needs in IFS, PyFS, or q-ROFS to be applied for more ambiguous and hesitant problems in fuzzy systems¹⁹. For example, in q-ROFS, SM and DM have been modified to give better differentiation between similarity and dissimilarity, which is important in operational tasks like medical diagnosis, pattern recognition, and speech matching²⁰. Besides, all these measures are significant in entropy-based information theory that uses SM and DM to give more details about the distribution of data, its entropy, and uncertainty to enhance the decision-making process²¹. Altogether, incorporating both SM and DM within contexts of IM enriches species of decision-making under uncertainty and enhances applications to machine learning²², intelligent computing²³, and situations with complexity problems where management of fuzziness and distance is critical. The ability to handle similarity and dissimilarity has made advanced fuzzy models the best models for the MCDM, making them very useful in different fields.

TOPSIS MCDM approach

TOPSIS method is widely used for MCDM solutions, developed by Hwang and Yoon²⁴ in 1981. TOPSIS ranks the alternatives based on how closely they are positioned to a positive ideal solution and the extent to which they are away from the negative ideal solution. Due to its computational simplicity and versatility, the program can handle both qualitative and quantitative data efficiently. This method has been extensively used in various fields, such as engineering, management, environmental sciences, and social decision-making systems in the past years according to Corrente and Tasiou²⁵. The use of the method has been adopted widely in MCDM real-life problems. It has gained popularity in such areas as green supplier selection²⁶, supply chain management²⁷, healthcare and medical decisions²⁸, and human resource management. This application has grown into the monitoring of air quality²⁹, energy management³⁰, selection of technologies³¹, and many others revealing that the application of the method is so diverse that it can be applied to a lot of industries. The research overview incorporates Table 1 to present important studies on CPFS and TOPSIS methods, along with their implementation approaches. The proposed SM and DM for CPFS are compared to existing works regarding their potential application for speech matching and sports training feature recognition. The current approach demonstrates a unique capability for managing uncertainty, along with cyclical patterns, in authentic decision-making contexts.

Table 1 Comparison of key studies and our proposed approach.

Preliminaries

Understanding the basic concepts of CPFS, SMs, and DMs is essential. The following is a concise summary of the fundamental ideas that underpin these concepts.

Definition I

³⁷ A CPFS $\text{M}$ on the universe of discourse ${{{\mathop u\limits_ \cdot }^\prime }}$ is an object of the form:

$$M = \left\{ {\left( {\mathop u\limits_{ \cdot }^{\prime } ,\left( {m_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),m_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),\left( {a_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),a_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),\left( {n_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),n_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)} \right):\mathop { u}\limits_{ \cdot }^{\prime } \varepsilon \mathop { u}\limits_{ \cdot }^{\prime } } \right\}$$

(1)

where $\left( {m_{M}^{r} \left( {\mathop u\limits_{ \cdot }^{\prime } } \right),m_{M}^{i} \left( {\mathop u\limits_{ \cdot }^{\prime } } \right)} \right) \in \left[ {0,1} \right]$ is known as MD,$\left( {a_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),a_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right) \in \left[ {0,1} \right]$ is known as AD, and $\left( {n_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),n_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right) \in \left[ {0,1} \right]$ is known as NMD, which satisfies the following condition:

$$0 \le m_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) + a_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) + n_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) \le 1 \forall \mathop { u}\limits_{ \cdot }^{\prime } \varepsilon \mathop { u}\limits_{ \cdot }^{\prime }$$

$$0 \le m_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) + a_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) + n_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) \le 1, \forall \mathop { u}\limits_{ \cdot }^{\prime } \varepsilon \mathop { u}\limits_{ \cdot }^{\prime }$$

The refusal degree (RD) is calculated by:

$$\begin{gathered} p_{{\text{M}}}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) = 1 - \left( {m_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) + a_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) + n_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right) \hfill \\ p_{{\text{M}}}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) = 1 - \left( {m_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) + a_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) + n_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right) \hfill \\ \end{gathered}$$

Definition II

³⁷ Let

${\text{M}}_{i} = \left( {\begin{array}{*{20}c} {\left( {m_{{{\text{M}}_{i} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),m_{{{\text{M}}_{i} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),} \\ {\left( {a_{{{\text{M}}_{i} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),a_{{{\text{M}}_{i} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),\left( {n_{{{\text{M}}_{i} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),n_{{{\text{M}}_{i} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)} \\ \end{array} } \right)$,

${\text{M}}_{j} = \left( {\begin{array}{*{20}c} {\left( {m_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),m_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),} \\ {\left( {a_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),a_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),\left( {n_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),n_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)} \\ \end{array} } \right)$

be two complex picture fuzzy values (CPFVs) and $\Delta >0$ be any scalar number, then the following operations are defined:

$${\text{M}}_{i} \oplus {\text{M}}_{j} = \left( {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} {\left( {m_{{{\text{M}}_{i} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) + m_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) - m_{{{\text{M}}_{i} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right).m_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),} \\ {\left( {m_{{{\text{M}}_{i} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) + m_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) - m_{{{\text{M}}_{i} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right).m_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)} \\ \end{array} } \right),} \\ {\left( {\left( {a_{{{\text{M}}_{i} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),a_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),\left( {a_{{{\text{M}}_{i} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),a_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)} \right),} \\ {\left( {\left( {n_{{{\text{M}}_{i} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),n_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),\left( {n_{{{\text{M}}_{i} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),n_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)} \right)} \\ \end{array} } \right)$$

$${\text{M}}_{i} \otimes {\text{M}}_{j} = \left( {\begin{array}{*{20}c} {\left( {\left( {m_{{{\text{M}}_{i} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),m_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),\left( {m_{{{\text{M}}_{i} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),m_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)} \right),} \\ {\left( {\begin{array}{*{20}c} {\left( {a_{{{\text{M}}_{i} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) + a_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) - a_{{{\text{M}}_{i} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right).a_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),} \\ {\left( {a_{{{\text{M}}_{i} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) + a_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) - a_{{{\text{M}}_{i} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right).a_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)} \\ \end{array} } \right),} \\ {\left( {\begin{array}{*{20}c} {\left( {n_{{{\text{M}}_{i} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) + n_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) - n_{{{\text{M}}_{i} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right).n_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),} \\ {\left( {n_{{{\text{M}}_{i} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) + n_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) - n_{{{\text{M}}_{i} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right).n_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)} \\ \end{array} } \right)} \\ \end{array} } \right)$$

$${\Delta }.M = \left( {\begin{array}{*{20}c} {\left( {\left( {1 - \left( {1 - m_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)^{{\Delta }} } \right),\left( {1 - \left( {1 - m_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)^{{\Delta }} } \right)} \right),} \\ {\left( {\left( {a_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)^{{\Delta }} ,\left( {a_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)^{{\Delta }} } \right),\left( {\left( {n_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)^{{\Delta }} ,\left( {n_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)^{{\Delta }} } \right)} \\ \end{array} } \right)$$

$$M^{{\Delta }} = \left( {\begin{array}{*{20}c} {\left( {\left( {m_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)^{{\Delta }} ,\left( {m_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)^{{\Delta }} } \right),} \\ {\left( {\left( {1 - \left( {1 - a_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)^{{\Delta }} } \right),\left( {1 - \left( {1 - a_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)^{{\Delta }} } \right)} \right),} \\ {\left( {\left( {1 - \left( {1 - n_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)^{{\Delta }} } \right),\left( {1 - \left( {1 - n_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)^{{\Delta }} } \right)} \right)} \\ \end{array} } \right)$$

$$M^{c} = \left( {\begin{array}{*{20}c} {\mathop { u}\limits_{ \cdot }^{\prime } ,\left( {n_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),n_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),\left( {a_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),a_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),} \\ {\left( {m_{M}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),m_{M}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)} \\ \end{array} } \right)$$

Definition III

¹⁵ Let ${\text{M}}_{i},{\text{M}}_{j}$ and ${\text{M}}_{k}$ be the collection of CPFVs. A SM is a real-valued function $S$ that must satisfy the following conditions.

$$S\left({M}_{i},{M}_{j}\right)\in \left[\text{0,1}\right]$$

$S\left({M}_{i},{M}_{j}\right)=1$ iff ${M}_{i}={M}_{j}$

$$S\left({M}_{i},{M}_{j}\right)=S\left({M}_{j},{M}_{i}\right)$$

If ${M}_{i}\subseteq {M}_{j}\subseteq {M}_{k}$ then $S({M}_{i},{M}_{j})\ge S({M}_{i},{M}_{k})$ and $S({M}_{j},{M}_{k})\ge S({M}_{i},{M}_{k})$

Definition IV

¹⁷ Let ${\text{M}}_{i},{\text{M}}_{j}$ and ${\text{M}}_{k}$ be the collection of CPFVs. A DM is a real-valued function $D$ that must satisfy the following conditions.

$$D\left({M}_{i},{M}_{j}\right)\in \left[\text{0,1}\right]$$

$D\left({M}_{i},{M}_{j}\right)=0$ iff ${M}_{i}={M}_{j}$

$$D\left({M}_{i},{M}_{j}\right)=D\left({M}_{j},{M}_{i}\right)$$

If ${M}_{i}\subseteq {M}_{j}\subseteq {M}_{k}$ then $D({M}_{i},{M}_{k})\ge D({M}_{i},{M}_{j})$ and $D({M}_{i},{M}_{k})\ge D({M}_{j},{M}_{k})$

Theorem I

³⁷Let ${\text{M}}_{j} = \left( {\begin{array}{*{20}c} {\left( {m_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),m_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),} \\ {\left( {a_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),a_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),\left( {n_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),n_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)} \\ \end{array} } \right)$ be the CPFVs then it holds the following properties:

$CPF\left({\text{M}}_{1},{\text{M}}_{2},{\text{M}}_{3},\dots ,{\text{M}}_{j}\right)=\text{M}$. i.e. (Idempotency).

If ${\text{M}}_{j}^{ - } = \left( {\left( {m_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)^{ - } m_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)^{ - } } \right),\left( {a_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)^{ - } ,a_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)^{ - } } \right),\left( {n_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)^{ - } ,n_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)^{ - } } \right)} \right)$ and.

${\text{M}}_{j}^{ + } = \left( {\left( {m_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)^{ + } m_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)^{ + } } \right),\left( {a_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)^{ + } ,a_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)^{ + } } \right),\left( {n_{{{\text{M}}_{j} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)^{ + } ,n_{{{\text{M}}_{j} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)^{ + } } \right)} \right)$ such that ${\text{M}}_{j}^{-}={\text{minM}}_{j}^{-}$ and ${\text{M}}_{j}^{+}={\text{maxM}}_{j}^{+}$, then, ${\text{M}}_{j}^{-}\le CPF\left({\text{M}}_{1},{\text{M}}_{2},{\text{M}}_{3},\dots ,{\text{M}}_{j}\right)\le {\text{M}}_{j}^{+}$ Which is boundedness.

If ${\text{M}}_{\mathcal{j}}\le {{\text{M}}_{\mathcal{j}}}{\prime}$. Then, $CPF\left({\text{M}}_{1},{\text{M}}_{2},{\text{M}}_{3},\dots ,{\text{M}}_{j}\right)\le CPF\left({\text{M}}_{1}{\prime},{\text{M}}_{2}{\prime},{\text{M}}_{3}{\prime},\dots ,{\text{M}}_{j}{\prime}\right)$ (monotonicity property).

Novel information measures

The evaluation of the TOPSIS approach with CPFS cannot be complete without a detailed look at IM, which is a critical quantitative tool in evaluating the characteristics of fuzzy systems, including SM and DM. These measures are essential tools that help quantify the degree of information content within a system, the level of fuzziness in that environment, and the amount of similarity or dissimilarity. They are critically important for improving decision-making and pattern analysis in various intelligent applications, especially speech recognition and sports performance analysis for intelligent computing training purposes. When incorporating these information measures into the TOPSIS model under the complex picture-fuzzy (CPF) environment, the model can better deal with ambiguity and uncertainty, making the recognition result more accurate and dependable. Based on this, we introduced a new SM and DM for CPFS that will be incorporated into the TOPSIS method to enhance the algorithm solutions within the CPF context.

Similarity measure (SM)

We introduce a novel SM tailored for CPFS, which incorporates the differences in MD, AD, and NMD between pairs of CPFS. The SM increases as the differences between these degrees decrease, providing a more precise evaluation of similarity. The following section provides a detailed explanation of this new SM.

Let

${\text{M}}_{1} = \left( {\begin{array}{*{20}c} {\left( {m_{{{\text{M}}_{1} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),m_{{{\text{M}}_{1} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),} \\ {\left( {a_{{{\text{M}}_{1} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),a_{{{\text{M}}_{1} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),\left( {n_{{{\text{M}}_{1} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),n_{{{\text{M}}_{1} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)} \\ \end{array} } \right)$ ,

${\text{M}}_{2} = \left( {\begin{array}{*{20}c} {\left( {m_{{{\text{M}}_{2} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),m_{{{\text{M}}_{2} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),} \\ {\left( {a_{{{\text{M}}_{2} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),a_{{{\text{M}}_{2} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right),\left( {n_{{{\text{M}}_{2} }}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right),n_{{{\text{M}}_{2} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right)} \\ \end{array} } \right)$

be two CPFVs then the distances between the MD, AD, and NMD of CPFS are determined as follows.

$$\mathop {u}\limits_{ \cdot } ^{\prime } \,_{m}^{r} \left( {\mathop {u}\limits_{ \cdot } ^{\prime } } \right) = m_{{{\text{M}}_{1} }}^{r} \left( {\mathop {u}\limits_{ \cdot } ^{\prime } } \right) - m_{{{\text{M}}_{2} }}^{r} \left( {\mathop {u}\limits_{ \cdot } ^{\prime } } \right)$$

$$\mathop {u}\limits_{ \cdot } ^{\prime } \,_{m}^{i} \left( {\mathop {u}\limits_{ \cdot } ^{\prime } } \right) = m_{{{\text{M}}_{1} }}^{i} \left( {\mathop {u}\limits_{ \cdot } ^{\prime } } \right) - m_{{{\text{M}}_{2} }}^{i} \left( {\mathop {u}\limits_{ \cdot } ^{\prime } } \right)$$

$$\mathop {u}\limits_{ \cdot } ^{\prime } \,_{a}^{r} \left( {\mathop {u}\limits_{ \cdot } ^{\prime } } \right) = a_{{{\text{M}}_{1} }}^{r} \left( {\mathop {u}\limits_{ \cdot } ^{\prime } } \right) - a_{{{\text{M}}_{1} }}^{r} \left( {\mathop {u}\limits_{ \cdot } ^{\prime } } \right)$$

$$\mathop {u}\limits_{ \cdot } ^{\prime } \,_{a}^{i} \left( {\mathop {u}\limits_{ \cdot } ^{\prime } } \right) = a_{{{\text{M}}_{1} }}^{i} \left( {\mathop {u}\limits_{ \cdot } ^{\prime } } \right) - a_{{{\text{M}}_{1} }}^{i} \left( {\mathop {u}\limits_{ \cdot } ^{\prime } } \right)$$

$$\mathop {u}\limits_{ \cdot } ^{\prime } \,_{n}^{r} \left( {\mathop {u}\limits_{ \cdot } ^{\prime } } \right) = n_{{{\text{M}}_{1} }}^{r} \left( {\mathop {u}\limits_{ \cdot } ^{\prime } } \right) - n_{{{\text{M}}_{2} }}^{r} \left( {\mathop {u}\limits_{ \cdot } ^{\prime } } \right)$$

And,

$$\mathop {\text{d}}\limits_{ \cdot } \,_{n}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) = n_{{{\text{M}}_{1} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right) - n_{{{\text{M}}_{2} }}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)$$

Therefore, a novel SM for CPFS is defined as follows.

$$S\left( {M_{1} ,M_{2} } \right) = \frac{1}{6n}\mathop \sum \limits_{i = 1}^{n} \left( {\begin{array}{*{20}c} {\left( {\frac{{\left( {1 - \left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{m}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right| + 1 - \left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{a}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right| + 1 - \left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{n}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right|} \right)}}{{\left( {\begin{array}{*{20}c} {1 + \left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{m}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right| + \left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{a}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right| + \left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{n}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right| + } \\ {\left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{m}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right|.\left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{a}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right|.\left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{n}^{r} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right|} \\ \end{array} } \right)}}} \right) + } \\ {\left( {\frac{{\left( {1 - \left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{m}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right| + 1 - \left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{a}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right| + 1 - \left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{n}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right|} \right)}}{{\left( {\begin{array}{*{20}c} {1 + \left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{m}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right| + \left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{a}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right| + \left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{n}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right| + } \\ {\left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{m}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right|.\left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{a}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right|.\left| {\mathop {\text{d}}\limits_{ \cdot } {\mkern 1mu}_{n}^{i} \left( {\mathop { u}\limits_{ \cdot }^{\prime } } \right)} \right|} \\ \end{array} } \right)}}} \right)} \\ \end{array} } \right)$$

(2)

Here $n$ represents the number of pairs of CPFS.

The novel SM in Eq. 2 satisfies the properties of SM as shown in Definition III.

Distance measure (DM)

We introduce a novel DM tailored for CPFS, which incorporates the MD, AD, and NMD between pairs of CPFS. The DM increases as the similarities between these degrees decrease, providing a more precise evaluation of dissimilarity.

Let ${{\varvec{M}}}_{1}=\left(\begin{array}{c}\left({{\varvec{m}}}_{{{\varvec{M}}}_{1}}^{{\varvec{r}}}\left({{{\mathop u\limits_ \cdot }^\prime }}\right),{{\varvec{m}}}_{{{\varvec{M}}}_{1}}^{{\varvec{i}}}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right),\\ \left({{\varvec{a}}}_{{{\varvec{M}}}_{1}}^{{\varvec{r}}}\left({{{\mathop u\limits_ \cdot }^\prime }}\right),{{\varvec{a}}}_{{{\varvec{M}}}_{1}}^{{\varvec{i}}}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right),\left({{\varvec{n}}}_{{{\varvec{M}}}_{1}}^{{\varvec{r}}}\left({{{\mathop u\limits_ \cdot }^\prime }}\right),{{\varvec{n}}}_{{{\varvec{M}}}_{1}}^{{\varvec{i}}}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right)\end{array}\right)$,

${{\varvec{M}}}_{2}=\left(\begin{array}{c}\left({{\varvec{m}}}_{{{\varvec{M}}}_{2}}^{{\varvec{r}}}\left({{{\mathop u\limits_ \cdot }^\prime }}\right),{{\varvec{m}}}_{{{\varvec{M}}}_{2}}^{{\varvec{i}}}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right),\\ \left({{\varvec{a}}}_{{{\varvec{M}}}_{2}}^{{\varvec{r}}}\left({{{\mathop u\limits_ \cdot }^\prime }}\right),{{\varvec{a}}}_{{{\varvec{M}}}_{2}}^{{\varvec{i}}}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right),\left({{\varvec{n}}}_{{{\varvec{M}}}_{2}}^{{\varvec{r}}}\left({{{\mathop u\limits_ \cdot }^\prime }}\right),{{\varvec{n}}}_{{{\varvec{M}}}_{2}}^{{\varvec{i}}}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right)\end{array}\right)$

be two CPFSVs then a novel DM for CPFS is defined as follows.

$$DM\left({M}_{1},{M}_{2}\right)=\frac{1}{6n}\sum_{i=1}^{n}\left(\begin{array}{c}\left|{m}_{{M}_{1}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)-{m}_{{M}_{2}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right|+\\ \left|{m}_{{M}_{1}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)-{m}_{{M}_{2}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right|+\\ \left|{a}_{{M}_{1}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)-{a}_{{M}_{2}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right|+\\ \left|{a}_{{M}_{1}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)-{a}_{{M}_{2}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right|+\\ \left|{n}_{{M}_{1}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)-{n}_{{M}_{2}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right|+\\ \left|{n}_{{M}_{1}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)-{n}_{{M}_{2}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right|+\\ \left|\begin{array}{c}{m}_{{M}_{1}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right).{a}_{{M}_{1}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right).{n}_{{M}_{2}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)-\\ {m}_{{M}_{2}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right).{a}_{{M}_{2}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right).{n}_{{M}_{1}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\end{array}\right|+\\ \left|\begin{array}{c}{m}_{{M}_{1}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right).{a}_{{M}_{1}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right).{n}_{{M}_{2}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)-\\ {m}_{{M}_{2}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right).{a}_{{M}_{2}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right).{n}_{{M}_{1}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\end{array}\right|\end{array}\right)$$

(3)

Here ${\varvec{n}}$ represents the number of pairs of CPFS.

The novel DM in Eq. 3 satisfies the properties of DM as shown in Definition IV.

Information measures based TOPSIS methodology

This section introduces a CPF-TOPSIS method with a novel IM, which provides an improved approach to MCDM implementation in the CPF context. To improve reliability, this approach incorporates newly developed SM and DM for CPFS distinct from the traditional methods. To compare the similarity of alternatives, the novel SM considers the differences in MD, AD, and NMD, resulting in a more accurate measure of similarity. At the same time, the DM records how alternatives diverge from the ideal and anti-ideal solutions, thus controlling for uncertainty and ambiguity typical to complex decision-making contexts. By creating these novel IMs, the methodology enhances the evaluation processes in applications to an enormous extent. The next section provides the steps for employing the PF-TOPSIS approach using the novel IMs.

Algorithm

Step 1: Define the decision matrix and find decision-maker weights:

• Formulate the decision matrix for the given problem with the help of the alternatives $\{{A}_{1},{A}_{2},\dots ,{A}_{m}\}$ and the criterion $\{{C}_{1}, {C}_{2},\dots , {C}_{n}\}$.

• Express all the elements of the decision matrix in the form of CPFVs characterized by its MD, AD, and NMD.

• By using the following Eq. 4, determine each expert’s weights ${{\varphi }}_{\text{e}}$.

  $$\left({w}_{e}^{r},{w}_{e}^{i}\right)=\left(\begin{array}{c}{\left(\frac{\left( {m}_{e}+ {a}_{e} . \left( \frac{{m}_{e}}{{m}_{e}+{n}_{e}} \right)\right)}{\sum_{k=1}^{l}\left({m}_{e} + {a}_{e} . \left( \frac{{m}_{e}}{{m}_{e}+{n}_{e}} \right)\right)}\right)}^{r},\\ {\left(\frac{\left({m}_{e} + {a}_{e} . \left( \frac{{m}_{e}}{{m}_{e}+{n}_{e}} \right)\right)}{\sum_{k=1}^{l}\left({m}_{e} + {a}_{e} . \left( \frac{{m}_{e}}{{m}_{e}+{n}_{e}} \right)\right)}\right)}^{i}\end{array}\right)$$

  (4)

Step 2: Aggregate the decision matrix and determine weights:

The CPFWA (Complex Picture Fuzzy Weighted Averaging) operator obtains the aggregated decision matrix as shown in Eq. (5). Let ${w}_{j}^{(k)}=\left(\left({{\text{m}}^{\text{r}}}_{j}^{\left(k\right)},{{\text{m}}^{\text{i}}}_{j}^{\left(k\right)}\right),\left({{\text{a}}^{\text{r}}}_{j}^{\left(k\right)},{{\text{a}}^{\text{i}}}_{j}^{\left(k\right)}\right), \left({{\text{n}}^{\text{r}}}_{j}^{\left(k\right)},{{\text{n}}^{\text{i}}}_{j}^{\left(k\right)}\right)\right)$ be the CPFVs assigned by the ${k}_{th}$ user $k=\text{1,2},\dots ,l$ to the specific criterion $j (j=1, 2,\dots ,n)$.

$$CPFWA\left(\begin{array}{c}\left({{m}^{r}}_{j}^{\left(k\right)},{{m}^{i}}_{j}^{\left(k\right)}\right),\\ \left({{a}^{r}}_{j}^{\left(k\right)},{{a}^{i}}_{j}^{\left(k\right)}\right), \left({{n}^{r}}_{j}^{\left(k\right)},{{n}^{i}}_{j}^{\left(k\right)}\right)\end{array}\right)=\left(\begin{array}{c}\left(\begin{array}{c}{\left(1-\prod_{e=1}^{f} {\left(1-{m}_{j}^{\left(k\right)}\right)}^{{w}_{e}}\right)}^{r},\\ {\left(1-\prod_{e=1}^{f} {\left(1-{m}_{j}^{\left(k\right)}\right)}^{{w}_{e}}\right)}^{i}\end{array}\right),\\ \left(\begin{array}{c}{\left(\prod_{e=1}^{f} {\left({a}_{j}^{\left(k\right)}\right)}^{{w}_{e}}\right)}^{r},\\ {\left(\prod_{e=1}^{f} {\left({a}_{j}^{\left(k\right)}\right)}^{{w}_{e}}\right)}^{i}\end{array}\right),\\ \left(\begin{array}{c}{\left(\prod_{e=1}^{f} {\left({n}_{j}^{\left(k\right)}\right)}^{{w}_{e}}\right)}^{r},\\ {\left(\prod_{e=1}^{f} {\left({n}_{j}^{\left(k\right)}\right)}^{{w}_{e}}\right)}^{i}\end{array}\right)\end{array}\right)$$

(5)

Consequently, a vector of criteria weights is produced in which every weight is a CPFV of the form $\left(\left({m}_{j}^{r},{m}_{j}^{i}\right), \left({a}_{j}^{r},{a}_{j}^{i}\right), \left({n}_{j}^{r},{n}_{j}^{i}\right)\right)$.

Step 3: Compute the weighted aggregated decision matrix:

Determine the weighted aggregated decision matrix by using the following multiplication operator of CPFS to multiply each of the aggregated CPFVs $\left(\left({{\text{m}}^{r}}_{j}^{\left(k\right)},{{\text{m}}^{i}}_{j}^{\left(k\right)}\right),\left({{\text{a}}^{r}}_{j}^{\left(k\right)},{{\text{a}}^{i}}_{j}^{\left(k\right)}\right), \left({{\text{n}}^{r}}_{j}^{\left(k\right)},{{\text{n}}^{i}}_{j}^{\left(k\right)}\right)\right)$ in Eq. (6), that follow the criteria weights mentioned in the previous step.

$${M}_{i}\otimes {M}_{j}=\left(\begin{array}{c}\left(\begin{array}{c}\left({m}_{{M}_{i}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right).{m}_{{M}_{j}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right),\\ \left({m}_{{M}_{i}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right).{m}_{{M}_{j}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right)\end{array}\right),\\ \left(\begin{array}{c}\left({a}_{{M}_{i}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right).{a}_{{M}_{j}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right),\\ \left({a}_{{M}_{i}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right).{a}_{{M}_{j}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\right),\end{array}\right)\\ \left(\begin{array}{c}\left(\begin{array}{c}{n}_{{M}_{i}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)+{n}_{{M}_{j}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\\ -{n}_{{M}_{i}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right).{n}_{{M}_{j}}^{r}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\end{array}\right),\\ \left(\begin{array}{c}{n}_{{M}_{i}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)+{n}_{{M}_{j}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\\ -{n}_{{M}_{i}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right).{n}_{{M}_{j}}^{i}\left({{{\mathop u\limits_ \cdot }^\prime }}\right)\end{array}\right)\end{array}\right)\end{array}\right)$$

(6)

Consequently, the weighted aggregated decision matrix is in the form of

$m_{{{\text{M}}_w}}^r({\mathop {{\text{ }}u}\limits_ \cdot ^\prime }),m_{{{\text{M}}_w}}^i({\mathop {{\text{ }}u}\limits_ \cdot ^\prime })$, $(a_{{{\text{M}}_w}}^r({\mathop {{\text{ }}u}\limits_ \cdot ^\prime }),a_{{{\text{M}}_w}}^i({\mathop {{\text{ }}u}\limits_ \cdot ^\prime }))$, $(n_{{{\text{M}}_w}}^r({\mathop {{\text{ }}u}\limits_ \cdot ^\prime }),n_{{{\text{M}}_w}}^i({\mathop {{\text{ }}u}\limits_ \cdot ^\prime }))$.

Step 4: Determine the CPF-positive ideal solution (CPFPIS)${(A}^{+})$ and CPF-negative ideal solution (CPFNIS)${(A}^{-})$:

Let $B$ and $C$ be the sets of benefit and cost criteria, then ${A}^{+}$ and ${A}^{-}$ are determined as follows.

$${A}^{+}=\left(\begin{array}{c}\left({m}_{{\text{M}}_{w}^{+}}^{r}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right),{m}_{{\text{M}}_{w}^{+}}^{i}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right)\right),\\ \left({a}_{{\text{M}}_{w}^{+}}^{r}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right),{a}_{{\text{M}}_{w}^{+}}^{i}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right)\right),\left({n}_{{\text{M}}_{w}^{+}}^{r}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right),{n}_{{\text{M}}_{w}^{+}}^{i}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right)\right)\end{array}\right)$$

and

$${A}^{-}=\left(\begin{array}{c}\left({m}_{{\text{M}}_{w}^{-}}^{r}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right),{m}_{{\text{M}}_{w}^{-}}^{i}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right)\right),\\ \left({a}_{{\text{M}}_{w}^{-}}^{r}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right),{a}_{{\text{M}}_{w}^{-}}^{i}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right)\right),\left({n}_{{\text{M}}_{w}^{-}}^{r}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right),{n}_{{\text{M}}_{w}^{-}}^{i}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right)\right)\end{array}\right)$$

where,

$$\left(\begin{array}{c}{m}_{{\text{M}}_{w}^{+}}^{r}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right),\\ {m}_{{\text{M}}_{w}^{+}}^{i}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right)\end{array}\right)=\left(\begin{array}{c}{\left(\begin{array}{c}\left(\underset{i}{\text{max}}{m}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in B\right),\\ \left(\underset{I}{\text{min}}{m}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in C\right)\end{array}\right)}^{r},\\ {\left(\begin{array}{c}\left(\underset{i}{\text{max}}{m}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in B\right),\\ \left(\underset{I}{\text{min}}{m}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in C\right)\end{array}\right)}^{i}\end{array}\right),$$

$$\left(\begin{array}{c}{a}_{{\text{M}}_{w}^{+}}^{r}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right),\\ {a}_{{\text{M}}_{w}^{+}}^{i}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right)\end{array}\right)=\left(\begin{array}{c}{\left(\begin{array}{c}\left(\underset{i}{\text{max}}{a}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in B\right),\\ \left(\underset{I}{\text{min}}{a}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in C\right)\end{array}\right)}^{r},\\ {\left(\begin{array}{c}\left(\underset{i}{\text{max}}{a}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in B\right),\\ \left(\underset{I}{\text{min}}{a}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in C\right)\end{array}\right)}^{i}\end{array}\right)$$

$$\left(\begin{array}{c}{n}_{{M}_{w}^{+}}^{r}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right),\\ {n}_{{M}_{w}^{+}}^{i}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right)\end{array}\right)=\left(\begin{array}{c}{\left(\begin{array}{c}\left(\underset{i}{\mathit{min}}{n}_{{M}_{w}^{i}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in B\right),\\ \left(\underset{I}{\mathit{max}}{n}_{{M}_{w}^{i}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in C\right)\end{array}\right)}^{r},\\ {\left(\begin{array}{c}\left(\underset{i}{\mathit{min}}{n}_{{M}_{w}^{i}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in B\right),\\ \left(\underset{I}{\mathit{max}}{n}_{{M}_{w}^{i}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in C\right)\end{array}\right)}^{i}\end{array}\right)$$

(7)

$$\left(\begin{array}{c}{m}_{{\text{M}}_{w}^{-}}^{r}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right),\\ {m}_{{\text{M}}_{w}^{-}}^{i}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right)\end{array}\right)=\left(\begin{array}{c}{\left(\begin{array}{c}\left(\underset{i}{\text{min}}{m}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in B\right),\\ \left(\underset{I}{\text{max}}{m}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in C\right)\end{array}\right)}^{r},\\ {\left(\begin{array}{c}\left(\underset{i}{\text{min}}{m}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in B\right),\\ \left(\underset{I}{\text{max}}{m}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in C\right)\end{array}\right)}^{i}\end{array}\right)$$

$$\left(\begin{array}{c}{a}_{{\text{M}}_{w}^{-}}^{r}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right),\\ {a}_{{\text{M}}_{w}^{-}}^{i}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right)\end{array}\right)=\left(\begin{array}{c}{\left(\begin{array}{c}\left(\underset{i}{\text{min}}{a}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in B\right),\\ \left(\underset{I}{\text{max}}{a}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in C\right)\end{array}\right)}^{r},\\ {\left(\begin{array}{c}\left(\underset{i}{\text{min}}{a}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in B\right),\\ \left(\underset{I}{\text{max}}{a}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in C\right)\end{array}\right)}^{i}\end{array}\right)$$

$$\left(\begin{array}{c}{n}_{{\text{M}}_{w}^{-}}^{r}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right),\\ {n}_{{\text{M}}_{w}^{-}}^{i}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right)\end{array}\right)=\left(\begin{array}{c}{\left(\begin{array}{c}\left(\underset{i}{\text{max}}{n}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in B\right),\\ \left(\underset{I}{\text{min}}{n}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in C\right)\end{array}\right)}^{r},\\ {\left(\begin{array}{c}\left(\underset{i}{\text{max}}{n}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in B\right),\\ \left(\underset{I}{\text{min}}{n}_{{\text{M}}_{w}^{\text{i}}}\left({{{{\mathop u\limits_ \cdot }^\prime }}}_{j}\right):j\in C\right)\end{array}\right)}^{i}\end{array}\right)$$

Step 5: Calculate the distance of each alternative from CPFPIS and CPFNIS by using the novel DM:

Using Eq. (3), apply the proposed DM to calculate the distance of each alternative from CPFPIS and CPFNIS.

Step 6: Compute the similarity of each alternative from CPFPIS and CPFNIS by using the novel SM:

Using Eq. (2), apply the proposed SM to calculate the similarity of each alternative to the ideal solution. The similarity score will be a value between $[\text{0,1}]$ and the higher the score, the closer we are to the ideal solution process.

Step 7: Calculate the closeness coefficient (CC) to the ideal solution:

Determine the closeness coefficient of each alternative to the ideal solution by using the following formulas for DM and SM, respectively.

$$C{C}_{D}=\frac{{D}^{-}}{{D}^{-}+{D}^{+}}$$

(8)

$$C{C}_{S}=\frac{{S}^{-}}{{S}^{-}+{S}^{+}}$$

(9)

The value of CC will fall within a range of $[0, 1],$ and the higher the value of CC, the closer the solution is to the ideal solution.

Step 8: Rank the Alternatives:

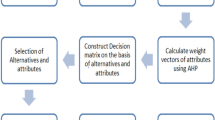
Rank the alternatives according to CC. Also, Fig. 2, shows the CPF-TOPSIS methodology.

Fig. 2

CPF-TOPSIS methodology.

Speech matching and sports training feature recognition

Speech matching involves comparing speech samples to identify similarities, classify spoken commands, or verify speaker identities. This process is especially popular in voice-based authentication systems, speaker identification applications, and speech recognition systems when the patterns of people’s voices or the content of commands can influence the decision-making process. This is a difficult task due to the inherent characteristics of the problem among which we have interfered with noise, feature overlapping, and uncertainty. The integration of CPFS into the evaluation process of the matching task ensures that these challenges are addressed because they include complex MD, AD, and NMD in the approach.

On the other hand, sports training feature recognition is concerned with the extraction and tagging of physical features in athletes such as posture, motion, flexibility, and steadiness among others. This recognition is important in assessing performance, recognizing problems, as well as in enhancing the results of training. For instance, evaluating whether a player sustains correct posture or executes movements within proper ranges defines skill enhancement or risk of injuries.

Thus, both speech matching and sports training which involve feature recognition can be modeled as MCDM problems. In this regard, strategies and options are compared through one criterion, and a table is used to select the best match or category. CPF-TOPSIS is a systematic approach for ranking the solutions obtained from problem-solving based on how close they are to the ideal solution taking into account fuzzy uncertainty in the alternative selection process.

The characteristics of speech matching and sports training feature recognition can then be assessed within the CPF-TOPSIS decision-making problem. In this case, four experts evaluate five alternatives regarding ten criteria for speech matching and sports training feature recognition.

Experts: Four experts $({E}_{1}, {E}_{2}, {E}_{3}, {E}_{4}$) evaluate the alternatives across all criteria as shown in Fig. 3:

• a) ${{\varvec{E}}}_{1}$ (Speech Specialist): Pertain to the qualities that include tone, intensity, intonation and also fluency.

• b) ${{\varvec{E}}}_{2}$ (Audio Engineer): Concentrates on signal features as the MFCC coefficients.

• c) ${{\varvec{E}}}_{3}$ (Sports Scientist): Remembers physical parameters for example posture angles.

• d) ${{\varvec{E}}}_{4}$ (Biomechanics Expert): Allows for measurement of dynamic properties such as; Balance and agility for instance.

Fig. 3

Decision-making experts.

This way, their experience guarantees a powerful and more complete analysis of the alternatives.

Alternatives: The five alternatives (${A}_{1},{A}_{2},{A}_{3},{A}_{4},{A}_{5}$) represents combinations of speech samples and sports movements, evaluated simultaneously:

${{\varvec{A}}}_{1}$: A bass-type vocal supported by a symmetrical movement.

${{\varvec{A}}}_{2}$: A model of a speaker that has high clarity but has an unstable condition about its posture.

${{\varvec{A}}}_{3}$: A talker with an average amount of speech activity and very good speech flexibility.

${{\varvec{A}}}_{4}$: A speaker with fluctuating pitch and high speed of vocal cord oscillations.

${{\varvec{A}}}_{5}$: A control of the voice a bit through good pacing and good standing position.

Criteria: The ten criteria (${C}_{1},{C}_{2}$,…,${C}_{10}$) are evaluated for speech matching and sports training feature recognition as shown in Fig. 4:

• a) Spectral features (${{{C}}}_{1}$): Histograms of the frequency of speech signals.

• b) Pitch (${{{C}}}_{2}$): This is the basic pitch of voice used in the communication of information by human beings.

• c) MFCC Coefficients (${{{C}}}_{3}$): A list of characterized acoustic parameters that make a representation of speech.

• d) Noise tolerance (${{{C}}}_{4}$): Spectral matching of the speech signals with different noises and their ability to oppose them.

• e) Clarity (${{{C}}}_{5}$): Identity of a speaker in terms of timbre of voice.

• f) Posture angles (${{{C}}}_{6}$): During the movement, angles are oriented to the correct movement.

• g) Joint velocity (${{{C}}}_{7}$): Rate at which the two articulations in the joint move during an activity.

• h) Acceleration (${{{C}}}_{8}$): Quantitative measure of acceleration in the motion.

• i) Balance (${{{C}}}_{9}$): Stability during movements.

• j) Agility (${{{C}}}_{10}$): Opportunity and flexibility to switch direction in a short time.

Fig. 4

Evaluation of criteria.

These criteria are then used to assess each of the alternatives utilizing CPFVs to model entropy in the estimation of controlling experts. As displayed in Table 2, linguistic expressions of experts’ expertise and criteria are illustrated with CPFVs and the identified MD ($m$), AD $(a),$ and NMD ($n$) during the evaluation. These values are important to ensure the effective usage of the IM-based TOPSIS method in assessing and ranking the alternatives where the experts are uncertain.

Table 2 Linguistic CPFVs for criteria.

Table 3 summarizes the linguistic expressions employed in the analysis of performance levels of the alternatives under the context of the CPFS framework. The corresponding CPFVs provide a systematic approach to incorporating the unpredictability and imprecision of decision-making situations, leading to a better understanding of the alternatives.

Table 3 Linguistic CPFVs for alternatives.

In Table 4, the significance values of criteria associated with sports training and speech match are represented based on three experts (${E}_{1}, {E}_{2}, {E}_{3}, {E}_{4}$). These are expressed in linguistic terms such as medium (M), important (I), and very important (VI) depending on the assessment of each expert about the level of importance of the criteria in the decision-making process.

Table 4 Evaluation of criteria based on experts’ opinions.

To determine the experts’ weights, we used Eq. 4, which shows how weights can be calculated using the information provided by the experts. Table 5 below shows the weight values obtained through the calculation for the experts. These weights matter a lot since they help in the decision-making process by specifying the degree of importance of each evaluation provided by the group of experts.

Table 5 Weights of each expert.

By applying Eq. 5, which utilizes the CPFWA operator, we derived the weights for various criteria as presented in Table 6. This table illustrates the weights for each criterion ${C}_{1}$ to ${C}_{10}$. These values show the weight of each criterion in the decision-making process and give an overall perspective on the other criteria’s importance in the evaluation.

Table 6 Criteria weights.

The assessment of the alternatives (${A}_{1} to {A}_{5}$) based on different criteria associated with sports training, feature recognition and speech matching are presented in Table 7. Here is the rating of the four experts (${E}_{1}, {E}_{2}, {E}_{3},{E}_{4}$) who have assessed the different alternatives using linguistic terms. These linguistic expressions reflect the qualitative measures that estimate the performance of every option against the different criteria.

Table 7 Evaluation of alternatives.

The aggregated CPF decision matrix is represented in Table 8. The values in this table are obtained by performing the CPFWA operator on linguistic ratings represented in Table 7. This aggregation process integrates the qualitative judgment of the four experts over the alternatives (${A}_{1}$ to ${A}_{5}$) for the criteria (${C}_{1}$ to ${C}_{10}$).

Table 8 Aggregated complex picture fuzzy decision matrix.

Table 9 displays the aggregated weighted CPF decision matrix for CPFS, which is determined by applying the multiplication operator, as defined in Eq. 6. In this process, each value in Table 8 is multiplied by the weight of the criteria given in Table 6 by multiplying the rules of the CPF environment.

Table 9 Weighted aggregated complex picture fuzzy decision matrix.

Table 10 depicts the CPFPIS ${(A}^{+})$ and CPFNIS $({A}^{-})$ obtained by employing Eq. 7 from the perspective of the TOPSIS technique. The table is developed using the positive and negative ideal solution derived from the aggregated weighted CPF decision matrix.

Table 10 Complex picture fuzzy positive and negative ideal solutions.

Table 11 shows the DM (${D}^{+}$ and ${D}^{-}$) and the $C{C}_{D}$ of each of the alternatives (${A}_{1}$ to ${A}_{5}$) which are calculated using the proposed DM from Eq. 3 and the CC from Eq. 8. ${D}^{+}$ refers to the distance from the positive ideal solution while ${D}^{-}$ is the distance from the negative ideal solution. The CC integrates these distances to give a comprehensive ranking measure for the alternatives. A higher CC value means an alternative is closer to the ideal solution and farther from the negative one. Figure 5, shows the ranking based on DM.

Table 11 Distance measure and closeness coefficient of each alternative.

Fig. 5

Ranking based on CPF-DM.

Similarly, Table 12 shows the SM (${S}^{+}$ and ${S}^{-}$) and the $C{C}_{S}$ of each of the alternatives (${A}_{1}$ to ${A}_{5}$) which are calculated using the proposed SM from Eq. 2 and the CC from Eq. 9. ${S}^{+}$ refers to the similarity from the positive ideal solution while ${S}^{-}$ is similar to the negative ideal solution. The CC integrates these similarities to give a comprehensive ranking measure for the alternatives. Also, Fig. 6, shows that the ranking is based on SM.

Table 12 Similarity measure and closeness coefficient of each alternative.

Fig. 6

Ranking based on CPF-SM.

Result discussion

The CPF-TOPSIS analysis yields optimal evaluation results for the alternatives in Speech Matching and Sports Training Feature Recognition, as per the DM and SM ranks, thus establishing the usefulness of the methodology. According to the data presented in Table 10 using DM, it is possible to determine that for Alternative ${{\varvec{A}}}_{1}$ with a bass-type vocal supported by symmetrical movement, the result is the highest closeness coefficient indicating the required level of CCD (${\varvec{C}}{{\varvec{C}}}_{{\varvec{D}}}=0.581$). This demonstrates its improved performance and representation of the optimal solution in ranking assessments based on distances. Next, ${{\varvec{A}}}_{2}$ (a model speaker with high clarity but unstable posture) and ${{\varvec{A}}}_{3}$ (a talker with average speech activity and excellent flexibility) are ranked second and the third, respectively, and can be heavily considered as moderate matches for the idealized criteria. Table 12, based on SM, presents related data to these discoveries. While the measures are inversely related, pacing and standing position contribute less to the computation of ${{\varvec{A}}}_{5}$, which turns out to be the best choice (${\varvec{C}}{{\varvec{C}}}_{{\varvec{S}}}=0.514$) in similarity-based comparisons to the ideal solution. ${{\varvec{A}}}_{4}$ which included fluctuating pitch and high speed of vocal cord oscillations, ${{\varvec{A}}}_{3}$ are relatively nearest with closeness coefficients of $0.508$ and $0.503$ respectively. These rankings confirm the efficacy of CPF-IM TOPSIS in incorporating both distance and similarity to allow comprehensive evaluation of alternatives. In this application, the CPF-IM TOPSIS approach is found efficient and beneficial. When CPF SM and DM are combined, the proposed methodology is able to account for uncertainties, cyclic behaviors, and hesitation often observed in real-world data. The findings reveal that the proposed method is effective in terms of generating consistent results and validating and ranking the alternatives against different criteria from two evaluation perspectives. This validation supports CPF-IM TOPSIS on identifying holistic, precise, and context-related decision-making solutions for highly demanding areas as speech matching and sports training feature recognition.

Comparison analysis

In this study, the evaluation was performed using hypothetical data to demonstrate the behavior and applicability of the proposed approach. A detailed comparative analysis has been conducted between the proposed approach and existing MCDM methods. The comparative analysis Table 13 shows that the proposed CPF-TOPSIS approach (IM-based) is better than the conventional MCDM techniques, namely MARCOS [38], WASPAS [39], VIKOR [40], TODIM [41], COCOSO [42], and DEMATEL [43]. CPF-TOPSIS performs better in complex uncertainties and cyclic behaviors, which highlights the applicability of the approach in scenarios where other approaches fail. It makes decision-making precise but is primarily used for large datasets, making it impractical for smaller datasets due to the algorithm’s lack of scalability for big data. Although methods such as WASPAS and VIKOR provide competitive decision accuracy, the presented approach is unable to handle cyclic behaviors and complex uncertainties. While DEMATEL and TODIM, on the other hand, have a few drawbacks in terms of computational efficiency and scalability. The CPF-TOPSIS approach combines the real and imaginary components of CPFS, providing a comprehensive solution for addressing MCDM issues, as demonstrated in speech matching and sports training feature recognition. This makes it ideal for use in situations involving complex decision-making processes because of its ability to perform better than other decision-making tools.

Table 13 Comparison analysis.

This characteristic-level comparison allows for a thorough assessment of performance, consistency, and decision-support capability. However, statistical analysis techniques such as Kendall’s tau correlation and p-value-based sensitivity tests were not incorporated, as this investigation focuses on the development and demonstration of proposed approach within the complex fuzzy framework. Moreover, the paper aims to define a methodological innovation and illustrate its operational benefits; however, statistical validation over real-world data is reserved for future extensions.

To validate the reliability and consistency of the proposed approach, we conducted a numerical comparison analysis and compared the ranking results with those of existing methods, such as CPFWA and CPFWG, as shown in Fig. 7. The ranking values obtained using the proposed approach confirm the robustness of the model. Although the closeness coefficient values differ due to the underlying computational mechanics, the consistency in final rankings demonstrates that the proposed operators behave similarly to existing ones while offering enhanced flexibility in modeling hesitation and complex information. This consistency supports the reliability of the proposed method in real-world MCDM scenarios.

Fig. 7

Numerical Comparison Analysis.

Sensitivity analysis

Sensitivity analysis in a CPF-TOPSIS approach is important to determine the changes in the ranking results of the alternatives in response to changes in the parameters used in acquiring the rankings. This process evaluates the variations in different weights, criteria, and other inputs that define the decision-making process to validate the model’s integrity. The sensitivity analysis in this study is performed for the purpose of confirming the adequacy of CPF-TOPSIS for decision-making under varying conditions.

The effects of weight factors on ranking outcome

The CPF-TOPSIS framework identifies criteria importance and allocate weights to them as per vicinity to the decision-making path. Using the method, various weight distribution scenarios are considered to determine the stability of rankings. As a result of the analysis, it is possible to identify that the primary ranked strategy always occupies leading place throughout all the tested conditions that confirms the effectiveness of introduced approach. In the same way, other alternatives show stability in their ranks hence strengthening the revealed model stability as shown in Fig. 8. This robustness attests for the flexibility of CPF-TOPSIS when it comes to dealing with vagaries of weight determination hence making it a reliable tool for MCDM.

Fig. 8

Effects of weight factors on ranking outcome.

Effect of changes in the criteria for the rankings

The analysis of changes in criteria demonstrates that the CPF-TOPSIS model can be effectively used when the conditions of the decision-making environment change. For instance, changes in criteria lead only to slight variations in the ranking, which suggests that the applied methodology is indeed close to grasping the nature of the problem. This result shows that the solution with high performance in the key selection criteria is more stable against the shifts in ranking as shown in Fig. 9.

Fig. 9

Effect of changes in the criteria for the rankings.

Validation of results

By observing changes in weights and criteria, the sensitivity analysis confirms that CPF-TOPSIS does provide robust rankings regardless of condition changes. To support it, this analysis reinforces the confidence in the effectiveness of the proposed methodology in realistic fields including the speech matching criteria, and training features identification of various sports. The ability of CPF-TOPSIS in maintaining similar ranks even in extreme variation also increases credibility in making decisions using the tool.

Practical implications

The CPF-TOPSIS model demonstrates practical relevance for use in three fundamental areas, including speech matching, sports training, and biometric applications. The model enables the development of enhanced voice recognition systems that utilize criteria such as tone, intensity, and clarity to improve speech pattern ranking accuracy. Conventional speech recognition systems often encounter difficulties when faced with noise interference and unclear speech characteristics. The inclusion of CPFS controls mitigates uncertainties in CPF-TOPSIS, enabling better recognition of security in unpredictable real-world situations. The decision-making capability of CPF-TOPSIS proves useful in various applications, from security systems to medical diagnostics, that require exact adaptation of critical evaluations in speech-related conditions. CPF-TOPSIS enables a comprehensive assessment of an athlete’s performance in sports training through the analysis of posture, balance testing, agility measurements, and hip and knee velocity measurements. The system enables sports science professionals to generate customized, data-driven training systems due to its ability to handle specific requirements. Through this model, trainers and coaches identify which athletic abilities require improvement and which ones the athlete masters most effectively, allowing them to focus on sessions that drive maximum performance. The combination of expert opinions across the fields of biomechanics and sports science provides CPF-TOPSIS with exceptional value when assessing complex, multidimensional evaluations that occur in multidisciplinary settings.

An expanded application of this method enables its use in biometric applications that require real-time analysis of physical performance for fitness tracking and health monitoring purposes. The technique can function effectively in conjunction with CPF-TOPSIS in wearable devices that monitor workout and rehabilitation performance, delivering customized feedback tailored to user development. The system presents value for voice-based biometric authentication by providing superior accuracy and security to protect speech pattern identification in different applications. The decision-making processes across various fields undergo transformation due to the implementation of CPF-TOPSIS, which provides a versatile model capable of handling actual data complexity and uncertainty. By incorporating expert systems and fuzzy logic, it has become a valuable tool to enhance operational results within sectors that rely on human involvement, offering superior decision quality, operational efficiency, and practical deployment potential across all industrial nodes.

Advantages

The proposed TOPSIS approach using new IM, which included both SM and DM in a CPFS environment, is proposed for the first time for speech recognition and sports training feature recognition in the pattern recognition context in this study and also offers the following important advantages.

• Enhanced handling of uncertainty: The incorporation of real and imaginary parts of MD, AD as well as NMD, results in a more extensive character of the representation of uncertainty in comparison to the utilization of fuzzy systems.

• Improved decision-making accuracy: The integration of SM and DM in the framework increases the reliability of the evaluations because it includes more than one opinion of the experts, solves the conflict of the criteria, and reduces hesitation in decision-making processes within the CPF-TOPSIS framework.

• Unified framework for MCDM: This work does put forth a unified framework for the use of MCDM in different contexts where it is required, which makes it universally versatile to address a wide range of real-life problems in the contexts of speech and sports-training match identifying features.

• Real-world application impact: This work directly advances methodology in speech-matching and sports-training feature recognition, beneficial to real-world systems that include biometric-authentication, voice-recognition, and sports science and the theoretical frameworks supporting them.

• Better representation of expert opinions: The CPF-TOPSIS method developed and proposed here is capable of handling the multi-attribute and expert-based evaluation models, and can combine both the quantitative and qualitative factors, which is more realistic in capturing the experts’ judgments in the real environment.

• Handling of conflicting criteria: The approach serves as the right answer to the conflict of criteria because it gives an opportunity to structure the problem and analyze it through a set of linguistic and sports-data parameters.

• Scalability and flexibility: The idea of the proposed model can be generalized for a variety of problems that belong to the class of MCDM problems different from speech and sports fields or can be applied to various branches, such as medical diagnostics, financial analysis, etc.

Limitations of this research

The following are the limitations of this study:

• Complexity of Computational Implementation: The CPF-TOPSIS which has been proposed in this study for determining SM and DM is likely to take quite a lot of computational resources and efficient algorithms. This could have problems in real-time applications or a system with less computational capacity.

• Assumption of Expert Consistency:

• The model also supposes all the ratings made by the experts are consistent which in real-life situations may not be true. The reviewers can have different levels of concerns, and preferences, or they may view criteria in a different way which in turn affects the reliability of the results.

• Dependency on Subjective Weight Assignments: The weights, for instance, in methods such as TOPSIS can be assigned given a lot of subjectivity, and the utility of these results depends on how well the weights incorporated into the formula do justice to the relative importance of each criterion. It emerged that poor assignment of weight to particular inputs can impact the decision of the organization.

• Data Quality and Availability: The capability of the CPF-TOPSIS model depends on the quality and availability of data required for speech matching and sports training features identification. Imprecise information is not perfect especially if it contains noise, missing values, or has errors, thus results from such information may not be ideal.

• Limited Consideration of Temporal Dynamics: While the cyclic uncertainty of the model is identified, temporal dynamics or changing characteristics over time may be lacking, though such an argument depends on the type of analog such that in a sport where behavior or performance changes with training and fatigue, the model could be considered lacking such details.

• Generalization to Other Complex Domains: Thus, although the applied work is more concrete and involves speech and sports, the authors admit that the method may require further improvements for situations where the noise level of data can be different, for example, in healthcare or when monitoring the environment, which, in turn, requires more nuanced decision-making.

Conclusion

In this work, we proposed a new integration of CPFS with the TOPSIS techniques to handle uncertainties, ambiguity, hesitation, and cyclic behavior when identifying speech matching and training the sports training feature. In proposing new SM and DM for CPFS, we incorporated the real and imaginary parts of MD, AD, and NMD into a very strong framework. The proposed methodology was then demonstrated on a real-world example or speech matching feature and sports training feature recognition. These included the vocal characteristic option, the posture stability option, and the speech flexibility options and it based on the multiple criteria that had been used to evaluate it by experts. The results also showed that the obtained CPF-TOPSIS scores for SM and DM were almost parallel, proving the effectiveness of the proposed ranking technique once again, and the alternative $A_1$ (bass-type vocal supported by symmetrical movement), was on top of rankings once more. The methodology deals with the complexity and ambiguity of the example adequately, thus proving the efficiency of its usage in decision-making. This work fills the gap between theory in fuzzy logic systems and application in complex environments such as artificial intelligence and sports science. The use of CPFS in MCDM frameworks ensures accuracy and consistency making MCDM an important aid in tackling great decision-making issues.

Future direction

This work also suggests numerous research directions for future investigations. Since hesitation and uncertainty are common in different areas, the proposed CPF-TOPSIS methodology can be applied to fields such as healthcare [44], social networks [45], and Tourism industry [46]. It is also possible to pose additional questions and include more criteria and a higher number of samples in new studies to evaluate the efficiency and applicability of the proposed approach. Comparing the advantages and considering the interconnection with other decision-making methodologies like, for example, VIKOR [40] or WASPAS [47], the further modification of CPF-TOPSIS may give a better outcome. Besides, the enhancement of the definitions of SM and DM can help to increase the efficiency of decision-making and apply it to solve various multifaceted tasks.