Study on comprehensive landslide risk zoning method in open pit mines under multi factor coupling effects

Abstract

Comprehensive landslide risk zoning in open-pit mines is fundamental to precise safety monitoring, early warning, and disaster prevention and control. Existing approaches often rely on single static indicators and exhibit limited capacity for dynamic risk regulation. To address these limitations, this study proposes a scientifically grounded slope zoning method that couples multiple factors across "engineering-geological-environmental (seasonal variations, distribution of infrastructure)". First, a hierarchical structure model comprising four key influencing degree of crack development, slope angle, slope height, and rock and soil properties—is constructed using the Analytic Hierarchy Process (AHP). By computing the weight coefficients of these evaluation indices and deriving a slope hazard index, we classify slope hazard zones. Additionally, the two-dimensional rigid-body Limit Equilibrium Method (LEM) is applied to calculate slope factor of safety for multiple cross-sections, facilitating the delineation of slope stability zones. To integrate these results, we employ a combined cross-matrix analysis and simple weighted averaging method, further refining the comprehensive risk zoning by dynamically incorporating factors such as slope along-strike surface shape, seasonal (climatic) variations, fault characteristics, and distribution of infrastructure. This approach is validated through application to a case study in an open-pit mine, where one higher-risk, five medium-risk, and six low-risk zones are identified. Notably, the higher-risk zone exhibits strong spatial agreement with actual landslide occurrences. The results demonstrate that the proposed method significantly enhances zoning accuracy, providing a theoretical basis for the optimized allocation of monitoring resources, the development of differentiated early-warning models, and the full-lifecycle management of slopes in open-pit mining operations.

Introduction

As open-pit mining operations expand, the frequency of landslides, collapses, and other geohazards has escalated, posing significant challenges for precise and slope hazard management¹. Open-pit coal mines, characterized by deep excavation and extensive coal seam strike, exhibit large slope spans and complex geological conditions. The substantial heterogeneity in rock mass structures, hydrogeological environments, and mining-induced disturbances across different sections results in pronounced spatial variability in slope stability. Consequently, there is an urgent need for a rigorous and precise slope zoning method to accurately identify hazardous areas, addressing the shortcomings of conventional uniform monitoring approaches. It provides a theoretical foundation for the optimized allocation of monitoring resources, the development of differentiated early warning models, and the full-lifecycle management of open-pit mine slopes.

The study of slope stability has evolved from the Coulomb’s earth pressure theory and static equilibrium methods analyzing ultimate states, to the Swedish slice method and limit equilibrium methods, and more recently to non-deterministic approaches such as reliability analysis, fuzzy mathematics, and numerical simulation². Zhang R.H. et al.³ proposed an improved LEM that accounts for both global and local failure modes. Deng D.P. et al.⁴ derived a stability evaluation equation for rocky slopes based on Taylor series expansion. Numerical simulation methods have been widely applied; for instance, Ding X.P.⁵ studied the impact of slope angles and the width-to-height ratio of coal pillars, while Wu S.C. et al.⁶ combined GEO-STUDIO and the grey relational analysis method to assess the impact of rainfall on stability. In terms of physical experiments, Cheng G. et al.⁷ and others employed Distributed Fiber Optic Sensing technology for multi-source, multi-field monitoring, and Yao Y.H. et al.⁸ found that slopes with water retention were less stable than dry soil slopes. Artificial intelligence technologies have also gradually been applied in slope stability analysis. Liu Z. et al.⁹ have utilized a BP neural network to investigate the non-linear relationship between slope safety factors and new components, while Liu Z. et al.¹⁰ proposed a new evaluation method based on extreme learning machines, which demonstrated higher application accuracy. These methods have enhanced the accuracy of stability evaluations; however, traditional overall analysis fails to accurately characterize local risks, limiting the implementation of refined control measures. Consequently, zoning studies have gradually become a key strategy for optimizing slope stability management.

Liu Z.P. et al.¹¹ employed maximum Lyapunov exponent analysis to divide slopes into unstable and marginally stable zones based on multi-variable deformation time series. Cao¹² classified slope stability zones using rock mass properties and discontinuity characteristics, incorporating Rock Mass Rating classification. Tao Z.G. et al.¹³ applied fuzzy mathematics for comprehensive evaluation, categorizing slopes into four stability levels. Zhang P. et al.¹⁴ developed the MSARMA model, enabling 3D visualization-based zoning and early warning using slope stability factor calculations. Han T.W, Li J.¹⁵ classified four engineering geological rock groups and subdivided slopes into five stability zones based on rock strength and structural types. Wang Y.M.¹⁶ identified three potential hazard zones by integrating rock mass structure and fault characteristics. Wang Y.Q. et al.¹⁷ combined structural discontinuities and numerical simulations to classify the Wushan Cu-Mo mine slopes into five engineering geological zones. Li Y. et al.¹⁸ used lithology, stratigraphy, and hydrogeological conditions to delineate four engineering geological zones, integrating Schmidt net projection and full-wave sonic logging for stability assessment. Ji C.¹⁹ analyzed rock mass deformation mechanisms by incorporating goaf effects and classifying slopes into three geological zones based on slope morphology and tectonic features. Li Q.Z. et al. ²⁰ differentiated geological regions based on rock mass strength and integrity, using back analysis to calibrate geotechnical strength parameters.Yin J.²¹ employed slope morphology and geological structure grading to further divide the eastern slope of an open-pit mine into multiple subzones, identifying high-risk collapse and landslide zones. Xu W.L. et al.²² constructed a weighting system using the AHP, classifying soil slopes into four hazard levels to optimize monitoring layouts.Chen S.S. et al.²³ employed a comprehensive index method integrated with ArcGIS technology to delineate a study area into four levels of geological hazard susceptibility zones based on six selected factors, providing a scientific basis for regional disaster prevention. Xu Y. et al.²⁴ utilized stereographic projection and acoustic logging techniques to categorize an open-pit copper mine slope into four zones, offering guidance for safe mining operations. Long S.L. et al.²⁵ focused on highway infrastructure and adopted the AHP in conjunction with GIS technology, incorporating eight factors to classify the region into low, medium, and high susceptibility zones, thereby contributing to disaster prevention modeling for linear engineering projects. Cao S.L. et al.²⁶ integrated AHP and GIS methodologies with geological and hydrogeological indicators to divide the study area into high-risk, medium-risk, and low-risk zones, further proposing monitoring, early warning strategies, and engineering mitigation measures. Zhao J.²⁷ conducted a stability zoning analysis of a mining area based on stratum bedding and slope configuration, classifying the region into four distinct stability categories.In recent years, multi-factor coupled geological hazard risk assessment has emerged as a major research focus internationally. Bathrellos et al.²⁸ proposed a multi-hazard coupling model-based suitability assessment framework for urban planning. Bathrellos et al.²⁹ conducted a GIS-based sensitivity analysis of landslide causative factors in tectonically active regions, revealing the coupling mechanisms between fault activity and slope parameters. Karpouza et al.³⁰ introduced a spatial-behavior integrated analytical approach for natural disaster emergency route evaluation, which provides a valuable reference for constructing the comprehensive landslide risk zoning framework proposed in this study.

Despite significant progress in slope zoning methods, certain limitations persist. On one hand, most existing studies focus on single-factor zoning approaches centered on technical indicators, lacking a unified analytical framework for multi-factor coupling. On the other hand, current research predominantly adopts static analyses, with insufficient capacity for dynamic risk regulation. Moreover, many zoning methods are tailored to specific open-pit slope conditions, resulting in limited generalizability. To accurately identify high-risk zones, support differentiated early warning model construction, and inform the development of targeted landslide mitigation measures, this study integrates slope hazard and slope stability zoning results using cross-matrix analysis and a simple weighted averaging method. A dynamic adjustment mechanism is incorporated to develop a comprehensive landslide risk zoning method that couples "engineering-geological-environmental (seasonal variations, distribution of infrastructure)". This approach enables precise delineation of landslide risk zones in open-pit mines, overcomes the limitations of single-method frameworks, and supports the formulation of differentiated control strategies for each zone. By avoiding the inefficiencies of one-size-fits-all management, the proposed method provides quantitative decision-making support for full-lifecycle safety management in open-pit mining.

Comprehensive landslide risk zoning methodology in open-pit mines

Analysis of influencing factors in comprehensive landslide risk zoning

Comprehensive landslide risk arises from the coupling of multiple factors, including slope geohazard susceptibility, engineering stability, and environmental influences,which collectively exhibit a complex and nonlinear risk response mechanism. Table 1 systematically elaborates on the mechanisms of various influencing factors, providing a theoretical foundation for subsequent multi-factor coupling analysis and dynamic optimization.

Table 1 Influencing Factors and Their Mechanisms in Comprehensive Landslide Risk Zoning.

Framework of comprehensive landslide risk zoning system

To achieve precise zoning of open-pit mine slopes, this methodology integrates the AHP, the LEM, cross-matrix analysis, and the simple weighted averaging method. Firstly, degree of crack development, slope angle, slope height, and rock and soil properties were selected as evaluation indices. A hierarchical structure model was established based on the AHP, wherein expert opinions and a pairwise comparison matrix were employed to determine the relative importance of each index. A judgment matrix was constructed and subjected to a consistency test to ensure the rationality of weight allocation. Subsequently, the weight coefficients of each index were computed, enabling the assessment of slope geological hazard risk. The hazard levels were classified into four categories: low, moderate, medium, and high. This approach achieves slope geological hazard zoning based on the AHP framework. Concurrently, the LEM is applied to compute the factor of safety (F_s), enabling a quantitative stability evaluation. Slopes are then classified into four stability categories: stable, marginally stable, less stable, and unstable.

The geohazard susceptibility zoning results and slope stability zoning results are integrated through cross-matrix analysis and a simple weighted averaging method to construct a cross-classification matrix. The Kappa coefficient³³ is used to measure consistency, followed by the calculation of a comprehensive risk index³⁴ for final risk level classification. Finally, the comprehensive risk classification is dynamically optimized by incorporating seasonal (climatic) variations, slope along-strike surface shape, fault characteristics, and distribution of infrastructure. Following dynamic adjustment rules that account for the influence of these factors on slope stability, the final landslide risk zoning is determined. The framework of the comprehensive landslide risk zoning methodology is illustrated in Fig. 1.

Fig. 1

Framework of Comprehensive Landslide Risk Zoning System.

Hazard assessment of slope instability hazards based on the AHP

Selection of slope geohazard evaluation indexes

Various geological and environmental factors influence the hazard level of slope instability hazards³⁵. In this study, four key factors are selected as weighting indicators for the hazard assessment: (1) Degree of crack development. (2) Slope angle. (3) Slope height. (4) Rock and soil properties. To enable unified processing of indicators with different physical dimensions, this study adopts a segmented value assignment approach inspired by the "indicator grading and mapping" concept in fuzzy comprehensive evaluation. Based on expert knowledge, the original value range of each indicator is partitioned into four intervals and mapped to corresponding recommended subranges within the normalized interval [0, 1]. This normalization allows for consistent and comparable expression of heterogeneous indicators, facilitating their integration into the overall risk assessment framework.Considering the impact of each factor on slope instability hazards, normalized recommended value ranges for these four indicators are determined, as shown in Table 2.

Table 2 Normalized Recommended Value Ranges for Assessment Indicators.

Construction of the Hierarchical model

Based on the influence of degree of crack development, slope angle, slope height, and rock and soil properties on slope stability, expert opinions are incorporated to assess the relative importance of these four factors in the indicator layer. A judgment matrix A = (a_ij) 4 × 4 is established, where the pairwise comparisons are conducted using a scale to quantify the relative importance of each factor. The scale definitions are presented in Table 3.

Table 3 Judgment Matrix Scale and Definitions.

To verify the consistency and reliability of the judgment matrix A, a Consistency Index (CI) and the Random Consistency Index (RI) are introduced for consistency testing.

The CI is calculated as:

$$CI = \frac{{\lambda_{max} - m}}{m - 1}$$

(1)

where λ_max is the maximum eigenvalue of the judgment matrix and m is the number of elements in the matrix ( m = 4 in this study ).

The RI is determined by constructing 500 random matrices A1, A2, A3,…,A500, calculating their consistency indices CI₁, CI₂, CI₃,…, CI₅₀₀, and computing their average to obtain the RI:

$$RI = \frac{{CI_{1} + CI_{2} + \cdots + CI{}_{500}}}{500}$$

(2)

For 1–9 order judgment matrices, the RI values are given in Table 4.

Table 4 Random Consistency Index (RI) for Different Matrix Orders.

For matrices with an order greater than 2, the ratio of CI to RI is defined as the Consistency Ratio (CR):

$$CR = \frac{CI}{{RI}}$$

(3)

If CR < 0.1,the judgment matrix is considered to have satisfactory consistency, meaning the assigned relative importance values are reasonable³⁶. Otherwise, the judgment matrix must be adjusted.Based on the impact of each indicator on slope stability and expert evaluations, a hierarchical ranking of the indicators is established, as presented in Table 5.

Table 5 Hierarchical Ranking of Evaluation Indicators.

Calculation of evaluation index weights

Based on the hierarchical ranking of indicators, the judgment matrix A is constructed as follows:

$$A\, = \,\left( {a_{ij} } \right){4}\, \times \,{4}\, = \left( {\begin{array}{*{20}c} 1 & {1.5} & 2 & {2.5} \\ {0.67} & 1 & {1.5} & 2 \\ {0.5} & {0.67} & 1 & {1.5} \\ {0.4} & {0.5} & {0.67} & 1 \\ \end{array} } \right)$$

(4)

Using SPSSPRO software, the maximum eigenvalue of the judgment matrix A is computed as λ_max = 4.009 . According to Table 3, the average random consistency index RI is 0.90. Applying Eqs. (1) and (3), the consistency ratio is calculated as CR = 0.003 < 0.1,indicating that the judgment matrix exhibits satisfactory consistency, and the relative importance ranking of factors is reasonable.

Applying the AHP to the judgment matrix A, the weight values of each indicator are obtained, as presented in Table 6. The ranking of influencing factors, in descending order of significance, is as follows: degree of crack development,slope angle, slope height, and rock and soil properties.

Table 6 Weights of Evaluation Indicators.

Classification of geologic hazards on slopes

Currently, several common methods are used in slope hazard zoning research, including multiple regression analysis, fuzzy comprehensive evaluation, and the indicator factor overlay method.Multiple regression analysis does not account for interaction effects and the nonlinear causality of influencing factors. The fuzzy comprehensive evaluation method is computationally complex and involves a high degree of subjectivity in determining indicator weight vectors. The indicator factor overlay method utilizes the characteristics of different indicators to achieve a combined assessment, effectively leveraging their respective strengths while compensating for their weaknesses. This approach facilitates mutual validation and ensures a more robust hazard classification.Given these considerations³⁷, the indicator factor overlay method is selected for hazard classification modeling.

Based on the zoning index overlay method, degree of crack development, slope height, slope angle, and rock and soil properties were selected as indices to establish a hazard zoning model.The model is expressed as follows:

$$P_{i} = \frac{{Y_{j} }}{{Y_{j/\max } }}X_{i}$$

(5)

where: P_i represents the slope hazard index. Y_j is the normalized value of the indicator, where j = 1, 2, 3, 4. Y_j/max is the upper limit of the normalized value range for the corresponding indicator. X_i denotes the weight of each indicator, where i = 1, 2, 3, 4.

The slope hazard classification model computes hazard levels, which are categorized as shown in Table 7.

Table 7 Classification of Slope Hazard Zoning Levels.

Quantitative analysis of slope stability based on the LEM

Determination of the slope design factor of safety

The slope design factor of safety is a threshold value for the slope factor of safety, determined by multiple factors, including the significance of the slope project, external influences, slope characteristics and scale, potential failure consequences, and the feasibility of remedial measures. The Chinese National Standard GB 51,289–2018 (Design Code for Open-Pit Mine Slopes), specifies differentiated design factor of safety requirements according to slope type and service life.This standard categorizes slopes into final pit slopes, non-working slopes, working slopes, dump slopes, and internal dump slopes and prescribes corresponding design factor of safety ranges based on service life.Specifically:For non-working slopes, the recommended design factor of safety ranges from 1.1 to 1.2 for a service life of less than 10 years, 1.2 to 1.3 for 10–20 years, and 1.3 to 1.5 for over 20 years. For internal dumps, slopes with a service life of less than 10 years should have design factor of safety of at least 1.2.For dumps, the recommended design factor of safety ranges from 1.2 to 1.5 for a service life of more than 20 years. For short-term or temporary slopes, such as working slopes, the design factor of safety requirements are more flexible, balancing safety considerations with economic feasibility.Therefore, a scientifically sound and rational determination of the design factor of safety is crucial for accurately assessing slope stability and ensuring safe and sustainable open-pit mining operations.

Selection of slope stability calculation profiles

The selection of calculation profiles is a critical step in slope stability analysis, directly influencing the accuracy and reliability of the results. To ensure that the selected profiles comprehensively and accurately reflect the overall stability conditions of the mine slope, the following scientifically grounded principles must be adhered to: (1) Profiles should be selected based on different slope categories to ensure comprehensive coverage and representativeness.. (2) Profiles should be oriented perpendicular to the strike of slope benches. (3) The selection should consider the locations of boreholes and monitoring points. (4) Profiles should be established in proximity to critical infrastructure and facilities. (5) Areas that have experienced landslides or are deemed relatively hazardous should be included. (6) Profiles should be set in areas where geological conditions exhibit significant variations. (7) The service life of the slope should be factored into profile selection. By adhering to these principles, the analysis can ensure a more representative and scientifically robust assessment of slope stability.

Classification of slope stability conditions

Based on the quantitative evaluation results of slope stability, the stability conditions of slopes can be categorized into four levels: stable, marginally stable, less stable, and unstable, as detailed in Table 8. By employing this classification approach, high-risk instability zones can be accurately identified, and a slope stability zoning map can be generated. This visualization provides an intuitive representation of slope stability across different zones and offers crucial insights for subsequent slope management and maintenance strategies.

Table 8 Classification of Slope Stability States.

Comprehensive landslide risk zoning under multi-factor coupling

The stability of open-pit mine slopes is influenced by the non-linear coupling of multiple factors, making it difficult for a single zoning method to fully represent its risk characteristics. The two methods discussed above focus on zoning from the perspectives of geohazard risk and engineering stability, However, they have not fully accounted for the influence of factors such as slope along-strike surface shape, seasonal (climatic) variations, fault characteristics, and the distribution of infrastructure. Therefore, based on these methods, dynamic adjustments to the comprehensive risk levels are made by considering these factors to achieve high-precision zoning.

Classification of comprehensive landslide risk levels

For the zoning results obtained by the two methods mentioned above, cross-matrix analysis and simple weighted average methods are used to integrate the results, providing a scientific basis for the classification of comprehensive risk levels.

• 1. Data Normalization.

To facilitate quantitative analysis, categorical variables are converted into numerical codes, as shown in Table 9. This coding approach enables stability levels and hazard levels to be computed and compared within a unified numerical framework, thus laying the foundation for subsequent cross-matrix construction and comprehensive risk index calculation.

• 2. Cross-Matrix Construction.

Table 9 Corresponding Coding Values for Stability and Hazard Levels.

By overlaying the zoning results, a 3 × 3 cross-classification matrix was constructed, as shown in Table 10, to quantify the distribution area or proportion of each classification combination. This cross-matrix effectively illustrates the relationship between the two zoning methods, providing an intuitive representation of the spatial distribution of different stability and hazard level combinations.

• 1) Consistency Measurement.

Table 10 Cross-Matrix of Stability and Hazard Zoning.

The Kappa coefficient (κ) was employed to evaluate the level of agreement between the two zoning outcomes. By cross-coding the slope stability and hazard zoning results, the observed agreement and the agreement expected by chance were compared to quantitatively assess the consistency between the two methods. The value of κ reflects the degree of concordance and is categorized into five levels: (–1 to 0) extremely poor agreement, (0.0–0.20) slight agreement, (0.21–0.40) fair agreement, (0.41–0.60) moderate agreement, (0.61–0.80) substantial agreement, and (0.81–1.00) almost perfect agreement.The Kappa coefficient is calculated as follows:

$$\kappa = \frac{{P_{o} - P_{e} }}{{1 - P_{e} }}$$

(6)

where $P_{o}$ is the observed consistency ratio, and $P_{e}$ is the expected random consistency ratio, The value of κ ranges from -1 to 1.

• 3. Simple Weighted Average.

The simple weighted averaging method was employed to integrate the results of stability and hazard zoning, using a comprehensive risk index to assess the overall risk level. This approach mitigates the limitations of any single method, enhancing the robustness of the risk assessment. Given the equal importance of the two zoning methods in this study, each method is assigned a weight of 0.5. After determining the weights, the Comprehensive Risk Index (CRI) is calculated using the formula:

$$CRI = \omega_{s} \cdot S_{i} + \omega_{H} \cdot H_{j}$$

(7)

where $S_{i}$ and $H_{j}$ are the stability and hazard zoning encoding values(1–3), and $\omega_{s}$ and $\omega_{H}$ are the corresponding weights.

• 2) Comprehensive Risk Level Classification.

Based on the CRI calculation results, comprehensive landslide risk zoning is classified into levels as shown in Table 11.

Table 11 Classification of Comprehensive Landslide Risk Zoning Levels.

Dynamic optimization of comprehensive landslide risk zoning

The previous zoning methods do not fully account for the influencing factors of comprehensive landslide risks. To improve the accuracy of the zoning, dynamic optimization of the comprehensive risk level is performed by incorporating key factors such as seasonal (climatic) variations, slope along-strike surface shape, fault characteristics, and distribution of infrastructure. The identification of unfavorable risk factors and the adjustment of factor classifications are outlined in Table 12.

Table 12 Adjustment of Factors and Their Impact on Slope Stability.

Following the preliminary classification of comprehensive risk levels, a dynamic adjustment mechanism is introduced to refine the zoning outcomes. As outlined in Table 12, factors such as seasonal (climatic) variations, slope along-strike surface shape, fault characteristics, and distribution of infrastructure are identified as key inputs for adjustment. Each factor is sequentially analyzed to determine its effect-classified as favorable, neutral, or unfavorable—on slope stability. These effects are then logically linked to the initial comprehensive risk level based on a dynamic adjustment protocol: if one or more unfavorable factors are present within a given area, the risk level is elevated accordingly; if only favorable or neutral factors are observed, the original classification remains unchanged. The detailed adjustment logic and decision-making framework are illustrated in the flowchart shown in Fig. 2.

Fig. 2

Dynamic Risk Level Adjustment Rules.

Application results and discussion

Overview of geotechnical conditions at a certain open-pit coal mine

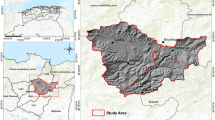
The region where the open-pit coal mine is located has a typical continental climate, with distinct seasons, arid conditions, low annual rainfall, and significant seasonal temperature variations. Winters are cold and windy, while summer rainfall is concentrated. The period from March to April is the peak of strong winds, with a maximum wind speed of 24 m/s and an mean wind speed of 2.3 m/s, and there are on average 32.8 dust storm days per year. The freeze period lasts from late October to early April, for about 200 days; the frost-free period is about 150 days. The maximum frost depth is 1.42 m (in 1972 and 1977), with the deepest frost occurring in February. The geographical location of the mining area is shown in Fig. 3. The first mining zone comprises, from top to bottom: discarded material, loess, interbedded mudstone-sandstone sequence, coal, interbedded mudstone-sandstone sequence, coal, and sandstone. The second mining zone comprises, from top to bottom: consist of interbedded sandstone and mudstone, coal, mudstone, coal, and interbedded mudstone and sandstone. The base of the internal dump is the coal seam floor, mainly consisting of mudstone and mud-rich siltstone. The layer of the dump A consists of discarded material, loess, and interbedded sandstone and mudstone from top to bottom. The layer of the dump C consists of discarded material, thinly interbedded loess, and sandstone. The layers of the dump B, D, and E consist mainly of discarded material, loess, and bedrock. The overall mining status of the mining area is shown in Fig. 4.

Fig. 3

Geographical Location Map of the Mining Area. The base map was generated using ArcGIS 10.8 (Esri, https://www.esri.com/) and Landsat image provided by the United States Geological Survey (USGS, https://earthexplorer.usgs.gov/).

Fig. 4

Overall Mining Status of the Mining Area.

Geological hazard risk assessment of slopes

Considering factors such as degree of crack development, slope angle, slope height, and rock and soil properties—the entire slope was divided into 16 zones for geological hazard assessment. A detailed evaluation table of zoning influence factors is presented in Table 13.

Table 13 Geological Hazard Hazard Assessment for Slope Zones.

Based on the relative importance ranking of the aforementioned slope evaluation indicators, the judgment matrix for the slope is constructed, as shown in the following equation.

$$A\, = \,\left( {a_{ij} } \right){4}\, \times \,{4}\, = \left( {\begin{array}{*{20}c} 1 & {1.5} & 2 & {2.5} \\ {0.67} & 1 & {1.5} & 2 \\ {0.5} & {0.67} & 1 & {1.5} \\ {0.4} & {0.5} & {0.67} & 1 \\ \end{array} } \right)$$

(8)

Using SPSSPRO software, the maximum eigenvalue of the matrix λ_max = 4.009 is calculated. The consistency index CI = 0.003 is obtained, and by referring to Table 3, the average random consistency index RI = 0.9 is found. Using Eq. (3), the consistency ratio CR = 0.003 < 0.1, indicating that the judgment matrix has good consistency, and the relative importance of the factors is reasonable.

The AHP analysis is conducted using Eq. (6), and the indicator weights are obtained as shown in Table 5. As seen in Table 5, the degree of crack development has the largest influence, followed by slope angle, slope height, and rock and soil properties.

Based on relevant data and Table 1, the normalization values for degree of crack development, slope angle, slope height, and rock and soil properties were determined for each zone. Utilizing Eq. (5) and the weight coefficients of each indicator listed in Table 5, the slope hazard index was computed. The corresponding hazard classification for each unit is presented in Table 14, where zone A1 exhibits high hazard potential, zones A2, A4, and A5 are classified as medium hazard zones, while other regions demonstrate relatively low hazard levels. Accordingly, the slope geological hazard zoning map was generated, as illustrated in Fig. 5.

Table 14 Normalized Values of Impact Indicators for Each Zone.

Fig. 5

Slope Geological Hazard Hazard Zoning Map.

Quantitative analysis of slope stability

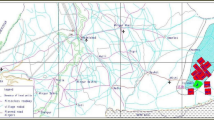
For final pit slopes with a service life of 10–20 years, a design factor of safetyof 1.20 is selected. For working slopes, the design factor of safety is also set at 1.20. For internal dump slopes with a service life of ≤ 10 years, a design factor of safety of 1.20 is adopted, and for dump slopes with a service life of > 20 years, the same factor is conservatively applied. Based on these principles, calculation profiles are selected for slope stability analysis, as shown in Fig. 6, while the summarized stability calculation results are presented in Table 15.

Fig. 6

Stability Calculation Profile Locations and Slope Stability Evaluation for the Mining Pit and Dump Slopes.

Table 15 Summary of Slope Stability Calculation Results.

Based on the stability analysis results, the overall slope stability within the study area is classified as stable. However, certain localized slopes exhibit a marginally stable condition. Specifically, in the initial mining area, the stability factors of local slopes along cross-sections C4 and C5 on the southern slope do not meet the design factor of safety, indicating a marginally stable state. Similarly, in the second mining area, local slopes along cross-sections C7 and C14 on the northern slope, as well as cross-sections C8, C9, and C10 on the working slope, fail to satisfy the design factor of safety, classifying them as marginally stable. Additionally, within the internal dump, the factor of safety of the local slope at cross-section N5 does not meet the design factor of safety, further indicating a marginally stable state. Based on these stability assessment results, the study area was zoned accordingly: Zones B1, B2, and B3 were classified as marginally stable, while all other zones were deemed stable, as illustrated in Fig. 7.

Fig. 7

Slope Stability Zoning Map.

Comprehensive landslide risk zoning and dynamic optimization

To facilitate risk assessment, categorical variables are converted into numerical codes, and a cross-matrix analysis is conducted, as shown in Table 16.

Table 16 Cross-Matrix of Stability and Hazard Zoning.

The Kappa coefficient (κ) is calculated to evaluate the consistency between the two zoning methods.$P_{o} = 0.89$,$P_{e} = 0.4994$,$\kappa = 0.78 > 0.6$. The analysis confirms a high degree of agreement between them.Finally, the CRI was calculated, and the zoning results were refined through a dynamic adjustment framework. The final integrated risk zoning results, obtained after these adjustments, are presented in Table 17. A total of one higher-risk zone, five medium-risk zones, and six lower-risk zones were identified.

Table 17 Comprehensive Risk Levels and Dynamic Adjustments.

Notably, three newly classified medium-risk zones R10, R11, and R12 were incorporated into the zoning scheme. The classification of R10 was primarily based on the adverse geological conditions of a convex slope, while R11 was identified due to the combined influence of the convex slope and the conveyor belt. R12 was designated as a medium-risk zone considering the impact of the northern crushing station, thereby enhancing the precision and applicability of the risk assessment. Additionally, R3 was classified as a higher-risk zone, demonstrating strong spatial agreement with actual landslide occurrences. Zones R2 and R4 were identified as medium-risk zones. The final comprehensive risk zoning results are illustrated in Fig. 8. Furthermore, during March and April, the overall slope stability of the mine is expected to be adversely affected by freeze–thaw cycles and wind erosion, leading to an upward adjustment of the comprehensive risk level by one category in the affected areas.

Fig. 8

Comprehensive Landslide Risk Zoning Map.

Discussion

The landslide comprehensive risk zoning method proposed in this study—by integrating slope hazard susceptibility and stability analysis, and introducing a dynamic adjustment mechanism—significantly enhances both the accuracy and rationality of slope risk identification in open-pit mines. This section discusses the method’s scientific merit and engineering applicability from four key perspectives: the performance of the multi-factor coupling approach, the practical effectiveness of the dynamic adjustment module, the reliability of risk index integration, and the method’s broader applicability and limitations.

• 1) Accuracy advantage of the multi-factor coupling approach.

The proposed "engineering–geological–environmental" multi-factor coupling method effectively combines slope hazard and stability assessments, while introducing a dynamic adjustment mechanism. Traditional zoning approaches based solely on either hazard susceptibility or stability are prone to false negatives and false positives. Through cross-matrix analysis and comprehensive risk index computation, this study partitions slope regions from both engineering and geological perspectives. The consistency of the integrated zoning results is supported by a Kappa coefficient (κ) of 0.78, indicating a high level of agreement. The change in risk zones before and after dynamic adjustment further demonstrates the method’s enhancement: three new medium-risk zones (R10, R11, R12) were identified, each corresponding to convex slope geometries, construction disturbances, or fractured zones—conditions verified in the field. Moreover, the identified higher-risk zone R3 closely aligns with historically recorded landslide events. Overall, the coupling of multiple factors with dynamic adjustment not only improves zoning precision but also effectively mitigates the shortcomings of single-factor approaches in identifying concealed risk areas, offering more robust data support for slope stability management in open-pit operations.

• 2) Effectiveness of the dynamic adjustment mechanism.

The dynamic adjustment framework—accounting for seasonal (climatic) variations, slope along-strike surface shape, fault characteristics, and distribution of infrastructure—enables the risk zoning to respond adaptively to environmental changes. Validation with field profiles and monitoring data confirmed that the three newly identified medium-risk zones (R10, R11, R12) strongly correlate with deformation anomalies. Among them, R10 and R11 are associated with convex slopes and transportation infrastructure, while R12 is located near a crushing station, consistent with geological surveys and engineering layouts. For instance, R10 initially had a risk index of 1, categorized as low risk. However, due to the presence of pronounced convex topography, the zone was upgraded to moderate risk following dynamic adjustment—an outcome later corroborated by early signs of deformation observed during field investigations. This adjustment mechanism enhances both the sensitivity and accuracy of risk identification, demonstrating the value of integrating static geological evaluation with dynamic environmental disturbance recognition. Compared to traditional static methods, the dynamic module exhibits superior adaptability and foresight, providing a solid basis for proactive landslide monitoring and mitigation strategies in open-pit mining.

• (3) Applicability analysis of the proposed risk zoning method

The proposed zoning framework, which integrates hazard assessment, slope stability analysis, and a dynamic adjustment mechanism, is characterized by a modular and structurally transparent design that supports method generalization. The hazard assessment component accommodates both qualitative and quantitative indicators depending on data availability; the stability analysis is based on the limit equilibrium theory, making it adaptable to diverse geological conditions; and the dynamic adjustment mechanism captures external perturbations, allowing flexible optimization of risk levels under varying environmental scenarios. Although the method was validated using a case study from an open-pit coal mine, the core input parameters—such as slope angle, height, lithology, and structural features—are standard across many types of surface mines. Therefore, this approach demonstrates not only robust performance in coal mining contexts but also strong generalizability, offering a viable technical pathway for establishing a unified landslide risk identification and zoning framework across different open-pit mining operations.

Conclusions

• 1. The landslide risk of open-pit mine slopes is influenced by the nonlinear coupling of multiple factors, including geomechanical properties, geotechnical engineering responses, geometric characteristics, and external dynamic disturbances. This study proposes a comprehensive landslide risk zoning method under the coupled effects of "engineering-geology-environment" factors, providing a novel approach to optimizing monitoring resource allocation and developing differentiated early-warning models.

• 2. Slope hazard zoning and stability zoning were conducted using the AHP and the rigid-body LEM. The results of these two zoning methods were integrated through cross-matrix analysis and a simple weighted averaging approach. A CRI was then used to classify landslide risk levels, with further refinement incorporating the effects of climate variability, fault conditions, and slope along-strike surface shape to dynamically optimize the risk zoning outcomes.

• 3. The proposed comprehensive landslide risk zoning method was applied to an open-pit mine in China, enabling precise delineation of landslide risk zones. The entire site was classified into one higher-risk zone, five medium-risk zones, and six lower-risk zones. The higher-risk zone exhibited strong spatial agreement with actual landslide occurrences, validating the reliability of the proposed risk zoning approach.

• 4. The landslide comprehensive risk zoning method proposed in this study demonstrates strong adaptability and potential for widespread application, making it suitable for open-pit mine slope scenarios with complete geological information. The core structure of the method features a high degree of modularity, allowing the hazard assessment and dynamic adjustment mechanisms to be flexibly configured based on the key influencing factors of different mine types. As a result, when applied to other open-pit mines, the method can be tailored to the specific geological conditions and disturbance characteristics, with evaluation indicators and adjustment factors selected accordingly. This flexibility ensures smooth adaptation and effective application, providing a practical and feasible approach for constructing a unified risk identification system across various mining operations.