Introduction

With the continual evolution of deep learning architectures, end-to-end models such as Connectionist Temporal Classification (CTC)1, Recurrent Neural Network Transducer (RNN-T)2, and Attention-Based Encoder-Decoder (AED)3 have emerged prominently in the domain of Automatic Speech Recognition (ASR). These models inherently treat the ASR task as a sequence modeling problem, employing multilayer neural networks to iteratively learn from training data and thereby construct direct mappings from speech to text. Specifically, CTC aligns speech frames with text using blank tokens during audio prediction; However, since CTC operates under the assumption of independence between tokens, it exhibits limitations in its ability to extract contextual information. Although RNN-T introduces a prediction module to learn contextual dependencies, this addition compromises model stability. In contrast, AED represents a revolutionary deep learning model composed of an attention-based encoder and decoder, where the encoder extracts high-level representations of speech and the decoder generates the corresponding text sequence. The encoder architectures most commonly utilized in this domain are variants based on the Transformer model, such as Conformer4, Squeezeformer5, and EfficientConformer6. These architectures enhance the encoder’s ability to capture global and local features by improving the Attention module or introducing new convolutional components, thereby achieving the goal of increasing accuracy in speech recognition tasks. However, encoders that solely rely on the Attention mechanism have a structural performance ceiling, necessitating the introduction of new modules to overcome this bottleneck.

State Space Models (SSM)7 offer a range of novel sequence modeling approaches, fundamentally conceptualizing model states and outputs through state variables. SSM typically encompass three primary processes: mapping the input sequence x(t), obtaining latent state representations h(t), and predicting the output sequence y(t). Common SSM variants include Gated State Space (GSS)8, Toeplitz Neural Network (TNN)9, and Mamba10. GSS optimizes Fast Fourier Transform (FFT) operations through gated units, achieving efficient sequence processing capabilities. TNN employs Toeplitz matrices with positional encoding for token mixing, reducing the model’s temporal and spatial complexity while yielding superior results. Mamba integrates the commonly used Gated MLP from Transformers with SSM modules, thereby enhancing feature extraction capabilities. Currently, Mamba has demonstrated strong performance in various domains, including tasks involving long text sequences8,11,12, biomedical fields13,14,15,16, video processing17,18,19, and image classification, segmentation, and object detection in the visual domain20,21,22,23,24,25. However, its exploration in the ASR field remains quite limited, with efforts primarily focused on improving the standalone Mamba module itself without investigating its integration with other modules. This design approach does not match the performance of mainstream Transformer-based encoders.

This study proposes an encoder named Mcformer, which integrates a parallel structure combining Conformer, Mamba, and Cgmlp modules. This design improves the model’s ability to capture both global and local features. The study utilizes the publicly available Mandarin datasets AISHELL-1 and Common Voice 14, as well as the English dataset TED-LIUM 3, for training, validation, and testing of the model. Experimental results demonstrate that the improved Mcformer encoder achieves CER of 4.15% and 4.48% on the AISHELL-1 validation and test sets, respectively, and 13.28% and 13.06% on Common Voice 14. After incorporating a language model, the CER further decreases to 3.88% and 4.08%, as well as 11.89% and 11.29%. On the TED-LIUM 3 English dataset, without the use of a language model, the WER for the validation and test sets are 7.26% and 6.95%, respectively.

The primary contributions of this paper are as follows:

  • This paper presents the Mamba module applied in parallel for the first time in the ASR field, achieving lower WER and CER on the Aishell-1, Common Voice 14 Mandarin public dataset, and TED-LIUM 3 English public dataset compared to mainstream encoders from recent years.

  • This paper demonstrates the effectiveness of the module through the analysis of relevant parameters and provides a visual analysis of the impact of the Mamba module and Cgmlp module on multi-head attention, highlighting the necessity of integrating the Mamba module with multi-head attention.

  • This paper tests the proposed McFormer encoder on audio files of varying durations, and the results show that the proposed McFormer encoder consistently achieves reductions in WER and CER across different duration ranges of audio.

The remainder of this paper is organized as follows. “Related work” reviews related work. “Methods” provides a detailed description of the components of the Mcformer encoder. “Experimental setup” and “Results” present the experimental parameters, detailed results, as well as ablation studies and analyses. Finally, “Conclusion” offers further conclusions.

Related work

End-to-end models are indisputably among the most prominent architectures in the current deep learning landscape. Since the Transformer encoder demonstrated strong performance in the field of Natural Language Processing (NLP), Transformer-based models have progressively been adopted for ASR tasks26. Compared to traditional Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs), the Transformer improves the model’s ability to capture global features of input audio through its distinctive self-attention mechanism. In ASR tasks, the extraction of global features is crucial for model performance, enabling the Transformer to achieve improved results in this domain. Gulati et al. integrated CNNs in a sequential manner into the Transformer and employed a “macaron”-style feedforward network structure to propose the Conformer encoder, thereby augmenting the model’s capacity for both global and local modeling and achieving state-of-the-art recognition performance at the time. To improve the flexibility and interpretability of ASR models, Peng et al.27 introduced the Branchformer encoder, which features parallel branches within each Branchformer module: one branch utilizes a self-attention mechanism to capture global information, while the other employs gated convolutions to capture local information. Building upon the Conformer framework, Burchi et al. proposed the Efficient Conformer, which reduces model complexity through progressive downsampling and lowers the computational complexity of attention through a group-based attention mechanism. Furthermore, Sehoon Kim et al. revisited the Conformer architecture and proposed the Squeezeformer encoder, which adopts a processing sequence consisting of multi-head self-attention layers, feed-forward network layers, convolutional layers, and additional feed-forward network layers, and they drew inspiration from the U-Net structure28, employing a dimensionality reduction approach in the intermediate encoder blocks and restoring the dimensions in the final layer, thereby further enhancing recognition accuracy. However, these models are all constructed around the Attention module, which creates a bottleneck in their ability to capture features, necessitating the introduction of new modules to guide the model towards deeper learning.

The Mamba module, based on SSM, has been extensively investigated in image processing, medical applications, video analysis, and long-sequence text-related tasks. However, its exploration within the realm of speech recognition remains relatively limited. Miyazaki et al.29 employed a bidirectional Mamba encoder, demonstrating its performance advantages in long-audio scenarios. Gao et al.30 serially combined the Mamba module with MHA mechanisms, similarly validating its effectiveness in handling long audio sequences. Fang et al.31 explored the efficiency of the Mamba module in streamable speech recognition. Yang et al.32 individually incorporated the Mamba module into the encoder, further investigating its role within the decoder. These efforts primarily involve making modifications within the Mamba module independently or integrating it sequentially with other modules. In most cases, such changes can overly steer the model to focus more on global features, thereby neglecting local features. As a result, the performance may not show substantial improvements compared to encoders built around the Attention mechanism, and could even lead to degradation in outcomes.

Therefore, this paper is the first to integrate the Mamba module with multi-head attention in parallel to enhance the model’s ability to capture global features. Subsequent experimental comparisons and analyses highlight the necessity of this hybrid structure. Additionally, to balance the capture of global features, this paper introduces a Cgmlp in parallel with the original Conformer’s standard convolution, thereby enhancing the extraction of local features. Ultimately, this approach achieves a balance between global and local feature extraction, leading to improved experimental results compared to commonly used encoders in recent years.

Methods

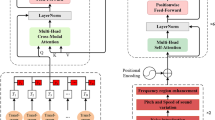
To enhance the capability of ASR models in capturing both global and local features, this paper introduces the Mcformer encoder, a novel architecture that integrates the Mamba module and Cgmlp module in parallel. As shown in Fig. 1, the core of the McFormer encoder primarily consists of two modules: the Parallel Mamba Attention (PMA) module, which operates in parallel with the multi-head attention and the Mamba module, and the Parallel Gated Convolution (PGC) module, which integrates the standard convolution of the original Conformer with the Cgmlp module.

Fig. 1
figure 1

Overall structure diagram of the Mcformer encoder.

Full size image

Specifically, within the PMA module, a parallel Mamba module is introduced alongside the MHA mechanism of the original Conformer encoder. These components are unified through learnable weights and ultimately combined via residual connections to produce the integrated output. The PGC module adopts a similar approach by parallelly introducing a Cgmlp module alongside the standard convolution module of the original Conformer encoder. This parallel integration is achieved through weight fusion and residual connections.Notably, in the PMA module, the input to the Mamba module is identical to that of the MHA. Conversely, in the PGC module, the standard convolution module receives input from the output of the PMA module, while the parallel Cgmlp module directly receives the same input as the PMA module. Subsequent experiments demonstrate that the Mcformer encoder achieves a delicate balance in capturing both global and local features through the combined effects of the PMA and PGC modules, leading to improved results across different datasets. Additionally, the Mcformer encoder retains the original ”macaron” structure of the Conformer encoder, consisting of a sequence of feedforward neural networks, PMA, PGC, and another feedforward neural network. The following sections provide a detailed introduction to the PMA and PGC modules.

PMA module

Within the proposed PMA module, the architecture fundamentally comprises the parallel operation of two distinct components: the MHA and the Mamba module. Both modules receive identical inputs and, upon processing through their respective networks, yield separate outputs denoted as \(y_{MHA}\) and \(y_{Mamba}\). Subsequently, an attention-based pooling technique is employed to ascertain the corresponding weights \(w_{MHA}\) and \(w_{Mamba}\) for each output. These weights are then utilized to scale the respective outputs, which are subsequently aggregated through addition, thereby effectuating the integration of global features. A comprehensive elucidation of this process is presented in the following sections.

Structure of multi-head self-attention and mamba module

As illustrated in Fig. 1, the proposed PMA module is primarily responsible for modeling the global context of the input audio information. It predominantly comprises a parallel architecture of a MHA mechanism and a Mamba module. The MHA mechanism receives input \(x\in R^{S\times d}\), where S denotes the sequence length corresponding to the audio, and d represents the dimensionality of the features. The input features are further processed using a scaled dot-product \(\frac{QK^T}{\sqrt{d}}\) to compute the interactions between queries (Q) and keys (K). These computed results are subsequently normalized, and the final self-attention output is the weighted product of the normalized scores and the values (V).

Within the MHA framework, the matrices Q, K, and V undergo h distinct projections to capture diverse representation subspaces. Each projected set is subjected to self-attention computation, and the resulting h outputs are concatenated to form the final output. The aforementioned process can be expressed using Eqs. (1) to (4) as follows:

$$\begin{aligned} Att(q,k,v)= & v \cdot Softmax(\frac{qk^T}{\sqrt{d}}) \end{aligned}$$
(1)
$$\begin{aligned} head_n= & Att(Q\cdot W_n^Q, K\cdot W_n^K,V\cdot W_n^V) \end{aligned}$$
(2)
$$\begin{aligned} MHA(Q,K,V)= & concat(head_1,head_2, \ldots , head_h) \end{aligned}$$
(3)
$$\begin{aligned} y_{MHA}= & DropOut(Linear(MHA(Q,K,V))) \end{aligned}$$
(4)

where \(W_n^Q,\ W_n^K,\ W_n^V \in R^{S\times \frac{d}{s} }\) and \({W\in R^{d\times d}}\)are linear transformation matrices.

The core of the Mamba module, operating in parallel with multi-head self-attention, is the optional SSM , which maps the input x to the final output y through a hidden state \(h_s\). he fundamental equations governing this process are expressed as Eqs. 5 and 6 as follows:

$$\begin{aligned} h_s= & A\cdot {\widehat{h}}_{s-1}+B\cdot {\widehat{x}}_s \end{aligned}$$
(5)
$$\begin{aligned} y_s= & C\cdot h_s \end{aligned}$$
(6)

In these equations, \({\widehat{A}}\) and \({\widehat{B}}\) denote the discretized matrices, as shown in Eqs. 7 and 8.

$$\begin{aligned} {\widehat{A}}= & exp(\Delta A) \end{aligned}$$
(7)
$$\begin{aligned} {\widehat{B}}= & (\Delta A)^{-1} (exp(\Delta A)-I)\cdot \Delta B \end{aligned}$$
(8)

Here, the matrix A is the HiPPO matrix33, while \(\Delta\), B, and C are all learnable linear layer structures. This configuration allows the system to dynamically adapt based on varying input features.

As depicted in Fig. 1, the Mamba module sequentially processes the input feature vector through a Linear layer, a one-dimensional convolutional layer, and the SSM module. Following these operations, a gated network performs element-wise multiplication, and the result is subsequently passed through another Linear layer, after which Dropout is applied to enhance the overall robustness of the Mamba module, resulting in the final output. The Sigmoid Linear Unit (SiLU) serves as the primary activation function throughout this process. The procedure is depicted in Eqs. 9 to 11 as follows:

$$\begin{aligned} U= & SSM(Conv1d(Linear(x))) \end{aligned}$$
(9)
$$\begin{aligned} V= & SiLU(Linear(x)) \end{aligned}$$
(10)
$$\begin{aligned} y_{Mamba}= & DropOut(Linear(U\otimes V)) \end{aligned}$$
(11)

In these equations, \(\otimes\) denotes element-wise multiplication. This architecture ensures that the Mamba module effectively captures and processes the intricate patterns within the input data, thereby enhancing the overall performance of the system.

Feature fusion between multi-head self-attention and mamba module

To enhance dynamic weight computation and improve interpretability, this study employ the attention-based pooling mechanism from Fastformer34 to determine the weights. This method facilitates the extraction of a singular vector encapsulating global information from a set of features through attention-like pooling. Subsequently, the resulting vectors from the two branches are projected into scalar values, and a softmax function is applied to derive the final branch weights. Specifically, assuming the input sequence is \(x_1, x_2, x_3,..., x_S\), the output vector is the weighted sum of \(x_S\):

$$\begin{aligned} AttPooling(X)=\sum _{i=1}^{S} A_i \cdot x_i \end{aligned}$$
(12)

Here, \(A_i\) denotes the class attention weight,which is calculated as shown in Eq. 13, by performing a scaled dot product between the input feature \(x_i\) and a learnable parameter vector w, followed by softmax normalization:

$$\begin{aligned} A_i=\frac{exp(\frac{w^S \cdot q_i}{ \sqrt{d}})}{\sum _{j=1}^S exp(\frac{w^S\ q_j}{\sqrt{d}})} \end{aligned}$$
(13)

Through attention-like pooling, the two branches generate two vectors, which are then normalized using softmax to obtain the final branch weights \(w_{MHA}\) and \(w_{Mamba}\), the calculation process is shown in Eqs. 14 to 16 as follows:

$$\begin{aligned} v_{MHA}= & AttPooling(y_{MHA}) \end{aligned}$$
(14)
$$\begin{aligned} v_{Mamba}= & AttPooling(y_{Mamba}) \end{aligned}$$
(15)
$$\begin{aligned} w_{MHA},w_{Mamba}= & softmax(\alpha _{MHA} \cdot v_{MHA}, \alpha _{Mamba} \cdot v_{Mamba}) \end{aligned}$$
(16)

In these equations, \(\alpha _{MHA}\) and \(\alpha _{Mamba}\) represent linear transformations. Finally, the output of the PMA module after weighted feature fusion and Dropout generalization enhancement is as follows:

$$\begin{aligned} y_{PMA}=Dropout(w_{MHA}\cdot y_{MHA} + w_{Mamba}\cdot y_{Mamba}) \end{aligned}$$
(17)

PGC module

Analogous to the architecture of the PMA module, the proposed PGC module similarly incorporates two parallel components: the original Conformer standard convolution and the Cgmlp module. However, the input configuration of the model diverges from that of the PMA module. Specifically, the input to the original Conformer standard convolution is the output following the residual connection of the PMA module, whereas the Cgmlp module receives the same input as the PMA module. The subsequent processing parallels that of the PMA module: initially, the outputs of the two components are aggregated, followed by the computation of their respective weights using an attention-based pooling mechanism. Finally, the weights are multiplied by the corresponding outputs and summed to achieve the integration of local features.

Structure of conformer standard convolution and Cgmlp module

The standard Conformer convolution initially performs layer normalization on the input x. It then processes the features using a 1D pointwise convolution with a kernel size of 1, followed by a Gated Linear Unit (GLU) activation function. Subsequently, a 1D depthwise convolution is applied to capture local dependencies, while batch normalization stabilizes training and the Swish activation function enhances linear expressive capacity. Finally, another pointwise convolution projects the output to the standard dimensionality. It is noteworthy that input originates from the output of the PMA module described in Section 3.1. Therefore, the inputs are defined as \(x^{PMA}_1, x^{PMA}_2, x^{PMA}_3, ..., x^{PMA}_S\). The detailed convolutional operations are shown in Equations 18 to 21 as follows:

$$\begin{aligned} y_{pwc1}(X^{PMA})= & PWConv(LN(X^{PMA})) \end{aligned}$$
(18)
$$\begin{aligned} y_{dwc}(X^{PMA})= & DWConv(GLU(y_{pwc1}(X^{PMA}))) \end{aligned}$$
(19)
$$\begin{aligned} y_{pwc2}(X^{PMA})= & PWConv(Swish(BN(y_{dwc}(X^{PMA})))) \end{aligned}$$
(20)
$$\begin{aligned} y_{conv}(X^{PMA})= & Dropout(y_{pwc2}(X^{PMA})) \end{aligned}$$
(21)

where PWConv denotes pointwise convolution, BN represents batch normalization, DWConv is depthwise convolution, and LN stands for layer normalization.

The original Conformer encoder block contains only a single serial standard convolutional layer. This design can create a bottleneck when the encoder extracts local features, thereby forcing the Attention module, which is intended to focus on global features, to learn to extract certain local feature content to some extent. Therefore, to more effectively decompose the tasks of extracting global and local features, as illustrated in Fig. 1, a parallel Cgmlp module is introduced. This module primarily consists of a channel projection, a GeLU activation function, a Convolutional Gated Unit (CSGU), another channel projection, and a series of layer normalization and dropout layers. Specifically, assuming that the input sequence is \(x_1, x_2, x_3,..., x_S\), identical to the input of the PMA module, the overall algorithm input flow is shown in Equation 22 as follows:

$$\begin{aligned} y_{Cgmlp}(X)=Dropout(Linear(CSGU(GeLU(Linear(LN(X)))))) \end{aligned}$$
(22)

Here, CSGU is the core component of Cgmlp, which first divides the feature dimension of the input feature sequence equally into two segments, obtaining two new sequences \(X_1\) and \(X_2\). Then, \(X_2\) undergoes layer normalization and is processed with depthwise convolution along the temporal dimension, with the calculation process shown in Eq. 23 as follows:

$$\begin{aligned} CSGU(X)=X_1\odot DWConv(LN(X_2)) \end{aligned}$$
(23)

where DWConv denotes depthwise convolution35, \(\odot\) represents element-wise multiplication, and LN stands for layer normalization.

Feature fusion between conformer standard convolution and Cgmlp module

Consistent with Section 3.1.2, the proposed methodology employs an attention pooling-based approach to compute the weights for the standard Conformer convolution(\(w_{conv}\)), and the Cgmlp module(\(w_{Cgmlp}\)), with the detailed calculation process formulated in Eqs. (24) to (26).

$$\begin{aligned} v_{conv}= & AttPooling(y_{conv}) \end{aligned}$$
(24)
$$\begin{aligned} v_{Cgmlp}= & AttPooling(y_{Cgmlp}) \end{aligned}$$
(25)
$$\begin{aligned} w_{conv}{,w}_{Cgmlp}= & softmax(\alpha _{conv}\cdot v_{conv},\alpha _{Cgmlp}\cdot v_{Cgmlp}) \end{aligned}$$
(26)

Finally, the output of the PGC module after Dropout generalization enhancement is as follows:

$$\begin{aligned} {y}_{PGC}=Dropout(w_{conv}\cdot y_{conv}+w_{Cgmlp}\cdot y_{Cgmlp}) \end{aligned}$$
(27)

Overall process of the Mcformer encoder

As illustrated in the Figure 1, the proposed McFormer encoder preserves the original Conformer encoder’s ”macaron” architecture and leverages the PMA and PGC modules to enhance the extraction of both global and local audio features. Given an input sequence \(x_1, x_2, x_3,..., x_S\), the process for obtaining the output \(y_{Mcformer}\) of each McFormer encoder is shown in Equations 28 to 31 as follows:

$$\begin{aligned} x_i^{FFN}= & x_i+\frac{1}{2}\cdot FFN(x_i) \end{aligned}$$
(28)
$$\begin{aligned} x_i^{PMA}= & x_i^{FFN}+PMA(x_i^{FFN}) \end{aligned}$$
(29)
$$\begin{aligned} x_i^{PGC}= & x_i^{PMA}+PGC(x_i^{PMA},x_i^{FFN}) \end{aligned}$$
(30)
$$\begin{aligned} y_{Mcformer}= & x_i^{PGC}+\frac{1}{2}\cdot FFN(x_i^{PGC}) \end{aligned}$$
(31)

In the above equations, the superscript FFN denotes the output of the feed-forward network block, PMA refers to the output of our proposed parallel MHA combined with Mamba’s PMA module, and PGC represents the output of our parallel Conformer standard convolution coupled with the Cgmlp PGC module.

Experimental setup

This section initially delineates the sources, durations, and pertinent attributes of the publicly available datasets employed. Subsequently, it provides a comprehensive exposition of the model’s parameter configurations and the nuanced details involved in the training process.

Datasets

Table 1 Duration information of three open source datasets.
Full size table

The Aishell-1 dataset36 is a Mandarin speech corpus specifically curated for the advancement of Chinese speech recognition technologies. It comprises recordings from approximately 400 speakers representing diverse dialect regions across China. The transcriptions encompass eleven domains, including smart home applications, autonomous driving, and industrial production, as detailed in the accompanying Table 1. The total duration of this corpus is approximately 178 h, partitioned into a training set of around 150 h, a development set of approximately 18 hours, and a validation set of roughly 10 h.

Common Voice zh 1437, orchestrated and maintained by the Mozilla Foundation, is an expansive, multilingual open-source speech recognition dataset predominantly sourced from audio contributions by global volunteers. For this study, the Mandarin subset of Common Voice 14 was selected as the training, development, and validation sets, totaling approximately 247 h. This includes roughly 214 h for training, and about 15 h and 17 h for the development and validation sets, respectively.

TED-LIUM 338 is an openly accessible English speech dataset derived from English TED talks, featuring contributions from over 2000 speakers. The corpus spans approximately 456 h in total, with the training set encompassing around 452 h, and the development and validation sets comprising approximately 1.6 h and 2.62 h, respectively.

Moreover, to ensure uniformity across all audio files, each recording was resampled to 16 kHz and subjected to normalization for subsequent experimental procedures. Correspondingly, the label texts associated with the audio files were cleansed of any punctuation marks that do not pertain to syllables.

Model configuration

All experiments in this work were conducted on a server equipped with two A40 GPUs. The experiments employed the classic joint CTC and Attention structure from the Wenet toolkit as the overall architecture of the model, using its default parameter configuration. This framework mainly consists of three parts: a shared encoder, a CTC decoder, and an Attention decoder. During training, the joint training loss is as follows:

$$\begin{aligned} Loss=\alpha \cdot Loss_{ctc}+(1-\alpha )\cdot Loss_{Att} \end{aligned}$$
(32)

Here, \(Loss_{ctc}\) represents the loss associated with the CTC decoder, \(Loss_{Att}\) corresponds to the loss of the Attention decoder, and \(\alpha\) denotes the weighting coefficient assigned to the CTC decoder’s loss, which is set to 0.3 in this study.

The baseline encoder adopts the classic 12-layer “Macaron” structure of Conformer encoding blocks. Each encoder layer comprises four self-attention layers with a dimensionality of 256, a standard 2D Conformer convolutional layer with a kernel size of 15, and two feedforward neural networks with a dimensionality of 2048. The decoder consists of a CTC decoder and a Transformer decoding block composed of six layers, each containing four attention heads and a feedforward neural network with a dimensionality of 2048. The final output dimensions are 4232, 4782, and 661, corresponding to the vocabulary sizes generated from the Aishell-1, Common Voice zh 14, and TED-LIUM 3 datasets, respectively.

During the model training process, a total of 240 epochs were conducted, utilizing the Adam optimizer with an initial warm-up of 25,000 steps and a peak learning rate of 0.0005. The batch size was configured to 8, with a gradient accumulation step of 10, and a dropout rate of 0.1. In the decoding phase, ctc greedy search, ctc prefix beam search, attention and attention rescoring strategies were employed, with a beam size of 10 and a CTC weight of 0.5 during decoding. For audio input, the frame length was set to 25 ms, with a frame shift of 10 ms, and 80 filters were used to extract Mel-spectrogram features. Additionally, audio jitter with a rate of 0.1 was applied to introduce random noise for enhancing robustness, and the SpecAug39 data augmentation strategy was employed with configurations including maximum frequency masking of 10, maximum time masking of 50, two frequency masks, and three time masks, along with speed perturbation at rates of 0.9, 1.0, and 1.1 to further increase variability in training data.

In the Mcformer encoder proposed in this study, the input and output dimensions of the Mamba module within the PMA module were set to 256, the SSM state expansion factor was set to 16, the convolutional width was 4, and the block expansion factor for linear projection was 2. Similarly, within the PGC module, the Cgmlp module’s input and output dimensions were set to 256, with a hidden layer dimensionality of 2048 and a convolution window size of 31. Moreover, the Mcformer encoder maintained consistency with the baseline model in terms of training parameters and strategy configurations.

Results

Comparative experiment

Table 2 Comparative experimental results on the Aishell-1 dataset.
Full size table
Table 3 Comparative experimental results on the CommonVoice zh 14 dataset.
Full size table
Table 4 Comparative experimental results on the TED-LIUM 3 dataset.
Full size table

This section provides a comparative analysis of the proposed Mcformer encoder and existing methodologies, with detailed experimental results summarized in Table 2. Compared to encoders such as Conformer, the Mcformer encoder achieves an absolute reduction in CER of 0.17% and 0.27% on the validation and test sets of the Mandarin dataset Aishell-1, respectively. Moreover, upon the integration of a language model, the CER further diminishes to outstanding levels of 3.88% and 4.08%.

Table 3 illustrates the performance of our Mcformer encoder in comparison with other frameworks on the publicly available CommonVoice zh 14 dataset. In the absence of a language model, the Mcformer encoder consistently outperforms Conformer and similar encoders, yielding CERs of 13.28% and 13.06% on the validation and test sets of the CommonVoice zh 14 dataset. Compared to Conformer, the absolute CER decreased by 0.42% and 0.75%, respectively. When a language model is incorporated, the CER further improves, reaching 11.86% and 11.29%.

The results on the open source dataset TED LIUM v3 are presented in Table 4. Compared to the Conformer encoder, the absolute Word Error Rate (WER) decreased by 2.27% and 1.74% on the validation and test sets, respectively. After incorporating the language model, the WER further improved to 6.53% and 6.34%.

Ablation experiment

As illustrated in Tables 5, 6, and 7, within the validation and test sets of the publicly available datasets Aishell-1, Common Voice zh 14, and TED-LIUM 3 across different languages, the incorporation of the Cgmlp module yielded only small improvements across the four distinct decoding strategies. Conversely, when solely integrating the Mamba module, the CER on the Aishell-1 validation and test sets under the optimal attention rescoring decoding method achieved 4.21% and 4.62%, respectively, representing reductions of 0.11% and 0.12% compared to the baseline. For the Common Voice zh 14 dataset, the CER on the validation and test sets was 13.51% and 13.42%, reflecting decreases of 0.19% and 0.39% relative to the baseline. Additionally, on the TED-LIUM 3 dataset, the WER for the validation and test sets was 7.24% and 6.92%, marking reductions of 0.85% and 0.64% compared to the baseline. These observations suggest that the exclusive inclusion of the Mamba module can notably enhance model performance.

Table 5 Results of ablation experiments on the Aishell-1 dataset.
Full size table
Table 6 Results of ablation experiments on the CommonVoice zh 14 dataset.
Full size table
Table 7 Results of ablation experiments on the TED-LIUM 3 dataset.
Full size table

To investigate the underlying reasons, a visualization of the model-extracted weights—specifically, and—using Aishell-1 as an exemplar, is conducted, as depicted in Fig. 2a. When only the Cgmlp module was incorporated, the Cgmlp module attained multiple high-weight values within encoders 6–12. It is hypothesized that this guides the model to focus more on extracting local features from the original input. However, in speech recognition tasks, the higher-level encoders rely more heavily on global contextual information. As a result, the improvement brought by this local enhancement is marginal.

In contrast, Fig. 2b demonstrates that upon the standalone addition of the Mamba module to the baseline model, the Mamba module commands comparatively higher weights. This prompted us to consider whether replacing the MHA with the Mamba module could lead to better performance. However, as demonstrated in the second rows of Tables 5, 6, and 7, which correspond to the Aishell-1, Common Voice zh 14, and TED LIUM 3 datasets respectively, substituting the MHA with the Mamba module alone results in an increase increase in CER, thereby degrading the model’s performance. Consequently, it is concluded that the inclusion of the MHA module is essential.

Fig. 2
figure 2

Learnable weight visualization. (a) adding Cgmlp module separately. (b) Join Mamba separately. (c) Conv and Cgmlp of Mcformer encoder. (d) MHA and Mamba for Mcformer encoder.

Full size image
Fig. 3
figure 3

Average attention weight matrix visualization, first row baseline, second row only Cgmlp added, third row only Mamba added, fourth row final Mcformer encoder.

Full size image

Results under long and short duration audio

Subsequently, both the Mamba and Cgmlp modules are concurrently integrated, thereby forming the final Mcformer encoder. Under the optimal decoding strategy without the incorporation of a language model, the CER for Aishell-1’s validation and test sets achieved 4.15% and 4.48%, representing reductions of 0.14% and 0.26% relative to the baseline. For Common Voice zh 14, the CER on the validation and test sets was 13.28% and 13.06%, reflecting decreases of 0.42% and 0.75%, respectively. Meanwhile, on the TED-LIUM 3 dataset, the WER on the validation and test sets was 7.24% and 6.92%, reflecting reductions of 0.58% and 0.64% compared to the baseline.

Similarly, utilizing Aishell-1 as an example, the model-extracted weights—specifically, and—are visualized upon the simultaneous incorporation of the Mamba and Cgmlp modules, as shown in Fig. 2c,d. Notably, the weight distributions for the MHA and Mamba modules in Fig. 2d resemble those observed when only the Mamba module is added. However, the two convolutional weights in Fig. 2c exhibit alterations, diverging from the predominantly posterior weight distribution seen with the exclusive addition of the Cgmlp module. Instead, the Mcformer encoder concentrates weights more intensively within the second and third encoders. This phenomenon is attributed to the enhanced provision of low-level local feature information by these encoders, which likely accounts for the negligible improvements observed when solely integrating the Cgmlp module.

To further explore the impact of the Mamba module and the Cgmlp module on the main network, as shown in Fig. 3, the four attention heads of the final encoder are chosen, and their average attention weight matrices are visualized to illustrate their effects. It is observed that in the weight matrices corresponding to the baseline in the first row, a very clear diagonal phenomenon appears in two attention heads. The main reason for this diagonal phenomenon is that the attention focuses excessively on local information. Compared to the baseline, after adding the Cgmlp module individually in the second row, the diagonal phenomenon appears in three attention heads. Combined with the phenomenon shown in Fig. 2a, where the Cgmlp module exhibits excessively high weights in the higher encoder layers (layers 6–12), it is believed that this is caused by the Cgmlp module guiding the attention to focus excessively on local information. In contrast, after adding the Mamba module individually in the third row, it is observed that the diagonal phenomenon is reduced. This is because the parallel Mamba module guides the attention mechanism to focus more on global information. This is the key reason why adding only the Mamba module can lead to a noticeable improvement in the model’s performance. In the fourth row, where both the Mamba module and the Cgmlp module are added simultaneously, it is observed that the diagonal phenomenon completely disappears. Combined with Fig. 2c,d, it can be seen that this combination allows the Cgmlp module to focus more on the lower layers (layers 2–3) for processing low-level local information in the encoder. This, in turn, enables the higher layers of attention to concentrate on extracting global high-level features. Ultimately, this allows the McFormer encoder to achieve a balanced capability between capturing global and local features.

Fig. 4
figure 4

Average cosine similarity curve between adjacent frames of an acoustic sequence. (a) The corresponding average cosine similarity curve for the Aishell-1 dataset, (b) The average cosine similarity curve corresponding to TED-LIUM 3.

Full size image

In addition, to provide a deeper and more intuitive representation of the effectiveness of the Mcformer encoder, this chapter uses the Aishell-1 Mandarin dataset and the TED-LIUM 3 English dataset as examples, randomly selecting 50 speech samples from the corresponding test sets for evaluation. By sampling the outputs of the Mcformer from layers 1 to 12 across the time dimension of the acoustic sequences, the average cosine similarity between the corresponding samples is calculated, as shown in Fig. 4. The Mcformer encoder exhibits lower average cosine similarity between different adjacent sampling points across most encoder layers compared to the baseline. This indicates that the Mcformer reduces redundancy in acoustic information to a certain extent, thereby effectively diminishing the propagation of redundant information. This enables the encoder to learn more new features, allowing for a more effective representation of acoustic information and ultimately achieving the goal of improving recognition accuracy.

Results across different duration intervals of audio

Fig. 5
figure 5

Results in the case of different interval speech durations. (a) Shows the results of the combined Aishell-1 dataset, and (b) shows the results of the combined TED LIUM v3 dataset.

Full size image

In this study, the performance across varying audio duration intervals is sought to be evaluated. However, the test sets of Aishell-1 and TED-LIUM 3 predominantly comprise audio segments ranging from 3 to 10 s. To assess the efficacy of the approach on audio files of diverse lengths, the audio files from the test sets of Aishell-1 and TED-LIUM 3 are randomly merged, resulting in a distribution spanning 0 to 40 s. As depicted in Fig. 5, Without incorporating a language model, our method achieved consistent reductions in Mandarin CER and English WER across audio files of varying durations (0–40 s) compared to the baseline. This demonstrates the effectiveness of our method for handling both short and long audio files across different languages.

Conclusion

In this work, the Mcformer encoder is proposed to enhance the capability of the encoder in ASR tasks for capturing both global and local information, thereby improving recognition accuracy. Specifically, the advantages of the Cgmlp and Mamba modules in extracting local and global features, along with the versatility of the Conformer structure, are leveraged. These two modules are successfully integrated in parallel with the multi-head attention and the original standard convolution of the Conformer, resulting in the creation of the PMA and PGC modules, which focus respectively on extracting global and local features. Experimental results on three public monolingual datasets, along with related comparative experiments and visualizations of relevant parameters, demonstrate that our Mcformer exhibits strong competitiveness in speech recognition tasks. However, the experiment did not explore the application of Mcformer in streaming speech recognition tasks, and this task will be explored in the future.