Abstract
General novel nonlinear second-gradient spectral constitutive models for rate dependent fiber-reinforced viscoelastic solids that consider bending stiffness are developed. The constitutive models are characterized by spectral invariants, each with a clearer physical meaning compared to the classical invariants. Hence, they are experimentally useful if a rigorous experimental curve fitting exercise is used to obtain a specific form of free energy function. The number of complete-irreducible-minimal spectral invariants is significantly less than the number of ‘classical’ complete-irreducible invariants given in the literature, and hence modelling complexity is drastically reduced when a spectral technique is used. Our spectral approach in this paper is different from the classical invariant approach that have been done in the last decades regarding nonlinear solid mechanics. A detailed proof to show that the spherical part of the couple stress is just a Lagrange multiplier, is given. Results for pure bending and, the extension and inflation of a solid cylinder, that could be useful for experiments and numerical validations, are given.
Similar content being viewed by others
Introduction
Fibre-reinforced viscoelastic composite solids with bending stiffness, are critical in numerous engineering applications, including aerospace, automotive, and civil structures. The ability to accurately predict the mechanical response of these materials under dynamic and static loading conditions is essential for their effective design and application; for example, in robotics design, Gour et al.4 present the fibre-reinforced constitutive modeling for the tear fracture and its impact on the mechanical behavior of artificial tissues used in the novel field of soft robotics. While the influence of fiber orientation in viscoelastic solids, in the absence of bending stiffness, has been widely studied (see, for example, references9,11,35 and references within), the role of fiber bending stiffness in the overall mechanical behavior of such viscoelastic solids remains an area that warrants deeper investigation. By integrating bending resistance into the governing equations, we aim to provide a more accurate prediction of the material’s performance, particularly in nonlinear large deformations. The results of this study offer potential for improving the design and optimization of advanced composite solids where fiber stiffness plays a critical role in their mechanical properties.
Recently, Shariff et al.31,33 managed to incorporate fiber bending stiffness into their non-viscoelastic models without using Cosserat (second-gradient) theory but these non-Cosserat models are different from the models proposed here. In this paper, based on the second-gradient (Cosserat) theory14 and on the work of Shariff et. al28,29 on non-viscoelastic solids, we present constitutive models that incorporate fiber bending stiffness into the rate dependent viscoelastic behavior of fiber-reinforced composites. This extension is motivated by the fact that fibers with significant bending stiffness contribute to the composite’s overall resistance to deformation, particularly under complex loading conditions where they cause fiber bending and twisting deformations. Due to the complexity of modelling bending stiffness effects, traditional constitutive models of viscoelastic fibrous composites often neglect these effects by assuming the reinforcing fibers are perfectly flexible, see, for example, references10,17,19,24,26,35 and references within. The mechanical behavior of fiber-reinforced viscoelastic solids with stiff bending curvatures is significantly different from those that are perfectly flexible12,21. Following the work of Shariff et al.35, we find it advantageous to develop a constitutive equation via invariants that have a clear physical interpretation in the sense that in a rigorous experimental curve fitting exercise to obtain a specific form of free energy function usually involve a test that vary one invariant in the free energy function and hold the rest of the invariants constant6,8 . If the invariants (such as the classical invariants40) have no direct physical interpretation, it is not easy, possibly impossible, to devise an experiment to do such a test: We also note that another advantage of spectral formulation is, it significantly reduces modelling complexity as indicated in references30. To achieve these advantages, we apply the generalized strain method (which uses spectral invariants), recently developed by Shariff27.
We prelude our paper in Section “Bending stiffness”, where a brief concept on bending stiffness is given. The governing equations are established in Sect. “Governing equations”. In Sect. “Constitutive equations for stress and couple stress” the constitutive equations for stress and couple stress are developed and their spectral formulations are given in Sect. “Spectral formulation”. Constitutive prototypes are proposed in Sect. “Prototype” and they are used to obtain results for specific deformations in Sect. “Boundary value problems”. The summary of the most important conclusions thus made is presented in Sect. “Conclusion”.
Bending stiffness
In non-linear elastic fiber-reinforced model with bending stiffness, the derivative of the deformed preferred direction41
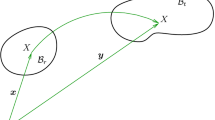
associated with bending stiffness, plays an important role in constitutive modelling of non-linear elastic composites with stiff curved fibers, where \({\varvec{F}}={\displaystyle \frac{\partial {\varvec{y}}}{\partial {\varvec{ x}}}}\) is the deformation gradient tensor, \({\varvec{ x}}\) and \({\varvec{y}}\) denote, respectively, the position vectors of a solid body particle in the current and reference configurations, \({\varvec{a}}({\varvec{ x}})\) is the fiber direction in the reference configuration and \({\varvec{b}}\) is the fiber direction in the deformed configuration. We can write (1)\(_2\) in the form
where \({\varvec{C}}={\varvec{F}}^T{\varvec{F}}\) is the right Cauchy-Green tensor and taking note that \({\varvec{f}}\) is a unit vector field. Hence, (1)\(_1\) takes the form
\({\displaystyle \frac{\partial \lambda }{\partial {\varvec{ x}}}}\) is associated with ”stretching” with respect to \({\varvec{ x}}\), since \(\lambda =\sqrt{{\varvec{a}}\cdot {\varvec{C}}{\varvec{a}}}\) is the stretch of the line element in the \({\varvec{a}}\) direction. Since \({\varvec{f}}\) is a unit vector, \({\displaystyle \frac{\partial {\varvec{f}}}{\partial {\varvec{ x}}}}\) is associated with ”rotating” of \({\varvec{f}}\) with respect to \({\varvec{ x}}\). Using the relation
we can express the Lagrangian relation
where
In view of \({\varvec{a}}\cdot {\varvec{\Lambda }}^T{\varvec{a}}={\varvec{a}}\cdot {\varvec{\Lambda }}{\varvec{a}}\) (an invariant) , we obtain
Hence from (3) and (7), we have
which shows that the invariant \({\varvec{a}}\cdot {\varvec{\Lambda }}{\varvec{a}}\) associated with stretching of the fiber not “bending” of fiber (see comment in34).
Governing equations
Let \({\varvec{T}}= {{\varvec{T}}}_{(s)} + {{\varvec{T}}}_{(a)}\) be the Cauchy stress, where \({{\varvec{T}}}_{(s)}\) and \({{\varvec{T}}}_{(a)}\) are, respectively, the symmetric and antisymmetric part of \({\varvec{T}}\). Here, we assume that the body forces are negligible and the equation motions derived in Mindlin and Tiersten14 are
where \(\varvec{M}\) is the couple stress, \(\mathbb {E}\) is the three-dimensional alternating tensor, \(\hbox{div}\) represents the divergence of a tensor in the current configuration, \(\rho\) is the current configuration mass density and \(\dot{{\varvec{v}}}\) is the convected derivative of particle velocity \({\varvec{v}}\). In this paper the notation \(\dot{(\,)}\) denotes the convected derivative.
Following the work Shariff et al.35, where their constitutive equation is only capable of modeling rate dependent deformations but not the common phenomenon such as stress-relaxation, we assume there exist a potential function \(W_v\) that is accountable for the internal dissipation D due to the viscous effects in the sense that3
where \({\displaystyle {\displaystyle \frac{\partial W_v}{\partial \dot{{\varvec{C}}}}}}\) is assumed to be symmetric3. The formulation
can be found in35, where \({\varvec{D}}\) is the rate of deformation tensor. Using the symmetry property of \({\displaystyle {\displaystyle \frac{\partial W_v}{\partial \dot{{\varvec{C}}}}}}\), we obtain
It is assumed that the Helmholtz potential \(\psi\) exists and the Second Law of Thermodynamics for an isothermal process then takes the form5,14
where \(\varvec{\omega } = {\displaystyle \frac{1}{2}}\nabla \times {\varvec{v}}\) is the spin vector.
Constitutive equations for stress and couple stress
Since, \({\displaystyle \frac{\partial {\varvec{f}}}{\partial {\varvec{ x}}}}\) is associated with bending (”rotating” of \({\varvec{f}}\) with respect to \({\varvec{ x}}\)) only, we assume the objective strain energy function
where \(W_e=\rho _0 \psi\), \(\rho _0\) is the reference configuration mass density and
\(\bar{{\varvec{\Lambda }}}\) is used instead of \({\varvec{F}}^T{\displaystyle \frac{\partial {\varvec{f}}}{\partial {\varvec{ x}}}}\) so that, at \({\varvec{F}}= {\varvec{I}}\) (the identity tensor), \(\bar{{\varvec{\Lambda }}} = {\varvec{0}}\). In view of (5) and (6)
Therefore \(\dot{\psi }= {\displaystyle \frac{1}{\rho _0}}\dot{W_e}\), where
taking note that \(\dot{{\varvec{a}}}={\varvec{0}}\) and \(\dot{{\varvec{H}}}={\varvec{0}}\) and the tensor derivative convention given in Ogden20 (see also Shariff22) is used. Using the relations
we can express (17) as
Using (12) and (13) and taking note that \(\hbox {tr}({\varvec{T}}_s{\varvec{D}})= \hbox {tr}({\varvec{T}}_s{\varvec{L}})\), we have
where \(J = \det {\varvec{F}}= {\displaystyle \frac{\rho _0}{\rho }}\) and \(\det\) is the determinant of a tensor. Since \({\varvec{L}}\) is arbitrary, we have, from (20)
and
The identity \(\hbox {tr}{\displaystyle \frac{\partial \varvec{\omega }}{\partial {\varvec{y}}}} \equiv {\displaystyle \frac{\partial \omega _i}{\partial y_i}} =0\)14 is a constraint in the sense that only eight of the nine variables \({\displaystyle \frac{\partial \omega _i}{\partial y_j}}\) are independent [Soldatos38,39 simply failed to understand that the identity \({\displaystyle \frac{\partial \omega _i}{\partial y_i}} =0\) is a constraint on the variables \({\displaystyle \frac{\partial \omega _i}{\partial y_j}}\)], where \(\omega _i\) and \(y_j\) are Cartesian components of \(\varvec{\omega }\) and \({\varvec{y}}\), respectively. We could, for example, let
to be the dependent variable. It is well known in the literature14 that a peculiarity of the Cosserat equations is that the scalar \({\displaystyle \frac{1}{3}} \hbox {tr}\varvec{M}\) is left indeterminate. Below, we prove that the indeterminate \(-{\displaystyle \frac{1}{3}} \hbox {tr}\varvec{M}\) is just a Lagrange multiplier. This proof invalidates the statement made by Soldatos39.
Proof
In view of the constraint \({\displaystyle \frac{\partial \omega _i}{\partial y_i}} =0\), we can write (22) in the form
where \(p_a\) (arbitrary) represents the Lagrange multiplier associated with the constraint \(\hbox {tr}{\displaystyle \frac{\partial \varvec{\omega }}{\partial {\varvec{y}}}}=0\), \(\Lambda _{RS}\), \(F_{iR}\) and \(v_i\), are respectively, the Cartesian components of \({\varvec{\Lambda }}\), \({\varvec{F}}\) and \({\varvec{v}}\).
Let
where \(e_{rik}\) are Cartesian components \(\mathbb {E}\) and
Using the property \(h_{kk}=0\), we have
From (25), we have
The above implies
Multiply (29) by \({\displaystyle {\displaystyle \frac{\partial ^2v_i}{\partial y_j\partial y_k}}}\) and in view of the symmetry property
we obtain
Using the relation
we obtain the proof
Hence
Using the method given in the optimization book of Walsh42 (see Section 1.3), we write
\(\forall i,j\), except \(i=j=1\). If we consider \({\displaystyle {\displaystyle \frac{\partial \omega _1}{\partial y_1}} }\) to be the dependent variable, we impose \(p_a\) to take the value
and, in view that the remaining \({\displaystyle \frac{\partial \omega _i}{\partial y_j}}\) are independent, we then have the result
Since \(h_{ii}=0\), we obtain from (37)
which proves that \({\displaystyle \frac{1}{3}}\hbox {tr}\varvec{M}\) is the arbitrary Lagrange multiplier \(-p_a\). We note that (34) can also be expressed as
but we must emphasize that, since not all of \({\displaystyle {\displaystyle \frac{\partial \omega _i}{\partial y_j}}}\) are independent, in general,
Substituting (38) in (34), we obtain the constitutive equation
which is exactly the constitutive equation obtained by Spencer and Soldatos41. The above proof further invalidate Soldatos39 statement that using \(W({\varvec{F}},{\varvec{G}},{\varvec{H}},{\varvec{a}})\) will not give the same constitutive equations, obtained by Spencer and Soldatos41; note that, in Shariff et al.34, we also give an alternative proof that our constitutive equations are exactly the same as those obtained in Spencer and Soldatos41. Equation (9)\(_3\) can also be expressed as
In tensor notation, the couple-stress relation (41) becomes
and (21) can be expressed as
For an incompressible material, we have
where p represents the Lagrange multiplier due to the incompressibility constraint \(\det {\varvec{F}}= 1\).
Fibre curvature constitutive equation
In fiber composite solids the change in fiber curvature plays a major factor. The change in fiber curvature can be described by the vector
Clearly at the reference configuration \({\varvec{F}}={\varvec{I}}\) and at rigid body motion \({\varvec{F}}={\varvec{R}}\) (independent of \({\varvec{ x}}\)), we obtain \({\varvec{d}}={\varvec{0}}\), which implies there is no change in fiber curvature. Since, \({\varvec{a}}\cdot {\varvec{a}}= 1\), we derive \({\displaystyle \left( {\displaystyle \frac{\partial {\varvec{a}}}{\partial {\varvec{ x}}}}\right) ^T{\varvec{a}}= {\varvec{H}}^T{\varvec{a}}= {\varvec{0}}}\) [there is a typo in28,29, \({\displaystyle \frac{\partial {\varvec{a}}}{\partial {\varvec{ x}}}}{\varvec{a}}= {\varvec{0}}\) should be replaced by \({\displaystyle \left( {\displaystyle \frac{\partial {\varvec{a}}}{\partial {\varvec{ x}}}}\right) ^T{\varvec{a}}= {\varvec{0}}}\)]
and in view of
we have the important result
which indicates that \({\varvec{d}}\) is perpendicular to \({\varvec{a}}\). The strain energy function for this type of material is described by
Spectral formulation
Spectral invariants
Using the polar decomposition or singular value decomposition theorem, the deformation gradient \({\varvec{F}}\) can be spectrally described by
where \(\lambda _i\) is a principal stretch, \({\varvec{v}}_i\) is an eigenvector of the left stretch tensor \({\varvec{V}}= \hat{{\varvec{F}}}(\lambda _i,{\varvec{v}}_i,{\varvec{v}}_i)\) and \({\varvec{u}}_i\) is an eigenvector of the right- stretch tensor \({\varvec{U}}= \hat{\varvec{F}}(\lambda _i,{\varvec{u}}_i,{\varvec{u}}_i)\). Note that the right Cauchy-Green tensor \({\varvec{C}}= \hat{{\varvec{F}}}(\lambda _i^2,{\varvec{u}}_i,{\varvec{u}}_i)\) and the rotation tensor \({\varvec{R}}= \hat{{\varvec{F}}}(\lambda _i=1,{\varvec{v}}_i,{\varvec{u}}_i)\), where \({\varvec{F}}={\varvec{R}}{\varvec{U}}\). The material with strain energy (14) should satisfy the form invariant
for all rotation tensor \({\varvec{Q}}\). Hence, we can express \(W_o\) in terms of the isotropic invariants of the set \(S=\{{\varvec{C}},\bar{{\varvec{\Lambda }}},{\varvec{a}}\}\). Following the work of Shariff30, the isotropic invariants are simply the spectral invariant-components
We note that the set of invariants in (52) is complete, irreducible and minimal as proven in Shariff30. Hence, we can express \(W_o\) in terms of the spectral invariants given in (52), i.e.,
Since \({\displaystyle \sum _{i=1}^3 \alpha _i=a_i^2 = 1 }\) and \(\lambda _1\lambda _2\lambda _3=1\), the number of independent invariants in (52) is 13 and, most importantly, \({W}_{(o)}\) must satisfy the P-property as described in22.
In the case of the material with the strain energy given in (49), we have,
where \(d_i ={\varvec{d}}\cdot {\varvec{u}}_i\) is a spectral invariant, \({W}_{(d)}\) contains only 7 independent invariants and it must satisfy the P-property.
If the viscous potential contains all the governing variables, then
taking note that \(G_{ij}\) is a spectral invariant. \({W}_{(v)}\) must satisfy the P-property and it contains only 20 independent invariants.
We strongly emphasize that the number of complete-irreducible-minimal spectral invariants is significantly less than the number of ‘classical’ complete-irreducible invariants given in the literature40 (See Appendix B). It is proven by Shariff30 that most of the classical-invariant irreducible number is not a minimal number. All classical invariants given in, say,40 can be expressed explicitly in terms of the spectral invariants as shown in Shariff30. Hence, modelling using spectral invariants is more general than using classical invariants and, due to the significantly reduced number of complete-irreducible-minimal spectral invariants, modelling complexity is significantly reduced as exemplified in this paper.
Spectral derivative components
We first note that
where \(\Omega _{ij} = -\Omega _{ji} = {\varvec{u}}_i\bullet \dot{{\varvec{u}}}_j\).
Let \({W}_{(h)}\) represents \({W}_{(o)}\) or \({W}_{(d)}\). Our spectral formulation needs the Lagrangian spectral tensor components35 of \({\displaystyle \frac{\partial {W}_{(h)}}{\partial {\varvec{C}}}}\) and \({\displaystyle \frac{\partial {W}_{(h)}}{\partial {\varvec{\Lambda }}}}\), i.e.,
where
Prototype
In view of the non-existent relevant experimental results for this class of materials, we are unable to meticulously construct specific constitutive equations for this class of materials. Hence, we nominate prototypes for \({W}_{(o)}\), \({W}_{(d)}\) and \({W}_{(v)}\) that can be easily amended if we are required to construct “better’ prototypes. We consider \({W}_{(o)}\), \({W}_{(d)}\) and \({W}_{(v)}\) to be independent of the sign of \({\varvec{a}}\) and only consider formulation for incompressible materials.
Infinitesimal deformation
When the gradient of the displacement field \({\varvec{u}}\) is very small
where \(\Vert \bullet \Vert\) is an appropriate norm and the magnitude of e is much less than unity. Since \({\varvec{G}}-{\varvec{H}}=O(e)\), it can be easily shown that
We also have \(\lambda _i-1 = e_i\) is of O(e), where \(e_i\) are the eigenvalues of the infinitesimal strain \({\varvec{E}}\) and we do not distinguish between the eigenvectors of \({\varvec{U}}\) and \({\varvec{E}}\). The infinitesimal relations
and
In the case when \({\varvec{a}}\) is independent of \({\varvec{ x}}\), \({\varvec{H}}= {\varvec{0}}\) and we have
\({W}_{(o)}\)
Taking into consideration that \({W}_{(o)}\) should be independent of the sign of \({\varvec{a}}\), and the fact that the invariant \({\varvec{a}}\cdot {\varvec{\Lambda }}{\varvec{a}}\) does not contribute to the couple stress (43)41, and in order that stress \({\varvec{T}}\) and the couple stress \(\bar{\varvec{M}}\) to be of O(e), the most general strain energy function takes the form
where23,
\(\mu _T\), \(\mu _L\) and \(\beta\) are ground state constants and their constraints are given in Shariff23.
For the Cauchy and the couple stresses to be of O(e), taking into account that \({W}_{(\Lambda )}\) must be independent of the signs of \({\varvec{a}}\), and in view of \({\varvec{a}}\cdot {\varvec{\bar{\Lambda }}}{\varvec{a}}=0\), we have,
where
and \(b_1,b_2\) and \(b_3\) are ground state constants.
To obtain a necessary condition for \({W}_{(\Lambda )} > 0\) for \({\varvec{\bar{\Lambda }}}\ne 0\), we consider a deformation where \({\varvec{b}}= b {\varvec{f}}\), where b has a constant value. For this type of deformation and when \({\varvec{a}}\) is independent of \({\varvec{ x}}\), we have
Following the work of36 and using the fiber direction \({\varvec{a}}\equiv [1,0,0]^T\), we obtain the necessary condition
\({W}_{(d)}\)
In this case, \({\varvec{d}}= O(e)\) and is even in \({\varvec{a}}\). To obtain \({W}_{(d)} = O(e^2)\) and even in \({\varvec{a}}\), we deduce that
The inequality \(b_4 >0\) ensures that \({W}_{(d)}>0\).
Finite strain
\({W}_{(o)}\)
For nonlinear \({W}_{(o)}\) to be consistent with infinitesimal elasticity, we propose the form
where23
\(r_\eta {\quad }\eta = 1,2,\ldots\) are generalized strains described in27 and have the property \(r_\eta (1) = 0\), \(r'_\eta (1) = 1\) and \(r'_\eta (x)> 0 {\quad }x> 0\). To be consistent with infinitesimal elasticity, we must impose \(q(0)=0\) and \(q'(0)=1\).
\({W}_{(d)}\)
For \({W}_{(d)}\), we propose a nonlinear form that is consistent with its infinitesimal counterpart
where \({W}_{(T)}\), is given by (74) and
where
\({W}_{(v)}\)
Based on the work of Shariff et al.35, we propose the specific form
where
where \(\nu _1,\nu _2,\nu _3,\nu _4\) are dimensionless parameters, \(\mu >0\) has a dimension of stress and
The derivatives
and
The internal dissipation (10) gives the relation
Since \(r_4^2,r_5^2,\chi _i, \gamma _i, H_3,H_4, \dot{{\varvec{C}}}{\varvec{u}}_i\cdot \dot{{\varvec{C}}}{\varvec{u}}_i,\hbox {tr}\dot{{\varvec{C}}}^2, \dot{{\varvec{C}}}{\varvec{a}}\cdot \dot{{\varvec{C}}}{\varvec{a}}\ge 0\), we have that
are sufficient for the inequality (85) to be satisfied.
Spectral components
The constitutive equation for \({\varvec{T}}_s\) given in (21) requires the following spectral formulation
where
and
Boundary value problems
In this Section, we give results for two boundary value problems, the pure bending of a slab and the extension and inflation of a solid cylinder, where their deformations are prescribed. We note that, up to our current knowledge, we believe that there are no experimental data on the mechanical behaviour of stiff fibre-reinforced viscoelastic composite to validate our theory. However, these boundary value problems could be important from the experimental and numerical point of view. We only study the material, where a change of fiber curvature plays a major factor, i.e. when \({W}_{(h)}= {W}_{(d)}\). Let \(\{ {\varvec{e}}_r, {\varvec{e}}_\theta , {\varvec{e}}_z \}\) be the polar basis for the current configuration. For these two-dimensional boundary value problems, it is reasonable to assume that the couple stress component \({\varvec{e}}_r\cdot \varvec{M}{\varvec{e}}_r =0\) (see for example, reference41), and in view of Appendix A, we show that if a component of the couple stress is prescribed then the Lagrange multiplier \(-{\displaystyle \frac{1}{3}}\hbox {tr}\varvec{M}\) is not indeterminate and hence from (42), the antisymetric part of the couple stress is prescribed.
For boundary value problems, where the deformations are not prescribed, numerical solutions for the proposed constitutive equations could be obtained via modifications of numerical procedures, such as those developed in references1,15,18,43 and some solution procedures are also described in14; it is beyond the scope of this paper to discuss such procedures.
To solve boundary value problems, we require the following derivatives
Pure bending
Consider the problem of plain strain pure bending, in which a rectangular slab of incompressible material is bent into a sector of a circular annulus defined by
where \((r,\theta ,z)\) is the cylindrical polar coordinate for the current configuration, \((x_1,x_2,x_3)\) is the Cartesian referential coordinate with the basis \(\{ {\varvec{g}}_1, {\varvec{g}}_2, {\varvec{g}}_3 ={\varvec{e}}_z \}\) and \(0 \le x_1 \le B\).
The formula employed here could be used to compare our theory with experiments, such as an experiment based on the modification of a three-point bending test experiment described in reference13.
The deformation tensor has the form
From the incompressibility condition ( \(\det {\varvec{F}}=1\)) and the boundary conditions \(\theta (0)=0\) and \(r(0)=a\), we obtain
where \(r(B) = b\). It is clear from (50), (94) and (95) that
and the spectral basis vectors are \({\varvec{u}}_i={\varvec{g}}_i\), \({\varvec{v}}_1={\varvec{e}}_r\), \({\varvec{v}}_2={\varvec{e}}_\theta\) and \({\varvec{v}}_3={\varvec{e}}_z\).
In this section we study the case \({\varvec{a}}={\varvec{g}}_2\) and a rate of deformation, where \(\dot{a}\) has a constant value when \(\chi\) is kept constant. We then have,
In view of the relation \({\displaystyle \frac{d {\varvec{e}}_{\theta }}{d x_2}} = -{\displaystyle \frac{{\varvec{e}}_r}{\chi }}\), we obtain
\({\varvec{d}}=- {\displaystyle \frac{1}{\lambda _2\chi }} {\varvec{g}}_1 , {\quad }\delta ={\displaystyle \frac{1}{\lambda _2\chi }}\). The derivative of (77) then simplify to
In view of \(\lambda _1\lambda _2=1\), we have \(\dot{\lambda }_1= -{\displaystyle \frac{\lambda _1}{\lambda _2}}\dot{\lambda }_2\), where \(\dot{\lambda }_2={\displaystyle \frac{a\dot{a}}{\chi r}}\). The symmetric part of the stress is simply
where
The couple stress
The values of the cylindrical components of \(\varvec{M}\) and \(\bar{\varvec{M}}\) are
From (105), we have \(m_{rr}=m_{\theta \theta } = m_{zz}\). As mentioned above, it is reasonable to assume that \({\varvec{e}}_r\varvec{M}{\varvec{e}}_r = m_{rr}=0\) (see41) and hence, we have (See the Appendix B) \(m_{rr}=m_{\theta \theta } = m_{zz}=0\). The cylindrical components of \({\varvec{T}}\) then have the relations
Hence, in view of the equilibrium equation (9)\(_2\) and (106), we have
and hence \({\varvec{T}}= {{\varvec{T}}}_{(s)}\). It is clear that \(\sigma _{rr}\) and \(\sigma _{\theta \theta }\) depends only on r, which implies the simplified equilibrium equation
If we assume that \(\sigma _{rr}=0\) at \(r=b\), we then have
The incompressible Lagrange multiplier the takes the form
and with the above expression for p we obtain the stress-strain relations for \(\sigma _{\theta \theta }\) and \(\sigma _{zz}\).
The bending moment BM, and the normal force \(\mathcal {N}\), per unit length in the \(x_3\) direction, and applied to a section of constant \(\theta\), are
To depict our results, we use the ground-state values
and the functions
with \(B=1\). We strongly emphasize that the above ad-hoc functions and ground-state-constant values may or may not represent real materials. They are merely used for graph plotting. Specific functional forms can be constructed and ground-state-constant values can be obtained via an appropriate set of experiment data.
In Fig. 1, we depict the behaviour of the radial stress \(\sigma _{rr}\) along the radius r when \({\displaystyle \frac{a}{B}}=1\) and \(\chi\) is fixed for various values of \(\dot{a}\). In general, as expected, the magnitude of the radial stress increases as the speed \(\dot{a}\) increases. For our proposed model, the value of BM given in (111) increases linearly with \(\dot{a}\) as depicted in Fig. 2.
Clearly these figures indicate that the rate of deformation significantly affect the behaviour of the stress and couple stress.
Extension and inflation of a thick-walled tube
Consider an incompressible thick-walled circular cylindrical tube that is deformed via an extension and inflation deformation described by20
where r, \(\theta\) and z are deformed cylindrical polar coordinates, a is the deformed internal radius of the tube and the axial stretch \(\lambda _z\) is constant. The deformation gradient
where
and the principal directions
The formulation developed in this Section could be used to compare our theory with experiments, such as an experiment based on the modification of an extension and inflation experiment described in Horny et al.7.
Here, we only consider the case when the preferred direction \({\varvec{a}}={\varvec{E}}_\Theta\), deformation rate associated with \(\dot{a}=\) constant and \(\lambda _z\ge 1\). Using the operator
where \({\varvec{h}}\) is a vector field, we then obtain
and
If we assume that \(\lambda _z\) is a constant, we then have
The deviatoric couple stress
We assume that \({\varvec{e}}_r\cdot \varvec{M}{\varvec{e}}_r = 0\), and in view of (122) and Appendix A , we have \({\varvec{e}}_z\cdot \varvec{M}{\varvec{e}}_z={\varvec{e}}_\theta \cdot \varvec{M}{\varvec{e}}_\theta =0\) and the results
where
and \({{\varvec{T}}}_{(V)}\) is given by (102). All values of \(a_ia_j\) are zero for \(i \ne j\). In view of (102), (124) and (125), all the shear stresses have a zero value, which gives the Cauchy stress \({\varvec{T}}= {{\varvec{T}}}_{(s)}\) to be coaxial with the left stretch tensor \({\varvec{V}}\). The Cauchy stress cylindrical principal components \(\sigma _{rr}\), \(\sigma _{\theta \theta }\) and \(\sigma _{zz}\) have the following relations
Since \({\varvec{T}}\) depends only on r, we have the simplified equilibrium equation,
with the boundary conditions
where \(P \ge 0\) is the pressure on the inside of the tube and b is the deformed external radius. In view of (127) and \(dr = \lambda _1 dR\), we obtain
In view of (114), for a fixed \(\lambda _z\), r(R, a) and, from (129), we deduce that P(a) (see Fig. 3).
Let N be the axial load needed to hold \(\lambda _z\) fixed, hence
Expressing the equilibrium equation (127) in the form
which implies
we obtain the relation
To depict our results, we use the ground-state constant values given in (112) and the functions given in (113). For simplicity we use the values \(A=1\) and \(B=2\).
The dependence of the pressure P on a is visualized in Fig. 3. It is clear from the curves that the presence of viscosity and/or the presence of bending stiffness significantly changes the mechanical behaviour of viscoelastic solids.
Figure 4 depicts the couple stress \(-m_{\theta z}\) vs R/A and from the figure it is indicated that magnitude of \(m_{\theta z}\) increases as the a increases; an increase in the value of a is associated with an increase in the change of radial curvature. We note that our proposed prototype, since \(b_4\) is a constant, the couple stress is independent of the rate of deformation. However, if we let \(b_4(\dot{{\varvec{C}}})\) then the couple stress is affected by the deformation rate.
Conclusion
We believe that a general spectral constitutive model for fiber-reinforced viscoelastic solids with bending stiffness does not exist in the literature and hence this paper may add to the understanding of the mechanical behaviour of such solids. The constitutive models, developed here, are characterized by spectral invariants, where each of them has a clearer physical meaning compared with the classical invariants given in, say, reference40 and hence, they are experimentally friendly. With the use of spectral invariants, we easily obtain the number of independent invariants and the minimal number of invariants in the corresponding minimal integrity or irreducible basis, and hence drastically reduce modelling complexity30. We note that classical invariants can be explicitly expressed in terms spectral invariants but, in general, a spectral invariant cannot be explicitly expressed in terms of classical invariants; this indicates the generality of the spectral-invariant formulation. The generalized strain tensor approach, employed here, differs from the classical invariant approach that has been done in the last decades regarding nonlinear solid mechanics. Our models can be implemented in a commercial finite element software with the aid of the spectral tangent formulation developed by Shariff25.
In Sect. "Constitutive equations for stress and couple stress", we gave a detailed proof (which was not done in the literature) that spherical part of the couple stress is just a Lagrange multiplier, i.e., \({\displaystyle \frac{1}{3}}\hbox {tr}\varvec{M}= - p_a\), associated with the constraint (identity) \(\hbox {tr}{\displaystyle \frac{\partial \varvec{\omega }}{\partial {\varvec{y}}}}=0\).
The results of the boundary value problem given in Sect. "Boundary value problems" could be used in experiments to study the performance of the proposed prototype models. In future, we will extend our current work to model stiff-bending- viscoelastic solids with two preferred directions, which we believe will have many applications.
Data availibility
All data generated or analysed during this study are included in this published article.
References
Andreaus, U. et al. Numerical simulations of classical problems in two-dimensional (non) linear second gradient elasticity. Int. J. Eng. Sci. 108, 34–50 (2016).
Boehler, J. P. On irreducible representations for isotropic scalar functions. Z. Angew. Math. Mech. 57, 323–327 (1977).
Germain, P. Mécanique-Tome I et II (Ellipses, Paris, 1986).
Gour, A., Kumar, D. & Khurana, A. Constitutive modeling for the tear fracture of artificial tissues in human-like soft robots. Eur J Mech: A/Solids 96, 104672 (2022).
Gurtin, M. E., Fried, E. & Anand, L. The mechanics and thermodynamics of continua (Cambridge University Press, New York, 2010).
Holzapfel, G. & Ogden, R. On planar biaxial tests for anisotropic nonlinearly elastic solids: A continuum mechanical framework. Math. Mech. Solids 14, 474–489 (2009).
Horny, L. et al. Inflation-extension test of silicon rubber- nitinol composite tube. IFMBE Proc. 37, 1027–1030. https://doi.org/10.1007/978-3-642-23508-5-267 (2011).
Humphrey, J., Strumpf, R. & Yin, F. Determination of a constitutive relation for passive myocardium: I. A new functional form.. J. Biomech. Eng. 112(3), 340–346 (1990).
Khurana, A., Sharma, A. K. & Jogleka, M. M. Nonlinear oscillations of electrically driven Aniso-Visco-hyperelastic dielectric elastomer minimum energy structures. Nonlinear Dyn. 104, 1991–2013. https://doi.org/10.1007/s11071-021-06392-5 (2021).
Kulkarni, S. G., Gao, X.-L., Horner, S. E., Mortlock, R. F. & Zheng, J. Q. A transversely isotropic visco-hyperelastic constitutive model for soft tissues. Math. Mech. Solids 21, 747–770 (2016).
Kumar, A., Khurana, A., Patra, A. K., Agrawal, Y. & Joglekar, M. M. Electromechanical performance of dielectric elastomer composites: Modeling and experimental characterization. Compos Struct 320, 117130 (2023).
Lee, M. G. et al. The viscoelastic bending stiffness of fiber-reinforced composite Ilizarov C-rings. Compos Sci Technol 61, 2491–2500 (2001).
Mathieu, S., Hamila, N., Bouillon, F. & Boisse, P. Enhanced modeling of 3D composite preform deformations taking into account local fiber bending stiffness. Compos. Sci. Technol. 117, 322–333 (2015).
Mindlin, R. D. & Tiersten, H. F. Effects of couple-stress in linear elasticity. Arch. Ration. Mech. Anal. 11, 415–448 (1962).
Nazarenko, L., Glüge, R. & Altenbach, H. On variational principles in coupled strain-gradient elasticity. Math. Mech. Solids https://doi.org/10.1177/10812865221081854 (2019).
Neff, P., Münch, I., Ghiba, I. & Madeo, A. On some fundamental misunderstandings in the indeterminate couple stress model. A comment on recent papers of A.R. Hadjesfandiari and G.F. Dargush. Int. J. Solids Struct. 81, 233–243 (2016).
Pandolfi, A., Gizzi, A. & Vasta, M. Visco-electro-elastic models of fiber-distributed active tissues. Meccanica 52, 3399–3415 (2017).
Placidi, L., Greco, L., Bucci, S., Turco, E. & Rizzi, N. L. A second gradient formulation for a 2D fabric sheet with inextensible fibres. Zeitschrift für angewandte Mathematik und Physik 67, 114 (2016).
Propp, A., Gizzi, A., Levrero-Florencio, F. & Ruiz-Baier, R. An orthotropic electro-viscoelastic model for the heart with stress-assisted diffusion. Biomech Model Mechanobiol 19, 633–659 (2020).
Ogden, R. W. Non-linear elastic deformations (Ellis Horwood, Chichester, 1984).
Rajan, S. et al. Characterization of viscoelastic bending stiffness of uncured carbon-epoxy prepreg slit tape. Compos Struct 275, 114295 (2021).
Shariff, M. H. B. M. Spectral derivatives in continuum mechanics. Quarterly J Mech Appl Math 70(4), 476–479 (2017).
Shariff, M. H. B. M. On the spectral constitutive modelling of transversely isotropic soft tissue: Physical invariants. Int J Eng Sci 120, 199–219 (2017).
Shariff, M. H. B. M., Bustamante, R. & Merodio, J. Rate type constitutive equations for fiber reinforced nonlinearly viscoelastic solids using spectral invariants. Mech. Res. Commun. 84, 60–64 (2017).
Shariff, M. H. B. M. A general spectral nonlinear elastic consistent tangent modulus tensor formula for finite element software. Results Appl. Math. 7, 100113 (2020).
Shariff, M. H. B. M., Bustamante, R. & Merodio, J. A nonlinear spectral rate-dependent constitutive equation for electro-viscoelastic solids. Z. Angew. Math. Phys. 71, 1–22 (2020).
Shariff, M. H. B. M. A generalized strain approach to anisotropic elasticity. Sci Rep 12(1), 1–22 (2022).
Shariff, M. H. B. M., Merodio, J. & Bustamante, R. Finite deformations of fiber-reinforced elastic solids with fiber bending stiffness: A spectral approach. J Appl Comput Mech 8(4), 1332–1342 (2022).
Shariff, M. H. B. M., Merodio, J. & Bustamante, R. Nonlinear elastic constitutive relations of residually stressed composites with stiff curved fibers. Appl Math Mech 43(10), 1515–1530 (2022).
Shariff, M. H. B. M. On the smallest number of functions representing isotropic functions of scalars, vectors tensors. Quarterly J Mech Appl Math 76(2), 143–161 (2023).
Shariff, M. H. B. M., Bustamante, R. & Merodio, J. A non-second-gradient model for nonlinear elastic bodies with fibre stiffness. Sci Rep 13(1), 6562 (2023).
Shariff, M. H. B. M., Bustamante, R. & Merodio, J. Spectral formulations in nonlinear solids: A brief summary. Math Mech Solids 30(2), 267–322 (2023).
Shariff, M. H. B. M., Merodio, J., Bustamante, R. & Laadhari, A. A non-second-gradient model for nonlinear electroelastic bodies with fibre stiffness. Symmetry 15(5), 1065 (2023).
Shariff, M. H. B. M., Merodio, J. & Bustamante, R. Basic errors in couple-stress hyperelasticity articles. Math Mech Solids 29(9), 1729–1738 (2024).
Shariff, M. H. B. M., Bustamante, R. & Merodio, J. A generalized strain model for spectral rate-dependent constitutive equation of transversely isotropic electro-viscoelastic solids. J Mech Phys Solids 192, 105838 (2024).
Soldatos, K. P., Shariff, M. H. B. M. & Merodio, J. On the constitution of polar fiber-reinforced materials. Mech Adv Meter Struct 28, 2255–2266 (2021).
Soldatos, K. P. Finite deformation of fibre-reinforced elastic solids with fiber bending stifness - Part II: Determination of the spherical part of the couple-stress. Math Mech Solids 28, 3–14 (2022).
Soldatos, K. P. New trends in couple-stress hyperelasticity. Math Mech Solids https://doi.org/10.1177/10812865231177673 (2023).
Soldatos, K. P. Author’s response to Shariff et al. [1]: Basic errors in couple-stress hyperelasticity articles. Math Mech Solids 29(9), 1739–1742 (2024).
Spencer, A. J. M. Theory of invariants. In Continuum physics I (ed. Eringen, A. C.) 239–253 (Academic Press, New York, 1971).
Spencer, A. J. M. & Soldatos, K. P. Finite deformations of fibre-reinforced elastic solids with fibre bending stiffness. Int J Non-Linear Mech 42, 355–368 (2007).
Walsh, G. R. Methods of optimization (Wiley, Hoboken, 1975).
Zervos, A. Finite elements for elasticity with microstructure and gradient elasticity. Int. J. Numer. Meth. Engng. 73, 564–595 (2008).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
Let \(\bar{m}_{ij}\) and \(m_{ij}\) be, respectively, the Cartesian components of \(\bar{\varvec{M}}\) and \(\varvec{M}\). From the relation \(\varvec{M}- {\displaystyle \frac{\hbox {tr}\varvec{M}}{3}} {\varvec{I}}=\bar{\varvec{M}}\), we have in Cartesian coordinates
It is clear the determinant of the matrix
is zero and that the matrix \({\varvec{N}}\) is of rank 2. Hence, we can write, for example
The values of \(\bar{m}_{22}\) and \(\bar{m}_{33}\) can be obtain from the constitutive equation (43). If one of the value of \(m_{11}\), \(m_{22}\) or \(m_{33}\) is specified then we can solve (A3) for the remaining values and hence we can uniquely determine the value of \(\hbox {tr}{\varvec{M}}\).
Appendix B
In this Appendix, we only discuss the isotropic invariants that describe the scalar function \(\bar{W}_v\). In order to simply obtain Boehler2 classical isotropic invariants for \(\bar{W}_v\), we write
where \(\bar{{\varvec{\Lambda }}}_s\) and \(\bar{{\varvec{\Lambda }}}_a\) are, respectively, symmetric and antisymmetric parts of \(\bar{{\varvec{\Lambda }}}\).
Boehler2 isotropic invariants are:
There are 63 Boehler’s isotropic invariants, where almost all of them do not have physical interpretation. However, in Sect. “Spectral formulation” we show that there are only 20 independent spectral invariants It is clear that the only invariant in the above list has a physical interpretation is
which is the stretch of the line element in the \({\varvec{a}}\) direction. If we replace the invariant \(\hbox {tr}{\varvec{A}}_1^3\) by the invariant \(\det {\varvec{A}}_1\), then \(\sqrt{\det {\varvec{A}}_1}= \sqrt{\det {\varvec{C}}}\) represents the volume change. Hence, at most, only two invariants in the above list have a physical interpretation.
A rigorous experimental curve fitting exercise to obtain a specific form of free energy function usually involve a test that vary one invariant in the free energy function and hold the rest of the invariants constant6,8 . If the invariants (such as those above) have no direct physical interpretation, it is not easy, possibly impossible, to devise an experiment to do such a test. An example, where spectral invariants, each with a clear physical interpretation, are used in a rigorous curve fitting exercise, is given in Section 7 of reference32.
Modelling a complex material (like the one in this paper) using established (classical) irreducible isotropic functions40 that are not minimal, where most of them have no direct physical interpretation, will give the resulting equations that are too complicated for practical applications and due to their unclear physical interpretation, it is not clear in the literature how to select an appropriate (or optimum) subset from the corresponding full sets (which generally contains non-physical numerous elements, as exemplified in this Appendix) of irreducible isotropic functions to represent a physical model. However, as indicated in this paper, the use of spectral invariants, not only reduce the modelling complexity but is also experimentally friendly.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Shariff, M.H.B.M. On the second gradient nonlinear spectral constitutive modelling of viscoelastic composites reinforced with stiff fibers. Sci Rep 15, 23279 (2025). https://doi.org/10.1038/s41598-025-05230-7
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41598-025-05230-7
Keywords
This article is cited by
-
A couple-stress formulation for electroactive stiff fibre-reinforced composites
Zeitschrift für angewandte Mathematik und Physik (2025)