Intense red emission from highly elastic and thermally stable phosphate glass doped with Ce³⁺, Nd³⁺, and Ce³⁺/Nd³⁺ ions

Abstract

Red emitting materials are critical to a wide range of optoelectronic devices, such as displays, lasers, and light-emitting diodes. Ongoing research efforts are focused on enhancing their emission efficiency and improving their thermal and mechanical stability to meet the demands of advanced device applications. Accordingly, a host glass network with the composition 50P₂O₅-20ZnO-20Bi₂O₃-10BaO (PZBB) was proposed and reinforced with 1 mol% of Ce³⁺, Nd³⁺, or Ce³⁺/Nd³⁺ ions to produce efficient red emission with high thermal and mechanical stability. Structural changes due to compositional variations were analyzed via X-ray diffraction (XRD), density measurements, and Fourier transform infrared (FTIR) spectroscopy. These analyses revealed a high network tightness with a very slight increase with the introduction of Ce³⁺, Nd³⁺, or Ce³⁺/Nd³⁺ ions. The produced host PZBB and developed PZBBCe³⁺, PZBBNd³⁺, or PZBBCe³⁺-Nd³⁺ glasses exhibited high thermal stability and elasticity, confirming their potential for use in optoelectronic device applications. Distinctive absorption bands of Ce³⁺ and Nd³⁺ ions were detected across the 200–2500 nm spectral range. Excitation of the PZBBCe³⁺, PZBBNd³⁺, or PZBBCe³⁺-Nd³⁺ glasses at 308 nm resulted in red emission at 619 & 639 nm, 616 & 677 nm, or 626 nm, respectively. Oscillator strength, Judd–Ofelt, and gain analyses confirm the suitability of PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ for efficient red emission applications. Gain cross section analysis reveals that PZBBCe³⁺-Nd³⁺ glass supports broadband and dual-ion emission, with potential energy transfer enhancing Nd³⁺-dominated red emission output, while Ce³⁺ (PZBBCe³⁺) and Nd³⁺ (PZBBNd³⁺) singly doped glasses show broad and selective gain, respectively—highlighting their suitability for tunable and narrow-linewidth red emission applications. Overall, the PZBBCe³⁺, PZBBNd³⁺, or PZBBCe³⁺-Nd³⁺ glasses demonstrated high photoluminescence efficiency in the red region, along with excellent thermal stability and elasticity, making them promising candidates for single- and dual-wavelength optoelectronic applications.

Introduction

Red emission materials exhibit distinct properties that make them highly valuable in a wide range of applications, including optical communication, night vision technology, laser systems, entertainment displays, and biomedical fields such as imaging, diagnosis, and therapeutic procedures^1,2. The choice of luminescent host materials plays a critical role for determining the performance and further development of red-emitting systems^1,2. Rare-earth (RE³⁺) ion-doped glass materials are recognized as one of most effective hosts for red-emitting applications^3,4,5. Their broad optical transparency across a broad wavelength range and their ability to be shaped into various geometric forms make glass a versatile option for a variety of optoelectronic devices. Furthermore, these materials can be engineered to exhibit high thermal stability, essential for maintaining performance under elevated operating temperatures^6,7. At high temperatures, glass materials may undergo crystallization, deleting emission efficiency by increasing scattering and absorption losses, altering dopant distribution, and raising the excitation threshold. The impact of crystallization on luminescent performance depends on the extent of crystallization, the nature of the formed crystalline phases, and the degree of control over the crystallization process. To ensure optimal red emission, the glass should retain a predominantly amorphous structure with minimal crystallization^8,9. Phosphate glass has proven to be an effective host for RE³⁺ ions, which are essential for luminescent materials. This type of glass offers high optical transparency, low melting point, low phonon energy, and superior rare-earth ion solubility^10,11. Despite these advantages, phosphate glass is relatively mechanically fragile, exhibits limited thermal stability, high hygroscopicity, and reduced chemical durability. To address these issues, it is often necessary to enhance phosphate glass with appropriate additives to improve its overall performance^12,13,14. Heavy metal oxides are particularly has proven effective in strengthening its mechanical integrity and thermal stability of phosphate glass while lowering its melting temperature —an advantage that facilitates easier glass processing. These oxides also help improve the chemical durability of phosphate glass. Bi₂O₃ and BaO, for example, integrate well within the phosphate glass network, altering its properties beneficially^15,16,17. Transition metal oxides such as ZnO play crucial roles in linking phosphate anions and preventing hydration reactions^18,19, and Zn²⁺ ions further stabilize the network by forming strong ionic bonds with neighboring oxygen atoms^19,20. Rare earth ions (RE³⁺) are particularly efficient as luminescent additives because of their extensive range of energy levels, which allows them to emit a wide spectrum of wavelengths with high intensity^21,22. Among these, Ce³⁺ and Nd³⁺ ions are notable for their strong emission across different regions via both up-conversion or down-conversion mechanisms, either independently or through energy transfer interactions^22,23,24. Ce³⁺ ion has a unique property: it undergoes an allowed $\:d-f$ transition, compared to the partially forbidden $\:f-f$ transitions of other RE³⁺ ions. This allowed transition gives Ce³⁺ ion high excitation efficiency and enhanced luminescence, making it an ideal emitter for various photonics applications^25,26. The Ce³⁺ is among the most prevalent RE³⁺ ions, and its relatively abundant availability leads to a lower price compared to many other RE³⁺ ions^27,28,29. One advantage of utilizing Ce³⁺ in photoluminescent media is its efficient energy transfer ability, which is attributed to its rapid fluorescence decay and the favorable overlap between its emission spectra and the absorption bands of other RE³⁺ ions. This synergy enhances the overall functionality of the photoluminescent systems by facilitating effective energy transfer processes^26,30,31. In contrast, Nd³⁺ is more expensive than Ce³⁺ due to its growing demand across various applications. While Nd³⁺ is less abundant than Ce³⁺, it remains more affordable than several other RE³⁺ ions, particularly those that are even rarer^28,32. Additionally, Nd³⁺ ion exhibits a wide range of energy levels like Er³⁺, but it is significantly cheaper^25,31,33. So, both Ce³⁺ and Nd³⁺ are often regarded as more cost-effective compared to other RE³⁺ ions. Ongoing research continues to explore the photoluminescence capabilities of various RE³⁺ ions, especially Ce³⁺, Nd³⁺, and Ce³⁺/Nd³⁺ ions in different host media across different wavelengths. This field remains dynamic, with studies focusing on enhancing the thermal, mechanical, thermomechanical, and chemical stability of luminescent materials, alongside improving their photoluminescence efficiency^{34,35,36,37,38}. The majority of research on energy transfer from cerium to neodymium primarily focuses on near-infrared (NIR) emission, as this is the most commonly observed outcome. In contrast, red emission resulting from this energy transfer is rare and has been reported infrequently. Meng et al.³⁹ generated NIR emission (880–930 nm) from CaSc₂O₄:Ce³⁺,Nd³⁺ phosphor under blue light excitation. It was showed the emitted NIR via Nd³⁺ strongly enhanced 200-fold by Ce³⁺ co-doping through efficient Ce³⁺→Nd³⁺ energy transfer, enabled by Ce³⁺’s 4f – 5d strong absorption and rapid energy relay. Tai et al.⁴⁰ demonstrated NIR quantum cutting via Ce³⁺→Nd³⁺ energy transfer in YAG: Ce³⁺,Nd³⁺, showing enhanced 1064 nm emission, with peak efficiency (160.7%) at 10 mol% Nd³⁺ without quenching. Ait Mellal et al.⁴¹ convert UV light to NIR emission (~ 1059 nm) via Ce³⁺→Nd³⁺ energy transfer in LaPO₄:Ce³⁺,Nd³⁺ phosphors, reaching ~ 172% quantum efficiency—ideal for enhancing c-Si solar cell spectral response.

Hence, to achieve a red emission, a host glass with the composition 50P₂O₅−20ZnO-20Bi₂O₃−10BaO (PZBB) was prepared and doped with 1 mol% of Ce³⁺, Nd³⁺, or Ce³⁺/Nd³⁺ ions (PZBBCe³⁺, PZBBNd³⁺, or PZBBCe³⁺-Nd3³⁺). The novelty of the current study lies in the successful generation of efficient red emission from Ce³⁺, Nd³⁺, and Ce³⁺/Nd³⁺ ions-based glass. This effectively addresses the challenges faced by other RE³⁺ glass-based red-emitting glasses, such as broad emission bandwidths, thermal quenching, energy transfer losses, and high cost. Additionally, it is important to highlight that the chosen Ce³⁺ and Nd³⁺ concentrations were carefully selected to overcome the photoluminescence quenching, a common issue that arises when RE³⁺ ions’ concentrations exceed permissible limits. A comprehensive analysis of the structural, thermal, mechanical, and optical characteristics of the synthesized PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd3³⁺ was conducted via techniques such as X-ray diffraction (XRD), density measurements, Fourier transform infrared (FTIR) spectroscopy, differential scanning calorimetry (DSC), ultrasonic, and UV-Vis optical absorption spectroscopy. Additionally, the red photoluminescence of the PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd3³⁺ glasses was investigated using a 308 nm excitation wavelength.

Experimental procedures

Material Preparation and chemical analysis

A glass matrix with the chemical formula 50P₂O₅−20ZnO-20Bi₂O₃−10BaO (PZBB host glass) was synthesized by the melt-quenching technique. A 1 mol % of Ce³⁺, Nd³⁺, or Ce³⁺/Nd³⁺ ions was incorporated into the produced host PZBB glass, producing a series of developed glasses PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd3³⁺ to generate a red-light emission. High-purity raw materials (sourced from Sigma-Aldrich), including (NH4)2HPO4 (99.99%), ZnO (99.98%), (BiO)₂CO₃ (99.95%), BaCO₃ (99.99%), CeO₂ (99.99%), and Nd₂O₃ (99.99%), were weighed and ground in a porcelain mortar for one hour to ensure uniformity. The mixture was then melted at $\:1200\pm\:1$ °C for two hours, followed by casting into a stainless-steel mold at $\:330\pm\:1$ °C for 30 min of annealing. During the melting process, the molten material was shaken at 10-minute intervals to ensure consistent homogeneity prior to casting. The precise chemical composition of the resulting host PZBB and developed PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses were determined via energy-dispersive X-ray spectroscopy (EDX) with a Hitachi S-3400 N SEM and a Thermo EDX Peltier-cooled X-ray detector. The results of the chemical analysis are provided in Table 1, alongside the targeted synthesis values.

Table 1 Synthesized and actual produced chemical composition of the considered host PZBB and the developed PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd3³⁺ glasses.

Materials examination

The amorphous nature of the host PZBB and the developed PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses was examined via X-ray diffraction (XRD). XRD patterns were recorded with a Philips diffractometer equipped with a Cu-Kα radiation source ($\:\lambda\:=1.54056\:\text{\AA\:}$). To determine the density of the host PZBB and the developed PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses, Archimedes’ principle was applied (Eq. 1)^42,43,44. Each glass sample was weighed in both air and toluene using a high-precision digital balance (± 0.001 g accuracy), with five measurements taken for each sample. The density was calculated from the average of these weight measurements. To assess the impact of the Ce³⁺, Nd³⁺, and Ce³⁺/Nd³⁺ ions on the structural properties of the proposed PZBB host glass, the measured densities were used to calculate molar volume ($\:{V}_{m}$), mean phosphor-phosphor separation ($\:{d}_{P-P}$), oxygen packing density (OPD), and total ionic packing density ($\:{V}_{t}$) values via Eqs. 2, 3, 4, and 5^42,43,44.

$$\:\rho\:=\frac{{W}_{a}}{{W}_{a}-{W}_{t}}\times\:{\rho\:}_{t}$$

(1)

$$\:\:\:\:\:{V}_{m}=\frac{M}{\rho}$$

(2)

$$\:{d}_{P-P}={\left(\frac{{V}_{m}^{P}}{{N}_{A}}\right)}^{1/3}$$

(3)

$$\:OPD=\frac{\rho\:}{M}\times\:n$$

(4)

$$\:{V}_{t}=\frac{\rho\:}{M}\sum\:_{i}{x}_{i}{V}_{i}$$

(5)

where $\:{W}_{a}$ and $\:{W}_{t}$ represent the measured weights of the PZBB, PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glass samples in air and toluene. $\:{\rho\:}_{t}$ is the density of toluene, $\:M$ is the molar mass of the considered glasses, $\:{N}_{A}$ is Avogadro’s number, $\:{V}_{m}^{P}$ is the volume occupied by one mole of phosphor ions in the glass, $\:n$ is the number of oxygen atoms per formula unit, $\:{x}_{i}$ is the mole fraction, and $\:{V}_{i}$ is the packing factor. The $\:{V}_{m}^{P}$ and $\:{V}_{i}$ were determined via the following formulas

$$\:{V}_{m}^{P}=\frac{{V}_{m}}{2\left(1-{X}_{P}\right)}$$

$$\:{V}_{i}=\frac{4\pi\:{N}_{A}}{3}\left(b{r}_{A}^{3}+c{r}_{O}^{3}\right)\:\:$$

where, $\:{X}_{P}$ represents the molar fraction of P₂O₅, while $\:{r}_{A}$ and $\:{r}_{B}$ denote the ionic radii of the cation and anion, respectively, for the oxide component $\:{A}_{b}{O}_{c}$.

A JASCO FT-IR 6200 spectrometer was utilized to record the FTIR spectra covering the wavenumber range of 400–4000 cm⁺¹ (± 2 cm⁻¹). This analysis was performed to investigate the vibrational modes of the fabricated PZBB, PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd3³⁺ glasses. Thermal behavior was analyzed via differential scanning calorimetry (DSC) with an SDT Q600 thermal analysis system, utilizing an open platinum crucible. The measurements were performed under a nitrogen atmosphere at a heating rate of 10 °C/min and a gas flow pressure of 15 psi. The resulting DSC curves were used to estimate the glass transition temperature ($\:{T}_{g}$), onset crystallization temperature ($\:{T}_{C1}\text{a}\text{n}\text{d}\:{T}_{C2}$), and peak crystallization temperature ($\:{T}_{P1}$and $\:{T}_{P2}$). Thermal stability ($\:\varDelta\:T$) of the PZBB, PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses were calculated from the difference between $\:{T}_{C2}$ and $\:{T}_{g}$ ($\:\varDelta\:T={T}_{C2}-{T}_{g}$)¹⁹. Ultrasonic longitudinal wave velocity ($\:{v}_{L}$) and shear wave velocity ($\:{v}_{S}$) were measured via the pulse-echo method with the SNAP, RAM-5000, RITEC system from Warwick, United States. Using the obtained values for $\:{v}_{L}$ and $\:{v}_{S}$, the longitudinal modulus ($\:{C}_{11}$), shear modulus ($\:{C}_{44}$), bulk modulus ($\:B$), Young’s modulus ($\:Y$), Poisson’s ratio ($\:\sigma\:$), microhardness ($\:{H}_{UT}$), acoustic impedance ($\:{Z}_{i}$), and Debye temperature ($\:{O}_{D}$) were estimated via the following Eqs^45,46.

$$\:{C}_{11}=\rho\:{v}_{L}^{2}$$

(6)

$$\:{C}_{44}=\rho\:{v}_{s}^{2}$$

(7)

$$\:B=\frac{\rho\:\left(3{v}_{L}^{2}-4{v}_{S}^{2}\right)}{3}$$

(8)

$$\:Y=\frac{\rho\:{v}_{S}^{2}\left(3{v}_{L}^{2}-4{v}_{S}^{2}\right)}{{v}_{L}^{2}-{v}_{S}^{2}}$$

(9)

$$\:\sigma\:=\frac{\left({v}_{L}^{2}-{2v}_{S}^{2}\right)}{2\left({v}_{L}^{2}-{v}_{S}^{2}\right)}$$

(10)

$$\:{H}_{UT}=\frac{\left(1-2\sigma\:\right)}{6\left(1+\sigma\:\right)}$$

(11)

$$\:{Z}_{i}={v}_{mean}\rho$$

(12)

$$\:{\theta\:}_{D}=\frac{h}{{K}_{B}}{\left(\frac{9{N}_{A}}{4\pi\:{V}_{m}}\right)}^{1/3}{v}_{mean}$$

(13)

where, $\:h$, and $\:{K}_{B}$ are Planck’s and Boltzmann constants, respectively. $\:{v}_{mean}$ represents the mean ultrasonic velocity and calculated by

$$\:{v}_{mean}={\left(\frac{1}{3}\left(\frac{1}{{v}_{L}^{3}}+\frac{2}{{v}_{s}^{3}}\right)\right)}^{-1/3}$$

Optical absorption spectra were measured via a Jenway 6405 UV/Vis spectrophotometer with a resolution of 2 nm. The measurements were conducted on highly-polished circular samples, each with a diameter of 2 cm and a thickness ranging from approximately 1.200 to 1.450 mm, over the spectral range of 200–1100 nm. The photoluminescence spectra of the PZBB, PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses were recorded via an Edinburgh FLS1000 steady-state/transient fluorescence spectrometer. Excitation was provided by a xenon lamp at a wavelength of 308 nm.

Results and discussion

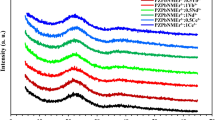
The X-ray diffraction pattern presented in Fig. 1 reveals the amorphous nature of the considered PZBB, PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd3³⁺ glasses. The broad, continuous diffraction feature observed is due to scattering from the irregular atomic arrangement within these glasses. As shown in Fig. 1, there was no significant change in the XRD patterns with the addition of Ce³⁺, Nd³⁺, and Ce³⁺/Nd³⁺ ions, indicating that the amorphous phase remained stable even with the incorporation of these ions into the host PZBB network.

Fig. 1

XRD patterns of the PZBB, PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses.

Initially, as shown in Table 2, the PZBB host glass exhibited a density of 4.202 g/cm³. Introducing CeO₂, Nd₂O₃, or CeO₂/Nd₂O₃ resulted in a minor growth in density compared to the PZBB, as shown in Table 2. Since CeO₂, Nd₂O₃, or CeO₂/Nd₂O₃ were added as dopants rather than substitutes, their presence within the glass network resulted in a higher network density due to their accumulation. The developed PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses exhibited the same density, as listed in Table 2. Conversely, the molar volume of all developed PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses decreased compared to the PZBB host, as indicated in Table 2. This implies that the incorporated Ce³⁺ and Nd³⁺ diffuse into the glass network, occupying interstitial voids, which results in a reduction in interstitial distances. Additionally, the incorporation of Ce³⁺, Nd³⁺, or Ce³⁺/Nd³⁺ ions caused the network constituents to move closer together, further decreasing the molar volume. This was supported by the reduction in the mean phosphor-phosphor separation, as detailed in Table 2. The decrease in molar volume and mean phosphor-phosphor separation highlights an increase in the network’s tightness. This is further supported by the changes in the oxygen packing density (OPD) and total ionic packing density ($\:{V}_{t}$), which refer to the tightness with which oxygen atoms are packed within the glass network and the fraction of the glass volume occupied by the constituent ions, respectively. As listed in Table 2, both OPD and $\:{V}_{t}$ increased in the developed PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses compared with the host glass PZBB. This indicates a more densely packed oxygen network, stronger interatomic interactions, and less free volume within the glass, suggesting greater network rigidity. A comparison of the roles of Ce³⁺ and Nd³⁺ ions within the glass network revealed that Ce³⁺ ions have a greater effect on increasing the tightness of the glass network. This is due to the larger ionic radius of Ce³⁺, which allows it to spread more effectively inside the glass network, fill more voids, and reduce inter-distances, thereby enhancing the overall tightness of the network.

Table 2 Density ($\:\rho\:$), molar volume ($\:{V}_{m}$), mean phosphor-phosphor separation ($\:{d}_{P-P}$), oxygen packing density (OPD), and total ionic packing density ($\:{V}_{t}$).

In the FTIR spectrum of the PZBB host glass shown in Fig. 2, the prominent absorption band at low-frequency centered at 460 cm⁻¹ corresponds to the deformation modes of the $\:{\text{P}\text{O}}_{4}^{3-}$groups ($\:{\text{Q}}^{0}$), bending modes of the $\:\text{O}=\text{P}-\text{O}$ linkages in $\:{\text{Q}}^{1}$ units, and the stretching of $\:\text{M}-\text{O}-\text{P}$ (where M denotes the metal ions in the current glass Zn²⁺, Bi³⁺, Ba²⁺)^47,48,49. The band at 680 cm⁻¹ corresponds to the symmetric stretching vibration of $\:\text{P}-\text{O}-\text{P}$ rings ($\:{\text{Q}}^{1}$)^47,48,49. The band centered at 865 cm⁻¹ is assigned to the stretching vibrations of $\:\text{P}-\text{O}-\text{P}$ linkages in $\:{\text{Q}}^{1}$ units^50,51. The broadband peak centered at 1035 cm⁻¹ was assigned to the stretching vibration of $\:\text{P}-{\text{O}}^{-}$ in $\:{Q}^{0}$ units, the stretching vibration in $\:{\text{P}\text{O}}_{3}^{2-}$ groups ($\:{Q}^{1}$), and the symmetric stretching vibrations of $\:\text{P}-\text{O}-\text{P}$ $\:{[\text{v}}_{\text{a}\text{s}}\left(\text{P}-\text{O}-\text{P}\right)]$ in the pyrophosphate units^52,53. The weak shoulder at 1391 cm⁻¹ is referred to the symmetric stretching vibrations of $\:\text{P}=\text{O}$ bonds^50,51,53. The bands observed in the higher energy region at 1667, 2381, 2942, and 3480 cm⁻¹ correspond to the bending vibrations of $\:\text{H}-\text{O}-\text{H}$ and $\:\text{P}-\text{O}\text{H}$ and the stretching vibration of $\:\text{H}-\text{O}-\text{H}$ in H₂O^48,50. With the introduction of Ce³⁺, Nd³⁺, or Ce³⁺/Nd³⁺, no significant shift in the FTIR band positions was observed. This stability at these sites indicates that the strength and length of the bonds are not affected by environmental changes in the host glass network as a result of the introduction of these ions.

Fig. 2

FTIR of the PZBB, PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses.

The thermal profiles of the fabricated PZBB, PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses, as shown in Fig. 3, reveal distinct exothermic peaks associated with crystallization temperatures and feature positions of glass transition temperatures. Table 3 presents the thermal parameters—glass transition temperature ($\:{T}_{g}$), onset crystallization temperatures ($\:{T}_{C1}$ and $\:{T}_{C2}$), and maximum crystallization temperatures ($\:{T}_{P1}$ and $\:{T}_{P2}$)—which are derived from Fig. 3. The glass transition temperature of the PZBB host glass is 390 °C, as indicated in Table 3. The introduction of Ce³⁺, Nd³⁺, or Ce³⁺/Nd³⁺ into the PZBB glass increases the glass transition temperature, suggesting enhanced network packing and cross-linking density. This observation aligns with the trends observed in the OPD and $\:{V}_{t}$ behavior detailed in Table 3. The OPD and $\:{V}_{t}\:$contribute to a stronger, more rigid glass structure with increased connectivity. As a result, a higher thermal energy is required to transform solid glass into a viscous liquid, which indicates that glasses with higher OPD and $\:{V}_{t}$ values within a given volume exhibit higher $\:{T}_{g}$ values. Conversely, for the Ce³⁺-doped glass (PZBBCe³⁺), the crystallization temperatures shift to higher values, implying that Ce³⁺ ions improve the glass-forming ability and reduce tendency to crystallization. In contrast, Nd³⁺ and Ce³⁺/Nd³⁺-doped glasses (PZBBNd³⁺ and PZBBCe³⁺-Nd³⁺) show a shift in crystallization temperatures toward lower values, indicating a greater likelihood of crystallization and a diminished glass-forming ability. According to Table 3, the PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses exhibit thermal stability and the presence of Ce³⁺, Nd³⁺, or Ce³⁺/Nd³⁺ ions slightly decreases this stability. The slight reduction in thermal stability of PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses can be ascribed to various factors: (a) The introduction of Ce³⁺ and Nd³⁺ ions may disrupt the structural connectivity of the glass matrix, reducing its overall stability. However, this explanation is contradicted by the structural changes discussed earlier, which indicate an increase in connectivity within the studied glasses. (b) The incorporation of Ce³⁺ and Nd³⁺ ions, which have larger ionic radii, may introduce localized regions of structural disorder, lowering the temperature at which the material can remain amorphous. This increase in disorder is confirmed for Ce-based glasses (PZBBCe³⁺ and PZBBCe³⁺-Nd³⁺) as indicated by the Urbach energy results discussed later. However, for the Nd-based glass (PZBBNd³⁺), the structure shows a higher degree of order, making this interpretation inconsistent with the thermal stability behavior of the PZBBNd³⁺. (c) The inclusion of Nd³⁺ may introduce defects, such as oxygen vacancies or other structural irregularities, which can act as nucleation sites for crystallization, thereby lowering thermal stability. This interpretation is strongly supported by the observed shift in the crystallization temperature of the PZBBNd³⁺ glass to a lower value, indicating reduced stability of the glass phase. However, despite these minor reductions in thermal stability, the overall high thermal stability of glasses containing Ce³⁺ and Nd³⁺ remains intact and unaffected. This high thermal stability ensures the structural integrity of the PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses, prevents unwanted crystallization, which maintains high photoluminescent efficiency and enhances the longevity and durability of the red emitting materials.

Fig. 3

DSC profiles of the fabricated PZBB, PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses.

Table 3 Thermal parameters of the host PZBB and the developed PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses.

Table 4 lists the behavior of various mechanical properties, including longitudinal$\: ({\varvec{v}}_{\varvec{l}})$ and shear $\:({\varvec{v}}_{\varvec{s}})$​ velocities, along with elastic moduli such as longitudinal $\:({C}_{11}),$ shear $\:({C}_{44}),$, bulk (B), Young’s modulus (Y), and the Poisson’s ratio $\:(\sigma).$ It also includes the microhardness ($\:{H}_{UT}$), acoustic impedance ($\:{Z}_{i}$​), and Debye temperature ($\:{\theta\:}_{D}$​). Initially, the variations in the obtained mechanical parameters were minor, as listed in Table 4, due to the slight increases in Ce³⁺, Nd³⁺, and Ce³⁺/Nd³⁺ contents. The elastic properties of glass materials are influenced primarily by factors such as the packing density, bond dissociation energy of metal-oxide bonds, cross-linking density, and coordination number. The addition of Ce³⁺, Nd³⁺, and Ce³⁺/Nd³⁺ ions increased the density and tightness of the proposed PZBB host glass, enhancing both the longitudinal and shear velocities. Furthermore, Ce³⁺, Nd³⁺, and Ce³⁺/Nd³⁺ ions played a significant role in filling network interstices and integrating into the glass network, which reduced the travel time of waves and consequently increased the ultrasonic velocity. The elastic moduli (longitudinal, shear, bulk, and Young) also follow a similar trend, increasing with the introduction of Ce³⁺, Nd³⁺, and Ce³⁺/Nd³⁺ ions, as indicated in Table 4. The increases in the microhardness ($\:{H}_{UT}$​) and Debye temperature ($\:{\theta\:}_{D}$​) further support the rigidity of the glasses and the observed elastic moduli results. The reduction in Poisson’s ratio ($\:\sigma\:$), as detailed in Table 4, reflects the increased cross-linking density due to the diffusion of Ce³⁺, Nd³⁺, and Ce³⁺/Nd³⁺ ions, which confirms the trends in the ultrasonic velocities and elastic moduli. Additionally, the increase in the acoustic impedance ($\:{Z}_{i}$), which denotes resistance to ultrasonic wave propagation, is attributed to the formation of PO_4​ chains and supports the compactness of the glass network.

Table 4 Ultrasonic velocities, elastic moduli, microhardness, passion’s ratio, impedance, and Debye temperature of the considered PZBB, PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses.

Figure 4a displays the optical absorption spectra for the PZBB, PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses. The PZBB host glass shows no absorption bands, as noted in the inset of Fig. 4. In contrast, the spectra for the PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses reveal several absorption bands, indicating the integration of Nd³⁺ and Ce³⁺ ions into the glass network. Ce-doped glasses typically exhibit absorption bands in the UV and blue regions due to $\:4F\to\:5d$ transitions. In PZBBCe³⁺, bands appear at 206, 222, 232, 246, 260, 266, 274, 292, 302, 308, 316, 326, 338, 346, 360, and 376 nm. The bands at 206, 222, 232, and 246 nm correspond to the transition in the split ²$\:{F}_{5/2}\to\:5{d}_{2}$ in Ce³⁺. The bands at 260 and 264 nm resulted from the charge transfer transitions in Ce⁴⁺. The bands at 274, 292, 302, 308, 316, 326, and 338 nm are attributed to the ²$\:{F}_{5/2}\to\:5{d}_{1}$ transitions in the Ce³⁺ ion. The bands at 346, 360, and 376 nm correspond to the transition in the ²$\:{F}_{7/2}\to\:5{d}_{1}$ of Ce³⁺ ion. For PZBBNd³⁺, bands are observed at 216, 230, 242, 250, 256, 262, 356, 528, 544, 744, and 806 nm. Nd³⁺ ions typically show absorption bands approximately $\:\sim$356, 432, 474, 515, 528, 586, 628, 684, 750, 806, and 882 nm, corresponding to various transitions from the ⁴I_9/2 ground state to various excited states. Here, the bands at 356, 528, 544, 744, and 806 correspond to transitions from the Nd³⁺ ground state ⁴I_9/2 to the excited state ⁴D_3/2 + ⁴D_3/2+⁴D_1/2, ⁴G_7/2, ⁴G_5/2, ⁴S_3/2, and ⁴F_5/2+²H_9/2. On the other hand, the bands that appeared in the region of 200–300 nm in the PZBBNd³⁺ glass arose from impurities, defects, and charge transfer. In PZBBCe³⁺-Nd³⁺, bands at 218, 240, 250, 262, 272, 284, 296, 302, 316, 326, 332, 342, 348, 354, 526, 584, 744, and 804 nm are observed as a result of transitions within Ce³⁺/Ce⁴⁺ and Nd³⁺ ions, indicating that the two ions were successfully integrated within the considered glass. Finally, it is important to note the presence of saturation or apparent cutoff in some absorption bands within the 200–400 nm range. These features, observed in the PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺–Nd³⁺ glasses, do not correspond to the intrinsic UV absorption edge of the host matrix. This is evident from the PZBB host glass, which exhibits no significant absorption in this region (as shown in the inset of Fig. 4), confirming its transparency, and ruling out host-related artifacts. Instead, the absorption bands observed are attributed to the electronic transitions of the dopant ions, specifically Ce³⁺/Ce⁴⁺, Nd³⁺, impurities, defects, and charge transfer. These transitions are well-documented in this spectral region and account for the distinct and structured features in the spectra. Although the fundamental absorption edge of the glass matrix may begin to contribute at wavelengths shorter than 200 nm (not fully captured in the current data), the absorption features between 200 and 400 nm are associated with the dopants and not spectrometer-related artifacts.

By applying the Lambert-Beer law (Eq. 14) and analyzing the absorption spectra, the absorption coefficient (α) of the fabricated glasses was calculated^11,17.

$$\:I={I}_{o}{e}^{-\alpha\:t}$$

(14)

where, $\:{I}_{o}$ and I represent the incident and transmitted photon intensities passing across the considered glasses of the thicknesses $\:t$.

The optical band gap ($\:{E}_{g}$) of the considered glasses was calculated based on Tauc’s theory and the supporting research by Mott and Davis using the following Eqs^11,17..

$$\:\alpha\:h\nu\:=\beta\:{\left(h\nu\:-{E}_{g}\right)}^{n}$$

(15)

By constructing a Tauc plot of $\:h\nu\:$ versus $\:{\left(\alpha\:h\nu\:\right)}^{0.5}$, as shown in Fig. 4b, the indirect optical band gap ($\:{E}_{g}$) was inferred. The $\:{E}_{g}$ values were determined by the slope of the linear region of the curve, where it intersects the $\:h\nu\:$ axis, noting the $\:h\nu\:$ value at αhν = 0.

The Urbach energies $\:\left(\varDelta\:E\right)$ of the considered glasses were calculated using the equation from references^13,19.

$$\:\alpha\:=\beta\:{e}^{\raisebox{1ex}{$h\nu\:$}\!\left/\:\!\raisebox{-1ex}{${\Delta\:}E$}\right.}$$

(16)

By applying Eq. 16, the relationship between $\:h\nu\:$ and $\:ln\alpha\:$ for the considered glasses was plotted, as shown in Fig. 4c. The Urbach energy $\:\left(\varDelta\:E\right)$ was obtained by finding the reciprocal of the intersection point of the curve’s linear extension with the x-axis.

The PZBB host glass exhibited a band gap and an Urbach energy of 3.20 and 0.328 eV, as tabulated in the inset of Figs. 4b and c. The incorporation of Ce³⁺ into the PZBB network (PZBBCe³⁺ glass) led to a notable reduction in the optical band gap and an increase in the Urbach energy. The presence of Ce³⁺ ions within the PZBB host glass generates localized states within the band gap, which promotes easier electronic transitions. This not only lowers the optical band gap but also increases structural disorder, broadening the density of states tail and thereby raising the Urbach energy. These changes result from the ion’s effects on the glass network, free carriers’ introduction, and defect states’ creation. Unlike Ce³⁺, Nd³⁺ (glass PZBBNd³⁺) slightly reduces the band gap and sharply reduces the Urbach energy. Nd³⁺ has a $\:{4f}^{4}$ electron configuration, and its electronic transitions typically involve intra-configurational 4f – 4f transitions, which are more localized than the conduction band electrons. Introducing Nd³⁺ ions into the glass network does not significantly disrupt the electronic structure but can induce subtle changes that slightly lower the optical band gap. The effect is small because Nd³⁺ does not introduce many defect states or new energy levels within the band gap. Nd³⁺ ions also tend to form more stable and ordered coordination environments within the glass matrix, which reduces structural disorder. As the glass network becomes more stable and less disordered, the density of states near the conduction band edge sharpens, and the tail of the density of states responsible for the Urbach energy narrows, resulting in a decrease in the Urbach energy. In the PZBBCe³⁺-Nd³⁺ glass, a balance between the effects of Ce³⁺ and Nd³⁺ is observed, as the glass exhibits an optical band gap that is higher than that of the PZBBCe³⁺ glass but lower than that of the PZBBNd³⁺ glass. Corresponding changes in the gap energy are also evident, as shown in the inset of Fig. 4c. This balance arises from the combined influence of the cerium and neodymium ions.

Based on the band gap results, the refractive index was determined using the following Eqs^19,43. and is provided in the inset table of Fig. 4c.

$$\:\frac{\left({n}^{2}-1\right)}{\left({n}^{2}+1\right)}=1-\sqrt{\frac{{E}_{g}}{20}}$$

(17)

The PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses all exhibited higher refractive indices than the PZBB host glass. The PZBBCe³⁺ glass had the highest refractive index, while PZBBNd³⁺ had the lowest. The PZBBCe³⁺-Nd³⁺ glass showed a refractive index that is relatively balanced between the two. Compared to the PZBB host glass, the higher refractive indices of the PZBBCe³⁺ and PZBBNd³⁺ glasses can be attributed to the higher polarizability of Ce³⁺ and Nd³⁺ ions. The higher refractive index of PZBBCe³⁺, compared to PZBBNd³⁺, is likely due to the larger ionic radius of Ce³⁺ and its more diffuse electron cloud, leading to higher polarizability and, consequently, a higher refractive index. The balanced refractive index in the PZBBCe³⁺-Nd³⁺ glass results from the combined polarizabilities of the two ions, producing an intermediate value between those of the individual Ce³⁺ and Nd³⁺ glasses.

Fig. 4

Optical absorption spectra of the considered PZBB, PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses.

The spectroscopic characteristics and photoluminescent parameters of produced materials are further examined using Judd–Ofelt (JO) theory. This theory is applied to extensively investigate the electric dipole transitions within the $\:4f$ configuration of RE³⁺ ions in various host media⁵⁴. For optical transitions involving both Ce³⁺ and Nd³⁺ ions, the experimental oscillator strength ($\:{f}_{exp}$) and the calculated oscillator strength ($\:{f}_{cal}$) for each absorption transition were determined using Eqs. 18 and 19, respectively^54,55,56.

$$\:{f}_{exp}=\frac{2.303m{c}^{2}}{N\pi\:{e}^{2}}\int\:\epsilon\:\left(\nu\:\right)d\nu\:=4.318\times\:{10}^{-9}\int\:\epsilon\:\left(\nu\:\right)d\nu$$

(18)

Here, the $\:m$ & $\:e$, $\:c$, and $\:N$ are the electron mass & charge, speed of light, and Avogadro’s number. The $\:\epsilon\:\left(\nu\:\right)$ represent the he molar absorption coefficient of absorption band corresponding to the energy $\:\nu\:$ (cm⁻¹) and $\:d\nu\:$ is the half bandwidth. The value of $\:\epsilon\:\left(\nu\:\right)$ deduce based on Beer–Lambert, as follows

$$\:\epsilon\:\left(\nu\:\right)=\frac{1}{Cl}\text{log}\left(\frac{{I}_{o}}{I}\right)$$

Where, $\:C$, $\:l$, and $\:\text{log}\left(\frac{{I}_{o}}{I}\right)$ represent the rare-earth ion concentration, the thickness of the glass sample, and the optical density.

$$\:{f}_{cal}=\frac{8{\pi\:}^{2}mc\nu\:}{3h\left(2J+1\right)}\frac{{\left({n}^{2}+2\right)}^{2}}{9n}\sum_{\lambda\:=2,\:4,\:6}{{\Omega\:}}_{\lambda\:}{\left({\Psi\:}J\parallel\:{U}^{\lambda\:}\parallel\:{{\Psi\:}}^{{\prime\:}}{J}^{{\prime\:}}\right)}^{2}$$

(19)

Where, $\:n$ and $\:J\:$represent the refractive index of the medium and the total angular momentum of the ground state. $\:{{\Omega\:}}_{\lambda\:}$ ($\:\lambda\:=2,\:4,\:\text{a}\text{n}\text{d}\:6$) and $\:{U}^{\lambda\:}$ are $\:\text{J}-\text{O}$ intensity parameters and the doubly reduced matrix elements of the unit tensor operator evaluated in the intermediate coupling scheme for a transition $\:{\Psi\:}J{\to\:{\Psi\:}}^{{\prime\:}}{J}^{{\prime\:}}$.

The peak positions of the absorption bands, along with their corresponding transitions and the derived values of $\:{f}_{exp}$ and $\:{f}_{cal}$, are presented in Table 5. It is important to note that in the case of Ce³⁺, multiple absorption bands were observed for each transition due to energy level splitting. To represent the possible transitions, only three characteristic wavelengths were selected for oscillator strength calculations, as shown in Table 5.

Table 5 The absorption band energies and the oscillator strengths ($\:\times\:{10}^{-6})\:$for PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses.

The results obtained for the experimental and calculated oscillator strengths demonstrated good convergence. The notable differences in oscillator strengths observed for both Ce³⁺ and Nd³⁺ in the co-doped PZBBCe³⁺-Nd³⁺ glass, compared to their singly doped counterparts (PZBBNd³⁺ and PZBBCe³⁺-Nd³⁺), provide strong evidence for interactions between the two ions within the glass matrix. These Ce³⁺–Nd³⁺ interactions can alter the local crystal field environment, thereby modifying both ions’ energy level structure and transition probabilities. Such modifications may arise from mechanisms such as energy transfer between Ce³⁺ and Nd³⁺ or changes in site symmetry and bonding characteristics within the glass network. Higher oscillator strengths for specific transitions were observed, indicating increased absorption efficiency at those wavelengths, which is crucial for photoluminescent systems. For instance, the absorption of Ce³⁺ near 274 nm and Nd³⁺ around 744 nm suggests these wavelengths are optimal for excitation, potentially facilitating effective energy transfer process.

Table 6 presents the Judd–Ofelt (J–O) intensity parameters ($\:{{\Omega\:}}_{2}$, $\:{{\Omega\:}}_{4}$, and $\:{{\Omega\:}}_{6}$) and their trends for PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses. In PZBBCe³⁺ glass, the relatively high $\:{{\Omega\:}}_{2}$ indicates a highly asymmetric local environment and significant $\:\text{C}\text{e}-\text{O}$ covalency. The lower $\:{{\Omega\:}}_{4}$ and $\:{{\Omega\:}}_{6}$ values suggest that asymmetry (linked to $\:{{\Omega}}_{2}$) primarily governs transition intensities. The trend $\:{{\Omega}}_{2}>{{\Omega\:}}_{6}>{{\Omega\:}}_{4}$ confirms the dominance of odd-parity crystal field components. In PZBBNd³⁺, $\:{{\Omega}}_{2}$ is lower than in the Ce³⁺-doped glass, suggesting a more symmetric environment or weaker $\:\text{N}\text{d}-\text{O}$ covalency. However, both $\:{{\Omega}}_{4}$ and especially $\:{{\Omega}}_{6}$ are significantly higher, with $\:{{\Omega}}_{6}\:$being crucial for transitions from the ⁴F_3/2 level— an essential factor in optimizing photoluminescence efficiency for practical applications. The typical trend $\:{{\Omega}}_{2}>{{\Omega}}_{6}>{{\Omega}}_{4}\:$reflects the strong role of higher-order crystal field effects. In PZBBCe³⁺-Nd³⁺, co-doping alters the J–O parameters for both ions. The reduced $\:{{\Omega\:}}_{2}$ suggests increased symmetry or altered covalency due to ion interaction. $\:{{\Omega\:}}_{4}$ increases markedly, indicating enhanced influence of even-parity fields, while $\:{{\Omega\:}}_{6}$ decreases compared to Nd³⁺-only glass but remains above the Ce³⁺-only level. The new trend $\:{{\Omega\:}}_{4}>{{\Omega\:}}_{2}>{{\Omega\:}}_{6}\:$highlights significant changes in the glass structure and local ion environments, with $\:{{\Omega\:}}_{4}$-driven transitions becoming more dominant.

Table 6 J–O intensity parameters ($\:{{\Omega\:}}_{\lambda\:}\times\:{10}^{-20}{\text{c}\text{m}}^{2},\:\lambda\:=2,\:4,\:\text{a}\text{n}\text{d}\:6)\:$and trend in the PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses.

Figure 5 shows the red emission beam from the proposed PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses, when pumped with 308 nm light. Initially, no emission was observed from the PZBB host glass, as shown in Fig. 5a. The absence of emission from the PZBB host glass network suggests that none of the components typically responsible for photoluminescence are present—this includes both key elements like bismuth, which is well known for its luminescent properties, as well as any luminescent impurities that might otherwise be present. Initially, although the Ce³⁺ ion is best known as an emitter in the UV and blue light regions, some earlier studies have also reported red emissions from Ce³⁺ ions in different host matrices. Hasegawa et al.⁵⁷ observed a broad reddish-yellow emission band spanning 500 to 750 nm in the BaCa₂(Y_0.998Ce_0.002)₆O₁₂ phosphor, attributing it to a spin-allowed $\:5\text{d}\:\to\:\:4\text{f}$ transition in Ce³⁺. Li et al.⁵⁸ reported emission band extending from 400 to 700 nm in the Ba₉Lu₂Si₆O₂₄:Ce³⁺ phosphor, originating from $\:5\text{d}\:\to\:\:4\text{f}$ transitions of Ce³⁺ ions located on Lu³⁺ sites. Finally, Kulesza et al.⁵⁹ observed a well-defined red emission band centered at 650 nm in SrSO₄:Ce powders, attributed to the spin-orbit splitting of the Ce³⁺ ground state into the ²F_5/2 and ²F_7/2 states, with the emission arising from transitions between these levels. On the other hand, regarding the red emission from Nd³⁺ ions, Nd³⁺ is widely known for its near-infrared (NIR) luminescence^60,61,62, but there are also some reports of red emission from this ion. Balda et al.⁶³ observed several red emission bands at 646, 656, 673, 675, and 686 nm from Nd³⁺ in a PB crystal, which were attributed to ⁴G_11/2$\:\to\:$⁴I_15/2, ⁴G_9/2 $\:\to\:$⁴I_13/2, ²G_9/2 $\:\to\:$⁴I_15/2, ⁴G_9/2 $\:\to\:$⁴I_13/2, ⁴G_7/2 $\:\to\:$⁴I_13/2, and ⁴G_5/2 $\:\to\:$⁴I_11/2 transitions, respectively. Additionally, Gaurkhede et al.⁶⁴ reported an emission band at 654 nm, which they attributed to the ⁴F_9/2 → ⁴I_9/2 transition.

When the PZBBCe³⁺ and PZBBNd³⁺ glasses are pumped at 308 nm, the 5d₃ and ²D_7/2 energy levels of Ce³⁺ and Nd³⁺, respectively, are excited through the ground state absorption (GSA) mechanism. For Ce³⁺, the excited 3 d state nonradiatively decays to the 5d₁ level, which then undergoes radiative decay to the ²F_5/2 and ²F_7/2 levels, emitting red light at 619 and 639 nm, as depicted in Fig. 6a. In the case of PZBBNd³⁺, the excited ²D_7/2 state nonradiatively decays to the ²H_11/2 and ⁴F_9/2 levels before ultimately decaying to the ⁴I_9/2 ground state, emitting red light at 616 and 677 nm, as shown in Fig. 6b. In comparison, the two red peaks formed in the PZBBCe³⁺glass had somewhat similar intensities, whereas in the PZBBNd³⁺glass, one of the bands had a higher intensity than the other, as observed in Figs. 5b and c, which occurred due to Stokes shift and the impact of the crystal field environment or the defects on Nd³⁺ emission. In PZBBCe³⁺-Nd³⁺ glass, single red light at 626 nm was generated, as shown in Fig. 5d, due to radiative decay from Ce³⁺ and Nd³⁺ and energy transfer between Ce³⁺ and Nd³⁺, as shown in Fig. 6c. The appearance of only one emission band in the PZBBCe³⁺-Nd³⁺ glass may be due to the energy transfer mechanism and spectral overlap.

Fig. 5

(a) The PL spectrum of the PZBB host glass and the red emission beam from (b) PZBBCe³⁺, (b) PZBBNd³⁺, and (d) PZBBCe³⁺-Nd³⁺ glasses.

Fig. 6

Potential electronic transitions in (a) PZBBCe³⁺, (b) PZBBNd³⁺, and (c) PZBBCe³⁺-Nd³⁺ glasses.

As shown in Fig. 6c, there are two possible excitation pathways at 308 nm: one for Ce³⁺, from the ground state ²F_5/2 to the highest excited state 5d₄, and another for Nd³⁺, from the ground state ⁴I₉/₂ to the excited state ²D_7/2. Three possible processes following this excitation led to red emission at 626 nm, as outlined below:

• 1. Ce³⁺ may undergo nonradiative decay from the 5d₄ excited state to the 5d₁ state, followed by radiative decay to the ground state (²F_5/2), resulting in red emission at 626 nm (as depicted in the right section of Fig. 6c).

• 2. Nd³⁺ may experience nonradiative decay from the ²D_7/2 excited state to the ²H_11/2 state, followed by radiative decay to the ground state (⁴I_9/2), also leading to red emission at 626 nm (as shown in the left section of Fig. 6c).

• 3. Key feature of Fig. 6c illustrates the nonradiative energy transfer between Ce³⁺ and Nd³⁺ ions. This energy transfer, driven by mechanisms such as dipole-dipole or exchange interactions, takes place when there is adequate overlap between the donor’s (Nd³⁺ or Ce³⁺) emission spectrum and the acceptor’s (Nd³⁺ or Ce³⁺) absorption spectrum, coupled with a small interionic distance. Specifically, energy transfer can occur from the 5d₃ state of Ce³⁺ to the ²H_11/2 state of Nd³⁺, or from the ²D_7/2 state of Nd³⁺ to the 5d₁ state of Ce³⁺, followed by radiative emission at 626 nm due to the transition to the ground state ²F_5/2 (Ce³⁺) and ⁴I_9/2 (Nd³⁺).

Finally, it is worth noting that the probability of energy transfer from Nd³⁺ to Ce³⁺ is significantly lower than the transfer from Ce³⁺ to Nd³⁺. This makes Ce³⁺ a strong candidate as a sensitizer for Nd³⁺. Ce³⁺ efficiently absorbs UV and blue light and exhibits fast relaxation dynamics. Moreover, its excited states lie at higher energies compared to those of Nd³⁺, allowing for an energetically favorable (downhill) transfer. In contrast, energy transfer from Nd³⁺ to Ce³⁺ is inefficient, as it would require an energetically uphill process^9,26,65.

To closely evaluate the red emission potential of the fabricated PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses, detailed analysis of the absorption cross section $\:\left({\sigma\:}_{abs.}\right(\lambda\:\left)\right)$, emission cross section ($\:{\sigma\:}_{em.}\left(\lambda\:\right))$, and gain $\:G\left(P,\:\lambda\:\right)\:$cross sections were calculated using Eqs. 20, 21, 22. These parameters provide critical insight into the light absorption and emission capabilities of the materials, as well as their potential for optical amplification—key factors in determining their suitability for laser and photonic applications in the red spectral region

$$\:{\sigma\:}_{abs.}\left(\lambda\:\right)=\frac{2.303\:O.D\:\left(\lambda\:\right)}{t{N}^{{RE}^{3+}}}$$

(20)

$$\:{\sigma\:}_{em.}\left(\lambda\:\right)={\sigma\:}_{abs.}\left(\lambda\:\right)\text{exp}\left[\frac{\left(\epsilon\:-\raisebox{1ex}{$hc$}\!\left/\:\!\raisebox{-1ex}{$\lambda\:$}\right.\right)}{kT}\right]$$

(21)

$$\:G\left(\lambda\:,\:P\right)=P\times\:{\sigma\:}_{em.}\left(\lambda\:\right)-\left(1-P\right)\times\:{\sigma\:}_{abs.}\left(\lambda\:\right)$$

(22)

where, $\:O.D\:\left(\lambda\:\right)$ is the optical density at wavelength $\:\lambda\:$, $\:t$ is glass samples thickness, and $\:{N}^{{RE}^{3+}}$ denotes the concentration of the studied rare-earth ions (here Ce³⁺ and Nd³⁺ ions). $\:\epsilon\:$ represents the excitation energy for Ce³⁺: ²F_5/2 →5d₁ (16155 cm⁻¹), Ce³⁺: ²F_7/2→5d₁ (15649 cm⁻¹), Nd³⁺: ⁴I_9/2 →²H_11/2 (16223 cm⁻¹), and Nd³⁺: ⁴I_9/2 →⁴F_9/2 (14771 cm⁻¹). $\:h$ and $\:k$ are the Plank and Boltzmann constants, respectively, and T is the ambient temperature. P represents the population inversion, where P is in the range of 0 to 1.

Figure 7 illustrates the absorption and emission cross sections of the PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses. As shown in Fig. 7a, the PZBBNd³⁺ glass exhibits two prominent absorption peaks with cross section values of $\:8.319\times10^{-19}$ cm² at 616 nm and $\:1.7482\times10^{-19}$ cm² at 677 nm. These related to the Nd³⁺: ⁴I_9/2 →²H_11/2 and ⁴I_9/2→ ⁴F_9/2 transitions, respectively. The PZBBCe³⁺ glass shows two absorption bands centered at 619 nm and 639 nm, with cross sections of $\:8.882\times10^{-19}$ cm² and $\:1.1328\times10^{-19}$ cm², respectively. These are attributed to Ce³⁺: ²F_5/2→5d₁ and ²F_7/2→5d₁ transitions. The relatively broad nature of these bands is characteristic of 4f →5d transitions in Ce³⁺, which are highly sensitive to the local crystal field environment provided by the glass matrix. In the PZBBCe³⁺-Nd³⁺ glass, a single absorption peak is observed at 626 nm with a cross section of $\:4.9\times10^{-20}$ cm² (inset of Fig. 7a). This feature likely arises from overlapping contributions of both the Nd³⁺: ⁴I_9/2 →²H_11/2 and Ce³⁺: ²F_5/2→5d₁ transitions, indicating potential spectral overlap and interaction between the dopants. The PZBBCe³⁺ glass exhibits broad emission bands near 619 nm and 639 nm, characteristic of the Ce³⁺: 5 d → 4f transitions, as shown in Fig. 7b. These broad emissions in the red spectral region confirm that Ce³⁺ can function as an efficient red emitting center when excited at higher energies (typically in the UV range). The spectral broadness also suggests a significant impact of the host glass on the Ce³⁺ emission characteristics. For the PZBBNd³⁺ glass, two emission peaks are detected at 616 nm and 677 nm, as shown in Fig. 7c, corresponding to radiative transitions from higher excited states of Nd³⁺ to lower-energy states, particularly ²H_11/2 →⁴I_9/2 and ⁴F_9/2 →⁴I_9/2, respectively. The strong emission around 677 nm is particularly noteworthy for its relevance to red emitting photonic applications. The PZBBCe³⁺-Nd³⁺ glass displays a broad emission band around 626 nm (Fig. 7d), overlapping with the emission features of both singly doped Ce³⁺ and Nd³⁺ glasses. This suggests simultaneous luminescence from both dopants. The observed spectral features suggest potential energy transfer interactions between Ce³⁺ and Nd³⁺ ions, enhancing or modifying the overall emission characteristics.

Fig. 7

(a) Absorption cross section ($\:{\sigma\:}_{abs.})$ of the PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses, and emission cross section ($\:{\sigma}_{em.})$ of (b) PZBBCe³⁺, (c) PZBBNd³⁺, and (d) PZBBCe³⁺-Nd³⁺ glasses.

Figure 8 presents the gain cross section spectra of PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses, evaluated across different population inversion levels (P). For PZBBCe³⁺, the gain cross section is negative (indicative of absorption) at both 619 and 639 nm at P = 0. As P increases, the gain becomes positive around 619 and 639 nm, corresponding to Ce³⁺ emission bands. At P = 1, significant gain is observed, demonstrating the suitability of Ce³⁺ for broadband red luminescence. In PZBBNd³⁺, gain profiles show broad and sharp peaks at 616 and 677 nm, respectively. These match Nd³⁺ emission transitions and become increasingly positive with higher P, suggesting strong potential for red emission action at discrete red wavelengths, suitable for narrow-linewidth photoluminescence applications. The PZBBCe³⁺-Nd³⁺ glass exhibits a complex gain profile combining features of both ions. A broad gain region centered around 626 nm is primarily attributed to Ce³⁺, with narrower peaks overlaying from Nd³⁺. As P increases, gain enhancement suggests the possibility of dual-ion emission or energy transfer-driven Nd³⁺ dominance, depending on excitation conditions and population dynamics. At a population inversion level of P = 0.8, all studied glasses exhibit a noticeable dip, turning negative, in the gain cross-section, as shown in Fig. 8. This indicates net absorption rather than gain and points to a complex interplay of underlying mechanisms affecting Ce³⁺ and Nd³⁺ ions. This trend is primarily attributed to excited state absorption (ESA), where a significant fraction of Ce³⁺ and Nd³⁺ ions in the excited state may absorb additional photons to reach higher energy levels. It can suppress the net gain when ESA is strong at specific wavelengths, such as around 625 nm. Furthermore, changes in population distribution among Stark sublevels with varying P can alter transition probabilities, impacting the gain spectrum. Interactions between Ce³⁺ and Nd³⁺ ions and the PZBB glass matrix may also enhance absorption under partial inversion, particularly in the inter-peak region. Overall, the observed non-monotonic gain behavior at P = 0.8 reflects the combined effects of ESA, incomplete inversion, Stark sublevel dynamics, and host matrix influence.

Finally, all three glasses demonstrate potential for red emission under adequate population inversion. Ce³⁺ provides broad gain bandwidth, ideal for tunable sources, while Nd³⁺ offers spectrally selective gain. The PZBBCe³⁺-Nd³⁺ glass presents opportunities for tailored emission behavior through ion interaction and energy transfer mechanisms.

Fig. 8

Gain cross-section profiles of (a) PZBBCe³⁺, (b) PZBBNd³⁺, and (c) PZBBCe³⁺-Nd³⁺ glasses.

Conclusion

In summary, three developed glasses containing 1 mol% of Ce³⁺, Nd³⁺, or Ce³⁺/Nd³⁺ ions as red emission (PZBBCe³⁺, PZBBNd³⁺, or PZBBCe³⁺-Nd³⁺) were fabricated and characterized. The proposed Ce³⁺, Nd³⁺, or Ce³⁺/Nd³⁺ ions were incorporated into a host glass with a chemical composition of 50P₂O₅−20ZnO-20Bi₂O₃−10BaO (PZBB). In terms of thermal stability, all the examined glasses demonstrated notable thermal stability. The elastic moduli—Young’s, bulk, shear, and longitudinal modulus—as well as hardness, slightly improved due to the diffusion of the Ce³⁺, Nd³⁺, or Ce³⁺/Nd³⁺ ions into the PZBB host network. In terms of optical properties, the incorporation of Ce³⁺, Nd³⁺, or Ce³⁺/Nd³⁺ ions into the glass network was confirmed by their distinct absorption bands in the UV-Vis-NIR region. The developed PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses exhibited high thermal stability and elasticity. Upon excitation at 308 nm, the fabricated PZBBCe³⁺ glass has two strong characteristic red emission peaks at 619 and 639 nm, whereas the PZBBNd³⁺ has a highly intense red peak at 677 nm and a lower peak at 616 nm. On the other hand, PZBBCe³⁺-Nd³⁺ exhibited a single red peak at 626 nm. Comprehensive oscillator strength, Judd–Ofelt, and gain cross section analyses demonstrate the potential of developed PZBBCe³⁺, PZBBNd³⁺, and PZBBCe³⁺-Nd³⁺ glasses for red emitting photonic applications. The PZBBCe³⁺-Nd³⁺ glass enables broadband, dual-ion emission with possible Ce³⁺→ Nd³⁺energy transfer, while the singly doped glasses offer broad (Ce³⁺) or narrow (Nd³⁺) gain—ideal for tunable red light sources. Therefore, the suitable mechanical and thermal properties, combined with highly efficient emissions in the red region of the studied PZBBCe³⁺, PZBBNd³⁺, or PZBBCe³⁺-Nd³⁺ glasses, make them strong candidates for use in optoelectronic devices such as red lasers, tunable light sources, and amplifiers. However, further investigations on emission lifetime and quantum efficiency should be conducted in the future to explore to fully evaluate photoluminescence performance.