CFD-based aerodynamic optimization of the fairing for a high-speed elevator

Abstract

This paper presents a computational fluid dynamics (CFD) analysis of the external flow field of a high-speed elevator car. A fairing with a varying cross-section is designed to improve the aerodynamics of the high-speed elevator car. An optimization study of the fairing is performed by combining the parametric optimization method and CFD. The cross-section of the fairing is parameterized by NURBS curves; then, the Latin experimental design method is used to generate test sample points, a mathematical model is formulated utilizing the response surface model approximation, and global optimization is conducted through the application of a multi-island genetic algorithm. The results show that by empirically adding the fairing, the aerodynamic resistance of the high-speed elevator car can be significantly reduced by 36.6% compared to that of the original model; moreover, by optimizing the designed fairing through modern optimization methods, the aerodynamic resistance of the high-speed elevator car can be further reduced by 39.3% compared to that of the original model. The structural parameters of the fairing have a significant impact on the aerodynamic performance of the high-speed elevator.

Introduction

During the operation of a high-speed elevator, airflow pulsation changes, variations in acoustic pressure inside the elevator car, and the piston effect, among other factors, can generate significant noise and vibrations. These disturbances can impact the elevator’s operational safety and stability. Therefore, it is essential to study the pneumatic characteristics of high-speed elevators^{1,2,3,4,5,6,7}.

Currently, two main research methods are used to characterize elevator aerodynamics. One approach involves obtaining flow field data through experimental measurements, which can be conducted using either real elevator tests or model experiments. Banerjee et al.⁸ studied the inlet flow field of a turbocharger compressor using three-dimensional example image velocimetry to observe the region of flow reversal. Zhang et al.⁹ developed a generalized theoretical model for unsteady airflow and validated it with experimental data from an elevator test tower. However, experimental methods are often constrained by high costs, limited scalability, and challenges in parameter control under realistic operating conditions. Another approach involves numerically simulating the elevator flow field using computational fluid dynamics (CFD) methods. Piston wind is generated when the elevator car travels at a high speed within the narrow and elongated hoistway. This leads to the creation of aerodynamic noise as it interacts with the car enclosure and the hoistway walls. This noise can negatively impact ride comfort. Qiao et al.¹⁰ performed sensitivity analysis of the piston wind in the hoistway of a super high-speed elevator. The analysis proved that when the building code permits, the larger the area of the ventilation holes, the more evident the weakening of the piston wind. Jing et al.¹¹ constructed a multi-parameter generalized model for an ultra-high-speed elevator and implemented a three-dimensional numerical simulation of incompressible airflow within the elevator. The validation of the model and methodology was accomplished via experimental trials and mesh-independent analysis, while the implications of diverse lane structures and vent parameters on aerodynamic forces and lane pressures were meticulously investigated. Recent studies have validated simplified models or empirical designs but lack systematic parameter optimization frameworks. For instance, Zhang et al.^12,13 demonstrated the effectiveness of curved fairings through trial-and-error adjustments, yet their approach relies heavily on designer experience and fails to exploit the full potential of automated optimization. Deng et al.^14,15 used modern optimization coupled with CFD for structural optimization, applied Pareto charts to analyze the effects of variables on the objective function, and obtained the optimal solution by the non-dominated sorting genetic algorithm-II (NSGA-II) method. Zhang et al.¹⁶ created an adaptive optimization method based on digital airfoil deformation and deep learning algorithms to generate airfoils using radial basis function (RBF) interpolation, obtain the response values of each sample from CFD simulations, and construct a deep neural network agent model to optimize the airfoil configuration. Furthermore, cutting-edge techniques such as deep learning-based aerodynamic optimization have shown promise in other domains but remain unexplored in high-speed elevator applications due to the complexity of geometric parameterization and multi-physics coupling. The genetic algorithm, a global optimization search algorithm developed in recent years, is based on Darwinian evolution and Mendelian genetics^17,18,19. It expresses the problem as a population, selects individuals adapted to the environment for copying according to the principle of survival of the fittest, generates a new generation of groups better suited to the environment through two basic operations: crossover and mutation, and finally converges to the optimal individual to find the optimal solution of the problem. The multi-island genetic algorithm, which is an advancement of the traditional genetic algorithm, divides the entire evolutionary population into a number of sub-populations called “islands” and independently performs genetic operations such as selection, crossover, and mutation of the traditional genetic algorithm on each of the islands. The multi-island genetic algorithm periodically randomly selects some individuals to perform “migration” operations and transfers them to other islands. Thereby, the variety within the population can be preserved, thus suppressing the phenomenon of early maturation. Functioning as a pseudo-parallel genetic algorithm, the multi-island genetic algorithm is more effective in identifying the global optimal solution within the optimization landscape. Recent studies have further advanced the understanding of high-speed elevator aerodynamics and optimization techniques. Xie et al.²⁰ proposed a digital twin-driven design framework for elevator fairings, utilizing multi-objective optimization methods such as neighborhood cultivation genetic algorithms (NCGA) to achieve notable reductions in air drag. While this study demonstrated the potential of digital twin technology in optimizing elevator fairing design, further research is needed to elucidate the intricate relationships between geometric parameters and aerodynamic performance, which remains an open challenge in the field. In conclusion, previous studies have primarily relied on experiments to study and improve the aerodynamic characteristics of high-speed elevators. Owing to the complexity of the factors involved in aerodynamic performance, the geometrical parameters of the elevator are not a function of its aerodynamic characteristics, and the mechanism of the influence of these geometrical parameters on aerodynamic performance is not fully understood. Such modern optimization algorithms have been applied in the field of aerodynamics but not yet in the field of high-speed elevators. Therefore, a critical gap exists in the integration of parametric design, advanced optimization algorithms, and high-fidelity CFD simulations for high-speed elevators.

While modern CFD-driven optimization methods are well-established in aerospace and automotive domains, their adaptation to high-speed elevators remains hindered by three critical barriers: (1) the confined hoistway environment amplifies wall-bounded flow complexities, (2) geometric constraints limit parametric freedom, and (3) traditional algorithms struggle with high-dimensional, nonlinear design spaces. To address these challenges, this study introduces a novel framework integrating NURBS parameterization, LHS sampling, and an enhanced MIGA. This approach not only adapts proven methodologies to elevator-specific conditions but also advances algorithmic efficiency and industrial applicability.

Methods

Parametric modeling

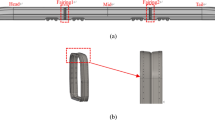
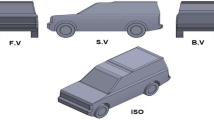
In this study, a high-speed elevator model with a machine room was considered as the research object, and NURBS (Non-Uniform Rational B-Splines) curves were applied to parametrically model the car fairing, essentially to study the effect of the fairing surface shape on the aerodynamic characteristics of the car. To reduce the amount of three-dimensional flow field calculation, the model was moderately simplified by ignoring the door machine, wire rope, spring, guide rail, and other components. Figure 1 (a) shows the simulation model of a high-speed elevator with car dimensions of 1.80 m x 1.78 m and hoistway dimensions of 2.20 m x 2.30 m.

Fig. 1

Elevator model.

For low-speed elevators, the Reynolds number is very low, and the airflow has little effect on the elevator operation. However, for high-speed elevators, the direct impact of the high-speed airflow on the top plane of the elevator produces a turbulent airflow. Owing to the turbulence of the airflow and the existence of some vortex holes, the airflow noise generated by the high-speed elevator increases abnormally. Therefore, the design of the fairing cover on the windward side of the high-speed elevator car can change the aerodynamic characteristics of the car, as illustrated in Fig. 1 (d) (e). The fairing model features a streamlined cross-section, with a thickness of 3 mm, a length of 1.80 m, a width of 1.78 m, and a height of 0.96 m, and its cross-sectional area was approximately 1.33m². These dimensions were determined based on factors such as the space constraints of the elevator shaft, structural strength, weight, and cost.

Conventionally, the improvement in the aerodynamic characteristics relies heavily on the experience of the designer, and the design-to-evaluate-redesign approach is inefficient and ineffective. Parametric modeling of the fairing enables the geometry of the fairing to be driven by design variables that control the fairing free deformation. A ventilation fan, traction components, and other components had to be installed on the top of the elevator, the top of the fairing was set horizontally with a height of 0.96 m, the cross-section was symmetrical, and the geometry of the windward surface was parameterized by applying NURBS curves.

The design variables are the coordinates of the NURBS control points defining the fairing profile. As shown in Fig. 1 (b), 7 control points (Y₁ - Y₇) were parameterized to adjust the curvature of the leading and trailing edges. The horizontal (x) takes empirical values, and the vertical (y) coordinates of these points were allowed to vary within predefined ranges, ensuring geometric feasibility within the elevator shaft dimensions.

The NURBS technique effectively captures conic sections and basic analytical surfaces, offering a consistent mathematical representation for curves and surfaces in the geometric definition of industrial products. At present, the NURBS method is extensively applied in geometric modeling across various sectors, including automotive, aerospace, and maritime industries²¹. The NURBS curve of degree K is expressed as a piecewise rational polynomial vector function. The parameter $\:{\omega\:}_{i}$ in the equation is the control point weight factor, which is associated with each of the n + 1 control points P_i (i = 0,1,2,.,n). The control points P_i (i = 0,1,2,.,n) are sequentially connected to form a control polygon. $\:{B}_{\begin{array}{c}i,k\end{array}}\left(u\right)$ is the kth normed B-spline basis function determined by the node vector $\:U=\left\{{U}_{0},{U}_{1},{U}_{2}\dots\:\dots\:,{U}_{n+k+1}\right\}$ according to the recursive Eq. (1)^22,23.

$$\:P\left(u\right)=\frac{\sum\:_{i=0}^{n}{\omega\:}_{i}{P}_{k}{B}_{\begin{array}{c}i,k\end{array}}\left(u\right)}{\sum\:_{i=0}^{n}{\omega\:}_{i}{B}_{\begin{array}{c}i,k\end{array}}\left(u\right)}$$

(1)

The two-dimensional contour lines of the fairing cross-section are modeled by fitting a fifth-order quadratic NURBS curve with seven points, and the fitted lines are then subjected to a stretching operation to obtain a parametric model, as shown in Fig. 1 (b) (c)²⁴.

CFD simulation

In the elevator hydrodynamics simulation model for the rectangular computational domain, the inlet and outlet of the computational domain were set to be five times the length of the elevator car, taking into account considerations of simulation efficiency.

To ensure the computational domain size does not artificially constrain flow development, a sensitivity analysis was performed by extending the upstream/downstream lengths.

Case 1

5× car length (original setup): F_D=1900.5 N.

Case 2

10× car length: F_D =1898.2 N (Δ = 0.12%).

Case 3

20× car length: F_D =1897.6 N (Δ = 0.15%).

The negligible variation (≤ 0.15%) confirms that the five domain lengths sufficiently minimizes boundary interference while balancing computational efficiency.

The computational domain was discretized using an unstructured tetrahedral mesh as shown in Fig. 1 (f) (g). To resolve the boundary layer, five prism layers were applied near the fairing and car surfaces, with a first-layer thickness of 0.1 mm and a growth rate of 1.2, ensuring y⁺<5. Local refinement zones were implemented around the fairing edges and the car-hoistway gap to capture flow separation and vortex shedding. The final mesh consisted of 4.7 million cells, balancing computational accuracy and efficiency.

To ensure grid independence, four mesh resolutions were tested:

Coarse mesh: 2.7 million cells, F_D=1927.1 N.

Medium mesh: 4.7 million cells, F_D =1900.5 N.

Refined mesh: 7.2 million cells, F_D =1879.8 N.

Fine mesh: 10.2 million cells, F_D =1878.0 N.

The drag force(N)variation between medium and fine meshes was less than 1.2%, confirming that the medium mesh (4.7 million cells) provided a grid-converged solution.

The basic laws of fluid motion can be described by the Navier–Stokes (N–S) equation, which comprises three parts: Eq. (2) is the continuity equation, Eq. (3) is the momentum equation, and Eq. (4) is the energy Eqs^25,26.

$$\:\frac{\partial\:\rho\:}{\partial\:t}+\frac{\partial\:\left(\rho\:{u}_{j}\right)}{\partial\:{x}_{j}}=0$$

(2)

$$\:\frac{\partial\:\left(\rho\:{u}_{j}\right)}{\partial\:t}+\frac{\partial\:\left(\rho\:{{u}_{i}u}_{j}\right)}{\partial\:{x}_{j}}=-\frac{\partial\:p}{\partial\:{x}_{i}}+\frac{\partial\:\left({{u}_{i}\tau\:}_{ij}\right)}{\partial\:{x}_{j}}$$

(3)

$$\:\frac{\partial\:\left(\rho\:e\right)}{\partial\:t}+\frac{\partial\:\left(\rho\:{u}_{j}h\right)}{\partial\:{x}_{j}}=div\left(kgradT\right)+\frac{\partial\:\left({{u}_{i}\tau\:}_{ij}\right)}{\partial\:{x}_{j}}$$

(4)

where t, ρ, u, and p are the time, density, velocity, and pressure, respectively; $\:{x}_{i}$ are the components of the rectangular coordinates (i = 1, 2, 3); e is the internal energy; k is the heat transfer coefficient; $\:{\tau\:}_{ij}=\mu\:\left(\frac{\partial\:{u}_{i}}{\partial\:{x}_{j}}+\frac{\partial\:{u}_{j}}{\partial\:{x}_{i}}\right)-\frac{2}{3}\mu\:\frac{\partial\:{u}_{k}}{\partial\:{x}_{k}}{\delta\:}_{ij}$ is the viscous stress tensor; µ is the dynamic viscosity of the incompressible fluid, and $\:h=e+\frac{1}{2}{u}^{2}+\frac{P}{\rho\:}$ is the enthalpy.

The Mach number of the air in the elevator hoistway is significantly smaller than 0.3, and the Reynolds number is larger than 4000; therefore, the airflow can be regarded as a non-constant incompressible turbulent motion²⁷. Assuming that the airflow temperature remains constant, Eqs. (2–4) can be simplified into Eqs. (5–6).

$$\:\frac{\partial\:{u}_{j}}{\partial\:{x}_{i}}=0\:\:\:\:\:\:\:\:$$

(5)

$$\:\rho\:\frac{\partial\:\left({u}_{j}\right)}{\partial\:t}+\rho\:\frac{\partial\:\left({{u}_{i}u}_{j}\right)}{\partial\:{x}_{j}}=-\frac{\partial\:p}{\partial\:{x}_{i}}+\frac{\partial\:\left({\tau\:}_{ij}\right)}{\partial\:{x}_{j}}$$

(6)

In this study, large-vortex simulation was used because it combines the characteristics of direct numerical simulation and Reynolds time-averaged equation simulation and divides the vortex motions into large vortex motions, which can be solved directly through simulation, and small vortex motions, which can be solved comprehensively by building, using filters, a pressure-lattice stress model that can be expressed by Eqs. (7–8)²⁸.

$$\:\frac{\partial\:\stackrel{-}{{u}_{j}}}{\partial\:{x}_{j}}=0$$

(7)

$$\:\frac{\partial\:\left(\rho\:\stackrel{-}{{u}_{i}}\right)}{\partial\:t}+\frac{\partial\:\left(\rho\:\stackrel{-}{{u}_{i}}\stackrel{-}{{u}_{j}}\right)}{\partial\:{x}_{j}}=-\frac{{\partial\:}_{p}}{\partial\:{x}_{i}}+\frac{\partial\:\stackrel{-}{{\tau\:}_{ij}}}{\partial\:{x}_{j}}-\frac{\partial\:{\tau\:}_{ij}^{{\prime\:}}}{\partial\:{x}_{j}}$$

(8)

where $\:{\tau\:}_{ij}^{{\prime\:}}$ is the sublattice stress. The vortex viscosity model, which is the most commonly used sublattice stress model, can be expressed by Eq. (9).

$$\:{\tau\:}_{ij}^{{\prime\:}}-\frac{1}{3}{\tau\:}_{kk}{\delta\:}_{ij}=-{u}_{i}{\left(\frac{\partial\:\stackrel{-}{{u}_{i}}}{\partial\:{x}_{j}}+\stackrel{-}{\frac{\partial\:{u}_{j}}{\partial\:{x}_{j}}}\right)}_{ij}$$

(9)

where $\:{u}_{i}$ is the pressure lattice turbulent viscosity coefficient, which must be obtained through the sublattice model.

The simulations were performed using ANSYS Fluent 2021 R1. The solver was set to a pressure-based, transient formulation with the SIMPLE algorithm for pressure-velocity coupling. The spatial discretization of momentum and turbulence equations employed a second-order upwind scheme to minimize numerical diffusion. The SST k-ω turbulence model was selected for its proven capability to accurately resolve near-wall flows, adverse pressure gradients, and flow separation—key phenomena in confined aerodynamic systems like elevator hoistways. Furthermore, the SST k-ω’s sensitivity to streamline curvature and pressure gradients aligns with the complex flow physics induced by the elevator’s streamlined fairing geometry. These advantages are well-documented in studies of wall-bounded, low-Reynolds-number flows, making it the optimal choice for capturing the interplay between turbulence, pressure pulsations, and drag generation in this work¹².

Boundary conditions included a uniform velocity inlet (v = 10 m/s) and a pressure outlet (p = 0 Pa). To model the relative motion between the elevator car and hoistway, the simulation was conducted in the car’s reference frame. The hoistway walls were defined as moving no-slip walls with a velocity of v = −10 m/s (opposite to the car’s direction of motion), while the car surface remained stationary. This approach eliminates the need for dynamic mesh deformation while preserving the relative velocity boundary layer effects. The fluid medium was air (density = 1.225 kg/m³, dynamic viscosity = 1.789 × 10⁻⁵ Pa·s), and the interior space of the hoistway was set to the interior. All simulations were run until residuals for continuity and momentum equations fell below 1 × 10⁻⁴, ensuring convergence.

The car was subjected to air resistance F in the direction of motion, as expressed in Eq. (10):

$$\:F=0.5\rho\:{C}_{d}A{u}^{2}$$

(10)

where C_d is the resistance coefficient, ρ is the air density, A is the reference area, and u is the flow rate of air relative to the car.

Aerodynamic forces were calculated by integrating surface pressure and viscous shear stress over the car and fairing surfaces using ANSYS Fluent’s force reports function. Calculations showed that the original model of the car had an air resistance of 1900.5 N when running at 10 m/s. With the fairing improvement, the air resistance on the car was reduced to 1204.6 N, which corresponds to a reduction of 36.6%. As shown in Fig. 2, a strong turbulence zone was formed at the rear of the car, thus increasing the irregular vibration of the car when traveling at a high speed. Comparing the turbulence energy of the model before and after the improvement, the turbulence at the rear of the car was found to be smaller after adding the fairing than before the improvement, which is conducive to improving the ride quality of the car. From the perspective of pressure gradient and separation control analysis, as shown in Fig. 7 (b), the high-pressure stagnation zone (ΔP = 2494) at the car’s windward surface creates a steep adverse pressure gradient, triggering early boundary layer separation. The improved fairing (Fig. 7 (c)) reduces this pressure differential (ΔP = 1023) by streamlining the leading-edge curvature, which accelerates flow around the car and delays separation.

Fig. 2

Comparison of turbulence kinetic energy.

Optimization model

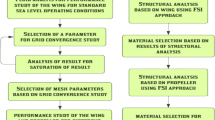
Traditional all-in-one algorithms are time-consuming and laborious when performing a complete multidisciplinary analysis at each iteration, mostly relying on manual experience. Using the parametric optimization method combined with CFD can significantly shorten the design cycle and improve the optimization efficiency²⁹. The optimization framework (Fig. 3) integrates four core modules:

Parametric modeling

NURBS curves define the fairing geometry, enabling smooth deformation controlled by seven design variables (Y₁–Y₇).

Design of experiments (DOE)

Latin Hypercube Sampling generates 70 sample points to uniformly explore the design space.

Surrogate model

A quartic response surface model (RSM) approximates the nonlinear relationship between variables and aerodynamic drag.

Multi-Island genetic algorithm (MIGA)

Ten sub-populations evolve independently, with periodic migration to preserve diversity and avoid premature convergence.

Fig. 3

Optimization flowchart.

The coordinates of the control point P_i (i = 0,1,2,…,n) are fixed in the x-direction, and the y-direction coordinate is the variable $\:{Y}_{i}$.The optimization problem is described as

$$\:Min\:\:f({Y}_{1},{Y}_{2},{Y}_{3}{,Y}_{4}{,Y}_{5}{,Y}_{6}{,Y}_{7})$$

(11)

$$\:s.t.\:\:\:\:{Y}_{1}\in\:\left[\text{1140,1151}\right],\:{Y}_{2}\in\:\left[\text{1076,1116}\right],{Y}_{3}\in\:\left[\text{967,996}\right]$$

$$\:{Y}_{4}\in\:\left[\text{756,768}\right],{Y}_{5}\in\:\left[\text{529,553}\right],{Y}_{6}\in\:\left[\text{329,341}\right],{Y}_{7}\in\:\left[\text{116,128}\right]$$

where $\:f({Y}_{1},{Y}_{2},{Y}_{3}{,Y}_{4}{,Y}_{5}{,Y}_{6}{,Y}_{7})$ denotes the objective function of optimization, i.e., the air drag force of the elevator car; $\:{Y}_{1},{Y}_{2},{Y}_{3}{,Y}_{4}{,Y}_{5}{,Y}_{6}{,Y}_{7}$ denote the design variables. The range of values of Y above is determined according to the basic shape measurements of the fairing, being all in millimeters. The design variable ranges were defined to preserve the fairing’s essential aerodynamic shape while adhering to mechanical and spatial constraints.

Design of experiments (DOE)

Considering the interaction effects between the variables, as well as the effects of averaging and nonlinearity, the DOE was used to obtain sample points³⁰. Different DOE methods produce different optimal estimates but optimize the design in the same direction. The Latin Hypercube Sampling (LHS) method was selected for its ability to uniformly explore the 7-dimensional design space. For each variable (Y₁–Y₇), the feasible range was divided into 70 equal intervals, and one sample was randomly placed within each interval. This stratification ensures that no two samples cluster in the same subregion, minimizing spatial bias and maximizing coverage of variable interactions³¹. The sample size (n = 70) adheres to the statistical rule of thumb (n ≥ 10 × number of variables), which is empirically proven to capture main effects and pairwise interactions in nonlinear systems. To further validate sufficiency, a post-hoc analysis compared the RSM prediction error for n = 70 and n = 100. The mean absolute error increased by only 1.8% (from 2.1 to 2.14%), confirming diminishing returns beyond 70 samples. CFD calculations were performed using the same simulation as for the original model, and 70 sets of response values were obtained.

The interactions between the variables are shown in Fig. 4, which reveals an interaction between all the variables. $\:{Y}_{2}$ and $\:{Y}_{3}$ have a large effect on the objective function, whereas the other variables have a small effect; in terms of the individual variables, the aerodynamic resistance is the smallest within the range of $\:{Y}_{2}$, and it increases with $\:{Y}_{3}$.

Fig. 4

Plot of the main effects for the drag force.

The sensitivity relationships of the design variables to the objective function are shown in Fig. 5. The Pareto plots illustrate the percentage contribution of each term in the model to every response following the fitting of the sample, where blue bars represent a positive effect and red bars denote a negative effect. The interaction of Y2 and Y3 had the largest effect on the objective function; for the individual variables, Y3 had the greatest impact on the objective function, followed by Y2, Y4, and Y6, with Y1 having the lowest sensitivity.

Fig. 5

Pareto plot for response drag.

Approximate surrogate model

Approximate models were used to simulate the response relationship between a set of input and output parameters. Their role was to replace or enhance computationally expensive simulations or analysis software to (1) dramatically improve the efficiency of the analysis task; (2) eliminate the “computational noise” of the simulation software where the input parameters vary gently while the output parameters oscillate violently because computational noise can produce numerous local peaks that can have a significant negative impact on the optimization process; and (3) understand the relationship between the variables and develop empirical relationships for further use in performance prediction and optimization. The methods used to construct approximate models include response surface models (RSM), kriging models, RBF neural network models, and Taylor series models.

Compared to other models, the RSM approximates the functional relationship on a local scale more accurately with fewer trials and presents it in a simple algebraic expression. By selecting an appropriate regression model, complex response relationships can be fitted with strong robustness. For the simulation of the nonlinear space, the higher the order, the higher the accuracy^32,33.

The quartic RSM function is constructed as Eq. (12):

$$\:F\left(y\right)={a}_{0}+\sum\:_{i=1}^{N}{b}_{i}{y}_{i}+\sum\:_{i=1}^{N}{c}_{ii}{{y}_{{i}_{i}}}^{2}\sum\:_{ij(i<j)}{c}_{ij}{y}_{i}{y}_{j}+\sum\:_{i=1}^{N}{d}_{i}{{y}_{{i}_{i}}}^{3}+\sum\:_{i=1}^{N}{e}_{i}{{y}_{{i}_{i}}}^{4}$$

(12)

where $\:F\left(y\right)$ denotes the objective function of optimization, i.e., the aerodynamic resistance; $\:{y}_{i}$ is the set of model inputs; N is the number of model inputs; a–e are the polynomial coefficients.

The RSM approximation is obtained after [(N + 1)(N + 2)/2] + 2 N exact calculations. The approximate relationship between the variables Y2 and Y3 and the objective function is shown in Fig. 6 (a), where the point corresponding to the lowest objective function exists in the yellow area.

The quartic RSM achieved an R² value of 0.963 and an RMSE of 18.7 N (1.5% of mean drag), confirming its reliability for optimization. The scatter plot (Fig. 6 (b)) references the alignment between RSM predictions and CFD results, stating: the quartic RSM demonstrates excellent agreement with CFD simulations, as evidenced by the clustering of sample points near the diagonal in response surface.

Fig. 6

Approximation model.

Results

Optimization based on the approximate model was carried out using the multi-island genetic algorithm, with the sub-population size set to 10, the number of islands set to 10, and the number of generations set to 100. The multi-island genetic algorithm (MIGA) exhibited stable convergence behavior across 100 generations. Sub-population diversity metrics and objective function residuals (< 0.5% after Generation 80) confirmed effective avoidance of local optima. The optimal design was identified at Generation 92, with subsequent iterations showing negligible improvements (< 0.2%). Table 1 summarizes the optimization results. The maximum deviation between the RSM-predicted drag (1119.7 N) and CFD validation (1153.3 N) was 2.9%, primarily attributed to localized flow separation near the fairing’s trailing edge (Y ~ 7 ~ control point), where the quartic RSM underestimated nonlinear pressure gradients. To mitigate this, elite candidates from each MIGA iteration were periodically re-evaluated via CFD, ensuring global convergence despite surrogate model approximations.

The model optimized using modern optimization algorithms reduced the drag value by 5.6% compared to the previous empirical improvement and by 39.3% compared to the original model.

Table 1 Optimization results.

In Fig. 7 (a), the dashed line shows the improved model without optimization, and the solid line shows the optimized model. The optimized model exhibits a greater change in curvature at the top, and the airflow can be directed to the sides faster.

As shown in Fig. 7 (b) (c) (d), compared to that of the original model, the positive pressure area on the windward side of the improved model is significantly weakened. Streamline patterns on the longitudinal symmetry plane (X-Z plane at Y = 0) reveal that the original model exhibits significant airflow separation at the car’s top edge (Fig. 7(a)), whereas the optimized model demonstrates smoother flow redirection (Fig. 7(b)). In comparison to the previous optimization, the optimization of the fairing further decreases the positive pressure region at the top of the car while increasing the negative pressure zone at the rear. As a result, the optimized model further decreases the aerodynamic resistance encountered by the car during operation.

Fig. 7

Model comparison.

Discussion

Aerodynamic performance improvements

High-speed elevator cars are subjected to airflow during high-speed operation, which affects their stability. The elevator car’s air resistance can be effectively improved at high speeds by adding a fairing. The optimized fairing reduced aerodynamic drag by 39.3% compared to the original model. These improvements correlate with weakened stagnation pressure at the car’s leading edge and suppressed wake vorticity, as evidenced by the streamlined flow patterns in the optimized design.

Flow physics underlying drag reduction

Three synergistic mechanisms drive the observed performance gains:

Flow field Redirection

The optimized model exhibits a more pronounced curvature at the top, enabling faster redirection of airflow to the sides. This design minimizes direct impact on the car’s windward surface, reducing flow separation and turbulence generation.

Pressure distribution

The addition of the fairing in the improved model reduced the front-rear pressure differential by 59.0% (from 2494 Pa to 1023 Pa). Further optimization of the fairing’s leading-edge curvature decreased the pressure differential by an additional 4.4% (from 1023 Pa to 980 Pa). The weakened positive pressure region on the windward side and enhanced negative pressure zone at the rear contribute to a smoother airflow transition, significantly lowering the car’s traveling resistance.

Wake Vortex structure and turbulent kinetic energy (TKE)

The original model exhibited large-scale vortices extending downstream, which were significantly reduced in the improved model and further minimized in the optimized model. Additionally, the peak TKE in the wake decreased by 27.0% (from 73.99 m²/s² to 54.02 m²/s²), indicating suppressed flow unsteadiness and reduced energy dissipation.

Reduction bridging optimization and industrial application

This study improved the design of a high-speed elevator and verified, through CFD simulation, that the addition of a fairing can effectively reduce the aerodynamic resistance when the car is running. A parametric model of the fairing was first developed to obtain the optimal geometric parameters of the fairing. Next, a modern optimization algorithm was applied to construct an approximate model that describes the relationship between the fairing parameter variables and aerodynamic resistance. Finally, the optimization results were achieved through numerical optimization. The proposed framework demonstrates superior performance in confined flow optimization, achieving a significantly surpassing prior empirical designs. Furthermore, the NURBS parameterization enables precise control of multi-curvature profiles, a capability absent in conventional B-spline methods.

Limitations and future work

While the current study focuses on drag reduction, future research should:

• (1) Validate the optimized design through wind tunnel or elevator test tower experiments.

• (2) Incorporate multi-objective optimization considering vibration, noise, and manufacturing costs.

• (3) Explore real-time adaptive control of fairing geometry under varying operational conditions.

These advancements will bridge the gap between computational optimization and industrial implementation.