Scrutinizing the applicability of blockchain in the sustainability of supply chains using an intelligent fuzzy multi criteria decision making

Abstract

Blockchain technology is a decentralized method of securely storing information in blocks. Over the past few decades, sustainability has gained importance and been shown to be a crucial component in building robust supply chains. Manufacturers and suppliers are pressured to become more globally sustainable by customers who want their products verified for sustainability. Furthermore, problems with social sustainability are becoming more complex. Multi-criteria decision-making (MCDM) is the best tool for addressing this issue. In this article, we aimed to propose a combined compromise solution (CoCoSo) method for ranking blockchain platform selection using spherical fuzzy set (SFS) information. SFS is a well-known framework that provides greater freedom to decision-makers and better reliability than intuitionistic fuzzy sets, Pythagorean fuzzy sets, q-rung ortho-pair fuzzy sets, and picture fuzzy set-based frameworks. The CoCoSo approach under the SFS framework is a renowned tool for complicated decision-making problems. In this method, we consider both linear and non-linear correlations among criteria; the technique aims to give decision-makers a more comprehensive assessment of the alternatives. In the MCDM field, the idea of a power aggregation operator (PAO) is a valuable tool for investigating the weightage of alternatives. We also introduce Sugeno Weber tnorm (TN) and tconorm (TCN) operations under the SFS framework. MCDM Sciences utilizes The Sugeno-Weber operations because it provides a solution for managing ambiguous yet unclear information. The approach enables users to mix diverse inputs through a versatile mechanism that proves valuable for selecting from multiple factors. The cartel theme of this article is to construct a new family of aggregation operators (AOs) called spherical fuzzy (SF) Sugeno Weber power weighted averaging (SFSWPWA) and SF Sugeno Weber power weighted geometric (SFSWPWG) operators, including investigation of some fundamental axioms of AOs. The MCDM algorithm for the CoCoSo method will also be constructed, and the SFSWPWA and SFSWPWG operators will be established. We solve a real-life numerical problem for selecting the best blockchain platform using diagnosed approaches. In the numerical example, we rank blockchain platforms like Hyperledger Fabric, Ethereum, IBM Food Trust, and VeChain. Applying the proposed CoCoSo method, SFSWPWA and SFSWPWG operators “Ethereum” are the best options. The proposed methodologies also apply in real-life Sanrio’s where decision-making is involved. To check the applicability of the developed technique, we made a comparison with existing approaches such as interval-valued intuitionistic fuzzy Heronian mean AOs, Pythagorean fuzzy Hamy mean AO, complex q-rung ortho-pair fuzzy Aczel Alsina AOs, and q-rung ortho-pair fuzzy Sugeno-Weber AOs. These discussed AOs are unable to handle SFS-based information. So, we concluded that the suggested framework is more reliable and superior to other discussed environments due to the presence of abstinence grade. Robust conclusions are given in the end.

Introduction

Before the discovery of fuzzy set theory, classical set theory was regarded as a renowned topic in decision-making science. There were just two choices: $"0"$ and $"1"$. When an element is a part of a set, the outcome is $1$. Conversely, the result is $"0"$ if a component is not a part of a set. The classical set theory is a well-recognized tool for assessing MCDM problems related to engineering, healthcare, business, management, public policies, and environmental sciences.

A brief introduction to fuzzy sets and their corresponding extensions

The information about whether an element fully or partially belongs to a set cannot be obtained from conventional set theory due to its narrow scope. To overcome this gap, Zadeh¹ established the thought of fuzzy set (FS) theory with the addition of truth grade (TG) is $\text{"}{\text{J}}\text{"}$ under the range of $\left[0, 1\right]$ that is ${\text{J}} \in \left[ {0,{ }1} \right]$. This concept got more attention than previous approaches. It is considered a powerful tool for the assessment of decision-making problems. However, with advancements in mathematics, this concept has failed to investigate problems involving false grade (FG)"Π."To fill this shortcoming, Atanassov² stabilized the theory of intuitionistic fuzzy set (IFS) theory with the addition of FG under the range of closed interval $\left[0, 1\right]$. It also satisfies the condition $0\le {\text{J}}\text{+}\Pi \le {1}$ where ${\text{J}} \in \left[ {0,{ }1} \right]$, and $\Pi \in \left[ {0, 1} \right]$. It is a more suitable and reliable approach than ordinary FS due to the presence of FG. Many researchers defined different operational laws based on the IFS, such as the IFS base Sugeno-Weber operation defined by³ and the Hamacher operations for IFS-based information developed by⁴. However, for many complicated situations, the scope of IFS is limited. For example, when we take ${\text{J}}\text{=0.6}$ and $\Pi = \text{0} \text{.5,}$ then the sum of ${\text{J}}$ and $\Pi$ is exceeded by the range of $\left[0, 1\right]$, which is a violation of the fuzzy set theory. In this critical situation, data scientists and mathematicians must develop new concepts to overcome this problem. In this crucial situation, Yager⁵ proposed a new framework known as Pythagorean fuzzy set (PyFS) by taking the square on TG and FG, such as $0\le {\mathcal{J}}^{2}\text{+}{\Pi }^{2}\le {1}$. This generalized tool format of IFS. The idea of PyFS is considered a better framework than IFS due to the extensive range of TG and FG under the range of closed interval $\left[0, 1\right]$. Some literature review based on PyFS framework is discussed in following references^6,7,8,9,10. Later on, for the assessment of a wide range of data when, we take ${\text{J}}\text{=0.81}$ and $\Pi \text{=0.51,}$ where the concept of PyFS failed to aggregate information. To address this issue, Yager⁶ proposed the theory of q-rung orthopair FS (q-ROFS) by taking the qth power on TG and FG such as $0\le {\mathcal{J}}^{q}\text{+}{\Pi }^{q}\le {1}$, where q is the positive integer. The thought of q-ROFS is a generalization of PyFS by extending the range from square to ${q}^{th}$ $\left(q\in {Z}^{+}\right)$. All problem decision-making problems are unable to be handled with the help of FS, IFS, PyFS, and q-ROFS, while abstinence grade (AG) $\text{\rm I}\in \left[0, 1\right]$ is involved in many decision-making problems. For this, Cuong⁷ developed the theory of picture FS (PFS) with the addition of AG along with TG and FG under the range of interval $\left[0, 1\right]$ such as $0\le \mathcal{J}\text{+}\text{\rm I}\text{+}\Pi \le {1}$.

For many complicated decision-making problems, the concept of PFS fails, such as when we take ${\text{J}}\text{=0.61}$, $\text{\rm I}=0.14$ and $\Pi \text{=0.55;}$ their sum exceeds the range $\left[0, 1\right]$. In this situation, it is necessary to define a new framework for assessing complex data. Mahmood et al.⁸ proposed the idea of SFS by making some amendments in the PFS framework by taking square on $0\le {\mathcal{J}}^{2}\text{+}{\text{\rm I}}^{2}\text{+}{\Pi }^{2}\le {1}$, where ${\mathcal{J}}^{2}\in \left[0, 1\right]$, ${\text{\rm I}}^{2}\in \left[0, 1\right]$, and ${\Pi }^{2} \in \left[ {0,{ }1} \right]$. Many mathematicians worked a lot on this novel approach for the solution of MCDM problems, such as the idea of the CoCoSo approach-based FS framework discussed by Deveci et al.⁹ and the PFS environment-based CoCoSo approach for precise assessment of decision-making problems discussed by Qiyas et al.¹⁰. The thought of the CoCoSo method based on the Fermatean FS provided by Dhruva et al.¹¹. Qiyas et al.¹⁰ proposed a decision support system based on the CoCoSo method. The CoCoSo method investigation of quality of deployment using SF values (SFVs) presented by Xu et al.¹² and Kieu et al.¹³ proposed the methodology for the assessment of central location using CoCoSo and SFS information. The investigation of Logistic autonomous vehicles using an SFS-based environment offered by Bonab et al.¹⁴ and the extended linguistic copula power AOs discussed by¹⁵. Figure 1 depicts the development from FS to SFS.

Fig. 1

Shows the development of FS to SFS.

CoCoSo approach and literature review

In decision-making sciences, ranking multiple alternatives based on defined characteristics is always an interesting topic for researchers and data scientists. In this regard, many scholars presented approaches like EDAS, VICOR, TODIM, PROMETHWEE, etc. The CoCoSo approach is a well-known tool for complicated problems in the decision-making sciences, providing a deep examination of various choices based on multiple attributes. The CoCoSo method was introduced by Yazdani et al.¹⁶. The main objective of this method is to address the limitation of MCDM problems dealing with fuzzy and uncertain information. By considering both linear and non-linear correlations among criteria, the technique aims to give decision-makers a more comprehensive assessment of the options. The CoCoSo method is used in various decision-making fields, such as economics, management, and engineering. Many mathematicians worked a lot using this crucial approach, such as the application of the CoCoSo method for insurance policy selection presented by Joshi¹⁷ and the assessment of site selection for floating offshore wind farm in Norway using the CoCoSo approach under the q-ROFS framework explored by Deveci et al.⁹. Nie¹⁸ proposed the CoCoSo approach using the IFS structure to solve group decision-making problems. An efficient CRITIC- CoCoSo approach using the PFS framework for supplier selection problem, discussed by Razzaq et al.¹⁹. The solution to urban transportation problems is based on the CoCoSo approach using the fuzzy ZE-Number framework discussed by Haseli et al.²⁰.

Some features of the CoCoSo approach

The CoCoSo approach is an efficient and organized technique for multi-critical decision-making problems. The following are some noteworthy benefits of the CoCoSo method:

Hybrid method

The CoCoSo method combines the weighted product model (WPM), weighted sum model (WSM), and logarithmic multiplicative model to reduce the chances of error and provide freedom to the decision maker to assess complex problems.

Flexibility

The CoCoSo approach is a valuable and efficient method for the evaluation of complicated MCDM problems related to business issues and management problems, as well as the.

Efficiency and simplicity

The CoCoSo is accessible for decision-makers since it combines several methodologies while maintaining a clear and understandable mathematical process. The CoCoSo approach is computationally efficient even for large and complicated SFS-based information.

Robustness

The system efficiently processes subjective and objective data, and it can link up with environments that deal with uncertainty, such as SFS and other fuzzy frameworks.

In the past, many data analyses developed many CoCoSo approaches using different fuzzy frameworks, such as the CoCoSo approach for the assessment of fuzzy information using IFS-based data for group decision-making presented by Nie¹⁸ and the application of the CoCoSo approach for the evaluation of teaching performance in sports colleges and universities presented by Li and Wen²¹. Zhang and Wei²² presented the CoCoSo and CRITIC approach for the location selection of charging stations for electric vehicles and advancement-based country ranking using the CoCoSo algorithm developed by Nişel²³. Dhruva et al.¹¹ proposed the CoCoSo approach for selecting cloud vendors for healthcare centers using fuzzy information.

Aggregation operators and triangular norm and triangular conorm operations

Yager gives the thought of PAOs²⁴. This is a crucial tool in decision-making science, which reduces the chances of error in aggregated outcomes. It has a keynote feature that combines each alternative with an attribute to evaluate the weightage of alternatives. The role of PAOs in decision-making science is vital. Multiple mathematicians and data scientists worked extensively in decision-making and presented numerous AOs to assess fuzzy data under different environments. For example, the concept of PAOs under q-ROFS is provided by Khan et al.²⁵, and the idea of PAOs under the SFS framework is discussed by Ali²⁶. The AOs for investigation of ventilation optimization in pharmaceutical rooms using the entropy weight method discussed by Wu and Li²⁷. The entropy method-based AOs for evaluation of evolution law and life prediction problems presented by Jiang et al.²⁸.

In decision-making sciences and statistical measurements, Menger²⁹ proposed the thought of the triangle norm. He also suggested some notable characteristics that expand the use of TN and TCN in statistical analysis. The probabilistic product TN and probabilistic sum TCN for the IFS framework were established by Xia et al.³⁰, and the generalization of the nilpotent TN with a few unique features was discussed by Sugen³¹. Weber³² investigated the asymptotic member’s product and drastic nilpotent TN product. Eventually, Sugeno-Weber TCN and TN are a mixture of the two concepts, and they are reliable and offer a versatile setting for accurately expressing the uncertainties of human ideas. Hwang et al.³³ investigated the IFS system based on Sugeno-Weber TN and TCN’s operations and similarity measures, and Sarkar et al.³⁴ developed the Sugeno-Weber TN and TCN operations for hypersoft t-SFS.

Problem questions and literature review

Before the invention of blockchain, data storage could be presented in a centralized way, but after the discovery of blockchain, data is stored in a decentralized manner. The major problem is that the real-time information is not updated in the centralized data strategy system, and finding the desired information is difficult. The idea of blockchain offers ease of seeing information from blocks of data. There are many types of blockchain systems available in the modern age. So, selecting the best blockchain system for the supply chain is challenging. This article aims to investigate four blockchains, Hyperledger Fabric, Ethereum, IBM Food Trust, and VeChain, used in the supply chain. Also, we made a comprehensive assessment of these discussed blockchains based on the following attributes: environmental impact, transparency and traceability, cost efficiency, scalability, and flexibility. We proposed the CoCoSo method and SFSWPWA and SFSWPWG operators using SFS information.

A literature review on the significance of blockchain is discussed as follows: In the past, many mathematicians proposed multiple approaches using different fuzzy frameworks to assess the best blockchain system. Such as evaluating blockchain implementation for a smooth supply chain based on fuzzy information discussed by Dehshiri and Amiri³⁵ and a digital supply chain partner selection using spherical fuzzy information explored by Gao et al.³⁶. A secure, intelligent, fuzzy blockchain system for the detection of IOT network was introduced by Yazdi Nejad et al.³⁷, and an integrated ISM-fuzzy and ANP-fuzzy approach for the selection of a sustainable supply chain was developed by Yadav and Singh³⁸. The hesitant fuzzy framework-based blockchain system provided by Çolak et al.³⁹. The risk analysis in a digital supply chain transformation system using the hybrid ISM-MICMAC method was discussed by Hasani et al.⁴⁰. The evaluation of factors affecting blockchain using prioritized operators for MCDM issues discussed by Seifi et al.⁴¹ and the viability of blockchain technology using the MCDM approach under the fuzzy theory framework provided by Babaei et al.⁴². The assessment of the supply chain of gas and oil at the industrial level using the fuzzy logic discussed by Mehdiabadi et al.⁴³ and sustainable supplier selection for food chains using fuzzy set base EDAS approach offered by Tufan and Ulutaş⁴⁴. The blockchain technology section using the using MCDM approach provided by Çodur and Erkayman⁴⁵.

The MCDM is a systematic approach to selecting the best blockchain system, considering multiple attributes, and enables decision experts to rank the many types of blockchains. There are many different features of blockchain systems, and choosing the best one for a given use case necessitates weighing organizational, financial, and technical considerations. The MCDM approaches offer a structure for handling these complex problems and facilitate the decision-maker.

Literature review on MCDM discussed as follows: In the past era, many mathematicians and data analysts worked a lot to investigate the blockchain systems for supply chain sustainability by using fuzzy set theory; for example, the assessment of blockchain performance using Aczel Alsina operations is discussed by Lei et al.⁴⁶, and the selection of blockchain technology using MCDM method under fuzzy environment discussed by Gardas et al.⁴⁷. Liu et al. proposed the TOPSIS method using fuzzy logic techniques to select the best service provider for the blockchain system. Andreoulaki et al.⁴⁸ developed the MCDM technique to evaluate energy sector blockchain selection barriers. Durán et al.⁴⁹ diagnosed the MCDM theory for Leveraging blockchain systems for maritime port supply. Dehshiri et al.⁵⁰ proposed the blockchain system to assess the reduction of renewable energy risk sources by applying the MCDM methodologies. An FS-based MCDM method for selecting the best blockchain system was developed by Liang et al.⁵¹, and the selection of healthcare blockchain suppliers using the MCDM approach was discussed by Mohamed et al.⁵². Suitable place selection for decomposing medical waste using SFVs is based on the information given by Ghoushchi et al.⁵³. Haseli et al.⁵⁴ provide climate-resilient land-use transport projects based on fuzzy ZE-number for decision-making problems and the solution of MCDM problems related to digital transformation technologies for sustainable supply chains offered by Hasani and Haseli⁵⁵. The investigation of MCDM problems using Bonferroni operators discussed by Hadzikadunic et al.⁵⁶ and the enhanced MCDM models based on the max AOs for assessment of green supply selection discussed by Riaz and Farid⁵⁷. The MCDM model for selecting a road map for the public was provided by Tamer et al.⁵⁸. The performance measurement of the decentralized digital blockchain system using the MCDM approach offered by Kassen⁵⁹ and the application of the blockchain system for assessment of social production logistic system selection discussed by Zhang et al.⁶⁰.

Research gap objectives of the proposed theory

In the past, many mathematicians proposed several methods to investigate fuzzy information under decision-making sciences. For example, the assessment of decision-making problems using the complex hesitant intuitionistic fuzzy set discussed by Ahmed et al.⁶¹ and the modern decision-making approach based on the confidence level complex polytopic AOs offered by Rahman and Muhammad⁶². However, many developed mechanisms have failed to aggregate SFVs-based details due to operational laws and framework limitations. For example, IFS, PyFS, and q-ROFS have no concept of abstinence degree. Hence, the SFS is a better format for assessing fuzzy information than IFS, PyFS, and q-ROFS. So, there is a need to overcome this limitation. These discussed environments are only based on the TG and FG under the range of closed interval $\left[0, 1\right]$. Moreover, there is a huge amount of information during the aggregation procedure. We aim to define new techniques to handle complicated information in which IFS, PyFS, and q-ROFS failed. The thought of cognitive decision-making science is based on FS theory concepts discussed by Yuan et al.⁶³ and the autonomous vehicle system for cyber-attacks based on FS theory proposed by Lian et al.⁶⁴.

This proposed methodology aims to present and express human thought precisely using the CoCoSo method, SFSWPWA, and SFSWPWG operators under the SFS framework. The present approach is more reliable and trustworthy than the existing methodology because we proposed the CoCoSo method and SFSWPWA and SFSWPWG operators in the same place for MCDM problems, including detailed algorithms of both approaches. Some more significant aspects are discussed as follows:

• i. For complicated MCDM problems, the CoCoSo method and proposed SFSWPWA and SFSWPWG operators are suitable approaches under the SFS framework, where IFS, PyFS, q-ROFS, and PFS frameworks fail to aggregate ambiguous information.

• ii. We investigated our proposed results with other present data aggregation techniques and noticed that many approaches failed to handle SFVs-based information.

Contribution to scientific society

The proposed methodology applies to all real-life practical seniors where decision-making is involved. The developed approach is a meaningful tool where we must rank the alternatives to select the best option considering a set of finite attributes.

The following are some contributions to scientific society are discussed as follows:

• i) A novel CoCoSo method using SFV was established for complex MCDM problems.

• ii)  We developed new operational laws using Sugeno Weber TN and TCN under the SFS environment.

• iii)  New theories were developed in the form of SFSWPWA and SFSWPWG operators on behalf of developed operational laws.

• iv)  Investigate some fundamental axioms of AOs, such as impotence, monotonicity, and boundedness of established AOs.

• v)  Present MCDM algorithms for both the CoCoSo method and diagnosed AOs.

• vi)  Provide a numerical solution for the MCDM problem using the derived CoCoSo method and AOs.

• vii)  To assess the applicability of diagnosed theories, we compare them with the present approaches to methodologies.

Arrangements of article

The remaining part of the article is imagined as follows: some necessary fundamental definitions are discussed in Section"Preliminaries". The proposed algorithm for the CoCoSo method for MCDM problems using SFS information is presented in Sect. “Proposed CoCoSo Method for SFVS”. Sect. “Proposed aggregation operators” introduces newly developed SFSWPWA and SFSWPWG operators. Section"MCDM algorithms for the CoCoSo METHOD and proposed AOS using SFS sinformation". discusses the algorithms for the CoCoSo method and diagnosed AOs. The case study on the selection of blockchain systems for supply chain management is presented in Section"Case study". The solution to real-life numerical problems related to selecting the best blockchain for data storage is provided in Section"Numerical problem". The sensitive analysis of the proposed theory is discussed in Section"Sensitivity analysis". A detailed and comprehensive comparative analysis of the reliability of the developed approach is presented in Section"Comparative analysis". Section"Result and discussion"discusses the result and discussion of the proposed work. The conclusions are given in Section"Conclusion".

Preliminaries

This segment offers some basic definitions related to the proposed approach and provides help in understanding the diagnosed CoCoSo method and SFSWPWA and SFSWPWG operators. The definitions of SFS and score function ($\mathcal{S}$F), accuracy function ($\mathbb{E}$F), and operational laws for SFVs are given as follows:

Before the invention of the SFS framework, the concept of PFS failed to handle MCDM problems with more extensive data. To overcome this shortcoming, Mahmood et al.⁸ presented the idea of SFS by taking the square on TG, FG, and AG and enlarging the range of the PFS framework under a fuzzy domain. The definition of SFS is given as follows:

Definition 1:

Ref⁸. Let Ө be a universal set, and SFS $\Delta$ on Ө is defined as follows:

$$\Delta =\left\{\left(\ddot{a} ,\mathcal{J}\left(\ddot{a} \right), {\rm I}\left( \ddot{a} \right),\Pi \left( \ddot{a} \right)\right)| \ddot{a} \in \Theta\right\}$$

(1)

The above-discussed Eq. 1 can present information in the shape of TG, AG, and FG under the range of interval $\left[0, 1\right]$.where ${\mathcal{J}}^{2} \left( {\ddot{a}} \right) \in \left[ {0,{ }1} \right]$ is TG, ${\rm I}^{2} \left( {\ddot{a}} \right) \in \left[ {0,{ }1} \right]$ is AG and $\Pi^{2} \left( {\ddot{a}} \right) \in \left[ {0, 1} \right]$ is FG and satisfies the condition $0 \le {\mathcal{J}}^{2} \left( {\ddot{a}} \right) + {\text{I}}^{2} \left( {\ddot{a}} \right) + \Pi^{2} \left( {\ddot{a}} \right) \le 1$. The hesitancy degree $H\left( {\ddot{a}} \right)$ is defined as follows:

$$H\left(\ddot{a} \right)={\left(1-\left({\mathcal{J}}^{2}\left(\ddot{a}\right)+{\rm I}^{2}\left(\ddot{a}\right)+{\Pi }^{2}\left(\ddot{a}\right)\right)\right)}^\frac{1}{2}$$

(2)

where $\left( {{\mathcal{J}}^{2} \left( {\ddot{a}} \right), {\text{I}}^{2} \left( {\ddot{a}} \right), \Pi^{2} \left( {\ddot{a}} \right)} \right)$ is called as SFVs.

Equation 2, which is discussed above, can present hesitant information.

Definition 2:

Ref⁸. Consider SFVs ${\mathcal{K}}\left( {\ddot{a}} \right) = \left( {{\mathcal{J}}^{2} \left( {\ddot{a}} \right), {\text{I}}^{2} \left( {\ddot{a}} \right), \Pi^{2} \left( {\ddot{a}} \right)} \right)$. The $\mathcal{S}$F formula is defined as follows:

$$\mathcal{S}F\left(\ddot{a} \right)=\left({\mathcal{J}}^{2}\left(\ddot{a} \right)-{\rm I}^{2}\left(\ddot{a} \right)-{\Pi }^{2}\left(\ddot{a} \right)\right)$$

(3)

The range of $\mathcal{S}$F is given as follows:

$$\mathcal{S}F\left(\ddot{a} \right)\in \left[-1, 1\right]$$

The main objective of Eq. 3. in decision-making sciences is to translate fuzzy values into scalar values that are easily comparable and useful for ranking fuzzy elements to determine their“preference”and"closeness."

Definition 3:

Ref⁸. Consider the SFVs ${\mathcal{K}}\left( {\ddot{a}} \right) = \left( {{\mathcal{J}}^{2} \left( {\ddot{a}} \right), {\text{I}}^{2} \left( {\ddot{a}} \right), \Pi^{2} \left( {\ddot{a}} \right)} \right)$. The F is defined as follows:

$${\mathbb{E}}F\left(\ddot{a}\right)=\left({\mathcal{J}}^{2}\left(\ddot{a}\right)+{\rm I}^{2}\left(\ddot{a}\right)+{\Pi }^{2}\left(\ddot{a}\right)\right)$$

(4)

The range of F is given as follows:

$${\mathbb{E}}\text{F}\left(\ddot{a}\right)\in \left[0, 1\right]$$

The above Definition 3 presents multiple fuzzy information in a single value.

Remark:

Consider two SFVs ${\mathcal{K}}_{1}$ and ${\mathcal{K}}_{2}$. By using the above principles of $\mathcal{S}F$ and ${\mathbb{E}}F$ the arrangement of SFVs can be presented as follows:

• i. If $\mathcal{S}\left({\mathcal{K}}_{1}\right)>\mathcal{S}\left({\mathcal{K}}_{1}\right)$, then ${\mathcal{K}}_{1}$ is higher to ${\mathcal{K}}_{2}$

• ii. If $\mathcal{S}\left({\mathcal{K}}_{1}\right)<\mathcal{S}\left({\mathcal{K}}_{1}\right)$, then ${\mathcal{K}}_{1}$ is smaller to ${\mathcal{K}}_{2}$

• iii. If $\mathcal{S}\left({\mathcal{K}}_{1}\right)=\mathcal{S}\left({\mathcal{K}}_{1}\right)$ for two SFVs, then.

• a. If ${\mathbb{E}}\left({\mathcal{K}}_{1}\right)>{\mathbb{E}}\left({\mathcal{K}}_{1}\right)$, then ${\mathcal{K}}_{1}$ is higher to ${\mathcal{K}}_{2}$

• b. If ${\mathbb{E}}\left({\mathcal{K}}_{1}\right)<{\mathbb{E}}\left({\mathcal{K}}_{1}\right)$, then ${\mathcal{K}}_{1}$ is smaller to ${\mathcal{K}}_{2}$

• c. If $\left({\mathcal{K}}_{1}\right)={\mathbb{E}}\left({\mathcal{K}}_{1}\right)$, then ${\mathcal{K}}_{1}$ is similar to ${\mathcal{K}}_{2}$

Definition 4:

Ref⁸. Some fundaments operational laws for three SFVs $\mathcal{K}=\left({\mathcal{J}}^{2}, {\rm I}^{2}, {\Pi }^{2}\right), {\mathcal{K}}_{1}=\left({\mathcal{J}}_{1}^{2}, {\rm I}_{1}^{2}, {\Pi }_{1}^{2}\right), {\mathcal{K}}_{2}=\left({\mathcal{J}}_{2}^{2}, {\rm I}_{2}^{2}, {\Pi }_{2}^{2}\right)$ such as scalar multiplication, power, and sum and product, are defined as follows:

• i. ${\mathcal{K}} = \left( {\left( {1 - \left( {1 - {\mathcal{J}}^{2} } \right) } \right)^{\frac{1}{2}} ,{ }\left( {\rm I} \right) ,{ }\left( {{{ \Pi }}} \right) } \right)$

• ii. ${\mathcal{K}}^{\text{\o}}=\left(, {\left(\mathcal{J}\right)}^{\text{\o}}, {\left(1-{\left(1-{\rm I}^{2}\right)}^{\text{\o}}\right)}^\frac{1}{2}, {\left(1-{\left(1-{\Pi }^{2}\right)}^{\text{\o}}\right)}^\frac{1}{2}\right)$

• iii. ${\mathcal{K}}_{1}\oplus{\mathcal{K}}_{2}=\left({\left({\mathcal{J}}_{1}^{2}+{\mathcal{J}}_{2}^{2}-{\mathcal{J}}_{1}^{2}{\mathcal{J}}_{2}^{2}\right)}^\frac{1}{2}, {\rm I}_{1}{\rm I}_{2}, {\Pi }_{1}{\Pi }_{2}\right)$

• iv. ${\mathcal{K}}_{1}\otimes {\mathcal{K}}_{2}=\left({\mathcal{J}}_{1}{\mathcal{J}}_{2}, {\left({\rm I}_{1}^{2}+{\rm I}_{2}^{2}-{\rm I}_{1}^{2}{\rm I}_{2}^{2}\right)}^\frac{1}{2}, {\left({\Pi }_{1}^{2}+{\Pi }_{2}^{2}-{\Pi }_{1}^{2}{\Pi }_{2}^{2}\right)}^\frac{1}{2}\right)$

Definition 5

Ref³⁴. The Sugeno-Weber TCN and TN are defined as follows:

$${\rm O}^{\chi }=\left\{\begin{array}{c}{\rm O}_{d}\left(\mathcal{W}, \eta \right), if \chi =-1\\ \text{min}\left(1,\mathcal{W}+\eta -\left(\frac{\chi }{1+\chi }\right)\mathcal{W}\eta \right), if-1<\chi <+\infty \\ {\rm O}_{p}\left(\mathcal{W}, \eta \right), \chi =+\infty \end{array}\right.$$

and

$${\Omega }^{\chi }=\left\{\begin{array}{c}{\Omega }_{d}\left(\mathcal{W}, \eta \right), if \chi =-1\\ \text{max}\left(0,\frac{\mathcal{W}+\eta -1+\chi \mathcal{W}\eta }{1+\chi }\right), if-1<\chi <+\infty \\ {\Omega }_{p}\left(\mathcal{W}, \eta \right), \chi =+\infty \end{array}\right.$$

where ${\rm O}_{d}\left(\mathcal{W}, \eta \right)$ and ${\Omega }_{d}\left(\mathcal{W}, \eta \right)$ Moreover, known as drastic TCN and TN.

Definition 6

Consider $\mathcal{K}=\left({\mathcal{J}}^{2}, {\rm I}^{2}, {\Pi }^{2}\right), {\mathcal{K}}_{1}=\left({\mathcal{J}}_{1}^{2}, {\rm I}_{1}^{2}, {\Pi }_{1}^{2}\right), {\mathcal{K}}_{2}=\left({\mathcal{J}}_{2}^{2}, {\rm I}_{2}^{2}, {\Pi }_{2}^{2}\right)$ There are three SFVs, and then, using Sugeno Weber TN and TCN operational laws such as scalar multiplication, power and sum, and product, they are defined as follows: Where $\text{\o}>0$.

• i. $\o\mathcal{K}=\left(\begin{array}{c}\sqrt{\frac{\chi }{1+\chi }\left(1-{\left(1-{\mathcal{J}}^{2}\frac{\chi }{1+\chi }\right)}^{\o}\right)},\\ \sqrt{\left(\left(1+\chi \right){\left(\frac{\chi {\rm I}^{2}+1}{1+\chi }\right)}^{\o}-1\right)\frac{1}{\chi }},\\ \sqrt{\left(\left(1+\chi \right){\left(\frac{\chi {\Pi }^{2}+1}{1+\chi }\right)}^{\o}-1\right)\frac{1}{\chi }}\end{array}\right)$

• ii. ${\mathcal{K}}^{\o}=\left(\begin{array}{c}\sqrt{\left(\left(1+\chi \right){\left(\frac{\chi {\mathcal{J}}^{2}+1}{1+\chi }\right)}^{\o}-1\right)\frac{1}{\chi }},\\ \sqrt{\frac{\chi }{1+\chi }\left(1-{\left(1-{\rm I}^{2}\frac{\chi }{1+\chi }\right)}^{\o}\right)},\\ \sqrt{\frac{\chi }{1+\chi }\left(1-{\left(1-{\Pi }^{2}\frac{\chi }{1+\chi }\right)}^{\o}\right)}\end{array}\right)$

• iii. ${\mathcal{K}}_{1}\oplus{\mathcal{K}}_{2}=\left(\begin{array}{c}\sqrt{{\mathcal{J}}_{1}^{2}+{\mathcal{J}}_{2}^{2}-\frac{\chi }{1+\chi }{\mathcal{J}}_{1}^{2}{\mathcal{J}}_{2}^{2}},\\ \sqrt{\frac{{\rm I}_{1}+{\rm I}_{1}-\chi {\rm I}_{1}{\rm I}_{2}}{1+\chi }},\sqrt{\frac{{\Pi }_{1}+{\Pi }_{1}-\chi {\Pi }_{1}{\Pi }_{2}}{1+\chi }}\end{array}\right)$

• iv. ${\mathcal{K}}_{1}\otimes {\mathcal{K}}_{2}=\left(\begin{array}{c}\sqrt{\frac{{\mathcal{J}}_{1}+{\mathcal{J}}_{2}-\chi {\mathcal{J}}_{1}{\mathcal{J}}_{2}}{1+\chi }},\\ \sqrt{{\rm I}_{1}^{2}+{\rm I}_{2}^{2}-\frac{\chi }{1+\chi }{\rm I}_{1}^{2}{\rm I}_{2}^{2}},\\ \sqrt{{\Pi }_{1}^{2}+{\Pi }_{2}^{2}-\frac{\chi }{1+\chi }{\Pi }_{1}^{2}{\Pi }_{2}^{2}}\end{array}\right)$

The concept of PAO is a powerful tool for investigating attribute weight vectors by combining each alternative with attribute value.

Definition 7

Ref²⁴. A PAO developed by Yager, the PAOs are defined as follows:

$$PA\left({\upepsilon }_{1}, {\upepsilon }_{2}, \dots , {\upepsilon }_{n}\right)=\frac{\sum_{{i}=1}^{n}\left(1+\mathcal{T}\left({\upepsilon }_{{i}}\right)\right){\upepsilon }_{{i}}}{\sum_{{i}=1}^{n}\left(1+\mathcal{T}\left({\upepsilon }_{{i}}\right)\right)}$$

where 

$$\mathcal{T}\left({\upepsilon }_i\right)= {\sum }_{\begin{array}{c}j=1\\ j\ne i\end{array}}^{n}Sup\left({\upepsilon }_i, {\upepsilon }_j\right),$$

and $Sup\left({\upepsilon }_{\mathcal{i}}, {\upepsilon }_{\mathcal{j}}\right)$ here, define the support function for ${\upepsilon }_{\mathcal{i}}$ from ${\upepsilon }_{\mathcal{j}}$, which must be fulfilled the following restrictions:

• 1. $Sup\left({\upepsilon }_i, {\upepsilon }_j\right) \in [0, 1]$

• 2. $Sup\left({\upepsilon }_i, {\upepsilon }_j\right)=Sup\left({\upepsilon }_i, {\upepsilon }_j\right)$

• 3. $Sup\left({\upepsilon }_i, {\upepsilon }_j\right)\ge Sup\left({\upepsilon }_k, {\upepsilon }_{{\ell}}\right), if \left|{\upepsilon }_i-{\upepsilon }_j\right|<\left|{\upepsilon }_k-{\upepsilon }_{{\ell}}\right|$

Proposed CoCoSo method for SFVS

Decision makers always carefully examine each algorithm’s selection procedure and justification for its inclusion in the study. Different aspects, including effectiveness, precision, intricacy, scalability, and data compatibility, guided the selection process. We preferred the CoCoSo method, which has a strong track record in related applications and a reputation for accuracy.

Another vital factor was efficiency since we required the CoCoSo techniques that could produce results quickly. Scalability was essential for the selected CoCoSo method to manage more extensive datasets without sacrificing performance.

The idea of the CoCoSo method is a valuable tool for MCDM issues. This method ranks the considered option by instigating the compromise programming approach and additive weighted sum. This method combines weighted product and sum to obtain the possible compromise solution by balancing the best and worst alternatives. The step-wise procedure of the CoCoSo method for MCDM problems is given as follows:

• i. First, define the collection of alternatives and attributes in a matrix using SFVs-based information; c. Assign weights to the attributes, where the sum of all weights vectors (WV) is one.

• ii. Normalize the decision matrix.

• iii. Construct the weighted normalized decision matrix (WNDM) using the formula defined in Definition 3.

• iv. Calculate the sum of the weighted normalized values (WNVs) for each attribute and alternative.

• v. Find the product of the WNVs of each attribute.

• vi. Calculate the average of the product and the sum of the WNVs.

• vii. Find the score values for each alternative.

• viii. Finally, we arrange the alternatives for ranking based on obtained score values.

Proposed aggregation operators

This section presents the diagnosed approach of SFSWPWA and SFSWPWG operators using SFS information. In the assessment of investigating AOs, we also derived some axioms of AOs, such as idempotency, monotonicity, and boundedness. Proves of diagnosed approaches are provided in the appendix section.

The Sugeno-Weber weighted averaging operation is crucial for SFS because it combines Sugeno-Weber processes with weighted averaging, giving more exact control over the influence of each component in the aggregation process.

Definition 8

Consider a family of SFVs ${}^\backprime \Upsilon _{{\text{o}}} = \left( {{\mathcal{J}}_{{\text{o}}}^{2} ,{\text{I}}_{{\text{o}}}^{2} ,\Pi _{{\text{o}}}^{2} } \right)$, where $\left(\text{o}=1, 2, \dots ,{\tilde{\grave{\eta}}}\right)$. And $\overline{\overline{{\uptau }_{\text{o}}}}$ be the WV with condition $\sum_{\text{o}=1}^{\tilde{\grave{\eta}}}\overline{\overline{{\uptau }_{\text{o}}}}=1, \chi \ge 1$.

$$SFSWPWA\left({{}^\backprime \Upsilon}_{1}, {{}^\backprime \Upsilon}_{2}, \dots , {{}^\backprime \Upsilon}_{{\tilde{\grave{\eta}}}}\right)=\begin{array}{c}{{\tilde{\grave{\eta}}}}\\ \oplus \\ \text{o}=1\end{array}\overline{\overline{{\uptau }_{\text{o}}}}{{}^\backprime \Upsilon}_{\text{o}}$$

The properties of the SFSWPWA operator must be shown since mathematical induction provides a comprehensive and systematic approach to verify the formula’s correctness in any circumstance. The primary case is established, and then it is demonstrated that if it holds for one instance, it has for the next, validating the dependability and generalizability of the proposed AOs.

Theorem 1

Let a family of SFVs ${}^\backprime \Upsilon _{{\text{o}}} = \left( {{\mathcal{J}}_{{\text{o}}}^{2} ,{\text{I}}_{{\text{o}}}^{2} ,\Pi _{{\text{o}}}^{2} } \right)$, where $\left(\text{o}=1, 2, \dots ,{\tilde{\grave{\eta}}}\right)$, $\overline{\overline{{\uptau }_{\text{o}}}}$ be the WV, whose sum is one and $\chi \ge 1$. Then, the aggregated outcome is SFVs. The achieved results are provided as follows:

$$SFSWPWA\left({{}^\backprime \Upsilon}_{1}, {{}^\backprime \Upsilon}_{2}, \dots , {{}^\backprime \Upsilon}_{{\tilde{\grave{\eta}}}}\right)$$

$$=\left(\begin{array}{c}\sqrt{\frac{1+\chi }{\chi }\left(1-\prod_{o=1}^{{\tilde{\grave{\eta}}}}{\left(1-{\mathcal{J}}_{o}^{2}\left(\frac{\chi }{1+\chi }\right)\right)}^{\overline{\overline{{\tau }_{o}}}}\right)},\\ \sqrt{\frac{1}{\chi }\left(\left(1+\chi \right)\prod_{o=1}^{{\tilde{\grave{\eta}}}}{\left(\frac{\chi {\rm I}_{o}^{2}+1}{1+\chi }\right)}^{\overline{\overline{{\tau }_{o}}}}-1 \right)},\\ \sqrt{\frac{1}{\chi }\left(\left(1+\chi \right)\prod_{o=1}^{{\tilde{\grave{\eta}}}}{\left(\frac{\chi {\Pi }_{o}^{2}+1}{1+\chi }\right)}^{\overline{\overline{{\tau }_{o}}}}-1\right)}\end{array}\right)$$

(5)

where $\overline{\overline{{\tau }_{o}}}=\frac{\sum_{{i}=1}^{n}\left(1+\mathcal{T}\left({\upepsilon }_{{i}}\right)\right){\upepsilon }_{{i}}}{\sum_{{i}=1}^{n}\left(1+\mathcal{T}\left({\upepsilon }_{{i}}\right)\right)}$ be the weight vectors of attributes.

The proposed SFSWPWA operator in Eq. 5 consists of the TG $\mathcal{J}$, AG ${\rm I},$ and FG $\Pi$, $\overline{\overline{{\uptau }_{\text{o}}}}$ shows the weightage of the alternatives, and $\chi \ge 2$ is the constant value.

Proof

The proof is given in the appendix section.

Idempotency is a crucial characteristic for verifying the proposed SFSWPWA operator, which ensures that the outcomes remain unchanged when identical inputs are mixed. This feature demonstrates how the aggregation process, which preserves consistency and prevents distortions, is essential to decision-making reliability.

Theorem 2

(Idempotency) Consider a collection ${}^\backprime \Upsilon _{{\text{o}}} = \left( {{\mathcal{J}}_{{\text{o}}}^{2} ,{\text{I}}_{{\text{o}}}^{2} ,\Pi _{{\text{o}}}^{2} } \right)$ be the SFVs, where $\left(\text{o}=1, 2, \dots ,{\tilde{\grave{\eta}}}\right)$. If ${}^\backprime \Upsilon _{1} = {}^\backprime \Upsilon _{2} = \ldots = {}^\backprime \Upsilon _{{\text{i}}} = {}^\backprime \Upsilon$. So,

$$SFSWPWA\left({{}^\backprime \Upsilon}_{1}, {{}^\backprime \Upsilon}_{2},\dots ,{{}^\backprime \Upsilon}_{\text{i}}\right)={{}^\backprime \Upsilon}$$

Proof

The proof is given in the appendix section.

Since the proposed SFSWPWA operator ensures that the aggregated output remains within a specific range, often between the minimum and maximum input values, it must be constrained to be checked. This feature offers stability and predictability by guaranteeing that the aggregation does not produce outliers or unexpected values.

Theorem 3

(Boundedness) Consider a collection ${ {}^\backprime \Upsilon}_{\text{o}}=\left({\mathcal{J}}_{\text{o}}^{2}, {\rm I}_{\text{o}}^{2}, {\Pi }_{\text{o}}^{2}\right)$ be the of SFVs. If ${{}^\backprime \Upsilon}^{-}=\left(\text{min}\left[{\mathcal{J}}_{\text{o}}^{2}\right],\text{max}\left[{\rm I}_{\text{o}}^{2}\right],\text{max}\left[{\Pi }_{\text{o}}^{2}\right]\right)$ and ${{}^\backprime \Upsilon}^{+}=\left(\text{max}\left[{\mathcal{J}}_{\text{o}}^{2}\right],\text{min}\left[{\rm I}_{\text{o}}^{2}\right],\text{min}\left[{\Pi }_{\text{o}}^{2}\right]\right)$, then we obtain as: So,

$${{}^\backprime \Upsilon}^{-}\le SFSWPWA\left({{}^\backprime \Upsilon}_{1}, {{}^\backprime \Upsilon}_{2},\dots ,{{}^\backprime \Upsilon}_{\text{i}}\right)\le {{}^\backprime \Upsilon}^{+}$$

Proof

The proof is given in the appendix section.

Since monotonicity ensures that the aggregated result will not decrease if input values increase, preserving the data’s intrinsic order is essential for validating the proposed SFSWPWA operator. Consistency depends on this feature since it confirms that the aggregation procedure respects the relative size of inputs.

Theorem 4

(Monotonicity) Consider a collection ${{}^\backprime \Upsilon}_{\text{o}}=\left({\mathcal{J}}_{\text{o}}^{2}, {\rm I}_{\text{o}}^{2}, {\Pi }_{\text{o}}^{2}\right)$, ${{}^\backprime \Upsilon}_{\text{o}}^{{^{\prime}}}=\left({{\mathcal{J}}^{2}}_{\text{o}}^{{^{\prime}}}, {{\rm I}^{2}}_{\text{o}}^{{^{\prime}}}, {{\Pi }^{2}}_{\text{o}}^{{^{\prime}}}\right)$ be the of SFVs., where $\left(\text{o}=1, 2, \dots ,{\tilde{\grave{\eta}}}\right)$ and satisfy the condition

$$SFSWPWA\left({{}^\backprime \Upsilon}_{1}, {{}^\backprime \Upsilon}_{2},\dots ,{{}^\backprime \Upsilon}_{\text{i}}\right)\le SFSWPWA\left({{}^\backprime \Upsilon}_{1}^{{^{\prime}}}, {{}^\backprime \Upsilon}_{2}^{{^{\prime}}},\dots ,{{}^\backprime \Upsilon}_{\text{i}}^{{^{\prime}}}\right)$$

Proof

The proof is easy to prove.

Definition 9

Consider a collection ${{}^\backprime \Upsilon}_{\text{o}}=\left({\mathcal{J}}_{\text{o}}^{2}, {\rm I}_{\text{o}}^{2}, {\Pi }_{\text{o}}^{2}\right)$ be the of SFVs. And $\overline{\overline{{\uptau }_{\text{o}}}}$ be the WV, $\sum_{\text{o}=1}^{\tilde{\grave{\eta}}}\overline{\overline{{\uptau }_{\text{o}}}}=1, \chi \ge 1$.

$$SFSWPWG\left({{}^\backprime \Upsilon}_{1}, {{}^\backprime \Upsilon}_{2}, \dots , {{}^\backprime \Upsilon}_{{\tilde{\grave{\eta}}}}\right)=\begin{array}{c}{{\tilde{\grave{\eta}}} }\\ \otimes \\ \text{o}=1\end{array}\overline{\overline{{\uptau }_{\text{o}}}}{{}^\backprime \Upsilon}_{\text{o}}$$

Theorem 5

Consider a collection ${{}^\backprime \Upsilon}_{\text{o}}=\left({\mathcal{J}}_{\text{o}}^{2}, {\rm I}_{\text{o}}^{2}, {\Pi }_{\text{o}}^{2}\right)$ be the SFVs, where $\left(\text{o}=1, 2, \dots ,{\tilde{\grave{\eta}}}\right)$, and $\overline{\overline{{\uptau }_{\text{o}}}}$ be the WV, whose sum is one and $\chi \ge 1$. Then, the aggregated outcomes are also SFVs. The achieved results are provided as follows:

$$SFSWPWGSFSWPWG\left({{}^\backprime \Upsilon}_{1}, {{}^\backprime \Upsilon}_{2}, \dots , {{}^\backprime \Upsilon}_{{\tilde{\grave{\eta}}}}\right)=$$

$$\left(\begin{array}{c}\sqrt{\frac{1}{\chi }\left(\left(1+\chi \right)\prod_{o=1}^{{\tilde{\grave{\eta}}}}{\left(\frac{\chi {\mathcal{J}}_{o}^{2}+1}{1+\chi }\right)}^{\overline{\overline{{\tau }_{o}}}}-1 \right)}, \\ \sqrt{\frac{1+\chi }{\chi }\left(1-\prod_{o=1}^{{\tilde{\grave{\eta}}}}{\left(1-{\rm I}_{o}^{2}\left(\frac{\chi }{1+\chi }\right)\right)}^{\overline{\overline{{\tau }_{o}}}}\right)},\\ \sqrt{\frac{1+\chi }{\chi }\left(1-\prod_{o=1}^{{\tilde{\grave{\eta}}}}{\left(1-{\Pi }_{o}^{2}\left(\frac{\chi }{1+\chi }\right)\right)}^{\overline{\overline{{\tau }_{o}}}}\right)}\end{array}\right)$$

(6)

where $\overline{\overline{{\tau }_{o}}}=\frac{\sum_{{i}=1}^{n}\left(1+\mathcal{T}\left({\upepsilon }_{{i}}\right)\right){\upepsilon }_{{i}}}{\sum_{{i}=1}^{n}\left(1+\mathcal{T}\left({\upepsilon }_{{i}}\right)\right)}$ be the weight vectors of attributes.

The proposed SFSWPWA operator in Eq. 6 consists of the TG $\mathcal{J}$, AG ${\rm I},$ and FG $\Pi$, $\overline{\overline{{\uptau }_{\text{o}}}}$ shows the weightage of the alternatives, and $\chi \ge 2$ is the constant value.

Proof

The proof of Theorem 5 is easy to prove, the same as Theorem 1. It also holds the fundamental axioms of AOs, such as boundedness, idempotency, and monotonicity.

MCDM algorithms for the CoCoSo method and proposed AOS using SFS sinformation

This segment presents the algorithm for the proposed COCOCO method using SFS information and diagnoses SFSWPWA and SFSWPWG operators for MCDM problems. For convenience, we also provide flowcharts of the working mechanism of both developed methodologies.

Algorithm of COCOCSO method

To enhance the precision of MCDM problems, we diagnosed the CoCoSo method using SFS information. The step-wise working mechanism of the CoCoSo method is given as follows:

Step 1. Define the collection of attributes $B=\left\{{C}_{1},{C}_{2},{C}_{3},\cdots ,{C}_{m}\right\}$ and alternatives $D=\left\{{\mathcalligra{t}}_{1},{\mathcalligra{t}}_{2},{\mathcalligra{t}}_{3},\cdots ,{\mathcalligra{t}}_{n}\right\}$ in the form of a decision matrix ${M}_{i\times j}$ using SFS informtion. Then considering WV $\left\{{\uptau }_{1},{\uptau }_{2},{\uptau }_{3},\cdots ,{\uptau }_{n}\right\}$ Moreover, assign WV to each attribute, where the sum of all weights must be one.

Step 2. Construct the organized decision matrix using SFS information, where all alternatives are presented column-wise, and attributes are written row-wise.

Step 3. Normalize the decision matrix: Usually, there are two types of attributes. We need to alter their nature to attain consistent results.

Step 4. To determine the WNDM, we use the score function formula discussed in Definition 2. and calculate the cumulative opinions about the alternatives regarding each factor.

Step 5. We calculate the WNDM ${\left[{M}_{mn}\right]}_{i\times j}$ I am using the information derived in step 2. Evaluate the WNDM using the following Equation.

$${\left(PR\right)}_{ij}={\tau }_{j}.{Scor\mathcal{X}}_{ij}^{n}$$

(7)

where ${\tau }_{j}$ be the WV of ${j}^{th}$ attribute, it also holds the condition $\sum_{j=1}^{n}{\tau }_{j}=1$.

Step 6. To find the sum of the weighted normalized values (VNVs) of the attributes using the given Equation as follows:

$${\mathcal{U}}_{i}=\sum_{j=1}^{n}{\left(PR\right)}_{ij}$$

(8)

Step 7. Evaluate the product of the WNVs of the attributes for each option by using the Equation given as follows:

$${\mathbb{Q}}_{i}=\prod_{j=1}^{n}{\left(PR\right)}_{ij}$$

(9)

Step 8. To find the average of the product and the sum of the WNVs obtained in Step 7. and Step 6.

$${\ddot{A} }_{i}=\frac{{\mathbb{Q}}_{i}+{\mathcal{U}}_{i}}{2}$$

(10)

Step 9. Find the score of each alternative based on relative importance using the Equation given as follows;

$${\left(PR\right)}_{i}={A}_{i}.\left(1+\frac{{\mathcal{U}}_{i}-min{\mathcal{U}}_{i}}{{max\mathcal{U}}_{i}-min{\mathcal{U}}_{i}}+\frac{{\mathbb{Q}}_{i}-min{\mathbb{Q}}_{i}}{{max{\mathbb{Q}}}_{i}-min{\mathbb{Q}}_{i}}\right)$$

(11)

Step 10. In the last step, we rank the alternatives in descending sequence based on the obtained score values.

For a better understanding, the working mechanism of the CoCoSo method is provided in Fig. 2.

Fig. 2

Shows the working mechanism of the CoCoSo method for MACM problems.

The MCDM algorithm proposed AOs

This subsection discussed the proposed algorithm for the diagnosed SFSWPWA and SFSWPWG operator using SFS data. The working mechanism step is provided as follows:

Step 1. Construct the decision matrix ${M}_{i\times j}$ in which collection of alternatives $\left\{{\mathcalligra{t}}_{1},{\mathcalligra{t}}_{2},{\mathcalligra{t}}_{3},\cdots ,{\mathcalligra{t}}_{n}\right\}$ and attributes $\left\{{C}_{1},{C}_{2},{C}_{3},\cdots ,{C}_{m}\right\}$ are provided column-wise and row-wise, respectively.

Step 2. Assign weights to each attribute by taking options for decision experts, where the sum of all weights should be one.

Step 3. To apply the diagnosed theory of SFSWPWA and SFSWPWG operator.

$$SFSWPWA\left({{}^\backprime \Upsilon}_{1}, {{}^\backprime \Upsilon}_{2}, \dots , {{}^\backprime \Upsilon}_{{\tilde{\grave{\eta}}}}\right)=$$

$$\left(\begin{array}{c}\sqrt{\frac{1+\chi }{\chi }\left(1-\prod_{o=1}^{{\tilde{\grave{\eta}}}}{\left(1-{\mathcal{J}}_{o}^{2}\left(\frac{\chi }{1+\chi }\right)\right)}^{\overline{\overline{{\tau }_{o}}}}\right)},\\ \sqrt{\frac{1}{\chi }\left(\left(1+\chi \right)\prod_{o=1}^{{\tilde{\grave{\eta}}}}{\left(\frac{\chi {\rm I}_{o}^{2}+1}{1+\chi }\right)}^{\overline{\overline{{\tau }_{o}}}}-1 \right)},\\ \sqrt{\frac{1}{\chi }\left(\left(1+\chi \right)\prod_{o=1}^{{\tilde{\grave{\eta}}}}{\left(\frac{\chi {\Pi }_{o}^{2}+1}{1+\chi }\right)}^{\overline{\overline{{\tau }_{o}}}}-1\right)}\end{array}\right)$$

and

$$SFSWPWG\left({{}^\backprime \Upsilon}_{1}, {{}^\backprime \Upsilon}_{2}, \dots , {{}^\backprime \Upsilon}_{{\tilde{\grave{\eta}}}}\right)=$$

$$\left(\begin{array}{c}\sqrt{\frac{1}{\chi }\left(\left(1+\chi \right)\prod_{o=1}^{{\tilde{\grave{\eta}}}}{\left(\frac{\chi {\mathcal{J}}_{o}^{2}+1}{1+\chi }\right)}^{\overline{\overline{{\tau }_{o}}}}-1 \right)}, \\ \sqrt{\frac{1+\chi }{\chi }\left(1-\prod_{o=1}^{{\tilde{\grave{\eta}}}}{\left(1-{\rm I}_{o}^{2}\left(\frac{\chi }{1+\chi }\right)\right)}^{\overline{\overline{{\tau }_{o}}}}\right)},\\ \sqrt{\frac{1+\chi }{\chi }\left(1-\prod_{o=1}^{{\tilde{\grave{\eta}}}}{\left(1-{\Pi }_{o}^{2}\left(\frac{\chi }{1+\chi }\right)\right)}^{\overline{\overline{{\tau }_{o}}}}\right)}\end{array}\right)$$

Step 4. Apply the defined $\mathcal{S}F$ formula for ranking the best alternative among all considered alternatives, give as follows:

$$\mathcal{S}F\left(\ddot{a}\right)=\left({\mathcal{J}}^{2}\left(\ddot{a}\right)-{\rm I}^{2}\left(\ddot{a}\right)-{\Pi }^{2}\left(\ddot{a}\right)\right)$$

Step 5. Arrange all aggregated score values in descending order.

Step 6. Ranking the alternatives based on obtained score values.

Step 7. End.

For a better understanding, the working mechanism of the developed SFSWPWA and SFSWPWG operator is provided in Fig. 3.

Fig. 3

Shows the data aggregation procedure using proposed AOs.

Case study

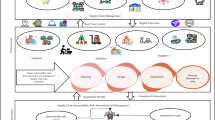
Blockchain is a decentralized method of storing data. The blockchain is the most modern way to save records. It moves more securely than previous technology, and we can accurately manage records. The working principle of blockchain is simple. If anyone changes the record, it cannot hide this activity because everyone is connected. At the start of time, blockchain technology was used in record-keeping transactions. Still, many blockchain applications, such as supply chain management, smart contracts, voting systems, and real estate business energy trading, are available nowadays. The structure of the blockchain is presented in Fig. 4.

Fig. 4

Presentation of the blockchain structure.

Blockchain is the modern way to store data in blocks; each block is connected, which is a very transparent way to store data. Two main types of blockchain are well-reputed in the modern age: public and private.

Public blockchain

The public blockchain means many users are connected, and everyone can access data. We can say that it is a non-resistive and permission-less ledger system. After connecting the public blockchain, we can access current and previous data.

Private blockchain

The second type is a private blockchain in which the users are connected, but not all users can access all data in the blockchain. We can say that a private blockchain is a resistive and closed chain of data blocks. The private blockchain is most of the time developed for a specific organization. It may be one organization or a combination of organizations.

In the supply chain, the couple or companies are connected via blockchain. For example, the supplier company provides raw materials to the makers (production company), and finally, the product reaches the end user by cargo or supplier company. The journey of a product from the production house (company) to the end user (customer) is presented in Fig. 5.

Fig. 5

Shows the simple structure of the supply chain.

In the modern age, things are converted into digital forms. E-commerce is a critical factor in the business field. All transactions and record keeping is done via a digital platform. It has a vital impact on the global world. So many businesses are running on digital platforms, and their work is smooth without any problems. It is also best for stakeholders to manage business. In any business, the supply chain directly affects the company’s performance. The whole working process will be less resistant if the supply chain works smoothly. When we use blockchain technology in the supply chain, we get insatiable advantages from the supply chain management system. The overall sustainability of the supply chain increases when we use a blockchain.

The stakeholders keep the updated record. If anyone does change the record, it is easy to trace. Here, four different blockchain platforms are discussed to improve the sustainability of the supply chain. The sustainability of the supply chain is essential for any product manufacturing company.

Hyperledger fabric ${\mathcalligra{t}}_{1}$

Hyperledger is the blockchain platform, which is an open-source and permissioned blockchain platform hosted by the Linux Foundation. It is specially designed for enterprises. It is widely used to develop the decentralized distribution system. The scope of the Hyperledger blockchain is vast. The Hyperledger blockchain can create a supply chain system. We can track the transactions and current situation of products in the supply chain. The Hyperledger is a permission blockchain, meaning all users or end-users must be authorized. After authorization, anyone can become part of this blockchain. The Hyperledger can also work as a modular architecture. We can convert the whole architecture into small modules and connect them. Each module can work as a separate part of the supply chain. Hyperledger also offers private blockchain architecture. The chain code is also a feature of Hyperledger. We can make contracts that govern transactions. The working mechanism of the Hyperledger blockchain is presented in Fig. 6.

Fig. 6

Presents the Hyperledger blockchain working principle.

Ethereum ${\mathcalligra{t}}_{2}$

Ethereum is a blockchain platform; it is an open-source platform that enables the development of smart contracts and decentralized applications. We can make an efficient supply chain management system using the Ethereum blockchain. It was launched in $2015$ by Vitalik Buterin. Today, the Ethereum blockchain is the most popular platform for developing decentralized applications worldwide. The best feature of the Ethereum blockchain platform is smart contracts. These contacts are directly written in code. The code is written in solidity. Competent contact means some action is automatically performed when the application meets certain conditions. Ethereum also works in a cryptocurrency transformation management system. Ethereum blockchain offers an efficient, secure, and traceable supply chain. When we use the Ethereum blockchain in a supply chain management system, we obtain many advantages; for example, when the end user places an order, the mart contract hits automatically and takes specific action to provide ease to the user. It can handle the transaction very quickly.

Ibm food trust ${\mathcalligra{t}}_{3}$

The IBM food trust is also a blockchain platform. It has been specially developed to make supply chain management systems. IBM Food Trust is responsible for increasing the supply chain management system’s traceability, transparency, and sustainability. IBM Food Trust is a better platform than the Hyperledger fabric. IBM food trust was developed with the contributions of IBM and leading global companies across the food industry. The main features of IBM Food Trust are its end-to-end transparency and traceability. IBM Food Trust is a public blockchain platform, but IBM Food Trust operates as a permission blockchain platform, which means that only one person can use this platform, which is authorized. IBM Food Trust offers immutable records of all transactions; anyone can not alter or delete them. IBM food trust is a reliable platform because every record must be accurate, secure, and trustworthy.

Vechain ${\mathcalligra{t}}_{4}$

VeChain is a blockchain platform. It is also designed for a supply chain management system. VeChain offers improving transparency, traceability, and efficiency for developing supply chain systems. VeChain works more effectively by collaborating with blockchain and the Internet of Things (IoT). VeChain offers security and immutable records-keeping architecture. VeChain tracks the products and assets throughout the whole lifecycle.

The VeChain was launched by Sunny Lu in $2015$. VeChain gained the global attention of developers who want to make enterprise systems. The primary focus of VeChain is to reduce security risks, reduce fraud, and enhance the system’s sustainability. It is a powerful tool for developing business, industry, food, healthcare, luxury goods, and logistics systems. The main key feature of VeChain is VET (VeChain Token) and VTHO (VeThor Token). VET is a primary token used for value transactions across a network. At the same time, VTHO is used to pay for the transaction fee and computational operations on the blockchain, including intelligent contracts.

The four significant attributes during the selection of blockchain systems that directly affect the sustainability of the supply chain are as follows: environmental impact, transparency and traceability, cost efficiency, and scalability and flexibility.

Environmental impact ${C}_{1}$

The study of environmental impact is essential. High energy consumption blockchains, such as Proof of Work (PoW) blockchains, are less common since they harm the environment. Rather, energy-efficient blockchains, such as Proof of Stake (PoS), are preferred by businesses because they enable them to achieve sustainability objectives and lower their carbon impact. A sound supply chain management system adheres to environmental regulations, saves money on energy expenses, and enhances its reputation/image with environmentally conscious clients.

Transparency and traceability ${C}_{2}$

A sound supply chain management system supports private transactions between participants while maintaining selective transactions, and it has robust traceability to improve the sustainability of the supply chain. It also checks all records quickly at any stage. This management system enables the participant to accurately trace the product’s journey from the production house (company) to the end user (customer).

Cost efficiency ${C}_{3}$

Cost efficiency is also one of the crucial components when selecting a blockchain system for supply chain management. Cost efficiency is a significant consideration because it directly impacts Blockchain systems with high transaction charges, making them less appealing to companies trying to optimize their supply chain operations. However, low-cost blockchains are more suitable for long-term supply chain management since they enable businesses to sustain profitability and growth.

Scalability and flexibility ${C}_{4}$

All the above-discussed blockchain systems are highly scalable for large organizations or enterprises, and they support pluggable consensus mechanisms and modular architecture. The flexibility of blockchain is a crucial factor affecting the supply chain’s sustainability. A sound blockchain system is designed for large-scale enterprises that offer high scalability and support large and complex supply chains. For example, it handles many transactions in the supply chain.

Numerical problem

The investigation of the best blockchain system for data storage in a secure way is a trending issue in the modern age. In decision-making problems involving multiple attributes and alternatives, the MCDM approach is suitable for handling complicated information.

For the assessment of the best blockchain system, we construct the decision matrix. ${M}_{i\times j}$. Where we have a collection of alternatives ${\mathcalligra{t}}_{1}$ is hyper ledger fabric, ${\mathcal{t}}_{2}$ is Ethereum, ${\mathcal{t}}_{3}$ is IBM food trust, and ${\mathcal{t}}_{4}$ be the VeChain. We wish to rank the alternative based on considered attributes such as environmental impact, transparency and traceability, cost efficiency, scalability, and flexibility. We assigned WVs to attributes such as ${C}_{1}=0.25$ is environmental impact, ${C}_{2}=0.28$ is transparency and traceability, ${C}_{3}=0.23$ is cost efficiency, ${C}_{4}=0.24$ is scalability and flexibility. The step-wise details of the CoCoSo method for the decision-making process are provided as follows:

Solution by using the developed CoCoSo approach.

Step 1. Construct the decision matrix by considering the opinions of decision experts. The decision matrix is presented in Table 1.

Table 1 Decision matrix ${M}_{i\times j}$ using SFS information.

Step 2. For defuzzification of SFS information, apply the score function formula defined in Definition 2. The resulting decision matrix after applying the score function is provided in Table 2.

Table 2 Defuzzification of decision matrix ${M}_{i\times j}$.

Step 4. Calculate the WNDM by using the formula defined in Eq. (10). The evaluated outcomes are presented in Table 3.

Table3 Defuzzification of decision matrix ${M}_{i\times j}$.

Step 5. Calculate the sum and product of all attributes and alternatives using Eq. (11) and Eq. (11), respectively. The results of the sum and product provide the combined solution of other options. Furthermore, we calculate the average sum and product of the alternatives and then calculate the relative scores of each alternative. The results obtained for the sum, product, average, and relative score are cited in Table 4.

Table 4 Sum, product, average, and the relative score values of alternatives.

Step 5. The relative ranking sequence of alternatives is presented in Table 5.

Table 5 The ordering of relative scores.

For better understanding, the ranking order of the relative score values is presented in geometrical format in Fig. 7.

Fig. 7

Presents the pictorial format of score values using the CoCoSo method.

It is observed from Fig. 6 that the ${\mathcalligra{t}}_{2}$ be the best alternative among all alternatives. The alternative ${\mathcalligra{t}}_{1}$ has relatively less worthwhile than ${\mathcalligra{t}}_{2}$ and least worthful alternatives are ${\mathcalligra{t}}_{3}$ using the CoCoSo approach.

The step-wise details of the algorithm by using developed AOs for the decision-making process are provided as follows:

Step 1. Take data from the decision experts and construct a ${M}_{i\times j}$ Using SFS information. The collection of decision information in the form of a decision matrix is provided in Table 1.

Step 3. The aggregated outcomes using the SFSWPWA and SFSWPWG operators are provided in Table 6.

Table 6 Aggregated results.

Step 4. Using Definition 2. evaluate the score values. The outcomes are given in Table 7.

Table 7 Presentations of the SVs of aggregated results.

Figure 8 depicts the final aggregated outcomes by using the diagnosed SFSWPWA and SFSWPWG operators, where we noticed that the ${\mathcalligra{t}}_{2}$ be the best alternative for the SFSWPWA and SFSWPWG operators. Also, the ranking sequence of score values using the SFSWPWA and SFSWPWG operators can be notified by blue and brown lines, respectively. For better convenience, the ranking order of score values is offered in Table 8.

Fig. 8

Presents the graphical shape of score values.

Table 8 Arrangement of the score function.

Step 5. The ranking sequence of the aggregated outcomes is provided in Table 8.

It is observed in Table 8. the option. ${\mathcalligra{t}}_{2}$ is the best among all considered alternatives. The ranking sequence of other options using the SFSWPWA and SFSWPWG operators is ${\mathcalligra{t}}_{2}>{\mathcalligra{t}}_{4}>{\mathcalligra{t}}_{1}>{\mathcalligra{t}}_{3}$, and ${\mathcalligra{t}}_{2}>{\mathcalligra{t}}_{3}>{\mathcalligra{t}}_{4}>{\mathcalligra{t}}_{1}$ respectively.

For several decision-making problems, including business, engineering, agriculture, medicine, etc., our suggested SFSWPWA, SFSWPWG operators, and CoCoSo methods for SFS-based data are suitable for investigating uncertain information. For example, when a construction company wants to evaluate cement quality for large-scale projects. We take five distinct construction companies as alternatives, and we aim to find the best construction company based on their defined set of attributes like price, long life, etc. Using the SFVs information, we construct the decision matrix and then aggregate the decision matrix by applying the developed SFSWPWA, SFSWPWG operators and CoCoSo method.

One of the new business people wants to invest a lot of money into the stock exchange industry. Initially, business people want to choose which company is the finest for a secure investment because several companies are in the market competition. So, first of all, the decision-makers need to define a list of companies as alternatives and define some parameters (attributes) for assessing companies. The information related to attributes and alternatives is collected in the form of SFVs and constructed as a decision matrix. Then, the information will be aggregated using the proposed SFSWPWA, SFSWPWG operators, and CoCoSo.

Sensitivity analysis

The main objective of the section is to analyze the sensitivity of the proposed theory. For this, we make a variation of parameter $\chi$ in proposed SFSWPWA and SFSWPWG operators.

Effect of ${\varvec{\chi}}$ in SFSWPWA

In this section, we aim to investigate the effect of parameter $\chi$ on our proposed SFSWPWA operators. For this, we take the value of $\chi =0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, \text{0.8,0.9}, 1.1, 1.2$ then observe the alternatives’ ranking. The ranking order is presented in Table 9.

Table 9 Shows the effect of parameter $\chi$ on the SFSWPWA operator.

Table 9 shows no effect on the ranking order of alternatives by changing the value of $\chi$ in proposed SFSWPWA operators under the $0\le \chi \le 1$ range. We noticed that when we take $\chi \ge 2$, no ranking result is obtained. For better understanding, we provided the graphical view of Table 9 in Fig. 9.

Fig. 9

Shows the effect of $\chi$ developed SFSWPWA operator.

From the above figure, we notice that. ${\mathcalligra{t}}_{2}$ is the best alternative among all choices. The proposed theory has no effect by making variations under the range of $\chi \le 2$.

Effect of ${\varvec{\chi}}$ in SFSWPWGS

The main objective of this subsection is to analyze the effect of parameter $\chi$ on our proposed SFSWPWG operators. For this, we take the value of $\chi =0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, \text{0.8,0.9}, 1.1, 1.2$ then observe the alternatives’ ranking. The ranking order is presented in Table 10.

Table 10 Shows the effect of parameter $\chi$ on the SFSWPWG operator.

There is no effect on the ranking of alternatives using the SFSWPWG operator. Also, there is no ranking outcome when the decision maker takes the parameter $\chi \ge 2$. The graphical representation of Table 10 is provided in Fig. 10.

Fig. 10

Shows the effect of $\chi$ developed SFSWPWG operator.

From the above figure, we observed that. ${\mathcalligra{t}}_{2}$ is the best alternative. There is no variation in ranking by making variation under the range of $\chi \le 2$ in the proposed theory.

Comparative analysis

This part of the article presents the effectiveness and applicability of the proposed AOs. For this, we made a comprehensive comparison with prevailing approaches and investigated the applicability of the developed theory. We compare our results with the spherical fuzzy Dombi (SFD) weighted averaging (SFDWA), SFD weighted geometric (SFDWG) operators given by Ashraf et al.⁶⁵, and spherical fuzzy Einstein (SFE) weighted averaging (SFEWA), and SFE weighted geometric (SFEWG) operators proposed by Ashraf et al.⁶⁶. Ayaz et al. presented the thought of spherical fuzzy Hamacher (SFHW) weighted averaging and SFHW geometric operators⁶⁷. The spherical fuzzy Aczel-Alsina weighted averaging (SFAAWA) and spherical fuzzy Aczel-Alsina weighted geometric (SFAAWG) AOs proposed by Riaz et al.⁶⁸. Spherical fuzzy Frank weighted averaging (SFFWA) and spherical fuzzy Frank weighted geometric (SFFWG) AOs presented by Punetha⁶⁹. It is also noticed that many other AOs are unable to handle SFS-based information such as complex q-rung ortho-pair fuzzy (Cq-ROF) Aczel Alsina power weighted averaging (Cq-ROFAAPWA) and Cq-ROF Aczel Alsina power weighted geometric (Cq-ROFAAPWG) operators established by Khan et al.⁷⁰. Q-rung ortho-pair fuzzy (q-ROF) Aczel Alsina weighted averaging (q-ROFAAWA) and q-ROF Aczel Alsina weighted geometric (q-ROFAAWG) operators diagnosed by Zhang et al.⁷¹. The thought of q-rung ortho-pair fuzzy Sugeno-Weber weighted averaging (q-ROFSWWA) and q-rung ortho-pair fuzzy Sugeno-Weber weighted geometric (q-ROFSWWG) operators developed by Wang et al.⁷². Some interval-valued intuitionistic fuzzy Heronian mean (Iv-IFHM) AOs proposed by Xiong⁷³ and Hussain et al.⁷⁴ explored the thought of Pythagorean fuzzy Hamy mean (PyFHM) AO for decision-making problems.

These discussed AOs failed to handle SFVs based on information because they do not have a concept of AG in their structure, so they cannot deal with SFVs. A comparison with some present approaches is presented in Table 11.

Table 11 Investigation of the suggested theory with currently present AOs.

Where they are used is observed. ${\mathcalligra{t}}_{2}$ be the finest option around all considered alternatives. On the other hand, by using SFDWA and SFDWG operator ${\mathcalligra{t}}_{2}$ be the best alternative, but the remaining sequence is changed while the ${\mathcalligra{t}}_{3}$ and ${\mathcalligra{t}}_{4}$ be the best alternatives by using the SFEWA and SFEWG operators, respectively. The ${\mathcalligra{t}}_{2}$ and ${\mathcalligra{t}}_{4}$ be the best alternative using SFCHWA and SFCHWG operators. While ${\mathcalligra{t}}_{4}$ be the best option by applying SFAAWA, SFAAWG operator. The alternative ${\mathcalligra{t}}_{2}$ and ${\mathcalligra{t}}_{2}$ be the finest alternative using SFFWA and SFFWG operators, respectively. The pictorial format of Table 9 is offered in Fig. 11.

Fig. 11

Shows the comparative analysis with existing AOs.

Figure 11 above shows that the brown line presents the results of SFDWA and SFDWG operators. In contrast, aggregated outcomes by SFEWA and SFEWG operators are presented in the green line. The proposed SFSWPWA and SFSWPWG results are shown in the blue line. Green lines presented the aggregated outcome using SFCHWA and SFCHWG, while blue lines gave SFAAWA and SFAAWA AO results. Orange lines represent the aggregated results using SFFWA and SFFWG operators.

The proposed AOs are more generalized than other existing AOs because they can handle some other existing fuzzy environments, such as IFS Sugeno-Weber operations-based AOs presented by Hussain et al.³ and some PyFS-based AOs discussed by Asif et al.⁷⁵. AOs are based on PFS information proposed by Hussain et al.⁷⁶.

Hence, our proposed AOs have a superior format to the discussed AOs. Because these approaches are only applicable to IFS, PyFS, and PFS information, at the same time, our proposed AOs can handle IFS, PyFS, and PFS information by making minor changes in their structure.

Result and discussion

The framework of SFS is a suitable tool for investigating complex information. The SFS is a more potent environment than other existing FS-based frameworks like IFS, PyFS, and PFS. It can handle all the IFS, PyFS, and PFS information.

In the modern age, the thought of decision-making sciences is one of the most reliable and suitable tools for assessing ambiguous and uncertain information. The scope of MCDM will increase daily due to the rapid increase in market competition. So, in this regard, many mathematicians provided many approaches for the solution of MCDM problems, such as the customized hospital recommendation based on the MCDM technique discussed by Bani-Doumi et al.⁷⁷ and electric vehicle selection using the MCDM approach based formation FS theory proposed by Golui et al.⁷⁸. Enhancing the MCDM approach based on the fuzzy logic concepts for ranking the alternatives developed by Tešić et al.⁷⁹ and the MCDM methodology based on the bipolar fuzzy approach and its application in economic conditions discussed by Jana et al.⁸⁰.

In MCDM, the AOs play a crucial role in aggregating complicated information. In past eras, many mathematicians and data scientists worked a lot to define several AOs, such as Hamacher TN and TCN-based AOs for PyFS discussed by Asif et al.⁷⁵ and some Frank TN and TCN-based AOs under SFS information developed by Alballa et al.⁸¹.

Assessing a blockchain platform to select the best supply chain is an exciting topic. We have proposed the SFSWPWA and SFSWPWG operators and the CoCoSo method for choosing the best blockchain platform. For this, we construct a decision matrix using SFVs-based information by using the list of alternatives like ${\mathcalligra{t}}_{1}$ is hyper ledger fabric, ${\mathcalligra{t}}_{2}$ is Ethereum, ${\mathcalligra{t}}_{3}$ is IBM food trust, and ${\mathcalligra{t}}_{4}$ be the VeChain under defined attributes such as environmental impact, transparency and traceability, cost efficiency, scalability, and flexibility. After applying the developed SFSWPWA and SFSWPWG operators and the CoCoSo method ${\mathcalligra{t}}_{2}$is Ethereum the best platform for the supply chain. To check the applicability of the diagnosed approach, we make a deep comparison with some existing approaches presented by Ashraf et al⁶⁵. and Ashraf et al⁶⁶.. On the other hand, we found that many other present methodologies do not apply to handling SFS-based information, such as Khan et al⁷⁰., Zhang et al.⁷¹, Wang et al.⁷², and Hussain et al.⁷⁴. For convenience, the comparative analysis is also presented in a graphical format in Fig. 9.

The proposed theories are applicable for all those real-life complex sarnies where decision makers need to rank the multiple alternatives based on a list of considered attributes. For example, a decision maker wants to rank five car companies based on multiple attributes like fuel efficiency, durability, manufacturing quality, and resell value. In this regard, we have to collect information in the shape of SFVs and make a decision matrix. Then, we apply our proposed CoCoSo approach and SFSWPWA and SFSWPWG operators to rank the list of alternatives.

The consequences of proposed work

The proposed SFSWPWA and SFSWPWG operators apply to PFS, PyFS, and IFS FS information. The consequences are discussed as follows:

• 1.  If we place $\left({\mathcal{J}}^{2}=\mathcal{J}\text{, }{\text{\rm I}}^{2}=\text{\rm I}\text{, }{\Pi }^{2}=\Pi \right)$ Then, the proposed AOs will be turned from the SFS framework to the PFS-based framework presented by Cuong⁷.

• 2.  If we place $\left({\mathcal{J}}^{2}\text{, }{\text{\rm I}}^{2}=0\text{, }{\Pi }^{2}\right)$ Then, the proposed AOs will turn from the SFS framework to the PyFS-based framework offered by Yager⁵.

• 3.  If we place $\left({\mathcal{J}}^{2}=\mathcal{J}\text{, }{\text{\rm I}}^{2}=0\text{, }{\Pi }^{2}=\Pi \right)$ Then, the proposed AOs will be turned from the SFS framework into the IFS-based framework provided by Atanassov².

• 4.  If we place $\left({\mathcal{J}}^{2}=\mathcal{J}\text{, }{\text{\rm I}}^{2}=0\text{, }{\Pi }^{2}=0\right)$ Then, the proposed AOs will be turned from the SFS framework into the FS-based framework Zadeh gave¹.

On the other hand, many researchers worked extensively in decision-making to aggregate complex information. They presented different methodologies like the VIKOR method, the TOPSIS method, the TODIM method, and many others. However, combining aggregation procedures and compromise solutions, the CoCoSo approach balances comprehensiveness and simplicity. CoCoSo integrates these elements for stronger resilience and flexible decision-making in multi-criteria analysis. While the VIKOR method emphasizes a trade-off solution, the TOPSIS method provides stress proximity to an ideal solution, and TODIM provides a behavioral pattern of alternatives.

In life scenarios where uncertainty and ambiguity are directly or indirectly involved in the decision-making process, the concept of SFVs-based CoCoSo approach, SFSWPWA, and SFSWPWG operators are well-organized and trustful tools for the assessment of information. A few real-life decision-making problems are discussed as follows:

Suppose we want to investigate the best construction company for dam construction based on attributes/characteristics such as previous company experiences, economic background, budget, long-lasting guarantee, etc. Because of these characteristics, we aim to rank the world’s four top-class companies: Bechtel (USA), ACS Group (Spain), VINCI (France), and ELC Electro consult (Italy). The proposed CoCoSo approach, SFSWPWA, and SFSWPWG operators are suitable tools for such a critical situation.

In another scenario, we aim to rank the best mobile phone based on memory storage, battery timing, screen resolution, and market-competitive price attributes. We have a list of the top five mobile manufacturing companies, including Apple (USA), Samsung (South Korea), Xiaomi (China), and Oppo (China). We assign weight to the attributes and then apply our proposed SFSWPWA, SFSWPWG, and CoCoSo methods based on the SFVs.

Conclusion

The topic of MCDM is one of the trending approaches for precise solutions to decision-making problems. In the age of technology, the selection of the best blockchain system for the assessment of supply chain management is a difficult task. In fuzzy set theory, SFS is considered the most generalized form of IFS, PyFS, q-ROFS, and PFS framework. By taking motivation from the concept of SFS, we proposed the CoCoSo method for SFVs-based information. We define Sugeno Weber TN and TCN operations and the concept of PAO, and we develop SFSWPWA and SFSWPWG operators, including essential characteristics of AOs. The detailed algorithms, including their pictorial format and implementation, are also part of the article. A comprehensive case study is presented on the blockchain systems under the investigated well-known blockchains such as Hyperledger Fabric, Ethereum, IBM Food Trust, and VeChain for supply chain by considering the following attributes: environmental impact, transparency, traceability, cost efficiency, scalability, and flexibility. The real-life application of the selection of blockchain for the supply chain is solved through both proposed methodologies. We also investigate the effect of parameters to assess the proposed theory’s reliability. Compare our proposed approach with present approaches to investigate the reliability and flexibility.

Limitations of the proposed

The developed CoCoSo approach, SFSWPWA, and SFSWPWG operators failed to investigate interval-valued based SFS information due to the absence of lower and upper terms in their structure. Also, the proposed theory could not aggregate periodic information (complex information) involving amplitudes and phase terms. The developed theory can also not handle circular SFVs-based details due to the absence of a circular degree.

In the near future, we aim to enhance our proposed work for other different fuzzy frameworks, such as Khan et al.⁸² proposal of the idea of the complex t-spherical fuzzy set (CTSFS) and Ali et al.⁸³ proposal of the complex interval-valued PyFS-based AOs. Ashraf et al.⁸⁴ developed the interval-valued SFS-based Maclaurin symmetric and interval-valued T-spherical by⁸⁵ and⁸⁶.