Static short-range laser circumferential detection using a transmissive-reflective optical architecture

Abstract

To address the problem of short-range laser circumferential detection, this paper proposes a static detection method based on a transmissive-reflective combined optical system, Building upon previous research on dynamic circumferential scanning mechanisms. In the transmissive-reflective optical system, the principle of equal energy distribution is applied to transform an incident Gaussian beam into a uniform-intensity conical detection beam capable of circumferential coverage. Drawing upon near-field laser detection theory and the geometric characteristics of the static detection field, the echo equation for single-pulse detection is derived, and a corresponding echo power distribution model is developed. Simulation results reveal that the annular light radius and beam Tilt angle vary systematically with changes in the cone angle and mirror displacement, while the echo amplitude increases with higher emission power, larger cone angles, greater displacements, and larger target areas. Furthermore, the reshaped flat-top beam achieves an energy RMS error of 3.2%, a peak intensity deviation within ± 4.5% of the mean, and a spot diameter variation of less than 2%, demonstrating excellent energy uniformity and Spatial stability. The proposed short-range laser circumferential detection method expands the detection range, enhances accuracy and energy uniformity, and achieves low-power static omnidirectional detection, offering a novel and efficient solution for target circumferential sensing

Introduction

The laser fuze is an optoelectronic device that utilizes a modulated laser beam to detect a target and initiate the detonation of a missile warhead. It offers high-ranging accuracy and strong anti-electromagnetic interference. It can accurately determine miss distances and is widely employed in air defense missile systems¹. However, the complex and diversified modern battlefield environment imposes stricter requirements on the short-range detection capability of laser fuzes. For example, high-precision strike munitions based on the concept of directional shaped charge detonation^2,3,4. The effective application of directional shaped charge warheads relies on the accurate identification of target orientation. Therefore, short-range laser detection technology must evolve from traditional point-to-point linear detection to enable omnidirectional sensing capabilities^5,6,7.

To address the challenge of short-range omnidirectional laser detection, Su et al.⁸ developed a 12-element laser detection model that enables precise target orientation identification and warhead detonation direction control. Cai et al.⁹ proposed an 8-channel panoramic laser fuze-warhead system designed to enhance target lethality. Systems such as the Thales missile (USA), the THOMSON-THORN missile (UK), and implementations by the Beijing Institute of Technology and the 8358 Institute¹⁰ have achieved omnidirectional spatial laser detection through the deployment of multiple transmitters and receivers. Although these methods cover a large detection space, the use of multiple transceiver modules and optical windows inevitably increases system complexity and reduces stability. In contrast to the static omnidirectional methods above, References^11,12,13 introduced a dynamic omnidirectional detection technique, employing motor-driven bilateral mirrors to achieve pulsed laser dynamic scanning at short range. However, the integration of motors and bilateral mirrors introduces redundant spatial layout and increases susceptibility to electromagnetic interference¹⁴.

However, the aforementioned methods mainly focus on modifying beam divergence along the fast and slow axes, while neglecting energy uniformity across the target surface within the effective detection range. Zhu et al.¹⁵ employed a combination of prism and cylindrical mirror surfaces to mix light, achieving uniform beam distribution within a 15-m range. Zheng et al.¹⁶ utilized an aspherical cylindrical lens arbeam to shape light distribution along the slow axis, resulting in an outgoing beam with uniform angular spread on the sagittal plane. Although these methods achieve local energy uniformity, the outgoing beams in different segments remain linear, and the overall field of view is still pyramidal. Compared to a conical field of view, a pyramidal field offers limited coverage and is prone to gaps or excessive overlap in the transition regions between beams, compromising overall energy uniformity, as well as detection accuracy and interference resistance. While early studies largely relied on linear or pyramidal segmentation strategies, recent efforts have explored more advanced configurations. For example, axisymmetric aspheric mirror (AAM)-based reflectors¹⁷ and metasurface-enabled flat-top beam generators¹⁸ aim to improve spatial coverage and energy consistency. Nevertheless, these approaches still encounter significant practical limitations, including high fabrication complexity, restricted adjustment flexibility, and difficulty in sustaining uniform irradiance over a full 360° range. Recent optical research confirms that conical beam configurations outperform pyramidal counterparts in maintaining spatial uniformity and reducing boundary interference, particularly in laser-based circumferential detection systems^15,19.

In contrast to conventional multi-channel static and motor-driven dynamic scanning systems, the proposed static circumferential detection architecture based on a transmissive-reflective optical configuration offers several key advantages regarding overall system performance. First, the static design removes reliance on mechanical scanning components, thereby reducing system response latency and enabling quasi-instantaneous target detection. Second, the elimination of moving components shortens the scanning cycle duration and significantly improves system operational reliability. Third, the optical layout is both compact and efficient, requiring fewer optical components and consuming significantly less power than conventional multi-laser or motor-driven counterparts. Lastly, by eliminating electromagnetic motor actuators and employing entirely passive optical beam shaping mechanisms, the proposed system demonstrates enhanced electromagnetic interference immunity, which is particularly advantageous in electromagnetically complex operational environments.

To overcome the limitations of existing laser short-range circumferential detection approaches, this study builds upon prior research on dynamic circumferential scanning mechanisms and proposes a static detection method based on a transmissive-reflective combined optical system. In the transmission subsystem, a mapping function is derived based on the principle of equal energy segmentation, relating the projection heights of incident and outgoing beams, followed by lens parameter optimization. The Gaussian input beam is first reshaped into a flat-topped circular beam, ensuring uniform intensity distribution. In the reflective subsystem, the geometric parameters of the fixed conical mirror, parabolic cylindrical mirror, and conical moving mirror are determined by adjusting the annular light diameter control range and working distance, based on geometrical beam tracing principles. The flat-topped beam is further reshaped into a conical detection beam with uniform intensity, whose radius and forward angle are tunable, enabling effective circumferential detection. Based on near-field laser detection theory and the spatial geometry of the static detection field, the echo equation for single-pulse short-range detection using the transmissive-reflective optical system is derived, and a corresponding echo power distribution model is established. The effects of key system parameters on the echo distribution of single-pulse short-range static circumferential detection are simulated and analyzed. A detailed design methodology for the short-range circumferential detection field is presented based on geometric optics, and its performance is further analyzed and validated using physical optics simulations. The overall system features a compact structure with minimal optical components, making it well-suited for short-range laser circumferential detection.

Optical system design

The operating principle of short-range static circumferential laser detection based on a transmissive-reflective optical configuration is illustrated in Fig. 1.

Fig. 1

The principle diagram of laser beam expanding short-range static circumferential detection based on transmissive-reflective combination.

The overall system primarily consists of two modules: the transmission flat-topped light shaping system and the reflective focusing circumferential detection field shaping system. A driving circuit triggers the Gaussian laser emitter to initiate emission. Simultaneously, the trigger signal also serves as the start signal for distance measurement. The Gaussian beam passes through two aspheric lenses to generate a collimated flat-top beam with uniform energy distribution. The beam then enters a hollow total reflector, guiding it into the reflective focusing module for circumferential field shaping. The flat-top beam is deflected by a conical reflector to form a uniform radial detection field (at a 90° angle), then converged by a focusing mirror and an adjustable conical moving mirror into a static circumferential field of view with a specified forward angle. While the fixed conical mirror and focusing mirror are fixed in place, the conical moving mirror can be either translated along the optical axis or have its cone angle adjusted, thereby enabling continuous tuning of the forward angle of the circumferential detection beam, this adjustment also contributes to more uniform energy distribution on the defocused plane, thereby enhancing detection accuracy. The target echo signal is first reflected by the focusing mirror to the hollow full-reflector, then directed to a receiving lens which focuses it onto a photosensitive detector. Finally, photoelectric signal processing is performed to complete the static circumferential target detection.

Transmission flat-top beam shaping design

The objective of transmitted flat-top beam shaping is to convert the centrally peaked Gaussian energy distribution into a flat-top beam with uniform intensity across the aperture. The design is based on the principle of equal energy segmentation. According to the conditions that the total incident energy equals the total output energy, and that incident and output intensity distributions are preserved over intervals R₁ and R₂¹⁹, the resulting transmission flat-top beam shaping system is illustrated in Fig. 2.

Fig. 2

Formation of transmission flat-top beam.

Given a known input energy A within radius R₁, r the system ensures that the output energy B within radius R₂ matches the input, thereby maintaining energy conservation. For an input Gaussian beam with waist radius $\:w$ and energy $\:\frac{1}{{\text{e}}^{2}}$, the output profile after shaping exhibits a uniform plateau within a radius R. The irradiance distribution of the input light is $\:P{\text{e}}^{\frac{-2{x}^{2}}{{w}^{2}}}$, while the output irradiance is modeled as a step function with constant intensity H within radius $\:R$. The input and output energy distributions over the intervals R₁ and R₂ are given by:

$$\:\begin{array}{c}A={\int\:}_{0}^{{R}_{1}}2{\uppi\:}xP{\text{e}}^{\frac{-2{x}^{2}}{{w}^{2}}}\text{d}x \end{array}$$

(1)

$$\:\begin{array}{c}B=\pi\:H{{R}_{2}}^{2} \end{array}$$

(2)

Let $\:A=B$, that is:

$$\:\begin{array}{c}{{R}_{2}}^{2}=\frac{P{w}^{2}}{2H}\left(1-{\text{e}}^{\frac{-2{{R}_{1}}^{2}}{{w}^{2}}}\right) \end{array}$$

(3)

Since input and output energies are equal, we obtain:

$$\:\begin{array}{c}\pi\:H{R}^{2}=-\frac{{\uppi\:}P{w}^{2}}{2}\left[{\text{e}}^{\frac{-2{x}^{2}}{{w}^{2}}}\right]\left|\genfrac{}{}{0pt}{}{{\infty\:}}{0}\right.=\frac{{\uppi\:}P{w}^{2}}{2} \end{array}$$

(4)

Combining Eqs. (3) and (4), we derive:

$$\:\begin{array}{c}{R}_{2}=R\sqrt{\left(1-{\text{e}}^{\frac{-2{{R}_{1}}^{2}}{{w}^{2}}}\right)} \end{array}$$

(5)

The relationship between the projection height R₁ of the incident Gaussian beam and the projection height R₂ of the output flat-top beam relative to the optical axis is established, as shown in Eq. (5). Using the mapping function, the projection heights of rays in the flat-top beam are computed for different incident angles and used in optical design software to optimize lens surface parameters accordingly.

The apodization factor is introduced and defined as:

$$\:\begin{array}{c}q={d}^{2}/{w}^{2} \end{array}$$

(6)

Here, $\:d$ denotes the radius of the incident pupil, and $\:w$ represents the waist radius of the incident Gaussian beam. The apodization factor $\:q$, introduced in beam shaping theory, quantifies the rate at which the light intensity decays along the $\:x$ -direction and plays a crucial role in shaping the output flat-top beam profile. This parameter has been widely employed in prior optical system designs²⁰, and its typical value for collimated Gaussian inputs ranges from 1.5 to 3.5, depending on the desired uniformity of the flat-top distribution.

Substitute Eq. (6) into Eq. (5), and assuming that the collimating lens radius is much larger than the pupil radius, the simplified mapping function becomes:

$$\:\begin{array}{c}{R}_{2}=R\sqrt{\left(1-{\text{e}}^{\frac{-2{q{R}_{1}}^{2}}{{d}^{2}}}\right)} \end{array}$$

(7)

In flat-top shaping systems with a large apodization factor, the lens must accommodate greater angular deflection compared to systems with smaller apodization values. This leads to smaller radii of curvature and more complex, non-uniform lens surface geometries. Consequently, wavefront aberration control becomes more challenging during collimation optimization.

Design of reflective focusing circumferential detection system

The reflective focusing system for shaping the circumferential detection field can be designed based on parameters such as detection field size and adjustment range, incident beam diameter, optical system dimensions, beam forward angle, and working distance, as illustrated in Fig. 3. The system comprises a fixed conical mirror, a parabolic cylindrical mirror, and a conical moving mirror, which are rotational surfaces generated by revolving the conical line U, parabola P and conical line M about the optical axis z, respectively. The parabola P has its symmetry axis aligned with a straight line $\:x$. The flat-top beam undergoes three reflections within the system and is focused at a point F₁. The focal point F₁ lies at an off-axis distance r from the z-axis, resulting in a focused annular beam with radius r on the focal plane. As the annular flat-top beam defocuses, its ring width increases with detection distance, forming a uniform-intensity circumferential detection field.

Fig. 3

Reflective focusing circumferential detection distribution shaping system.

In Fig. 3, the half-apex angle of the fixed conical mirror is $\:\phi\:=45^\circ\:$, and the vertex coordinate is$\:\left(0,{z}_{U}\right)$. The corresponding cone line equation is then given by:

$$\:\begin{array}{c}z=x-{z}_{U}\end{array}$$

(8)

where $\:{z}_{U}$ is the distance between the vertex of the fixed conical mirror and the $\:x$-axis, which is determined by the actual laser working distance and the radius of the incident flat-toppedped light.

Let the coordinates of point Q and point K on the conical moving mirror be known as $\:Q({x}_{Q},{z}_{Q})$ and $\:K(0,{z}_{K})$, respectively. The generating line M is then defined by:

$$\:\begin{array}{c}z=\frac{{x}_{Q}-x}{\text{tan}\alpha\:}-{z}_{Q}\:,\:{z}_{Q}\le\:z\le\:{z}_{Q}+{x}_{Q}/\text{tan}\alpha \end{array}$$

(9)

When selecting point Q, factors such as lateral system size, mirror diameter, and translation distance L should be comprehensively considered.

The parabolic cylindrical mirror is generated by rotating a parabola P, whose equation is:

$$\:\begin{array}{c}{\left(z-{z}_{F}\right)}^{2}=-4f\left(x-\left(f+{x}_{F}\right)\right) \end{array}$$

(10)

The focus F has coordinates $\:({x}_{F},{z}_{F})$, and the parabola’s focal length is denoted as f. As shown in Fig. 3, the focus F is the symmetric point of $\:{F}_{1}$ with respect to the generating line M of the conical moving mirror. The focal point on the focal plane essentially moves along the line segment $\:F{F}_{1}$ perpendicular to the cone line $\:W({x}_{W},{z}_{U})$. Substituting point w into the parabola equation, the focal length f can be determined. The value of $\:{x}_{W}$ should take into account the radial size of the system, the focus F position and the transverse length of the conical moving mirror.

If the focus coordinates are known, then $\:r$ can be expressed by $\:({x}_{F},{z}_{F})$:

$$\:\begin{array}{c}r=\frac{{x}_{F}\left(1+{\text{t}\text{a}\text{n}}^{2}\alpha\:\right)-2{x}_{Q}-2{z}_{Q}\text{tan}\alpha\:}{{\text{t}\text{a}\text{n}}^{2}\alpha\:-1}\\\:={x}_{Q}+{z}_{Q}\text{tan}\alpha\:+\frac{{z}_{F}\left(1+{\text{t}\text{a}\text{n}}^{2}\alpha\:\right)}{-2\text{tan}\alpha\:}\end{array}$$

(11)

Fig. 4

The change curve between L and radius $\:{\text{r}}_{\text{1,2}}$.

Fig. 5

The variation curve between α and radius $\:{\text{r}}_{\text{1,2}}$.

Figure 4 shows that when the conical moving mirror displacement is fixed at 5 mm, and the cone angle α varies from 7° to 23°, the annular beam radius $\:{r}_{\text{1,2}}$ on the focal plane decreases as α increases. Figure 5 illustrates that with the cone angle fixed at 15°, increasing the mirror displacement L from 0 to 10 mm results in a larger annular beam radius $\:{r}_{\text{1,2}}$ on the focal plane.

The tilt angle of the beam reflected at point Q is given by:

$$\:\begin{array}{c}{\theta\:}_{1}=\text{arctan}\left(\frac{r-{x}_{Q}}{{z}_{Q}+L}\right)\end{array}$$

(12)

For the beam reflected by the K point, the beam forward tilt angle is expressed as:

$$\:\begin{array}{c}{\theta\:}_{2}=\text{arctan}\left(\frac{r\text{tan}\alpha\:}{({z}_{Q}+L)\bullet\:\text{tan}\alpha\:-{x}_{Q}}\right)\end{array}$$

(13)

The beam forward tilt angle of the circumferential detection field of view can be approximately expressed as:

$$\:\begin{array}{c}\theta\:=\frac{{\theta\:}_{1}+{\theta\:}_{2}}{2}\\\:=\frac{1}{2}\text{arctan}\left(\frac{({z}_{Q}+L)\bullet\:\text{tan}\alpha\:\left(2r-{x}_{Q}\right)+{x}_{Q}\left({x}_{Q}-r\right)}{{({z}_{Q}+L)}^{2}\bullet\:\left(\text{tan}\alpha\:-{x}_{Q}\right)+r\text{tan}\alpha\:\left({x}_{Q}-r\right)}\right) \end{array}$$

(14)

Fig. 6

The variation curve between α and θ.

Fig. 7

The variation curve between L and θ.

From Eqs. (13) and (16), it is evident that the forward angle of the focused annular beam changes with variations in the cone angle $\:\alpha\:$ and displacement L of the conical moving mirror, as shown in Figs. 6 and 7. As shown in the figures, the forward angle decreases as the cone angle $\:\alpha\:$ increases, and increases with greater displacement L. The cone angle has a more pronounced effect on the beam angle than the displacement.

Echo characteristics

For a detection system using a Gaussian laser as the emission source, the pulse echo power can be described by²¹:

$$\:\begin{array}{c}{P}_{r}=\frac{{P}_{t}{G}_{t}}{4{\uppi\:}{R}_{t}^{2}}\frac{\sigma\:}{4{\uppi\:}{R}_{r}^{2}}\frac{{\uppi\:}{D}^{2}}{4}{\eta\:}_{a}^{2}{\eta\:}_{s} \end{array}$$

(15)

where $\:{P}_{t}$ is the laser emission power; $\:{G}_{t}$ is the emission gain; $\:{R}_{t}$ and $\:{R}_{r}$ are the distance between the laser transmitting system and the receiving system and the target, respectively. $\:\sigma\:$ is the scattering cross-section area; $\:D$ is the receiver aperture diameter; $\:{\eta\:}_{a}$ is the atmospheric transmittance; $\:{\eta\:}_{s}$ is the optical transmittance of the laser detection system.

Gaussian beams exhibit energy concentration at the center, resulting in inefficient edge utilization. In contrast, flat-top beams have uniform energy distribution, significantly improving illumination efficiency over the target area. Therefore, when using a flat-top laser source, the echo power equation must be reformulated to account for its distinct intensity profile. The flat-top laser features a uniform spatial intensity distribution and a narrow beam divergence angle. Assuming the target depth is negligible relative to the detection distance, the transverse intensity distribution can be modeled as a function of x and y, with negligible variation along the z-axis. The spatial intensity distribution is expressed as:

$$\:\begin{array}{c}I\left(x,y\right)=\left\{\begin{array}{c}\frac{{P}_{t}}{{\uppi\:}{R}_{0}^{2}},\:\sqrt{{x}^{2}+{y}^{2}}\le\:{R}_{0}\\\:0,\sqrt{{x}^{2}+{y}^{2}}\ge\:{R}_{0}\end{array}\right.\end{array}$$

(16)

where $\:{R}_{0}$ is the radius of the flat-topped beam.

The radar cross section (RCS) is obtained by integrating the differential RCS over each surface element of the target:

$$\:\begin{array}{c}\sigma\:=\rho\:\iint\:I\left(x,y\right)\text{cos}\beta\:\text{d}A\end{array}$$

(17)

where ρ denotes the target surface reflectivity; $\:\beta\:$ is the incidence angle; $\:dA=dxdy$ is the unit facet of the scattering cross section.

Substituting Eq. (16) into Eq. (17) yields the following expression for the total RCS:

$$\:\begin{array}{c}\sigma\:=\rho\:{A}_{t}\text{cos}\beta\:\bullet\:\frac{{P}_{t}}{{\uppi\:}{R}_{0}^{2}} \end{array}$$

(18)

where $\:{A}_{t}$ denotes the effective projection area of the target.

The time-integrated expression of the flat-top laser echo power is given by:

$$\:\begin{array}{c}{P}_{r}\left(t\right)=\frac{{\uppi\:}{D}^{2}{\eta\:}_{a}^{2}{\eta\:}_{s}}{4{R}_{r}^{2}}\iint\:I\left(x,y\right){P}_{t}\left({t}^{,}\right){f}_{r}\left({\upbeta\:}\right)\text{cos}\beta\:\text{d}x\text{d}y \end{array}$$

(19)

where $\:{f}_{r}\left(\bullet\:\right)$ represents the bidirectional reflectance distribution function^22,23,24.

For a Gaussian laser, the temporal pulse profile follows a heavy-tailed distribution, whereas a flat-top pulse maintains a constant intensity throughout the duration. To account for the rise and fall edges of a real laser pulse, a transition region is introduced. The temporal intensity profile of the flat-top pulse is represented by the following piecewise-defined function:

$$\:\begin{array}{c}f\left(t\right)=\left\{\begin{array}{c}{P}_{0}{\left(\frac{t}{{\tau\:}_{1}}\right)}^{2}\text{exp}\left(-\frac{t}{{\tau\:}_{1}}\right),0\le\:t<{t}_{1}\left(ascent\:stage\right)\\\:{P}_{0},{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:t}_{1}\le\:t<{t}_{2}\:\:\:\:\:(flat\_topped\:stage)\\\:{P}_{0}exp(-\frac{t-{t}_{2}}{{\tau\:}_{2}}),t>{t}_{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\left(waning\:stage\right)\end{array}\right. \end{array}$$

(20)

where $\:{P}_{0}$ denotes the constant peak power of the flat-top laser, and t denotes the pulse duration.

Substituting the temporal profile, spatial irradiance, and scattering model into Eq. (19) leads to the final expression for the received echo energy:

$$\:\begin{array}{c}{P}_{r}={P}_{0}\bullet\:\frac{{{\uppi\:}D}^{2}}{{4R}_{r}^{2}}\bullet\:{\eta\:}_{a}^{2}{\eta\:}_{s}\bullet\:\frac{{P}_{t}}{{\uppi\:}{R}_{0}^{2}}\bullet\:{\iint\:}_{{x}^{2}+{y}^{2}\le\:{R}^{2}}^{}{f}_{r}\left({\upbeta\:}\right)\text{cos}\beta\:\text{d}x\text{d}y \end{array}$$

(21)

The relationship between $\:{P}_{0}$ and the peak power of a Gaussian pulse $\:{P}_{G}$ is given by:

$$\:\begin{array}{c}{P}_{G}=\frac{2{P}_{0}{R}_{0}}{{w}^{2}} \end{array}$$

(22)

$$\:\begin{array}{c}{P}_{t}={P}_{G}{\text{e}}^{\frac{-2{\left(x-{x}_{0}\right)}^{2}}{{w}^{2}}}\#\left(25\right)\end{array}$$

(23)

Fig. 8

Spatial distribution model of laser static circumferential detection field.

In this paper, a transmissive-reflective combined optical detection system is proposed to extend the spatial coverage of laser-based circumferential scanning, as illustrated in Fig. 8. After passing through the focusing circumferential reflection system, the pulsed laser beam forms a static circumferential scanning field of view for the detection of ultra-short-range approaching targets. Let us define the vertex of the conical moving mirror as the coordinate origin. The half cone angle is denoted as $\:\alpha\:$, and the distance from the vertex to the post-expansion laser detection plane is d.

It is assumed that the projected area of the target on the detection plane is $\:{L}_{1}^{{\prime\:}}\times\:{L}_{2}^{{\prime\:}}$, with four vertices denoted as $\:{A}^{{\prime\:}}$, $\:{B}^{{\prime\:}}$, $\:{C}^{{\prime\:}}$ and $\:{D}^{{\prime\:}}$, respectively. The corresponding projection of this target area onto the laser emission beam plane (at the cone vertex) is $\:{L}_{1}\times\:{L}_{2}$, with vertices labeled A, B, C and D, respectively. Then the pulse laser echo power corresponding to this projected area is given by:

$$\:\begin{array}{c}{P}_{r}={P}_{0}\bullet\:\frac{{{\uppi\:}D}^{2}}{{4R}_{r}^{2}}\bullet\:{\eta\:}_{a}^{2}{\eta\:}_{s}\bullet\:\frac{{P}_{t}}{{\uppi\:}{R}_{0}^{2}}\bullet\:{\int\:}_{{x}_{D}}^{{x}_{A}}{\int\:}_{{y}_{A}}^{{y}_{B}}{f}_{r}\left({\upbeta\:}\right)\text{cos}\beta\:\text{d}x\text{d}y\\\:=\frac{{\eta\:}_{a}^{2}{\eta\:}_{s}{P}_{0}{{P}_{t}D}^{2}{L}_{1}{L}_{2}}{{4R}_{r}^{2}{R}_{0}^{2}}\bullet\:{f}_{r}\left({\upbeta\:}\right)\text{cos}\beta\: \end{array}$$

(24)

After passing through the reflection system, the spatial distribution characteristics of the flat-topped laser beam are altered. The laser echo power $\:{P}_{r}^{{\prime\:}}$ of the detection plane after shaping is affected by the reflectivity $\:{\eta\:}_{r}^{{\prime\:}}$ of the shaping system. The pulse laser echo power due to the target located within the projected region on the detection plane is expressed as:

$$\:\begin{array}{c}{P}_{r}^{{\prime\:}}=\frac{{\eta\:}_{r}^{3}{\eta\:}_{a}^{2}{\eta\:}_{s}{P}_{0}{{P}_{t}D}^{2}{L}_{1}^{{\prime\:}}{L}_{2}^{{\prime\:}}}{{4R}_{r}^{2}{R}_{1}^{2}}\bullet\:{f}_{r}\left({\upbeta\:}\right)\text{cos}\beta\:\end{array}$$

(25)

where $\:{R}_{1}$ denotes the beam radius after passing through the reflection system. The specific value is related to the cone reflection angle $\:\beta\:$ and the cone vertex position. When the detection distance is much greater than the length of the conical moving mirror, the following approximation holds:

$$\:\begin{array}{c}{R}_{1}^{2}={d}^{2}\left({\text{tan}}^{2}{\theta\:}_{2}-{\text{tan}}^{2}{\theta\:}_{1}\right) \end{array}$$

(26)

From the above derivation and Eqs. (25) and (26), it is evident that the echo distribution function for single-pulse short-range static circumferential detection is proportional to the transmitted laser power $\:{P}_{t}$, and strongly influenced by parameters such as the half cone angle $\:\alpha\:$, the moving distance L, and the effective projection area of the target. The influence of these parameters on the single-pulse short-range static circumferential echo distribution will be analyzed individually through simulation. The relevant simulation model parameters used for analysis are listed in Table 1.

Table 1 Simulation calculation model parameter setting.

The pulse laser emission power plays a critical role in determining the echo signal characteristics of single-pulse short-range static circumferential detection. The target projection area is fixed at $\:30\:\text{c}\text{m}\times\:30\:\text{c}\text{m}$, the half cone angle of the conical moving mirror is 15°, and the moving distance is set to 0 mm, the emission peak power is varied from 10 W to 30 W in steps of 5 W. The pulse laser echo signals at different emission power levels are illustrated in Fig. 9.

Fig. 9

Laser echo signals with different pulse emission power.

As shown in Fig. 9, the echo amplitude increases noticeably with a larger cone angle. This enhancement is primarily attributed to improved beam concentration and reduced angular divergence, which allow more optical energy to be directed toward the target region.

The conical moving mirror is a key element of the system architecture. Its cone angle and axial displacement govern the spatial coverage of the single-pulse laser beam and significantly influence the target echo power. To evaluate how the cone angle of the conical moving mirror affects the echo signal, the following conditions are applied: the emission power is fixed at 20 W, the target projection area is $\:30\:\text{c}\text{m}\times\:30\:\text{c}\text{m}$, and the moving mirror remains stationary (L = 0 mm), The half cone angle is varied from 8° to 20° in 3° increments. From Fig. 4, it can be seen that the radius of the circumferential detection beam changes with the half cone angle of the cone. Therefore, the pulse laser echo signals at different half cone angles of the conical moving mirror are shown in Fig. 10.

Fig. 10

Laser echo signals of different conical moving mirror half cone angle.

As shown in Fig. 10, increasing the mirror displacement expands the annular footprint of the beam, which increases the illuminated area and results in stronger echoes from targets within the field of view, particularly in mid-range sectors.

To investigate the effect of the axial displacement L of the conical moving mirror on the echo signal, the following parameters are held constant, the laser emission power is set to 20 W, the target projection area is $\:30\:\text{c}\text{m}\times\:30\:\text{c}\text{m}$, and half cone angle fixed at 15°. The displacement L is varied from 0 mm to 16 mm in 4 mm increments. As demonstrated in Fig. 5, the detection beam radius varies with the displacement of the conical moving mirror. The corresponding echo waveforms for different values of L are presented in Fig. 11.

Fig. 11

Laser echo signals of different moving distances of conical moving mirrors.

As illustrated in Fig. 11, the echo amplitude exhibits a nearly linear increase with respect to the laser emission power, validating the consistency of the model with fundamental energy conservation principles.

The target’s projected area represents the region illuminated by the laser circumferential detection field, and the echo signal corresponds to the laser energy reflected from this region. Next, the influence of varying target projected area sizes on the echo signal in single-pulse short-range static circumferential detection is analyzed. The laser emission power is set to 20 W, the half cone angle is set to 15°, and the mirror displacement is 0 mm. The target projection area is varied from 10 cm×10 cm to 50 cm×50 cm. The corresponding pulse echo signals for different target projection areas are illustrated in Fig. 12.

Fig. 12

The laser echo signal of different target size projection area.

As presented in Fig. 12, larger target projection areas intercept more of the beam’s energy, thereby reflecting stronger signals. This effect becomes increasingly pronounced when the target size approaches the beam diameter.

In summary, as the pulse emission power, cone angle, mirror displacement, and target projection area increase, the amplitude of the echo signal also increases accordingly. The influence of the cone angle of the conical moving mirror on the echo signal is especially pronounced.

Simulation and analysis

A comprehensive design of the transmissive-reflective optical system for circumferential detection is presented in Fig. 13. The length of the parabolic cylindrical mirror is limited to match the height of the fixed conical mirror, which simplifies fabrication and reduces the overall system size.

Using a semiconductor laser as the light source, the incident beam is assumed to be a Gaussian collimated beam with a wavelength of 905 nm, a pupil radius of 9 mm, a waist radius of 6.36 mm, and an apodization factor of 2. The flat-topped beam radius is specified as 16.8 mm, with high collimation quality. Firstly, R₁ is obtained by equal interval sampling of pupil radius, and the corresponding R₂ is calculated. In the optical design software, the incident beam projection height is normalized, and the normalized pupil coordinate is expressed as R₁/$\:{R}_{\text{p}\text{u}\text{p}\text{i}\text{l}}$, with the corresponding target value set as R₂. Finally, the mapping data is entered using the REAY operand, and the ANAR operand is used to optimize beam collimation.

Fig. 13

Non-sequential solid model.

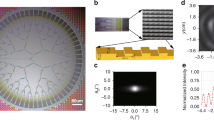
In the ZEMAX sequence mode, Fig. 14a illustrates the designed transmissive flat-top beam shaping system, which consists of two flat-convex high-order aspheric surfaces. The material used is K9 glass, featuring regular optical geometry and smoothly varying curvature. Figure 14b,c show the energy distribution and intensity profile of the incident Gaussian beam, while Fig. 14d,e present those of the shaped flat-top beam. The results demonstrate that the outgoing beam exhibits high spatial uniformity.

Fig. 14

Design results of transmissive flat-topped beam shaping system.

In the ZEMAX non-sequential mode, Fig. 15 depicts the reflective focusing system for circumferential beam shaping, composed of a parabolic cylindrical mirror, a fixed conical mirror, and a conical moving mirror. Figure 15b,c show the simulated intensity distributions of the annular beam received at the detector plane located at the system’s focal plane. Figure 15d,e present the corresponding intensity distributions at a defocused plane. If the Gaussian laser beam bypasses the initial flat-top shaping stage and directly enters the reflective shaping system, the resulting focal-plane beam remains annular but follows a Gaussian intensity distribution. When defocused, the annular beam broadens, but its energy becomes asymmetrically concentrated, reducing the system’s robustness against interference and degrading detection accuracy. Figure 15d illustrates the intensity distribution of the defocused annular detection beam shaped by the flat-top optics. As shown in the defocus curve of the flat-topped beam in Fig. 15e, the intensity remains relatively uniform across the full beam width, which effectively enhances both detection accuracy and coverage. This demonstrates clear advantages over Gaussian-beam-based configurations.

Fig. 15

Design results of reflective focusing circumferential detection beam shaping system.

As analyzed in Sect. 2.2, adjusting the cone angle and axial displacement of the conical moving mirror allows control over the forward angle and radius of the annular circumferential detection beam, as illustrated in Fig. 16.

From Fig. 16, it is evident that the effects of the cone angle and axial displacement on the focal-plane beam size align with the analysis presented in Sect. 1.2. The axial displacement of the fixed conical mirror has a limited effect on beam size, making it suitable for fine-tuning applications. In contrast, changes in the cone angle significantly impact the beam size, allowing for adjustment of the system’s detection range. However, as the detection radius increases, the peak intensity of the annular beam is inevitably reduced due to energy conservation. In practical applications, the laser output power can be increased as needed to enhance both detection range and accuracy.

In the non-sequential mode of ZEMAX, we evaluated three key performance metrics based on the simulated irradiance distribution at the focal plane: the root-mean-square (RMS) error of energy uniformity, the peak intensity deviation, and the variation in focal spot diameter. The simulation results indicate that the flat-top beam produced by the proposed shaping method yields an RMS error of 3.2%, with the peak intensity deviation confined within ± 4.5% of the mean, and a spot diameter variation of less than 2% along the annular direction. These metrics collectively verify the high uniformity and spatial stability of the system.

Compared with the conventional configuration that directly focuses Gaussian input beams using reflective optics, the proposed method achieves substantially improved irradiance uniformity, along with enhanced system robustness and reduced susceptibility to beam distortion.

Fig. 16

Design results of reflective focusing circumferential detection beam shaping system. (a) The influence of the cone angle of the conical moving mirror on the beam size. (b) The influence of the moving distance of the conical moving mirror on the beam size.

Conclusion

To address the requirements of short-range circumferential detection in terms of coverage, accuracy, and energy uniformity, this study proposes a static laser detection method based on a transmissive-reflective combined optical architecture. By applying equal-energy segmentation and integrating aspherical lenses with reflectors, the system reshapes an incident Gaussian beam into a conical beam with uniform intensity, adjustable radius, and forward tilt.

Based on near-field laser detection theory and the geometric configuration of the static detection field, the echo equation for single-pulse detection is derived, and a corresponding echo power distribution model is established. Simulation results show that the annular spot radius and beam tilt angle vary systematically with changes in cone angle and mirror displacement, while the echo amplitude increases with higher laser power, larger cone angles, greater mirror displacements, and expanded target areas. The spatial symmetry of the detection field remains consistent across different configurations. Quantitative analysis further confirms the system’s beam-shaping performance, yielding an energy RMS error of 3.2%, a peak intensity deviation within ± 4.5% of the mean, and a spot diameter variation of less than 2%, thereby demonstrating excellent beam uniformity and spatial stability. Compared with conventional motor-driven scanning systems²⁵, which typically consume 5–15 W to achieve full coverage, the proposed static architecture operates at less than 1 W under equivalent conditions, resulting in power savings of up to 80-90%.

Overall, the proposed method enables efficient, low-power, and omnidirectional target sensing with reduced system complexity, offering a promising solution for static short-range laser circumferential detection.