Introduction

Decreasing uncertainty of multi-element geochemical anomaly mapping is a challenging procedure. Decreasing uncertainty is so necessary for geochemical anomaly mapping in a study area. Because, recognition of multi-element geochemical anomalies can facilitate to detect hidden deposits1. In regional scale, multi-element geochemical anomaly detection is performed employing stream sediments geochemical data. The stream sediments geochemical data is extremely under efficacy of complex geological features2,3,4,5. Hence, this data is a nonlinear multivariate input which requires capable processing models5,6. Whereas, traditional procedures have not necessary capability to process them but advanced machine learning (AML) frameworks are appropriate substitutes to perform this task1,3,7,8,9,10,11,12,13,14. Among applied machine learning models, random forest (RF), artificial neural networks and support vector machine were the most useful methods for multi-element geochemical anomaly detection15,16,17. The RF method is a developed form of decision trees which can be applied for classification and regression18,19,20,21. Three known hyperparameters of the RF comprising number of trees (NT), number of splits (NS) and depth (D) extremely need to be optimized for reduction of uncertainties in multi-element geochemical anomaly detection. Although, applied ML models have better conclusions than traditional methods but majority users tune their hyperparameters through performing trial-and-error procedure. While, applying trial-and-error is an onerous and time-consuming way which can not be eventuated to reliable results22,23,24. Fortunately, numerous nature-inspired optimization techniques have been designed to remove trial-and-error procedure of tuning stage of the ML hyperparameters in recent decade. These techniques commonly inspire by the social life behavior of creatures. In this regard, firefly algorithm25,26, dolphin echolocation27,28, cuckoo search29, bat algorithm30, whale optimization algorithm24 and grey wolf optimizer31, wild horse optimizer32, Harris hawks optimization (HHO) algorithm23 and so on were introduced to optimize ML models applied in medical, industrial, agriculture and geoscience fields33,34,35,36. Indeed, these optimization techniques have been widely regarded due to i) inspiring from nature, ii) considering problems as black boxes, iii) avoidance of falling to great local optima, iv) containing gradient-free mechanism37. Optimization techniques are usually selected based on: 1) which does hyperparameter of a specific ML model need to be optimized? and 2) should that hyperparameter be maximized or minimized? In recent decade, several AML frameworks were constructed hybridizing the ML models with nature-inspired optimization techniques to recognize multi-element geochemical anomalies38,39,40. Accordingly, research proposal is integration of the RF model due to its popularity, computational attractiveness, great inference power with the HHO algorithm due to its robust conclusions in comparison to 11 optimization algorithms23. In fact, hybridization of the RF model with HHO was applied to eliminate trial-and-error of training stages and decreases uncertainties of geochemical anomaly mapping. It is noteworthy, results demonstrate effect of eliminating trial-and-error procedure in tuning hyperparameters of the RF model. Difference of performance of the AML model applied to conventional RF model is rather than 6% which can be confirmed considering success-rate curves.

Region of interest

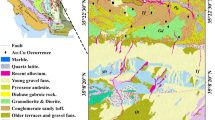
A main mineral potential zone from NE Iran is the Feyzabad district. The Feyzabad is known as a high potential area of the iron oxide copper–gold (IOCG) and vein-type Au-Cu mineralizations which is restricted between 58° 30´ 0˝ E and 59° 0´ 0˝ E longitudes and 35° 0´ 0˝ N and 35° 30´ 0˝ N latitudes4,41. Its significant mineralization occurrences are Zarmehr (IOCG), Tanourjeh (vein-type), Baharieh (IOCG), Sarsefidal (IOCG), Kamarmard (IOCG) and Kalateh timor. This area is a segment of the boundaries of the internal Iranian microcontinent which places between the Loot Block and the Central Iran zones. It is seen, numerous faults and fractures are related to mineralization occurrences in this area. In this regard, the darouneh fault as the longest fracture plays a significant role in forming deposits of the Feyzabad district. Granodiorite, diorite, pyroxene andesite and diabase gabbroic rock are the most significant volcanic structures which are frequently observed there (Fig. 1). Also, alternations of sedimentary and carbonated rock units comprising reddish and sandstone conglomerate, gypsiferous marl, dolomitic limestone, silty shale and quartz latite which belong to middle- to upper-Cambrian era and accompany mentioned volcanic rock units (Fig. 1)42. The vein-type Au-Cu and the IOCG deposits are mainly hosted by diorite and granodiorite intrusions of Eocene–Oligocene age in this area. Elements Au, Cu, Bi, Pb, Zn, Sb and As demonstrated spatial correlation to mineralization occurrences. But, Appropriate pathfinder elements Au, Cu, Sb, Zn and Pb with specific thresholds were chosen based on a novel deep framework presented by7,18 to trace mineralization occurrences in the study area43.

Fig. 1
figure 1

Simplified geological map (1:100,000) of the Feyzabad district, NE Iran. This map is an improved version of its original version presented by geological survey & mineral exploration organization from Iran as public (https://gsi.ir/). This version has been improved applying GIS software 10.6 toolbox.

Full size image

Methods and materials

Conventional random forest method

The RF method is applied for classification and regression which was first introduced by44. Training process in the RF method is performed applying “bagging” procedure. This method creates many decision trees and integrates them to predict information precisely. Each decision tree is trained by a random sample of inputs. Within the forest, a sample is classified into a class which get majority votes of overall decision trees. A schematic flowchart of the conventional RF classification algorithm has been shown in Fig. 2. Three hyperparameters of the RF comprising NT, NS and D should be tuned to present reliable data classification. In this concept, increasing NT value can increase accuracy of classification but value of the NT should be optimized because additional NT wastes training time. Unsuitable NS value can create under-fitting problem in prediction procedure45. Because, each decision tree with rather splits is considered deeper. Also, unsuitable D value can create over-fitting problem in training procedure45. More information of the conventional RF methodology can be investigated in10,40,44,46,47,48.

Fig. 2
figure 2

Flowchart of classification procedure applying the CRF algorithm.

Full size image

Harris hawks optimization algorithm

Superb performance of the HHO algorithm in comparison to 11 powerful optimization algorithms was demonstrated by23. Harris hawk is a predator bird in the Arizona, USA. Because, this creature seeks, attacks and shares victims with other family members. Nature-inspired algorithms generally include two stages comprising exploration and exploitation. In the exploration stage, Harris hawks seek and find the prey from the highest altitude applying their eyes in a desert region. In this regard, the best location of the Harris hawks to the prey is the closest distance to it which can be mathematically simulated as follow:

$$X \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}c} {X_{rand} \left( t \right) - r_{1} \left| {X_{rand} \left( t \right) - 2r_{2} X\left( t \right)} \right| q \ge 0.5} \\ {\left( {X_{prey} \left( t \right) - X_{m} \left( t \right)} \right) - r_{3} \left( {LB + r_{4} \left( {UB - LB} \right)} \right) q < 0.5} \\ \end{array} } \right.$$
(1)

where r1, r2, r3, r4 and q (perching chance of the Harris hawks) are the random values in range (0, 1) and LB, UB, Xprey, Xrand, X(t) and X(t + 1) are lower bound, upper bound, location of the prey in the t iteration, randomly chosen Harris hawk in the current population, location of the Harris hawk in the t iteration and t + 1 iteration respectively. Also, Xm(t) as mean location of the Harris hawks should be calculated as follow:

$$X_{m} \left( t \right) = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} X_{i} \left( t \right)$$
(2)

where Xi(t) is location of each Harris hawk in iteration t and N is number of Harris hawks. It is noteworthy, fleeing condition of the prey can change response of the Harris hawks in the HHO algorithm. In this case, escaping energy factor can be defined using Eq. (3). While, escaping energy parameter be \(\text{E}\ge 1\), seeking for the prey is continued by Harris hawks but the exploitation behavior is started when escaping energy parameter is \(\text{E}<1\).

$$\text{E }= {2\text{E}}_{0}(1-\frac{\text{t}}{\text{T}})$$
(3)

where T is maximum number of iteration. E and E0 are escaping energy in iteration t and initial escaping energy respectively. For each iteration, E0 varies inside range (− 1, 1). Decreasing E0 from 0 to − 1 demonstrates exhausting the prey and increasing E0 from 0 to 1 demonstrates strengthening of the prey. In the exploitation stage, Harris hawks have targeted their prey and intend to attack it. Consequently, targeted prey tries to flee the surprising pounce by performing random jumps. In this regard, the prey chance for successful feeling can be considered as r < 0.5 and while fleeing be not successful r ≥ 0.5. Based on different fleeing chances and escaping energy factor of the prey, four possible strategies are mathematically simulated in the HHO algorithm. At the first strategy (\(r \ge 0.5\) and \(\left| E \right| \ge 0.5\)), Harris hawks intend to tire the prey before attacking because the prey still has enough escaping energy but it will be eventually capitulated. In this strategy which named soft besiege, location of the Harris hawks in iteration t + 1 is expressed as follow:

$$X (t + 1) = \left(\Delta X(t)\right)-E\left|J{X}_{prey}\left(t\right)-X(t)\right|$$
(4)
$$\Delta X(t) = \left({X}_{prey}\left(t\right)-X\left(t\right)\right)$$
(5)
$$J=2(1-{r}_{5})$$
(6)

where r5 is also a random value in (0, 1) and J is random jump strength of the prey during fleeing procedure which varies in each iteration randomly to model the nature of the prey movements. At the second strategy (\(r \ge 0.5\) and \(\left| E \right| < 0.5\)), the prey has been capitulated and Harris hawk can apply surprising pounce. In this strategy (hard besiege), locations of the Harris hawks in iteration t + 1 can also be considered by following equation:

$$X (t + 1) = {X}_{prey}\left(t\right)-E\left|\Delta X(t)\right|$$
(7)

At the third strategy (\(r < 0.5\) and \(\left| E \right| \ge 0.5\)), the prey has enough escaping energy and a soft besiege can still be performed before surprising pounce. This stage (soft besiege with progressive rapid dives) is rather intelligent than the first stage. Accordingly, locations of Harris hawks are updated via Eqs. (8–10):

$$\text{Y }= {X}_{prey}\left(t\right)-E\left|J{X}_{prey}\left(t\right)-X(t)\right|$$
(8)

The Harris hawks compare previous motion of the prey to their previous dive, whether was dive response appropriate or not? Accordingly, along deceptive movements of the prey, those also carry irregular, suddenly and rapid dives out. In23 suggested an LF(x) function to consider various dives of the Harris hawks along zigzag deceptive movements of the prey during scape as follow:

$$Z = Y + S \times LF(x)$$
(9)
$$LF\left( x \right) = 0.01{ } \times { }\frac{u \times \sigma }{{\left| \omega \right|^{{\frac{1}{\beta }}} }},{{ \sigma }} = \left( {\frac{{\Gamma \left( {1 + \beta } \right) \times \sin \left( {\frac{\pi \beta }{2}} \right)}}{{\Gamma \left( {\frac{1 + \beta }{2}} \right) \times \beta \times 2^{{\left( {\frac{\beta - 1}{2}} \right)}} }}} \right)^{{\frac{1}{\beta }}}$$
(10)

where LF(x) named levy flight function and β value is equal to 1.5 and Г is Gamma function. Also, u, ω and S are the random value in range (0, 1) and a random vector respectively. Eventually, location of the Harris hawk in iteration t + 1 can be expressed as follow:

$$X (t + 1) = \left\{\begin{array}{c}Y if F\left(Y\right)<F(X\left(t\right))\\ Z if F\left(Z\right)<F(X\left(t\right))\end{array}\right.$$
(11)

At the forth strategy (\(r<0․5\) and \(\left|E\right|<0․5\)), the prey has been exhausted and the escaping chance is very low. Accordingly, the Harris hawks apply hard besiege behavior with progressive rapid dives which can be simulated as:

$$X (t + 1) = \left\{\begin{array}{c}Y if F\left(Y\right)<F(X\left(t\right))\\ Z if F\left(Z\right)<F(X\left(t\right))\end{array}\right.$$
(12)
$$Y ={X}_{prey}\left(t\right)-E\left|{JX}_{prey}\left(t\right)-{X}_{m}\left(t\right)\right|$$
(13)
$$Z = Y + S \times LF(x)$$
(14)

Examples of the soft and hard besiege behaviors have been presented in Fig. 3.

Fig. 3
figure 3

Some cases of exploitation phase, (a) example of overall vectors in the case of hard besiege, (b) example of overall vectors in the case of soft besiege with progressive rapid dives.

Full size image

Appropriate validation

Area under the receiver operating characteristic (ROC) curve (AUC) was employed as aggregated classification method to validate geochemical samples classified. The AUC value mostly lies in range [0.5, 1]. While, the AUC values be 0.5, performance of applied machine learning model is similar to guess randomly. Also, performance of applied machine learning model is completed if its AUC values be 1. In other word, applied machine learning model has been perfectly trained. The success-rate curve method was initially presented to evaluate spatial accuracy of targeting models employed by49. In this validation tool, proportion of mineralization occurrences which have correctly placed within recognized anomaly zones is exhibited in the vertical axis. In contrast, proportion of the corresponding study area is exhibited in the horizontal axis. A diagonal gauge line is discriminant factor of inefficiency and efficiency of applied targeting model and its geochemical map produced. If, success-rate curve of an employed model be above the gauge line meaning a strong spatial correlation between its geochemical map produced and mineralization occurrences. While, success-rate curve of an employed model be below the gauge line meaning a weak spatial correlation between its geochemical map produced and mineralization occurrences. Indeed, each curve which be higher than other includes more prediction ability.

Geochemical sample preparation and analysis

The study area has dimensions of 44 × 54 km2 which a dense sampling grid (1.4 × 1.4 km2) has been performed there. Stream sediments samples (1033) were collected to check changing rate of concentrations of 27 elements across the Feyzabad district. Collected geochemical samples were analyzed using a combined inductively coupled plasma-optic emission spectroscopy (ICP-OES) after a near-total 4-acid digestion (hydrochloric, nitric, perchloric, and hydrofluoric acids)50. Also, analyzing precision (< 10%) was measured applying duplicated sub-samples for each 20 measurements.

Prepare training data

Classification of the stream sediments geochemical data is critical for producing requirement geochemical layers. Stream sediments geochemical data includes inherent closure problem5,51. Hence, the centered log-ratio (clr) transformation was performed to eliminate data closure problem using Eq. (15).

$$clr \left( x \right) = \left( {\log \left( {\frac{{x_{1} }}{g\left( x \right)}} \right), \ldots ,\left( {\log \frac{{x_{D} }}{g\left( x \right)}} \right)} \right)$$
(15)

where x, xD and g(x) are vector of the composition with D dimensions, Euclidean distances between distinct variables and geometric mean of the composition x respectively52. Then, data table values were transformed in range [0, 1]. Accordingly, a geochemical data table comprising transformed values of elements Au, Cu, Sb, Zn and Pb was classified to map geochemical anomalies in the study area. Indeed, a geochemical data table with 5 columns including transformed values of pathfinder elements with 1 column including their labels for whole of 1033 collected samples was constructed to train model (Fig. 4). For assigning pre-defined labels of training data, we applied several ranges of transformed values (Table 1). Accordingly, geochemical data table was consisted of the four class types comprising strong anomaly, weak anomaly, high background and low background based on suggested ranges and their labels were allocated to samples. Accordingly, for instance, a geochemical sample which is contained transformed values Au = 0.648, Cu = 0.703, Sb = 0.927, Zn = 0.811 and Pb = 0.806 has a great spatial correlation to close mineralization occurrences and is member of the strong anomaly population and achieves label 4 (Table 1). In this research, we also implemented a cost function of root mean squared error (RMSE) values during the training procedure based on Eq. (16).

$$RMSE =\sqrt{\frac{1}{n}(\sum_{i=1}^{n}({C}_{R}-{C}_{p}))}$$
(16)

where n, CR and Cp are number of samples, allocated real class to sample and predicted class respectively.

Fig. 4
figure 4

Hybridization of the RF model with the HHO algorithm using training and testing data.

Full size image
Table 1 Classes defined for training data with criterions.
Full size table

Results and discussion

Training conventional RF

In this regard, the MATLAB R2022a environment was applied to conduct conventional RF (CRF) and Harris hawks optimized random forest (HHORF) networks. 70% samples (in-bag data) were randomly applied to train and 30% samples (out-of-bag data) were employed to test networks designed. For training conventional RF network, relevant hyperparameters NT, NS and D were experimentally assigned in range 1–300, 1–8 and 1–4 respectively. These tuned hyperparameters using trial-and-error procedure were presented in Table 2. Optimum value of the parameter NT (280) was applied to train CRF with tenfold cross-validation. It is noteworthy, increasing the NT value is not necessarily eventuated to decrease the uncertainties but also increases the calculating time. Furthermore, NS and D values were chosen 5 and 2 respectively while these parameters include lower impact on the CRF performance (Table 2).

Table 2 Tuned hyperparameter values of the CRF and HHORF models.
Full size table

Training HHORF and comparison

A schematic flowchart of the hybridization of the HHO algorithm with the RF method has been presented in Fig. 4. Here, the HHO is fittingly attracted to optimal solutions in the best locations of the search spaces, and the number of random parameters is restricted in the HHO. Therefore, the initial population of Harris hawks is significant in this algorithm. Before optimizing hyperparameters of the HHORF model, appropriate number of iterations (100), Harris hawks population (30), lower bound value (100) and upper bound value (1) with tenfold cross-validation were set. In the HHORF procedure, the best location of the prey (Xprey) is considered as relevant hyperparameters of the RF method in the selected features for all cross validation folds. Tuned hyperparameters of the RF by employing HHO algorithm were demonstrated as NT = 636, NS = 7 and D = 3 (Table 2). Cost function of optimizing procedure for all iterations has also been exhibited in Fig. 5. It is displayed, minimizing procedure is finalized after 58th iteration with a cost value 0.466. Indeed, stable part of the cost function after 58th iteration with the lowest cost value can insure perfect tuning of the model hyperparameters. The AUCs presented in Fig. 6 can compare prediction ability of the trained models in this research. It is cleared, the HHORF has rather accuracy than the CRF method. The AUC values of classified samples (class 4 = 0.931, class 3 = 0.937, class 2 = 0.943, class 1 = 0.925) by applying the HHORF (Fig. 6b) are greater than the AUC values of the classified samples (class 4 = 0.811, class 3 = 0.916, class 2 = 0.802, class 1 = 0.797) through the CRF (Fig. 6a; Table 3).

Fig. 5
figure 5

Minimizing procedure of the cost values in whole of iterations.

Full size image
Fig. 6
figure 6figure 6

Area under the receiver operating characteristic curve (AUC) for geochemical data classified via employing, (a) the CRF model and (b) the HHORF model.

Full size image
Table 3 The AUC values for geochemical data classified applying the CRF and HHORF models.
Full size table

Multi-element geochemical anomaly mapping and validation

Testing data classified were applied to map multi-element geochemical anomalies through inverse distance weighted (IDW) interpolation tool in the GIS software 10.6 toolbox (Fig. 7). Due to greater classification accuracy of the HHORF procedure, map plotted of its samples classified obviously presents better prediction of the geochemical anomalies linked to the mineralization occurrences. In other word, high potential zones of multi-element geochemical map produced through HHORF approach (Fig. 7b) has catched up more mineralization occurrences. This claim can also be demonstrated regarding the success-rate curves achieved for both plots (Fig. 8). In this concept, two cases are regardable. The first, both success-rate curves are meaningfully above the diagonal gauge line meaning both produced maps have acceptable ability in predicting geochemical anomalies. The second, success-rate curve of the produced map by classified samples of the HHORF procedure is above other curve. It is meaning, prediction ability of the HHORF procedure is greater due to higher proportion of the mineralization occurrences have detected in lower proportion of the corresponding area. For instance, the HHORF has predicted 86.53% mineralization occurrences in the 30% corresponded area while the CRF has predicted 80.14% mineralization occurrences in same corresponding area (Fig. 8).

Fig. 7
figure 7figure 7

Multi-element geochemical anomaly maps plotted applying, (a) the CRF model and (b) the HHORF model.

Full size image
Fig. 8
figure 8

The success-rate curve for achieved results employing, (a) the CRF model and (b) the HHORF model.

Full size image

Conclusions

In this research, a hybridized random forest model was successfully constructed to classify multi-element geochemical data table linked to the mineralization occurrences in the Feyzabad district, NE Iran. Accordingly, conclusion remarks are presented as follow:

  • The CRF is a powerful and popular method for classification of geochemical data which its relevant hyperparameters extremely require to be optimized for achieving reliable conclusions.

  • Optimization of hyperparameters of the CRF method is time consuming and onerous while trial-and-error procedure be executed.

  • A nature-inspired procedure named Harris hawks optimization algorithm could reliably tune hyperparameters of the CRF without wasting a lot time.

  • Advanced machine learning frameworks can be constructed hybridizing appropriate optimization algorithms with powerful machine learning models.

  • Advanced machine learning frameworks can meaningfully decrease uncertainties yielding reasonable geochemical anomaly maps.