Introduction

Concrete bridges that have been in service for decades often experience overload, material aging, shrinkage, creep, and fatigue. To ensure the continued normal operation of these transportation infrastructures, structural health monitoring and detection have become pivotal topics in academic research and engineering. Among these structural defects, cracks are crucial indicators for monitoring and inspection purposes because they provide vital information about structural conditions. This information forms the basis for decision-making in bridge condition identification, safety assessment, and damage management1,2. Therefore, the detection of cracks in concrete structures is indispensable for informed and strategic decision making related to structural maintenance.

In its early stages, crack detection was mainly done manually. With the development of digital image processing technology, a large number of semi-automatic detection methods based on visual damage detection have been proposed3. Due to the fact that cracks often appear in different colors and geometric features in images, such as changes in brightness or sharp edges. These digital image processing methods typically locate the location of damage by searching for color and geometric features in the image4. These methods mainly include Sobel operator5, Prewitt operator6, Laplacian operator7, and Canny operator8 based on gradient calculation and direction filtering. Meanwhile, edge detection in images can also be achieved by designing match filter algorithms that correspond to the corresponding features9,10. Zhang et al.11 achieved segmentation and detection of crack images by establishing a matched filter using Gaussian functions. Compared to algorithms that obtain crack information through geometric integration, it has higher anti-interference ability, but lower operational efficiency. These algorithms have strong interpretability and fast validation capabilities, but are often limited in practical applications due to their sensitivity to noise and low efficiency.

In recent years, computer vision technology has witnessed tremendous progress with the emergence of deep learning. In 2012, the AlexNet developed by Krizhevsky et al.12 using deep convolutional neural networks (CNNs), achieved first place in the ImageNet Large Scale Visual Recognition Challenge. Since then, computer vision tasks have entered the deep learning era dominated by CNN architectures. For instance, Cha et al.13 developed a CNN-based method for automatic crack recognition, achieving high accuracy in classifying various crack types. Similarly, Cha et al.14 proposed a region-based deep learning framework capable of detecting multiple types of structural damage from images, demonstrating promising results for autonomous visual inspection in complex environments. Lau et al.15 introduced an image segmentation algorithm based on a U-net architecture to isolate damage regions from the background. Yang et al.16 proposed YOLOv8-GSD, integrating DySnakeConv, BiLevelRoutingAttention, and the Gather-and-Distribute Mechanism into the single-stage model YOLO (You Only Look Once), realizing tunnel crack detection and segmentation. Liu et al.17 combined a fully convolutional neural network with a deeply supervised network, achieving pixel-level crack segmentation via an end-to-end approach and demonstrating favorable results. Recent studies have demonstrated the effectiveness of advanced deep learning models for pixel-wise crack segmentation, especially in real-world conditions with complex backgrounds. Choi et al.18 achieved real-time crack detection through an optimized architecture, while a hybrid framework integrating multi-scale context19 and attention based encoder decoder design20 achieved state-of-the-art IoU performance on different datasets. These methods exhibit significant robustness under varying lighting conditions, background noise, and surface textures. However, these deep learning models are computationally intensive, requiring substantial raw data for training and high-performance hardware. Detection performance may be suboptimal in scenarios with limited access and data scarcity, such as bridge crack inspection.

Quantification of crack detection or segmentation is necessary to provide reliable reference information (e.g., crack length and width) for maintenance personnel. Schlicke et al.21 achieved favorable results in predicting concrete crack widths using machine learning models. Zhou et al.22 calculated crack width by integrating an eight-direction algorithm with depth camera distance information. Yuan et al.23 obtained crack length information by marking calibration points on experimental structural components and calculating the pixel-to-scale conversion ratio. Research on calculating crack length remains relatively scarce compared to studies on crack width calculation.

Meanwhile, most existing models primarily validate their performance on public or custom datasets. However, these individual image data often prove inadequate for structural maintenance applications due to their inability to provide spatial context for damage localization. Consequently, data visualization that facilitates crack positioning is crucial. 3D reconstruction techniques offer a viable solution for such visualization24. 3D reconstruction creates opportunities for effective computer vision applications in engineering structures25,26,27. Kim et al.28 developed an Attention-Based Modified Nerfacto (ABM-Nerfacto) model that achieves remarkable visualization effectiveness by mapping damage onto 3D models. Additionally, Kim et al.29 introduced deep learning into 3D model reconstruction using Neural Radiance Fields (Nerfacto), providing solutions to address the time-consuming nature of traditional 3D reconstruction. Integrating detection results into models for enhanced visualization remains an active research area.

Bridges represent large-scale infrastructure structures, whereas cracks constitute typical small targets. Consequently, the detection of bridge cracks exemplifies a low-data target scenario. Sheiati et al.30,31 utilized unmanned aerial vehicles (UAVs) to collect data from large-scale wind power facilities and employed deep learning methods to isolate wind turbine blades from the background for subsequent damage analysis. Recent advancements demonstrate that autonomous UAV platforms integrated with deep learning facilitate real-time structural damage detection32,33,34. These systems combine onboard navigation, obstacle avoidance, and crack detection using convolutional neural networks (CNNs) or region-based detectors, enabling autonomous inspection in GPS-denied or complex environments. However, they typically demand extensive labeled datasets, high computational resources, and precise localization infrastructure, potentially limiting their applicability in resource-constrained field scenarios. When training data is insufficient for small target detection, such as cracks, traditional digital image processing methods offer a viable alternative. Nonetheless, deep learning approaches hold significant promise for the future; as data resources expand, detection methodologies are anticipated to transition from traditional techniques to deep learning.

In this study, we propose improvements to the matched filter algorithm to address low operational efficiency while maintaining detection accuracy. This research focuses on a lightweight and interpretable detection and quantification method based on enhanced matched filter and UAV imaging parameters. This approach proves more practical for short-term deployments where deep models and autonomous systems are infeasible, while permitting future integration into autonomous frameworks as technology matures. Additionally, the actual length of cracks is calculated based on shooting distance and camera parameters. UAV-acquired images are reconstructed into 3D models for visualizing detection results. The primary research contributions are as follows:

(1) An improved matched filter algorithm is proposed, which improves the processing efficiency by 30 times without affecting the detection accuracy;

(2) The enhanced algorithm is benchmarked against Sobel, Laplacian, Canny, and U-Net algorithms. Results demonstrate superior segmentation performance, achieving average scores of 97.9% (PA), 72.5% (F1-score), and 58.1% (IoU) on public crack datasets;

(3) A crack length quantification method combining image processing, shooting distance, and camera parameters is developed, with measurement errors below 2% compared to manual measurements;

(4) 3D damage projection via reconstructed models provides a visualization solution.

The remainder of this paper is structured as follows: Section II outlines the UAV inspection workflow and details each procedural step. Section III elaborates on crack detection using enhanced matched filter, including skeleton extraction and length quantification, alongside 3D reconstruction techniques. Section IV presents experimental results and comparative analyses. Finally, Section V concludes the study.

Framework overview

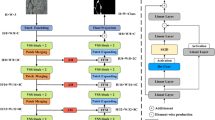
Developing an optimal flight plan is crucial for UAV-based bridge data collection and crack detection. SEO et al.35 employed a DJI Phantom 4 UAV to inspect a glued timber bridge in South Dakota and developed a five-phase inspection methodology, comprising information review, risk assessment, pre-flight preparation, inspection implementation, and damage identification. Post-implementation, the UAV demonstrated excellent image quality and damage identification capabilities, with results consistent with traditional inspection methods, confirming its effectiveness as a bridge inspection aid. Building on this methodology, the present study conducted preliminary research on bridge inspection to familiarize with the bridge scale, structure, and surrounding environment, identifying key observation points. Subsequently, the flight path was planned based on bridge orientation and terrain to ensure full coverage, efficiency, and obstacle avoidance. Periods with stable lighting and weather conditions were selected to minimize environmental interference. Finally, emergency procedures were implemented to ensure flight safety and data acquisition completion, preparing for contingencies such as low battery and signal loss. The main workflow is illustrated in Fig. 1.

  1. (1)

    Preliminary Preparation. This phase focused on collecting bridge-related information, including prior inspection reports and construction drawings. A risk assessment of the on-site environment surrounding the bridge was then conducted, followed by developing a compliant flight plan based on local regulations.

  2. (2)

    UAV Pre-flight Setup. Before executing the flight plan, the UAV required inspection and configuration, covering software and hardware components, as well as specific checks of the camera, battery, and propellers. Flight parameters were subsequently determined, and the compass was calibrated to prevent GPS signal loss during flight.

  3. (3)

    Bridge Inspection. During flight, image information was collected from designated bridge inspection areas according to the flight plan, emphasizing detailed data acquisition from critical regions. Parameters related to capture were recorded, as they are essential for subsequent crack quantification and calculation.

  4. (4)

    Data Processing. A Gaussian matched filter was designed to enhance crack detection based on the matched filter algorithm, segmenting cracks from the surrounding environment. The segmentation results were processed via skeleton extraction to generate crack skeletons composed of single-pixel lines. Actual crack length was calculated considering shooting distance, focal length, and skeleton pixel count. Additionally, 3D models were reconstructed using image data of the bridge and its surroundings.

  5. (5)

    Structural Safety Assessment. Based on quantitative results, specific damage extent in inspected areas (e.g., crack distribution density) was evaluated. By comparing these outcomes with actual structural dimensions and expert assessments, the final damage degree was determined, and corresponding repair and maintenance plans were formulated.

Fig. 1
figure 1

Workflow of using UAV for bridge crack detection.

Full size image

Enhanced matched filter-based method for crack detection and quantification

UAV imagery and crack characteristics

Based on their morphology and propagation trends, cracks in bridge pavements can be classified into four types: transverse, longitudinal, block, and grid cracks. The two types share several common characteristics.

  1. (1)

    They propagate in irregular and unpredictable directions.

  2. (2)

    The crack width remains relatively uniform over short distances in the longitudinal direction.

  3. (3)

    Within the crack area, the optical reflectivity (or pixel value) consistently showed a lower intensity than the surrounding areas.

Owing to these properties, when cracks are segmented into sufficiently small sections, they can be approximated as a series of relatively uniform rectangular strips. Using grayscale data from these sections and plotting them as a curve, a characteristic U-shaped grayscale pattern was obtained, as illustrated in Fig. 2. The nadir of this curve corresponds to the lowest grayscale value. By leveraging these properties, a specific function template that optimally fits the cracks can be obtained, thereby enabling the extraction of highly correlated data for crack identification. Subsequently, the skeleton of the segmented image is extracted, from which the length data and the degree of damage in the area can be captured.

Fig. 2
figure 2

Gray value curve of crack section.

Full size image

Design of enhanced matched filter algorithm

The gray-scale intensity within crack regions is typically lower than that of surrounding areas. Consequently, crack locations can be detected by identifying morphological features or geometric shapes4. Traditional digital image processing methods for crack detection based on gray-scale variations can be broadly categorized into two groups according to gradient calculations:

  1. (1)

    First-derivative-based methods: These simulate the first-derivative acquisition process, where extreme derivative values correspond to crack locations. Examples include Roberts, Sobel5, Prewitt6, Canny operators8, and wavelet-based detection techniques.

  2. (2)

    Second-derivative-based methods: These focus on identifying zero-crossing points of the second derivative, interpreted as edges. Representative approaches include Laplacian of Gaussian (LoG) detection7 and zero-crossing detection, which exhibit heightened sensitivity to subtle curvature changes in edges.

The choice between these methods depends on application-specific requirements and desired edge-detection precision.

Matched filter is a robust technique for distinguishing known signals from noisy backgrounds. By convolving input signals with predefined templates, it optimizes the signal-to-noise ratio (SNR) to enhance detection accuracy. Widely applied in radar, communications, and biomedical signal processing—particularly for extracting weak signals from noise—its core principle in image processing involves designing customized filters that capture target-specific attributes. This enables precise localization of image segments exhibiting strong correlation with filter characteristics. Historically, O’Gorman et al.9 pioneered cosine-based filters for fingerprint detection by leveraging ridge patterns. Chaudhuri et al.10 advanced this field with Gaussian filters for retinal vessel detection, achieving notable results. Recently, Zhang et al.11 successfully extended its application to pavement crack detection.

Building on these foundations, this study enhances the matched filter algorithm for crack detection (methodological flowchart shown in Fig. 3.

The grayscale value data in the crack area are roughly similar to the inverse Gaussian function. Therefore, using the Gaussian function to convolute and fit the grayscale value in the crack area can also be referred to as a Gaussian matched filter. The crack area f (x, y) in the image was simulated using a Gaussian function as follows:

$$f(x,y)=A[1 - k{\text{ }}\text{e}\text{x}\text{p}(\frac{{ - {d^2}}}{{2{\sigma ^2}}})]$$
(1)

where f (x, y) represents the intensity of the grayscale values in the image, (x, y) represents the coordinates of the points in the image, A represents the local background intensity, k is the reflectivity of the measured object, d is the distance between point (x, y) and the line segment passing through the center of the object, σ represents the intensity distribution.

The designed optimal filter must have the same grayscale value morphology as the crack area.

$$hopt= - \text{e}\text{x}\text{p}(\frac{{ - {d^2}}}{{2{\sigma ^2}}}).$$
(2)

Where hopt is the optimal filter function.

Owing to the hypothetical segmentation of the crack area into different small segments, the cracks were approximated using small rectangular segments. Therefore, a linear function is required to estimate it, and the designed small convolution kernel is

$$K(x,y) = - \exp (\frac{{ - x^{2} }}{{2\sigma ^{2} }}){\text{ }}|y| \le \frac{L}{2}$$
(3)
Fig. 3
figure 3

Enhanced matched filter algorithm’s flow-process diagram.

Full size image

where L is the length of the line segment, x is perpendicular to the line segment, and y is in the direction of the line segment. To match the line segments in different directions, kernel K (x, y) must be rotated accordingly. The correlation between the points in the rotation kernel and the points in the horizontal kernel is given by the following equation:

$${p_i}=p{\left[ \begin{gathered} \cos \theta i{\text{ }} - \sin \theta i \hfill \\ \sin \theta i{\text{ }}\cos \theta i \hfill \\ \end{gathered} \right]^\text{T}}$$
(4)

where pi is the position of the point in the i-th θ angle, P is the corresponding point in the horizontal kernel, and T is the transpose of the matrix.

Because the two sides of the Gaussian curve extend to infinity, the neighborhood N={(x) is used for computational convenience, y)||x|≤3σ, |y|≤L/2} and truncates at x = ± 3σ on the Gaussian curve. Therefore, the i-th kernel is given by the following equation:

$$Ki(x,y)= - \text{e}\text{x}\text{p}(\frac{{ - {x^2}}}{{2{\sigma ^2}}}){\text{ }}\forall pi \in N$$
(5)

An additive Gaussian white noise model was used to describe the noise. Because the mean of the kernel function should be zero, the i-th kernel function is

$$Ki^{'} (x,y) = Ki(x,y) - mi{\text{ }}\forall pi \in N$$
(6)

where mi is the mean of kernel Ki (x, y).

Crack information in multiple directions was extracted by convolving the image with omnidirectional kernels. The maximum value per direction was retained as the initial crack identification. Subsequently, a connected-domain-based threshold was applied to filter these results and obtain crack detection outputs. Final results were achievable when image quality was adequate. For images containing speckle noise, connected-domain denoising was employed: segmented regions below the threshold were discarded to eliminate noise. This denoising step provided supplemental robustness when initial screening results were reliable.

The matched filter algorithm employing direction-specific kernels for multi-orientation feature extraction offers advantages over gradient-based methods, including higher detection accuracy and reduced sensitivity to noise. However, its dual-loop computational structure suffers from low operational efficiency. To enhance processing speed while preserving the algorithmic framework and detection precision, this study implements the following improvements:

  1. (1)

    Vectorization of Gaussian-matched filter kernels coupled with coordinate transformation via broadcasting mechanisms, enabling batch computation to reduce loop iterations;

  2. (2)

    Parallel processing integration, treating convolution operations of directional filters as independent tasks to leverage multi-core CPU capabilities through parallel computing frameworks;

  3. (3)

    Dynamic path generation with result caching mechanisms to improve file handling flexibility and manageability.

Crack skeleton extraction and length calculation

Crack skeleton extraction involves the segmentation and extraction of a crack image to simplify it into a skeleton of a single pixel. Crack length can be obtained by calculating the number of pixels and estimating the extent to which each pixel represents the actual length. The degree of crack damage in this range can be determined to a certain extent by calculating the crack length per unit area.

Fig. 4
figure 4

Principles of crack imaging.

Full size image

Currently, the primary skeleton extraction methods include morphological refinement, distance transformation, and central axis transformation. A morphological refinement method was adopted in this study. Morphological corrosion is an image processing technique based on set operations, the core idea of which is to use a structural element (usually a small, predefined shape, such as a circle or square) to slide over an image and compare it with the pixels in the image.

If the structural elements match the pixels perfectly, then the pixels are preserved; otherwise, they are removed. In this manner, the boundary of the object shrinks inward, and the object smaller than the structural element is completely removed. The fracture skeleton was obtained by refining the extracted and segmented crack images using a morphological method.

The principle of crack imaging is illustrated in Fig. 4. The image captured by the camera follows the principle of aperture imaging, in which the light passing through the aperture forms a real image on the screen. This real image is a projection of the object (crack) onto the screen, inverted both vertically and horizontally, compared with the actual object. According to the principles of crack imaging, a real crack is projected on a screen. The relationships among the distances from the object to the camera lens, from the lens to the image, the actual size of the object, and the size of the object in the image form similar triangles. By obtaining the length k represented by each pixel in the camera in the real world, the pixel counts p  of the crack skeleton, the camera’s focal length f, and the shooting distance d, along with the camera’s pixel size c, number of combined pixels x, the actual length l  of the crack can be calculated through simple proportional mapping.

The specific calculation method is as follows:

$$l=\frac{{d{\text{ }} \times {\text{ }}p{\text{ }} \times {\text{ }}c{\text{ }} \times {\text{ }}x}}{f}$$
(7)
$$k{\text{ }}={\text{ }}\frac{{d{\text{ }} \times {\text{ }}c{\text{ }}\times {\text{ }}x}}{f}$$
(8)

3D modeling reconstruction of cracked bridges

In bridge structures, different components experience varying stress states. For instance, in reinforced concrete box-girder bridges, the bottom flanges near mid-span typically undergo tension, while the top slabs endure compression. Cracks in bottom tension zones may indicate rebar yielding or fatigue, posing substantial safety risks. Conversely, surface cracks on top slabs—often caused by shrinkage or temperature variations—may be less critical for load-bearing capacity. Therefore, identifying crack locations is essential for assessing structural severity.

3D reconstruction technology utilizes UAV-collected field data to reconstruct 3D models of actual scenes24. Based on data reconstruction typology, it can be categorized into point cloud reverse reconstruction, photo reverse reconstruction, and 3D scanning reverse reconstruction36. By integrating crack detection results with UAV flight and imaging parameters, each crack can be precisely mapped to its actual spatial location, allowing engineers to assess both the existence and functional impact of damage.

This spatially resolved modeling enables time-variant damage tracking, supports cross-temporal comparisons, and helps prioritize maintenance based on crack severity and structural relevance. While close-up images ensure fine-grained detection, 3D reconstruction consolidates these insights into a comprehensive damage assessment framework. Notably, Kim et al.28,29integrated damage detection results by projecting crack shapes onto 3D models, achieving exceptional visualization effects. Displaying spatial crack locations through 3D image reconstruction is critically significant for the performance evaluation of bridge structures. The overall process of data acquisition and modeling is illustrated in Fig. 5.

Fig. 5
figure 5

Data collection and modeling flowchart of 3D reconsrtuction.

Full size image
  1. (1)

    Data collection: The oblique photography system collects image data from five different angles (vertical, forward, left, right, and backward) by installing multiple sensors on the same flight platform. It also saves the GPS and shooting angle data.

  2. (2)

    Preprocessing: The acquired image data undergo preprocessing, which includes denoising, color balancing, and other operations, to enhance the image quality.

  3. (3)

    Camera calibration: To ensure that the captured photos or videos can accurately restore the three-dimensional information of objects, camera calibration is necessary. The purpose of calibration is to determine the internal and external parameters of the camera, specifically the conversion relationship between the camera coordinate system and world coordinate system.

  4. (4)

    Image matching and orientation: Algorithms, such as feature point detection and descriptor extraction, are used to find the corresponding relationships between photos from different angles to achieve image matching.

  5. (5)

    3D model reconstruction: based on on-site data combined with internal and external parameters, 3D modeling of objects is performed. Using the method of regional network joint adjustment and multi-view image matching, an irregular triangular network was constructed to generate a three-dimensional box model. Finally, by integrating the 3D model with the real spatial information of the image, the automatic mapping of the surface texture of the 3D model was achieved, thereby establishing a high-resolution real-world 3D model with realistic and natural textures.

Model development and validation

Detect results with different thresholds and comparison of operating speed

An appropriate threshold selection is critical for achieving optimal detection performance in the matched filter algorithm. Consequently, this experiment systematically evaluates the impact of varying thresholds (0.05 to 0.2) on the final detection results, with other parameters fixed (σ = 2, L = 9, θ = 15) and no connected-component denoising applied, providing a reference for subsequent threshold optimization. The detected data is from the CFD dataset37. The detection outcomes are assessed using the intersection over union (IOU) metric and plotted as a curve, and the results are shown in Fig. 6. The results indicate that as the threshold increases from 0.05 to 0.2, the IOU value initially rises and then declines, peaking at a threshold of 0.15. Therefore, a fixed threshold of 0.15 is adopted for subsequent detection. A comparative assessment of computational efficiency was performed between the enhanced matched filter algorithm and its original counterpart using the CFD validation dataset37. As detailed in Table 1, the enhanced algorithm demonstrates an approximate 30-fold speedup relative to the original version.

Fig. 6
figure 6

Different thresholds with Iou results.

Full size image
Table 1 Performance comparison between original and improved algorithms.
Full size table

Test results comparison

This section compares the detection results of the matched filter algorithm with other prevalent crack detection algorithms based on digital image processing, namely the Sobel5, Laplacian7, and Canny operators8. To demonstrate the segmentation efficacy of the proposed algorithm, a U-Net segmentation network is included for comparison15.

All digital image processing methods utilize a 5 × 5 mean filter for denoising. The gradient threshold for the Sobel operator is set at 75. Thresholds for the Canny operator are selected as 75 and 150. The matched filter algorithm employs parameters σ = 2, L = 9, θ = 15, without connected-component denoising, and a screening threshold of 0.15. The U-Net adopts the original U-shaped architecture with binary cross-entropy as the loss function. It is trained on publicly available datasets (CFD37 and Crack50038), comprising 2,083 training samples. The network undergoes 150 training epochs with a batch size of 1. Reflection padding with a padding size of 1 maintains consistent image dimensions before and after training, while the remaining architecture follows the standard U-Net design. All algorithms are executed on a PC equipped with an NVIDIA GeForce RTX 4060Ti GPU and an Intel i5-12400 F CPU.

The test images comprise three components: six images selected from the CFD validation dataset37 and six from the DeepCrack dataset17. Detection results of all algorithms are illustrated in Figs. 7, 8 and 9, where columns from left to right depict the original image, ground truth, Sobel operator result, Laplacian operator result, Canny algorithm result, U-Net model result, and matched filter algorithm result.

To objectively evaluate the enhanced matched filter algorithm, segmentation outcomes in Figs. 7, 8 and 9 are assessed using quantitative metrics (i.e., IoU, PA, and F1-score), with detailed results listed in Tables 2,3 and 4(maximum values in bold).

Results indicate that Sobel, Laplacian, and Canny detections all contain speckle noise. Sobel detection simulates first-derivative solutions, identifying cracks at regions of abrupt grayscale changes; consequently, it performs poorly on images with low-grayscale contamination (e.g., speckles). Laplacian detection models second-derivative solutions but exhibits no significant improvement over Sobel in suppressing speckles or contaminants, though it avoids gradient-dependent variability. Canny detection utilizes Sobel-derived gradients, enhancing performance versus predecessors but still suboptimal suppressing isolated speckle noise and generating false detections. In contrast, the U-Net segmentation model significantly improves detection through training on extensive samples, demonstrating strong anti-interference capability that effectively suppresses non-crack regions (e.g., speckles).

As illustrated in Fig. 7, detection results from the CFD dataset demonstrate that both the matched filter algorithm and U-Net model exhibit excellent performance. Among traditional methods, Sobel detection yields optimal outcomes with.

Fig. 7
figure 7

Crack detection results on CFD dataset.

Full size image
Table 2 Evaluation index values on cfd crack images.
Full size table
Fig. 8
figure 8

Crack detection results on deepCrack dataset.

Full size image
Table 3 Evaluation index values on deepcrack images.
Full size table
Fig. 9
figure 9

Crack detection results on tunnel cracks.

Full size image

minimal noise contamination. This conclusion is reinforced by quantitative metrics, where the matched filter algorithm and U-Net model significantly outperform other approaches.

Results shown in Fig. 8, derived from images selected in the DeepCrack dataset, reveal that both the matched filter algorithm and U-Net achieve robust detection performance, displaying strong interference resistance and negligible speckle noise. Similar trends are observed in objective evaluation metrics. The U-Net model consistently attains higher scores for most.

images, particularly those with pronounced noise and uneven illumination. However, the matched filter algorithm surpasses U-Net in high-quality images, achieving peak scores.

Tunnel crack images in Fig. 9 present the most challenging detection scenario due to significant illumination variations and interfering potholes. The U-Net model demonstrates superior performance, delivering exceptional results with robust interference resistance and outperforming other algorithms in objective metrics. The matched filter algorithm exhibits better anti-interference capability than conventional methods, producing satisfactory detection outcomes. Nevertheless, reliance on a single filter for crack detection proves infeasible, as performance varies with variance values; thus, adjusting the filter kernel constitutes a critical future research focus.

Extraction of crack skeleton and estimation of length error

The crack skeleton is extracted using morphological methods described in Chapter C of Section III,, and the fracture skeleton diagram is obtained as shown in Fig. 10. Meanwhile, a precision verification experiment is conducted to quantitatively evaluate the accuracy of the crack length calculation method, thereby validating the practicality and accuracy of the computational algorithm. In this experiment, a mobile phone equipped with an OV64b imaging sensor (focal length: 4.71 mm) is utilized. This sensor, developed by OmniVision specifically for mobile photography, has a pixel size of 0.702 μm based on official specifications39. To ensure lens perpendicularity to the road surface and simplify calculations, calibration is performed using a ruler and level, with the shooting distance maintained at 1 m. Four in one pixelmode is adopted for shooting, which doubles the photosensitive area compared to full-pixel mode. Consequently, the experimental parameters are as follows: shooting distance of d 1 m, focal length f of 4.71 mm, and pixel size c of 0.7.2 μm, number of combined pixels x of 2.

Table 4 Evaluation index values on tunnel crack images.
Full size table
Fig. 10
figure 10

Crack detection results and their skeleton.

Full size image

Four crack images are collected for verification, with manual crack length measurements yielding results of 703.4 mm, 692.3 mm, 674.5 mm, and 754.6 mm, as shown in Fig. 11. After preprocessing the acquired images, crack segmentation is performed using the enhanced matched filter algorithm, followed by skeleton extraction and pixel counting. The actual crack lengths are calculated using formulas (7) and (8), resulting in values of 717.6 mm, 710.1 mm, 688.1 mm, and 735.7 mm. Comparison with manual test results confirms the algorithm’s feasibility, and the final error verification table (Table 5) is obtained. Based on the analysis, the error between the detection by the combined matched filter and morphological operations algorithm and manual measurement is approximately 2%. Considering manual measurement errors and time costs, this algorithm is deemed referential.

Fig. 11
figure 11

Shooting a schematic diagram of cracks and their lengths.

Full size image
Table 5 Algorithm error verification.
Full size table

Engineering applications

Description of bridges and UAVs

The entire procedure was applied to a practical case study at the Engineering Training Center of Shijiazhuang Tiedao University, where field testing was conducted on an experimental bridge (schematic shown in Fig. 12). The bridge has a 24-m main span, 5.2-m width, and 1-m-high railings, with its reinforced concrete arch standing 5.5 m high featuring 0.75-m segment heights and 0.6-m width. Five hangers spaced at 3.5-m intervals connect the single arch rib to the main girder. A DJI MAVIC 3 CLASSIC UAV equipped with an L2D-20 C camera (co-developed by Hasselblad and DJI) was deployed40. This Micro Four Thirds (M4/3) format camera has a 12.7042-mm focal length, maximum resolution of 5,280 × 3,956 pixels, and 20-megapixel effective resolution41, with the M4/3 industry-standard sensor measuring 17.3 mm × 13.0 mm yielding a 3-µm pixel size during full-frame imaging42. For close-range photogrammetry, onboard radar maintained a 1-m shooting distance while marked observation points enabled positioning; flight trajectories generated from these points ensured consistent distance.

According to the guidance in Section III, Chapter A, a UAV flight test was conducted, all types of data required were collected, and the GPS and shooting attitude information were recorded during each collection. During flight, the actual distance between the drone and bridge was set in advance. Multiple rounds of repeated collections of key monitoring areas, such as bridge arches and piers, were conducted to ensure rich and accurate data. A total of 384 high-definition pictures were collected, and all data were run on a 2667 MHz 16GB notebook equipped with an i5-8300 H CPU and a GTX1050 graphics card.

Fig. 12
figure 12

Schematic diagram of the bridge in the engineering training center.

Full size image
Fig. 13
figure 13

GPS point and 3D reconstruct model.

Full size image

3D modeling and data visualization

As described in Section III, Chapter D, to obtain a complete 3D model, it is necessary to process GPS points. Using the principle of oblique photography, 384 images were reverse-3D modeled. The GPS point position and the 3D model diagram are shown in Fig. 13.

The top half shows the data before processing and GPS point position information, and the bottom half shows the 3D model. The left side shows the full picture of the model, and the right side shows the top, front, and side views.

By analyzing the scenario model shown in Fig. 13, the current model was fully usable. Using this model, the field situation can be determined and understood quickly. After selecting the key site and retrieving the site data, more detailed damage detection can be performed. This refined detection capability provides strong data support for subsequent maintenance and repairs.

Crack detection and structural damage state calculation

An enhanced matched filter was used to detect cracks in the detected image. The experimental framework and specific parameters of this section are as follows.

(1) All pictures were captured using a UAV.

(2) The image was denoised using a 3×3 mean filtering.

(3) Using the parameters σ=2, L=9, θ=15, calculate the weight of the horizontal kernel using the above formula, calculate the convolutional kernel after rotation through the rotation matrix, and then apply all convolutional kernels to the image.

(4) The threshold selection is a fixed threshold with a size of 0.15.

(5) The detection results were screened and the threshold of the connected area was set to 1% of the photo.

(6) The skeleton was extracted from the crack-detection results, and its length was calculated.

(7) The crack length per unit area was calculated.

For the part of the bridge arch to be tested, shooting was performed in a vertical manner, and the shooting distance was strictly controlled at 1000 mm. The sampling positions and test results are shown in Fig. 14. From top to bottom are the original drawings, crack drawings, and skeleton drawings. The original drawing shows the original state of the crack in the bridge arch.

Fig. 14
figure 14

Image sampling location and detection result diagram.

Full size image

The crack plan clearly shows the crack after segmentation, and the skeleton further highlighted the main skeleton of the crack, which provides convenience for subsequent length calculations.

From the information in Chapter A of Section V, we can see that the actual size of the CMOS is 0.003 mm, the distance is 12.7042 mm, and the pixel integration mode is not used for shooting at a distance of 1000 mm. At this point, we obtained the necessary parameters for calculating the crack length, including the pixel size c = 0.003 mm, number of combined pixels x = 1, shooting distance d = 1000 mm, and focal length f = 12.7042 mm.

After extracting the skeleton of the crack, its length is calculated. According to the guidance in Chapter C in the Section III,, the required shooting parameters and other data are obtained, and calculate the actual length of the crack according to formulas 7 and 8, which are 355.1 mm, respectively, 393.5 mm, 268.1 mm, 160.5 mm, 789.7 mm, 1797.0 mm. The degree of damage to the bridge arch in the local area can be obtained by calculating the total length of the cracks per unit area. The results are presented in Table 6.

According to the above detailed data and the results of the crack detection in Fig. 14, the damage degree in region f is particularly serious. The length and distribution density of the fractures were significantly higher than those in other regions. The degrees of damage in regions a, b, and c were similar. Although the severity of Area F has not yet been reached, prompt attention and treatment are required. The damage degree of region e was between those of regions f and a, b, and c. Area d, which had the least degree of damage, should not be taken lightly and requires regular testing and maintenance.

In summary, in view of the damage in each area of the bridge reflected by the above data, corresponding repair or maintenance measures should be taken in time. For the seriously damaged area f, priority should be given to repair to ensure the overall safety of the bridge arch. Areas a, b, c, d, and e also need to be maintained and reinforced. Through scientific repair and maintenance measures, we can ensure the safe operation of bridges and provide a solid guarantee for human travel.

Table 6 Local damage status data of bridge arches.
Full size table

Conclusion

This study proposes a crack-detection method for digital image processing using UAV photography and an enhanced matched-filter algorithm. Compared to traditional visual methods, this method demonstrates strong anti-interference abilities and wide adaptability. This method applies morphological operations to extract the crack skeleton and actual crack length using the ratio of the shooting distance to the focal length. Based on this data, the crack distribution density in the detected area can be quantified, offering a valuable foundation for subsequent maintenance and repair decisions. In addition, the scene data captured by the drone were processed using reverse 3D modeling, enhancing its visualization and providing a more comprehensive view of the inspected structure.

Although this method requires no training and achieves superior performance compared to traditional approaches, it exhibits inherent limitations. In this study, crack detection and segmentation are exclusively applied to bridge scenarios, where fixed thresholds yield satisfactory results. However, extending to large datasets necessitates determining optimal thresholds as a primary research focus. For instance, image contrast can be estimated using the standard deviation of gray-scale values: high-contrast images permit wider threshold ranges and more directional filters, whereas low-contrast images benefit from narrower thresholds and fewer directional filters, enabling adaptive threshold filtering. Additionally, pre-filtering image scaling adjustments (e.g., scaling ratios of 0.75, 1.0, 1.25) accommodate varying resolutions or field-of-view settings.

Concurrently, diverse lighting conditions impact detection outcomes, making algorithm robustness under such variations a critical future research priority. We note existing efforts employ infrared cameras to capture thermal crack data, compensating for lighting-induced information disparities. Consequently, developing advanced fusion algorithms to generate integrated images that fully incorporate dual-image information represents a key future direction.