Introduction

Diabetic retinopathy (DR) is a age-related macular degeneration eye diseases problem that cause pathological changes of retinal neural and vascular system. It is one of the leading causes of blindness DR and is a frequent complication of diabetes mellitus. According to a survey, around \(77\%\) of diabetic people live in low and middle-income countries, and 179 million diabetes people are undiagnosed1 due to limited access of advance devices and skilled ophthalmologists. It is evident from the literature that early detection and adequate treatment \(98\%\) of DR-related vision loss can be prevented2,3,4,5,6,7; In computer aid DR detection, high-quality images to carry enough information for clinical decisions are mandatory8. It is evident from the literature that various imaging models have been proposed in past for achieving high-quality retinal imaging. The Image processing algorithms enhance the low-quality images including decomposition methods9,10. They divide the image into high-frequency and low-frequency signals11,12. The histogram feature changes the image by generating a pixel mapping function, thereby redistributing the original image histogram to increase the image contrast. Various recent methods have received the researchers attention because of their intuitive and straightforward use.

For instance; Dai et al.10 proposed to improve the fundus image by extracting the background image from the original one using the normalized convolution algorithm13. In phase 2 background removal, the new image intensity can be increased and combined with the original image. Finally, noise is removed by applying a fourth-order and average median filter partial differential equation13. It can reduce unexpected changes and improve the visibility of retinal details. However, in this scheme, the analysis of the decomposition is complex. Histogram equalization (HE) is often used to enhance grayscale images by improving contrast using the cumulative distribution function (CDF) to expand the dynamic ranges; however, it produces unwanted artifacts, color imbalance and loss of the detail of color images. Moreover, the average intensity value may change to the mean intensity range14,15,16. It is observed that these brightness preservation algorithms provide an average brightness of the output image and the output is close to the original one, which is unsuitable for color retinal images. Furthermore, the contrast threshold function, contrast-limited adaptive histogram equalization (CLAHE) algorithm17 used to improve the channel illumination. Similarly, Deep convocational networks (DCNN) has significant progress in image processing and classification. The use of DCNN in precise evaluation and DR fundus images are helpful, However, to achieve a reliable diagnosis and the treatment remains a crucial task18,19,20,21,22,23. The optic nerve is a serious condition in glaucoma that causes blindness and is a key area of medical image analysis. The clinical perspective highlights the potential of machine learning in glaucoma diagnosis and Computer-Aided Diagnosis (CAD) that permits the ophthalmologist to avail the benefit of CAD24. Singh et al.25 proposed a machine-learning model for the automatic detection of glaucoma disease, retinal image acquisition, feature extraction, and glaucoma symptoms detection in affected images. Furthermore, the Kumar et al.26 investigates the application of multi-objective feature selection techniques based on differential evolution. The author used K-Nearest Neighbors (KNN) classification schemes to evaluate the performance of subclass precise features. Singh et al.27,28 proposed a correlation filter-based technique for glaucoma detection and hybridized feature selection scheme for funds images. Preprocessing done initially in order to extract the appropriate features, removal of noise and to detect the optic cup and disc. The author presented fast fuzzy C-mean algorithm for fundus image processing to automatically classify the boundaries between the optical disc and cup.

In addition, these are not efficient and also has quality issues. The low-quality retinal images make the subsequent precise segmentation complex. Therefore, in order to solve these issues. In this paper, we propose adaptive enhancement based Deep convolutional neural model for Diabatetic reintopathy cataractous. Our proposed quantitative retinal image analysis provide a new pathway for computer-aid objective diagnosis and the treatment assessment of eye disease. We employ hyperparameter tuning and transfer learning for accurate classifying. Our approach improves the luminance and contrast of poor and average retinal images and is superior to state of the art image-enhancing methods. The proposed model adds enough contrast to an image and keep the cover image’s structural information similar to the original image. Furthermore, it improves the local details of a specific color image without varying the color information. For image enhancement, our proposed model improves the image’s texture and local details to avoid altering its structural information; therefore, we use the Structural Similarity Index (SSIM) to check the structural similarity between the cover and the output image. The performance metrics used to evaluate the outcomes of classification schemes are sensitivity, accuracy, and specificity. The detected precision is the proportion of adequately classified samples to the total sample, and is an excellent way to measure model performance. We observed the training process used hyperparameter-tuning and transfer learning to more accurately classify the fundus images. We have performed several experiments and the efficiency is evaluated using a public dataset named Messidor’s. The average assessment score for the original and enhanced images is 0.1942, standard deviation (SD): 0.0799, Peak Signal-to-Noise Ratio (PSNR) 28.62 and Structural Similarity Index (SSIM) is 0.71. The best classification accuracy is 95.80, indicating that CNNs and transfer learning are superior to traditional methods.

  1. (1)

    We proposed a Deep Convolutional Neural Network (DCNN) model for Diabetic retinopathy (DR).

  2. (2)

    In our proposed model, we have used adaptive gamma enhancement matrix to optimize the image color channels and contrast standardization.

  3. (3)

    The proposed model integrates Quantile-based histogram equalization to expand the perceptibility of the fundus images.

  4. (4)

    The blurriness grading loss limits the contrast of image, reduce the over- and under contract enhancement image problems.

  5. (5)

    We have performed several experiments and the efficiency is evaluated using a public dataset named Messidor’s. The average assessment score for the original and enhanced images is 0.1942 (standard deviation: 0.0799), PSNR 28.79 and SSIM 0.71. The best classification accuracy is 95.88 indicating that CNNs and transfer learning are superior to traditional methods.

The rest of this article is organized as follows. we have presented introduction in section “Introduction” . Section “Related work” describes the related work. It illustrates the details of the proposed techniques in section “Methods”. Results and performance evaluation are deliberated in section “Experiments”, while the conclusion is illustrated in section “Conclusions”.

Related work

In recent years, fundus image enhancement has become a vital area of research, and several advanced retinal techniques have been proposed. The transform domain converts a raw image into a new function with additional parameters, i.e., the spatial frequency domain. A new image with improved contrast is generated by processing the image in different domains. It allows us to change the weights of various structures in the image. However, the image-domain approach is preferred because of its low computational cost29,30,31,32.

According to the Retinex theory33, an image may be divided into a reflectance and an illumination map. The Retinex hypothesis opens new doors for low-illumination image improvement. This process’s main concept is to employ a bilateral-filter to approximate the illumination map, thus getting the reflection map. Elad’s method worked well, but due to the intensity structure’s blindness, bilateral-filtering may reduce image quality33,34.

Lee et al.33 introduced an adaptive MSR algorithm to improve image contrast. The technique improved image contrast well. However, the image outcomes may appear unnatural and over-enhanced. MSR were initially proposed for low-illumination enhancement. SSR and MSR have substantially advanced Retinex theory in image low-illumination enhancement. However, SSR and MSR frequently create halo effects.

They are implemented in logarithmic domains to decrease computing complexity. Because the logarithmic transformation suppresses changes in gradient magnitude in bright regions, addressing an ill-posed challenge might result in the loss of refined structural features. Our approach significantly enhances low-illumination images while keeping the overall structure and feature information. In contrast, enhancement, histogram equalization, and gamma map indicate better adaptability in various enhancement schemes, improving various retinal images.

Histogram equalization expands areas with lower local contrast to produce higher contrast. It does this by setting the most common intensity value. Early approaches generally increase the overall contrast, which results in over-enhancement. This issue has been unravelled by the CLAHE, which can reallocate the brightness in different portions30,35,36,37. In Gamma mapping, the nonlinear function commonly used in image enhancement systems to encode and decode pixel values30,38, can be defined as follows:

$$\begin{aligned} F_{gamma} (x,y) = In(x,y)^{\beta } \end{aligned}$$
(1)

where x and y are the row index and column index of pixels, In (x, y) and \(F_{gamma} (x, y)\) represents the input image and the enhanced image. If the scale coefficient \({\beta }\) is less than 1, the detailed visibility of dark images can be improved and more significant than 1 for an image of sufficient brightness. In the retina theory, the image is composed of a replication of light and reflection. Illumination is seen as the cause of the low frequency and the source of a blur. The luminosity and reflection can be converted further using the logarithmic process.

CLAHE can be useful for non-color channels instead of direct use in RGB images. Adjusting grayscale intensity without any apparent artefact using a Gamma map and the retinal cortex theory can increase the contrast significantly, so the idea of eliminating low-frequency mechanisms can be helpful. The luminosity-based contrast enhancement of the fundus color image suggested R, G, and B channels to improve by luminance gain matrix. The matrix obtains a gamma correction value V channel in the hue saturation value (HSV) of color space. The contrast of the \(L * a * b\) luminance channel can be Increased by applying the CLAHE technique, but the color balance is not adjusted to improve the quality of color images.

Intajag et al.12 suggested a general way to indicate generalized extreme value distribution for Auto adjustment by restructuring image data’s brightness, contrast, and color balance. That supports screening for age-related macular degeneration (AMD) lesions. Automatic DR image detection can effectively diagnose at an early stage. Early diagnosis and treatment are critical to delaying or preventing vision impairment. In the past few years, deep learning technology has revolutionized the field of computer vision. CNN’s use of image classification is attracting the attention of many researchers39,40,41,42. CNN deep domain initially proposed a solution for standard image classification, and the current study has rapidly developed in classifying DR fundus images. Wang et al.43 proposed LeNet-5, which is used to extract image features to solve the problem of blood vessel segmentation; however, this method has some limitations. The data set was small and of poor image quality. Subsequently, several excellent CNN models were proposed, such as GoogleNet44. VggNet45 and ResNet46 model which enhanced CNN’s efficiency in classifying images. We use transfer Learning to expedite the learning time and precise feature detection to reduce visual damage.

Acquiring pixel-to-pixel retinal image pairs of different clarities under the same imaging condition such as angle, focal length, and exposure is extremely difficult in retinal photography. Some fundus image enhancement methods employ the cycle consistency through unpaired image translation. This is to loosen the constraint of insufficient paired training data . However, unreal artifacts sometimes appear without the pixel level constraint in these methods. Therefore, researchers use the degradation of high-quality fundus images to obtain corresponding blurred fundus images.

Methods

The unbalanced luminance can affect the visual sensitivity of fundus images, making it challenging to detect diagnostic information. First, it is vital to improving the luminance effect, but the color would not modify with each pixel’s color image to avoid image distortion. 0 degenerates high-quality fundus images and then trains enhancement networks, which belongs to enhancement based on retinal image degradation. It is difficult to obtain cataractous and high-quality image pairs clinically. Therefore, we propose a degradation model for cataractous fundus image synthesis. The degradation process is based on the image formation model [16], which is widely used in natural image dehazing and has shown good performance in the synthesis of hazy images

Initially, we generate 35 degraded retinal images for each high-quality image by adjusting the transmissivity of t, 0 the step of t is 0.05 and the range is from 0 to 1. These images are then assessed and compared visually with the real cataractous retinal images. Based on the suggestions of two ophthalmologists, we determine to generate the retinal images when the transmissivity t is 0.0, 0.30, and 0.35 The synthetic image has similar blurriness to the real cataractous image, where the contrast and visibility of their blood vessels are similar.

We propose an adaptive enhancement strategy for different cataractous images. Specifically, a classifier for cataract grading and three sets of generative adversarial networks with the same structure are employed in the adaptive enhancement strategy. The enhancement is adjusted according to cataract grading. During training, the blurriness classifier is trained in advance using multi-level cataractous fundus images synthesized through the degradation model to determine the blurriness of input images. Then, three enhancement models of generative adversarial networks are trained independently with synthetic data of different cataract grades to enhance different blurriness. The blurriness in the training set is quantified through the degradation model, so the enhancement ability for each network is guaranteed. In addition, we use the welltrained classifier to calculate the blurriness grading loss to further constrain the enhancement ability of the model. Our blurriness classifier adopts the structure of ResNet-18. Training the classifier requires cataractous fundus images of three different blurriness, high-quality fundus images, and the over-enhanced fundus image. generator adopts the U-net structure. Skip connections are utilized between the downsampling layers and the corresponding upsampling layers.

The fundus image’s color is kept and shown in the RGB color space. R, G, and B channels also contain brightness information which is associated with each color information.

$$\begin{aligned} \frac{ r^{\prime }(i, j) }{ r(i, j)} = \frac{ g^{\prime }(i, j)}{g(i, j)} = \frac{ b^{\prime }(i, j) }{ b(i, j)} = L(i, j) \end{aligned}$$
(2)

The R, G, and B channels are set to the same rate to increase luminosity and reserve the image color [20]. The intensity gain matrix L(i, j). It is distinguished as follows: where \(r^{\prime }(i, j)\), \(g^{\prime }(i, j)\) and \(b^{\prime }(i, j)\) are the R, G, and B enhanced pixel value at (i, j); beside r(i, j), g(i, j) and b(i, j) are the original values of R, G, and B. Converting a color image to the \(\alpha \beta \gamma\) color space, the intensity channel \(\alpha\) is separated from the saturation \(\beta\) and hue \(\gamma\) components. It is easier to get an invariant matrix and make the image brighter. The brightness concentration of the pixel at the location (i, j) is the more significant value of the R, G, and B values; thus, the intensity enhancement matrix can be obtained as follows:

$$\begin{aligned} L(i, j) = \frac{ \alpha ^{\prime }(i, j) }{ \alpha (i, j)} = \frac{ \alpha ^{\prime }(i, j)}{max (r(i, j) g(i, j) b(i, j))} \end{aligned}$$
(3)

\(\alpha (i, j)\) is the brightness of the pixel at location (i, j), and \(\alpha ^{\prime }(i, j)\) is the function \(\alpha (i, j)\), which describes the influence of increasing the intensity enhancement. Processing can be done directly in the RGB color space, reducing the amount of calculation. We slightly increased the dynamic range of low-gray areas to improve the adequate gray level area for pixel \(\alpha ^{\prime }(i, j)\) and retain the high-gray areas. Gamma correction1,16,36 is a standard image processing technique used to convert nonlinear intensity. The transformation curve is expressed as:

$$\begin{aligned} n=m^{\lambda } \end{aligned}$$
(4)

\(m \epsilon [0, 1]\) represents the luminance channel’s expected pixel value, n is the standard output, and \(\lambda\) is constant. The conversion takes place in the form of simple point-wise operations. The transformation, \(\alpha (i, j)\) is normalized to the input of m and \(\alpha ^{\prime }(i, j)\) is the inverse normalization of output n. The value of \(\lambda\) is usually greater than 1.0; however, compared with the pattern line at \(\lambda = 1\), nonlinear transformation can effectively improve the intensity.

The L(i, j) value in the calculated brightness gain matrix is always larger than or equal to 1. The gray scale range in the intensity channel \(\alpha\) is converted to [0, 50] to [0, 122], [100, 150] is converted to [167, 200], and [200, 255] is converted to [228, 255]. Increase the conversion of low dynamic range grayscale and keep a high grayscale level which can simplify the fundus image details; furthermore, increasing the brightness of the \(\alpha \beta \gamma\) color space can efficiently solve the color gamut problem [23]. The pixel value in the intensity \(\alpha\) channel is the additional value in the R, G, and B channels, as well as the gamma correction, which does not transform the grayscale range. Furthermore, \(r^{\prime }(i, j)\), \(g^{\prime }(i, j)\) and \(b^{\prime }(i, j)\) are enhanced values which multiply the original L(i, j) and R, G, and B values correspondingly.

Fig. 1
figure 1

Block diagram of the proposed method for fundus color image enhancement.

Full size image

Adaptive contrast enhancement

The enhancement in intensity is attained through the ’adaptive gamma correction’ (AGC) method, which can compensate for the overall intensity, which leads to a certain degree of contrast enhancement. However, to improve the contrast of the low fundus image, it is necessary to increase its overall contrast. Khan et al.32 proposed automated retinal vascular tree extraction pre-processing procedures for denoising and contrast enhancement (green channel extraction, GLM training, morphological filters, Frangi filter and masking) are followed by preserve threshold for segregating vessel and background pixels. To ensure this, we applied a quantile-based histogram equalization technique where the quantile value of the data point divides into sample data. We use probability distributions to calculate into equal proportion for Pixel intensity data. The quantiles q provides q discrete values which distribute luminosity distribution into q equal portion, shown in Fig. 1.

The random variable R, the tth value and the q quantile are the \(i_{t}\) value. For this:

$$\begin{aligned} R[V]= G[V\leqslant i_{t}] = \frac{t}{q}, t= 0,1,2,...,q. \end{aligned}$$
(5)

The brightness range of the histogram of an input image is \([V_{0}, V_{I-1}]\) where we used the q quantile to distribute the input graph H(V) into q sub-histograms.

\(S_{1} = [s_{0}, s_{1}], S_{2} = [s_{1}, s_{2}],...,S{q} = [s_{q-1}, s_{q}]\), such that:

$$\begin{aligned} G[V \epsilon s_{t}]= G[s_{t}-1 = V \leqslant s_{t}] = \frac{1}{q}, t= 0,1,2,...,q \end{aligned}$$
(6)

where \(s_{0}=V_{0}, s_{q}= V_{I-1} s_{q} \epsilon V_{0}, V_{1},..., V_{I-1}, t= 0,1,..., q\) and I is entire no of grey ranks

while sub-histogram probability of \(S_{t}\), represent by \(G_{t}\) define as:

$$\begin{aligned} G_{t}= \sum _{s \epsilon [s_{t-1}, s_{t} ]} G[V_{n}=s], n= 0, 1,..., I-1 \end{aligned}$$
(7)

So, the pixel intensity normalized the probability mass function. (PMF) in the \(S_{t}\) will be

$$\begin{aligned} G_{t} [V_{n}] = \sum ^{G[V_{n}]} _{G_{t}}, \end{aligned}$$
(8)

then, cumulative distribution function (CDF) defined as:

$$\begin{aligned} F_{t} [V_{n}] = \sum ^{V_{n}} _{s=s_{t-1}} \frac{G[V_{m}=s]}{G_{t}} \end{aligned}$$
(9)

The transformation function of a histogram for \(S_{t}\) will be

$$\begin{aligned} c_{t}(V_{n})= s_{t-1} + (s_{t}-s_{t-1}) F_{t} [V_{n}], t=1,2,3,..., q. \end{aligned}$$
(10)

Assume \(V^{\prime }\) is a processed image; It can be characterized as collecting all processed sub-Histograms.

$$\begin{aligned} V^{\prime }= \bigcup ^{q} _{t=1} c_{t} (V_{n}) \end{aligned}$$
(11)
Table 1 Average PSNR and SSIM result of 1000 test images used in our proposed scheme.
Full size table
Fig. 2
figure 2

Fundus images dataset.

Full size image

Histogram weighting

Sub-histogram \(S_{t}(n)\), we now substitute the PMF of the input image G(m) with the weighted image PMF \(G_{\psi } (m)\), distinct as:

$$\begin{aligned} G_{\psi } (m) = G_{mx} ( \frac{G(m)-G_{mn}}{G_{mx}- G_{mn}} ) ^{G_{k}} + \theta \end{aligned}$$
(12)

Choose ¦E for best consequences, \(G_{mx}.|VE_{1}- VE_{2}| /V_{mx}- V_{mn}\), where average intensity \(VE_{1}\), center gray level, \(VE_{2}\), and Maximum and minimum of \(V_{mx}\), \(V_{mn}\) gray level of the input image. The higher weight is assigned to smaller intensities and provides a smaller weight to the high-frequency intensity. These weights drop transformations between intensity value and intensity distribution, which are constant intensity distributions. The resultant normalize output \(G_{\psi }(m)\):

$$\begin{aligned} G_{\psi r}(t)= \frac{ G_{\psi }(t) }{\sum ^{I-1} _{m=0} G_{\psi }(m)} , \quad 0 \leqslant t \leqslant I-1 \end{aligned}$$
(13)

Image classification

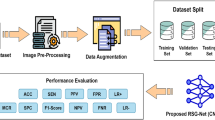
Transfer learning (TL) is widely used to overcome the absence of labeled data by reusing previously trained deep CNN for similar work. TL and hyperparameter tuning are valuable approaches for improving the classification accuracy and significantly reducing the training time when adapting the model and minimizing the demand for training the data. TL enhanced the robustness of diverse datasets, accuracy, and generalization, leveraging pre-trained models and optimizing model tuning over specialized medical image data domains. CNN has made excellent performance in image classification; meanwhile, we integrated hyperparameter-tuning and transfer learning as well as AlexNet43, GoogleNet44, VggNet45, and ResNet46 model which enhanced CNN’s efficiency in classifying DR image dataset. Transfer learning is a mode to remove the last associated layer of a previously trained CNN and treat it as a tool for feature extraction. We can train the classifier on the novel dataset if we extract all the retinal images’ features. The network itself has not started the hyperparameter tuning; these parameters should be refined and optimized according to DR image training outcomes to improve performance. The proposed procedure for using CNN to detect DR is shown in Fig. 1. DL model including CNN network proficient in tasks like feature extraction, image segmentation, and classification. The proposed approach is highly proficient in terms of feature extraction, and a high amount of training data to refine the feature to facilitate accurate localization, early disease detection, and diagnosis of diseases. Thus, the proposed model is not only computationally efficient in retinal image analysis but also significantly enhances the classification accuracy, by reducing the manual feature extraction, automatically learning complex features and patterns, enable faster and more precise automated diabetic retinopathy detection.

Experiments

we have used a a public database47 named retinal Fundus Multi-disease Images dataset (RFMiD)48, and kaggle49 is used to analyze and verify the effectiveness of the image enhancement method based on the intensity and contrast of the fundus image. The AUC (Area Under the Curve) value of 0.9 is considered excellent performance and accuracy of our model which performs outstanding in comparison with other methods, we have chosen the lowest and average value AUC as for the average PNSR value. We got high AUC and accuracy with the comparatively lower value of the PSNR ratio. We have also used RFMiD image database, which include very low-resolution images, even have less than \(1000 \times 1000\) pixels, which can make it difficult for AI models to accurately detect and classify diseases. We used two forms of RGB or Lab color space approaches, CLAHE and HE. We randomly selected these images, as shown in Fig. 2. First we apply the proposed enhancement scheme using large retinal images. However, only the luminance improvement provides a uniform luminance enhancement, and the intensity of the fundus image still needs to be improved. Moreover, CLAHE17 applied to the \(L*x*y\) color space for channel L will significantly increase the contrast of the fundus image1,4,35. The Generalized Linear Model (GLM)32 contrast enhancement method performs better than the CLAHE17 technique. In the literature, Zhou et al.4 provide the optimal approach for RetImg augmentation. We employed histogram equalization and CLAHE schemes in RGB and Lab color spaces, respectively, i.e., HERGB, HELab, CLAHERGB, CLAHELab.

Fig. 3
figure 3

(C) Cover fundus image; \(P_{1}\), \(P_{2}\) and \(P_{3}\) are intensity and contrast enhanced image; Selected areas in the image frame with zoomed in the bottom row.

Full size image

To increase the intensity enhancement, gray values in all channels become more significant due to the intensity gain matrix G(x, y), which illustrates the best illuminance. Besides, the dynamic series of the histogram is also expanded in the lower gray area. Hence, the contrast can be slightly improved by increasing the intensity enhancement.

Fig. 4
figure 4

Enhancement outcomes of lowest luminosity images of proposed method, (C) Cover fundus image; \(P_{1}\), \(P_{2}\), \(P_{3}\), \(P_{4}\), \(P_{4}\) and \(P_{5}\) are proposed different intensity and contrast value of enhanced image.

Full size image

The fundus image enhancement shows better visualization of blood vessels and other significant functional structures of the retinal and the prominence lesions structure. The proposed scheme reserves the fundus image naturalness while enhancing the critical image details, which can help ophthalmologists better analyze the fundus images.

Fig. 5
figure 5

Enhancement outcomes of lighest luminosity images of proposed method, (C) Cover fundus image; \(P_{1}\), \(P_{2}\), \(P_{3}\), \(P_{4}\), \(P_{4}\) and \(P_{5}\) are proposed different intensity and contrast value of enhanced image.

Full size image

The proposed scheme, which is based on improving the intensity and contrast enhancement, the CLAHE method17,35 can only expand the contrast of fundus images with standard illumination in the L channel of \(L*x*y\) color space, but incapable of balancing brightness for low illumine fundus images, displayed in Figs. 3, 4, 5 and 6.

Table 2 Average PSNR result of 1000 test images used in our proposed work.
Full size table

Using CLAHE17 to improve the image in channels R, G, and B can result in severe discolouration, possibly leading to a clinical misdiagnosis. Whereas an enhancement technique based on controlled filtering of an image can effectually improve the entire image’s information, this scheme consequences in an unnatural appearance due to the extra-refinement of details and boundaries. These two approaches cannot expand luminosity; thus, it is necessary to increase the brightness, specifically for low-quality retinal images. Improving the contrast and providing balance illumination for high-contrast images is more effective.

Table 3 Average SSIM result of 1000 test images used in our proposed work.
Full size table

The \(HE_{RGB}\) and \(HE_{Lab}\) methods over-enhance the processed image, altering the useful information in the input image; consequently, many essential input image information is wholly erased during the processing phase. Improved outcomes with the \(CLAHE_{RGB}\) and \(CLAHE_Lab\) approaches expand the processed images’ perceptibility. These approaches do not enhance adequate contrast and cannot maintain a structural similarity of the cover image in the output image, while Zhou et al.4. expand the detail of output images.

Fig. 6
figure 6

Enhanced processed images. The blurred image vessel tracking and after segmentation of enhance image.

Full size image

However, this technique changes the cover image’s color and other visually significant data in the processed image. Furthermore, the proposed technique’s enhancement outcomes increase the contrast without changing the color and structural similarity of the processed image as shown in Fig. 6. The proposed method does not transform the other data of the cover image and structural similarity in the processed appearance; hence our scheme is an appropriate choice for preprocessing to optimize the color image, shown in Tables 1, 2 and 3.

The use of CLAHE17 in the R, G, and B channels cause significant color alteration, potentially leading to experimental misanalysis. Finally, while direct image filtering may efficiently improve the features of the entire image, the over-enhancing of details and boundaries results in a non-natural appearance.

Fig. 7
figure 7

(a) Classification, specificity, sensitivity and PSNR outcome of original images (b) Classification, Sensitivity, Specificity and PSNR performance outcome of enhanced image. Lowest and higher performance outcome (Accuracy: 91.01–96.94) for the ratio of PSNR (28.60–29.17).

Full size image

The retinal images in the Messidor dataset were likewise enhanced and evaluated using our technique. The average assessment score for the original and enhanced images is 0.1942 (standard deviation: 0.0799). The assessment consequences show that our approach can also improve standard retinal images. Compared to the evaluated scores of the two datasets, the Messidor-enhanced images average marginally better, but the original images average considerably higher. However, our technique outperforms both datasets in the low-quality retinal images. Our approach improves the luminance and contrast of poor and average retinal images and is superior to existing image-enhancing methods. The classification accuracy of the blurriness reached 98.91 In the case of misclassification, they are only classified into adjacent categories, which has less impact than other wrong categories. We randomly select the enhancement networks when we test without the assistance of the classifier The proposed adaptive enhancement strategy can grade and enhance cataractous fundus images with the help of the classifier.

The adjusted brightness is easier to observe for images with imperfect illumination, but it will increase the standard deviation for PSNR and SSIM.

The inappropriate enhancement may lead to the decline of the enhancement visually and quantitatively.

Performance analysis

These retinal images’ poor contrast, uneven illumination, and blurriness make clinical diagnosis challenging. The Messidor public database47, Retinal Fundus Multi-disease Image Dataset (RFMiD)48, and kaggle49 used to analyze and verify the effectiveness of the image enhancement method based on the intensity and contrast of the fundus image. We used two forms of RGB or Lab color space approaches, CLAHE and HE. We have randomly selected these images.

The proposed model add enough contrast to an image and keep the cover image’s structural information similar to the original image. Furthermore, it improve the local details of a specific color image without varying the color information. We use the PSNR (Peak Signal-to-Noise Ratio) to measure the information in the cover and processed image. It is widely used to measure properties such as enhancing texture detail, improving contrast, etc. A high PSNR value in Fig. 6 shows that processed images have minimum visual distortion and excellent visual quality. The proposed model extends the contract and illumination of fundus color images by non-linearly fine-tuning the pixels’ intensities, which are used in image contrast enhancement, color protection, illumination correction, and detail preservation to encode and decode the pixel values. Furthermore, the fundus image, image formation, non-linear perception, and the Gamma correction mechanisms make this enhancement more uniform and natural by squeezing the dynamic range of dark pixels and intensifying the dynamic range of bright pixels. The PSNR is a non-linear metric that compares the pixel values of degraded images and original reference images. First, we calculate mean squared error (MSE). If the value of MSE is lower, then higher the PSNR value and lowers the error ratio. Higher PSNR values indicate better contrast improvement while at the same time retaining high-frequency details (edges and textures). The average PSNR for other techniques is lower than that of the proposed scheme, which means that the proposed approach outperforms concerning PSNR. Improve the texture information and local data in the image for additional analysis by an ophthalmologist.

Enhancing retinal images presents challenges like preserving color fidelity, managing uneven illumination, and dealing with noise and artifacts, while also ensuring that enhanced images accurately reflect the underlying retinal structures for better diagnosis. Challenges to address illuminated retinal images without over-enhancing or introducing artifacts (1) Inconsistent brightness might impact the visual sensitivity of fundus images, making it challenging to identify diagnostic information. First, it is essential to enhance the brightness impact; however, to prevent image distortion, the color would not change with each pixel’s color image. The RGB color space retains and displays the color of the fundus image. The brightness information that corresponds to each color information is presented in the R, G, and B channels. (2) Although to improve the contrast of the low fundus image, it is necessary to increase its overall contrast. We applied a quantile-based histogram equalization technique where the quantile value of the data point is divided into sample data. We use probability distributions to calculate into equal proportion for pixel intensity data. (3) Retinal images can be noisy, especially when captured in low-light conditions. Enhancement methods effectively reduced the noise while preserving important details of retinal images. For image enhancement, we need to improve an image’s texture and local details to avoid altering its structural information; therefore, we use the Structural Similarity Index (SSIM) to check the structural similarity between the cover and the output image. The higher the SSIM value, which specifies that the resultant image retains the structural details of the cover image. The proposed method has a higher SSIM and PSNR value, ensuring the processed image’s structural details and no misconceptions in the ophthalmologist process’s advanced diagnosis. The proposed technique improve standard fundus images and be used during the image diagnosis phase. The above consequences show that the proposed enhancement approach is significant for both weak and standard fundus images to expand luminosity and contrast.

Table 4 Classification results of original images. Lowest and higher performance outcome (Accuracy: 91.01–96.94) for the ratio of PSNR (28.60–29.17).
Full size table
Table 5 Hyperparameter-tuning based classification results of enhanced images. Lowest and higher performance outcome (Accuracy: 91.01–96.94) for the ratio of PSNR (28.60–29.17).
Full size table

The performance metrics used to evaluate the outcomes of classification schemes are sensitivity, accuracy, and specificity. The detected precision is the proportion of adequately classified samples to the total sample is an excellent way to measure model performance. The classification performance of different CNN architectures’ overall classification consequences could be better. Furthermore, we observed the training process used hyperparameter-tuning and transfer learning to more accurately classified the fundus images.

$$\begin{aligned} ACC= & \frac{TP+TN}{TP+FP+TN+FN } \end{aligned}$$
(14)
$$\begin{aligned} SE= & \frac{TP}{TP+ FN } \end{aligned}$$
(15)
$$\begin{aligned} SP= & \frac{TN}{TN+ FP } \end{aligned}$$
(16)

After 30 to 40 training iterations, the fundus image data is enlarged 20–25 times compared to the original image; the learning factor varies linearly within the range \([0.0\, 0\, 01-0.1]\) and a randomized gradient optimization technique employed to improve weight values. Five-fold validation is used to analyze the consequence, shown in Tables 4 and 5, the classification accuracy of the VggNet-s model. The less training data and extra tracking parameters lead to the overfitting occurrence, leading to lower classification accuracy.

Conclusions

In this paper we proposed a efficient image enhancement and classification model to expand the illumination and contrast of fundus color images. Herein, we provide a remarkable improvement in fundus color images, which can be used particularly for low-contrast quality images. The proposed model not only strengthens the critical anatomical structure of the retinal image but also preserves the visual perception of the image; furthermore, it significantly supports ophthalmologists in diagnosing diseases by analyzing fundus images and utilizing an automated image analysis system. In the future, we can consider our model to evaluate the efficiency of obtaining real high-quality retinal images for stability and robustness using a large real-time database.