Introduction

Community detection 1 is a well-liked research hotspot in complex networks, which is widely used in electronic commerce, social media, and other fields. Community detection can reveal the structures and functions that are hidden inside complex networks. For example, in social networks, analyzing users’ behavioral patterns and identifying user groups with similar interests and behaviors can predict user behavior, recommend friends or content, and enhance user experience 2. In biological networks, community detection is often used to study the interaction between proteins and genes, which helps understand the basic laws of life processes. On the Internet, it can help users discover the themes of their interest to deliver a customized recommendation page. In traffic networks, community detection is used to identify the areas of traffic jams and identify its key nodes to improve traffic efficiency. In financial networks, it can reveal the relationship between financial institutions and the path of risk communication, which is used to evaluate market risks and predict financial crises, to provide favorable tools for financial supervision. Dynamic community detection has become more difficult but also more practically significant by turning the dynamic network into a sequence of snapshots and watching the evolution of the interactions between nodes across successive snapshots. The work of forebears has led to the proposal of an increasing number of community detection techniques. For static networks, such as spectral clustering 3,4,5, modularity optimization6,7, random walking 8,9, and Graph Partitioning 10,11,12. However, in dynamic networks, most of the existing methods have certain limitations, such as optimization problems, and scalability of the model.

For dynamic networks, there are several classes of methods to detect the dynamic community structure 13,14. The first is the intuitive two-step method, which is based on the static community detection method. By obtaining the community structure under different snapshots in the dynamic network, it is analyzed according to a similar methodology to calculate its evolution. However, this method is greatly affected by noise, if the interference of noise is very powerful, it becomes impractical. In another approach, dynamic networks can be analyzed by generating models. This method can not only excellently accomplish the task of community detection, but also be applied to link prediction 15,16 in complex networks. The main idea of this method is to generate dynamic networks 17 through certain assumptions and potential variables and treat the network as a sample. As a result, community detection is transformed into a parameter estimation problem, such as a dynamic Bayesian model 18 and a dynamic random block model 19. However, these models tend to have high time complexity and are difficult to scale.

In recent years, non-negative matrix factorization 20,21 has become the focus of dynamic network analysis for community detection. This method can well integrate other types of methods and is easy to expand. Li et al. 22 proposed a dynamic community detection method called NE2NMF based on NMF in dynamic networks. They proved the equivalence between network embedding and NMF, providing the theoretical foundation for algorithms. Yu et al. 23 proposed a novel evolutionary clustering framework, which is based on Graph regularized nonnegative matrix factorization (ECGNMF), to detect dynamic communities and the evolution patterns and predict the varying structure across the dynamic networks. However, in terms of this research progress, NMF-based dynamic community detection cannot use structural characteristics well.

In this paper, we propose a dynamic community detection method based on graph and symmetry bi-regularized non-negative matrix factorization, called GrSrNMF, for detecting the dynamic communities, exploring their evolution pattern, and predicting the structure changes in dynamic networks. The graph- and symmetry-regularization are added to the model as penalty terms, making it more effective at addressing structural changes. In principle, we detect the evolutionary model in different community networks over time and across spatial locations. Finally, we discover that GrSrNMF for community detection in dynamic networks has major benefits over several state-of-the-art models. Notably, our approach is also capable of capturing changes in the number of communities in dynamic networks. The following are several important outstanding contributions of this work:

  • We suggest a new framework called GrSrNMF, which is more likely to be used for dynamic network growth. It inherits the constraint optimization of its predecessor, evolution clustering, and regular items.

  • GrSrNMF can enhance the learning ability of ECGNMF by adding the learning goals of the symmetry-regularization item, and can be integrated into any other types of dynamic networks, and it is also easy to expand and optimize.

  • The proposed model may successfully identify the community structures in addition to appropriately handling variations in the number of communities hiding in network snapshots. In conclusion, the evolution of the communities may be anticipated and investigated by mining the community evolution pattern.

Experiments conducted on two synthetic networks and two real networks indicate that, compared with other advanced methods, our community detection based on GrSrNMF achieves more significant accuracy improvement. Section "Related work" conducts a preliminary summary of related work. Section "Models" puts forward the method of GrSrNMF. Section "Experiments analyses" shows the experimental results and analyzes and discusses them, and Section "Discussion" concludes this work.

Related work

In the context of dynamic networks, community detection for dynamic networks is often classified into two groups: heuristic-based methods and model-based methods.

For the heuristic-based methods, for example, the modularity optimization algorithm, it mainly identifies the community by meeting the predefined evaluation indicators as the goal and then searches the node information of the target network. In recent years, maximum modularity frameworks have been widely used in community detection, for example, label propagation algorithms24 and random walk-based algorithms25. Not only that, there are scholars who solve problems by traversing the entire solution space through methods such as greedy search optimization or extreme value optimization. The strategic methods of such methods mainly include the following: two-step based strategies26,27, incremental clustering28,29, evolutionary clustering30,31,32, spectral clustering3,4 and multi-agent perspective33,34. By periodically updating the most recent snapshot in dynamic networks, these techniques are mostly used to predict communities that are changing. Abernathy et al.  28 proposed a new partition color quantization algorithm based on MacQueen’s online K-means binary splitting formula. This framework can solve the initialization and acceleration problems of K-means without sacrificing the simplicity of the algorithm. Ye et al. 30 proposed an efficient evolutionary clustering algorithm, which finds sparsely optimum solutions to extremely large-scale multi-objective optimization problems. By maximizing each solution’s binary vector, the algorithm determines the sparse distribution of the ideal solution and offers a quick clustering technique to significantly lower the search space’s dimension. Xiao et al. 4 proposed a spectral clustering algorithm based on a Gaussian mixture type model, and chose to formalize two intuitions, which significantly improved the accuracy of its community detection. Chreim et al. 34 transformed the community detection problem corresponding to power network management into a modeling-constrained optimization problem, for which the Lagrange multiplier approach was used to centrally solve. Moreover, the decentralized method based on a multi-agent system (MAS) enabled it to be effectively solved. So far, although the heuristic-based methods have been widely used in the community detection of dynamic networks, they also have some shortcomings. These methods do not have a strict model interpretation, and the models have high computational complexity. In addition, these heuristic methods either ignore the evolution of the community or only consider the two-step strategy, thus ignoring the information connection between neighboring snapshots during the task process, resulting in unclear information processing results of the community detection in the dynamic network.

The majority of current model-based methods, by modeling the dynamic network generative mechanism, treat community detection as a learning challenge and convert it into a parameter estimation issue based on maximizing posterior probability. To represent a dynamic network, a dynamic latent space model is first built, and the network nodes are mapped to Euclidean space positions. Next, the hidden Markov hypothesis is used to build the link between the hidden and observable variables. Finally, the evolution pattern of the community is captured by the method of the random block model, and then the estimated parameters are calculated based on the maximization of the posterior probability by clarifying the transition of individual nodes of the model. For the above methods, for example, weighted random block model (MSBM)35, degree corrected random block model (DCSBM)36, bisect random block model SBM(CUSUM)19, etc. The model-based method has a good theoretical explanation, and it is able to accurately depict the features of the dynamic network’s progression. Nevertheless, there are also drawbacks to this approach. Specifically, the corresponding optimization procedure has a high computational cost, and there are typically a lot of model parameters. Furthermore, model-based methods for detecting communities in dynamic networks often presuppose that the quantity of communities remains constant across time, which also leads to their defects in capturing dynamic network information in real-world applications of dynamic networks, and a lack of adaptability to network environments with rapidly changing community structures in the real world.

In recent years, community detection using graph neural networks has emerged as a significant research topic. Wang et al. 37 proposed a novel autoencoder-based model for self-supervised graph representation learning with redundancy reduction. Their approach incorporates a multi-scale module built upon the Graph Autoencoder (GAE) framework, specifically designed for community detection tasks. Experimental results on real-world network datasets demonstrate the superior performance of this method compared to existing approaches. Cheng et al. 38 proposed a novel approach that integrates deep non-negative matrix factorization (DNMF) with graph neural networks (GNNs). This method not only mitigates the oversmoothing issue inherent in GNNs but also enhances DNMF’s ability to reconstruct nonlinear network structures, thereby compensating for the respective limitations of both techniques.

Our most related method is based on non-negative matrix factorization (NMF). This is among the most accurate techniques for detecting communities in actual networks. The community detection model based on NMF learns its low-rank representation 39 by decomposing its target matrix into two potential eigenmatrices, namely the eigen matrix and the coefficient matrix. Then, by considering the factors in the coefficient matrix as a soft indicator of the probability of a node merging into a specific community, NMF is well suited to graph clustering, which has been proved to be equivalent to classical and complex clustering methods, such as K-means, through its potential clustering effect and its complex variants. It also has good interpretability for clustering tasks. Liu et al. 40 provided an NMF architecture that allows the implemented detector to effectively learn the symmetric structure among communities in the target network while maintaining the local invariance of the network’s intrinsic geometry. Nevertheless, the dynamic networks’ evolutionary process remains elusive to this technique. Ma et al. 41 suggested an evolutionary non-negative matrix factorization technique that is co-regularized and based on evolutionary communities (called Cr-ENMF), which characterizes cluster drift using the network and community from the preceding time step. Nevertheless, rather than concentrating on the dynamics of any one community, the similarity determined by this technique measures cluster drift as the total of all communities’ dynamics. This can lead to poor performance of the algorithm, and the computational complexity of this framework is high. Li et al. 42 proposed a new NMF algorithm for dynamic embedding and cluster joint learning, and used it for dynamic community detection. This algorithm integrates network embedding, edge dynamics, and clustering into a framework through joint learning, integrates the graph representation of edge layers with dynamics, and provides innovative ideas for dynamic community detection based on representations. However, it lacks the quantification of dynamic communities. However, their model works either when evolutionary patterns and community numbers in dynamic networks are time-varying, or the model fails to process and take advantage of structural features. For instance, in modeling dynamic networks, information processing is crucial in determining the microevolutionary properties of nodes.

In view of some problems and shortcomings in the above related methods, GrSrNMF can well solve and optimize. For example, GrSrNMF can not only work on static networks, but also divide the dynamic networks under snapshots into communities, and learn and adapt to the evolutionary mechanism of dynamic networks to describe them. Moreover, this method takes advantage of the limitation of the regular term of the Laplace diagram, which can solve the problem that the above methods cannot deal with the network feature structure 43,44,45. The most important thing is that in undirected graphs, the symmetric relationships between nodes represent a critical topological characteristic. The symmetry constraint introduced by our model effectively captures this structural property, thereby enhancing the accuracy of community detection. GrSrNMF can learn the symmetry of undirected graphs based on its characteristics, and through this feature, it can learn and explore the correlation between the structures of the community nodes 46,47 in the snapshots of the undirected graph under the dynamic network, to better divide communities at different times in the different snapshots of time series under the dynamic network.

Models

Preliminaries

In this work, we primarily investigate the performance of this symmetric learning device using an unweighted, undirected dynamic network. From this, we represent a dynamic network as G = (V, \(E_t\)), when snapshot \(t = 1, 2, 3,..., T\) represents different snapshots of dynamic network. V represents the set of nodes, and \(N=|V |\) represents the number of nodes. \(E_t\) represents the set of edges, and \(M_t=|E_t |\) represents the number of edges in the snapshot t. Because this is a dynamic network, we also expressed \(K_t\) as the number of communities divided at the time of t, and the network of networks at different times is represented by the adjacency matrix and recorded as \(A_t\). Among them, if the node i is connected to the node j in the network, then \(A_{ij,t} = 1\), otherwise, the summary of all characters is introduced as 0. Table 1 shows the interpretations of all symbols.

Table 1 Table of symbols.
Full size table

Nonnegative matrix factorization

The Classical Nonnegative Matrix Factorization (NMF) has been widely used in different fields. The most important core idea is to break down the observation matrix, so as essence for the challenge of locating the community in dynamic networks. For a dynamic network G with T snapshots, different snapshots are independent of each other. SNMF is used independently for every snapshot with the following objective function:

$$\begin{aligned} \min _{U_t\ge 0,A_t\ge 0} O_t = \Vert A_t - U_tH_t^T \Vert _F^2 \end{aligned}$$
(1)

GrSrNMF

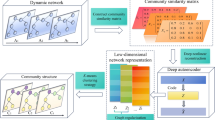
In this work, we proposed a dynamic community detection framework based on a non-negative matrix factorization model combining graph- and symmetry-regularization (GrSrNMF). GrSrNMF is an efficient learning algorithm that uses non-negative matrix factorization techniques to represent the undirected network in each snapshot of the time-series network, and maintains its ability to learn the network through continuous iteration. It achieves local invariance through graph regularization and combines it with symmetric regularization to decompose the low-rank matrices into those that preserve the intrinsic geometric features of the target network under the assumption of symmetric adjacency matrices. The illustration of the proposed GrSrNMF is shown in Fig. 1. The introduction of GrSrNMF is detailed as follows.

First, we introduce evolutionary clustering as taking into account the differences in the effects of various network architectures on community discovery in historical snapshots. CB is the snapshot cost, CG is the time cost, and \(\gamma\) is a balanced parameter,

Fig. 1
figure 1

The illustration of the proposed GrSrNMF.

Full size image

The cost function might be set up like this: \(cost = \gamma \cdot CB + (1-\gamma )\cdot CG\). Furthermore, we take into account the dynamic network’s manner of evolution over time. Thus, \(H_t \approx H_{t-1} Z_{t-1}\) may be considered, where \(Z_{t-1}\) represents the transition matrix from the community of the snapshot \(t-1\) to t. Based on evolutionary clustering, its objective function (called ECNMF) is as follows:

$$\begin{aligned} \min _{U_t,H_t,Z_t\ge 0} O_t =\left\{ \begin{aligned}&\Vert A_t - U_tH_t^T\Vert _F^2,&\, t = 1 \\&\Vert A_t - U_tH_t^T\Vert _F^2 \\&+ \alpha \Vert H_{t-1}Z_{t-1}-H_t\Vert _F^2,&\, t\ge 2 \end{aligned} \right. \end{aligned}$$
(2)

where the community transition matrix in the different snapshot is \(Z_{t-1}\) \(\in\) \(R_+^{K_{t-1\times K_t}}\); typically, we have \(\sum _{EMPTY}{EMPTY}_kZ_{lk,t-1} = 1\), with \(\alpha\) serving as the equilibrium parameter. We can eventually obtain community labels for various snapshots by continuously updating the iterative \(U_t\), \(H_t\), and \(Z_{t-1}\) until their convergence. In addition, under continuous snapshots of dynamic networks, the transition matrix \(Z_{t-1}\) can quantify the nodes’ inclination to transfer to distinct communities. The evolution pattern of dynamic networks can be obtained spontaneously, but it only contains information about the historical network structure under different community structures and lacks information about the microscopic changes of nodes.

Second, inspired by graph regularization, we introduce a graph regularization term to make up for the lack of information observation between nodes with the micro changes of the node. As per the hypothesis of evolutionary clustering, the higher the consistency for the nodes i and j in the last snapshot, the higher the likelihood that it belong to the same community of snapshot t. So we express similarities for nodes i and j at the snapshot \(t-1\) as \(S_{ij,t-1}\). Then a term \(S_{ij,t-1}\cdot \Vert H_{i,t}-H_{j,t}\Vert _F^2\) will be introduced, where \(H_{i,t}\) indicates the membership vector of the node i in the different time of the snapshot t. To the similar of \(S_{ij,t-1}\), the more likely it is that the community member vectors \(H_{i,t}\) and \(H_{j,t}\) have stable distributions at the snapshot t. As a result, we can present a fresh image of common products in the manner shown below:

$$\begin{aligned} \begin{aligned} R_t&= \sum _{i=1}^{N}\sum _{j=1}^{N}S_{ij,t-1}\cdot \Vert H_{i,t}-H_{j,t}\Vert _F^2\\&= \sum _{i=1}^{N}\sum _{j=1}^{N}S_{ij,t-1}\cdot ((H_{i,t} - H_{j,t})(H_{i,t}-H_{j,t})^T)\\&= \sum _{i=1}^{N}\sum _{j=1}^{N}S_{ij,t-1}\cdot (H_{i,t}H_{i,t}^T + H_{j,t}H_{j,t}^T - 2H_{i,t}H_{j,t}^T)\\&= 2\sum _{i=1}^{N}H_{i,t}H_{i,t}^TD_{ii,t1}^{(S)}-2\sum _{i=1}^{N}\sum _{j=1}^{N}S_{ij,t-1}H_{i,t}H_{j,t}^T\\&= 2tr(H_t^TD_{t-1}^{(S)}H_t) - 2tr(H_t^TS_{t-1}H_t)\\&= 2tr(H_t^TL_{t-1}H_t) \end{aligned} \end{aligned}$$
(3)

where tr(\(\cdot\)) indicates the trace to matrix, \(D_{t-1}^{(S)}\) is a diagonal matrix, of which the element \(D_{ii,t-1}^{(S)}\) = \(\sum _{j=1}^{N}S_{ij,t-1}\), and \(L_{t-1}\) = \(D_{t-1}^{(S)}\)-\(S_{t-1}\), which is the Laplacian matrix of \(S_{t-1}\). When analyzing the evolution of a dynamic network, the local structural information is crucial. Based on local similarity indices, for example, Common Neighbors, Adamic Adar48, Salton49, Jaccard Coefficient50, and so forth, we can create the similarity matrix \(S_{t-1}\). If not, Eq. (4) states that the similarity can combine any local similarity.

$$\begin{aligned} \overline{S}_{t-1} = \sum _{\omega =1}^{\Omega }\lambda _\omega S_{t-1}^{\omega } + \tau \Vert \lambda \Vert _2^2 ,\sum _{\lambda _\omega }^{\Omega }\lambda _{\omega } = 1 ,\lambda _{\omega } \ge 0 \end{aligned}$$
(4)

where \(\lambda\) is the weight vector and \(\Omega\) indicates the number of local similarity among nodes. To prevent overfitting, a nonnegative parameter called \(\tau \Vert r \Vert ^2\) is included. We take into consideration one similarity index in this work.

Then, by introducing graph regularization, we constitute an evolutionary clustering framework (called ECGNMF) with the following objective functions:

$$\begin{aligned} \min _{U_t,H_t,Z_t\ge 0} O_t =\left\{ \begin{aligned}&\Vert A_t - U_tH_t^T\Vert _F^2,&\,t = 1 \\&\Vert A_t - U_tH_t^T\Vert _F^2 \\&+ \alpha \Vert H_{t-1}Z_{t-1}-H_t\Vert _F^2\\&+ \beta Tr(H_t^TL_{t-1}H_t),&\text {EMPTY}t\ge 2 \end{aligned} \right. \end{aligned}$$
(5)

Another equilibrium parameter that regulates the weight of the graph’s regularized details is \(\beta\).

Last, to understand the direct information relationships between nodes, we try to add a symmetric regularization term to ensure that the symmetry of the objective network across continuous snapshots in dynamic networks can be maintained. We attempt to combine graph and symmetry-regularization terms into NMF. This learning mechanism can consider the relationship between two latent matrices through the restriction for the low-rank matrix and its transpose. As a result, it may both effectively preserve the original model’s learning capacity and identify the symmetry connections in networks, as well as enhance them. So we introduced a new symmetric regularization term, as follows:

$$\begin{aligned} \min _{U_t,H_t,Z_{t-1}\ge 0} O_t =\left\{ \begin{aligned}&\Vert A_t - U_tH_t^T\Vert _F^2,&\, t = 1 \\&\Vert A_t - U_tH_t^T\Vert _F^2 \\&+ \alpha \Vert H_{t-1}Z_{t-1}-H_t\Vert _F^2\\&+ \gamma \Vert U_tH_t^T - H_tU_t^T\Vert _F^2\\&+ \beta Tr(H_t^TL_{t-1}H_t),&\text {EMPTY}t\ge 2 \end{aligned} \right. \end{aligned}$$
(6)

Among them, \(\gamma\) is a new equilibrium parameter that controls the weight of the regularization information of the symmetry term. In the case when \(t \ge\) 2, \(O_t\) is not a convex function. Consequently, we minimize the objective function \(O_t\) by using the gradient descent estimation algorithm51, which can be express as:

$$\begin{aligned} \begin{aligned} O_t&= Tr(H_tU_t^TU_tH_t - A_t^TU_tH_t^T-H_tU_t^TA_t)\\&+ \alpha Tr(Z_{t-1}^TH_{t-1}^TH_{t-1}Z_{t-1}\\&- Z_{t-1}^TH_{t-1}^TH_t - H_t^TH_{t-1}Z_{t-1}\\&+ H_t^TH_t) + \gamma (H_tU_t^TU_tH_t^T - H_tU_t^TH_tU_t^T - U_tH_t^TU_tH_t^T \\&+ U_tH_t^TH_tU_t^T) + \beta \sum _{s=1}^{t-1}\theta ^{t-s} Tr(H_t^TL_{t-1}H_t) + const \end{aligned} \end{aligned}$$
(7)

The Lagrange multipliers are shown to \(\Psi _{ik,t}\), \(\Phi _{jk,t}\) and \(\xi _{lk,t-1}\) for constraints \(U_{ik,t}\) \(\ge\) 0, \(H_{jk,t}\) \(\ge\) 0 and \(Z_{lk,t}\) \(\ge\) 0, respectively. Letting \(\Psi _t\) = [\(\psi _t\),t], \(\Phi _t\) = [\(\phi _t\),t], and \(\Xi _t\) = [\(\xi _{lk,t}\),\(t-1\)], we obtain the minimum value of the loss function by constructing the Lagrange function \(L_t\) as

$$\begin{aligned} \begin{aligned} L_t&= Tr(H_tU_t^TU_tH_t - A_t^TU_tH_t^T-H_tU_t^TA_t)\\&+ \alpha Tr(Z_{t-1}^TH_{t-1}^TH_{t-1}Z_{t-1}\\&- Z_{t-1}^TH_{t-1}^TH_t - H_t^TH_{t-1}Z_{t-1} \\&+ H_t^TH_t) + \gamma (H_tU_t^TU_tH_t^T - H_tU_t^TH_tU_t^T - U_tH_t^TU_tH_t^T \\&+ U_tH_t^TH_tU_t^T) + \beta \sum _{s=1}^{t-1}\theta ^{t-s} Tr(H_t^TL_{t-1}H_t) \\&+ Tr(\Psi _tU_t^T) + Tr(\Phi _tH_t^T) + Tr(\Xi _{t-1}Z_{t-1}^T) +const \end{aligned} \end{aligned}$$
(8)

The partial derivatives of \(L_t\) about \(U_t\), \(H_t\), and \(Z_{t-1}\) are as follows:

$$\begin{aligned} \frac{\partial L_t}{\partial U_t} = 2U_tH_t^TH_t - 2A_tH_t + 4\beta U_tH_t^TH_t - 4\beta H_tU_t^TH_t + \psi _t \end{aligned}$$
(9)
$$\begin{aligned} \frac{\partial L_t}{\partial H_t}= & 2H_tU_t^TU_t - 2A_t^TU_t - 2\alpha H_{t-1}Z_{t-1} + 2\alpha H_t \nonumber \\ & + 4\beta H_tU_t^TU_t - 4\beta U_tH_t^TU_t + 2 \gamma L_{t-1}H_t +\Phi _t \end{aligned}$$
(10)
$$\begin{aligned} \frac{\partial L_t}{\partial Z_{t-1}} = 2\beta H_{t-1}^TH_{t-1}Z_{t-1} - 2\beta H_{t-1}^TH_t + \Xi _t \end{aligned}$$
(11)

The Karush-Kuhn-Tucker criteria are as follows: \(\psi _{ik,t}\) \(U_{ik,t}\) = 0, \(\phi _{jk,t}\) \(H_{jk,t}\) = 0, and \(\xi _{lk,t-1}\)The following equations may be used to derive \(U_{ij,t}\), \(H_{jk,t}\), and \(Z_{lk,t-1}\) when \(Z_{lk,t-1}\) = 0:

$$\begin{aligned} & 2(U_tH_t^TH_t)_{ik}\psi _{ik,t} - 2(A_tH_t)_{ik}\psi _{ik,t} \nonumber \\ & + 4\beta (U_tH_t^TH_t)_{ik}\psi _{ik,t} - 4\beta (H_tU_t^TH_t)_{ik,t} = 0 \end{aligned}$$
(12)
$$\begin{aligned} & \begin{aligned}&2(H_tU_t^TH_t)_{jk}\phi _{jk,t} - 2(A_t^TU_t)_{jk}\phi _{jk,t} - 2\alpha (H_{t-1}Z_{t-1})_{jk}\phi _{jk,t} \\&+ 2\alpha (H_t)_{jk}\phi _{jk,t} - 4\beta (U_tH_t^TU_t)_{jk}\phi _{jk,t} \\&+ 2\gamma (L_{t-1}H_t)_{jk}\phi _{jk,t} = 0 \end{aligned} \end{aligned}$$
(13)
$$\begin{aligned} & 2\beta (H_{t-1}^TH_{t-1}Z_{Z-1})_{lk}\xi _{lk,t} - 2\beta (H_{t-1}^TH_t)lk\xi _{lk,t} = 0 \end{aligned}$$
(14)

Then, using the following updating rules, we may minimize the object function \(O_t\)(t \(\ge\) 2):

$$\begin{aligned}&U_{ik,t} \leftarrow U_{ik,t} \cdot \frac{(2\beta H_tU_t^TH_t + A_tH_t)_{ik}}{(2\beta U_tH_t^TH_t + U_tH_t^TH_t)_{ik}} \end{aligned}$$
(15)
$$\begin{aligned}&H_{jk,t} \leftarrow H_{jk,t} \cdot \frac{(2\beta U_tH_t^TU_t + A_t^TU_t + \gamma S_{t-1}H_t + \alpha H_{t-1}Z_{t-1})_{jk}}{(H_tU_t^TU_t + \alpha H_t + 2\beta H_tU_t^TU_t + \gamma D_{t-1}H_t)_{jk}} \end{aligned}$$
(16)
$$\begin{aligned}&Z_{lk,t-1} \leftarrow Z_{lk,t-1} \cdot \frac{(H_{t-1}^TH_t)_{lk}}{(H_{t-1}^TH_{t-1}Z_{t-1})_{lk}} \end{aligned}$$
(17)

We summarize the algorithm for GrSrNMFFootnote 1 in Alogorithm 1. Regarding this algorithm, most of the time is spent updating \(U_t\), \(H_t\), and \(Z_t\) to the time for every iteration is \(O(N^2\hat{K} + N\hat{K^2})\). Consequently, the overall time complexity is almost \(O(n_{iter}T(N^2\hat{K} + N\hat{K^2}))\), where \(\hat{K}\) symbolizes the average number of communities and nitrate represents the average quantity of iterations. The average number of edges \(\hat{M}\) between snapshots can be used to estimate \(N^2\) in dynamic networks, which are known to be quite sparse. In addition, \(\hat{K}\) is often substantially less than \(\hat{M}\) and N, and it is basically negligible. Consequently, our suggested algorithm’s time complexity is lowered to \(O(n_{iter}T(\hat{M} + N))\).

Algorithm 1
figure a

GrSrNMF-based community detection.

Full size image

We perform all experiments on a PC with Windows and Intel Core i7-11800H CPU at 4.60 GHz and 32GB RAM. The software is MATLAB in R2020a version.

Experiments analyses

We demonstrate the results of our proposed GrSrNMF in various artificial and real-world dynamic networks, which include community structure prediction, evolutionary pattern discovery, and dynamic community detection. In these experiments, we use the AA index as the local similarity to generate the similarity matrix S. The balancing parameters are as follows, without compromising generality: \(\alpha\) = 20, \(\beta\) = 2, and \(\lambda\) = 100.

Metrics. To measure the performance of different community detection methods, many evaluation indicators have been studied. Here, we have selected three widely used evaluation indicators: Normalized Mutual Information (NMI), Error Rate (ER), and Completeness Ratio (CR). The \(NMI = \frac{2I(\hat{C},C)}{H(\hat{C})+H(C)}\), \(ER = \Vert \hat{C}\hat{C^T} - CC^T\Vert _F^2\) and \({CR} = \frac{\text {Trace}(\hat{C} C^T)}{\text {Trace}(C C^T)}\). To be more precise, C stands for ground truth, and \(\hat{C}\) represents the community structure that the algorithm has identified. The entropies of \(\hat{C}\) and C are denoted by \(H(\hat{C})\) and H(C), respectively, while the mutual information between \(\hat{C}\) and C is denoted by \(I(\hat{C},C)\). Here, the formulas for calculating entropy and mutual information are \(H(X) = \sum _{EMPTY}{EMPTY}_{k=1}^KN_klog\frac{N_k}{N}\), and I(X;Y) = \(\sum _{EMPTY}{EMPTY}_{k=1}^{K^X}\sum _{EMPTY}{EMPTY}_{l=1}^{K^Y}N_{kl}log\frac{N\cdot N_{kl}}{N_k^X\cdot N_l^Y}\), where N is the number of nodes in the community and K is the number of communities in the current network. NMI is used as a normalized entropy metric ranging from [0, 1] and is often employed to evaluate the consistency or similarity in two separators. On the other hand, ER is often used to quantify the difference between two different community structures, and a lower ER value indicates better performance. In general, as the size of the network increases, ER tends to increase as well. CR calculates the degree of alignment between the community structure detected by the algorithm and the actual community structure. The higher the degree of matching, the higher the CR value, indicating better performance of the algorithm.

Baselines. For an extensive comparative analysis, we compared GrSrNMF with 7 methods: SNMF, Multislice52, FaceNet53, FVI-NMF54, MSSC55, AFFECT56, Cr-ENMF41 and JLMDC57.

Datasets. For our experiments, we use four datasets, of which details are as follows.

  • Synthetic dataset #1. It is based on the Girvan Newman58 benchmark’s dynamic generalization and the following settings: number of communities K = 4, quantity of nodes N = 128 at each snapshot, and quantity of snapshots T = 10. The values of 4, 5, and 6 are the mixing parameter z, which regulates the noise interference rank in community detection. Furthermore, we establish these community transfer parameters nc = 30% and nc = 90%, which regulate the dynamic level of nodes randomly moving between communities throughout a series of snapshots, and \(\hat{d}\) = 20 is the average degree of nodes.

  • Synthetic dataset #2. This network was generated from its description by Greene59. In this network, we generate embedded synthetic network samples by exchanging events with seven integrated dynamic communities and 100 nodes, the tiny switch network simulates user mobility between communities by randomly assigning 20% of the node members to each snapshot. There are mixed parameters \(\mu = 0.8\), which control the overlap of communities, and node transfer probability p. In this experiment, we used three different groups of mixed parameter time networks: (\(\mu = 0.7\), \(p = 60\%\)), (\(\mu = 0.8\), \(p = 50\%\)), and (\(\mu = 0.8\), \(p = 60\%\)) for communities.

  • Real dataset #1, which is a communication network about emails, gathered by KIT’s Department of Informatics58. From September 2006 to August 2010, it was a dynamic network structure that changed for 48 consecutive months under real-world conditions. A member of a KIT computer science department is represented by each node, several research groups are represented by the community structure, and the weights of the edges indicate how many emails each member has sent to another. In this instance, we divide the network into snapshots representing varying month counts. As a result, we divide the successive 2, 3, and 6 photos into three networks, each containing 24, 16, and 8 snapshots. Each snapshot for these dynamic networks contains 138, 170, and 195 nodes as well as 23, 25, and 25 communities.

  • Real dataset #2, which contains calls from members of the fictional Palaiso movement, covering 10 days in June 200657. The mobile phone network records the communication between the members of the movement every day. Each individual communication is treated as a node, and the communication between every two members is represented as an edge. The communication between the members of the movement is recorded daily, and the total number of mobile phones used is 400.

The synthetic networks #1 and #2 not only validate GrSrNMF’s capability in managing dynamic properties and robustness to noise but also rigorously evaluate its performance in detecting community overlap and modeling user mobility. Furthermore, the real-world networks #1 and #2, characterized by their dynamic properties and real-world attributes, effectively demonstrate GrSrNMF’s ability to handle sparsity, noise, and large-scale networks in dynamic environments.

Dynamic community detection

Fig. 2
figure 2

The results of NMI and ER on synthetic dataset #1 with different noise levels.

Full size image
Fig. 3
figure 3

The results of NMI and ER on synthetic dataset #2 with different noise levels.

Full size image
Fig. 4
figure 4

All snapshots of NMI and ER on real-world dataset #1.

Full size image
Fig. 5
figure 5

The results of NMI and ER on real dataset #2 with different snapshot intervals.

Full size image

  • Case 1: Comparison of methods under synthetic datasets. As shown in Figs. 2 and 3, we designed comparative experiments of 7 baseline methods. The dynamic network’s snapshot t is shown by the Y-axis, while the evaluation index’s NMI or ER value is represented by the Y-axis. In this case, we set the parameters of GrSrNMF to: \(\alpha =2\), \(\beta =2\), and \(\gamma =100\).

    Figure 2 displays approach in a synthetic dataset #1 at various noise interference levels. Accordingly, the parameter Settings for the network in Figs. 2 are (a, b) \(z = 6\), \(nc = 30\%\), satin \(\hat{d}=16\), (c, d) z = 5, \(nc = 90\%\), satin \(\hat{d}\)=16, \((e, f) z = 4\), \(nc = 30\%\), satin \(\hat{d}=16\). It can be seen from Figs. 2(a), 2(c), and 2(e) that the NMI of GrSrNMF is higher than those of most of the other methods, which indicates that our proposed method has certain significance. In addition, we can see from Figs. 2(b), 2(d), and 2(f) that the value of ER is basically lower than that of most methods, and the variance bars in NMI and ER are relatively small. It is worth mentioning that GrSrNMF is slightly inferior to MSSC in terms of NMI and other indices, because this network has good adaptability to MSSC, but GrSrNMF can adapt to most different topological networks. The above situation also indicates the excellent performance of our GrSrNMF in the synthetic dataset #1.

    Figure  3 is the small switch network of synthetic dataset #2. As can be seen from the NMI and ER values in Figs. 3 (a, b), 3(c, d), and 3(e, f), our GrSrNMF can compete with most excellent algorithms or even advanced algorithms, although GrSrNMF is slightly lower than MSSC in terms of NMI index. However, MSSC suffers from a critical limitation: its computational complexity is significantly higher than that of the proposed GrSrNMF framework. The lower computational complexity of GrSrNMF makes it particularly advantageous for large-scale dynamic network analysis. Moreover, it is not satisfactory in the index of ER, and on the contrary, the proposed GrSrNMF shows superior performance in the value of ER. Overall, our suggested technique, GrSrNMF, consistently produces outstanding performance on the NMI and ER of the synthetic dataset #2, as shown in Fig. 3.

  • Case 2: Comparison of methods under real network datasets. As seen in Figs. 4 and 5, which can design comparative experiments of 5 comparison methods. The X-axis is the snapshot t under the dynamic network, and the Y-axis is the NMI or ER value of the evaluation index. In this case, we set the parameters of GrSrNMF to: \(\alpha =0.2\), \(\beta =0.2\), and \(\gamma =10\).

    For Figure 4, we designed a comparison experiment on the real dataset #1. In Figure 4, we set the snapshot length of 2 months, 3 months, and 6 months of the KIT email dataset to form three dynamic networks, whose corresponding network snapshots are T=24, T=16, and T=8 respectively. Figures 4 (a, b), 4(c, d), and 4(e, f) can still reflect the advantage of GrSrNMF. Regarding performance, it performs extremely well in this real network through NMI and ER values. In summary, on the whole, the algorithm we proposed also embodies superior performance in the real network.

    Figure 5 is a comparative experiment in the real dataset #2, for which we predict communities in the network over a longer period of time by not only predicting the community division of the network for each day but also by an interval of one day. As for the NMI changes in Figs. 5 (a) and 5(c), we can clearly see that in the real dynamic network with the number of snapshots T being 10, although the start time of GrSrNMF is slightly lower than those of FVI-NMF and FaceNet, the NMI value of GrSrNMF immediately increases with the advance of time. This is also related to GrSrNMF’s ability to learn the characteristics of undirected networks well with the time progression of dynamic networks. The NMI value of GrSrNMF also increases gradually in the time-series network with an interval of one day With T = 5, and finally is slightly lower than that of FVI-NMF. In addition, compared with other methods, ER values in Figs. 5 (b) and 5(d) show that our model has a good performance from ER, indicating that our algorithm has excellent adaptability to tasks under real networks, and thus has a very superior performance, indicating that our proposed method is successful.

Ablation experiment and evolution analysis

Ablation experiments are an important process to evaluate whether a model has optimized its performance and whether the modification of the model is successful. In this section, we use several generations of GrSrNMF precursors, SNMF, ECNMF, and ECGNMF, as competing algorithms for the GrSrNMF model, so as to judge that the improvement of GrSrNMF has a significant performance optimization effect on the model.

In this experiment, we selected different network structures of the real dataset #1 and the synthetic dataset #1 for comparative experiments. We use CR and ER to compare the performance of the GrSrNMF algorithm and its comparison algorithms. All the algorithms in this experiment are run 10 times, and we give the results of the mean with variance obtained in the following Figs. 6 and 7. In the real dataset #1, we set the parameters of GrSrNMF to: \(\alpha =0.2\), \(\beta =0.2\), and \(\gamma =10\). In the synthetic dataset #1, we set the parameters of GrSrNMF to: \(\alpha =0.2\), \(\beta =0.2\), and \(\gamma =10\).

Fig. 6
figure 6

The results of NMI and CR on synthetic dataset #1 with different noise levels.

Full size image
Fig. 7
figure 7

All snapshots of CR, CR and NMI on real-world dataset #1.

Full size image

  • First Case: The model performance of the GrSrNMF method and its comparison methods on the synthetic dataset #1 at various noise levels is displayed in Fig. 6. In accordance with this, we have (a, b) z \(= 6\), nc \(= 30\%\), \(\hat{d}\) \(= 16\), (c, d) z \(= 5\), nc = \(90\%\), \(\hat{d}\) \(= 16\), (e, f) z \(= 4\), nc = \(30\%\), \(\hat{d}\) \(= 16\) set as the network’s parameters in Figs. 6(a), 6(c), and 6(e) demonstrate that our suggested GrSrNMF outperforms other comparison methods in the CR method in terms of accuracy.

    Similarly, we can observe in Figs. 6(b), 6(d), and 6(f), GrSrNMF has a good result performance on the ER as well. In addition, we can clearly observe that the variance bar of GrSrNMF is significantly smaller than those of other previous generations of algorithms, indicating that our improved algorithm model has obvious performance optimization compared to other comparison methods in the synthetic dataset.

  • Case 2: In addition, Fig. 7 shows the performance of the GrSrNMF algorithm compared with the comparison methods in the real dataset #1 under different slice snapshots. In addition, we split network snapshots with different time lengths to construct three different dynamic networks with real dataset #1: (1) T \(= 24\), 2 months as a snapshot in Fig. 7(a, b); (2) T \(= 16\), 3 months as a snapshot in Fig. 7(c, d); (3) T \(= 8\), 6 months as a snapshot in Fig. 7(e, f). Obviously, we can clearly observe from Fig. 7(a), 7(c) and 7(e) in Fig. 7 that the CR values of our improved model can also well reflect the model performance of several generations of comparison methods in different snapshots in real networks, and for the evaluation index of ER, Fig. 7(b), (d) and (f) are also much superior to other comparison methods, and it can be clearly observed that the variance bars of CR and ER in real datasets are basically smaller than those of other types of algorithms.

From the above experiments, we can observe the performance improvement of the new model over the comparison methods under the evaluation of different indicators. This not only demonstrates that our symmetry learning regular term is reliable and effective, but also indicates that our model improvement is successful compared with the comparison methods.

Convergence of algorithms and parameter analysis

The choice and arrangement of parameters, along with the convergence of algorithms, determine a model’s performance. In this part, by varying and matching different parameters, we examine the sensitivity of the GrSrNMF parameters and the algorithm’s convergence after several iterations.

Table 2 Parameters \(\gamma\) and \(\beta\) from 0.01 to 100 for NMI on the real dataset #1.
Full size table
Table 3 Parameters \(\gamma\) and \(\alpha\) from 0.01 to 100 for NMI on the real dataset #1.
Full size table
Table 4 Parameters \(\beta\) and \(\alpha\) from 0.01 to 100 for NMI on the real dataset #1.
Full size table
Fig. 8
figure 8

The objective function’s convergence across various snapshots within two distinct datasets: (a) the real dataset #1 (b) the synthetic dataset #2.

Full size image

We chose the snapshot of T = 10 in real dataset #1 to test the effect of parameters on GrSrNMF performance. Set the parameter to \(\alpha\), \(\beta\), \(\gamma \in \{0, 0.01, 0.1, 1, 10, 100\}\). During the experiment, we changed the \(\alpha\) and \(\beta\) from 0 to 100 and fixed the \(\gamma\) to 0.1 to examine the combined effects of \(\alpha\) and \(\beta\). Similarly, we changed the \(\alpha\) and \(\gamma\) from 0 to 100 and fixed the \(\beta\) to 0.1 to examine the combined impact of \(\alpha\) and \(\beta\). Also, we changed the \(\beta\) and \(\gamma\) from 0 to 100 and fixed the \(\alpha\) to 0.1 to check the combined impact of \(\beta\) and \(\gamma\). We will also show Table 4 for the parameter sensitivity of the \(\alpha\) and \(\beta\), and Table 3 for the parameter sensitivity of the \(\alpha\) and \(\gamma\). Table 2 shows the sensitivity of the \(\beta\) and \(\gamma\) parameters. We can see that when \(\alpha\) = 0, \(\beta\) = 0, and \(\gamma\) = 0, the accuracy is often relatively low. From Tables 3 and 4, we can see that as the parameters increase from 0 to 10, the overall accuracy increases, and after \(\alpha \in\)[0.1, 10] interval, the accuracy tends to stabilize. The same phenomenon can also be easily observed in Table 2 and Table 4, where accuracy increases when \(\beta\) increases from 0 to 100, and stabilizes within this range. In Table 2 and Table 3, we can also clearly observe a change in \(\gamma\), where the accuracy improves and stabilizes within the [0.01, 1] interval. Therefore, we can conclude that the performance of GrSrNMF is not overly sensitive to the changes in \(\alpha\), \(\beta\), and \(\gamma\), and overall, the model’s performance has a good balance when \(\alpha\), \(\beta\), and \(\gamma\) increase from 0.1 to 1. Taking all these factors into consideration, choosing \(\alpha\), \(\beta\), and \(\gamma\) within the range of [0.1, 1] can yield better performance. The results of this experiment are favorable for us, which is a good indication of the effectiveness of the three parameters \(\alpha\), \(\beta\), and \(\gamma\), and also indicates the excellent performance of our model.

Furthermore, we confirm that the GrSrNMF method converges under two different kinds of time series networks. The objective function’s convergence under various snapshots in two types of networks is depicted in Fig. 8(a), which is a real-world dataset with values of T = 8, and Fig. 8(b), which is a synthetic dataset with values of T = 10, \(\mu = 0.8\), \(p = 50\%\). The objective function value is displayed on the y-axis of the graph, the number of iterations is displayed on the x-axis, and the value of the objective function under snapshot \(2-T\) is displayed as a function of the number of iterations on the line. As observed in Fig. 8, under the two types of networks, the objective function at different snapshots tends to converge when the number of GrSrNMF \(n_{iter}\) reaches 50-100. Our suggested methodology is superior to various sampling-based techniques. In addition, this model is useful for extensive network applications.

We use ECGNMF as a contrasting method for community evolution and prediction in comparison to GrSrNMF. Here, we’ll use real-world dataset #1 as an illustration. we set the parameters of GrSrNMF to: \(\alpha =0.2\), \(\beta =0.2\), and \(\gamma =10\).

The analysis of community evolution is essential to dynamic network analysis. The community time transition matrix \(Z_{t-1}\), which shows the likelihood of a transfer across communities from snapshot \(t-1\) to snapshot t, may be obtained using GrSrNMF with certain calculations. The community evolution model of dynamic networks is effectively captured by the Community Transition Matrix (\(Z_1,......, Z_{T-1}\)).

Fig. 9
figure 9

Tracking the evolution of community transition matrices through ECGNMF and GrSrNMF analyses on a real dataset #1 across various resolutions.

Full size image

We normalized each \(Z_t\) by row, followed by \(\forall\) l, \(\sum _{EMPTY}{EMPTY}_kZ_{lk,t} = 1\), because the element values in the transition matrix \(Z_t\) between distinct snapshots may be in different ranges. Thus it is possible to calculate the traces of the normalized community transfer matrix, i.e., \(Tr(Z_t) = \sum _{EMPTY}{EMPTY}_lZ_{ll}\). Fig. 9 shows the trajectories of the community transition matrix over time on real dataset #1 using ECGNMF and GrSrNMF. The higher the value of the trace, the slower the evolution of the community. We can see from Figs. 9(a) to 10(c) that the average traces at the snapshots progressively get better and that there is generally little fluctuation in magnitude between neighboring snapshots. We believe that the main reason for this is the smoothness of community evolution between adjacent snapshots in a dynamic network. Each snapshot requires time to adapt and reach a stable structure.

Fig. 10
figure 10

Community prediction using the ECGNMF and GrSrNMF methods on a real dataset #1 with various resolutions.

Full size image

As the evolution of a dynamic network slows down over time, we can use the historical transition matrix \(Z_{T-\upsilon }\) to to predict \(Z_T\) by folding the historical transition matrix and using \(Z_{T-\upsilon +1}\)..., \(Z_{T-1}\), where \(\upsilon\) is the size of the sliding window. It is important to note that these transfer matrices are also standardized. In order to analyze its predictive ability, we design a strategy: \(\hat{Z}_T = \sum _{t=max(1, T-1-\upsilon )}^{T-1}Z_t/\upsilon\).

Based on the characteristics of GrSrNMF, we can use \(\hat{H}_{T+1} = H_T\hat{Z}_T\) to predict its community member matrix. Thus, the community structure in t + 1 can be predicted by using \(\hat{C}_{i,t+1} = arg max_k (\hat{H}_{ik,t+1})\). We also use NMI as a metric to judge the performance of its predictive power.

As shown in Fig. 10, we set the parameters of GrSrNMF to: \(\alpha =0.2\), \(\beta =0.2\), and \(\gamma =10\). we give the community prediction results for real dataset #1 using ECGNMF and GrSrNMF. where Figs. 10(a), 11(b), and 11(c) correspond to the results of the three networks, respectively. In Fig. 10, we calculated the temporal community prediction results of ECGNMF and GrSrNMF based on varying sliding window sizes \(\upsilon\). Notably, GrSrNMF’s prediction results typically outperform ECGNMF’s ones.

Discussion

In this work, we propose a new framework for community detection in dynamic networks, GrSrNMF, by introducing a regularization term for symmetry learning. The model can accurately learn the network’s symmetries by using symmetry learning regularizers when NMF is extended to evolutionary clustering of dynamic networks. It also maintains the internal network structure and organization by utilizing graph regularizers to explore dynamic networks, enabling applications such as dynamic community detection, evolutionary pattern detection, and prediction. This allows for an accurate representation of the target network. In addition, we analyze its complexity. GrSrNMF can simultaneously detect dynamic community structures and corresponding evolutionary patterns. The model can accurately learn the network’s symmetries by using symmetry learning regularizers when NMF is extended to the evolutionary clustering of dynamic networks. Parameter tuning: GrSrNMF offers several parameters (such as \(\alpha\), \(\beta\), \(\gamma\)) to balance the impact of various regularization terms. These parameters can be tailored based on the specific characteristics of the data to adapt to varying levels of noise and incompleteness. GrSrNMF has six main advantages: (1) For dynamic network architectures where the number of communities varies over time, GrSrNMF can be used; (2) the time-varying network changes are more in line with real-world situations; (3) the dynamic network feature structure in the data space can be utilized as a regularization of the graph; (4) to investigate the existing network structure and forecast patterns of community evolution, GrSrNMF exclusively uses the data from past and current snapshots; (5) GrSrNMF can mine the inherent characteristics of undirected networks. Not only can it learn the structural characteristics of historical networks and the evolution of community structure, but it can also effectively apply this knowledge to predict the structure of undirected networks in the future; (6) By adjusting the parameters in GrSrNMF, it is possible to find the optimal performance balance across networks of varying sizes. Adjusting these parameters helps the model maintain efficiency and accuracy when processing large networks. This capability gives GrSrNMF a significant advantage in network structure prediction. Furthermore, extensive experiments demonstrate that our approach outperforms certain commonly used baseline methods in community discovery. However, in the presence of significant noise in dynamic networks or when the network structure is not distinct, graph regularization might not enhance the model’s performance and could even lead to over-smoothing.

In our experiment, two potential problems need to be addressed. First of all, it is how to automatically and accurately set the equilibrium parameters \(\alpha\), \(\beta\), and \(\gamma\) under different dynamic networks, as this is directly related to the rationality and accuracy of our experimental settings. Secondly, it is also an intriguing question of how to directly and accurately identify the number of communities in each dynamic network snapshot within a single model, in order to avoid the limitations and errors that may be introduced by the traditional two-step method. This presents an important and intriguing topic for further investigation. To address these issues, we plan to delve into the evolutionary patterns of dynamic networks, as well as the complex relationships between community structure, similarity index, and topology. Moreover, extending community detection to directed graphs will be a significant area of future work for us. We will explore modifications to the Laplacian matrix to adapt it to the context of directed graphs. These are not only interesting and challenging research directions, but alsoa crucial step towards more accurate network analysis and prediction of community evolution. We anticipate that additional research will help us comprehend and predict the dynamic evolution of undirected networks.