Introduction

Water is indispensable for human survival, with access to ample and clean supplies pivotal for sustainable societal advancement1,2,3,4. In recent years, human activities such as industrialization5, urbanization6 and rapid population growth7, as well as climate changes such as extreme rainfall and increased temperature frequency have greatly affected the hydrological cycle8 and led to changes in water quality9,10,11. Changes in water quality may pose a threat to the ecosystem, thus affecting human health12. Assessment can effectively identify the water quality of water bodies and provide scientific suggestions for their utilization and protection13,14,15.

An appropriate water quality assessment framework can accurately reflect the water quality status of a given area. While univariate water quality parameters and trophic state models offer value in specific contexts, their limited scope restricts a comprehensive understanding of aquatic ecosystems16,17. Up to now, many tools and technologies have been developed for evaluating water quality18. The water quality index (WQI) model is a widely used tool to evaluate water quality, which helps transform a large number of complex and interrelated water quality data into a single value19,20. Because of its simple structure, easy application, and direct interpretation of results, it has been widely used to evaluate surface water quality21. Previous studies have shown that there are seven basic -WQI models in the world. Most other WQI models are based on these models22. For example, Horton Index23, National Sanitation Foundation Index (NSF index)24, and Scottish Research Development Department Index (SRDD Index)25 and so on, for other water quality index models and their detailed information, please refer to Uddin et al.22. However, this technology has also been criticized. The main reasons include uncertainty, model reliability, transparency, and model sensitivity18. Recently, many studies have shown that the existing WQI model will produce considerable uncertainty when converting a large number of water quality index data into digital form26. At the same time, improper classification schemes may lead to wrong classification or wrong rating in water quality assessment, and also increase the uncertainty of the results27. In recent years, to reduce the uncertainty of the model, many studies have been carried out. For example, Uddin et al.28 compared 18 different feature selection technologies to evaluate their effects in selecting key coastal water quality indicators in constructing the WQI model. Sajib et al.29 used the root mean square water quality index (RMS-WQI) model and eight machine learning algorithms to evaluate the water quality of Tongi Canal in Bangladesh, among which the Gaussian Process Regression (GPR) model showed excellent performance in predicting WQI scores. By improving the WQI model, Uddin et al.30 effectively reduced the eclipsing and ambiguity of the model and successfully applied it to Cork Harbour, Ireland. By combining machine learning with game theory, Ding et al.31 optimized the parameter weight and aggregation function of the water quality index (WQI) evaluation model, proposed a new aggregation function to reduce the uncertainty of the model, and established a new water quality evaluation system. Therefore, it is very important to reduce the uncertainty of the model for scientific and reasonable evaluation of water quality32. Given that WQI models are typically tailored to reflect the unique environmental conditions of a particular area, this customization leads to spatial variations in how water quality is assessed across different regions33,34. To effectively apply a WQI model to a specific target water body, it becomes imperative to develop a new WQI model that is specifically adapted to its unique characteristics and conditions.

Typically, a WQI model comprises five key components: indicator selection, sub-index, weighting, aggregation function, and classification scheme35,36. Prior research has reported that uncertainties in WQI models arise from several factors, including the validity of the data used, the selection of parameters, the distribution of weights among these parameters, and the choice of aggregation function37. Within WQI models, the selection of parameters and the allocation of weights are critical factors that can influence the outcomes38. Considering the costs associated with monitoring plans, particularly in developing countries, data availability emerges as a significant constraint in selecting appropriate parameters for the WQI model39. Consequently, the careful selection of key water quality indicators becomes paramount. Although principal component analysis (PCA) and correlation analysis can be used to derive the main parameters, these methods may have data interpretation and applicability limitations35. In many methods of assigning weights, expert weights are usually determined by a panel of experts22,25. Still, this weighting method may make collecting expert opinions based on watersheds challenging and may need a better correlation with water quality data22. The aggregation function, a core component of the WQI model, stands as a primary source of uncertainty in the model’s outcomes. Most studies have compared various WQI aggregation functions40,41. Adapting classification schemes to represent regional water quality conditions accurately is necessary, given the observed significant variances in such schemes across different regions42,43. A deeper exploration into the selection and application of aggregation functions within WQI models is imperative to diminish model uncertainty and enhance the precision of calculated results.

In recent years, machine learning algorithms have become practical tools for solving many environmental problems44. Machine learning algorithms have been widely used to optimize the water quality parameters and weights of the WQI model, thereby reducing its uncertainty. Robust and reliable models, including random forests, support vector regression, and artificial neural networks, are used to improve performance accuracy45,46,47. These machine learning algorithms select and sort critical parameters according to the importance of features, reduce measurement costs, and determine which parameter has the most robust predictive ability among many parameters. It has become a promising model and practical surface water quality evaluation tool48. Machine learning can process a large amount of data and high-dimensional features and is usually used to allocate weights in water quality assessment objectively31,49. The machine learning-informed weighting strategy assigns higher weights to water quality indicators that rank more prominently, reflecting their critical importance to the overall health of water bodies42,43. Exploring the standardization of the data-driven WQI customization process represents a significant and novel area of research, offering potential advancements in water quality management50. Therefore, leveraging surface water environmental quality classification scheme, investigating the application of machine learning, and developing novel aggregation functions for area-specific are of great significance for reducing model uncertainty, improving the accuracy, reliability, and practicability of water quality assessment, and for future water quality protection and policy.

This study improved the WQI model by selecting water quality parameters, using different weighting methods, and comparing and analyzing existing and newly proposed aggregation functions. The largest artificial lake in Asia, i.e., the Danjiangkou Reservoir (DJKR) of China, was selected as the study case. The study aims to (1) Utilize machine learning algorithms for the identification of critical water quality indicators, thereby enhancing the accuracy of water quality assessments; (2) Determine the most appropriate weighting strategy by comparing various weighting methods employed in different WQI models; (3) compare and verify the robustness of the optimized WQI model to comprehensively evaluate the water quality regime in different types of water bodies. This study offers crucial insights into identifying key water quality parameters in extensive reservoir basins. It will aid decision-makers and water resource management entities in understanding water quality dynamics comprehensively, facilitating informed decision-making, and developing effective water quality management and environmental protection strategies.

Methodology

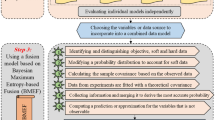
Figure 1 shows the major steps in the proposed framework of the WQI optimization. The initial step involves selecting water quality indicators that accurately reflect the water’s condition. Subsequently, each chosen indicator is assigned a sub-index (Si) from 0 to 100, quantifying its quality status for standardized assessment. The third step is to determine the weight of each indicator, reflecting their relative importance in the water quality assessment. After selecting the indicators and assigning weights, the process involves comparing various aggregation methods to integrate each Si into a unified, dimensionless water quality score. The final step is the classification of comprehensive WQI scores into distinct water quality grades, this classification intuitively communicates the overall water quality status.

Fig. 1
figure 1

Comparative optimization framework for water quality index (WQI) improvement.

Full size image

Selection of water quality indicator

For the analysis of multi-class problems, the most commonly used machine learning algorithms mainly include support vector machines (SVM), Naïve Bayes (NB), random forest (RF), k-nearest neighbor (KNN) and gradient boosting (XGBoost) and so on36. To predict and classify water quality, in recent years, some studies have used machine learning technology to evaluate the performance of water quality models in binary classification of water quality51. For example, Uddin et al.18 tested the water quality classification performance of SVM, NB, KNN, and XGBoost, and finally concluded that XGBoost had the best water quality prediction classification performance. Uddin et al.30 evaluated decision tree, random forest, Boruta, and XGBoost, and the results showed that XGBoost achieved the highest prediction accuracy of 97%, while random forest achieved 92%. XGboost has superior prediction performance, which is due to the lower prediction error compared with other algorithms. Therefore random forest and XGBoost, have become integral to water quality analysis due to their high predictive accuracy30. This study employs both algorithms to assess the relative importance of water quality indicators, and the XGBoost method combined with recursive feature elimination (RFE) was introduced to identify critical water quality indicators. This method effectively performs feature selection. The process includes (1) The XGBoost model is first trained on the dataset, ranking features by their importance to establish a preliminary understanding of each indicator’s impact. (2) RFE technology is applied to eliminate the unimportant features by recursion, retaining only those significantly enhancing the model’s performance. (3) Use the filtered features to retrain the XGBoost model. This process aims to select the most significant and representative features from complex data to enhance the explanatory and predictive ability of the model. Incorporating recursive feature elimination cross-validation (RFECV) in the feature selection phase streamlines the process by automating identifying the most impactful features, eliminating the need for manual intervention. RFECV thoroughly evaluates different feature combinations, assessing the significance of each feature individually and leveraging cross-validation to determine the optimal set of features that enhance the model’s efficacy.

Formulation of sub-index (Si)

This study employs both linear and non-linear interpolation functions to compute the sub-indexes for each water quality indicator. The Si calculations are based on the threshold values specified by environmental quality standards for surface water in China (EQSSWC), as detailed in Table S1. Notably, the presence of consistent thresholds across various water quality grades for certain indices in the EQSSWC necessitates the formulation of two distinct types of equations to accurately construct water quality indices. The equation is as follows:

$$S_{i} = \left\{ {\begin{array}{*{20}c} {\left( {S_{i,max} - S_{i,min} } \right) - \frac{{T_{i} }}{{S_{i,k + n} }} \times 20n, T_{i} \in \left[ {0,\left. {S_{i,k} } \right)} \right.} \\ {\left( {S_{i,max} - S_{i,min} } \right) - \left[ {\frac{{T_{i} - S_{i,k} }}{{S_{i,k + n} - S_{i,k} }} \times 20n + I_{i,k} } \right], T_{i} \in \left[ {S_{i,k} ,\left. {S_{i,k + n} } \right)} \right.} \\ \end{array} } \right.$$
(1)

where Si, max is the standard normalized value of the water quality indicator concentration reaching the ideal value conversion, and Si, min is the standard normalized value of the most unacceptable value conversion of the water quality indicator concentration. Ti is the real measured concentration of the i-th indicator; Si,k and Si,k+n are the standard thresholds of the i-th indicator at level k and (k + n), respectively; is the standard normalization value of the indicator classification; n is the number of the equal values of the threshold, and if no equal threshold exists then n = 1. Due to the lack of clear classification level of WT and pH in EQSSSWC, this study uses nonlinear interpolation method to construct rating curve. For more details, please refer to the supplementary material Methodology section.

Data processing

The determination of water quality status entailed a comparison of observed water quality indicator values against the benchmark thresholds defined by environmental quality standards for surface water, as detailed in Table S1 (supplementary material). In this study, nine water quality indicators were chosen as input variables for the machine learning model. Data for these indicators were collected from 31 monitoring stations in the study case. This comprehensive dataset was employed to ascertain the monthly water quality status at each station, serving as the model’s output variable.

The classification rules were established as follows: A water quality status value of '0', indicating ‘good’ water quality, is assigned to sites where all indicator values satisfy or are superior to the Class II standard. Should any indicator align with the Class III standard, the site’s status is marked as '1', signifying ‘medium’ water quality. Conversely, a status of '2' is allocated when any indicator falls below the Class III standard, reflecting ‘low’ water quality. The water quality grade of each monitoring site is recorded in time series and associated with a specific site, all of which can be found in supplementary materials (Tables S2 and S3).

To accurately evaluate the machine learning algorithm’s performance, this study divides the input data into a training set and a test set, of which 80% of the data is used for training the model and the remaining 20% is used for testing. Within the dataset, the river station comprises 1152 sample points, split into 921 for training and 231 for testing, whereas the lake site dataset includes 1080 samples, with 964 allocated for training and 216 designated for testing. To counteract the issues of high variance and the likelihood of overfitting inherent in simple data partitioning, the study utilizes the k-fold cross-validation technique. K-fold cross-validation divides the dataset into k-equal subsets30. Each subset sequentially serves as the test set, with the remaining subsets combined as the training set, facilitating k rounds of independent training and evaluation. After each training round, the model’s performance on the test set is meticulously recorded and assessed using key metrics, including the average accuracy and mean square error, to evaluate the overall performance of the model. To mitigate overfitting, fivefold cross-validation was employed, dividing the dataset into five subsets for iterative training and testing. Hyperparameter tuning (e.g., tree depth, gamma value for XGBoost) was conducted to optimize model complexity, ensuring that shallow trees (depth ≤ 3 for reservoirs) were a result of optimal configuration rather than underfitting. For detailed information about model performance evaluation, please refer to the Methodology section of supplementary material. Hyperparameters are parameters whose values control the learning process in machine learning and must be adjusted for each application52. For details of hyperparameter tuning, please refer to Uddin et al.30.

Determination of weight

The study adopts three methodologies to ascertain the weights of water quality indicators: expert-derived weights, percentage weighting of water quality indicators, and their importance rankings.

Expert weight

Weights ranging from 1 to 4 are assigned to each water quality indicator based on expert evaluations, reflecting the extent of their impact on water health1,53,54. Specifically, a weight value of 4 is indicative of an indicator having a paramount impact on water health, signifying its critical role in the ecosystem. In contrast, a weight value of 1 denotes a comparatively minor influence, suggesting that the indicator has a less substantial effect on overall water quality.

Percentage weighting of water quality indicators

All nine water quality indicators were adopted, without partitioning the dataset into training and testing subsets. In a preceding phase of model evaluation, the RF algorithm was employed for feature selection, during which the predictive accuracy of the RF model was assessed, and a ranking of the water quality indicators based on their importance was established. At this stage, the application of the RF model shifts away from concerns such as overfitting prevention and prediction enhancement, focusing solely on deriving the absolute weights of the water quality indicators50. The weight assigned to each indicator is computed as the ratio of that indicator’s importance to the aggregate importance of all indicators, with the resulting weights expressed as percentages.

$$w_{i} = \frac{{I_{i} }}{{\mathop \sum \nolimits_{i = 1}^{n} I_{i} }} \times 100{ }$$
(2)

where Ii is the important value of the indicator derived from the RF model, wi is the corresponding indicator weight value, and n is the total number of indicators.

Ranking of water quality indicators

Weight values for each water quality indicator are determined by their ranked importance in the overall assessment of water quality, ensuring that each weight accurately reflects the indicator’s contribution to evaluating the water body’s health. To achieve a more comprehensive evaluation of each index’s importance, four distinct weighting methods are employed. For more details, please refer to Uddin et al.55.

Rank sum (RS) weighting method:

$$w_{i} = \frac{n + 1 - i}{{\mathop \sum \nolimits_{j = 1}^{n} j}} = \frac{{2\left( {n + 1 - i} \right)}}{{n\left( {n + 1} \right)}},i = 1,2,3 \ldots \ldots ,n$$
(3)

Rank reciprocal (RR) weighting method:

$$w_{i} = \frac{1}{i}/\mathop \sum \limits_{j = 1}^{n} \frac{1}{j},i = 1,2,3 \ldots \ldots ,n$$
(4)

Rank order centroid (ROC) weighting method:

$$w_{i} = \frac{1}{n}/\mathop \sum \limits_{j = i}^{n} \frac{1}{j},i = 1,2,3 \ldots \ldots ,n$$
(5)

Equal (EQ) weighting method:

$$w_{i} = \frac{1}{n},i = 1,2,3 \ldots \ldots ,n$$
(6)

where i is rank from 1 to n, j is the sum of ranks, n is the total numb of selected parameters, and wi is the i-th weight value.

Aggregation function

Selecting an appropriate aggregation function is crucial in the construction of a WQI model, as it fundamentally influences the model’s framework and outcome. The choice of aggregation functions, encompassing weighted, non-weighted, multiplicative, and additive-multiplicative combinations, introduces varying degrees of uncertainty into the WQI model, affecting its overall reliability. In an effort to mitigate these uncertainties and bolster the model’s accuracy and dependability, this study embarked on an exhaustive comparative analysis of eight distinct aggregation functions.—six from existing WQI models (please refer to the Methodology section of supplementary materials for details) and two proposed by the authors. The aim was to rigorously evaluate their effectiveness and robustness in the context of water quality assessment, thereby identifying the most suitable function for the WQI model.

The Bhattacharyya mean originates from the Bhattacharyya coefficient, a statistical measure quantifying the similarity between two probability distributions. The Bhattacharyya mean generalizes the similarity assessment to multiple distributions, emphasizing nonlinear interactions and distributional overlaps—critical for aggregating heterogeneous water quality indicators with varying scales and environmental impacts. The BMWQI enhances reliability by integrating a logarithmic transformation to compress score ranges (reducing ambiguity between classifications like “Good” and “Excellent”) and leveraging the Bhattacharyya framework to accommodate skewed or multimodal parameter distributions, ensuring robust performance across diverse water quality regimes. Based on the Bhattacharyya mean, this study proposes a new BMWQI model as follow:

$$BMWQI = \left( {ln\mathop \sum \limits_{i = 1}^{n} w_{i} e^{{ - \sqrt {S_{i} } }} } \right)^{2}$$
(7)

The harmonic mean is a statistical measure particularly suited for rates or ratios, emphasizing the influence of lower values in a dataset. In water quality assessment, the weighted harmonic average (WHA) penalizes severely degraded sub-indices more heavily than linear methods, ensuring that critical pollutants disproportionately impact the final WQI score. Based on the harmonic weighted average method, this study proposes:

$$WHA = \frac{1}{{\mathop \sum \nolimits_{i = 1}^{n} \frac{{w_{i} }}{{S_{i} }}}}$$
(8)

WQI calculation

In this study, to precisely assess the impact of surrounding major rivers on reservoir water quality, sampling sites from rivers and reservoirs were analyzed separately. Water quality status was classified into three categories based on environmental quality standards for surface water thresholds, serving as the output variable, with the nine water quality indicators employed as input variables. To identify the optimal model, various machine learning techniques, including XGBoost and RF models, were evaluated using hyper-parameter grid search and fivefold cross-validation. The process determined the relative importance of water quality indicators, with key indicators automatically identified through a combined application of XGBoost & RFE. Model validation was conducted using a comprehensive set of metrics, including accuracy, precision, recall, and F1 score, among others. In addition, WQI values were calculated by integrating various weighting methods with the aggregation function, with the machine learning-predicted water quality states compared against these WQI values to ascertain the most accurate WQI formulation. After screening, WQIs derived from different weighting methods were employed as response variables, with key water quality indicators serving as input variables. The predictive performance of these configurations was assessed using a random forest regression model. Ultimately, the selected WQI model was applied to evaluate the region’s water quality. Utilizing Python and SPSS as the primary tools for statistical analysis and the implementation of machine learning techniques.

Study case and data collection

Study case

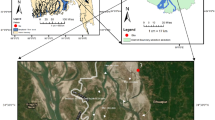
The DJKR is the largest artificial lake in Asia and serves as the core water source for the MRSNWDPC. The formation of this reservoir originated from the DJKR Dam built in 1973, across Hubei and Henan provinces. Sixteen tributary rivers flow into the reservoir, of which 12 tributaries flow into the sub-reservoir and consist of the “Hanjiang Reservoir”, and the rest of the four tributaries enter the other sub-reservoir and consist of the “Danjiang Reservoir”. To facilitate the operational needs of the MRSNWDPC, the project to heighten the DJKR dam was completed in 2013. The dam’s height was raised from 162 to 176.6 m, elevating the water storage level from 157 to 170 m and expanding its capacity from 17.45 billion cubic meters to 29.05 billion cubic meters. Consequently, the current water surface area of the DJKR extends over 1,050 km256. The DJKR basin is located in the northern subtropical monsoon climate, with an annual average air temperature of 15.9 °C57, and annual rainfall of 800 to 1,000 mm58. The main soil types are yellow–brown soil, brown soil, and yellow cinnamon soil59. The local economy and industry are underdeveloped, mainly agriculture60. As the water source area of the MRSNWDPC, DJKR area and its upper reaches are facing a series of challenges in ecological environment protection and high-quality development. Therefore, it is of great practical significance to scientifically and reasonably evaluate the water quality of the DJKR basin to ensure the safety of water resources and implement effective management. Detailed information on the DJKR, river systems, and water quality sampling sites can be found in Fig. 2.

Fig. 2
figure 2

Locations of water quality sampling sites in the study case, the Danjiangkou Reservior, China.

Full size image

Data collection

The water quality monitoring of the DJKR has been supported and validated by the Chinese government and local authorities, for which a network of water quality monitoring stations in the DJKR area has been set up, allowing for a comprehensive system of quality assurance and control of water quality in the reservoir area. This study using the data from monthly water sample collectioncampaign from 16 esturay control sites in the river systems and 15 sites in the reservoir areas during 2017 to 2022 based on re-analysis. These sites were strategically chosen from national monitoring programs by the Ministry of Ecology and Environment of the People’s Republic of China (MEEPRC, https://www.mee.gov.cn/xxgk2018/) to monitor the water quality characteristics of the entire DJKR basin (Tables S2).

The parameter selection scheme of WQI is based on data availability, expert advice, or environmental significance of parameters22,25. Common parameters include dissolved oxygen (DO), pH, and temperature, ranging from 4 to more than 2022. A total of nine water quality indicators were used in this study, including water temperature (WT), pH value, dissolved oxygen (DO), chemical oxygen demand (COD), permanganate index (CODMn), five-day biochemical oxygen demand (BOD5), ammonia nitrogen (NH3-N), total phosphorus (TP), and fluoride (F−). Specifically, WT affects the biological activity and DO content of water, thus affecting water quality and ecological health. The pH value reflects the acid–base levels, and deviation from the average value may cause pressure on aquatic organisms. DO is an important indicator to measure the self-purification ability and ecological health of water body. CODMn, COD, and BOD5 are used to evaluate the concentration of organic pollutants in water. NH3-N and TP mainly come from agriculture, domestic sewage and industrial wastewater. Too high concentration will lead to eutrophication of water body and destroy ecological balance. For the DJKR basin, because agricultural activities in this area are dominant, these emissions from agriculture have a particularly significant impact on water quality60. As the water source area of the MRSNWDPC, DJKR monitoring F− concentration is very important to ensure the safety of drinking water. In contrast, the National Water Quality Monitoring Station of MEEPRC only takes pH, DO, CODMn, NH3-N, and TP as the core indicators of water quality evaluation.

For detailed information about the sample determination method, please refer to supplementary material Tables S4. The MEEPRC has established a comprehensive quality control/quality assurance specification to ensure that the data generated by the national monitoring plan are reliable and have sufficient accuracy and precision. For more details, please refer to technical specifications for surface water environmental quality monitoring (https://www.mee.gov.cn/ywgz/fgbz/bz/bzwb/jcffbz/202205/t20220506_977066.shtml). To ensure the precision of the sampling data, collections were typically conducted under sunny or cloudy conditions, thereby minimizing data variances that could arise from rainfall, strong winds, and surface runoff.

Results and discussion

Validation of the ML model

RF and XGBoost model

The feature selection process leveraged parameter grid search combined with cross-validation techniques to fine-tune and identify the optimal settings for the machine learning models. The results are shown in Tables S5–S7. For both river and reservoir sites, the models were configured with a uniform maximum tree depth of 7 and a total of 300 trees. The leaf node of the river site is 2, and the minimum sample size is 5; the number of leaf node in the reservoir site is 1, and the minimum sample size is 3. Performance evaluations indicated that the models achieved higher performance metrics on the training set, with a slight decrease observed on the test set. On the test set, the river site achieved an accuracy of 0.95 and the reservoir site achieved perfect accuracy of 1. Similarly, precision rates were 0.94 for the river site and 1 for the reservoir site, with recall rates at 0.89 and 1, and F1 scores at 0.91 and 1, respectively, demonstrating high predictive accuracy across both sites. Logarithmic losses for the river and reservoir sites were 0.17 and 0.03, respectively, suggesting low divergence between the models’ predicted probability distributions and the actual labels, thereby indicating the RF model’s superior performance. For the XGBoost model applied to the river site, parameter settings included a maximum tree depth of 5, a gamma value of 0.2, a feature selection ratio of 0.5, a learning rate of 0.1, with 300 trees, and a subsample set to 1. The maximum tree depth of the reservoir site is 3, the gamma value is 0, the feature selection ratio is 0.2, the learning rate is 0.1, the number of trees is 500, and the number of subsample is 0.6. The accuracy rate, precision rate, recall rate, and F1 score of the river station are 0.95, 0.94, 0.91, and 0.92 respectively, and the reservoir station is 1. A comparative analysis revealed that the XGBoost model surpassed the RF model in performance metrics, further evidenced by lower logarithmic loss values. The river station and reservoir station are 0.15 and 0.01 respectively.

XGBoost & RFE model

For the river site, the model was configured with a maximum depth of 5, a gamma value of 0.2, a learning rate of 0.05, and a total of 300 trees. The maximum depth of the tree in the reservoir site is 3, the gamma value is 0, the learning rate is 0.01, and the number of trees is 2000. The river site model achieved high-performance metrics, with an accuracy of 0.97, precision of 0.98, recall of 0.97, and an F1 score of 0.97, alongside a logarithmic loss of 0.12. Figure S1 shows the iterative relationship between the training and test sets, indicating that the model performance of the reservoir site is better than that of the river site, and performs better during the training period than during the test period. Figure 3 shows the classification performance of the model for each category in the river and reservoir data sets. For the river site, category 0 saw 167 true positives, only 1 false positive, and no false negatives, indicating that the model has excellent classification performance in classes 0 and 2. But only in category 1, the model performance is slightly lower than the other two classes, with a recall rate of 0.89. The reservoir area’s water quality was predominantly stable, with only 5.56% of samples exceeding Class II standards (TP as the primary indicator). This severe class imbalance (94:6 for Class 0: Class 1) facilitated binary classification, as the model could leverage the dominant class for high accuracy. However, cross-validation and feature selection processes ensured the model’s focus on critical indicators (WT and TP) rather than mere class memorization. The reservoir’s model performance reflects its ecological stability, where water quality is primarily influenced by WT and TP with minimal fluctuations. In contrast, riverine systems exhibit dynamic multi-class variations, leading to more moderate model metrics. The disparity in performance underscores the models’ ability to adapt to differing environmental complexities rather than memorization. Overall, the reservoir area’s dataset yielded superior model performance compared to the river site, suggesting that water quality fluctuations are more pronounced in the river, whereas the reservoir’s water quality exhibits stability.

Fig. 3
figure 3

Results of true classification and prediction classification of testing set.

Full size image

Selection of water quality indicator

The results depicted in Fig. 4 show a consistent ranking of water quality indicators’ importance across both RF and XGBoost models for river stations. For reservoir sites, the analysis underscores the dominant influence of WT and TP, with the relative significance of other indicators markedly reduced in comparison. In the RF model, pH and DO exhibited lower importance values of 0.0105 and 0.0083, respectively. The XGBoost model assigned NH3–N, the third-ranked indicator, a value of only 0.0312, considerably lower than WT’s second-ranked value of 0.2488, highlighting the substantial gap in their relative importance. The utilization of the XGBoost & RFE method proved instrumental in pinpointing key water quality indicators, effectively discerning the most impactful parameters for both river and reservoir settings. It was found that all water quality indicators of river sites could not be ignored except F–, and their importance ranking was consistent with the results of the first two models. The importance of the key indicators were TP, CODMn, NH3–N, COD, WT, DO, BOD5, and pH. For the reservoir site, WT and TP were determined as key water quality indicators after screening. Throughout the study area, TP was identified as the paramount water quality indicator, with WT also recognized for its significant impact. The important impact of TP on rivers and reservoirs has been reported in many studies61. As an important nutritional parameter in water quality, TP may lead to eutrophication when the total phosphorus concentration in water increases. While WT exhibits natural seasonal variability, its long-term shifts, influenced by global climatic trends, carry significant consequences for the vitality and equilibrium of aquatic ecosystems62.

Fig. 4
figure 4

Ranking of water quality indicators by importance across three machine learning algorithms.

Full size image

The determination of weight

Expert weight

In the weighting of water quality indicators, WT and pH were assigned a minimal weight of 1, reflecting their relatively small impact on water quality assessment. Under natural conditions, pH levels remain relatively stable, whereas WT varies in response to ambient temperature changes. DO is a critical parameter indicative of water quality status and has been a focal point of concern in previous water quality studies due to its vital role in aquatic ecosystems63. It can affect the growth of aquatic organisms and many complex biochemical processes, so it is given the highest weight 4; COD, CODMn, BOD5, and NH3–N were assigned a weight of 3, signifying their substantial influence on water quality, particularly due to their implications for organic matter content and nitrogen levels. F– received a moderate weight of 2, reflecting its discernible but less critical impact on water quality, given its typically low and stable concentrations in surface waters. TP was weighted differently across water bodies, with a weight of 1 in rivers and 4 in lakes and reservoirs, reflecting the difference in the impact of total phosphorus on water quality in different water types. The elevated hydrodynamic conditions in rivers, characterized by higher flow velocities, facilitate the dilution and transport of nutrients, thus mitigating the risk of total phosphorus accumulation and eutrophication. In addition, in EQSSWC, the water quality grade threshold of TP in lakes and reservoirs is more stringent.

Percentage of weight

Table S8 shows the weight percentage of each water quality indicator in the river and reservoir area. At river stations, the distribution of weight percentages for each water quality indicator is as follows: TP leads with 18.45%, followed by CODMn at 16.13%, NH3-N at 15.41%, and COD at 12.14%, with the remaining indicators, BOD5, DO, pH, WT, and F–, contributing lesser percentages in descending order. This order of weight percentages aligns with the importance rankings of the top four water quality indicators as assessed by three other machine learning models. At lake and reservoir sites, WT and TP dominate the weight distribution with percentages of 54.42% and 35.78%, respectively, with the combined weight of all other indicators amounting to only 9.8%. In reservoir areas, the influence of other indicators beyond WT and TP is markedly minor, with BOD5’s weight percentage at a mere 0.09%, rendering its impact on water quality nearly negligible.

Importance ranking of water quality indicators

Here, the XGBoost & RFE model serves to systematically rank water quality indicators by importance, subsequently guiding the assignment of weights to each indicator based on their respective rankings. The methods used include RR, RS, and ROC, differentiate weights based on each indicator’s position within the importance hierarchy, ensuring that higher-ranked indicators receive greater weights. Contrastingly, the EQ method adopts an equal weighting strategy, allocating identical weights to each indicator, irrespective of their ranked importance. Specifically for reservoir sites, which feature only two key indicators, TP and WT, the RR and RS methods assign identical weights of 0.6667 and 0.3333, respectively. For details on weight values and the associated methodology, refer to the supplementary materials presented in Table S9.

Sub-index (Si)

Each water quality indicator value was converted into Si, utilizing linear or non-linear interpolation functions to standardize measurements across different scales, as detailed in Table S10. Across both river and reservoir sites, the Si values for WT, pH, and F– exhibited minimal variation, indicating consistent water quality characteristics in these parameters. The mean and standard deviation were: WT: 77.03 ± 17.95 and 76.12 ± 18.89; pH: 91.55 ± 8.43 and 90.09 ± 6.66; F–: 91.91 ± 2.43 and 93.22 ± 1.73. It is worth noting that at river sites R7 and R8, NH3-N and TP displayed notably lower mean Si values compared to other stations, with TP’s minimum Si value reaching as low as 27.64. Additionally, COD, BOD5, and CODMn presented lower Si values, with CODMn registering the lowest at 53.08. The Si values at these river sites can be attributed to their urban, where heightened TP and NH3–N emissions from the city could potentially compromise the DJKR’s water quality. Conversely, within the reservoir area, Si values for CODMn, NH3–N, and BOD5 are generally higher than in the river sites, indicating a more stable water quality profile, likely due to the reservoir’s buffering capacity64.

WQI classification scheme

This study introduced a five-tier water quality classification scheme, based on the EQSSWC, to facilitate a comprehensive comparison of the effectiveness of various aggregation functions within the WQI model. The scheme utilizes specific threshold levels for each grade, uniformly applied across the scores derived from all aggregation functions, ensuring consistent categorization across different methods. As detailed in Table S11, the water quality classifications extend from ‘Excellent’ to 'Bad,' where a higher score directly corresponds to better water quality. The classification scheme is developed based on the classification and corresponding intervals described in Table S12. The adaptation of the WQIw classification scheme, originally applied within China’s water system65, the scheme undergoes further subdivision to align with the national standard requirements set.

Comparison of aggregation functions

In this study, eight different aggregation functions were utilized to calculate WQI values for river and reservoir sites, assessing their respective water quality. Figure 5 shows varied WQI scores, and it is found that the WQI values of river and reservoir stations are at a ‘Good’ level and above. Notably, the CCME model rated the water quality at all evaluated sites as 'Excellent.' The CCME stands out due to its unique calculation methodology, which differs significantly from that of other WQI models. It generally requires four water quality indicators to calculate, while there are only two key indicators at the reservoir site in this study. Therefore, all water quality indicators are used when calculating CCME at river and reservoir sites, which may be the reason why the CCME score is significantly higher than other WQIs. Within the NSF, WQM, WHA, and BMWQI models, the WQI values of different weighting methods are not much different, but the BMWQI values are relatively low, consistently categorizing water quality as ‘Good’. In the river stations, the WQM model scores are more than 81, and the water quality is ‘Excellent’, which is significantly different from other weighted WQI. The WQM model was put forward by Uddin et al.30 to improve the evaluation method of the coastal water quality index (WQI) model. Its initial score was divided into '80–100’, which belongs to the ‘Good’ level, suitable for various applications. This study’s '81–100’ score range, deemed ‘Excellent’, applies to source water and national nature reserves, and of course, can be applied to any place. The application of different weighting methods did not definitively determine the most suitable WQI for the DJKR.

Fig. 5
figure 5

Comparison of WQI results using varied weighting methods (the dashed line indicates the WQIs higher than “81” is excellent).

Full size image

To address this issue, the study examined the ‘eclipsing problem’ associated with WQI calculations, where aggregation functions might overestimate the index, masking instances where individual water quality indicators exceed their thresholds. This issue was investigated by checking whether measured values of water quality indicators within the WQI model conformed to their established thresholds, using the worst Si as the evaluative standard for water quality grading. Instances where the water quality index fell within the expected range of WQI were marked as '0', indicating no eclipsing problem, while deviations were marked as '1'. For example, if the water quality grade of a station WT is ‘III’ and the water quality grade of other indicators is 'I', the water quality grade of the station in that month should be judged as ‘III’, and the corresponding WQI score should be within the range of '41–60’, then marked as '0', indicating no eclipsing problem.

Table 1 shows the eclipsing percentages for each WQI model and Tables S13 and S14, enumerates instances of the ‘eclipsing’ phenomenon across all aggregation functions used in WQI calculations. The results show that eclipsing is a pervasive issue across all WQI models, with river stations exhibiting a higher eclipsing percentage compared to reservoir stations. The higher eclipsing rates at river sites can be attributed to the inclusion of eight key water quality indicators in the WQI calculations, as opposed to reservoir areas where calculations predominantly rely on WT and TP, resulting in reduced eclipsing. Across all sites, the BMWQI model demonstrated the lowest eclipsing rates, below 20%, with the WHA model also showing lower eclipsing rates compared to other WQI models, indicating their relative effectiveness in minimizing eclipsing. These improvements translate to targeted pollution mitigation, enhanced drinking water security through early reservoir parameter monitoring, quantifiable policy evaluation evidence, and optimized monitoring via key indicator prioritization for robust water governance. The introduction of two new WQI models in this study has markedly reduced the uncertainty associated with WQI calculations. The eclipsing rates of different weighting methods were ranked as BMWQI > WHA > NSF > WQM. Employing the ROC weighting method resulted in the lowest eclipsing rates for both river and reservoir sites, at 17.62% and 4.35% respectively. The CCME-WQI exhibited the highest eclipsing rates, a factor closely linked to its specific selection and calculation approach for water quality indicators, which may inadvertently mask certain water quality issues. As a model closely related to the over-standard rate of water quality indicators, CCME usually reflects a better water quality status when evaluating multiple water quality indicators or only a few indicators exceeding the standard, which may obscure certain water quality assessments.

Table 1 Eclipsing rates of WQI function categories in water quality analysis.
Full size table

Eclipsing in the WQI model is usually accompanied by ambiguity, which may hide the actual water quality information contained in the model input, potentially leading to misclassification of water quality by environmental managers and assessors. As indicated in Table S15 of the supplementary material, the WQI model for the reservoir area incorporates only two significant water quality indicators. This restricted selection could result in underestimation or overestimation of the model’s water quality assessments. At the river site, WQI is almost Overestimation ambiguity, because the river selects most of the water quality indicators, which are at the I or II level, and occasionally an indicator is inferior to the II water quality standard, and its impact is often obscured. Crucially, the assigned weights to these indicators may not accurately reflect their true significance, potentially skewing the WQI results. Therefore, it is very important to select the key water quality indicators and adopt the optimal weighting method to improve the performance of the WQI model.

The incorporation of various weighting methods in the BMWQI model has markedly reduced the prediction uncertainty, enhancing the reliability of its water quality forecasts. To ascertain the optimal BMWQI variant for water quality prediction, we constructed a random forest regression model and used the R2, RMSE, MSE, and MAE (Fig. 6) as performance test indicators. The results revealed that the R2 reached 0.98 for both river and reservoir sites, demonstrating an excellent fit of the model to the data. The values of the other three parameters of the river station are higher than those of the reservoir area, and the values of RMSE, MSE, and MAE in the ROC weighting method are the lowest, which are 3.19, 10.19, and 1.78, respectively. At the reservoir site, the limited selection of only two indicators led to identical results for both RR and RS weighting methods, slightly lower than the ROC, but the ROC weighting method had the least eclipsing. Therefore, the ROC weighting method is the most suitable weighting method for the BMWQI model.

Fig. 6
figure 6

Performance evaluation of the BMWQI model.

Full size image

Water quality evaluation using the optimal WQI model

Figure 7 shows the spatial distribution of water quality across the DJKR, as assessed by the BMWQIROC model on an annual basis. The river stations consistently exhibited water quality levels of ‘Good’ or better throughout the years. Except for the R7 and R8 stations, the water quality of these two stations increased from ‘Bad’ to ‘Medium’ according to the annual BMWQI results. The rivers corresponding to stations R7 and R8 traverse Shiyan City in Hubei Province, a region characterized by its significant industrial activity, dense population, and rapid economic growth. In the past decade, the increase of industrial wastewater and domestic sewage discharge has become the main pollution source of these rivers. Fortunately, these previously heavily polluted rivers have exhibited significant water quality improvements over the past five years, which is inseparable from the Chinese government’s vigorous development of sewage treatment capacity, including the construction of sewage pipe network systems and sewage treatment plants, which has effectively improved the surface water environment2. Moreover, among the four rivers proximal to the Danjiang reservoir, all sites except for R16 have attained ‘Excellent’ water quality levels, showcasing the overall health of the basin. The reservoir site uses the Purkin interpolation method to observe the distribution of water quality in the DJKR. The water quality of the Hanjiang reservoir is significantly lower than that of the Danjiang reservoir due to the influence of different rivers, and the closer to the Danjiang reservoir, the better the water quality. Site L15 is the water intake of the MRSNWDPC. After increasing the flow of water in 2017, the water quality still maintained a good level. Overall, the trend of water quality improvement in the DJKR has benefited from the Chinese government’s efforts in pollution control and management over the past decade66.

Fig. 7
figure 7

Assessment of water quality using the proposed optimal BMWQI model in the study case, DJKR.

Full size image

Key indicators affecting water quality variation in DJKR

Figure S2 shows the effects of precipitation (Pre) and temperature (AT) on BMWQI. The results show that AT significantly influences BMWQI in the reservoir area, with extremes in temperature both high and low, correlating with reduced BMWQI values. This may be because WT is selected as a key water quality indicator, and WT is closely related to AT. Conversely, precipitation appears to have a minimal impact on BMWQI fluctuations at both river and reservoir sites, suggesting a weak correlation between water quality changes and precipitation levels in the DJKR. Seasonal analysis reveals that BMWQI values tend to be lowest during the summer across both river and reservoir sites, as depicted in Fig. S3, pointing to seasonal variations in water quality. In the EQSSWC evaluation, the water quality grade of the worst water quality indicator is usually taken as the water quality grade of the site for the month, that is, the minimum Si value determines the water quality status of the site for the month. Figure 8 shows the relationship between BMWQI and the water quality indicator over time. The water quality of the river and the reservoir area is basically at the ‘Good’ level. WT frequently emerges as the indicator with the lowest Si value, underscoring its critical role in determining the overall water quality assessment. In the river, WT is the fifth key water quality indicator. The previous indicators include CODMn, NH3-N, TP, and COD, which were selected in this study. TP and WT stand out as pivotal indicators for the DJKR’s water quality, a finding that aligns with observations from the MRSNWDPC1. TP is a water quality parameter representing nutrients and is the first selected water quality indicator in both rivers and reservoirs.

Fig. 8
figure 8

Correlation between BMWQI values and water quality indicators.

Full size image

Conclusion

The study aims to propose a new aggregation function to improve the water quality index WQI model and evaluate the water quality of rivers and reservoirs. Based on the nine water quality indicators, utilizing three machine learning algorithms, key water quality indicators were identified, and different weighting methods were used to determine the weights. To evaluate the performance of standard and newly proposed WQI models and determine the applicability of BMWQI. The main conclusions are as follows:

  1. 1.

    In feature selection, the XGBoost method combined with recursive feature elimination (RFE) performs better than random forest and XGBoost models.

  2. 2.

    The XGBoost & RFE model was used to identify the key water quality indicators of the river and the reservoir area. For river sites, indicators were ranked in importance from TP, CODMn, NH3–N, COD, WT, DO, and BOD5, to pH. In contrast, only TP and WT were identified as key indicators for reservoir sites.

  3. 3.

    The BMWQI model exhibited the lowest eclipsing among the various WQI models. Among them, the BMWQI weighting demonstrated the lowest eclipsing rates: 17.62% for rivers and 4.35%for reservoirs.

  4. 4.

    Over six years, 83.4% of river sites of the DJKR maintained “Good” or better water quality. In the reservoir, the water quality of the Hanjiang reservoir was observed to be lower than that of the Danjiang reservoir, with the latter consistently maintaining ‘Good’ water quality levels. Temperature was found to have a more pronounced effect on water quality in the reservoir area than in rivers, and seasonal variations revealed that BMWQI scores were generally lower in summer.

The limitation of this study is that it does not consider the time variation of the water quality index of DJKR. Also, the research lacks consideration of emerging contaminants, such as microplastics and pharmaceutical. Further research should be conducted to evaluate the performance of the WQI model using the temporal resolution of indicators. However, despite the limitations, the results of this study are helpful in reducing the obscurity of the WQI model, which will provide insightful information for researchers, policymakers, and water researchers.

This study advances surface water quality assessment by integrating machine learning and innovative aggregation functions, demonstrating that the proposed framework can serve as a flexible template for customizing WQI models in various environmental settings. While the case-specific findings are rooted in the Danjiangkou Reservoir system, the methodology—including feature selection via XGBoost&RFE, weight optimization through machine learning, and aggregation function comparison—offers a scalable approach for tailoring WQI models to region-specific hydrological conditions, data availability, and policy priorities.