Introduction

As a pivotal greenhouse gas, water vapor exerts profound influence upon the Earth’s climate1. Its transformation from vapor to liquid or solid states gives rise to clouds, rain, snow, and other forms of precipitation, which are among the most significant determinants of weather patterns2. Therefore, comprehending and observing the spatial and temporal distribution of atmospheric water vapor in near real-time are indispensable for numerical weather prediction3.

Several techniques have been developed to estimate atmospheric water vapor as integrated water vapor (IWV) or precipitable water vapor (PWV), each offering distinct advantages and limitations. For instance, radiosonde data is popular for its good quality; however, it suffers from limitations in both spatial and temporal resolution. Besides, the inherent inhomogeneity arising from variations in radiosonde sensors may introduce uncertainties when analyzing long-term climate trends4. Satellite remote sensing techniques, such as the Moderate Resolution Imaging Spectroradiometer (MODIS), provide high spatial resolution but face challenges in delivering real-time, all-weather, high-accuracy IWV estimates, particularly under cloudy conditions and during diurnal changes5. Reanalysis products, such as the European Centre for Medium-Range Weather Forecast (ECMWF) third-generation reanalysis ERA-Interim and fifth-generation reanalysis ERA-5 provide continuous and spatially uniform IWV data by assimilating diverse datasets with quality control. However, these products suffer from time latency issues6. For instance, ERA5 has a latency of 5 days, which is significantly shorter than the 2–3 months latency of ERA-Interim. Nonetheless, this delay renders them unsuitable for real-time or near real-time applications. Global Navigation Satellite System (GNSS) has demonstrated robust capabilities in providing quantifying IWV measurements with all-weather availability, high temporal and spatial resolution, and long-term stability7; however, GNSS-derived IWV measurements are inherently point-based observations restricted to fixed ground stations, resulting in limiting comprehensive atmospheric water vapor monitoring in regions with sparse infrastructure.

Since the emergence of GPS meteorology in the 1990s8GNSS has emerged as a highly effective method for retrieving water vapor9,10,11. Although monitoring water vapor with GNSS has historically been restricted by the discrete distribution of ground-based receivers, recent advancements have substantially enhanced the spatial representativeness of these observations. Driven by significant advancements in receiver, antenna, and processing technologies, the manufacturing costs of GNSS receivers and antennas have been significantly reduced. This has resulted in a dramatic decrease in the acquisition cost of a single low-cost GNSS unit, with the cost of a receiver and antenna now typically 10–20% of that of a geodetic-grade unit12. This cost advantage facilitates the establishment of densified networks of low-cost GNSS units, significantly enhancing spatial coverage and improving water vapor monitoring capabilities. A notable example can be observed in the city of Wroclaw, Poland, where a network of low-cost multi-GNSS receivers has been established, achieving a spatial resolution of several kilometers across an urban area13. This initiative demonstrates the feasibility and practicality of utilizing such networks for high-resolution water vapor monitoring, highlighting their potential for urban-scale atmospheric studies14.

In Switzerland, a parallel research initiative has implemented dense networks utilizing of GNSS low-cost receivers for environmental monitoring applications, specifically focusing on atmospheric water vapor and soil moisture content15. The CentipedeRTK network, initiated in 2019 at an extended regional scale across mainland France, aims to provide free real-time centimeter-level positioning16. As of September 2024, the network includes over 700 permanent stations, predominantly equipped with low-cost GNSS receivers and antennas. The network follows a collaborative model, where each station is built and maintained by its individual owner. This structure enables the network to function as a wide-area, distributed system, supporting a variety of GNSS-based applications, from precise positioning to atmospheric monitoring and beyond.

The accuracy and applicability of IWV retrieval from low-cost GNSS networks are highly dependent on precise orbit and clock products. Although real-time orbit and clock products are available, challenges remain in terms of stability, accuracy, reliability, and reconvergence during orbit determination, primarily due to unavoidable interruptions in the real-time data stream17. In contrast, ultra-rapid orbit products have gained widespread adoption due to their feasibility and robustness, offering a practical alternative for maintaining high-precision GNSS applications. However, the standard ultra-rapid orbit products typically exhibit a latency of up to three hours18 which poses a significant limitation for near real-time atmospheric water vapor monitoring. Moreover, a variety of empirical models19,20,21,22,23,24,25independent of direct meteorological observations, have been developed to estimate the weighted mean temperature (\(\:{T}_{m}\)), a key parameter in converting zenith wet delay (ZWD) to IWV when direct temperature observations are unavailable. However, a comprehensive evaluation of the accuracy of these empirical models remains lacking. This study aims to achieve high spatial and temporal resolution IWV monitoring in near real-time using a network of low-cost GNSS receivers. It assesses the performance of newly released near real-time precise orbit and clock products with lower latency and compares the efficacy of various empirical \(\:{T}_{m}\) models. Additionally, this study provides an assessment of the impact of missing phase center variation (PCV) corrections for low-cost receivers in GNSS data processing and examines the sensitivity of the conversion factor to \(\:{T}_{m}\) deviations during ZWD to IWV conversion.

This manuscript begins with an introduction to the IWV retrieval process and \(\:{T}_{m}\) determination. Section 2 provides a comprehensive description of the study area, datasets, and GNSS data processing strategies. The analysis examines several key aspects, including the performance of near real-time IWV products, validation of ZWD estimates from low-cost stations, comparison of \(\:{T}_{m}\) models for IWV conversion, and the spatiotemporal variation of IWV within the study area. The manuscript concludes with key findings and discussions, emphasizing the implications of the results and potential applications.

Methods

IWV retrieval method

GNSS signals traveling from a satellite experience a delay as they pass through the troposphere, compared to their propagation in a vacuum. This phenomenon, known as the tropospheric delay, can be estimated during GNSS data processing. The tropospheric delay is typically divided into two components: hydrostatic and wet. The hydrostatic delay, which represents about 90% of the total delay, can be accurately corrected using an a priori model with surface air pressure measurements. In contrast, the wet delay, caused by atmospheric water vapor, constitutes the remaining 10%. Due to its variability and complexity, the wet delay is more challenging to predict and is treated as an unknown parameter, estimated during GNSS data processing26. By analyzing the wet delay using a ground-based GNSS receiver, it is possible to infer the IWV present in the troposphere.

The Precise Point Positioning (PPP) technique is a promising approach for estimating tropospheric delay27,28. The ionosphere-free (IF) carrier-phase \(\:{\varPhi\:}_{r,IF}^{s}\) and pseudo-range \(\:{P}_{r,IF}^{s}\) observations for satellites s and receiver r can be formulated as29,30:

$$\:\begin{array}{c}\left\{\begin{array}{c}{\varPhi\:}_{r,IF}^{s}={\rho\:}_{r}^{s}+c\left(\delta\:{t}_{r}-\delta\:{t}^{s}\right)+{T}_{r}^{s}+{\lambda\:}_{IF}\cdot\:{N}_{IF}+{\epsilon\:}_{\varPhi\:}\\\:{P}_{r,IF}^{s}={\rho\:}_{r}^{s}+c\left(\delta\:{t}_{r}-\delta\:{t}^{s}\right)+{T}_{r}^{s}+{\epsilon\:}_{P}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\end{array}\right.\end{array}$$
(1)

where \(\:{\rho\:}_{r}^{s}\) is the geometric distance between the satellite and receiver; c is the speed of light in vacuum; \(\:{\updelta\:}{t}_{r}\) is the reparametrized receiver clock offset and \(\:{\updelta\:}{t}^{s}\) is satellite clock offset; \(\:{T}_{r}^{s}\) represent the tropospheric delay; \(\:{\lambda\:}_{IF}\) is the IF combined carrier wavelength and \(\:{N}_{IF}\) is the reparametrized ambiguity parameter; \(\:{\epsilon\:}_{{\Phi\:}}\) and \(\:{\epsilon\:}_{P}\) are respectively the carrier-phase and pseudo-range observation noises. Since the fixed PPP solutions do not show a significant improvement in tropospheric estimates compared to the float solutions31,32only the float solutions will be considered in this study. Consequently, the code and phase hardware delays from both the receiver and satellite are fully absorbed by the reparametrized receiver clock offset and ambiguity parameters.

The tropospheric delay, as previously mentioned, can be divided into two components: the hydrostatic component and the wet component. Each of these components is associated with a corresponding mapping function, as expressed in Eq. (2):

$$\:\begin{array}{c}{T}_{r}^{s}={m}_{h}\left(e\right)\cdot\:{T}_{h}+{m}_{w}\left(e\right)\cdot\:{T}_{w}\end{array}$$
(2)

where \(\:{T}_{h}\) is the zenith hydrostatic delay, \(\:{T}_{w}\) represents the ZWD, \(\:{m}_{h}\left(e\right)\) and \(\:{m}_{w}\left(e\right)\) are the corresponding mapping functions, which typically depend on the satellite elevation e as observed from the receiver. ZWD is one of the parameters estimated in the PPP solution, along with receiver clock offset and receiver coordinates. Once ZWD estimates are obtained, the IWV can be converted by:

$$\:\begin{array}{c}IWV=Q\cdot\:ZWD\end{array}$$
(3)

where Q represents the conversion factor, which is defined as19

$$\:\begin{array}{c}Q=\frac{{10}^{6}}{{\rho\:}_{w}{R}_{w}\left(\frac{{k}_{3}}{{T}_{m}}+\left({k}_{2}-{k}_{1}\frac{{M}_{w}}{{M}_{d}}\right)\right)}\end{array}.$$
(4)

where \({\rho}_{w}=997\,\text{kg} \! \cdot \! \text{m}^{-3},\) \({R}_{w}=461.525\, \text{J} \! \cdot \! {\text{kg}}^{-1}\! \cdot \! {\text{K}}^{-1},\) \({k}_{3}=3754.63\, {\text{K}}^{2}\!\cdot {\text{Pa}}^{-1},\) \({k}_{2}=0.712952\,\text{K} \! \cdot\!{\text{Pa}}^{-1},\) \({k}_{1}=0.776890\,\text{K} \! \cdot \! {\text{P}\text{a}}^{-1},\) \({M}_{w}=15.9994\, \text{g}\! \cdot \! {\text{m}\text{o}\text{l}}^{-1}\) and \({M}_{d}=28.9644\, \text{g}\! \cdot \! {\text{m}\text{o}\text{l}}^{-1}\) are physical constants, while \(\:{T}_{m}\) is the sole variable, exhibiting both spatial and temporal variations influenced by factors such as geographic location, altitude, seasonal fluctuations, and meteorological conditions.

Determination of \(\:{T}_{m}\)

From Eq. (4), it is evident that \(\:{T}_{m}\) is a crucial variable for the conversion of ZWD to IWV. Theoretically, \(\:{T}_{m}\) can be calculated with the following Eq. 20:

$$\:\begin{array}{c}{T}_{m}=\frac{\int\:\frac{e}{T}dh}{\int\:\frac{e}{{T}^{2}}dh}\approx\:\frac{{\sum\:}_{1}^{n}\frac{{\stackrel{-}{e}}_{i}}{{\stackrel{-}{T}}_{i}}\varDelta\:{h}_{i}}{{\sum\:}_{1}^{n}\frac{{\stackrel{-}{e}}_{i}}{{\stackrel{-}{T}}_{i}^{2}}\varDelta\:{h}_{i}}\end{array}$$
(5)

where e and T are the water vapor pressure (hPa) and absolute temperature (K), respectively; n represents the number of atmospheric layers; \(\:{\stackrel{-}{e}}_{i}\),\(\:\:{\stackrel{-}{T}}_{i}\), and \(\:{{\Delta\:}h}_{i}\) are the mean water vapor pressure, mean temperature, and thickness of the i-th layer, respectively. To obtain \(\:{T}_{m}\) for a specific GNSS site, a straightforward and accurate approach involves using vertical profiles of atmospheric temperature and humidity, typically derived from radiosonde data. However, GNSS stations are rarely co-located with radiosonde stations. Even when they are located closely, the low temporal resolution of radiosonde data may restrict its applicability. Consequently, the derived \(\:{T}_{m}\) lacks the temporal resolution required in near real-time or real-time applications. As a result, Eq. (2) is generally inapplicable for most GNSS stations.

Alternatively, based on an analysis of extensive radiosonde profiles, \(\:{T}_{m}\) can be estimated using an empirical model expressed as a linear function8 of the surface air temperature \(\:{T}_{s}\):

$$\:\begin{array}{c}{T}_{m}=70.2+0.72\times\:{T}_{s}\end{array}$$
(6)

While the ideal scenario involves directly acquiring surface air temperature data from in situ temperature instruments, logistical constraints often make this impractical. For example, the CentipedeRTK network was originally designed to provide free Real-Time Kinematic (RTK) positioning with centimeter-level accuracy for users, with meteorological applications not being a primary consideration. As a result, real-time surface air temperature measurements are not available in this network, making Eq. (6) inapplicable for the context of this study.

In this study, three latest empirical models are employed and validated. The first model is Global Pressure and Temperature 3 (GPT3), serving as the successor to the Global Pressure and Temperature 2 Wet model (GPT2w). GPT3 was developed using a ten-year mean of monthly pressure level data derived from the ERA-Interim reanalysis dataset. This model is available in two spatial resolutions, specifically 1°×1° and 5°×5° grids23,33. The second model, GTrop, is similar to GPT3 in that it also uses data from the ERA-Interim reanalysis dataset; however, GTrop incorporates data spanning up to four decades, providing a longer temporal coverage24. The third model, GGNTm, accounts for the vertical nonlinear variation in the \(\:{T}_{m}\) by using a third-order polynomial function and ERA5 monthly mean reanalysis data over a 10-year period. Additionally, the temporal variation of the four coefficients in the fitting function is modeled with variables representing the mean, annual, and semi-annual amplitudes of the 10-year time series coefficients25.

Experiment

Data collection

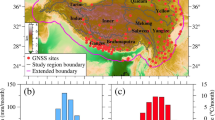
This study analyzes a significant heavy precipitation event that occurred on September 25–26, 2024, in France using data from CentipedeRTK network. To maintain consistency, stations equipped with geodetic receivers or geodetic antennas were excluded, resulting in 439 low-cost stations available during the experimental period. Among these, 98.4% of the stations are equipped with Ublox F9P receivers, while the remaining stations utilize receivers from Septentrio and Unicore. Regarding antennas, 75.2% of the stations are equipped with JCA228F0001 antennas supplied by ZHEJIANG JC Antenna Co., Ltd., while the rest use antennas manufactured by Ardusimple, Beitian, and other providers.

To evaluate the accuracy of ZWD estimates from low-cost stations, these estimates were validated against references derived from nearby high-grade GNSS reference stations. In this study, six reference stations from the Réseau GNSS Permanent (RGP) network were carefully selected as references, each located within 1 km of a corresponding low-cost station. Table 1 provides details of the RGP stations, including names, hardware configurations, and distances to the nearest low-cost station. Similarly, to assess the efficiency of empirical models for determining the \(\:{T}_{m}\), six meteorological stations were chosen, each situated within 1 km of a corresponding low-cost station. Table 2 lists the names of the meteorological stations and their respective distances to the nearest low-cost station. The geographic distribution of all stations is illustrated in Fig. 1.

Table 1 Configuration of RGP stations and their distances to the nearest low-cost station.
Full size table
Table 2 Meteorological stations and their distances to the nearest low-cost station.
Full size table
Fig. 1
figure 1

Geographical distribution of GNSS and meteorological stations.

Full size image

During the experiment period between September 25 and 26, all GNSS stations recorded observations at a 30-second sampling rate, while the meteorological stations provided hourly measurements, including precipitation and air temperature data.

GNSS data processing strategies

Both low-cost stations and RGP stations adopted identical strategies for PPP processing to ensure consistency and comparability in the results. As receiver antenna phase center variation (PCV) corrections are predominantly available for GPS satellites, only GPS satellites were employed in the data processing for this study. The observation elevation mask was set to 7 degrees, and station coordinates were treated as constant values, with daily estimates derived from the PPP solutions. The tropospheric delay was modeled using the Saastamoinen model34 for the hydrostatic delay, while ZWD was estimated as a random walk process, combined with a global mapping function to account for the tropospheric delay along the slant path35,36. Corrections for solid Earth tides, ocean tides, and pole tides were applied following the IERS Conventions37. Near real-time precise orbit and clock products provided by Wuhan University (WHU)38 were used in the processing. These ultra-rapid products released with 1-hour latency—compared to the 3-hour latency of products from other agencies—are well-suited for near real-time monitoring of water vapor transport during severe rainfall events.

Results

Performance of near real-time products for ZWD Estimation

The near real-time products have lower latency compared to the final products, albeit at the cost of reduced precision. To evaluate their performance in ZWD estimation, ZWD values were independently derived using both near real-time and final products. The comparison was conducted by analyzing the ZWD estimates from near real-time products against those from the final products. Figure 2 illustrates the comparison at selected stations, where each subfigure shows a strong agreement in ZWD trends between the two products, with only systematic and slight differences observed. Table 3 provides a quantitative assessment, presenting the correlation coefficients (R), root mean square error (RMSE), and bias of ZWD estimates derived from near real-time products compared to those from final products.

Fig. 2
figure 2

Comparison of ZWD from near real-time and final products at selected stations.

Full size image
Table 3 ZWD statistics of near real-time products against final products.
Full size table

The average correlation coefficient, i.e., R in Table 3, reaches 0.9998, indicating an exceptionally strong agreement between the ZWD estimates from near real-time and final products. Furthermore, the average RMSE and bias values are both 4.4 mm, highlighting that the differences between the two products in retrieving ZWD are minimal. Given the low time latency of near real-time products, they are particularly advantageous for applications requiring near real-time numerical weather prediction.

Validation of ZWD estimates from low-cost stations

The ZWD estimates at low-cost stations are validated against external ZWD references. As described in Sect. 3.1, six low-cost stations were selected based on their proximity—less than 1 km—to the nearest RGP station, ensuring that the ZWD values at both locations would be highly similar. The dual-frequency geodetic-grade equipment at RGP stations provides millimeter-level precision in ZWD estimates through PPP processing, making the ZWD estimates from the RGP stations a truth benchmark for evaluating the accuracy of the ZWD values obtained from the low-cost stations. Figure 3 compares the ZWD estimates from selected low-cost stations with those from their corresponding RGP stations, illustrating the consistency between the two datasets. Table 4 provides a quantitative assessment of the comparison, using the same metrics presented in Table 3, including correlation coefficients, root mean square error, and bias.

Fig. 3
figure 3

Comparison of ZWD at low-cost stations against RGP stations.

Full size image
Table 4 ZWD statistics of low-cost stations against RGP stations.
Full size table

As shown in Fig. 3, the differences between the two datasets fluctuate over time without any discernible systematic pattern. The correlation coefficients in Table 3 remain consistently high, with an average value of 0.993. Additionally, the average bias and RMSE are 4.4 mm and 6.6 mm, respectively, indicating minimal differences between the ZWD estimates from low-cost stations and their corresponding RGP stations. However, the bias and RMSE for low-cost station A349 are notably larger than those for the other low-cost stations. This discrepancy can be attributed to significant variations observed during the last few hours of the experiment, likely caused by localized ZWD variations, as water vapor can exhibit significant spatial variability under certain conditions.

Comparison of \(\:{T}_{m}\) models on IWV conversion

Since the air temperature data at the meteorological stations were recorded at hourly intervals, they were interpolated to 30-second intervals using cubic spline interpolation39. Subsequently, the interpolated air temperature data were converted into \(\:{T}_{m}\) using Eq. (5), referred to as the observed \(\:{T}_{m}\) in the following context. Simultaneously, the GPT3 model with a spatial resolution of 5° × 5°, the GTrop model, and the GGNTm model were independently employed to compute \(\:{T}_{m}\), which were then validated against the observed \(\:{T}_{m}\). Figure 4 provides a comparative analysis of \(\:{T}_{m}\) obtained using different methods at selected low-cost stations. Table 5 complements this by presenting a statistical evaluation.

Fig. 4
figure 4

Comparison of modeled \(\:{T}_{m}\) with respect to the observed \(\:{T}_{m}\).

Full size image
Table 5 Statistics of modeled \(\:{T}_{m}\).
Full size table

As shown in Fig. 4, the modeled \(\:{T}_{m}\) values derived from the three empirical models generally agree with the observed \(\:{T}_{m}\) values. However, these empirical models may have limitations in capturing daily variations in \(\:{T}_{m}\). Since these models often rely on linear regression techniques, they may exhibit significant errors during periods of abrupt or short-term fluctuations, thereby reducing their accuracy in certain dynamic conditions. According to Table 4, the GTrop model exhibits slightly better performance than the other two models, with an average bias of −0.19 K and an average RMSE of 1.56 K. In comparison, the GPT3 model shows an average bias of −1.08 K and an RMSE of 1.94 K, while the GGNTm model exhibits an average bias of −0.67 K and an RMSE of 1.69 K, respectively.

Figure 5 compares the IWV values converted from ZWD at selected low-cost stations and \(\:{T}_{m}\) obtained using different methods. As observed in each subfigure of Fig. 5, the IWV estimates from different methods nearly overlap, indicating minimal differences among the methods. Table 6 presents the statistical evaluation of IWV derived from three empirical models relative to the IWV computed using the observed \(\:{T}_{m}\).

Fig. 5
figure 5

Comparison of IWV at low-cost stations using different \(\:{T}_{m}\) models.

Full size image
Table 6 IWV statistics: modeled vs. observed temperature.
Full size table

Based on the metrics presented in Table 4, the correlation coefficients show exceptionally high values, while the bias and RMSE magnitudes are extremely low. However, the GTrop model still demonstrates a slight advantage over the other two models, as evidenced by its marginally lower RMSE and bias values. This finding aligns with previous research, which has shown that the GTrop model performs slightly better than the GPT3 and GGNTm models in providing \(\:{T}_{m}\) estimates. This performance is likely attributed to the fact that GTrop utilizes a longer temporal coverage, which allows for the detection and modeling of longer-term trends in the data. Nevertheless, all three models exhibit negligible discrepancies when compared to the observed \(\:{T}_{m}\) in IWV conversion, indicating that all models are suitable for IWV conversion in this study. Given that the GTrop model demonstrates the best performance in both accuracy and computation efficiency, it will be adopted for subsequent analysis in this study.

Relation of IWV retrieved from low-cost receiver and rainfall measurement

Figure 6 presents the comparison of IWV retrieved from low-cost receiver and precipitation data from the meteorological stations listed in Table 2. It can be seen that the IWV and precipitation shows a good consistency. A biduous rainfall appeared in the upper panel region with precipitation peaking around the 12th–24th and 32nd–38th hours. The IWV follows a similar trend and displays obvious two distinct crests during the same periods. The lower panel region demonstrates a unique phenomenon that the IWV increases steadily prior to the precipitation, and the rainfall occurs actually during the subsequent IWV decline. This is not contrary to the existing acknowledge because IWV represent the water vapor content of the atmosphere, and precipitation occurs once the water vapor concentration reaches a critical threshold40. During the latter stages of precipitation, the IWV begins to decrease even before the precipitation concludes, as atmospheric water vapor content is gradually transferred to the ground. This phenomenon is observed consistently for both the upper and lower panel receivers.

Fig. 6
figure 6

Comparison of IWV retrieved from low-cost receiver and precipitation.

Full size image

Figure 6 demonstrates that IWV data retrieved from low-cost GNSS receivers can reliably reflect the atmospheric moisture dynamics and precipitation processes. A clear temporal relationship between IWV variations and rainfall has been observed with IWV peaks aligning with significant precipitation events, suggesting that low-cost receivers can capture the buildup and release of atmospheric moisture with a certain level of accuracy. To further investigate the predictive value of IWV in anticipating rainfall, the precipitation onset is defined as the hour when rainfall exceeded 1 mm following a sustained dry period of at least 3 h, while the corresponding IWV peak is identified as the last local maximum preceding this precipitation onset. As demonstrated by the six representative stations in Fig. 6, the IWV peak generally precedes the onset of peak precipitation by 1.5 to 3 h. An average lead time of approximately 2.3 h across all stations of the study region. These lead times are consistent with prior findings that show IWV accumulation as a precursor to convective precipitation, particularly when atmospheric saturation conditions are approached.

Lag correlation analysis is performed on paired IWV and precipitation time series from the above six representative stations. At each station, IWV are interpolated to hourly temporal resolution to align with precipitation records. Pearson correlation coefficients are calculated systematically between the IWV series and time-shifted precipitation data, with lags ranging from 0 to 6 h in 0.5-hour increments. A consistent lead time of 2 to 2.5 h between IWV peaks and rainfall onset, with statistically significant correlation coefficient ranges between 0.68 and 0.82 are observed across multiple stations.

The findings highlight the potential of these receivers to provide valuable insights into precipitation timing and intensity. Moreover, low-cost receivers offer a cost-effective alternative for advancing precipitation research, enabling more accessible and precise monitoring of rainfall events and contributing to improved weather prediction models.

Spatio-temporal variation of IWV

Figure 7 illustrates the spatio-temporal evolution of IWV across the study area over a two-day period, with each subfigure representing a 2-hour interval, providing a clear visualization of atmospheric moisture dynamics.

Fig. 7
figure 7

Spatial visualization of IWV in 48 h.

Full size image

At the beginning of the observation period, as depicted in subfigure (a) to (c), IWV values are relatively low across most regions, with dominant blue and green shades indicating IWV levels between 5 and 20 mm. As time progresses, from subfigures (d) to (h), a gradual increase in IWV becomes apparent, particularly in the southern and central regions. Here, green shades transition to yellow and orange, representing IWV levels rising to 25–35 mm. Notably, between 14:00 and 22:00 on September 25, a significant accumulation of IWV is observed in the southern and southwestern parts of the study area, as highlighted in subfigures (h) to (l). During this period, orange and red shades emerge, signifying IWV levels exceeding 30–40 mm, suggesting an influx of atmospheric moisture influenced by local or regional weather dynamics. Meanwhile, the northern and northeastern regions retain relatively lower IWV levels, reflected by persistent blue and green shades.

On September 26, the IWV distribution undergoes a noticeable shift, as shown in subfigures (m) to (p). While the southern regions continue to exhibit elevated IWV levels during the early hours, a decline in atmospheric moisture becomes evident starting at 08:00. The previously dominant orange and red regions progressively recede, replaced by green and blue shades, indicating a reduction in IWV levels. By the final hours of the observation period, as shown in subfigures (w) and (x), IWV values return to relatively low levels across most regions, with blue and green shades reemerging to signify depleted atmospheric water vapor content.

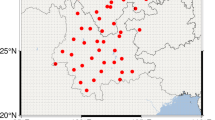
Figure 8 depicts the daily precipitation recorded on September 25–26, 2024. The circles indicate the locations of meteorological stations, while the fill color represents the corresponding precipitation magnitude. As shown in subfigure (a), stations experiencing substantial daily precipitation are primarily concentrated in the western regions. During the same period, these western regions exhibited higher IWV levels than other areas, as evidenced in subfigures (a) to (m) of Fig. 7. On September 26, a greater number of stations with significant daily precipitation emerged in the south-central regions, where IWV levels were notably higher than in other areas, as illustrated in subfigures (n) to (p) of Fig. 7. Overall, both the intensity and spatial extent of precipitation on the second day exceed those of the first day. This aligns with the observation that regions exhibiting higher IWV levels on the second day are significantly more widespread compared to the first day.

Fig. 8
figure 8

Daily precipitation on September 25–26, 2024.

Full size image

The spatiotemporal evolution of IWV, as illustrated in Fig. 7, underscores the capability of low-cost GNSS stations to effectively capture dynamic variations in atmospheric moisture. These cost-efficient and practical solutions enable continuous monitoring of the gradual accumulation, peak, and subsequent dissipation of water vapor with high temporal and spatial resolution. Furthermore, analysis of Figs. 7 and 8 reveals a significant correlation between daily precipitation recorded at meteorological stations and IWV levels. This alignment suggests that regions with elevated IWV levels exhibit a higher propensity for significant precipitation.

Discussions

PCV correction for low-cost antennas

Noting that low-cost antennas mostly exhibit significantly larger PCV magnitudes, often reaching several centimeters, this directly impacts the accuracy of ZWD estimation41,42. While many survey-grade antennas come with readily available PCV corrections stored in Antenna Exchange Format (ANTEX) files provided by the International GNSS Service (IGS), such corrections are frequently unavailable for low-cost antennas. This limitation can introduce significant biases into ZWD and, consequently, into IWV estimates when low-cost antennas are used for atmospheric water vapor monitoring. The National Geodetic Survey (NGS) provides antenna calibration information for a variety of low-cost antennas, including those used in this study, such as the JCA228F0001 and AS-ANT3BCAL. This calibration data, including PCV corrections, can be downloaded from their official website as ANTEX files for specific antennas43helping mitigate the biases introduced by the PCV.

Importantly, the original PCV information provided in the corresponding ANTEX file is confined to an elevation angle range of 10° to 90°. To accommodate data processing requirements where the elevation angle cutoff is set below 10°, typically 7°, a fourth-order polynomial function was utilized to extrapolate the PCV data. The left panel of Fig. 9 illustrates the ionosphere-free PCV pattern for the JCA228F0001 antenna alongside its corresponding fourth-order polynomial fit. As shown, the two curves exhibit excellent concordance, with an R-squared value of 0.992. The RMSE of the fitting residuals is 0.32 mm—substantially lower than the typical noise level in phase observations, which generally lies within the range of several millimeters. This fitting process ensures that PCV corrections are available for lower elevation angles, extending the coverage of the corrections across all observed data above the cutoff angle. The right panel of Fig. 9 shows ZWD estimation discrepancies for selected low-cost stations when PCV corrections are omitted. These discrepancies are calculated by comparing ZWD estimates without PCV corrections to those with corrections applied. The red dashed line is diagonal, while each colored line corresponds to a specific low-cost station.

Fig. 9
figure 9

(a) PCV data for the JCA228F0001 antenna. (b) PCV effect on ZWD estimations.

Full size image

As depicted, the PCV pattern for the JCA228F0001 antenna exhibits peak-to-peak variations of approximately 1 centimeter. Notably, the magnitude of these PCV fluctuations is more pronounced at lower elevation angles, particularly below 10 degrees. The PCV data for the JCA228F0001 antenna predominantly exhibits negative values. This characteristic leads to an underestimation of the actual ZWD when PCV corrections were not applied, as evidenced in the right subfigure. Notably, the metrics for each selected station exhibit similar levels, with both RMSE and bias exceeding 4 mm. This suggests that the impact of PCV on ZWD estimation for the JCA228F0001 antenna is moderate, as the magnitude of PCV for this antenna is slightly larger than that of typical geodetic antennas but significantly lower than that of low-cost patch antennas.

Selection of \(\:{T}_{m}\) model

In the preceding section, the three latest empirical models for determining \(\:{T}_{m}\), independent of meteorological observations, were introduced and evaluated. Although these models exhibit varying levels of accuracy in estimating \(\:{T}_{m}\) compared to observed values, the differences in their impact on the resulting IWV estimates were found to be negligible.

A range of surface air temperatures from − 40 °C to + 65 °C is considered, corresponding to a \(\:{T}_{m}\) range of 238.068 K to 313.668 K. This range encompasses the standard operating temperature range for most receivers. Figure 10 illustrates the relationship between the conversion factor and \(\:{T}_{m}\), offering insights into the sensitivity of the conversion factor to variations in \(\:{T}_{m}\).

Fig. 10
figure 10

(a) conversion factor versus \(\:{T}_{m}\). (b) variation of conversion factor with deviation in \(\:{T}_{m}\).

Full size image

As shown by the curves in the left subfigure, the conversion factor exhibits a gradual increase from approximately 0.14 to 0.18 as \(\:{T}_{m}\) increases from 238.068 K to 313.668 K, suggesting a relatively low sensitivity of the conversion factor to changes in \(\:{T}_{m}\). The left subfigure also includes scenarios where \(\:{T}_{m}\) is considered with deviations of ± 5 K and ± 10 K. It can be observed that deviations in \(\:{T}_{m}\) introduce biases in the conversion factor relative to its true value, with the magnitude of the bias increasing proportionally to the magnitude of the deviation.

For clarity, the right subfigure highlights the variations in the conversion factor when deviations are present in \(\:{T}_{m}\). The deviations of ± 5 K and ± 10 K in \(\:{T}_{m}\) result in variations of ± 0.0028 and ± 0.0056 in the conversion factor, respectively. Previous research has shown that the mean bias and RMSE of \(\:{T}_{m}\) estimates at the Earth’s surface, as determined by all three models, are within 5 K25. For a typical ZWD value of 0.25 m, a deviation of 5 K in \(\:{T}_{m}\) introduces biases of less than 0.7 mm in the IWV estimates, which are generally negligible for most applications. Even during heavy rainstorms, where the ZWD may double, this deviation results in biases of less than 1.4 mm in the IWV estimates. This demonstrates that all three models are well-suited for IWV conversion applications, with negligible differences observed in the conversion of ZWD to IWV. Notably, there are many other models with comparable accuracy to those investigated in this study, all of which are also suitable for this application.

The high temporal resolution and near real-time availability of IWV estimates derived from low-cost GNSS networks make them valuable for assimilation into operational numerical weather prediction models. These measurements can be incorporated via variational methods to directly constrain humidity analysis or through ensemble-based techniques to probabilistically adjust moisture fields using flow-dependent error covariances. This study has demonstrated that assimilating GNSS-derived IWV improves the representation of moisture fields and enhances short-term precipitation forecasts. The 2–3 h lead time observed between IWV peaks and rainfall in this study supports the utility of GNSS-IWV for nowcasting and high-frequency forecasting cycles. Furthermore, the affordability and scalability of low-cost GNSS networks offer a practical solution for extending moisture observations into regions with sparse conventional coverage.

Conclusion

This study aims to achieve near real-time monitoring of IWV with high spatial and temporal resolution using a network of low-cost GNSS receivers. It provides a comprehensive assessment of the performance of near real-time precise orbit and clock products, the efficacy of empirical models for \(\:{T}_{m}\) determination, and the impact of missing PCV corrections on atmospheric parameter estimation. Through comparative analysis across various scenarios, this study provides valuable insights into the relative importance of these factors in ensuring accurate IWV retrievals.

The results show that: (1) The ZWD estimates from near real-time and final products demonstrate strong agreement, with average RMSE and bias values at the level of a few millimeters. This suggests that near real-time products are not only comparable in accuracy to final products but also effective, providing reliable precision in ZWD estimation. (2) The ZWD estimates from low-cost stations, with a spatial separation of less than 1 km from high-grade stations, show strong agreement with those from high-grade stations. (3) The GTrop model demonstrates superior performance over the GPT3 and GGNTm models. This advantage is largely due to its utilization of ERA-Interim data spanning four decades. The spatial resolution of this model can be further improved by integrating higher-resolution datasets, such as ERA5. However, all three models display negligible discrepancies compared to the observed \(\:{T}_{m}\) in IWV conversion. A further investigation shows that the conversion factor has relatively low sensitivity to deviations in \(\:{T}_{m}\). Within the typical operating temperature range for most receivers, all these recent models will suffice in the conversion of ZWD to IWV. (4) The IWV estimates from low-cost stations, with a spatial separation of less than 1 km from meteorological stations, exhibit strong consistency with precipitation data. (5) PCV data for low-cost antennas are often unavailable in standard ANTEX files. Users should retrieve these files from the official NGS website and incorporate them into the PPP processing. For example, in the case of the JCA228F0001 antenna, the absence of PCV correction can lead to a decrease in ZWD estimates by several millimeters.

This study demonstrates that low-cost GNSS stations effectively capture the dynamic evolution of atmospheric moisture by tracking the spatio-temporal variations of IWV. These stations serve as a valuable tool for monitoring the gradual accumulation, peak, and subsequent dissipation of water vapor with high temporal and spatial resolution. However, translating these variations into accurate rainfall forecasts requires further investigation. While this study does not explicitly address forecasting lead times, future research should focus on establishing quantitative relationships between IWV evolution and precipitation probability to enhance the reliability of IWV-based forecasting.