Introduction

Electrohydrodynamic(EHD) printing is a novel micro-nano manufacturing technology, characterized by low cost, ease of integration, good material compatibility and high resolution. It has a great application prospect in flexible electronics1,2,3, biological tissue engineering4,5, micro-nano sensing6,7, etc. Unlike traditional inkjet printing methods that rely on extrusion pressure, EHD printing utilizes a high-voltage electric field to induce fluid motion8. It enables precise control for high-resolution printing. When the liquid surface is applied a sufficient electric potential, the liquid meniscus forms the stable Taylor cone9,10,11. When the electric field force overcomes the surface tension of the droplet, the cone ejects the charged jet from the tip, and deposit the desired droplet or fiber structure on the collector. Several injection modes can be observed in EHD printing, including the droplet jet mode, Taylor cone jet mode, retractive jet mode, forked jet mode, etc12. Among these, the Taylor cone jet mode is particularly valued for its stable jet and precise deposition capabilities, which are essential for producing well-defined micro-nano structures13,14.

Orderly and accurately patterned printing can be used to make patterned electrodes15, LED displays16, sensors17, and other devices that require uniform deposition and stable printing. However, there are various interference such as charge repulsion, electric field, air flow and platform motion in the EHD printing process, leading to the whipping jet and other unstable states, and they result in nonuniform deposition morphology18. Therefore, robust monitoring and controls are crucial to ensure stable and uniform deposition, and thus the precise fabrication of micro-nano structures19,20.

At present, microscopic imaging systems and current measurement and control systems are commonly used for printing process monitoring. Sun et al.21 monitored the manufacturing process of the EHD printing scaffold by collecting digital microscopic images, and evaluated the influence of process parameters on the cone and jet through characteristics such as the center of droplet and jet diameter. Similarly, Nguyen et al.22 used a image processing technology technique called the meniscus characterization to monitor EHD jetting, thereby controlling and improving jet stability. The meniscus height was used as the feedback data. However, they did not segment the image regions, and the fast response speed could lead to significant errors in feature detection data. In contrast, the image recognition algorithm employed in this study segments the needle, droplet, and jet regions of the image, resulting in more accurate feature data for each region. Li et al.23 designed an instrument of drop-on-demand electrohydrodynamic jet (DoD E-Jet) printing device controlled by a current measurement and control system. However in EHD printing, the current value is too small to isolate the environmental interference, so current measurement itself is insufficient for achieving accurate close-loop control.

Several control schemes have been implemented in jet printing systems. Barton et al.24 discussed the development of a sensing and feedback–feedforward control system for EHD printing. The feedforward voltage signal is used to compensate for repeatable changes in the operating conditionsand is obtained using an Iterative Learning Control (ILC) algorithm. However, their control system merely adjusts the control of jetting frequency and cannot mitigate deposition instability resulting from variations in jet mode. Guo et al.25 proposed two control-oriented models to describe the layer-to-layer height evolution of the ink-jet 3D printing process. The first is based on droplet geometry superposition, while the other is based on a graph-based characterization of local flow dynamics. These control-oriented models will ultimately enable the design of model-based closed-loop control for high resolution ink-jet 3D printing.

However, the EHD printing process is complex and susceptible to various interference. There is yet no clear functional relationship between the jet mode, characteristic current and voltage, so it is difficult to develop the mathematical fitting model, and model-based control methods are complex for EHD printing26. Compared with other control schemes, fuzzy control is based on linguistic rules rather than a clear mathematical model, making it powerful to handle the systems with nonlinear, time-varying characteristics27,28. This approach offers strong reliability, rapid response, and robust anti-interference capabilities, making it well-suited for managing the intricate and variable aspects of the EHD printing process29.

In this paper, a double closed-loop fuzzy control method based on jet image recognition and micro-current measurement was designed to monitor and control the EHD printing process. The system takes the micro-current and jet image characteristics data as feedbacks, and carries out the closed-loop control upon the EHD printing by fuzzy control algorithm. The experimental results show that the closed-loop control greatly improves the uniformity and stability of the fiber deposition.

Materials and methods

EHD printing system

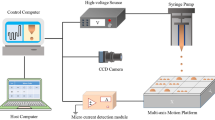
Figure 1 shows the EHD printing system. It is composed of a high voltage power supply (RIGOL DG1022Z, Beijing, China; HVA-502NP5, Tianjin, China), a precision syringe pump (Pump 11 Pico Plus Elite, Harvard Apparatus America, Cambridge, MA, USA), a metallic nozzle (the inner diameter of the nozzle is 60 μm, and the outer diameter is 200 μm), a collector (silicon wafer), a multi-axis motion platform (REI95LM-050, Shenzhen Borui Automation Equipment Co., Ltd., Shenzhen, China), a jet monitoring module, a micro-current detection module, and workstation. The nozzle is connected to high voltage positive supply, and the collection plate to the negative supply. A high electric field is formed between the nozzle tip and the collector, which force the solution to overcome the viscous tension and form the jet. The collector is carried by a multi-axis motion platform, whose speed and trajectory are pre-designed. The solution feeding rate is accurately controlled by the precision syringe pump, and the jet injection behavior is monitored in real time by the high-speed CCD (UI-3130CP-C-HQ, IDS Imaging Development Systems GmbH, Obersulm, Germany). The nano-ampere (nA) scale jet current is amplified by the micro-current module and the current data is collected. The jet solution consists of a 12% PEO solution dissolved in a solvent mixture of 25%v/v ethanol in water.

In the jet monitoring module, the real-time images were collected by CCD industrial camera. The original images underwent preprocessing, which includes gray-scale, binarization and feature screening to eliminate the noises. Three regions were automatically sorted: the needle, liquid drop and jet. Features of each region were extracted and recorded, including droplet area, cone length, cone angle and center coordinate. Figure 1c shows the jet monitoring GUI, in which real-time jet image and the image region segmentation are presented. The droplet area, droplet center coordinates, cone length, cone width and other characteristic parameters are also displayed.

Fig. 1
figure 1

The EHD printing system: (a) The schematic of the EHD printing system. (b) The actual setup of the EHD printing system. (c) Jet image monitoring interface. (d) The actual setup of the micro-current detection module.

Full size image

The micro-current detection module includes micro-current amplifier and signal collection circuit as shown in Fig. 1(d). The jet micro-current is too small to be directly detected and recorded by the data acquisition (DAQ) card. The micro-current amplifier circuit is used to transfer the nA-scale current to the µV-scale voltage signal. The microcontroller collects the amplified voltage data at a certain frequency, and transmits to the upper computer software through RS-232 serial port communication. When the current measurement gear operates at nA level,1-V signal is equivalent to 1000-nA current signal.

Fuzzy control algorithm

In EHD printing system, processing parameters such as applied voltage between nozzle and collector, liquid feeding rate, platform trajectory, and the dependent parameters including micro-current and jet image feature parameters are all effective inputs of morphology of deposited fibers and droplets. Figure 2 shows the block diagram of the EHD printing fuzzy control closed-loop system.

Firstly, launch the starting parameters that set the Taylor cone injection mode. The closed-loop fuzzy control is in operation once the printing process starts. CCD camera captures the jet images, and the image recognition algorithm is used to extract the measured image features. The micro-current detection module is used for current amplification and acquisition, and the current measurement value during printing is obtained. The current deviation, jet image feature deviation, and the deviation gradients of both information can be calculated through feedback to the preset image and current predicted value. The fuzzy logic is operating to control the output voltage, liquid feeding rate and platform motion parameters.

Fig. 2
figure 2

The block diagram of the EHD printing fuzzy control closed-loop system.

Full size image

It is necessary to fuzzy-process deviation (E), deviation gradient (EC), and voltage increment (U). Figure 3 shows the triangle membership function of E, EC, and U. The triangular membership function was chosen because it is simple to calculate and adjust, and is often used in real-time control.

Each of the three fuzzy attributes are classified into 7 conditions: large negative deviation (NB) for range -∞~-4, medium negative deviation (NM) for range − 6~-2, small negative deviation (NS) for range − 4 ~ 0, no deviation (ZO) for range − 2 ~ 2, small positive deviation (PS) for range 0 ~ 4, medium positive deviation (PM) for range 2 ~ 6, and large positive deviation (PB) for range 4~∞.

Upon confirming the membership function, E, EC and U are normalised to the range − 6 ~ 6. They are expressed by \(\:{\text{e}}^{\text{*}}\), \(\:{\text{r}}^{\text{*}}\), \(\:{\text{u}}^{\text{*}}\):

$$\:{\text{e}}^{\text{*}}\text{=}{\text{K}}_{\text{e}}\text{e}$$
(1)
$$\:{\text{r}}^{\text{*}}\text{=}{\text{K}}_{\text{r}}\text{r}$$
(2)
$$\:\text{u}\text{=}{\text{K}}_{\text{u}}{\text{u}}^{\text{*}}$$
(3)

Then the coefficient \(\:{\text{K}}_{\text{e}}\), \(\:{\text{K}}_{\text{r}}\), \(\:{\text{K}}_{\text{u}}\) are defined as:

$$\:{\text{K}}_{\text{e}}\text{=}\frac{\text{S}\text{u}\text{b}\text{o}\text{r}\text{d}\text{i}\text{n}\text{a}\text{t}\text{e}\:\text{f}\text{u}\text{n}\text{c}\text{t}\text{i}\text{o}\text{n}\:\text{r}\text{a}\text{n}\text{g}\text{e}}{\text{M}\text{a}\text{x}\text{i}\text{m}\text{u}\text{m}\:\text{d}\text{e}\text{v}\text{i}\text{a}\text{t}\text{i}\text{o}\text{n}}$$
(4)
$$\:{\text{K}}_{\text{r}}\text{=}\frac{\text{S}\text{u}\text{b}\text{o}\text{r}\text{d}\text{i}\text{n}\text{a}\text{t}\text{e}\:\text{f}\text{u}\text{n}\text{c}\text{t}\text{i}\text{o}\text{n}\:\text{r}\text{a}\text{n}\text{g}\text{e}}{\text{M}\text{a}\text{x}\text{i}\text{m}\text{u}\text{m}\:\text{d}\text{e}\text{v}\text{i}\text{a}\text{t}\text{i}\text{o}\text{n}\:\text{g}\text{r}\text{a}\text{d}\text{i}\text{e}\text{n}\text{t}}$$
(5)
$$\:{\text{K}}_{\text{u}}\text{=}\frac{\text{I}\text{n}\text{i}\text{t}\text{i}\text{a}\text{l}\:\text{a}\text{p}\text{p}\text{l}\text{i}\text{e}\text{d}\:\text{v}\text{o}\text{l}\text{t}\text{a}\text{g}\text{e}\times\:\text{n}\text{\%}}{\text{S}\text{u}\text{b}\text{o}\text{r}\text{d}\text{i}\text{n}\text{a}\text{t}\text{e}\:\text{f}\text{u}\text{n}\text{c}\text{t}\text{i}\text{o}\text{n}\:\text{r}\text{a}\text{n}\text{g}\text{e}}$$
(6)

Where n is a variable, which is used to adjust proportion of the jet image and the current value. Since the jet image feature parameters are the main parameters of the control, and the current is the auxiliary parameter, the n of the jet image feedback is set to be larger, and the n of the current feedback is set to be smaller.

After the EHD printing experiment, the dynamic behavior characteristics of the injection were obtained, and the droplet area was selected as the feedback value of the jet image. The detailed experimental results are shown in the “Results and Discussion”. The Taylor cone angle is about 60° in Taylor cone jet mode. In this mode, the predicted droplet area is approximately equal to the equilateral triangle area S whose side length is the nozzle diameter d, which is \(\:S\:\text{= }\frac{\sqrt{\text{3}}}{\text{4}}{\text{d}}^{\text{2}}\). The predicted value can also be obtained by real-time monitoring of the droplet area. The predicted current value is the average current in Taylor cone jet mode in the experiment. The maximum deviation and deviation gradient of current and droplet area can be calculated by experiments.

Fig. 3
figure 3

The membership function of fuzzy control: (a) Current and image deviation (E). (b) Current and image deviation gradient (EC). (c) Output voltage increment(U).

Full size image

The fuzzy control rules of the EHD printing system were established, as shown in Table 1. When the droplet area deviation is NS and the deviation gradient is PB, the compensation voltage outputs NM. In other words, when the droplet area has a small negative deviation but the deviation gradient has a clear trend to larger value, the compensation voltage is still set to a small negative value to prevent the rapid increase of droplet area beyond the predicted value. When the current deviation is PS and the deviation gradient is NM, the compensation voltage is set to PS.

However, only fuzzy results are obtained by the fuzzy control algorithm. The output must be transformed into precise numerical value for the processing control. The gravity center method was used to transform the fuzzy quantities into numerical ones.

Table 1 The fuzzy control rules of EHD printing system.
Full size table

Results and discussion

Jet dynamic behavior characteristics

EHD printing experiment was carried out without fuzzy closed-loop control, with liquid feeding rate of 10 µL/h, nozzle-collector distance of 2 mm, and collector speed of 30 mm/s. The jet solution in the experiment was 12% PEO dissolved in a solvent mixture of 25%v/v ethanol in water. Fibers are printed and deposited due to the high viscosity of 12% PEO solution. As voltage increases, the droplet jet mode, Taylor cone jet mode, retractive jet mode appeared successively, corresponding to the applied voltages of 1.9 kV, 2.1 kV and 2.3 kV respectively, as shown in Fig. 4(a-c). The specific details of the three jet modes can be seen in supplementary videos.

The fiber deposition morphologies in different jet modes are shown in Fig. 4(d-f). In the droplet jet mode, the fibers has small and nonuniform diameters, and the phenomenon of disconnection occurs, but the fiber interval is stable. In the Taylor cone jet mode, the fiber deposition is continuous and uniform, with even intervals. In the retractive jet mode, the jet rotates, resulting in unstable fiber interval and poor uniformity. Therefore, one should set and operate in the Taylor cone jet mode to generate uniform and even-spacing fibers.

The jet image recognition algorithm was used to monitor the printing process. The dynamic jet behavior characteristics in Taylor cone jet mode were obtained as in Fig. 5. The jet dynamic behavior characteristics in other jet mode can be seen in Fig.S1 and Fig.S2. The original images at 0 s, 0.5 s, 1 s and 2 s are shown in Fig. 5(a). The droplet images extracted from the droplet part are shown in Fig. 5(b). The droplet area in Taylor cone jet mode ranges from 0.0135 mm2 to 0.0152 mm2 as in Fig. 5(c). The geometric centers of drops range from 0.936 mm to 0.948 mm in horizontal coordinates. The geometric center deviation of droplets is related to the collector movement. The jet is stretched and deformed and the geometric center position moves with the collector motion. In different jet modes, the droplet area range has a large difference and small fluctuation, compared to other image feature values. Therefore, the jet mode recognition and close-loop control can be realized by the droplet area data.

Fig. 4
figure 4

Different jet modes and fiber deposition morphologies: (a,d) Droplet jet mode and its fiber deposition morphology; (b,e) Taylor cone jet mode and its fiber deposition morphology; (c,f) Retractive jet mode and its fiber deposition morphology.

Full size image
Fig. 5
figure 5

Droplet area and center position in Taylor cone jet mode.

Full size image

Current characteristics

In fact, there is also a strong relationship between current, jet mode and printing parameters. Larger average current is benefit to the stable deposition of fibers. However, the current fluctuation increases when the current exceeds a critical value, which destroys stable deposition. The EHD printing experiments were carried out to study the current characteristics under different jet modes.

The current waveforms in different jet modes are shown in Fig. 6(a-c). Y-ordinate of each graph ranges from 0 to 300 nA for easier comparison of current characteristics in different modes. The current fluctuates slightly in both the droplet jet mode and the Taylor cone jet mode. But in the droplet jet mode, the supply voltage is smaller, the jet diameter is smaller, and the current value is lower. In contrast, retractive jet mode has larger average current with larger fluctuation. Figure 6(d) shows the variation of average current value with the applied voltage. The forked jet mode appears at 2.5 kV voltage supply. At this time, the jet is in a very unstable state, so the instantaneous current value fluctuates greatly and the average current error is relatively large. The average current value increases from 71.24 nA to 304.93 nA with the increase of applied voltage. The current fluctuation range is 72.4 nA in the droplet jet mode, 44.6 nA in the Taylor cone jet mode, 302.6 nA in the retractive jet mode, and 597.09 nA in the forked jet mode. The larger the current fluctuation, the more nonuniform the resulting fiber. The current must be stabilized.

Fig. 6
figure 6

(a) The current waveform in the droplet jet mode; (b) The current waveform in the Taylor cone jet mode; (c) The current waveform in the retractive jet mode; (d) The variation of average current value with applied voltage.

Full size image

Results of closed-loop fuzzy control

The preliminary EHD printing test verifies that the jet in Taylor cone jet mode is most stabilized and uniform fibers can be fabricated. The dynamic jet behavior characteristics in the Taylor cone jet mode were obtained by the jet image recognition algorithm, and the droplet area data was selected as the jet image feedback variable. The average value and fluctuation of current are read and recorded by the micro-current detection module.

The Taylor cone jet mode is established and operates at a corresponding voltage of 2.1 kV under the experimental conditions of a 0.25 mm needle diameter, 2 mm polar distance, 10 µL/h liquid feeding rate, and 12% PEO solution. The predicted droplet area is 0.0143 mm2 with a maximum deviation of 0.01 mm2 and a maximum deviation gradient of 0.0053 mm²/ms. The predicted current value is 132.75 nA with a maximum deviation of 20 nA and a maximum deviation gradient of 30 nA/ms. The n value corresponding to the droplet area is 30, and the n value corresponding to the current is 3.

Corresponding \(\:{\text{K}}_{\text{e}}\), \(\:{\text{K}}_{\text{r}}\), \(\:{\text{K}}_{\text{u}}\) values of the two control parameters were calculated respectively. The \(\:{\text{K}}_{\text{e}}\), \(\:{\text{K}}_{\text{r}}\), \(\:{\text{K}}_{\text{u}}\) of the droplet area are 600, 1132 and 105 respectively, and those of the current are 0.3, 0.2 and 10.5 respectively. All the coefficients were normalized and calculated for the fuzzy control of the printing system.

Fig. 7
figure 7

The jet images and current waveform: (a) Open-loop control; (b) Closed-loop fuzzy control.

Full size image
Fig. 8
figure 8

Morphology and diameter distribution of fiber deposition: (a) Open-loop control; (b) Closed-loop fuzzy control.

Full size image

EHD printing test were carried out with both open-loop control and current-jet binary closed-loop fuzzy control to investigate the fuzzy control effect on the printing, under the conditions of 10 µL/h liquid supply speed, 2 mm needle-to-collector distance, 30 mm/s collector speed, and 12% PEO jet solution. The input and output of fuzzy control can be seen in Fig.S3. The jet images and current waveforms before and after fuzzy control are shown in Fig. 7. The closed-loop-controlled injection exhibited greater stability compared to the open-loop controlled method and effectively minimized current fluctuations. The volatility percentage of the current decreased from 34% to 12%. Figure 8 shows the fiber deposition morphology with and without fuzzy control. Closed-loop control made fibers with higher uniformity and stable even interval. The fluctuation range of fiber diameter was reduced from 35 μm to 15 μm.

The stability of EHD printing process ensures uniform and orderly deposition morphology of fibers. Moreover, the rapid response of jet mode conversion in the printing system can reduce the ineffective deposition area on the collection plate and contribute to the realization of EHD printing on demand printing.

The response speeds of EHD printing mode conversions under both open-loop and close-loop controls were investigated. In open-loop controlled printing, the EHD printing jet is easily disturbed by surroundings, and manual voltage adjustment incurs a delay. Figure 9(a) shows the jet mode conversion under open-loop manual control. After voltage was applied, higher voltage supply is required to overcome the surface tension and initiate jetting from the bending liquid surface.Therefore, the retractive jet mode occurred at 1 s, with the fiber spacing unstable and the fiber uniformity poor. Through empirical analysis, the applied voltage was reduced but the jet does not respond in real-time to voltage change. It was observed that the voltage was reduced significantly at 3 s, causing it to transition into the droplet jet mode, and the deposited fibers show significant fluctuations in diameter. The Taylor cone jet mode was established by fine-tuning the voltage at 5 s. The fibers exhibit favorable characteristics with stable and uniform diameters and intervals.

Fig. 9
figure 9

EHD printing jet mode conversion: (a) Open-loop control; (b) Closed-loop fuzzy control.

Full size image

In the closed-loop control system, the response speed of EHD printing mode conversion is notably accelerated. This enhancement is achieved through fuzzy control, which initially increases the voltage to minimize delay time and allows the jet to quickly reach the collector for spraying. Once the jet stabilizes, the close-loop control effectively regulates the jet, ensuring it remains in a stable Taylor cone mode. Real-time voltage adjustments further contribute to stabilizing the jet and reducing the jet whipping.

The jet mode conversion under fuzzy closed-loop control is depicted in Fig. 9(b). The Taylor cone jet mode is achieved by 2.2 s, resulting in more uniform deposited fibers and stable interval under the current-jet double close-loop fuzzy control. The addition of close-loop control reduces the response time for printing to reach a stable mode from 5 s to 2.2 s.

Finally, ordered patterning printing was carried out on the EHD printing system to obtain a grid pattern, as shown in Fig. 10. Ordered and accurate grid patterns can be applied to patterned electrodes, LED displays, sensors and so on. However, without closed-loop control, the deposition point of the jet is inconsistent with the motion trajectory of the platform due to charge repulsion and other effects, and the fiber spacing will deviate from the set value, as shown in Fig. 10 (a). In addition, the uniformity of fiber diameter is poor, and the bead structure appears in the fiber, which reduces the print quality. After the closed-loop control was added, the system works in a stable Taylor cone mode. Not only can the pattern be accurately deposited according to the motion trajectory of platform, but also the fiber diameter is relatively uniform, as shown in Fig. 10 (b). The jet mode control suppresses the overall fluctuation of the jet, while the current control reduces the local fluctuation. Compared with open-loop control, the fluctuation range of fiber spacing under closed-loop fuzzy control was reduced from 116 μm to 38 μm, and the volatility percentage of fiber spacing was reduced from 29 to 9.5%.

Fig. 10
figure 10

Ordered grid pattern: (a) Open-loop control; (b) Closed-loop fuzzy control.

Full size image

Conclusions

This article presents a double close-loop fuzzy control method designed for monitoring and regulating the EHD printing process using jet image recognition and micro-current analysis. Initial EHD printing experiments confirms that stable Taylor cone jet mode results in stable and uniform fibers deposition. Dynamic characteristics of the jet in the Taylor cone jet mode are analyzed using the jet image recognition algorithm, with the droplet area serving as feedback. Micro-current detection provides average current values and fluctuation data, which are integrated into real-time feedback for fuzzy control implementation.

Experimental results demonstrate significant improvements in fiber deposition uniformity and stability after close-loop control implementation: current volatility decreases from 34% to 12%, fiber diameter fluctuation narrows from 35 μm to 15 μm, and fiber spacing volatility decreases from 29% to 9.5%. Moreover, the response time to reach a stable mode improves from 5 s to 2.2 s, effectively reducing ineffective deposition on the collection plate. This approach enhances the quality of micro-nano structure printing, advancing its application in high-resolution additive manufacturing.