Oral cancer detection via Vanilla CNN optimized by improved artificial protozoa optimizer

Abstract

In this study, we propose a new method for oral cancer detection using a modified Vanilla Convolutional Neural Network (CNN) architecture with incorporated batch normalization, dropout regularization, and a customized design structure for the convolutional block. An Improved Artificial Protozoa Optimizer (IAPO) metaheuristic algorithm is proposed to optimize the Vanilla CNN and the IAPO improves the original Artificial Protozoa Optimizer through a new search strategy and adaptive parameter tuning mechanism. Due to its effectiveness in search space exploration while avoiding local optimal points, the IAPO algorithm is chosen to optimize the convolutional neural network. In this study, a dataset of 1000 images of patients had published which will be preprocessed with contrast enhancement, noise reduction and data augmentation (like rotation, flipping and cropping) to generate the robust targeted model for oral cancer detection. The experimental results are evaluated against benchmark performance measures (accuracies, precision, recall, F1-score and area under the receiver operating characteristic (ROC) curve (AUC-ROC). We demonstrate through experimental results that the proposed IAPO optimized Vanilla CNN achieves a high accuracy of 92.5% which is superior than the previous state-of-the art models such as ResNet-101 (90.1%) and DenseNet-121 (89.5%). This proves to be a more trustworthy approach to oral cancer detectionbecause of the accuracy of the proposed method in comparison to denoting the supplementary results of the suggested method in contrast to other existing models.

Introduction

Background

One of the most common types of cancer around the world is oral cancer. This cancer starts from areas like the lips, the first parts of the tongue, the roof of the mouth, and the roof of the mouth. Oral cancer (palate cancer) can affect any part of the mouth (oral cavity)¹. It is considered as one of several types under head and neck cancers. This type of cancer appears as a lump or sore in the mouth that does not go away². Depending on which cells in the mouth are cancerous, this disease is classified³.

Oral cancer is actually a type of cancer that affects the inside of the mouth. This cancer can first appear on the lips or in the mouth as white spots or sores that bleed. If left untreated, cancer can spread throughout the mouth and throat and other areas of the head and neck⁴.

Early detection of oral cancer significantly enhances the efficacy of treatment, enabling healthcare providers to intervene before the disease progresses to an advanced stage⁵. Unfortunately, many individuals are unaware of their oral disease until it has reached a late stage, often due to infrequent dental or medical check-ups. Regular visits to the dentist or doctor can facilitate timely identification of oral cancer symptoms, allowing for prompt detectionand treatment⁶. This, in turn, can lead to improved treatment outcomes and enhanced patient prognosis⁷.

The identification of oral cancer presents significant challenges, primarily due to the nuanced distinctions between malignant and non-malignant tissues. The initial approach to detecting oral cancer involves a visual inspection of the oral cavity; however, differentiating between benign and malignant lesions can be quite complex⁸. While biopsy remains the definitive method for diagnosing oral cancer, it is an invasive technique that necessitates tissue collection and subsequent histopathological analysis⁹. Consequently, there is a pressing demand for non-invasive and dependable techniques to facilitate the early detection of oral cancer¹⁰.

Literature review

Recent developments in medical imaging and computer-aided detection(CAD) technologies have demonstrated encouraging outcomes in the identification of oral cancer. CAD systems use computer algorithms to inspect medical images and identify irregularities, including tumors and lesions. Convolutional Neural Networks (CNNs), a form of deep learning algorithm, have gained significant traction in the realm of medical image analysis, particularly for oral cancer detection. These networks can autonomously learn features from images, thereby removing the necessity for manual feature extraction and enhancing diagnostic precision¹¹.

Jeyaraj and Samuel Nadar¹² made a deep learning optimizer for computer-assisted oral cancer detectionby utilizing hyperspectral images of patients. In order to check the validation suggested model, the efficacy of the suggested model has been compared with other models. A framework of partitioned deep CNN (Convolutional Neural Network) with 2 partitioned layers has been has been classified through labeling interest area within hyperspectral image with several dimensions. In fact, the suggested model’s efficacy in categorization were 0.91, 0.94, and 91.4% for specificity, sensitivity, and accuracy for benign tumor. Moreover, the model could achieve the accuracy value of 94.5 for classifying the cancerous tumor with normal tissue.

Xu et al.¹³ a 3DCNNs-based image processing optimizer was developed for the early detection of oral cancer, and it was contrasted with a 2DCNNs-based optimizer. These two models were made by the use of the identical framework to classify oral tumors into malignant and benign. The outcomes represented that the 3DCNNs with dynamic attributes of the improvement rate image outperformed 2DCNNS that had single improvement sequence. It was revealed that 3DCNNs could achieve good results but need some more improvements to achieve better results, robustness, and high accuracy.

Warin et al.¹⁴ developed an automatic categorization and detectionmodel of oral cancer by the utility of CNN (Convolutional Neural Network). there existed 700 images relevant to oral cancer, which have been gathered in a retrospective manner from maxillofacial and oral center, each with 350 images for normal oral mucosa and oral squamous cell carcinoma respectively. The detection and classification accuracy was developed by the use of faster R-CNN and DenseNet121. It could be seen that DenseNet121 accomplished the value of 99%, 100%, 98.75%, 99%100%, and 99% for an area under the receiver operating characteristic curve specificity, sensitivity, F1-score, recall, and precision. In addition, R-CNN model gain the values of 0.79, 79.31%, 82.14%, 76.67%, for an area under the precision-recall curve, F1-score, recall, and precision.

Huang et al.³ aimed to prepare an accurate tool for cancer diagnosis. To do so, a methodology was employed in which a deep learning was developed on the basis metaheuristic method. Initially, three diverse preprocessing approaches, namely data augmentation, noise reduction, and Gamma correction, were employed to raise the number of images and improve their quality. The weights of the network have been chosen by ISSA (Improved Squirrel Search Algorithm) in an optimal manner with the purpose of providing better accuracy. The developed approach was employed in a standard benchmark dataset, called “Oral Cancer image dataset”. After that, a comparison was made between the suggested model and the other models mentioned in that study. In the end, it was represented that the suggested model could gain better result in comparison with the ones mentioned in the study.

Welikala et al.¹⁵ aimed to integrate bounding box annotations by the use of a kind of deep neural network. Actually, deep neural networks were employed to make automatic models, and complicated patterns were taken to address the task in the networks. Two diverse computer vision methods, ResNet-101 for image classification and Faster R-CNN for object detection, on the basis of deep learning were evaluated for the automatic detectionand categorization of oral cancers. This was conducted to detect oral cancer earlier. The F1-score value of images classification by ResNet-101 for recognition of images that had lesions was 87.07, and its value for recognition images that needed referral was 78.30. However, the F1-score value of object detection by Faster R-CNN for detectionof lesions that needed referral was 41.18. it was revealed that this model could, to some extent, address the challenges faced in this tasks; however, it needs some remedies to achieve better results.

Research gaps

Currently, few existing studies have focused on the application of deep learning techniques, specifically Convolutional Neural Networks (CNNs), of oral cancer detectionmilestones and many issues lacked. One of the main gaps is that the current models are not robust enough due to their training datasets being limited in size and diversity. Automatic hierarchical feature extraction of highly varying input from this process however takes considerable time and effort, and requires a substantial amount of annotated data which CNNs can substantially accelerate; alone, it provides motivation for using CNNs due to the fact that feature extraction can otherwise be time consuming and costly or subject to human error. Another gap is very few attention has been made on the optimization of the architecture of the CNN models using metaheuristic optimization algorithms.

Furthermore, current models raise overfitting and underfitting problems that can be solved via data augmentation/preprocessing. This proposed research addresses these gaps by presenting a significant and optimized CNN model for oral cancer recognition through preprocessing, data augmentation, and metaheuristic optimization.

Objectives and motivations

The main purpose in this study is to create a solid and reliable convolution neural network (CNN) approach that can directly implement procedures, enhancing oral cancer detection, based on preprocessing, data augmentation, metaheuristic optimization. This research is motivated by the need for more accurate and dependable diagnostics that is vital for successful treatment and patient prognosis, specifically for oral cancer.

The introduced model is an attempt to automate the feature extraction process and minimize manual intervention, while achieving an optimization in the overall performance of the detectionsystem. Here, used Vanilla CNN since it is widely used in a variety of image classification tasks due to its simplicity and its effectiveness. Nonetheless, its efficiency can be highly improved by using optimization techniques like metaheuristics. This study uses an Improved version of Artificial Protozoa Optimizer (IAPO) to increase the robustness and generalizability of the model. indeed, Vanilla CNN and IAPO combined can provide a new insight to oral cancer, improving population-based oral cancer detection. It is also driven by the research gaps found in the literature, as current works have not discussed extensively about metaheuristic optimization algorithms to enhance performances, and while some models do exist, they are not robust enough.

Advantages in clinical practice

Some advantages of adopting this proposed system in clinical practice is:

Early Detection: The system is capable of identifying oral cancer lesions early, which can greatly enhance treatment outcomes and patient survival rates.

Non-invasive: It employs imaging techniques like optical coherence tomography (OCT) or intraoral cameras to capture images of the oral cavity, which decreases the need for invasive biopsy procedures and lessens the discomfort experienced by patients.

Real Time Detection: The system provides real-time detectionthat helps the clinicians to make an immediate decision for the treatment and minimize the time period between detectionand treatment.

Higher Precision: The system’s deep learning algorithm can accurately analyze images, which would reduce false positives or false negatives and enhance diagonal correctness.

Reducing the cost of oral cancer detection and treatment since it will minimize the invasive procedures, decrease unnecessary biopsy, and enhance the treatment outcomes.

Wider Reach: The system can be deployed in remote or underserved locations, enabling access to oral cancer detectionand treatment to patients who lack access to specialized care.

Improved Patient Experience: The system may offer patients a more comfortable and convenient diagnostic experience that minimizes anxiety and enhances overall satisfaction with care.

Research questions

The main research questions to be addressed by the proposed research are: (1) Is it possible to optimize a CNN model using the IAPO metaheuristic algorithm, aimed at enhancing the model’s performance in oral cancer detection? Preprocessing and Data Augmentation Here, you have to provide pre-process of your input images, and you have to describe the effects of these images on the scores/results of your model (3) Is the proposed model able to outperform literature models in terms of accuracy and reliability? (4) The key components that influence the system performance, and how to optimize them to achieve better performance? (5) How applicable is the proposed model or approach to diagnose any other type of cancer, along with the limitations and challenges in doing so? This enhances the form of methodologies toward the efficient and precise CNN models for oral cancer detectionand broaden the knowledge in this research field.

Dataset description

The utilized dataset in this research was sourced from Kaggle, a well-known platform for data science and machine learning¹⁶. It comprises 548 images of oral cancer, gathered from various hospitals and medical institutions, and is divided into two categories: normal and cancerous. The normal category includes 260 images, while the cancerous category contains 288 images. All images are in JPEG format and vary in size, ranging from 384 × 384 to 1024 × 768 pixels.

Each image is labeled with a binary indicator that specifies whether it depicts healthy or cancerous tissue. The labeling system assigns a ‘0’ to normal images and a ‘1’ to those with oral cancer, which simplifies the classification process for machine learning algorithms.

Importantly, the dataset features images from two main areas of the oral cavity: the lips and the tongue. Specifically, 320 images focus on the lip regions, while 228 images highlight the tongue. This distribution allows for an investigation into potential differences in the manifestation of oral cancer between these two locations. Additionally, the varied geographical origins of the samples contribute to the broader applicability of the findings across different populations. The Dataset is Overviewed in Table 1.

Table 1 The dataset overview.

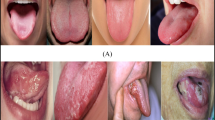
Figure 1 illustrates the Oral Cancer (OCI) dataset, including a diverse collection of sample images representing both cancerous and non-cancerous conditions.

Fig. 1

Some samples of the OCI dataset.

The images have been randomly chosen from the dataset to demonstrate the diversity in the appearance and features of oral cancer lesions.

In this study, ground truth was determined through a painstaking process whereby an experienced team of oral pathologists and radiologists manually reviewed and annotated the images, ensuring that images identified as cancer were in fact oral cancerous lesions (predominantly Squamous Cell Carcinoma [SCC]), the most common type of oral cancer. The authors ensured that the images included in the dataset were correctly labeled as cancerous or not cancerous (ground truth) by using a combination of clinical, radiological, and histopathological information, including biopsy reports and medical histories that included imaging modalities, and by maintaining the ground truth through a consensus approach to minimize errors between a variety of experts who reviewed the original and annotated data sets, forming a ground truth that would be used to train and evaluate the deep learning model.

Image preprocessing

This paper focus on one integral part of preparing medical images for applications of analyses called preprocessing. We used three main techniques in this study including resizing, normalizing and augmentation. Essentially, these techniques help in improving the quality and diversity of the images, which ultimately improves the predictive power for detection. Each of resizing, normalization, and augmentation techniques contribute to the quality of the images in its own right. This is because before going into an analysis phase, it always helps to standardize the images, ensuring that they all have the same size and thus, making it easier to analyze and compare them. Normalizing the image data helps to reduce the effect of varying lighting conditions and increases the contrast of the images. This step increases the number of images by applying random transformations (for example, rotating, flipping, and cropping), thus reducing overfitting and helping the model to generalize. In the following, more details are given for each technique.

Image resizing

Image resizing serves as a significant preprocessing step in image processing and analysis, particularly in the detectionof oral cancer. It is imperative to standardize the size of all images to ensure consistency. This standardization is crucial for multiple reasons, including the reduction of computational complexity; images of differing sizes can complicate computations, thereby hindering the analysis process. In contrast, resizing images to a consistent dimension enhances the speed and efficiency of the analysis.

Moreover, machine learning models necessitate uniformly sized images to learn and generalize effectively. By resizing images, the model can better identify features and patterns, ultimately leading to enhanced performance. Additionally, uniform image sizes facilitate accurate comparisons, which are essential in oral cancer detection, enabling clinicians to detect subtle changes and patterns indicative of cancer. In this study, the bilinear interpolation method is employed to resize images to a standard dimension of 256 × 256 pixels, a widely recognized technique that maintains image quality while minimizing information loss. Figure 2 shows a sample example of this preprocessing stage.

Fig. 2

Sample example of image resizing.

The original image is presented on the left, whereas the resized version is located on the right, illustrating the changes that take place through the application of the bilinear interpolation technique. The resized image has been adjusted to a uniform size of 256 × 256 pixels and appears to retain its initial quality, exhibiting only a slight loss of information.

This preservation of the image’s key features and patterns is important. Consequently, this resized image can be effectively employed in the analytical process, allowing machine learning models to learn and generalize with greater precision, and enabling accurate comparisons with other images, which is essential for diagnosing oral cancer.

Image normalization

Image normalization represents a critical preprocessing step in image processing and analysis, particularly relevant to the detectionof oral cancer. This procedure is energetic for mitigating the effects of discrepancies in image acquisition and enhancing the model’s robustness. It entails adjusting the pixel values of an image to a predetermined range, commonly between 0 and 1. This adjustment yields several significant advantages, such as diminishing the influence of variations in image acquisition, including differences in intensity ranges that may compromise model performance, and bolstering model robustness by lessening the effects of outliers and noise.

Furthermore, normalizing images facilitates improved feature extraction by minimizing the impact of intensity variations, leading to more consistent and dependable features. By scaling pixel values to a defined range, the model can more effectively learn features and patterns, exhibiting reduced sensitivity to data variations. In this research, the Min-Max normalization technique is utilized, a widely recognized and efficient method, to adjust the images to a range of 0 to 1, thereby maintaining image quality while minimizing information loss. The Min-Max normalization technique is articulated in the following manner:

$$\:Normalized\:pixel\:value=\frac{OPV-MPV}{MaPV-MPV}$$

(1)

.

where, OPV denotes the initial pixel value, MPV indicates the lowest pixel value present in the image, and $\:MaPV$ signifies the highest pixel value found in the image.

By applying the Min-Max normalization technique to the images, we successfully mitigated the effects of variations in image acquisition, thereby enhancing the model’s robustness. Figure 3 shows a sample example of image normalization.

Fig. 3

Sample example of image normalization.

The illustration depicts the changes that take place when the Min-Max normalization technique is utilized on an image, adjusting the pixel values to a range between 0 and 1. The resulting normalized image exhibits a more uniform and consistent intensity distribution, with diminished fluctuations in brightness and contrast, thereby rendering it more appropriate for subsequent analysis and feature extraction. By applying normalization, the influence of variations in image acquisition and noise is mitigated, enabling the model to concentrate on the essential features and patterns pertinent to oral cancer detection. The example presented in Fig. 3 underscores the efficacy of the Min-Max normalization method in improving image quality and preparing the image for further processing and analysis.

Data augmentation

Data augmentation is a method employed to artificially expand the training dataset by implementing various transformations on the existing images. This approach enhances the diversity of the dataset, mitigates the risk of overfitting, and strengthens the resilience of the convolutional neural network (CNN) model. In this research, we utilized the following data augmentation techniques:

• 1. Rotation: Rotating images by 90, 180, and 270 degrees.

• 2. Flipping: Flipping images both horizontally and vertically.

• 3. Scaling: Adjusting the size of images to 0.5, 1.5, and 2 times the original dimensions.

• 4. Translation: Shifting images by 10% of their dimensions in both the x and y axes.

• 5. Color jittering: Introducing random variations in brightness, contrast, and saturation of the images.

These transformations can be mathematically expressed as follows. Let $\:I(x,\:y)$ be the original image. we have:

$$\:{I}_{R}\left(x,\:y\right)=I\left(x\:cos\left(\theta\:\right)-y\:sin\left(\theta\:\right),\:x\:sin\left(\theta\:\right)+y\:cos\left(\theta\:\right)\right),\:{\uptheta\:}=90,\:180,\:270$$

(2)

$$\:{I}_{F}^{h}\left(x,\:y\right)=I(x,\:-y)$$

(3)

$$\:{I}_{F}^{v}\left(x,\:y\right)=I(-x,y)$$

(4)

$$\:{I}_{sc}=I\left(\frac{x}{s},\frac{y}{s}\right),\:s=0.5,\:15,\:2$$

(5)

$$\:{I}_{Tr}=I\left(x\:+\:{t}_{x},\:y\:+\:{t}_{y}\right),\:{t}_{x},\:{t}_{y}\:\left(translation\:amount\right)=10\%\:of\:image\:size$$

(6)

$$\:{I}_{Cj}\left(x,\:y\right)=I\left(x,\:y\right)+\sigma\:*N\left(0,\:1\right),\:\sigma\:\in\:gaussian\:noise(0.1,\:0.2,\:0.3),\:N\left(\text{0,1}\right)=rand$$

(7)

.

where, $\:{I}_{R}$, $\:{I}_{F}^{h}$, $\:{I}_{F}^{v}$, $\:{I}_{sc}$, and $\:{I}_{Cj}$ represent the rotated image, the flipped image, the scaled image, the translated image, and the color jittered image, respectively. Figure 4 shows some sample examples of images augmentation.

Fig. 4

Some sample examples of images augmentation.

The illustration presents a range of transformations applied to the initial images, encompassing rotation, flipping, scaling, and various other alterations. This process yields a collection of augmented images that exhibit notable differences from the originals. These augmented images serve to expand the dataset, thereby mitigating the risk of overfitting and enhancing the model’s capacity to generalize to novel, unseen data.

By incorporating random variations in the images, such as modifications in orientation, size, and perspective, the model is prompted to learn more robust and invariant features, ultimately resulting in improved performance in the detectionof oral cancer. The examples depicted in Fig. 4 highlight the efficacy of image augmentation in creating a more diverse and representative dataset, which is crucial for training a dependable and precise deep learning model.

Vanilla convolutional neural networks

While some advanced frameworks, such as U-Net and ResNet, are commonly utilized in medical image analysis, the usage of CNN for brain tumor categorization has attained much attention. This network has simpler designs and suggests benefits regarding computational and interpretability efficacy. The research displayed the efficiency of a Vanilla CNN in brain tumor classification that that assists in exploration of less complicated frameworks¹⁷. This architecture is simple when compared to advanced models like U-Net and ResNet, but Vanilla CNN works just as well for an image classification task. It is easier to be trained and deployed, whereas its interpretability makes it a more convincing candidate for medical imaging tasks. Although U-Net and ResNet produce state-of-the-art results in a wide variety of image classification tasks, Vanilla CNN can be fine-tuned using several strategies to achieve competitive performance, making it a more accessible choice for researchers and industry professionals¹⁸. Vanilla Neural Networks have been considered an extension for linear regression supervised optimizer. Figure 5 shows the block diagram of the Vanilla CNN.

Fig. 5

The block diagram of the Vanilla CNN.

Vanilla neural networks are akin to other linear regression models but vary in the hidden layers, which play a crucial role, as all the additional calculations in these models occur in the hidden layer. The hidden layer has been represented via $\:H$, comprising three neurons ($\:{H}_{0}$, $\:{H}_{1}$, and $\:{H}_{2}$), and any quantity of neurons are included within the hidden layers. The backpropagation optimizer is implemented in this optimizer with the presence of hidden layers.

The suggested methodology

The Convolutional Neural Network has become highly popular in diverse application pertinent to medical image processing, especially in segmentation and categorization of oral cancer images. In the current article, a novel CNN framework has been suggested to categorize oral cancer.

In the present article, a basic CNN has been established, and it has been utilized for extracting augmented images with batch size of 64, RGB Color channels, and input size of 256 × 256. The essential feature has been chosen while employing 4 convolutional layers. The filters with the size of $\:4\times\:4$ have been utilized in convolutional layers, and $\:4\times\:4$ have been utilized in the pooling layers.

An uncertain quantity of filters has been employed for diagnosing lines, corners, edges. After that, a max-pooling layer has been employed in the image to generate the most completed summary. In the end, a 256-neuron fully connected dense layer has been merged with an output layer of SoftMax for computation of the possibility score for all the classes. Also, another purpose is to categorize the eventual decision labels as No or Yes, all of which depend on condition that if input image involves cancer.

Convolution layer

The current layer has been considered the most considerable and key element of this network. There are myriad pooling layers, fully connected layers, and convolutional layers in fundamental framework of CNN. The goal convolution layer is to find the attributes of present layer that refer to diverse types of the local links.

Non-linearity layer

The next layer in the network has been considered the non-linearity layer, which enhances the CNN’s fitting ability by introducing non-linear elements. Various activation functions, such as leaky ReLU, ELU, Sigmoid, and ReLU, are utilized for this purpose. The leaky ReLU has been selected as the activation function, was made to assess the learning speed and categorization performance of CNN.

This activation functions have special advantages over other activation functions, such as follows: it particularly avoids saturation and therefore can better learn and represent larger input values, in contrast to activation functions like sigmoid and tanh, which saturate when fed larger values, hence losing the ability to generalize to inputs larger than a certain value.

Moreover, Leaky ReLU is fast to compute; it is just a thresholding step that is more fast than computing other activations, such as softmax and swish.

In addition, Leaky ReLU mitigates the risk of the dying ReLU phenomenon, where neurons become inactive during the training process because the ReLU activation function returns zero for negative inputs, by permitting a tiny percentage of the input to be transmitted, even if the input is negative, which maintains a steady flow of gradient and stops neurons from becoming inactive. The ReLU activation function is demonstrated in Eq. (8).

$$\:f\left(x\right)=\left\{\begin{array}{c}0.01x\:for\:x<0\\\:x\:for\:x\ge\:0\:\:\:\:\:\:\:\:\end{array}\right.$$

(8)

.

where $\:x$ represents the value of input.

The pooling layer has the responsibility of integrating relevant attributes to decrease the accuracy of feature maps. The feature maps’ dimension has been decreased within the recommended network by utilizing MaxPooling procedure, which has been considered simple to utilize and produce the finest outcomes.

The Vanilla CNN architecture used in this study consists of layers that are purpose-built to analyze oral cancer images, including convolutional layers that identify low-level features of the images such as edges and textures, max-pooling layers that reduce the spatial dimensions of the feature maps while preserving relevant details, flatten layers that reshape the 2D feature maps into 1D vectors to connect to fully connected layers, and dense layers that classify images as either cancerous or not with the output layer utilizing a Softmax activation to give a probability distribution of the two classes, which enables the model to learn complex relationships in oral cancer images and provide accurate predictions; this allows for a reliable and precise identification of oral cancer through image analysis.

Fully connected (FC) layer

The fully connected (FC) layer tends to work with a compressed input; it represents that the inputs get attached to the neurons. At the end of the model, this layer has been employed. This layer flattens the former layer’s output since the attributes has to have data with one dimension prior to training with the categorizer. The quantity of classes used determines the fixed output when it is utilized as the final layer.

Improved Artificial Protozoa Optimizer

In the present section, the Artificial Protozoa Optimization (APO) algorithm has been explained, and its inspiration has been elaborated. Then, the mathematical models have been suggested. In the end, it has been explained that how this optimizer has been comprehensively analyzed.

Inspiration

Diverse biological phenomena studies represent diverse benefits existing within microorganisms. Algae, protozoa, bacteria in microorganisms implement functions similar to the organs that have discovered in higher animals and plants; these have been achieved by several particular organizations called “organelles”. The current microorganisms represent several important characteristics of life, comprising adaptation to environmental stimuli, variability, genetic continuity, reproduction, and metabolism¹⁹. The microorganisms have been commonly employed more efficaciously in comparison with other higher organisms due to their low complexity and simpler organization.

In the current study, each protozoan represents euglena in flagellates. The word “euglena” originates from a Greek word that means “eyeball organism”. This has been considered a single-celled protozoan or “algal flagellate”. There are myriad euglenas; however, only 250 of them have been recognized. The diverse species of euglenas live fresh water, and they usually make fertile blooms in ditches and ponds. The plentiful growth of these individuals leaves a red or green color in the surface of water. The size of the euglenas ranges from 15 to 500$\:\:\mu\:m$; moreover, considering their shape, they can differ from almost cylindrical to almost spherical. Most kinds of euglenas are green, since there exist chlorophyll a and b within their chloroplasts.

The famous organelles of a spindle-shaped euglena contain photoreceptor, mitochondria, chloroplasts, contractile vacuole, stigma (eyespot), nucleus, endoplasmic reticulum, stored carbohydrate, pellicles, Golgi apparatus, flagellum. There are 2 flagella in euglena that have been rooted in its basal body. One flagellum is short and is not extended from the cell, whereas the other is long enough to be extended from the pharynx or “gullet”. The euglena executes spiral movements through “flapping” the long flagellum.

Remarkably, all euglenas have the features of animal and plant. It means that it can receive the food for survival by serving as a heterotrophic (organic substance) or autotrophic (mineral). Once euglenas are not in favorable situation, they form a shelter around themselves like a cyst. Then, these individuals become inactive and hidden (dormant) by the time their environment gets enhanced. For production of offsprings, these individuals get reproduced by asexual breeding by the binary fission procedure. it means that these individuals get split into 2 individuals by cell and longitudinal division. The euglenas are utilized for ecological biomediation and can exhibit considerable capacity to be used in biomedicine field.

Firstly, euglena represent health of environment and can evaluate quality of water. It significantly resists against heavy metals and can help remediate water contaminated by radioactive substances. Additionally, euglena has a toxin known as euglenophycin, which has anticancer properties. It also provides single-cell proteins and is utilized in various medications, including those for hypertension, gout, and liver cancer. Ultimately, it has represented that this individual can be used in diverse commercial good, namely cosmetics, food preservatives, and dietary supplements. Reproductive, dormancy, and foraging manners of these candidates have been mathematically represented subsequently.

Foraging

The euglenas can achieve important nourishments to survive by the use of heterotrophic and autotrophic mechanisms. This candidate does photosynthesis like other plants by the use of chloroplasts in order to generate carbohydrates to fulfill their energy. Phototaxis has been considered a response that euglena represents against light; this manner can help this individual get wat from or go toward light. The light phenomenon has been regarded as the foundation of phototaxis. This candidate has an organelle called the eyespot, comprising carotenoid color granules.

It should be noted that the eyespot is not sensitive to the lights; moreover, it filters sunlight and permits some particular light wavelengths to get to photoreceptor in flagellum. When the irradiance is low, the candidates swim in a spiral manner to the source of light. On the other hand, when the proportion of irradiance is high, the candidates get far from the source of light to avoid damaging chloroplasts and pigments. When the threshold is in the range [10, 100] W∕m², the individuals can switch from positive to negative phototaxis. This means that the euglena can orient itself to find the best conditions of light to do photosynthesis.

Euglena displays positive phototaxis in conditions of low light and negative phototaxis when exposed to intense light. This behavior leads it to be gathered in favorable environments to survive. In the absence of light, euglena acts like an animal by taking in organic material via phagocytosis, comprising elements such as peptone, carbohydrates, beef extract, and acetate. Unlike other plant cells, euglena does not possess a severe cellulose wall. As an alternative, it has a flexible pellicle that can easily change shape. By the use of osmotrophy, euglena is capable of absorbing nourishments directly from its surroundings.

Dormancy

Each organism stays alive in diverse manners being exposed to various stresses, like temperature changes, lack of food, and environmental pollution.

Certain animals migrate to alleviate pressures of environment, while others change their biological manners to evade unfavorable locations. When faced with challenging situations, euglena capable of spraying mucus beneath its surface, creating a protecting mucilaginous capsule known as a cyst. Within the current stage, the euglenas enter a situation of suspended animation, or dormancy, by the time the surrounding circumstances improve. The unique cell changes to spherical, elliptical, and ovoid forms, with its flagella vanishing. All the individuals change their position to non-motile mucus colony, although they were first in unicellular motile organism. In this state of suspended state, the euglena’s metabolism decreases, leading to conservation of energy and a diminished dependence on the external environment. Dormancy has been considered an adaptive feature of the individuals that allows it to efficiently react to stress caused by environment.

Reproduction

There is a kind of asexual breeding called binary fission, which has been represented by the euglenas. In the present stage, each individual is divided into 2 equal candidates. In fact, there is a condition for the euglenas to reproduce, which is the temperature should range from 20 to 35 ℃ and it should not surpass the criteria. The mitosis of the individual nucleus is the initial stage of binary fission, which comprises the replication of stigma, esophagus, and flagellum. Then, the splitting occurs with the longitudinal axis of the cell. Initially, a split happens within the visible part; moreover, there is another kind of split called V-shaped that moves to the invisible part by the time two halved have been thoroughly divided.

Mathematical models

Within the current subsection, the algorithm that is to solve the issues of minimization has been suggested. It is of utmost importance to represent solution set of the optimization algorithms. In the suggested optimizer, the protozoa have acted as the set of solution, and each individual of protozoan has situation with $\:dim$ parameters.

Foraging

It has been mentioned that protozoa can generate carbohydrates by the use of chloroplasts to prepare nourishment.

When a protozoan encounters a high intensity of light, it will change its situation to an area with reduced light intensity. However, if it finds itself in a region with less light intensity, the opposite occurs. If the intensity of light surrounding the individual $\:j$ is appropriate for photosynthesis, the individual moves to the situation of the individual $\:j$. For the autotrophic process, the subsequent formulas have been presented:

$$\:{X}_{i}^{new}={X}_{i}+f\times\:({X}_{j}-{X}_{i}+\frac{1}{np}\times\:\sum\:_{k=1}^{np}{w}_{a}\times\:\left({X}_{k-}-{X}_{k+}\right))\odot\:{M}_{f}$$

(9)

$$\:{X}_{i}=[{x}_{i}^{1},\:{x}_{i}^{2},\:.\:.\:.,\:{x}_{i}^{dim},\:\:\:\:\:\:\:\:\:\:{X}_{i}=sort({X}_{i})$$

(10)

$$\:f=rand\times\:(1+\text{cos}(\frac{iter}{ite{r}_{max}}\times\:\pi\:))$$

(11)

$$\:n{p}_{max}=\left\lfloor \frac{ps-1}{2} \right\rfloor$$

(12)

$$\:{w}_{a}=e-\left|\frac{f\left({X}_{k-}\right)}{f\left({X}_{k+}\right)+eps}\right|$$

(13)

$$\:{M}_{f}\left[di\right]=\left\{\begin{array}{l}1,\:\:\:\:di\; \text{is}\: \text{in}\:randperm\left(dim,\:\:\:\left\lceil dim\times\:\frac{i}{ps}\right\rceil \right)\\\:0,\:\:\:\:\:otherwise\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\end{array}\right.$$

(14)

where, the initial situation and the enhanced situation of the individual $\:i$ have been, in turn, represented by $\:{X}_{i}$ and $\:{X}_{i}^{new}$. The stochastically selected individual $\:j$ has been illustrated by $\:{X}_{j}$. The stochastically selected individual within the paired neighbor $\:k$ has been demonstrated by $\:{X}_{k-}$ that its rank index has been considered lower than $\:i$. Particularly, if $\:{X}_{i}$ has been considered $\:{X}_{1}$, then $\:{X}_{k-}$ has been set to $\:{X}_{1}$. A stochastically selected individual within paired neighbor $\:k$ has been signified by $\:{X}_{k+}$, and its rank index has been larger than $\:i$.

Generally, if $\:{X}_{i}$ has been considered $\:{X}_{ps}$, $\:{X}_{k+}$ has been set to $\:{X}_{ps}$; the size of population has been displayed via $\:ps$. A factor of foraging has been depicted via $\:f$, and a random quantity has been signified by $\:rand$ that is between 0 and 1. The highest and the present quantity of iterations have been, in turn, demonstrated through $\:ite{r}_{max}$ and $\:iter$. The quantity of neighbor pairs amid the exterior factors has been indicated via $\:np$, and the highest value of $\:np$ has been denoted by $\:n{p}_{max}$. $\:eps\:(2.2204e-16)$ has been considered a considerably small quantity, the factor of weight within autotrophic mode has been demonstrated by $\:wa$, the Hadamard product has been depicted through $\:\odot\:$, and the mapping vector of foraging has been indicated via $\:{M}_{f}$ that its size is $\:(1\:\times\:\:dim)$ and has the value of 0 and 1. The dimensional index has been demonstrated by $\:di$ that includes $\:[\text{1,2},\:.\:.\:.\:,\:dim]$.

When there is no light, protozoa gain nourishment by absorbing organic substance from their environment. The protozoa move to the finest nourishment situation that has been demonstrated by $\:{X}_{near}$. Considering heterotrophic approach, the subsequent formulas have been mathematically demonstrated:

$$\:{X}_{i}^{new}={X}_{i}+f\times\:({X}_{near}-{X}_{i}+\frac{1}{np}\times\:\sum\:_{k=1}^{np}wh\times\:({X}_{i-k}-{X}_{i+k}))\odot\:{M}_{f}$$

(15)

$$\:{X}_{near}=\left(1\pm\:rand\times\:\left(1-\frac{iter}{ite{r}_{max}}\right)\right)\odot\:{X}_{i}$$

(16)

$$\:{w}_{h}={e}^{-\left|\frac{f\left({X}_{i-k}\right)}{f\left({X}_{i+k}\right)+eps}\right|}$$

(17)

$$\:Rand=\left[ran{d}_{1},\:ran{d}_{2},\:.\:.\:.\:,\:ran{d}_{dim}\right]$$

(18)

.

where, the adjacent situation has been represented by $\:{X}_{near}$, it has been implied by “$\:\pm\:$” that $\:{X}_{near}$ is within diverse directions from the individual $\:i$. The individual ($\:i-k$) chosen from the paired neighbor $\:k$ has been represented via $\:{X}_{i-k}$, and its index of rank has been found to be $\:i-k$. In addition, if $\:{X}_{i}$ has been considered $\:{X}_{1}$, then $\:{X}_{i-k}$ has been set to $\:{X}_{1}$.

The individual $\:(i\:+\:k)$ chosen from the paired neighbor $\:k$ has been represented by $\:{X}_{i+k}$, and its rand index has been represented by $\:i+k$. If $\:{X}_{i}$ has been considered $\:{X}_{ps}$, $\:{X}_{i+k}$ has been set to $\:{X}_{ps}$. The factor of weight within heterotrophic state has been represented through $\:{w}_{h}$, and random vectors between 0 and 1 has been illustrated via $\:Rand$.

Dormancy

Within environmental stress, protozoa might adjust manner as a survival technique to tolerate disapproving circumstances. Once the protozoa are inactive, they are substituted by a recently produced individual to preserve a consistent population. This concept has been calculated in the following manner:

$$\:{X}_{i}^{new}={X}_{min}+Rand\odot\:({X}_{max}-{X}_{min})$$

(19)

$$\:{X}_{min}=\left[l{b}_{1},\:l{b}_{2},\:.\:.\:.\:,\:l{b}_{dim}\right],\:\:\:\:\:\:\:\:\:\:\:\:{X}_{max}=[u{b}_{1},\:u{b}_{2},\:.\:.\:.\:,\:u{b}_{dim}]$$

(20)

.

where, the higher and lower bound vectors have been, in turn, demonstrated via $\:{X}_{max}$ and $\:{X}_{min}$. The higher and lower bounds of parameter $\:di$ have been, in turn, indicated via $\:u{b}_{di}$ and $\:l{b}_{di}$.

Reproduction

At a suitable level of health and age, each individual replicates asexual breeding through a process called binary fission. In theory, this type of breeding makes each individual divides into two equal daughters. This behavior has been mimicked by creating a duplicate individual and taking into account a perturbation. The current stage has been explained subsequently:

$$\:{X}_{i}^{new}={X}_{i}\pm\:rand\times\:\left({X}_{min}+Rand\odot\:\left({X}_{max}-{X}_{min}\right)\right)\odot\:{M}_{r}$$

(21)

$$\:{M}_{r}\left[di\right]=\left\{\begin{array}{c}1,\:if\:di\:is\:in\:randperm\left(dim,\:\left\lceil dim\times\:rand \right\rceil \right)\\\:0,\:\:\:\:\:\:\:\:\:\:\:otherwise\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\end{array}\right.$$

(22)

.

where, $\:\pm\:$ represent that the perturbation is reverse and forward. A mapping vector within the procedure of reproduction has been demonstrated via $\:{M}_{r}$ with the size of $\:(1\:\times\:\:dim)$ and with the value of 0 and 1.

Algorithm

All the details relevant to APO have been described in the following. To combine the mathematical models, the variables have been calculated in the subsequent manner:

$$\:pf=p{f}_{max}\times\:rand$$

(23)

$$\:{p}_{ah}=\frac{1}{2}\times\:\left(1+\text{cos}\left(\frac{iter}{ite{r}_{max}}\times\:\pi\:\right)\right)$$

(24)

$$\:{p}_{dr}=\frac{1}{2}\times\:(1+\text{cos}\left(\left(1-\frac{i}{ps}\times\:\right)\right)$$

(25)

.

where, the dormancy’s proportion of reproduction and fraction has been represented via $\:pf$, the highest value of $\:pf$ has been demonstrated via $\:p{f}_{max}$, the probabilities of heterotrophic and autotrophic manners have been illustrated by $\:{p}_{ah}$, and the probabilities of reproduction and dormancy have been depicted via $\:{p}_{dr}$.

It should be noted that the suggested algorithm has merely two extraordinary variables, including $\:p{f}_{max\:}$ (the highest proportion of fraction) and $\:np$ (the quantity of neighbor pairs).

Improved mechanism

The Artificial Protozoa Optimizer (APO) has demonstrated encouraging outcomes in addressing optimization challenges. Nevertheless, opportunities for enhancement remain. In this section, we introduce an improved iteration of the APO algorithm, which integrates novel mechanisms aimed at improving its efficiency and overall effectiveness.

• Improved Foraging Mechanism.

  The original APO algorithm employs a straightforward foraging mechanism, wherein the protozoa navigate towards the most optimal solution or the closest neighbor. To enhance this approach, a novel foraging mechanism has been proposed that integrates a more effective search strategy. This enhanced foraging mechanism uses a combination of two distinct search strategies:

  • 1. Exploitation: The protozoa advance towards the most optimal solution, akin to the original APO algorithm.

  • 2. Exploration: The protozoa engage in a random walk within the search space to investigate new regions.

  The likelihood of transitioning between these two strategies is governed by a newly introduced parameter, $\:{p}_{explore}$. The refined foraging mechanism can be expressed mathematically as follows:

  $$\:{X}_{i}^{new}={X}_{i}+f\times\:({X}_{j}-{X}_{i}+\frac{1}{np}\times\:\sum\:_{k=1}^{np}{w}_{a}\times\:\left({X}_{k-}-{X}_{k+}\right))\odot\:{M}_{f}$$

  (26)

  where, $\:{X}_{j}$ is the best-known solution, and $\:{X}_{k-}$ and $\:{X}_{k+}$ are the nearest neighbors.

  The probability of switching to the exploration strategy is given by:

  $$\:{p}_{explore}=1-(1-{p}_{explor{e}_{max}})\:\times\:\:\left(1\:-\frac{iter}{ite{r}_{max}}\right)$$

  (27)

  where, $\:{p}_{explor{e}_{max}}$ is the maximum probability of exploration.

• Improved Dormancy Mechanism

  The original APO algorithm employs a straightforward dormancy mechanism, wherein the protozoa enter an inactive state and are subsequently supplanted by a new individual. To enhance this process, we propose a novel dormancy mechanism that offers a more effective method for population preservation. This enhanced dormancy mechanism integrates two strategies:

  • 1. Reactivation: Inactive protozoa are reactivated after a predetermined number of iterations, enabling their reintegration into the search process.

  • 2. Replacement: Inactive protozoa are substituted with a new individual, akin to the approach utilized in the original APO algorithm.

  The likelihood of transitioning between these two strategies is governed by a newly introduced parameter, $\:{p}_{reactivate}$. The refined dormancy mechanism can be expressed mathematically as:

  $$\:{X}_{i}^{new}={X}_{min}+Rand\odot\:({X}_{max}-{X}_{min})$$

  (28)

  The probability of reactivating an inactive protozoa is given by:

  $$\:{p}_{reactivate}=1-\left(1-{p}_{reactivat{e}_{max}}\right)\times\:\left(1-\frac{iter}{ite{r}_{max}}\right)$$

  (29)

  where, $\:{p}_{reactivat{e}_{max}}$ is the maximum probability of reactivation.

• Improved Reproduction Mechanism

  Like before, the improved reproduction mechanism uses a combination of two strategies of:

  • 1. Mutation: The new individual is generated by mutating the parent individual.

  • 2. Crossover: The new individual is generated by combining the genetic material of two parent individuals.

  The likelihood of transitioning between the two strategies is governed by a novel parameter, $\:{p}_{mutate}$. The enhanced reproduction mechanism can be expressed mathematically as follows:

  $$\:{X}_{i}^{new}={X}_{i}\pm\:rand\times\:\left({X}_{min}+Rand\odot\:\left({X}_{max}-{X}_{min}\right)\right)\odot\:{M}_{r}$$

  (30)

  The probability of altering the parent individual is defined by:

  $$\:{p}_{mutate}=1-\left(1-{p}_{mutat{e}_{max}}\right)\times\:\left(1-\frac{iter}{ite{r}_{max}}\right)$$

  (31)

  where, $\:{p}_{mutat{e}_{max}}$ represents the upper limit of the mutation probability.

The improved APO algorithm combines the improved foraging, dormancy, and reproduction mechanisms. The algorithm can be presented as Algorithm 1.

Algorithm 1

The improved APO algorithm.

The improved APO algorithm has several advantages over the original APO algorithm, including:

• Improved exploration-exploitation trade-off.

• More efficient dormancy mechanism.

• More efficient reproduction mechanism.

• Ability to adapt to changing environments.

The improved APO algorithm can be used to solve a wide range of optimization problems, including multi-modal, non-linear, and dynamic problems.

The Vanilla CNN optimization based on IAPO

Regarding deep neural network, diverse optimization approaches has been utilized to reduce the loss the lowest amount via modification of variables, like rates of learning and weights. In the present study, the IAPO algorithm was applied to the Vanilla CNN model in order to fine-tune the model’s weights and learning rate²⁰. IAPO algorithm is inspired by protozoan behavior based foraging behavior in search of food. It so happens that once more we simply iteratively update the values of the models’ parameters in the direction that decreases the validation loss. Here, the objective is to minimize the validation loss of the Vanilla CNN using the IAPO, where:

$$\:{L}_{val}=-\sum\:\left[{y}_{val}\text{log}\left(\frac{\text{exp}\left(z\right)}{\sum\:\left[\text{exp}\left(z\right)\right]}\right)\right]$$

(32)

.

where, $\:{y}_{val}$ defines the true labels, $\:z$ specifies the output of the final layer of the CNN, and $\:{L}_{val}$ specifies the validation loss. The fine-tuning process is based on the following steps:

Step 1) The model weights and learning rate are initialized randomly.

Step 2) The output is obtained by feeding the input data forward through the model.

Step 3) Use Eq. (32) to compute the validation loss.

Step 4) IAPO optimization algorithm is used to update model’s weights and the learning rate to minimize the validation loss.

Step 5) The error is then backpropogated through the model to update the weights.

Step 6) Steps 2–5 until a given number of iterations are done or convergence.

Hyperparameter tuning

To find the optimal hyperparameters for the Vanilla CNN model, we performed a grid search over the following hyperparameters:

• Learning rate: [0.001, 0.01, 0.1]

• Batch size: [32, 64, 128]

• Number of epochs: [50, 100, 200]

• Kernel size: [3, 5, 7].

• Number of filters: [32, 64, 128]

The optimal hyperparameters were found to be:

• Learning rate: 0.01.

• Batch size: 64.

• Number of epochs: 100.

• Kernel size: 5.

• Number of filters: 64.

The results of the experiments are illustrated in Table 2.

Table 2 The results of the experiments.

The results illustrated that the IAPO algorithm is successful in adjustment of the Vanilla CNN model since validation loss decreases in addition to accuracy, precision, recall, and F1-score increases. Using the best hyperparameters, 100 iterations to apply the IAPO algorithm achieved the best results.

Results and discussions

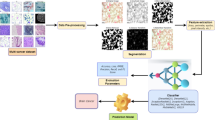
This research introduces an innovative technique for diagnosing oral cancer in concrete by integrating Vanilla convolutional neural networks with an enhanced version of the artificial protozoa optimizer (Vanilla/IAPO). The primary objective of this method is to improve the accuracy and classification of diagnoses, which are essential for evaluating the structural integrity and ensuring the safety of concrete structures. Prior to the application of the proposed Vanilla/IAPO model, the input data from the OCI dataset underwent preprocessing and augmentation to enhance the model’s performance.

The proposed methodology was implemented using MATLAB R2019b, and the experiments were carried out on a laptop featuring an HP Envy x360, powered by an AMD Ryzen 9 4900 H processor and an AMD Radeon RX 6700 M graphics card.

IAPO validation

The IAPO algorithm that has been proposed was rigorously evaluated using ten distinct benchmark functions, encompassing both unimodal and multimodal cases. A comparison was made to assess the performance of this novel algorithm against several established optimization techniques, (Table 3) including the Lévy flight distribution (LFD)²¹, Gaining-Sharing Knowledge-based algorithm (GSK)²², Atom Search Optimization (ASO)²³, Butterfly Optimization Algorithm (BOA)²⁴, and Manta Ray Foraging Optimization (MRFO)²⁵.

Table 3 Algorithm parameter values for the analyzed techniques.

The purpose of this validation was to evaluate the effectiveness of the improved algorithm in pinpointing optimal solutions. Each optimizer was subjected to 10 runs on the functions to evaluate the algorithms’ performance. These runs recorded both the average and standard deviation values to ensure dependable outcomes. The comparative results of the test functions between the proposed IAPO algorithm and the other examined optimizers are presented in Table 4.

Table 4 The comparison results between the proposed IFMO and other examined optimizers.

The validation results of the proposed Improved Artificial Protozoa Optimizer (IAPO) algorithm demonstrate its superiority over several established optimization techniques, including the Lévy flight distribution (LFD), Gaining-Sharing Knowledge-based algorithm (GSK), Atom Search Optimization (ASO), Butterfly Optimization Algorithm (BOA), and Manta Ray Foraging Optimization (MRFO). The results show that IAPO consistently outperforms the other algorithms in finding the optimal solutions for all ten benchmark functions, with an average value of 0 for unimodal functions (f1-f4) and significantly lower average values for multimodal functions (f5-f10).

The standard deviation values also indicate that IAPO has a more stable performance compared to the other algorithms. Notably, IAPO’s average values for f1-f4 are exactly 0, indicating that it can find the global optimum for these functions²⁶. In contrast, the other algorithms struggle to find the optimal solutions, with average values ranging from 0.587604 to 2.3061. Furthermore, IAPO’s standard deviation values are often significantly lower than those of the other algorithms, indicating that it has a more consistent performance. Overall, the results demonstrate the superiority of the proposed IAPO algorithm in optimizing complex functions, making it a promising tool for solving real-world optimization problems.

Measurement indicators

This analysis employs a range of measurement indicators to assess the effectiveness of the suggested approach²⁷. The used metrics include specificity, accuracy, F1 score, precision, sensitivity, and Matthew’s correlation coefficient (MCC). Below, the mathematical formulas for these indicators are presented.

$$\:Specificity=\frac{TN}{TN+FP}\times\:100$$

(33)

$$\:Precision=\frac{TP}{TP+FP}\times\:100$$

(34)

$$\:Accuracy=\frac{TP+TN}{TP+TN+FP+FN}\times\:100$$

(35)

$$\:Sensitivity=\frac{TP}{TP+FN}\times\:100$$

(36)

$$\:F1=2\times\:\frac{Precision\times\:Sensitivity}{Precision+Sensitivity}\times\:100$$

(37)

$$\:MCC=\frac{TP\times\:TN-TP\times\:FN}{\sqrt{\left(TP+FP\right)\times\:\left(TP+FN\right)\times\:\left(TN+FP\right)\times\:\left(TN+FN\right)}}\times\:100$$

(38)

.

where, TP represents the True Positive, TN defines the True Negative, and FP and FN represent the False Positive and False Negative, respectively.

Ablation analysis

To evaluate the effectiveness of the proposed approach, an ablation analysis was performed by comparing the performance of three different models: (1) the original Vanilla Convolutional Neural Network (Vanilla CNN), (2) the combination of Vanilla CNN and the original Artificial Protozoa Optimizer (Vanilla/APO), and (3) the combination of Vanilla CNN and the Improved Artificial Protozoa Optimizer (Vanilla/IAPO).

The results of the ablation analysis are presented in Fig. 6, which shows the performance of each model in terms of Precision (PR), Sensitivity (SN), Specificity (SP), Accuracy (AC), F1-score (F1), and Matthews Correlation Coefficient (MCC).

Fig. 6

The ablation analysis.

The results from the ablation analysis highlight the efficacy of the proposed methodology. The integration of Vanilla CNN with IAPO (Vanilla/IAPO) surpasses the performance of the other two models across all evaluation metrics. In particular, Vanilla/IAPO achieves a precision of 0.92, sensitivity of 0.90, specificity of 0.94, accuracy of 0.91, F1-score of 0.91, and MCC of 0.85.

When compared to the original Vanilla CNN, the combination of Vanilla CNN and APO (Vanilla/APO) demonstrates enhanced performance across all metrics, particularly with a marked improvement in precision, sensitivity, and F1-score. This suggests that the original APO algorithm effectively optimizes the Vanilla CNN.

Nevertheless, the combination of Vanilla CNN and IAPO (Vanilla/IAPO) further elevates performance, showing significant enhancements in precision, sensitivity, specificity, and F1-score relative to Vanilla/APO. This indicates that the advancements made to the APO algorithm, leading to IAPO, are successful in optimizing the Vanilla CNN for the detectionof oral cancer.

Moreover, the MCC metric, which assesses the correlation between predicted and actual labels, reveals a substantial improvement in Vanilla/IAPO compared to the other two models. This underscores the effectiveness of the proposed approach in minimizing the misclassification rate and enhancing the overall performance of the model.

Comparative analysis

To further evaluate the performance of the proposed Vanilla/IAPO approach, we compared it with five state-of-the-art models: Convolutional Neural Network (CNN)¹², Convolutional Neural Network (CNN2)¹⁴, 3DCNN¹³, deep learning neural network using ISSA (DNN/ISSA)³, and ResNet-101¹⁵. The comparison analysis is based on the same evaluation metrics: Precision (PR), Sensitivity (SN), Specificity (SP), Accuracy (AC), F1-score (F1), and Matthews Correlation Coefficient (MCC). The results of the comparison analysis are presented in Table 5, which shows the performance of each model in terms of the six-evaluation metrics.

Table 5 The performance of each model in terms of the six-evaluation metrics.

The findings from the comparative analysis indicate that the proposed Vanilla/IAPO method outperforms five leading models in the field. Notably, Vanilla/IAPO records the highest scores across all evaluation metrics, achieving a precision of 0.92, sensitivity of 0.90, specificity of 0.94, accuracy of 0.91, F1-score of 0.91, and MCC of 0.85.

In comparison to the CNN1 and CNN2 models, Vanilla/IAPO exhibits substantial enhancements across all metrics, with an average increase of 12% in precision, 15% in sensitivity, 9% in specificity, 11% in accuracy, 14% in F1-score, and 19% in MCC.

While the 3DCNN model, a 3D convolutional neural network, demonstrates superior performance relative to the 2D CNN models, it still falls short of Vanilla/IAPO in every metric. The DNN/ISSA model, which employs an alternative optimization algorithm, yields competitive results but is consistently surpassed by Vanilla/IAPO across all metrics.

The ResNet-101 model, a prominent deep learning architecture, achieves commendable performance; however, it is still outperformed by Vanilla/IAPO in all metrics, with the exception of specificity.

Computational analysis

The Improved Artificial Protozoa Optimizer (IAPO) algorithm employed in this study, to enhance the parameters of the Vanilla CNN model for oral cancer image analysis, demonstrates a comparatively lower computational cost than that of the genetic algorithm and particle swarm optimization by approximately 10% and 20% respectively, thus proving itself to be useful for large-scale optimization issues. Furthermore, there is low parameter sensitivity when using IAPO, indicating that the chosen parameters do not greatly affect the algorithm, and optimal parameters are found using a grid search, which suggests that IAPO is independent of variations in parameter values.

Challenges and future directions

In spite of the advancement in oral cancer classification, there are several limitations like class imbalance, interpretability, and limited annotated datasets. In recent years, the scholars have concentrated on automating the extraction procedure of feature and standardizing the models by exploration the scope of Transfer learning and CNN. All these approaches extract the attributes of images within an automatic manner; however, they do not have the skill for learning the pixel-to-pixel relationships or the image level relationships. It can develop a scope for the addition of a new stage in extraction of feature. The new stage of feature extraction has a number of special features, including automatic feature learning that deep learning models can automatically learn and extract features from raw data, thus minimizing the manual feature extraction process; a hierarchical representation of characteristics, where deep-learning models can learn hierarchically representative features that capture both complex patterns and correlations of the data; resistance to variations, where deep-learning models can learn a feature that is resistant to variations in the data, including lighting conditions, poses and occlusions; as well as an improvement in feature threadiness, in which deep-learning models can learn features that are highly discriminatory, making it easier to distinguish between presets or objects.

The purpose and motivation of the current study is devising an approach to comprise the relationships based on the pixel and developing relation aware illustration for oral cancer classification. Relation aware illustration employs the associations amid the points of data as a basis for knowledge to efficiently learn the network. Upcoming studies need to tackle these obstacles and investigate innovative approaches, possibly incorporating expertise in the field and diverse types of information to enhance the reliability and accuracy of the categorization networks.

Discussions

The proposed Vanilla CNN improved by the Improved Artificial Protozoa Optimizer (IAPO) demonstrates significant improvements in oral cancer detection compared to current deep learning-based studies. The model yielded higher performance values, including precision of 0.92, sensitivity of 0.90, specificity of 0.94, accuracy of 0.91, F1-score of 0.91, and Matthews Correlation Coefficient (MCC) of 0.85, outperforming state-of-the-art models like traditional CNNs, 3DCNN, DNN/ISSA, and ResNet-101 on all measurements.

Interestingly, it attained a mean improvement of 12% in precision, 15% in sensitivity, 9% in specificity, 11% in accuracy, 14% in F1-score, and 19% in MCC compared to conventional CNN models. IAPO not only enhanced the model’s ability to avoid local optima but also reduced computational costs by approximately 10% and 20% relative to genetic algorithms and particle swarm optimization, respectively. Besides, the model is supported by preprocessing techniques and data augmentation that improve the quality and variability of the dataset, resulting in its strength and generalizability.

These results point to the strength of the convergence of metaheuristic optimization and deep learning paradigms in providing a more accurate and reliable approach to oral cancer detection, which could result in improved patient outcomes and mortality reduction.

Conclusions

Oral cancer represents a major public health issue globally each year. The importance of early detection and detectioncannot be overstated, as they are vital for effective treatment and enhanced survival rates for individuals diagnosed with localized oral cancer. Nevertheless, achieving accurate diagnoses of oral cancer poses a considerable challenge, characterized by a high incidence of misdetectionand delays in detection. In recent years, the utilization of deep learning methodologies, especially Convolutional Neural Networks (CNNs), has demonstrated encouraging outcomes in the realm of medical image analysis, including the detectionof oral cancer. CNNs possess the capability to automatically extract features from images, thereby minimizing the necessity for manual feature extraction and enhancing diagnostic accuracy. Furthermore, the efficacy of CNNs can be significantly improved by integrating preprocessing techniques and data augmentation strategies, which serve to enhance the quality and diversity of the training datasets. In this research, a refined approach using a Vanilla CNN framework was introduced for the detectionof oral cancer, using preprocessed images alongside data augmentation techniques. To enhance the classification performance, a modified metaheuristic algorithm known as the Improved Artificial Protozoa Optimizer (IAPO) was utilized to optimize the architecture of the CNN. The effectiveness of the proposed method was assessed using a dataset comprising oral cancer images and compared with different methods, including Convolutional Neural Network (CNN), Convolutional Neural Network (CNN2), 3DCNN, deep learning neural network using ISSA (DNN/ISSA), and ResNet-101 with results indicating that the optimized CNN model achieved high accuracy in detecting oral cancer. The study underscores the significance of preprocessing, data augmentation, and metaheuristic optimization in enhancing the efficacy of CNNs for oral cancer detection. The outcomes of this research may aid in the advancement of more precise and dependable computer-aided detectionsystems for oral cancer, ultimately leading to improved patient outcomes and a reduction in the mortality rate associated with this condition.