Introduction

High-ash Indian coal, with its low calorific value and high mineral content, makes burning and pyrolysis difficult1,2. On the other hand, fly ash found intensive applications in concretes and also researchers have received enhancement in the performance also3,4. The chemical and physical characteristics of High-ash coal, metal chloride modification may improve pyrolysis, kinetics, and burnout5,6. This literature review examines experimental research on metal chloride modification of coal, focusing on pyrolysis, reaction kinetics, and burnout7. India’s coal reserves are primarily High-ash (30–50% ash). Silica, alumina, and iron oxides are the main causes of this High-ash level. High-ash concentrations lower calorific value, increase combustion slagging and fouling, and increase particulate matter and pollutant emissions like SO2 and NOx8. Pyrolysis, the heat degradation of organic material without oxygen, is essential to coal thermal conversion9,10,11,12. Several studies have shown that High-ash Indian coal’s mineral content inhibits volatile release and reduces pyrolysis efficiency13,14,15. Various works highlighted on High-ash Indian coal pyrolysis and found that ash components like silica and alumina make it harder for organic matter to break down4. This means that there are fewer volatile yields and more char residue. The research stressed the need for coal modification for pyrolysis. Metal chlorides such as CaCl2, MgCl2, and FeCl3 modify coal by altering its chemical structure and thermal behavior16,17,18,19. These metal chlorides catalyzed pyrolysis and combustion, breaking down organic materials and enhancing coal reactivity20,21. In parallel, many investigations discovered that CaCl2 modification on High-ash Indian coal boosted volatile output during pyrolysis and lowered coal decomposition activation energy22,23,24. Furthermore, many researchers demonstrated that altering metal chloride could improve pyrolysis efficiency and combustion25,26.Various works have been highlighted that metal chloride treatment may improve coal-fired power production efficiency and sustainability by reducing fuel costs and environmental compliance27,28,29. The metal chlorides reduced combustion activation energy and changed the combustion process, thoroughly burning the coal. The data imply that metal chloride alteration improves pyrolysis and combustion kinetics, improving thermal performance5,30,31,32.In recent years, investigators have employed multivariate statistical approaches to ascertain the impact of process factors on process responses. We employ experimental design to examine the primary and interactive impacts of process factors using a minimal number of experimental runs. Artificial neural networks and response surface technique are used to project process behavior in many spheres, including syngas generation33., modeling of fin and tube condenser34, prediction of floatation column grade and recovery35, extraction of Bauhinia monandra seed oil36. RSM functions as a statistical tool designed to identify and establish functional relationships between dependent and independent variables. The ANN is employed as a different statistical method, showing enhanced goodness of fit. It has the notable quality to derive significance from complex data, and define patterns and perceive trends from highly non-linear complicated data sets. In addition to this it also gives an insight from intermittent, inadequate and insufficient data sets and this is a kind of advantage for using ANN.

This study investigates the use of the coal pyrolysis technique to improve high-ash coal utilization. The Machine Learning Approach inherently presupposes that the primary method of moving from input to output parameters is largely established in advance. In this context, the present work uses machine learning approach which includes Artificial Neural Networks (ANN) and Response Surface Methodology (BBD), leveraging a feed forward back propagation neural network to predict the responses, specifically burn-out, based on input variables including pyrolysis temperature, pyrolysis time, and catalyst concentration.

Materials and methods

Methods of experiment and analysis

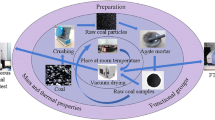
For the present study, High-ash coal was collected from a local vendor, located in Dhanbad district, Jharkhand, India. The process of High-ash coal preparation is shown in Fig. 1. The proximate and ultimate analysis of the feed sample employ for catalytic decomposition was prearranged in Table 137.

Table 1 Proximate and elemental analysis of coal sample.
Full size table
Fig. 1
figure 1

Process of high-ash coal collection and preparation.

Full size image

Chemical impregnation method was used to load Tin in coal samples. Tin chloride (Sigma Aldrich, purity 99.7%) was the chosen impregnant source of Tin based on the procedure employed by Macedo LAd, et al.38. The standard solutions of anhydrous SnCl2 were prepared by mixing Distilled water and SnCl2 (Sigma Aldrich, purity 99.7%) pursuant to the requisites concentrations. Five grammes of dry coal samples were placed in a beaker filled with prepared standard solutions of anhydrous SnCl2 at a 10 mL g−1 ratio; then, after one hour at 25 °C, stirred. The coal samples impregnated with SnCl2 were then filtered and then dried at 100 °C for 24 h. The Coal samples were then packed in plastic bags until the tests were carried out, as shown in Fig. 2, to protect them from moisture and dust. In the present study, three low Sn2+concentrations (0.003 M, 0.006 M, 0.009 M) were elected for study. Pyrolysis study was performed at the CSIR-CSMCRI facility in Bhavnagar, India. The experiments of High-ash coalsample (10 ± 0.05 mg) was heated from 510 °C, 610 °C and 710 °C into a platinum crucible at different heating rates (10 °C/min) under an inert high-purity nitrogen flow of 0.50 L/min. To impel the morphology changes on the surface of coal particles before pyrolysis process, were performed by FE-SEM analyses. A gold-coated evacuated die was used to compress (−72#) coal samples into conductive pellets. As shown in Fig. 2, the coal sample pellets at the CSIR-CSMCRI facility in Bhavnagar, India, have undergone inspection utilizing an airtight chamber and a JEOL JSM 7100 F.

Fig. 2
figure 2

Sncl2 impregnation method and analysis of data.

Full size image

Artificial neural network for prediction

Artificial neural networks, also known as neural networks, serve as statistical modeling tools based on the same principles as biological neural networks (BNNs). The neural network implementation’s purpose is to transform various data inputs into valuable data outputs. There are many approaches for artificial neural networks (ANN), the most often used one being the feed forward back propagation neural network methodology based on the multilayer Perceptron (MLP). The back propagation method is used to train data sets39,40,41. The comprising an input layer, many hidden layers, and an output layer, a multilayer perceptron is a kind of feed-forward neural network. A three-layer perceptron using feed forward back propagation learning technique has been acknowledged for its capacity to represent nonlinear interactions with considerable precision. Each layer of neurons in an artificial neural network interconnects with the next layer through distinct weights. The modified these weights throughout training to institute an experiential relationship between both output and input variables.

Response surface methodology (RSM) for prediction

Statistical analysis is performed using RSM method for forecasting the correlation between process variables and responses42,43,44. The three components of analytical investigations are the ANOVA table, regression analysis, and the creation of 3D graphics, aimed at determining ideal conditions and forecasting future responses. We deduced by fitting a second-order polyn (SOP) equation to the gathered data that the variables are associated. We assessed the excellence of the fitted model manner ANOVA and a significance experiment (p-value). The fitted model equation is specified as:

$${\text{y = }}{{\text{\varvec{\upbeta}}}_{\text{0}}}+\sum\limits_{{i=1}}^{k} {{{\text{\varvec{\upbeta}}}_i}} {x_i}+\sum\limits_{{j=1}}^{k} {{{\text{\varvec{\upbeta}}}_{jj}}{x_j}^{{\text{2}}}} +\sum {\sum\limits_{{ij}}^{k} {{{\text{\varvec{\upbeta}}}_i}_{j}} } {x_i}{x_j}+e$$
(1)

Where\(\:{x}_{1}\text{,}{x}_{2}\text{,}{x}_{3}\text{,\:\:}.\:..\:\:,\:{x}_{k}\) are the input variable factors which impact the response y; β0, βii,….βij, in which (i = 1, 2, …,k), and (j = 1,2, …,k). The parameters remain unknown; e denotes a random error that in this case could be considered minor. Design Expert-13 software helped the analysis using the Box Behnken Design (BBD).

Results and discussion

Structure characteristics of samples

The catalytic effects of metal chlorides on coal surfaces may be thoroughly and informatively investigated using scanning electron microscopy (SEM). The morphological properties of both raw and chemically processed materials are investigated using scanning electron microscopy45. The research found that by changing surface morphology, porosity, and structural fragmentation, metal greatly enhances the pyrolysis process. The SnCl2 maintains the structural integrity of coal more effectively than other metal chlorides. The coal surface displays less cracking, indicating regulated thermal breakdown. SnCl2 interacts with the coal matrix by stabilizing free radicals and promoting selective bond cleavage, especially for C-H bonds. This regulated fragmentation yields fewer by-products and enhances selectivity for the intended compounds. SEM pictures of SnCl2 impregnated samples are shown in Fig. 3.

Fig. 3
figure 3

SEM micrographs samples.

Full size image

.

Effect of pyrolysis time

It is observed in many previous studies that pyrolysis time significantly affect the burnout behavior of coal46. In present study SnCl2 used as catalysis for pyrolysis process and it was observed in study that presence of SnCl2 accelerates the thermal decomposition process, significantly reducing the duration of pyrolysis47. In parallel, finding illustrate that SnCl2 specifically helps to cleave both aliphatic and aromatic bonds. Furthermore, SnCl₂ has a modest effect in the advanced stages of breakdown on lowering the pyrolysis time and helps to stabilize intermediate products and free radicals, its disintegration happens more precisely and under control. A considerable weight loss was seen for periods of up to 30 min at 510 °C; yet, the change in responsiveness reduced after this time. Extended pyrolysis duration at a constant temperature seems to increase the reactivity of coal. After up to 30 min, the pyrolysis temperature of 610 °C produced a noticeable rise; thereafter, a steady weight loss was seen as shown in Fig. 4.

Fig. 4
figure 4

Effect of pyrolysis time on burnout at 510 °C (a), 610 °C (b) and 710 °C (c).

Full size image

Effect of chemical concentration

The coal pyrolysis processes is significantly influenced by numerous experimental factors, including the, chemical or catalysis concentration, operating temperature, process time, and the heating rate48. The effect of chemical or catalysis concentration is crucial; usually, a rise in this variable encourages cross-linking processes. This lowers the average molecular weight of tar and results in lower yields of tar and liquids49. The SnCl2 interaction with the coal matrix, catalysts influence thermal behavior, breakdown paths, and product distribution in certain ways. In present study it was found that as we are increasing the concentration of SnCl2 causes a remarkable burn-out increase, up to 9%, whilst at lower concentrations a consistent temperature and pyrolysis time shows a considerable decrease. At 610 and 710 degrees Celsius, 9% SnCl2-impregnated coal produced the most notable decrease, as shown in Fig. 5. Previous studies have revealed that, SnCl2 reduces the pyrolysis temperature; its effect is not as pronounced as that of other metal chloride. However, SnCl2 enhances tar production and quality through the stabilization of aromatic intermediates, rendering it suitable for liquid product recovery processes.

Fig. 5
figure 5

Effect of chemical concentration on burnout at 510 °C (a), 610 °C (b) and 710 °C (c).

Full size image

Effect of pyrolysis temperature

The current work shows that by enabling dehydrogenation and de-polymerization processes in the coal matrix, SnCl2 drastically lowers the pyrolysis temperature50. Meanwhile, SnCl₂ reduces the pyrolysis temperature through the selective decomposition of coal constituents and stabilizes intermediate radicals and promotes the controlled breakdown of both aromatic and aliphatic compounds51. The catalytic effect of SnCl2 was also studied in present investigation and it’s confirmed that as we increasing the concentration of SnCl2 cause a remarkable burn-out increase, up to 9%, whilst at lower concentrations a consistent temperature and pyrolysis time shows a considerable decrease52. Furthermore, at 610 and 710 degrees Celsius, 9% SnCl2-impregnated coal produced the most notable decrease, as shown in Fig. 6. However, SnCl₂ facilitates the targeted cleavage of C-H and C-C bonds, particularly within aromatic rings and mitigates the impact of free radicals produced during pyrolysis, thus averting significant thermal degradation.

Fig. 6
figure 6

Effect of Pyrolysis temperature on Burnout at 510 °C (a), 610 °C (b) and 710 °C (c).

Full size image

RSM for the prediction of output

In the current research, process variables Catalyst concentration, Pyrolysis temperature, Pyrolysis time and were varied and their response is compiled into tables. Table 2 displays the coded and uncoded levels of the process variables.

Table 2 Coded and uncoded levels of variables for box Behnken Design.
Full size table

In the present study, The Box-Behnken design that included 15 tests to investigate the influence of different type of burn-out rate namely(A) Pyrolysis time, (B) catalyst concentration and (C) Pyrolysis temperature are listed in below Table 3. A combination of Variables of significance resulted in % burn-out varied between 18.23 and 71.18%. The anticipated values derived from the model provided by the BBD model varied between 14.20 and 75.21%. Based on the information provided in Table 3, a second-order quadratic equation represented the relationship between the response and process variables as follow:

$$\begin{gathered} \% {\text{ }}BO{\text{ }}={\text{ }}52.37{\text{ }}+14.92A{\text{ }}+{\text{ }}4.52B{\text{ }}+{\text{ }}15.58C{\text{ }} - 2.94{A^2} - {\text{ }}2.27{B^2}-{\text{ }}4.44{C^2}{\text{+ }}0.59AB \hfill \\ {{- }}0.28AC{\text{ + }}0.39BC \hfill \\ \end{gathered}$$
(2)

The significance of model was verified by ANOVA results which are presented in Table 4, the model prediction was noteworthy as p < 0.001 to predict % burn-out. The coefficient of determination (R2) recognized to be 0.9807 which implies that the total variation in % Burn-out is attributed to the studied experimental variables. The contribution of linear terms (95.33%) found to be much higher than quadratic terms (2.68%) and cross-product (interactional) terms (0.06%). The obtained adj. R2 is 0.9807. The close value of adj. R2 to coefficient of determination (R2) suggests a high significance of the model. The positive sign for the coefficient indicate that variables have synergistic effect on the % burn-out whereas negative sign of coefficient indicate that variables have antagonistic effect. The results showed that Pyrolysis time, Pyrolysis temperature and catalyst concentration had positive significant linear effect whereas quadratic terms are non-prominent with p > 0.05. Furthermore, the interactive effects between the variables are found to be insignificant. The F-value of the model is 28.19 and p-value < 0.001, the high F-values indicate that model is significant. The contribution of Pyrolysis temperature is highest among the process variables with 47.63% followed by Pyrolysis time (43.69%) and catalyst concentration (4.01%). Thus, the order of significance for burn-out can be mentioned as Pyrolysis temperature > Pyrolysis time > Catalyst concentration.

Table 3 BBD matrix showing observed response and predicted response.
Full size table
Table 4 ANOVA table of the quadratic model for the catalytic thermal conversion of coal.
Full size table

The RSM 2D and 3D plots were used to examine the effects of process variables. RSM plots explain the effect of two factors on the response, keeping other variables at mid-level. From the Fig. 7a–c, it can be seen that increase in Pyrolysis time and catalyst concentration the pyrolysis rate is increasing significantly. The highest pyrolysis rate found to be achieved at high concentration and time. Similar trend of change was observed with increase in Pyrolysis temperature. For the same concentration and Pyrolysis time, the pyrolysis rate was higher at high temperature (710°C). The close value between observed and predicted values (high R2) assures the significance of model predicted by RSM box behnken design.

Fig. 7
figure 7

Shows the effect of time, temperature and concentration on % burn-out.

Full size image

ANN for the prediction of output

In this investigation, 3-layer architecture of FFNN (feed forward neural network) has been established by untrustworthy parameters, viz., Pyrolysis temperature, Pyrolysis time and Catalyst concentration and the results were evaluated for Burn-out % and are presented in Table 5. Schematic flow diagram is shown Fig. 8. Out of 27 experimental data, 70% data were employed for training, remanent was utilizing for testing. MATLAB software was used toimplement ANN. Every input and output variable in the present work underwent normalization. A MLP with algorithm of feed forward back proliferation was applied with Tan-Sigmoid as a transfer function. For knowledge of network algorithm of Levenberg-Marquardt (LM) has been adopted.

Fig. 8
figure 8

Schematic diagram of ANN.

Full size image
Table 5 Design-matrix for observed and ANN predicted values for % burn-out.
Full size table

ANN is characteristically constituted of individual, inter-connected unit called neuron or node. Each layer of neurones is fully connected to the layers below it. These connections, or nodes, are called artificial neurones, and each one copies the value of the inputs with its own weights. The data is trained using allied weight are adjusted to engender an experimental correlation between the process variables. Table 6 portrays the connection weight and biases in order to assessment of burn-out percentage.

Table 6 Connection weight and biases.
Full size table

The Coefficient of efficiency was estimated for contrast of ANN models; calculation is distinct as prearranged in Eq. 3:

$$\:E=\frac{({E}_{1}-{E}_{2})}{{E}_{1}}$$
(3)

Where,

$$\:{E}_{1}=\:\sum\:_{i=1}^{N}(AV-{\stackrel{-}{AV}}_{avg})^2$$
(4)
$$\:{\:\:\:E}_{2}=\sum\:_{i=1}^{N}(PV-AV)^2$$
(5)

While E signifies the Nash Coefficient, PV, AV, and (AV) avg reflect predicted values, the mean of actual values, and the actual values themselves across the board.

Sensitivity analysis

This approach establishes the link between variations in an independent variable and their effect on a particular dependent variable and is essential for the precise choosing of important input parameters. This performance operates within certain constraints depending on many inputs. Still, other techniques have been suggested to meet necessary criteria like the connection weights method, Garson’s algorithm, and Pearson correlation coefficient53,54,55,56.

Table 7 illustrates the cross correlation of inputs for burn-out %. It can be easily seen in the table that burn-out % is exceedingly correlated to Pyrolysistime as implythrough the cross relationship values of 0.67, pursued by Pyrolysis temperature and then catalyst concentration. The sensitivity analysis related to Garson’s method is illustrated in Table 8. Garson’s approach highlighted a significant pittance indicated by the Pyrolysis time for burn-out %, which shared a value of 39.80% in comparison to other inputs. The Connection Weight approach, exemplify that the Pyrolysis temperature is significant as an input parameter, with a Si value of 1.97, followed by Pyrolysis time and catalyst concentration.From the above results, it could be accomplished that Pyrolysis time has been establish as efficient parameter accompany by Pyrolysis temperature and catalyst concentration determined from all the sensitivity analysis methods (as shown in Table 8).

Table 7 Cross-correlation of input and output for the % burn-out.
Full size table
Table 8 Garson’s algorithm and connectionweight approach.
Full size table

ANN based model equation for the prediction of output

Formulating a predictive model equation using artificial neural networks is quite complex. Nonetheless, in this research, based on three factors (Pyrolysis time, catalyst concentration, and Pyrolysis temperature) a model equation can be established.Goh50 has suggested formulating the model equation by using the connection weights as the parameters of the model. The established relationship can be expressed in the following manner as shown in Eq. 6

$${O_n}={f_{sig}}\{ {b_0}+\sum\nolimits_{{k=1}}^{h} {[{W_k} \times {f_{sig}}({b_{hk}}+\sum\nolimits_{{i=1}}^{m} {{W_{ik}}{X_i}]\} } }$$
(6)

In this context, On represents the normalised output; b0 denotes the bias at the output layer; Wk indicates the connection weight between the kth neurone of the hidden layer and the single output neurone; bhk refers to the bias at the kth neurone of the hidden layer; and h signifies the number of neurones in the hidden layer. The connection weight is represented by Wik, linking the ith input variable to the kth neurone in the hidden layer. Xi denotes the normalised input variable i, while fsig refers to the sigmoid transfer function.

The values displayed in Table 9 permits for the consequential expressions to have been formulated as a subjective constant, which ultimately yields an output for the burn off percentage.

Equations for burn-out percentage using artificial neural network are given below

$${A_1}={\text{ }} - 2.94+{\text{ }}0.1046Py.Time{\text{ }}+{\text{ }}0.2942Cat.Conc.-{\text{ }}0.6998Py.Temp$$
(7)
$${A_2}={\text{ }} - 0.0989{\text{ }} - {\text{ }}0.9426Py.Time{\text{ }}+{\text{ }}0.1136Cat.Conc.{\text{ }}+{\text{ }}0.5608Py.Temp$$
(8)
$${A_3}={\text{ }} - 1.2953{\text{ + }}1.0637Py.Time{\text{ + }}0.4318Cat.Conc.{\text{ + }}3.4528Py.Temp$$
(9)
$${B_1}={\text{ }} - 0.2117{\text{ }}*{\text{ }}\left[ {\left( {{e^{A1}} - {e^{ - A1}}} \right)/{\text{ }}\left( {{e^{A1}}+{e^{ - A1}}} \right)} \right]~$$
(10)
$${B_2}={\text{ }}2.6366*{\text{ }}\left[ {\left( {{e^{A2}} - {e^{ - A2}}} \right)/{\text{ }}\left( {{e^{A2}}+{e^{ - A2}}} \right)} \right]$$
(11)
$${B_3}={\text{ }} - 0.2845*{\text{ }}\left[ {\left( {{e^{A3}} - {e^{ - A3}}} \right)/\left( {{e^{A3}}+{e^{ - A3}}} \right)} \right]$$
(12)
$${C_1}={\text{ 0}}{\text{.1026 }}+{\text{ }}{B_1}+{\text{ }}{B_2}+{\text{ }}{B_3}$$
(13)
$$B{O_n}={\text{ }}\left[ {\left( {{e^{C1}} - {e^{ - C1}}} \right)/\left( {{e^{C1}}+{e^{ - C1}}} \right)} \right]$$
(14)

The \(\:{BO}_{n}\) value as obtained from Eq. (14) this needs to be denormalized as

$$BO{\text{ }}={\text{ }}0.5\left( {B{O_{max}}-{\text{ }}B{o_{min}}} \right)\left( {B{O_n}+1} \right){\text{ }}+{\text{ }}B{O_{min}}~$$
(15)

where, A, B, C are the constant and BO is the Burn-out percentage, BOmax and BOmin are the maximum and minimum values of BO.

Assessment between RSM and ANN models

Assessment of the best -suited model for data interpretation, a comparative study of both ANN and RSM models was carried out.Various statistical methods for analysis were employed, including the Nash Coefficient, RMSE, and MAPE. The results provided in a form of table in Table 10. Analysis was carried out for ANN (Fig. 9a) and RSM (Fig. 9b) the approach between the inputs (Pyrolysis time, catalyst concentration and Pyrolysis temperature) and response (% BO) values as revealed in Tables 2 and 7. Upon comparison of the two models, the ANN model demonstrated superior performance in non-linear data fitting and estimation capabilities relative to the RSM model, as illustrated in Table 10. Nonetheless, ANN has reliably outperformed the RSM across all dimensions.

Fig. 9
figure 9

Comparison between observed % vs. predicted % burnout (a) ANN and (b) BBD.

Full size image
Table 9 Comparative studyof the evaluation of ANN model using different statistical coefficient.
Full size table
Table 10 Comparison between RSM and ANN by different statistical parameters.
Full size table

Conclusion

The coal pyrolysis processes is significantly influenced by numerous experimental factors, including the, chemical or catalysis concentration, operating temperature, process time, and the heating rate. However, SnCl2 has shown promise in improving the pyrolysis of high ash coal. A considerable weight loss was seen for periods of up to 30 min at 510 °C; yet, the change in responsiveness reduced after this time. It was found that as an increasing the concentration of SnCl2 causes a remarkable burn-out increase, up to 9%, whilst at lower concentrations a consistent temperature and pyrolysis time shows a considerable decrease. At 610 and 710 °C, 9% SnCl2-impregnated coal. Meanwhile, SnCl₂ reduces the pyrolysis temperature through the selective decomposition of coal constituents and stabilizes intermediate radicals and promotes the controlled breakdown of both aromatic and aliphatic compounds.

Present study also employed artificial neural networks and response surface methodology for predicting % burn-out. The feed-forward back propagation, method of neural has been utilized and could be effectively envisage the % burn-out. The values of % Burn-out is witnessed from coefficient of determination (R2).Based on node and bias weights obtainedfrom ANN a model equation is suggested to predict the % Burn-out. Through sensitivity analyses, it was found that the pyrolysis temperature stands out as the most critical input parameter; with pyrolysis time and catalyst concentration following in consequence.Similar results was observed using response surface methodology. ANN and RSM both were deputed for the prediction of % burn-out. The over study depicts that ANN (R2 = 0.9965) suggests the better predictability than that of RSM.