Introduction

Rock masses, as fundamental components of the Earth’s lithosphere, naturally contain inherent defects such as fractures, joints, and voids resulting from long-term geological processes and anthropogenic activities1,2,3,4,5,6. Moreover, under sustained external actions, these defects can induce the nucleation of new cracks, leading to damage propagation and coalescence7,8,9,10. As key construction materials in infrastructure projects including roads, bridges, hydropower facilities, and mines, understanding fracture-driven rock behavior is therefore pivotal for ensuring geotechnical safety and optimizing engineering design strategies11,12.

The mechanical response of fractured rocks has been extensively investigated in recent decades13,14,15,16. Early experimental studies by Bobet & Einstein17 elucidated the patterns of crack coalescence in rock specimens under biaxial compression, while Prudencio et al.18 classified four distinct failure modes of jointed rock masses. For specimens with dual fractures, Chen et al.19,20 demonstrated that joint connectivity significantly governs the strength anisotropy of rock masses, and Cho et al.21 established a link between fracture geometry and macroscopic deformation behavior. Sang et al.22 conducted a detailed investigation on the effects of fissure geometric characteristics on the mechanical behavior and failure mechanism of granite under uniaxial compression, highlighting the significant influence of fracture geometry on strength and failure patterns. Similarly, Xu et al.23 explored the dynamic mechanical behavior and energy dissipation characteristics of low-temperature saturated granite under cyclic impact loading, revealing the complex interactions between fracture geometry and loading conditions. These studies underscore the importance of fracture geometry in determining the mechanical response of fractured rocks.

With the advancement of numerical simulation techniques, grain-based models (GBM) have emerged as powerful tools for simulating the fracturing processes in crystalline rocks24,25. Potyondy & Cundall26 pioneered the development of bonded-particle GBMs. Zhang et al.27 investigated the fracture behavior of thermally treated granite under compression-shear loading, demonstrating that thermal treatment can alter the mechanical properties and failure modes of granite. Additionally, Wang et al.28 conducted detailed investigations on the macro-meso mechanical properties and energy dissipation mechanisms of granite shear fractures under dynamic disturbance, providing valuable insights into the complex interactions between fracture geometry and dynamic loading condition. However, traditional smooth-joint (SJ) models often oversimplify the inter-grain mechanics, failing to accurately capture realistic crack paths29,30. Recent studies have made progress in improving boundary modeling31,32, but these efforts still lack comprehensive multiscale validation against experimental data.

Despite these advances, two critical gaps remain: (1) Cross-scale linkage: Most studies focus either on macro-scale experiments or micro-scale simulations, neglecting integrated analyses bridging crack initiation (mineral boundaries) to macro-fracture formation. (2) Model limitations: Existing GBMs inadequately simulate intra-crystalline cracking and multi-mineral interactions, limiting their predictive accuracy.

To address these gaps, this study combines multiscale experiments (mechanical testing, acoustic emission monitoring) with an innovative Multilevel Parallel Bonded-GBM (Multi Pb-GBM). Using granite from the Jiaodong Group, we systematically investigate how fracture geometry (angle, rock bridge configuration) controls strength and failure modes, the evolution of micro-to-macro crack networks under uniaxial compression, and the role of mineral heterogeneity in fracture propagation. The research findings provided a database for in-depth study on mechanical properties of rock materials.

Mechanical experiment

Test scheme

Granite specimens were sourced from the Jiaodong Group and machined to dimensions of 100 mm (length) × 50 mm (height) × 30 mm (thickness)33,34. Pre-existing cracks were prefabricated using a diamond saw, with standardized geometries of 15 mm length and 1 mm width. This crack length represents 15% of the specimen height, a proportion selected based on preliminary tests confirming its effectiveness in simulating natural fracture behaviors and aligned with established scaling relationships35,36. Two crack configurations were investigated: single-crack and double-crack specimens (Fig. 1), with crack inclination angles of 0°, 30°, 60°, and 90° relative to the loading direction. To mitigate experimental variability, three identical specimens were tested per configuration, ensuring statistical reliability of failure mode observations.

Fig. 1
figure 1

Rock specimens: (a) single crack; (b) double cracks.

Full size image

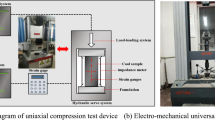
Uniaxial compression tests were conducted using a WES-2000 digital hydraulic servo testing machine, and the uniaxial compressive strength (UCS) was recorded. A constant loading speed of 0.02 kN/s was maintained until sample failure. Acoustic emission (AE) data were collected using a PCI-2 system37. To avoid interfering with crack development observation, AE sensors were attached to both sides of the sample. The boundary conditions of the model samples are illustrated in Fig. 230,35.

Fig. 2
figure 2

The boundary conditions of the model.

Full size image

Failure mode

Figure 3 showed the single crack test sample and failure results. During the loading process, the crack tip was the first area where the stress was concentrated. The failure of the sample with a crack angle of 0° started from the end of the horizontal crack and extended to the sample boundary from the upper right side and the lower left side, respectively. As a hard brittle rock mass, the macroscopic fracture of granite was instantaneous, so no new fracture point was observed during the experiment. In the sample with a crack angle of 30°, wing-like cracks were first generated at the crack tip, which expanded along the direction perpendicular to the prefabricated crack, and then developed in the direction of the maximum compressive stress. Secondary cracks gathered in large numbers at the lower end of the primary crack, and then a third main crack appeared on the lower right side, extending through the entire rock mass. No obvious sliding shear plane was generated in this process. The failure mode of specimens with 60° fracture angle was similar to that of 30° specimen, and the reverse wing fracture was obvious. When the dip angle increased to 90°, the end crack only expanded in a small amplitude after initiation, and multiple points in the specimen appeared cracks simultaneously. The main crack generated by the splitting failure extended along the loading direction and finally directly penetrated to the surface of the loading plate.

Fig. 3
figure 3

Failure mode of single crack samples: (a) 0°; (b) 30°; (c) 60°; (d) 90°.

Full size image

In order to study the compressive strength characteristics and crack propagation laws of intermittently fractured rock, uniaxial compression tests were conducted on double primary fracture samples, and the test results were shown in Fig. 4. When the rock bridge angle was 0°, shear-splitting failure occurred at the tips of the two prefabricated cracks. After penetrating the primary fissures, the two split cracks extended towards the loading plate, and shear cracks developed between the prefabricated cracks. When the rock bridge angle was 30°, minor secondary cracks appeared at the tip of the prefabricated crack, and then winglike cracks began to gather near the left primary fissures, resulting in the main fracture zone, which may be caused by the uneven force of the sample during loading. The rock bridge specimens with 60° and 90° rock bridge inclination angle maintained good integrity during loading, and the double joints of the specimens with 60° were almost collinear, and the prefabricated cracks above the rock bridge angle started to produce a wing-like fracture, forming a 60°damage surface. On the other hand, the rock bridge dip angle of 90° was affected by the boundary effect, and the splitting failure occurred directly next to the precast fissure, and the lateral expansion deformation was obvious.

Fig. 4
figure 4

Failure mode of double crack samples: (a) 0°; (b) 30°; (c) 60°; (d) 90°.

Full size image

Stress-strain law

The stress-strain curve was recorded during the test. As can be seen from Fig. 5, samples with different crack inclination angles had a compaction stage in the initial loading stage, and then the rock entered into a linear elastic stage, and the axial stress increased linearly with the increase of strain. With the progress of loading, invisible micro-cracks appeared inside the rock, and the failure entered into plastic deformation stage, and unrecoverable deformation developed. The stress load continued to increase until the peak strength was reached, the specimen entered into failure stage, the stress-strain curve dropped rapidly, and the brittle rock had no obvious residual strength. The peak uniaxial compressive strength of single-fracture rock with different angles was 104.76, 112.82, 120.54 and 134.98 MPa, respectively. With the increasing of fracture inclination angle, the uniaxial compressive strength increased, while the elastic modulus was basically the same. With the increasing of rock bridge angle, the strength of rock with intermittent double fracture had compressive strength of 109.88, 124.10, 51.68 and 116.98 MPa, respectively. Rock was most prone to failure when the rock bridge inclination angle was 60°, because the fracture inclination angle selected by the intermittent double joint test was also 60°, and when the rock bridge was in line with the primary cracks, the compressive strength of rock mass was reduced.

Fig. 5
figure 5

Stress-strain relationship in uniaxial compression test: (a) single crack; (b) double cracks.

Full size image

AE characteristics

Acoustic emission refers to a phenomenon that occurs when the external load exceeds a certain critical value, micro-yielding or deformation occurs in the internal defect region of a solid, and excess energy is released instantaneously in the form of elastic waves8,13. The ringing count in acoustic emission monitoring represents the number of cracks in the specimen. The acoustic emission characteristics of rock samples are obviously different due to the different fracture results.

The acoustic emission monitoring results of single fracture specimens were shown in Fig. 6. As the stress increased, the impact count and cumulative energy of 30°, 60° and 90° joint specimens increased slowly. When the stress reached the peak strength, the impact number increased sharply and attained the maximum value. The 0° fracture sample exhibited two concentrated periods of microcrack formation, which were the two main fracture surfaces that developed at the upper and lower ends of the pre-existing fissure.

Fig. 6
figure 6

Results of acoustic emission ringing in single fractured rock samples: (a) 0°; (b) 30°; (c) 60°; (d) 90°.

Full size image

As shown in Fig. 7, the acoustic emission results of the interrupted double-fractured rock mass showed that when the rock bridge inclination angle was 60°, a large number of acoustic emission signals appeared, and the number of ringing had been at a higher level since 15 s of the test, the sample was prone to failure and the stress-strain curve was smoother. By comparing the deformation failure process characteristics of fractured rock mass, the AE process can be divided into three stages, including initial compaction and rising stage, peak stage and stable stage. First of all, under axial stress loading, micro-cracks and pores in fractured rock mass were compressed and closed. At this time, there were only a few acoustic emission events and a slight increasing trend. In the peak zone, cracks inside the specimen were connected to form a large fracture surface, and acoustic emission events increased sharply. In the stable zone, the number of cracks did not change after macroscopic failure, and the cumulative ringing number became stable.

Fig. 7
figure 7

Results of acoustic emission ringing in double fractured rock samples: (a) 0°; (b) 30°; (c) 60°; (d) 90°.

Full size image

Numerical simulations

Through physical simulation testing, comprehensive conclusions of fracture initiation and propagation, stress-strain relationship and failure modes of fractured rock mass can be obtained. However, a large number of experiments demonstrate that granite fracture occurs not only around mineral boundaries but also inside minerals29,30. It is difficult to directly observe the process of microscopic damage and crystal scale fracture order in rock mass during physical tests, but numerical simulation technology is a reasonable and effective way to simulate rock mechanics issues31,32.

Multilevel parallel bonded -grain based modeling

The Grain-Based Model (GBM) exhibits strong capability in simulating the fracture behavior of crystalline rocks and is well-suited for granite simulations. Potyondy and Cundall integrated GBM into Particle Flow Code (PFC) to simulate the microstructure of crystalline rocks38,39. Each crystal is composed of multiple bonded particles, enabling deformation and fracture of the crystal. The GBM in PFC2D can not only simulate the initiation of microcracks and their interaction with crystal boundaries but also capture cracking behavior within the crystal structure30,31,40.

The traditional GBM approach employs polygons to simulate crystals in granite samples, which are bonded via a parallel bond model, while smooth joint (SJ) models are used to simulate grain boundaries due to their ease of generation. However, the SJ model has notable limitations: (1) Crystal boundaries are treated as cracks with bond strength but do not exhibit local geometric expansion effects, thereby losing the capability to facilitate particle rolling; (2) Contacts neglect the initial cohesion around boundaries, and rotational resistance between particles is absent; (3) Under large strains, the SJ model is only effective when surface clearance is negative30,37,41.

To address these limitations, a multi-parallel bond GBM (multi-Pb-GBM) is proposed to simulate the microstructure of crystalline granite. Instead of the traditional SJ model, a parallel contact model is employed to characterize crystal boundaries. The parallel contact model is categorized into three types: intra-crystal contact, intra-crystal boundary contact of the same mineral, and inter-mineral boundary contact, as illustrated in Fig. 8. Detailed modeling principles and optimization procedures are available in the literature37,42.

Fig. 8
figure 8

Multistage PBM import GBM. (a) Grain-based model; (b) a parallel bonded model; (c) classification of the three Pb-GBM.

Full size image

Micro parameters calibration

The numerical calibration model, with dimensions matching experimental specimens (100 mm × 50 mm), comprised 14,558 particles (radius range: 0.1–0.155 mm). Mineral grains were randomly distributed according to granite petrology with specified sizes and volume fractions: K-feldspar (40 vol%, 3.3 mm), plagioclase (20 vol%, 3.8 mm), quartz (30 vol%, 2.8 mm), and biotite (10 vol%, 2.2 mm)36,37 (Fig. 9). Parameters put into the calculation model must be calibrated to the results of UCS and UTS tests. By adjusting the microscopic parameters, the stress-strain curve of the numerical experiment is basically consistent with the physical experiments (Fig. 10). The calibrated micro-parameters and the experiment results were shown in Table 1. Validation followed a multi-scale framework: macroscopic stress-strain alignment, microscopic crack path matching with acoustic emission data, and theoretical consistency with the grain-breakage mechanics. This confirms the model’s capability to replicate both global mechanical behavior and localized fracture mechanisms42.

Fig. 9
figure 9

Calibration model and microcrack distributions in numerical tests: (a) UCS tests; (b) UTS tests.

Full size image
Fig. 10
figure 10

The stress–strain curves: (a) UCS tests; (b) UTS tests.

Full size image
Table 1 Microscopic parameters of the numerical simulation.
Full size table

Simulation results

The calculation results of the 60° specimen that was most prone to failure were taken as an example to discuss the fracture characteristics of the rock material at the microscopic scale, as shown in Fig. 11. Four characteristic time points had been selected: I was the crack initiation point at the tip of the prefabricated fissure; II was the expansion and bending of the wing-shaped crack and the germination point of micro-cracks; III was the peak strength point where a large number of internal micro-fractures gathered; IV was the point of overall failure of the specimen. The fracture development of the single fissure specimen at these four time points was shown in Fig. 11 (a). The thickness of the line segments reflected the number of micro-cracks within those areas, offering a more detailed account of the fracture evolution process of the fissured rock mass during the experiment. Figure 11 (b) depicted the stress-strain curve corresponding to the number of cracks. And Fig. 11 (c) showed the sequence of multi-level crack generation at the same time step, which helped us clearly understand the process of fracturing within the crystal during the uniaxial compression process, including the internal contact of crystals, contact at the boundaries of the same type of mineral crystals, and contact at the boundaries of different types of mineral crystals.

During the loading process, stress concentration zones first emerged at the tips of the fissures. For the 60° specimen, wing-shaped cracks initiated earliest at the tip of the prefabricated fissure and began to expand perpendicular to the direction of the pre-existing fissure. Subsequently, the upper end of the prefabricated fissure propagated downward, and the lower end propagated upward, both curving to develop in the direction of maximum compressive stress. Secondary fractures accumulated extensively at the ends of the prefabricated fissures, followed by the generation of two additional collinear joints along the plane of the prefabricated fissure, which inclined the specimen as a whole towards shear failure, revealing a macroscopic shear surface. Eventually, the wing-shaped crack that first formed at the upper end turned towards the direction of maximum compressive stress, communicating with the lower boundary and forming the rock mass failure plane with the collinear joints, transforming local shear fractures into local splitting fractures. The rock mass underwent overall fragmentation, and the stress-strain curve decreased.

Fig. 11
figure 11

Analysis of damage characteristics of single fractured rock mass: (a) fracture development; (b) stress-strain curve and crack count; (c) sequence of multi-level crack generation.

Full size image

Figure 12 presented the numerical experiment results of double fracture with 60° fracture and 30° rock bridge, showing the fracture conditions of the specimen at four characteristic points, as well as the corresponding types and quantities of fractures. From the figure, it was observed that secondary fractures first occurred at the tips of the two prefabricated fissures, and both extended along the direction of the principal compressive stress. Subsequently, the upper prefabricated fissure began to bifurcate at its tip, giving rise to several secondary wing-shaped fractures. Following this, the upper extension of the upper prefabricated fissure and the lower extension of the lower prefabricated fissure started to accumulate micro-cracks, resulting in two distinct bands of micro-cracks. Upon further loading, the fracture band on the upper left side expanded to the specimen’s boundary, causing the specimen to undergo macroscopic shear failure in that area. It was evident that micro-cracks first appeared at the grain boundaries of different minerals, followed by fractures occurring at the grain boundaries within the same mineral, and finally, the number of internal contact fractures within the crystals rapidly increased to form a macroscopic fracture surface.

Fig. 12
figure 12

Analysis of damage characteristics of double fractured rock mass: (a) fracture development; (b) stress-strain curve and crack count; (c) sequence of multi-level crack generation.

Full size image

Discussion

The findings of this study hold substantial implications for practical geotechnical engineering design and risk assessment in fractured rock environments. Firstly, the critical role of fracture geometry-particularly the 60° rock bridge angle in double-fractured specimens, where uniaxial compressive strength (UCS) is minimized-provides actionable guidance for underground excavation design. Engineers should prioritize pre-construction fracture mapping to identify high-risk zones with collinear fracture alignments and implement targeted reinforcement measures, such as reducing cable bolt spacing to lower-risk zones, as inferred from the UCS reduction observed in this study. This proactive approach can mitigate the risk of sudden instability in tunnels, mines, or slope projects.

Secondly, the triphasic evolution of acoustic emission (AE) activity-characterized by compaction, peak, and stabilization phases-offers a robust framework for real-time risk monitoring. Field monitoring systems can be calibrated to trigger alerts during the compaction phase when minor AE events exceed 85% of the loading duration, coupled with thresholds for abrupt energy surges during the peak phase. Such monitoring protocols enable early warning of impending failure, facilitating timely evacuation or temporary support reinforcement in critical infrastructure like dam foundations or rock slopes.

Thirdly, the distinct failure modes of single- and double-fractured specimens inform material selection and reinforcement strategies. For single-fractured rock masses, which exhibit progressive tensile-dominated failure, flexible support systems can accommodate localized shear deformation and prevent catastrophic collapse. In contrast, double-fractured zones prone to sudden tensile-shear hybrid failure require more rigid reinforcement to counteract stress interference between fractures.

Finally, the Multi Pb-GBM’s ability to replicate multiscale fracture propagation-from inter-mineral boundary initiation to macroscopic rupture-enhances predictive accuracy in engineering design. This model can be deployed to simulate excavation-induced damage propagation, optimizing pit wall angles or tunnel boring machine cutterhead configurations to minimize stress concentration at mineral boundaries. By bridging microscale heterogeneity with macroscale behavior, the model supports data-driven decisions in projects such as nuclear waste repositories or deep geological storage, where fracture-driven instability poses significant risks.

Collectively, these applications translate laboratory-derived mechanisms into practical tools, improving the safety and efficiency of geotechnical engineering projects in fractured granite formations.

Conclusion

  1. 1.

    The inclination angle of pre-existing fractures exerts a significant influence on the mechanical properties of granite. Experimental results demonstrate that uniaxial compressive strength (UCS) increases systematically with fracture inclination angle, while the elastic modulus remains nearly constant across all tested configurations. For double-fractured specimens, the rock bridge angle plays a critical role: strength peaks at 60°, where collinear alignment of fractures and rock bridge amplifies stress localization, leading to reduced load-bearing capacity. This geometric dependency underscores the importance of fracture orientation in predicting rock mass stability.

  2. 2.

    Acoustic emission monitoring reveals a triphasic failure process in fractured granite. During initial loading, microcrack closure induces sparse AE activity (compaction phase). As stress escalates, rapid crack coalescence triggers an abrupt surge in AE signals (peak phase), correlating with macroscopic fracture formation. Post-failure, AE activity stabilizes as crack networks reach equilibrium (stable phase). This temporal pattern provides a diagnostic framework for real-time monitoring of fracture-driven instability.

  3. 3.

    Single-fractured specimens exhibit progressive tensile-dominated failure, with minor shear components localized near fracture tips, preserving partial structural integrity. In contrast, double-fractured specimens undergo sudden tensile-shear hybrid failure due to stress interference between fractures, resulting in complete disintegration. The dominance of tensile behavior in double fractures highlights the synergistic effects of multiple defects on catastrophic failure.

  4. 4.

    The Multilevel Parallel Bonded-GBM (Multi Pb-GBM) successfully replicates fracture evolution from mineral-scale initiation to macroscopic rupture. Simulations confirm that microcracks first nucleate at inter-mineral boundaries, propagate along intra-mineral interfaces, and culminate in intra-crystalline coalescence. Tensile cracks dominate, while shear cracks concentrate near mineral boundaries. This model bridges microscale heterogeneity to macroscale nonlinear behavior, offering a predictive tool for assessing brittle fractures in engineering contexts such as underground excavations and slope stability.