Exploring QSPR in breast cancer drugs via entire neighborhood indices and regression models

Abstract

Cancer is a life-threatening disease that can attack humans at any part of the body as a consequence of abnormal cell growth and proliferation, leading to tumors that can be fatal. Breast cancer is one of the deadliest ailments in the world after lung cancer. Through hormonal and genetic changes that occur in DNA, breast cancer can affect women. The quantitative structural-property relationship (QSPR) is used to provide a comprehensive study of 16 drugs involved in the treatment of breast cancer. According to their chemical structure, the drugs being studied are modeled as molecular graphs. The purpose of this study is to examine the utility of new entire neighborhood topological indices in characterizing the physicochemical properties of a range of breast cancer drugs. Cubic regression analysis was initially employed, followed by multiple linear regression modeling to enhance the correlation between the entire neighborhood topological indices and some properties of the aforementioned drugs. The analysis results are presented and discussed, leading to conclusions about the potential of these new indices for pharmaceutical and chemical research on breast cancer treatments.

Introduction

Irrespective of gender or age, cancer is a life-threatening disease and can form in human beings at any part of the body. Our bodies are perfectly made up of a tremendous number of cells that divide naturally every day. When the division and growth of some cells happen abnormally and spread to surrounding tissues to form lumps or tumors, cancer forms. This happens due to some cells that divide more than they should or do not die when they should¹. According to², there are more than 200 types of cancer, and each is classified as the part of the body it originates from, such as breast cancer. Usually, women are affected by breast cancer, more often than other types. In 2020, 2.3 million women got affected by breast cancer, and 685,000 of them died. Mostly breast cancer forms in the lining of milk ducts, or in the lobules which what supplies the milk to the ducts³. Until 15 years ago, there were not a lot of options when it comes to breast cancer treatment. Either chemotherapy medication or hormone therapy would be the only treatment solutions for breast cancer patients. Unlike nowadays, treatment for such a disease has developed tremendously and more efficiently, newer, more effective chemotherapy and intelligent drugs taken by vascular access or by taking it through the mouth would target the cancer cells accurately and effectively. At research centers, developing new drug medication is very costly. It would require an average of 14 years, and its cost can rise to 1.5 billion dollars, only to get one drug approved. The most important objective in contemporary pharmaceutical and medicinal chemistry research is to design novel compounds with particular biological effects, and absolutes in a short time and at a lower cost. Quantitative structure-property [activity] relationship analysis is one of the tools employed to achieve this purpose in discovering and developing compounds that can be an efficient ingredient for new drugs. For more details see^4,5,6

Chemical graph theory is defined as a field of mathematical chemistry that handles with applications of graph theory to solve molecular issues. A molecular graph is a graph model used to present the chemical structure of a compound by considering atoms as graph vertices and chemical bonds as edges. The quantitative structure-property relationship (QSPR) and quantitative structure-activity relationship (QSAR) analysis are used to study and estimate the relationship between the characteristics of various chemical compounds and their biological activities via mathematical methods. A topological index is a numerical value that characterizes the topological structures of the molecular graph. Topological descriptors play a crucial role in describing the physical and chemical properties of numerous chemical compounds. In recent years, the application of these invariants in investigations of QSPR and QSAR analysis has received significant scholarly interest and is employed considerably in diverse fields such as mathematics, bioinformatics, and cheminformatics. Also, QSPR can be useful in determining the optimal association between topological indices and pharmacological properties. In order to avoid excessive and time-consuming laboratory experiments, numerous topological descriptors are applied^7,8,9

QSPR is an essential computational method used in modern drug design and materials science. It involves creating mathematical relationships between the chemical structure of compounds, usually represented by topological indices and their physico-chemical or biological properties. In drug discovery, especially for cancer treatment, QSPR is crucial as it allows researchers to predict important properties such as solubility, permeability, and toxicity before synthesizing compounds and conducting biological evaluations. This predictive ability significantly reduces the time, cost, and risks associated with experimental procedures and late-stage drug development failures.

By accurately modeling the Quantitative structure–property relationships, QSPR helps optimize lead compounds, enhancing their selectivity and effectiveness against cancer cells while minimizing potential side effects. This method is particularly beneficial in the early stages of drug design, where computational screening and prioritization of compounds streamline the identification of promising candidates.

Therefore, based on the significance of QSPR in drug design, and given that degree-based topological indices have been proven to be valuable tools for investigating drug compounds related to breast cancer, this has motivated us to apply these novel indices to some breast cancer drugs.Hence, through this study, we conduct a comprehensive QSPR based analysis of 16 drugs used in breast cancer treatment. We compute several topological indices to characterize their molecular structures, aiding chemists and researchers in understanding structure–activity relationships and guiding the development of more effective therapeutic agents.

Since 1947 until now, numerous topological indices have been introduced and have several applications. For more details about the indices, see^{10,11,12,13,14,15,16,17}. A relationship between these invariants and the characteristics of drugs used in the treatment of some diseases has been explored by many researchers such as cardiovascular disease¹⁸, heart attack¹⁹, infertility²⁰, HIV/AIDS²¹, blood cancer²², bone marrow cancer²³, breast cancer^3,6,24, malaria²⁵, and colorectal cancer²⁶.

The concept of neighborhood indices was started in 2018 by Mondal, De, and Pal²⁷. The neighborhood indices have significant applications in various areas of computational chemistry and drug discovery. There are numerous studies in this field, along with a wide range of applications, which can be explored through many published articles. For more details, see^{28,29,30,31,32} The initial appearance of the entire topological indices was in 2018 by A. Alwardi et al.³³. Subsequently, the entire indices were proposed for several known indices such as the entire forgotten index³⁴, the entire ABC index³⁵, the entire Randić index³⁶, the entire Sombor index³⁷, the entire harmonic index³⁸, and the recently introduced, the entire Albertson index and the entire sigma index³⁹. The field of topological indices has recently seen the development of neighborhood indices (focused on local atomic environments) and entire topological indices (providing a comprehensive view of atomic and bond interactions). Recognizing the strengths of both, we have introduced the first, modified, and second entire neighborhood indices. These new descriptors integrate the localized insights of neighborhood indices within the broader scope of entire indices, resulting in a more balanced and informative representation of molecular structure. This unique combination is anticipated to substantially improve the accuracy of predictions for diverse molecular properties. Previous research has already shown strong correlations between entire neighborhood topological indices and the physico-chemical properties of octane isomers and benzenoid hydrocarbons⁴⁰. Leveraging the known connection between anticancer drugs and alkane properties^41,42, this work applies these novel descriptors to a set of 16 breast cancer treatment drugs. The entire neighborhood topological indices present high correlations with physico-chemical properties of octan isomers and benzenoid hydrocarbons⁴⁰. Moreover, according to the interrelation between anticancer drugs and characteristics of alkans^41,42, we aim to apply these new descriptors to 16 drugs used for breast cancer treatment in this work.

In this work, first we obtain the molecular graph for the considered drugs based on their chemical molecular structures, which are Azacitidine, Cytarabine, Daunorubicin, Dexamethasone, Docetaxel, Doxorubicin, Glasdegib, Gilteritinib, Ivosidenib, Paclitaxel, Palbociclib, Pamidronic, Prednisone, Ribociclib, Tioguanine, and Toremifene. Then, in addition to the previously submitted research, which introduced three new indices: first, second, and modified entire neighborhood indices⁴⁰, we introduce two more types, the entire neighborhood forgotten and modified entire neighborhood forgotten, to further extend the study’s application. The values of these entire neighborhood indices are calculated in “Materials and methods”. In “Regression approaches and quantitative analysis”, we propose the relationship between the respective descriptors and the physical characteristics of the 16 mentioned drugs by applying two types of QSPR modeling which are cubic and multiple linear regression analysis. The explanation of the study and analysis of the finding data are illustrated and discussed in “Discussion”, where it presents a significant relationship between the entire neighborhood indices and the physical characteristics of the relevant 16 drugs.

For the readers, Let $\Gamma$ be a graph with vertex set V and edge set E. Two vertices v and u are adjacent, or neighbors, if there is an edge between them, and the set of all neighbors of v is called an open neighborhood of v, N(v). For any vertex $v\in V$, the degree d(v) of the vertex v is defined to be the number of edges that are incident to it. Also, for any edge $e\in E$, the degree d(e) of the edge e is the number of edges adjacent to e in the graph; that is, $d(e)=d(u)+d(v)-2$, where u and v are endpoints of e. For standard graph notations and terminologies, see⁴³.

For an element $x \in V \cup E$ of the graph, the neighborhood degree $\delta (x)$ is defined to be $\delta (x) = \displaystyle \sum _{y\in N(x)} d(y)$. Then, the entire neighborhood forgotten and modified entire neighborhood forgotten indices are defined as follows.

Definition 1

Consider the graph $\Gamma (V,E)$. Then, the entire neighborhood forgotten, and modified entire neighborhood forgotten indices are defined as follows,

$$\begin{aligned} NF^{\varepsilon }(\Gamma )&= \displaystyle \sum _{x \in V(\Gamma ) \cup E(\Gamma )} \delta ^3(x), \end{aligned}$$

and

$$\begin{aligned} MNF^{\varepsilon }(\Gamma )&= \displaystyle \sum _{\begin{array}{c} x \text { is either adjacent} \\ \text {or incident to }y \end{array}} \big [ \delta ^2(x) + \delta ^2(y) \big ]. \end{aligned}$$

Materials and methods

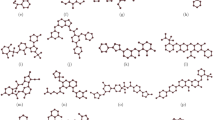
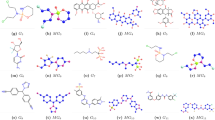
In the field of chemical graph theory, vertices represent atoms, and the corresponding bonds are referred to as edges in the molecular graph of the molecular structure of a chemical compound. The molecular structures of 16 drugs used for breast cancer treatment are displayed in Tables 1 and 2, and their corresponding resulting graphs.

Table 1 Molecular and graph structures of drugs.

Table 2 Continue molecular and graph structures of drugs.

In this study, we analyze these sixteen drugs that are either directly used in the treatment of breast cancer or have known pharmacological relevance in oncology. Many of these agents, such as Doxorubicin, Docetaxel, Paclitaxel, and Palbociclib, are widely used in clinical protocols for breast cancer chemotherapy. Others, including Ribociclib and Toremifene, are targeted therapies or hormone modulators used in specific breast cancer subtypes. The inclusion of these compounds allows for a diverse evaluation of the proposed topological indices across different drug classes and mechanisms of action. Their selection was based on their established therapeutic roles and the availability of structural data necessary for index computation.

The topological indices used in our study are illustrated in Table 3

Table 3 Entire neighborhood topological indices.

The experimental values of the physico-chemical characteristics of these drugs are listed in Table 4, including boiling point (BP), enthalpy of vaporization (EV), flash point (FP), molar refractivity (MR), LogP, and molar volume (MV), which are taken from http://pubchem.ncbi.nim.nih.gov/ and http://www.chemspider.com/Search.aspx.

Table 4 Experimental values for physico-chemical properties of breast cancer drugs.

This research highlights the essential pharmacokinetic and pharmacodynamic properties of the breast cancer drugs being studied. For example, LogP is directly related to lipophilicity and affects absorption, membrane permeability, and distribution within biological compartments. Molar refractivity (MR) and molar volume (MV) can influence drug-receptor binding affinity and the volume of distribution (Vd). Additionally, the boiling point (BP), enthalpy of vaporization (EV), and flash point (FP) are associated with the volatility and stability of compounds, which can impact formulation and metabolism.

The first, modified, second entire neighborhood, entire neighborhood forgotten, and modified entire neighborhood forgotten indices are calculated for the considered 16 drugs using the partition method for vertices and edges. The process of this computation involves the classification of adjacent vertices, adjacent edges, and incident vertices and edges for the molecular graph of each of the aforementioned drugs based on the neighborhood degree of these vertices and edges and applying the definitions of the considered entire neighborhood indices. For instance, consider the molecular graph of Azacitidine, say $\Gamma$. Then, the partition of this graph is depicted in Tables 5 and 6.

Table 5 The partition of the vertices and edges of the molecular graph of Azacitidine.

Table 6 The hole partition of the molecular graph of Azacitidine.

Then, we have

$$\begin{aligned} NM_{1}^{\varepsilon }(\Gamma )&=4+4(9) + 16+2(25)+3(36)+3(49)+2(64) + 9+2(36)+2(49)\\&+4(64)+81+2(100)+121+3(144)+169+196=2148,\\ MNM_{1}^{\varepsilon }(\Gamma )&= 210+514+538 =1262,\\ NM_{2}^{\varepsilon }(\Gamma )&= 623+2604+2040=5267. \end{aligned}$$

The calculation of the entire neighborhood indices for the reminder drugs can be made via the equivalent procedure and their values are illustrated in Table 7.

Table 7 Numerical values of the entire neighborhood indices.

Regression approaches and quantitative analysis

Regression analysis is employed to find the most effective options for breast cancer treatment by examining the predictive power of the physico-chemical properties of these compounds. In this section, we apply the entire neighborhood indices for the statistical QSPR analysis with the physical properties of 16 breast cancer drugs namely, Azacitidine, Cytarabine, Daunorubicin, Dexamethasone, Docetaxel, Doxorubicin, Glasdegib, Gilteritinib, Ivosidenib, Paclitaxel, Palbociclib, Pamidronic, Prednisone, Ribociclib, Tioguanine, and Toremifene. For this purpose, two types of regression modeling are used in this research and it has been presented in detail as demonstrated in the following two subsections.

The statistical parameters which are correlation coefficients (R), the square of the correlation coefficients ($R^2$), adjusted R square (Adj. $R^2$), standard error (Std. error), F change (F), and significance (s-value) are taken into account in the regression model tables.

Cubic regression

In this subsection initially, we investigate the compatibility among the entire neighborhood indices and the physical properties of the breast cancer drugs that are considered in this work using cubic regression analysis. The statistical properties for this QSPR modeling were obtained using (SPSS software 25) and illustrated in Tables 8, 9, 10, 11 and 12. The observations indicate that the correlation coefficient R should be greater than 0.6, and if the s-value is less than 0.05, then the result is considered statistically significant. Otherwise, it is insignificant. The cubic QSPR modeling produced the following predictive regression equations that established a connection between the entire neighborhood indices and the physico-chemical properties of the 16 drugs used in the treatment of breast cancer. The general formula for the cubic regression equation is given by

$$\begin{aligned} P= a_1 (TI) + a_2 (TI)^2 + a_3 (TI)^3 + a_0, \end{aligned}$$

(1)

where P denotes the physical property, $a_0$ for the constant, and $a_1,a_2,a_3$ denote the regression coefficients. Then, using equation 1, the regression equations for the respective topological indices examined in the current study are determined. Later, Figs. 1, 2, 3, 4 and 5 demonstrate the relationships between the correlations of all neighborhood indices and the physical properties.

• 1. The first entire neighborhood index ($NM_{1}^{\varepsilon }$):

  $$\begin{aligned} BP&= 0.312 (NM_{1}^{\varepsilon }) -4.948 \times 10^{-5} (NM_{1}^{\varepsilon })^2 + 2.485 \times 10^{-9} ( NM_{1}^{\varepsilon })^3 + 88.623,\\ EV&= 0.032 (NM_{1}^{\varepsilon }) - 4.842 \times 10^{-6} (NM_{1}^{\varepsilon })^2 + 2.454 \times 10^{-10} (NM_{1}^{\varepsilon })^3 + 40.603,\\ FP&= 0.189 (NM_{1}^{\varepsilon }) - 2.976 \times 10^{-5} (NM_{1}^{\varepsilon })^2 + 1.490 \times 10^{-9} (NM_{1}^{\varepsilon })^3 + 6.694,\\ MR&= 0.111 (NM_{1}^{\varepsilon }) - 1.790 \times 10^{-5} (NM_{1}^{\varepsilon })^2 + 9.134 \times 10^{-10} (NM_{1}^{\varepsilon })^3 -97.254,\\ LogP&= 0.004 (NM_{1}^{\varepsilon }) -5.713 \times 10^{-7} (NM_{1}^{\varepsilon })^2 + 3.087 \times 10^{-11} (NM_{1}^{\varepsilon })^3 - 5.313,\\ MV&= 0.337 (NM_{1}^{\varepsilon }) - 5.407 \times 10^{-5} (NM_{1}^{\varepsilon })^2 + 2.754 \times 10^{-9} (NM_{1}^{\varepsilon })^3 -326.010. \end{aligned}$$

Table 8 Statistical specifications for the cubic model of $NM_{1}^{\varepsilon }$.

Fig. 1

Correlations of the physical properties with the first entire neighborhood index for 16 breast cancer drugs.

• 2. The modified entire neighborhood index ($MNM_{1}^{\varepsilon }$):

  $$\begin{aligned} BP&= 0.204 (MNM_{1}^{\varepsilon }) - 4.083 \times 10^{-5} (MNM_{1}^{\varepsilon })^2 + 4.039 \times 10^{-9} (MNM_{1}^{\varepsilon })^3 + 355.372,\\ EV&= 0.012 (MNM_{1}^{\varepsilon }) - 7.876 \times 10^{-7} (MNM_{1}^{\varepsilon })^2 + 1.291 \times 10^{-10} (MNM_{1}^{\varepsilon })^3 + 75.800,\\ FP&= 0.129 (MNM_{1}^{\varepsilon }) - 2.635 \times 10^{-5} (MNM_{1}^{\varepsilon })^2 + 2.578 \times 10^{-9} (MNM_{1}^{\varepsilon })^3 + 163.945,\\ MR&= 0.196 (MNM_{1}^{\varepsilon }) - 5.748 \times 10^{-5} (MNM_{1}^{\varepsilon })^2 + 5.775 \times 10^{-9} (MNM_{1}^{\varepsilon })^3 - 101.089,\\ LogP&= 0.012 (MNM_{1}^{\varepsilon }) - 3.786 \times 10^{-6} (MNM_{1}^{\varepsilon })^2 + 3.914 \times 10^{-10} (MNM_{1}^{\varepsilon })^3 - 10.088,\\ MV&= 0.637 (MNM_{1}^{\varepsilon }) + 1.916 \times 10^{-8} (MNM_{1}^{\varepsilon })^3 - 366.795. \end{aligned}$$

Table 9 Statistical specifications for the cubic model of $MNM_{1}^{\varepsilon }$.

Fig. 2

Correlations of the physical properties with the modified entire neighborhood index for 16 breast cancer drugs.

• 3. The second entire neighborhood index ($NM_{2}^{\varepsilon }$):

  $$\begin{aligned} BP&= 0.129 (NM_{2}^{\varepsilon }) - 8.016 \times 10^{-6} (NM_{2}^{\varepsilon })^2 + 1.540 \times 10^{-10} (NM_{2}^{\varepsilon })^3 + 75.355,\\ EV&= 0.014 (NM_{2}^{\varepsilon }) - 8.256 \times 10^{-7} (NM_{2}^{\varepsilon })^2 + 1.594 \times 10^{-11} (NM_{2}^{\varepsilon })^3 + 36.956,\\ FP&= 0.078 (NM_{2}^{\varepsilon }) - 4.815 \times 10^{-6} (NM_{2}^{\varepsilon })^2 + 9.221 \times 10^{-11} (NM_{2}^{\varepsilon })^3 - 0.957,\\ MR&= 0.041 (NM_{2}^{\varepsilon }) - 2.573 \times 10^{-6} (NM_{2}^{\varepsilon })^2 + 5.044 \times 10^{-11} (NM_{2}^{\varepsilon })^3 - 82.835,\\ LogP&= 0.001 (NM_{2}^{\varepsilon }) - 7.038 \times 10^{-8} (NM_{2}^{\varepsilon })^2 + 1.486 \times 10^{-12} (NM_{2}^{\varepsilon })^3 - 4.109,\\ MV&= 0.122 (NM_{2}^{\varepsilon }) - 7.584 \times 10^{-6} (NM_{2}^{\varepsilon })^2 + 1.484 \times 10^{-10} (NM_{2}^{\varepsilon })^3 - 273.970. \end{aligned}$$

Table 10 Statistical specifications for the cubic model of $NM_{2}^{\varepsilon }$.

Fig. 3

Correlations of the physical properties with the second entire neighborhood index for 16 breast cancer drugs.

• 4. The entire neighborhood forgotten index ($NF^{\varepsilon }$):

  $$\begin{aligned} BP&= 0.027 (NF^{\varepsilon }) - 3.613 \times 10^{-7} (NF^{\varepsilon })^2 + 1.392 \times 10^{-12} (NF^{\varepsilon })^3 + 129.838, \\ EV&= 0.003 (NF^{\varepsilon }) -4.076 \times 10^{-8} (NF^{\varepsilon })^2 +1.560 \times 10^{-13} (NF^{\varepsilon })^3 +37.760, \\ FP&= 0.016 (NF^{\varepsilon }) -2.154 \times 10^{-7} (NF^{\varepsilon })^2 + 8.271 \times 10^{-13} (NF^{\varepsilon })^3 +33.502, \\ MR&= 0.007 (NF^{\varepsilon }) -9.237 \times 10^{-8} (NF^{\varepsilon })^2 + 3.704 \times 10^{-13} (NF^{\varepsilon })^3 -29.593, \\ LogP&= -1.805 \times 10^{-9} (NF^{\varepsilon })^2 +8.363 \times 10^{-15} (NF^{\varepsilon })^3 -1.397, \\ MV&= 0.020 (NF^{\varepsilon }) -2.616 \times 10^{-7} (NF^{\varepsilon })^2 +1.047 \times 10^{-12} (NF^{\varepsilon })^3 -107.248. \end{aligned}$$

Table 11 Statistical specifications for the cubic model of $NF^{\varepsilon }$.

Fig. 4

Correlations of the physical properties with the entire neighborhood forgotten index for 16 breast cancer drugs.

• 5. The modified entire neighborhood forgotten index ($MNF^{\varepsilon }$):

  $$\begin{aligned} BP&= 0.061 (MNF^{\varepsilon }) -1.731 \times 10^{-6} (MNF^{\varepsilon })^2 +1.508 \times 10^{-11} (MNF^{\varepsilon })^3 +63.718, \\ EV&= 0.007 (MNF^{\varepsilon }) -1.832 \times 10^{-7} (MNF^{\varepsilon })^2 +1.599 \times 10^{-12} (MNF^{\varepsilon })^3 +34.137, \\ FP&= 0.037 (MNF^{\varepsilon }) -1.037 \times 10^{-6} (MNF^{\varepsilon })^2 +9.006 \times 10^{-12} (MNF^{\varepsilon })^3 -7.429, \\ MR&= 0.018 (MNF^{\varepsilon }) -5.201 \times 10^{-7} (MNF^{\varepsilon })^2 +4.643 \times 10^{-12} (MNF^{\varepsilon })^3 -75.174, \\ LogP&= -1.306 \times 10^{-8} (MNF^{\varepsilon })^2 +1.275 \times 10^{-13} (MNF^{\varepsilon })^3 -3.487, \\ MV&= 0.053 (MNF^{\varepsilon }) -1.522 \times 10^{-6} (MNF^{\varepsilon })^2 +1.356 \times 10^{-11} (MNF^{\varepsilon })^3 -249.571. \end{aligned}$$

Table 12 Statistical specifications for the cubic model of $MNF^{\varepsilon }$.

Fig. 5

Correlations of the physical properties with the modified entire neighborhood forgotten index for 16 breast cancer drugs.

Multiple linear regression

In this part, we perform the multiple linear regression model to predict the physical characteristics of the aforementioned 16 drugs used in breast cancer treatment. The signification of this analysis can be determined from the value of the statistical parameters R, $R^2$, Adj. $R^2$, Std. error, F, and s-value which displayed in Table 13

Table 13 Statistical specifications for the multiple linear model.

The multiple linear regression model yields the following predictive equations, such that the general formula is given by

$$\begin{aligned} P= a_0 + a_1 (NM_{1}^{\varepsilon }) + a_2 (MNM_{1}^{\varepsilon }) + a_3 (NM_{2}^{\varepsilon }) + a_4 (NF^{\varepsilon }) + a_5 (MNF^{\varepsilon }), \end{aligned}$$

(2)

where $P,a_0,a_1,a_2,a_3, a_4$, and $a_5$ are as mentioned in Eq. (1). Therefore, the following equations are obtained by utilizing the formula in (2).

$$\begin{aligned} BP&= 410.129 + 0.294 (NM_{1}^{\varepsilon }) - 0.182 (MNM_{1}^{\varepsilon }) - 0.010 (NF^{\varepsilon }) -0.004 (MNF^{\varepsilon }),\\ EV&= 74.651 + 0.051 (NM_{1}^{\varepsilon }) - 0.056 (MNM_{1}^{\varepsilon }) - 0.002 (NF^{\varepsilon }) + 0.002 (MNF^{\varepsilon }),\\ FP&= 203.779 + 0.177 (NM_{1}^{\varepsilon }) - 0.117 (MNM_{1}^{\varepsilon }) - 0.006 (NF^{\varepsilon }) - 0.001 (MNF^{\varepsilon }),\\ MR&= 1.309 - 0.114 (NM_{1}^{\varepsilon }) + 0.252 (MNM_{1}^{\varepsilon }) + 0.005 (NF^{\varepsilon }) - 0.011 (MNF^{\varepsilon }),\\ LogP&= -3.694 - 0.012 (NM_{1}^{\varepsilon }) + 0.022 (MNM_{1}^{\varepsilon }) + 0.001 (NF^{\varepsilon }) -0.001 (MNF^{\varepsilon }),\\ MV&= -11.106 - 0.408 (NM_{1}^{\varepsilon }) + 0.840 (MNM_{1}^{\varepsilon }) + 0.020 (NF^{\varepsilon }) -0.039 (MNF^{\varepsilon }). \end{aligned}$$

The comparison between the experimental and predicted values of the physical properties of the treatments mentioned in this study are displayed in Figure 6, where (1) Azacitidine, (2) Cytarabine, (3) Daunorubicin, (4) Dexamethasone, (5) Docetaxel, (6) Doxorubicin, (7) Glasdegib, (8) Gilteritinib, (9) Ivosidenib, (10) Paclitaxel, (11) Palbociclib, (12) Pamidronic, (13) Prednisone, (14) Ribociclib, (15) Tioguanine, and (16) Toremifene.

Fig. 6

Comparative between the multiple linear prediction and experimental values of the properties for 16 breast cancer drugs.

Discussion

This study employs five novel entire neighborhood topological indices alongside numerical molecular descriptors to investigate the structural and physicochemical properties of drugs used in the treatment of breast cancer. It is common knowledge that the greater value of the statistical properties R, $R^2$, Adj. $R^2$, and F, as well as the small value of the Std. error indicates that there is a relationship between the dependent and independent variables. The effectiveness of this relationship is based on the significant value if it is greater or less than 0.05.

In the consideration of cubic regression modeling, we observe that BP, EV, and FP have their highest correlations with $NF^{\varepsilon }$ with $R=0.921, 0.937$, and 0.927, respectively. Moreover, MR, LogP, and MV possess good correlations with $MNM_{1}^{\varepsilon }$ where in this case $R=0.936, 0.727$, and 0.941, respectively. In general, the results obtained in this QSPR modeling type provide significant correlations between the entire neighborhood indices and the physical properties of the breast cancer drugs which are all over 0.85, in which the correlation coefficients ranged between (0.851-0.921) for BP, (0.864-0.937) for EV, (0.858-0.927) for FP, (0.846-0.936) for MR, and (0.854-0.941) for MV, except for the Log P which has values ranging between (0.603-0.727) with these descriptors. The s-value is less than or equal to 0.001 for BP, EV, FP, MR, and MV, indicating the significance of the result. The cubic regression model for LogP only shows significant results with the modified entire neighborhood index.

Now, regarding the multiple linear regression analysis, it provides correlation coefficients for the considered physical properties with the first, modified, second entire neighborhood, entire neighborhood forgotten, and modified entire neighborhood forgotten indices greater than those shown in the cubic one. Constructed multiple linear modeling in SPSS demonstrates an excellent correlation value with MR, (R = 0.994). It is evident that R values greater than 0.91 are shown for BP (R = 0.915), FP (R = 0.919), and MV (R = 0.985). Also, EV, and LogP have high correlation coefficients with $R= 0.895$, and 0.805, respectively. The s-value for LogP is 0.015 while other properties have 0.000, which elucidates a statistically significant relationship between these physical properties and the proposed indices.

As it is demonstrated in Tables 8 to 13, we found that the multiple linear regression analysis provided considerable results as compared with the cubic modeling type for boiling point, enthalpy of vaporization, flash point, molar refractivity, LogP, and molar volume as it is shown in Fig. 7. This means that those physical characteristics can be predicted efficiently using multiple linear regression modeling of entire neighborhood indices. The outcomes of this study indicate that first, modified, second entire neighborhood, entire neighborhood forgotten, and modified entire neighborhood forgotten indices have the potential to contribute to the discovery of novel treatments for several diseases.

Fig. 7

Comparison between the correlation coefficients of two regression models.

Conclusion

The QSPR analysis included in this work is a valuable tools using for figuring and understanding the physical and chemical properties of chemical compounds. In addition, it assists researchers in comprehending the effective properties of anti-cancer drugs that are required for the treatment of breast cancer or in discovering new drugs. The prediction of the physico-chemical characteristics is widely done using topological descriptors. The aim of this study is to extract structural information through topological indices in a cost-effective and time-efficient manner. In this research, we introduced the concept of the entire neighborhood forgotten and modified the entire neighborhood forgotten indices to complement the previously defined indices, which are the first, modified, and second entire neighborhood indices⁴⁰. Then, the graph structures of the chosen 16 drugs used in the treatment of breast cancer are obtained based on their chemical molecular structures. The values of the entire neighborhood indices of these drugs were calculated in order to understand their physical properties considered in the study, which are boiling point, enthalpy of vaporization, flash point, molar refractivity, LogP, and molar volume. Afterward, two types of QSPR modeling are applied to determine the prediction power of the first, modified, second entire neighborhood, entire neighborhood forgotten, and modified entire neighborhood forgotten indices with the considered compounds. These models include cubic and multiple linear regression analysis and their predictive equations are obtained. We observed that the physical properties of the mentioned breast cancer drugs have a strong correlation, and the respective indices have a significant relationship with them. This finding indicates that the entire neighborhood indices have the potential to be utilized in the discovery of novel drugs for various ailments.

Future research directions stemming from this work include expanding the dataset of breast cancer drugs for model validation and refinement, exploring additional physicochemical and biological properties like toxicity and pharmacokinetic parameters, and conducting comparative studies against established topological descriptors to assess the relative performance of the entire neighborhood indices. Investigating the chemical basis of observed index-property correlations could provide insights into drug mechanisms of action. Furthermore, virtual screening using the developed QSPR models could identify novel drug candidates, and the applicability of these indices to other disease targets warrants investigation to broaden the research’s impact.

Limitations

Despite the extensive development of topological indices designed to convey structural information about molecular graphs and computer networks, it remains challenging to capture all the relevant characteristics of a substance. Therefore, additional molecular descriptors are needed to provide a more comprehensive and theoretically grounded approach to characterizing chemical structures, particularly those of drug compounds used in the treatment of breast cancer.