Evaluation of sports teaching quality in universities based on fuzzy decision support system

Abstract

Sports teaching in universities relies on staff experience, training modes., evaluated by the student’s performance and competitive outcomes. The teaching quality assessment requires a large volume of data related to teaching patterns, training. A Teaching Convoluted Quality Assessment Model (TCQAM) is proposed in this article to provide a robust teaching quality assessment. The proposed model intakes different factors, such as training patterns, sessions, time, associated with the teaching sessions. Based on the sports training requisites, the above, like associated factors, are validated using a fuzzy decision system. In this decision system, the possible factors for maximum teaching quality are convoluted with each of the above-mentioned factors. The fuzzy membership derivatives identify the least performance factor to perform an improvement assessment. This improvement assessment replaces the low teaching quality factors with the recommended or novel inputs. The fuzzy performs high-quality membership derivatives on this improved assessment to ensure better teaching is provided. Therefore, a balanced teaching input improves the quality of sports teaching for different training sessions.

Introduction

Evaluation of education quality is necessary to improve results and stimulate student athletic growth in university sports education¹. Traditional assessment techniques rely on instructors’ and students’ subjective experiences and struggle to capture sports education’s complexity and change. In the classroom, these techniques fail because they cannot handle large datasets or intangibles like student engagement, motivation, and enjoyment². Utilizing modern methodologies for analyzing and improving instructional practices is required to evaluate sports education programs. Since current methods don’t always adjust to real-time performance, training patterns, and session dynamics, we don’t always get the best results from our courses³. These gaps must be filled to build a complete evaluation model that meets training needs, educational goals, and student needs⁴.

Student survey responses might reveal a teacher’s level of education. These questionnaires can help instructors assess their strengths and weaknesses in the many elements that affect classroom performance⁵. Today’s universities value students’ critical and creative thinking, which has increased the requirement for reliable assessment methods that can measure more than faculty competency⁶. Innovative evaluation methods are more important than ever for enhancing learning outcomes and student growth. Data-driven sports education program evaluation is becoming mainstream⁷. Data collection, which involves maintaining and arranging information over time, allows monitoring of educators’ activities. Many schools evaluate athletic programs using KPIs like student participation, information retention, and instructor efficiency⁸. FDSS, or fuzzy decision support systems, can handle ambiguity and subjective input, making them excellent for assessing instructional quality. Improved interpretability, systematic categorization, and improvement recommendations are FDSS benefits⁹. It organizes and analyzes generic data like teacher lecture outcomes and class performance. Membership functions enable targeted changes by distinguishing high- and low-quality educational results¹⁰. The method suggests optimizing training schedules and low-quality instructional inputs to improve education¹¹.

Current research on evaluating sports education quality addresses novel approaches, such as data-driven frameworks that use machine learning to identify actions and provide feedback, blockchain-enabled models to evaluate performance securely, and IoT-enabled systems to recognize activities¹². These methods have pros and cons. They offer real-time monitoring and higher accuracy and scalability¹³. However, they are too costly, cannot adjust to varied athletic venues, and struggle to measure subjective factors like student interest and enjoyment¹⁴. Most techniques merely address some issues rather than providing a complete assessment framework¹⁵. This study provides a paradigm that may adapt to the organization’s changing needs to address these issues¹⁶. This uses a fuzzy decision-support system and theoretical and practical assessment methods. It evaluates sports education using quantifiable performance and intangible learning outcomes to provide a complete picture¹⁷.

The research provides a thorough framework for solving these issues in the Teaching Convoluted Quality Assessment Model (TCQAM). Large-scale data collection on teaching patterns, session forms, and time allocation is needed to evaluate and improve education. Using performance-driven real-time training adjustments to provide an effective and personalized learning environment. Traditional evaluation techniques disregard non-cognitive factors like student fun and participation. The selection of a Fuzzy Decision Support System (FDSS) over other assessment approaches was motivated by the inherent complexity and subjectivity of evaluating sports instruction quality at the university level. Conventional statistical or rule-based systems sometimes lack the suppleness to manage vague, qualitative elements such as instructional efficacy, student involvement, and the flexibility of training methodologies. FDSS facilitates modeling uncertainties using fuzzy logic, offering a more sophisticated and realistic evaluative framework. Its capacity to amalgamate quantitative metrics (e.g., performance scores, improvement rates) and qualitative assessments (e.g., expert evaluations, instructional delivery) renders it especially appropriate for educational contexts where multifaceted, ambiguous, or intersecting criteria shape decisions. The flexibility and interpretability of FDSS validate its role as the primary decision-making mechanism in the TCQAM paradigm.

The main contribution of the article include:

• The creation of an innovative TCQAM that uses FDSS to accurately assess the quality of instruction by combining training patterns, session dynamics, and performance data.

• Improvement evaluations can help address problems that hinder performance, leading to better sports teaching methods.

• Experimental datasets will be used to validate the proposed model and show that it can adapt to different training conditions and participant ratios.

The remaining research is arranged as follows: Sect. 2 summarizes the Quality Assessment Model literature. Section 3: Theory and Practice of the Teaching Convoluted Quality Assessment Model. Present and discuss results in Sect. 4. Section 5 summarizes the findings, makes conclusions, and recommends future research.

Related works

Intelligent systems for skill and activity recognition

To improve basketball training efficiency, Zhou et al.¹⁸ created a smart system to help beginners in basketball by using IoT to recognize their activities. Their goal is to improve basketball training by accurately recognizing activities. The method combines IoT edge-cloud architecture with Adaptive Binary PSO (IoT-EC-ABPSO) for feature selection. The proposed method achieved a remarkable 97.26% average accuracy in recognizing five basic basketball activities. Although the system uses swarm intelligence to improve accuracy, its dependence on many IoT devices may make installation more expensive. The research does not assess the system’s adaptability to different game scenarios and long-term performance. Research should lower resource utilization and generalize to more sporting settings.

Lin et al. (2023)¹⁹ offer a new badminton teaching approach that uses gyroscopes and electromyography better than earlier methods. This system’s real-time input can increase skill training accuracy. The technique accurately measures muscle activity and movement patterns, but scalability and cost issues occur in more extensive educational contexts. The research does not account for real-world factors like student capabilities and external influences. This is because the research only considers controlled conditions, not real-world situations. Future studies should examine ways to make it more adaptive and cheaper for different learning contexts. This helps us learn how to improve its usefulness.

He et al.²⁰ developed an accurate track and field sports action recognition system using ant colony optimization. They aimed to integrate cutting-edge technologies like AI, machine learning, IoT, and virtual reality into sports Decision Support Systems (DSS). These systems help coaches make accurate, unbiased decisions about player skills and selection, leading to improved performance. DSS swiftly addresses player misconduct, promoting a safe sports environment. The system needs high-quality sensor data, which may not be accurate across sports and technologies. This may lower system efficiency. The literature does not indicate if the system can handle larger datasets or many track-and-field events, which may limit its application. Little research has been done on how it works in less-than-ideal conditions, such as environmental issues or weary athletes. Future studies should focus on improving the algorithm’s effectiveness in other sporting circumstances and expanding its applicability.

Data-driven approaches to injury prevention and physical monitoring

Cui et al.²¹ examined sports training data to determine wearable technology’s benefits. They sought to improve physical recovery and minimize injury risk. Wearable sensors that collected real-time data were used to avoid athlete training injuries. Artificial neural networks, machine learning, and time series analysis are used to study injury prevention and rehabilitation. Although it gives precise recovery characteristics, the study needs pricey devices and raises privacy concerns, limiting its use. Scalability concerns are compounded by uncertainty about system performance in controlled conditions. The idea is useless since it has not been tested across many sports. Researchers should make it more versatile and affordable for additional applications.

To optimize basketball instruction and mitigate injury risks, Yin et al.²² proposed an algorithm to prevent injuries in basketball training. The goal is to improve basketball teaching by creating an online platform for learning basic techniques. Ultra-Wideband Sensor Networks and node localization technology highlight the challenges and opportunities in basketball teaching. The proposed method improved accuracy in player tracking and injury prevention in basketball teaching. The study does not assess the sensor’s accuracy in outdoor settings or lighting conditions. Furthermore, institutions with limited resources may find it difficult to implement due to the reliance on high-end equipment. Securing cost-effective implementation for wider accessibility and optimizing the algorithm for varied situations should be the focus of future studies.

Advanced computational models for teaching quality and administration

De-kun et al. developed an innovative mobile PE class assessment approach²³. To create a quantitative evaluation model, the program analyzes assessment indices and sports resource administration factors. The author seek to increase PE class mobile intelligent assessment accuracy and efficiency. Data processing in 1 millisecond shows the algorithm’s efficiency. The approach fails to address scalability in larger class sizes, where several examinations could overwhelm the system. There has also been minimal research on its application in outdoor or mixed-ability classrooms. Future research should focus on expanding the algorithm’s applicability and demonstrating its flexibility in other educational contexts.

Xie et al.²⁴ designed a multi-agent physical education teaching management system. This technique aims to improve PE classroom efficiency and subject mastery. The technology lets teachers and students quickly exchange and receive information, encouraging cooperation and resource sharing. The multi-agent model-based system exhibits outstanding efficiency and stability. Due to its intricacy, teachers without technical knowledge may find it difficult to use. It hasn’t been tested with different sports or student demographics. Research should focus on simplifying user interfaces and testing system adaptation in varied educational environments.

According to Bao and colleagues, hybrid PE combines online and offline learning and has a new evaluative framework²⁵. The method’s goal is to build an evaluation system for online/offline hybrid physical education programs using mobile edge computing. Using analysis to simplify index items creates a comprehensive hybrid physical education evaluation system. This strategy improves hybrid PE quality and reduces evaluation expenses and mistakes. Because it requires a fast internet connection, the strategy may not operate in areas with poor network infrastructure. The evaluation technique may fail in certain cases, such as when equipment fails or when doing outside activities. Future research should make the system more customizable for several educational situations and assure excellence regardless of the conditions.

Machine learning and deep learning for educational enhancement

Liu²⁶ used ResNet34 and big data (ResNet34-BD) to create this long-term online physical education system. We wanted to permanently solve online physical education problems using cutting-edge photo recognition algorithms. ResNet34, the system’s base, allows real-time student behavior analysis and correction across sports. Technology has greatly improved online physical education and virtual sports teaching. However, many classes, especially low-resource ones, may lack the expertise to implement this method correctly. The model’s inability to handle larger classes or physical activities raises concerns about its scalability. Big data in educational technology platforms may raise ethical and privacy concerns. Scientists must find a way to simplify data collecting and test it in additional courses.

Wu²⁷ assessed a brand new algorithm in volleyball coaching to enhance evaluation effectiveness. The aim is to conquer hurdles in traditional assessment, especially in complex scenarios of kernel characteristic selection for non-sparse models. The set of rules iteratively selects simple classifiers and applies constraints on kernel feature proportions through elastic net-kind normalization. The method mixes L1 and L2 norms to improve coaching assessment in sports training. The algorithm’s need on many training data may be troublesome in sparse or expensive data environments. Scalability improvements would help the study handle larger datasets and more volleyball techniques. This would broaden the algorithm’s instructional applications. Future research should improve the algorithm for more use cases and test it in academic and sporting settings.

Emerging technologies in teaching evaluation and predictive modeling

Cao et al. (2021)²⁸ offer a blockchain-compatible Hidden Markov Model (BCHMM) that can predict sports performance. This method enhances performance projections, secure data sharing, and secure data interchange. The technique demands a lot of computer power, which may slow real-time performance analysis, but blockchain technology ensures data integrity and objectivity. This technique ignores confounding factors like the learner’s mood or the teaching environment in favor of statistical trends. However, massive sports networks still face scalability and practicability challenges. Future study should focus on developing lightweight blockchain models that employ multi-dimensional data to anticipate.

Zhang et al. developed a way to assess standard college physical education²⁹. Edge computing and artificial intelligence are used to improve physical education teacher evaluations. The model emphasizes the physical fitness compliance rate in student evaluations and adjusts final examination scores accordingly. A real-time system monitors teaching quality and enables continuous student evaluation during the learning process. Cost-effective testing and implementations in numerous physical education scenarios should be studied.

Pedagogical techniques with targeted instruction

Huang et al.³⁰ used a focused teaching approach and phased evaluation to address the highlighted issue in public tennis classes. Their primary goals were to improve students’ interest and enthusiasm in tennis sessions and their basic tennis abilities. The method blends targeted teaching methods with a structured evaluation process. The technique is effective and scalable in smaller classrooms but struggles in larger ones. There has also been little investigation into its potential use in varied learning contexts, such as those with students of varied skill levels and in natural settings. The phased evaluation has no real-time adjustment capability, which would lessen its usefulness in classrooms with much change. Improving the approach for wider application and evaluating its efficacy in different settings should be the primary goals of future studies.

Using wireless sensors, Zhu et al.³¹ started tracking college students’ sports and mental health in real-time. The aim is to make wireless sensor networks safer and more effective for tracking college students’ sports and mental health. The model proposes a system with multiple wireless sensor stations, using advanced encryption and blockchain for secure communication among different parts. The model includes a live system to monitor students’ sports participation and mental well-being.

Wang and Jian³² developed an intelligent assessment technique for basketball, teaching reliability to improve quality and fairness. They expect this new system will make basketball teaching evaluations more reliable and fair. The model objectively assesses class basketball skills using swarm intelligence and edge computing. The method improves students’ basketball skills and interests.

The literature survey is shown in Table 1.

Table 1 Literature survey.

The lack of a holistic model that can combine quantitative performance indicators with qualitative factors like engagement, contentment, and motivation is one of the gaps that these studies have pointed out. Regarding real-time adaptation and individualized recommendations for instructional improvements, current techniques prioritize technology-driven solutions that aren’t scalable or completely ignore these issues. Given the fragmented environment, a unified framework that links theoretical ideas to real-world applications is needed. This research proposes a fuzzy decision-support system-based teaching Convoluted Quality Assessment Model (TCQAM) to address these issues. This strategy considers conceptual and empirical factors to ensure scalability, practical sports education quality recommendations, and dynamic adaptability. The established technique of evaluating sports education includes improved technology. This is done by integrating coordinated improvement techniques with real-time feedback.

Teaching convoluted quality assessment model

The Teaching Convoluted Quality Assessment Model (TCQAM) is developed to address critical limitations in conventional sports teaching evaluation methods at the university level, particularly their lack of adaptability, precision, and real-time responsiveness. This study proposes the integration of a Fuzzy Decision Support System (FDSS) to solve these challenges by:

• Enabling real-time diagnostic and corrective feedback through fuzzy membership functions to detect and address deficiencies in teaching quality across training sessions and instructional patterns.

• Designing a dynamic, data-driven instructional framework that personalizes training content based on student performance metrics and learning needs, thereby enhancing engagement and outcomes.

• Applying fuzzy inference mechanisms to systematically classify, evaluate, and improve both tangible (skill acquisition) and intangible (strategic understanding) components of sports education.

The TCQAM solves these limits using data-driven insights and a fuzzy decision-making framework to redefine sports instructor assessment. The approach aims to evaluate and improve university gym classes by providing a comprehensive, adaptable, and dynamic framework.

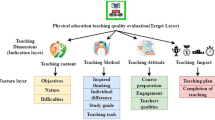
The TCQAM may be enhanced by incorporating factors such as teaching staff expertise, student performance, and training methods to enhance suggestions for assessing sports education quality. Sports education must be evaluated for college students to succeed in a competitive environment. One of the most crucial parts of a successful curriculum is university athletics. TCQAM synchronizes to minimize the negative effects of demanding requests such as high-performance student data access, storage, sharing, and delivery delay. In Fig. 1, the TCQAM is illustrated. Alternative evaluation methods like the Teaching Convoluted Quality evaluation Model (TCQAM) were created to improve collegiate athletics programs while addressing concerns with current approaches. The model analyzes training patterns, sessions, and time allocations to assess instruction quality. Fuzzy decision support systems (FDSS) underpin TCQAM. They grade teaching as good or bad to concentrate on therapy. We may categorize using student performance data, root cause analysis, and iterative assessments. Enhancements are possible using these strategies. By balancing training inputs and student needs, the TCQAM can personalize quality development in sports education.

TCQAM’s ability to adapt to training session conditions sets it apart. The model validates training data through a fuzzy membership function, including agility, engagement, and time deployment. Using this procedure, TCQAM can pinpoint causes of poor teaching quality and find solutions by suggesting new approaches. The model also carries out an improvement assessment, which entails substituting ineffective teaching methods with new inputs specified for the pupils’ requirements. That way, the training sessions are fine-tuned all the time, improving instruction quality and decreasing the probability of session failures.

Fig. 1

Illustration of the TCQAM.

The quality assessment of teaching for sports can enhance the management of sports teaching in universities. In universities, sports teaching is highly emphasized on the merging of theoretical and practical sessions; it requires a large volume of data related to training patterns, sessions, and not only the systematic theoretical basis, and professional knowledge, but also a rational exercise system. In this paper, the high teaching quality is satisfied by universities through a fuzzy decision system. In this sports teaching analysis, the training patterns, training sessions, and training time are changed to match the requisites and performance of the students. In this teaching quality assessment, the fuzzy decision system is used to identify and classify the high and low teaching quality in university sports training for time intervals. Therefore, the training patterns, sessions, and time associated with sports training sessions are validated using a fuzzy decision system to provide appropriate recommendations to achieve a successful teaching model.

Regarding teaching quality, the TCQAM’s enhancement method uses a rigorous procedure for assessing results as sufficient or unsatisfactory. Classification uses fuzzy decision-making and evaluates individual achievement, competitive outcomes, and session-specific features. The program considers both physical performance metrics and intangible (student satisfaction) discoveries, which modify training approaches in real-time. TCQAM promotes a holistic instructional framework that maximizes teaching quality and student engagement. Through repeated analysis and validation, this framework is advanced. This all-encompassing method shows that the concept can be scaled up or changed to fit several sports instructional environments.

Sport teaching in universities relies on the training patterns, sessions, and time provided to the students based on their requirements. The sports training requisites of each student are identified using the fuzzy decision system to combine the maximum teaching quality with possible factors. The students’ performance and competitive outcomes are the input for sports teaching quality assessment to validate the associated factors using a fuzzy decision system. The requisites and performance output serve as input to the fuzzy system for improving sports teaching quality, from which the membership derivatives are used to perform an improvement assessment.

Training patterns

The training patterns are designed based on students’ understanding of sports training. These rely on different training modes such as basic, traditional, modified, and recommended. This model aims to evaluate university sports teaching quality with students’ performance and competitive outcomes. The specific features are observed from the training patterns of individual students. That specific feature is matched with other students for similarity analysis under TCQAM. Hard matching is identified as the least performance factor from the fuzzy membership derivatives. The training patterns are given input to the proposed model for identifying the sports training requisites to validate the training patterns and from which the appropriate sports teaching model is implemented to the university students. For instance, the training patterns are inputs, as shown in Eq. (1).

$$\:{Tr}_{Pattern}\left(\varphi\:+1\right)={Tr}_{Pattern}\left(\varphi\:\right)-\epsilon\:\left(\alpha\:+\beta\:\right)$$

(1)

where Eqs. (2),

$$\:\epsilon\:\left(\alpha\:+\beta\:\right)={Tr}_{Pattern}\left(\varphi\:\right)-L\left(D\right)$$

(2)

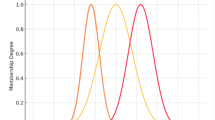
In the above equations, $\:{Tr}_{Pattern}\left(\varphi\:\right)$ and $\:\epsilon\:\left(\alpha\:+\beta\:\right)$ is the training patterns of sports teaching and evaluating students’ performance and competitive outcomes in random time intervals. Where, $\:L\left(D\right)$ signifies that a large volume of data related to training patterns is observed during the active sessions. The training pattern relies on the teaching modes described in Fig. 2.

Fig. 2

Training pattern based on teaching modes.

In Fig. 2, the 4 teaching modes are considered to validate student factors. The physical factors, participant ratio, individual performance, and their assessments are used to define the teaching patterns. The notable patterns are different sequences, time, agility, physical involvement, instructions given, and recommendations. The fuzzy process validates the teaching quality by combining the patterns and student factors for each teaching mode. The fuzzy implication defines mode changes and outcomes for improving the teaching quality.

Training sessions

In these active sports training sessions, the proposed model is applied to identify an accurate teaching model for all the students based on their interests. In these sessions, continuously monitoring the students for performance evaluation reduces failure sessions. The actual process of the proposed model is to intake the training patterns, sessions, time. Based on the requisites, the above factors are evaluated through a fuzzy decision system. A maximum teaching quality is achieved by using this technique. If the least performance is identified in any teaching sessions, it leads to modifying the training patterns, sessions, and time. The proposed model aims to overcome the least performance factor in sports teaching. It also maximizes the quality of the training session, which is evaluated from the proposed model, as shown in Eq. (3).

$$\:{Tr}_{Session}\left(\varphi\:\right)={Req}_{i,j}+{Perf}_{i,j}\:$$

(3)

Here,$\:\:{Tr}_{Session}\left(\varphi\:\right)$ is the training sessions of sports teaching and from which $\:{Req}_{i,j}$ and $\:{Perf}_{i,j}\:$ are the requisites and performance outcomes of the students in particular sessions. Those factors are used for the accurate sports teaching quality assessment of university students using TCQAM based on a fuzzy decision system. The proposed model based on a large volume of data is observed from the training patterns; sessions and time are analyzed to find hard and soft matching independently in any instance. Based on the requisites and performance, the teaching quality classification is to perform an improvement assessment with either 0 or 1 outcome.

Training time

In this assessment, the data observed from sports training patterns and sessions in random time intervals is evaluated to identify the hard matching of specific features between the students. The sports training requisites and specific features of university students are extracted. The extracted factors are used to compute the probability of hard matching. The training session time intervals are utilized to improve the teaching quality and student performance outcomes. Therefore, the sports training session is allocated for all the students based on their requirements at a given time interval. Hence, the fuzzy decision is as shown in Eq. (4).

$$\:FDS\left(\varphi\:+1\right)=\frac{{\left({Teach}_{Q}\right)}_{High}}{{\left({Teach}_{Q}\right)}_{High}+{\left({Teach}_{Q}\right)}_{Low}}$$

(4)

where, $\:{\left({Teach}_{Q}\right)}_{High}$ and $\:{\left({Teach}_{Q}\right)}_{Low}$ is the high teaching quality and low teaching quality identified from the sports training sessions, as shown in Eq. (5).

$$\:{Tr}_{time}\left(\varphi\:\right)=\frac{{Req}_{i,j}}{{Req}_{i,j}+\:{Perf}_{i,j}}$$

(5)

Here,$\:\:{Tr}_{time}\left(\varphi\:\right)$ is defined as the training time of sports teaching sessions allocated based on the student’s requirements and is validated using fuzzy decisions.

Fuzzy decision system

The TCQAM relies on the fuzzy decision system (FDS) to facilitate accurate categorization and ongoing enhancement of the quality of instruction. The fuzzy decision system implemented to classify high and low teaching quality is an important assessment in this model. From the instance, the design goal of the proposed model is to match the specific features observed from each student with others to identify the variations in their performance outcomes. Sports education is ambiguous and subjective; hence, the FDS uses spectrum membership functions rather than binary options. Due to its versatility, it may evaluate teaching based on training patterns, session dynamics, and time intervals. The system can adapt to various settings since these inputs are taken from real-time workout data.

The FDS uses fuzzy logic to assess how different teaching methods affect student progress and happiness. It determines the importance of each element’s membership and how training methods and time distribution affect results. By researching these derivatives, identify poor performance or instructional quality and evaluate progression trajectories. To fix problems, the system suggests changes like new training inputs or changing session styles. The FDS guarantees a constant trajectory toward improved teaching quality by offering a systematic and iterative evaluation mechanism.

The associated factors are validated to improve the sports teaching quality in universities by balancing requisites and performance outcomes to provide appropriate training sessions to the students to improve their sports performance. This validation provides the number of student data, training patterns, training sessions, in the fuzzy system. The fuzzy decision provides different membership derivatives are identified from the least performance factor. The fuzzy membership functions provide high teaching quality that intakes successful recommendation$\:\:{Succ}_{recomd}$, as shown in Eqs. (6) and (7).

$$\:{Succ}_{recomd}=2{Req}_{i,j}.{p}_{1}-{Perf}_{i,j}$$

(6)

And,

$$\:{C}_{i}=2{p}_{2}+\frac{\epsilon\:\left(\alpha\:+\beta\:\right)}{FDS\left(\varphi\:+1\right)}$$

(7)

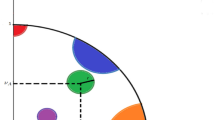
Here, the variables$\:{\:p}_{1}$,$\:\:{p}_{2}$ and$\:\:{C}_{i}$ signifies the random integers and classification of teaching quality, including the appropriate training patterns and sessions for university students. The fuzzy decision process for different outcomes is illustrated in Fig. 3.

Fig. 3

Fuzzy decision process for different outcomes.

The fuzzy decision process relies on $\:\:{C}_{i}$defined in Eq. (7). This requires$\:\:Re{q}_{i,j}$ and it’s associated $\:\:Per{f}_{i,j}$ to ensure maximum student factor association. In this case, the $\:\:T{r}_{time}\left(\varphi\:\right)$ is the output-generating interval for successful recommendations. By differentiating the derivative outcomes as$\:\:\varphi\:$ and $\:\:\left(\varphi\:+Re{q}_{i,j}\right)$ the improvement check is performed. The $\:\:{C}_{i}$ using $\:\:{p}_{1}$ and $\:\:{p}_{2}$ for FDS$\:\:\left(\varphi\:H\right)$ is useful to accumulate$\:\:L\left(D\right)$. This $\:\:L\left(D\right)$is validated for $\:\:\epsilon\:\left(\alpha\:+\beta\:\right)$ under different$\:\:T{r}_{pattern}\left(\varphi\:+1\right)$. Therefore, the higher the$\:\:\left(Teac{h}_{Q}\right)$, the lower the decision on$\:\:Im{p}_{{A}_{n}}$. In this process, both classifications require $\:\:suc{c}_{recomd}$ and $\:\:\left(p1,\:p2\right)$ combinations across $\:\:Re{q}_{i,j}$ (Fig. 3).

Pseudocode 1

Fuzzy decision process for different outcomes

The fuzzy decision system (FDS) looks at the quality of sports education by taking into account a number of criteria, including training patterns (TP), training sessions (TS), training time (TT), student needs (R), and performance results (P). At first, each clear input undergoes a fuzzification process. This means that it is turned into degrees of membership that match language categories like “Low,” “Medium,” or “High” using the right membership functions. Next, these fuzzified inputs are evaluated against a set of IF-THEN criteria that have already been set out (for example, IF TP is High AND TS is Medium THEN Quality is High). The lowest value of the membership functions that are involved is used for figuring off the activation intensity, or firing degree, of each rule. This shows that the input meets the rule criteria.

The FDS also plays a key role in controlling the dynamic interplay of different training factors. It simultaneously validates several session and student aspects, such as agility levels, physical involvement, and participation ratios. To find the most effective ways to educate, the FDS compares several approaches and finds patterns of inefficiency. One way the algorithm improves its accuracy is by distinguishing between hard and soft matching of performance characteristics. In the end, the FDS does more than merely address causes of poor teaching quality; it also guarantees that the changes result in long-term enhancements to physical education programs. The FDS is a vital resource for encouraging creativity and flexibility in pedagogical approaches because of its dynamic and iterative nature.

Teaching quality classification

The teaching quality classification is based on high and low student performance outcomes in the training sessions. The implication of the training model is verified using the fuzzy decision system, respectively. The possible factors are supported for all the training sessions with specific feature matching, which avoids failed sports training sessions. The above-mentioned factor in each session is $\:{Session}_{1}$ which is trained and$\:\:{Session}_{2}$,$\:\:{Session}_{3}$ are also trained to avoid further failed sessions during sports teaching. All the training sessions are stacked patterns-wise and provide training to perform an improvement assessment. The proposed model and fuzzy decision system prevent the least performance factor and failed session intervals. This improvement assessment also gives successful recommendations to replace the low teaching quality with high teaching quality factors. The actual sports teaching model of the university students may vary based on the proposed model, which uses the improvement assessment for achieving high teaching quality. The proposed model allows the fuzzy decision to achieve the maximum teaching quality with possible factors. Hence, the classification based on the sequence of low teaching quality and least performance factors $\:{\left({Teach}_{Q}\right)}_{Low}.{\left({Perf}_{i,j}\right)}_{Low}$ is validated as shown in Eqs. (8) and (9).

$$\:{C}_{i}\left(\varphi\:+1\right)=\frac{{\left({Teach}_{Q}\right)}_{{Low}_{1}}.{\left({Perf}_{i,j}\right)}_{{Low}_{1}}+{\left({Teach}_{Q}\right)}_{{Low}_{2}}.{\left({Perf}_{i,j}\right)}_{{Low}_{2}}+\dots\:+{\left({Teach}_{Q}\right)}_{{Low}_{n}}.{\left({Perf}_{i,j}\right)}_{{Low}_{n}}\:}{N\left({{\Theta\:}}_{{S}_{n}}\right)}$$

(8)

And,

$$\:\left.\begin{array}{c}{C}_{1}=\left|{Imp}_{{A}_{1}}-\:{\mathcal{N}}_{1}.\:{Memb}_{\alpha\:}\:\right|\\\:{C}_{2}=\left|{Imp}_{{A}_{2}}-\:{\mathcal{N}}_{2}.\:{Memb}_{\beta\:}\:\right|\\\:\vdots\\\:{C}_{n}=\left|{Imp}_{{A}_{n}}-\:{\mathcal{N}}_{m}\:.\:{Memb}_{\gamma\:}\:\right|\end{array}\right\}$$

(9)

In the above equations,$\:\:{Imp}_{{A}_{1}}$,$\:\:{Imp}_{{A}_{2}}$ and$\:\:{Imp}_{{A}_{n}}$ signifies the improvement assessment under varying performance outcomes with less session failure. The least performance factor detected sequence from the fuzzy decision system. The variables$\:\:{\mathcal{N}}_{1}$,$\:\:{\mathcal{N}}_{2}$ and$\:\:{\mathcal{N}}_{m}$ is the novel input observed as per Eq. (6) using teaching quality classification and derivatives.$\:\:{Memb}_{\alpha\:}$,$\:\:{Memb}_{\beta\:}$ and$\:\:{Memb}_{\gamma\:}$ are the membership functions validated using the fuzzy decision to ensure high teaching quality membership derivatives? The variable$\:\:N\left({{\Theta\:}}_{{S}_{n}}\right)$ is the number of failed training session intervals.

Improvement assessment based on classification

The fuzzy decision identified the least performance factors on the student side and low teaching quality on the staff side for providing better teaching recommendations to the universities. The minimum teaching quality identified in any session is halted, generating a new successful session that achieves better teaching quality based on novel inputs. The improvement assessment is performed on both the high-quality and low-quality membership derivatives to balance the teaching inputs. Based on the decision system, the improvement assessment and novel inputs are some of the possible factors used to maximize the teaching quality. The low teaching quality is avoided to provide better teaching to the students. To avoid such issues, this paper proposes that TCQAM focus on requisites and competitive outcomes based on a fuzzy decision system. The improvement assessment process is illustrated in Fig. 4.

Fig. 4

Improvement Assessment Process.

The improvement assessment is performed under two prime conditions:$\:\:N\left({{\Theta\:}}_{{S}_{n}}\right)=1$ and$\:\:{C}_{n}=True$. These two conditions are linear for$\:\:{{T}_{r}}_{time}\left(\varphi\:\right)$ such that$\:\:Im{p}_{{A}_{n}}$ is observed for$\:\:\left(Teac{h}_{Q}\right)\in\:low$ and high. The fuzzy derivatives are $\:\:{C}_{i}\:\left(\varphi\:+1\right)$ and $\:\:{C}_{i}\forall\:\:{p}_{1}\:and\:{p}_{2}$ under$\:\:{\mathcal{N}}_{m}$. If$\:\:{\mathcal{N}}_{m}$ is the conventional output extracted from the $\:\:Mem{b}_{\gamma\:}$ is observed in $\:\:T{r}_{time}\left(\varphi\:\right)$ such that the outcome of sessions is used for balanced assessment. In the $\:\:suc{c}_{recomd}$ phase, the $\:\:{c}_{i}\left(\varphi\:+1\right)$ is alone augmented until $\:\:Im{p}_{{A}_{n}}$ is observed. Thus either$\:\:{\mathcal{N}}_{m}$ or$\:\:Im{p}_{{A}_{n}}$ is used to teach quality assessment for precise improvement (Fig. 4). In this assessment, the students’ requisites are identified in the training patterns and sessions under fuzzy decision. The high-quality membership derivative on this improved assessment is achieved to improve teaching quality and prevent failed sessions and low-quality teaching models. The overall proposed model validates different factors following session failure. Here, the classification of high- and low-quality membership derivatives is the input to the improvement assessment that is validated to ensure high-teaching quality.

Balanced teaching

This study aims to achieve high teaching quality using the fuzzy decision system by differentiating the least performance factor and low-teaching quality instances in particular sessions. It stabilizes the fuzzy decisions during the improvement assessment, reducing the number of session failures. Therefore, it is given as Eq. (10).

$$\:{Sports}_{tqi}\left(\frac{i}{j}\right)=\:\frac{\theta\:\left({Req}_{ij}+{Perf}_{ji}\right)+\:{\left({Imp}_{{A}_{n}}\right)}_{i}}{\:\theta\:\left({Req}_{ji}+{Perf}_{ij}\right)+\:{\left({Imp}_{{A}_{n}}\right)}_{j}}$$

(10)

In Eq. (10), $\:{Sports}_{tqi}$ shows the sports teaching quality improvements assessment based on requisites and competitive outcomes validated from the student’s performance in training sessions is to identify the teaching quality easily. The conditions of $\:\theta\:\left({Req}_{ij}+{Perf}_{ji}\right)$ and $\:\theta\:\left({Req}_{ji}+{Perf}_{ij}\right)$ represents the requisites and performance outputs based on membership functions aided by a fuzzy decision system to avoid session failures and low-quality teaching. The high teaching quality is achieved using the membership derivatives. The teaching inputs are balanced to improve the chances of improving the quality of sports teaching in universities. The $\:{\left({Imp}_{{A}_{n}}\right)}_{i}$ and $\:{\left({Imp}_{{A}_{n}}\right)}_{j}$ are identified from the varying membership derivatives on this improved assessment to ensure better sports teaching.

Sports teaching quality improvement

The main goal of sports teaching quality improvement is achieved by validating the students’ performance and competitive outcomes to provide accurate teaching to the students based on their requisites. The least performance factors identified are that students are continuously trained with new training models to improve their performance in sports. It also minimizes the low-quality membership derivatives during sports training sessions. The high-quality membership derivatives balance the teaching inputs and provide high teaching quality with fuzzy decisions in the neural network, as shown in Eqs. (11) and (12).

$$\:{Teach}_{Q}\left(\mu\:\right)=\frac{{\left({Teach}_{Q}\right)}_{High}-{\left({Teach}_{Q}\right)}_{Low}}{N\left({{\Theta\:}}_{{S}_{n}}\right)}$$

(11)

and,

$$\:{Teach}_{Q}\left(\mu\:+1\right)=\frac{1}{\sqrt{2\pi\:}}\left[\frac{\left(\frac{{\left({Teach}_{Q}\right)}_{Low}}{{\left({Teach}_{Q}\right)}_{High}}-\frac{Perf}{N\left({{\Theta\:}}_{{S}_{n}}\right)}\right)}{2\left({Imp}_{{A}_{n}}-\:{\mathcal{N}}_{m}\:.\:{Memb}_{\gamma\:}\right)}\right]$$

(12)

In the above Equation, $\:\mu\:$ and $\:\mu\:+1$ are the teaching quality improvement between the active and upcoming sessions observed using the fuzzy decision. The recommendation for quality improvement assessment is presented in Fig. 5.

Fig. 5

Recommendation process for quality improvement.

The classified outputs are the input for deciding recommendations through intermediate conditions. If$\:\:Re{q}_{i,j}=0$ other recommendation is successful, and this is combined with$\:\:{t}_{q}i=\left(\frac{i}{j}\right)$ improvements for new assessments. The modification requiring combinations are recommendations are two-fold for $\:\:{C}_{1}$ to $\:\:{C}_{n}$ until any one $\:\:Im{p}_{A}$is observed. Therefore $\:\:Sport{s}_{{t}_{qi}}\left(\frac{i}{j}\right)$ is the balanced assessment for $\:\:{\mathcal{N}}_{m}$identified for new combination-based teaching quality improvements (Fig. 5). The TCQAM identifies the sports training requisites with the associated factors for maximizing teaching quality with less training time. Both high and low teaching inputs are balanced to perform the improvement assessment that reduces the least performance factor identified from fuzzy membership derivatives. The sports training data observed from the different sessions are analyzed to improve the chances of sports teaching quality improvements.

Data analysis

The article is validated using the resemblance data provided in (https://doi.org/10.3390/electronics12040874). This source provides sports teaching using conventional and new models with different patterns. A maximum of 400 students trained for basketball, football, athletics, and long jump are considered in this data analysis. The conventional teaching and new models are categorized into 4 components based on score points. This is accounted for the outcomes based on teaching quality and$\:\:Im{p}_{A}$. The validation part is represented as illustrated below (Fig. 6).

Fig. 6

Validation process flow.

This research expands upon prior work in educational innovation; namely, that focused on using intelligent technologies to facilitate individualized instruction. It is well-known that adaptive teaching models can improve learning outcomes by filling individual performance gaps; fuzzy decision systems (FDS) are examples. In sports education, comparable frameworks have highlighted the need for dynamic evaluation and iterative feedback for training program refinement. Studies aiming at eliminating inefficiencies in performance evaluations, a major concern in sports and general education, complement the focus on minimizing complex elements. This study adds to the existing body of knowledge by providing empirical evidence that FDS may successfully and systematically improve the quality of instruction. This study adds to the existing body of research on data-driven pedagogy by demonstrating how hybrid instructional frameworks might improve learning outcomes in various subject areas.

The validation flow relies on student performance scores per assessment week with the participant’s ratio and recommendation. The dataset provides a 7-week training program augmenting (6 h.×7) for each sport. The improvements for $\:\:{\left(Teac{h}_{Q}\right)}_{Low}$classified is decided based on the average score. Thus, the classification of $\:\:\left(Teac{h}_{Q}\right)$for low and high is assessed in Fig. 7.

Fig. 7

$\:\:Teac{h}_{Q}$classification based on score.

The teaching quality assessment is performed between $\:FDS\:\:\left(\varphi\:\right)$ and $\:FDS\:\:\left(\varphi\:+1\right)$instances for$\:\:Re{q}_{i,j}$. In this case, the derivatives $\:\:\in\:{\left(Teac{h}_{Q}\right)}_{low}$ are revisited for $\:\:Suc{c}_{recomd}$ under different assessment criteria and weeks. The increasing weak augments the $\:\:Im{p}_{A}$ for $\:\:{\mathcal{N}}_{m}$ and $\:\:Mem{b}_{\gamma\:}$ such that $\:\:Re{q}_{i,j}$ is balanced for any$\:\:L\left(D\right)$. This case requires $\:\:\epsilon\:\left(\alpha\:+\beta\:\right)$ for the ratio of participants for which modification/ recommendation is given (Fig. 7). The modification and (or) recommendation for the 4 teaching modes is assessed in Fig. 8.

Fig. 8

Recommendation & modification assessment.

The above assessment analyzes the modified and its ratio for (basic, traditional) modes and 7-week training patterns. This requires the $\:\:FDS(\varphi\:+1)$under the classified qualities. Though the $\:\:{c}_{i}$and $\:\:{C}_{i}\left(\varphi\:+1\right)$are useful in $\:\:Mem{b}_{\gamma\:}$ derivatives the $\:\:{\mathcal{N}}_{m}$ is used to validate if it is a modification or recommendation. Therefore the $\:\:{T}_{{r}_{time}}\left(\varphi\:\right)$ is optimal for $\:\:{C}_{1}$to $\:\:{C}_{n}$ across $\:\:Im{p}_{A}$for new$\:\:Mem{b}_{\gamma\:}$. In this case, the requirement and performance assessment are vital to deciding the quality improvement with a less convoluted factor (Fig. 8). The convoluted factor analysis is presented in Fig. 9.

Fig. 9

Convoluted factor analyses.

The convoluted factor relies on the maximum modification provided under different weeks and$\:\:{C}_{i}$. In this case, the convoluted factor is useful for increasing modifications based on recommendations. Therefore the $\:\:Mem{b}_{\gamma\:}$ is the further derivative for $\:\:FDS\left(\varphi\:+1\right)$ based classified. The teaching quality improvement is performed under$\:\:{\mathcal{N}}_{m}$ for preventing convoluted factors (Fig. 9).

Discussion

The discussion is preceded by quality improvement, improvement assessment, assessment time, convoluted factors, and training patterns. These metrics are identified from the above-mentioned discussions with the participant variant as 20%, 40%, 60%, and 80%. Besides, the session (Hrs) (0.5–6.0) and the teaching modes (basic, traditional, modified, and recommended) are used to validate the above metrics. A discussion of this is given below.

Quality improvement

Fig. 10

Quality Improvement Discussion.

In this article, the proposed model is applied to achieve high-quality improvement based on the requisites outcomes of students (Refer to Fig. 10). The improvement assessment maximizes the teaching quality based on student performance. The proposed model and fuzzy decision system suppress the least performance factor and low-quality teaching. For instance, the above factors are validated using fuzzy decisions to identify the least performance factors from the membership derivatives. The proposed model nevertheless takes the hard matching features for sports teaching to provide better sports teaching. The low teaching quality model is identified and replaced with the recommended inputs for better teaching quality. The large data from the training patterns, sessions, and time is analyzed to provide appropriate teaching to the students. The current sports training data compares with the previous dataset for classifying high and low teaching quality to reduce convoluted factors. Hence, high-quality improvement is achieved using a fuzzy decision system.

Improvement assessment

Fig. 11

Improvement assessment discussion.

This proposed model is applied sequentially, evaluating students’ performance and competitive outcomes. This is to provide accurate training sessions based on their interests without convoluted factors (Refer to Fig. 11). The occurrence of convoluted factors is identified using the conditions of$\:\:{Tr}_{Pattern}\left(\varphi\:\right)$ and $\:\epsilon\:\left(\alpha\:+\beta\:\right)$ at any training sessions. The fuzzy performs high-quality membership derivatives on this improved assessment to maximize the chances of improving sports teaching quality. The condition of $\:FDS\left(\varphi\:+1\right)$ is validated to satisfy all the students’ requisites and performance outcomes from which the convoluted factors are identified. The proposed model analyzes the sports training-based data observed from the different students’ performances in this decision system. A maximum teaching quality is satisfied using the quality assessment and fuzzy decision system. If the lowest performance factor is identified in teaching sessions based on the sports training requisites, The proposed model helps satisfy the high-quality membership derivatives of this improved assessment. The specific features are matched to satisfy high improvement assessment.

Assessment time

Fig. 12

Assessment time discussion.

This article applies the TCQAM to identify the convoluted factors for maximum teaching quality with each of the above-mentioned factors (Refer to Fig. 12). This improvement assessment relies on training patterns and possible factors observed at different time intervals to identify the convoluted factors to achieve high training patterns. In this article, the student’s training data is continuously analyzed to improve students’ performance and thereby reduce failure sessions. Due to convoluted factors, occurrence in sports training sessions is identified using a fuzzy decision system. The proposed model is applied to overcome the low teaching quality and low-performance factors in university sports training. It also maximizes the improvement of sports teaching quality, from which the student’s performance is evaluated. The high and low sports teaching quality-based training outcomes are pursued to satisfy high training patterns. Based on the $\:{Req}_{i,j}$ and$\:\:{Perf}_{i,j}$ the output of students is analyzed, the accurate sports teaching quality assessment jointly produces the outcome of$\:\:{Sports}_{tqi}\left(\frac{i}{j}\right)$ at its least possible factors. Therefore, the quality of sports teaching is pursued with less assessment time than other factors.

Convoluted factor

Fig. 13

Convoluted factor discussion.

The fuzzy decision system is implemented to improve the quality of sports teaching based on sports training requisites to ensure that better teaching is achievable. Based on the improvement assessment, the high-quality membership derivatives on this improved assessment are detected from the highest performance factor. In particular, the balanced teaching input analysis is to satisfy either$\:\:\theta\:\left({Req}_{ij}+{Perf}_{ji}\right)$ or $\:\theta\:\left({Req}_{ji}+{Perf}_{ij}\right)$ for preventing convoluted factors. The less convoluted factors are required to compare with the previous features for identifying low-quality teaching. The low teaching quality factors are replaced with novel inputs for performing improvement assessments using a fuzzy decision system. High teaching quality is achieved based on membership derivatives to improve sports teaching. The training inputs are balanced to improve the chances of sports teaching quality for different training sessions. Such a low performance factor is identified under training patterns, and specific features are matched to improve the training patterns. In this article, the convoluted factors are addressed using the fuzzy decision, thereby improving teaching quality, as represented in Fig. 13.

Training patterns

Fig. 14

Training Patterns Discussion.

The actual sports teaching of students may vary based on students’ performance and competitive outcomes. The improvement assessment is pursued to ensure high teaching quality (Refer to Fig. 14). This article addresses the requisites and performance outcomes to provide high teaching quality to students using fuzzy derivatives. The improvement assessment also gives successful recommendations to replace the low teaching quality with high teaching quality factors based on their requisites. Based on the sports training requisites, the hard matching of specific features is identified and modified to improve teaching quality. The recommended inputs are used from Eq. (6) based on teaching quality classification and derivatives to ensure high teaching quality. The membership functions are validated using fuzzy decisions to maximize sports teaching quality improvements with high training patterns and sessions. In this model, the fuzzy decision system improves the quality of sports teaching with less assessment time.

In sports education, the study shows that a fuzzy decision system (FDS) can fix low-performance elements and complicated variables, greatly enhancing instruction quality. Analyses conducted over seven weeks with four hundred basketball, football, sports, and long jump students showed that performance-based metrics drove adaptive adjustments and suggestions that significantly improved instructional results. As shown in the research, successfully classifying instructional models into low- and high-quality categories allowed for targeted interventions that decreased inefficiencies and increased student results. The technique showed its potential for wider use in education by improving teaching quality, reducing assessment time, and better meeting student needs by using data-driven judgments.

Importantly, the study’s conclusions affect educational policy and practice. The recommended paradigm integrates common sense and empirical evidence to create flexible educational materials that may satisfy the needs of various student populations. Through tailored, performance-based interventions, this approach might alter arts, STEM, and professional development. It also has the potential to transform sports education. According to the findings, AI-driven systems like FDS might revolutionize evaluation and education. If schools want to increase enrollment in high-quality programs, they should streamline their processes to create more efficient and fair learning environments. These statistics may assist policymakers in improving teacher training, funding, and student achievement. This technique prepares students for the workplace by teaching them job-related skills. The authors of this study believe that artificial intelligence and data analytics will promote education and improve classroom outcomes.

According to the experts who reviewed the paper, incorporating the Fuzzy Decision Support System (FDSS) into the TCQAM model allows for a more precise and dynamic evaluation of the quality of sports education. Their main point was that the model is applicable in real-world classrooms since it can adjust to different training patterns and degrees of participant engagement. Researchers noticed the model’s excellent training pattern accuracy and a noticeable increase in the quality evaluation as signs that it was resilient and might be used for many things. Furthermore, experts emphasized that convolutional aspects enhance the assessment, providing a more comprehensive view of educational efficacy.

Conclusion

The innovative Teaching Convoluted Quality Assessment Model (TCQAM) enhances university sports teaching assessments. The topic is provided in the paper. The approach uses fuzzy decision support systems (FDSS) to evaluate real-time instructional quality. Complex training patterns, session dynamics, and performance measurements inform these decisions. Key results that show TCQAM can recognize poor teaching quality and adapt to student needs show that students will receive a tailored and adaptable education that will boost their engagement, motivation, and performance in various sports. The trials reveal that the proposed approach works across several training settings, participant ratios, and sports. The evaluation system considers intangible factors like student pleasure, which are usually ignored. The Teaching and Learning Quality Assessment Method (TCQAM) improves sports education quality and efficiency by continuously assessing and improving teaching approaches. This study expands educational technology research by providing a scalable real-time training efficacy evaluation mechanism. Adaptive and tailored training in higher education is growing, and the model’s effectiveness in enhancing sports instruction may be applied there. To expand its use in education, future research may examine how TCQAM is applied in different classrooms. Finally, the results stress the need for data-driven, adaptive evaluation methods to raise the bar for sports education instruction at the university level. The experimental results demonstrate that the proposed TCQAM model increases the Training Pattern Score by 98.2%, Assessment Time Efficiency by 13.1%, Convoluted Factor by 0.29%, teaching quality improvement by 32.1%, and improvement assessment by 95.2% compared to other existing methods such as IoT-EC-ABPSO, BCHMM, and ResNet34-BD. To improve educational results, the TCQAM provides a strong framework for addressing the shortcomings of conventional evaluation tools and gaining useful insights. The model helps institutions pursue ever-improving educational experiences by providing a balanced approach to assessing student and teacher performance. There are still limitations to the proposed TCQAM model, even if it improves the assessment of sports instruction quality via fuzzy decision-making. The amount and quality of the input data determine the system’s performance, which might differ across institutions. Furthermore, further adjustments can be necessary to accommodate sport-specific training subtleties since the model now focuses on broad sports education. To further customize training input, it is advised that future studies integrate deep learning approaches with real-time sensor data. To further enhance the model’s robustness and generalizability, expanding the dataset across other colleges and including longitudinal performance monitoring might be beneficial.